Abbreviations: AOP: Advanced oxidation process; Azi: Azithromycin; DP: Degradation Product; Ery: Erythromycin; ESI: Electrospray ionization; HPLC: high performance liquid chromatography; LC50: lethal concentration; MS: mass spectrometer; Q: TOF quadrupole time-of-flight; QSAR: quantitative structure-activity relationship; Spi: Spiramycin; Tyl: Tylosin; UV: Ultra violet; VUV: Vacuum ultra violet; MIC: minimal inhibitory concentration
1. Introduction
One of the major current trends in water studies is the research towards a fourth purification stage in wastewater treatment plants (WWTP), as more and more micropollutants are detected in WWTP effluents and in various water bodies [1,2,3,4]. The use of activated carbon, ozonation and advanced oxidation processes (AOPs), such as the irradiation with UV light often in combination with photocatalysts or degradation accelerating agents, e.g. titaniumdioxide or hydrogenperoxide, are being intensely discussed. A common goal of many of these AOPs is the generation of hydroxyl radicals. These are formed by homolysis of water under vacuum UV radiation [5,6,7]. Hydroxyl radicals are highly reactive and react quickly with any organic compound in the solution. The presence of hydroxyl radicals has been previously demonstrated and was also observed under the conditions as used in the present study [8,9]. Yet, these oxidations processes are often assumed to give rise to products more toxic or ecologically toxic than the parent compound. These new products will negatively affect the environment. Many degradation products cannot be detected analytically with a reasonable effort due to their low concentrations. Using activated carbon for adsorption requires the treatment of the contaminated sorbent either by recycling or by combustion.
This study focuses on improved and more recent methods. Current findings reveal concentrations in ng L–1 ranges depending on the compounds [4]. The reliable, experimental evaluation and prediction of the toxicity of the degradation products are often a challenge, since most products are not commercially available and chemical synthesis would be too lengthy and costly. Alternative approaches to assess toxicity rely on computational methods, such as QSAR analysis [10,11]. QSAR analysis predicts a relationship between biological activity and chemical structure [12,13,14]. Thus, it can also be used to evaluate the eco-toxicity of the resulting photodegradation products. For this purpose, two different software products were applied in this study to calculate ecotoxicity. An experimental approach to access ecotoxicity is the determination of minimal inhibitory concentration (MIC) values. These two methods will be deployed in the field of ecotoxicology to selected macrolide antibiotics.
Today, macrolide antibiotics occur worldwide in water. In Germany, azithromycin was found in concentrations of 7–22 ng L–1 and erythromycin in concentrations of 4–190 ng L–1 in surface water. In Spanish surface waters, observed concentrations of spiramycin and tylosin were up to 488 ng L–1 [15,16,17]. In Mexico, azithromycin was observed in different canals with concentrations up to 211 ng L–1 [18]. The concentration of erythromycin was 7–1149 ng L–1 in river water in Ghana and up to 60 ng L–1 in Chinese surface waters [19,20,21]. The concentration of azithromycin and erythromycin in Portuguese rivers was measured by Pereira et al. [22]. The observed macrolide concentrations amounted to 39 ng L–1. In seawater, the concentration of azithromycin was found as high as 138.9 ng L–1 near China [23]. The occurrence of azithromycin in groundwater was confirmed by Boy-Roura et al. for Catalonia (Spain) to 7 ng L–1 [24]. The highest concentration of macrolides was observed in WWTP effluents, with macrolide concentrations in the feed samples being at least twice as high as the effluent samples [25,26,27,28,29,30]. Thus, a part of the macrolides can be eliminated by the conventional three stage sewage treatment plant. Yet, for a complete and sustainable removal of the macrolides, another stage is required. In this respect, azithromycin, erythromycin, spiramycin and tylosin were irradiated with UVC/VUV-light at pH 6–7. The products formed were identified using high-performance liquid chromatography coupled to electrospray ionization quadrupole time-of-flight mass spectrometry (HPLC-ESI-Q-TOF-MS) and examined with respect to their ecotoxicological potential. The gram-positive Bacillus subtilis and the gram-negative Pseudomonas fluorescens minimal inhibitory concentrations (MIC) of the four macrolides and their solutions were determined as a function of irradiation time to assess potential ecotoxicological hazards. Both bacterial strains occur ubiquitously in soil and waters, allowing the evaluation of the environmental impact [31].
2. Materials and methods
2.1. Chemicals and reagents
Azithromycin dihydrate (Alfa Aesar, purity 98%) consisting of form A (Azi A) and B (Azi B), erythromycin free base (BioChemica AppliChem, purity 95%) consisting of form A (Ery A), B (Ery B) and F (Ery F), spiramycin (Alfa Aesar, 90%), consisting of form spiramycin I (Spi I) and spiramycin Ⅲ (Spi Ⅲ), and tylosin tartrate (Alfa Aesar, purity 95%) consisting of form A (Tyl A) and B (Tyl B) were used for photodegradation experiments. Hydrochloric acid and ammonia (approximately 25% Riedel-de Haen; pro analysis, Reag ISO, Reag Ph. Eur.) were used to adjust the pH value of the solution. Methanol (LiChrosolv Merck for liquid chromatography), MilliQ water (Simplicity 185, Merck Millipore, Billerica, MA, USA) and formic acid (Fluka, LC-MS-Grade) were used as eluent for HPLC-ESI-Q-TOF-MS experiments.
2.2. Photodegradation experiments
The photodegradation experiments of macrolides were carried out in a 1 L-batch reactor (Peschl Ultraviolet, Mainz, Germany) wrapped in aluminum foil to prevent penetration of irradiation. A low-pressure mercury immersion lamp (TNN 15/32, 15 W, Heraeus, Hanau, Germany), which emits polychromatic light with maximum radiation intensities at 185,254,313,365 405,437,547,578, and 580 nm, was located in the center of the batch reactor. Each of the four macrolides was dissolved separately in 800 mL MilliQ water (Simplicity 185, Merck Millipore, Billerica, MA, USA) to yield a final concentration of 20 mg L–1. The solution was irradiated in the batch reactor for 10 min. The total photon flux of the UV lamp was determined to 2 mmol min–1 L–1 by ferrioxalate actinometry [32,33]. The temperature in the reactor was kept at 22 ± 2 ℃ for all photodegradation experiments. A magnetic stirrer (500 rpm) was used for mixing. For comparison purposes, the absorption spectrum of each compound was recorded using a UV/Vis spectrophotometer (UV-1601 PC, Shimadzu, Kyoto, Japan).
2.3. HPLC-ESI-Q-TOF-MS analyses
Samples from photodegradation experiments were analyzed using HPLC Agilent 1200 (Agilent, Santa Clara, USA) coupled with an ESI-Q-TOF mass spectrometer Agilent 6530 (Agilent, Santa Clara, USA). The column used for chromatographic separation was a reversed-phase C-18 CoreShell column (Thermo Scientific, Dreieich, Deutschland) having dimensions of 50 mm × 2.1 mm and 2.6 μm particle size. The column temperature was kept constant at 40 ℃. Two eluents were used during the gradient-program: MilliQ water with 0.1% formic acid as eluent A and methanol with 0.1% formic acid as eluent B. The gradient steps over a total run time of 12 min were: during 1 min 1–30% B, during the next 10 min 30–75% B, till 11.1 min 75–99% B, hold 99% for 0.1 min, return to starting conditions (1% B) within 0.8 min.
The mass spectrometer was equipped with a Jet-Stream Electrospray-Ion-source (ESI), which was operated in positive detection mode. The collision gas flow was set to 8 L min–1, the gas temperature was 300 ℃ and the fragmentor voltage was 175 V. Mass spectrometer and HPLC system were controlled via MassHunter Workstation B.06.00 (Agilent, Santa Clara, USA) running under Windows 7 Professional. Chromatograms and mass spectra were processed and analyzed using the same software.
Using a syringe, samples of 2 mL volume were taken from the reactor at 30 second intervals during the first 5 min, and thereafter at 1 minute intervals. The total irradiation time was 10 min. Samples were transferred to the HPCL-ESI-Q-TOF-MS and for MIC determination.
2.4. Determination of the kinetic rate constants and quantum efficiencies
Photolysis proceeds following first order or pseudo-first order reaction kinetics according to Equations 1 and 2, where ν is the reaction velocity, cA is the concentration of each macrolide, the index 0 denotes the starting concentration, k1 is the reaction rate constant and t the time [9,34,35,36,37]. In this work, the concentration-time (c-t) curves were determined as mass area-under-the-curve depending on irradiation time resulting from the HPCL-ESI-Q-TOF-MS experiments. They were described according to first order kinetics. The degradation products are considered intermediates and their c-t curves can be described as a consecutive and subsequent follow-up reaction [9,36]. All c-t curves were fitted mathematically using the curve fitting toolbox within the software MatLab R2016b (MathWorks, Natrick, USA).
The quantum efficiencies Φ254 at 254 nm were determined according to Equation 3 as described in detail in former studies [8,9].
|
Φ254=k2.303⋅l⋅ε254⋅I0,254
|
(3)
|
The quantum efficiency at 254 nm Φ254is the fraction of photons leading to a reaction compared to the total number of photons emitted by the lamp, where k (min–1) is the first-order reaction rate constant, l the reactor width, which was 3 cm, I0,254 the photon fluence rate in mmol min–1 L–1 and ε254 the molar extinction coefficient in L mol–1 cm–1.
2.5. Determination of minimal inhibitory concentration (MIC)
The minimal inhibitory concentration (MIC) assay was performed according to ISO 20776-1:2007 [38] Two bacterial strains were selected: Pseudomonas fluorescens (DSMZ-No. 50090), and Bacillus subtilis (DSMZ-No. 10). The method followed the protocol described by Wiegand, Hilpert and Hancock [39].
2.6. Quantitative structure-activity relationship (QSAR)
For QSAR analysis, the software T.E.S.T. and the software OECD QSAR Toolbox were used [40]. QSAR was calculated using the corresponding option in the software T.E.S.T. The following organisms were selected as indicators: Daphnia magna LC50 (48 h) in mg L–1 and fathead minnow LC50 (96 h) as target organisms and 'Photoinduced Toxicity on D. magna' and 'Mortality LC50 (48 h) of brachiopoda' for non-specified test organisms. These organisms represent species of the aquatic environment. The structure of each compound was sketched using ACD/ChemSketch 2016.1.1 (ACDLabs, Inc., Toronto, ON, Canada) and imported into the software T.E.S.T and QSAR toolbox.
3. Results and discussion
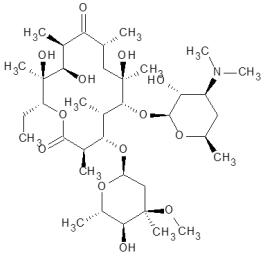
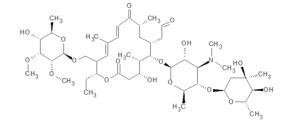
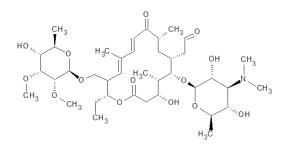
The chemical structures of the four macrolides investigated are depicted in Table 1 together with the m/z value of their quasi-molecular ion and the major fragments observed in MS. In water, erythromycin is often found as anhydro-erythromycin [18,23,26,41,42]. This is formed from erythromycin A by elimination of a water molecule. This reaction is especially preferred in acidic solutions [9,43,44,45]. Among the other macrolides, this dehydration has not been observed. Macrolides are often unstable in an acidic environment, such that a chemical degradation may occur even before irradiation [9,44,45,46,47,48,49,50,51,52].
The experimental [M+H]+ values agreed well with the theoretical values. The detected fragments all possessed the lactone ring, from which sugar moieties had already been eliminated.
3.1. Photoinduced degradation rate constants of macrolides
Table 2 shows the first order rate constants determined from the degradation experiments using UVC irradiation. Quantum efficiencies at 254 nm according to Equation 3 are also given.
Table 2. Rate constants, half-lives and the calculated quantum efficiencies of the individual macrolides at pH 7.
| Substance |
k /min–1 |
t1/2 /min |
Φ254 |
| Azi A |
0.39 |
1.80 |
1.02 |
| Azi B |
0.31 |
2.23 |
0.81 |
| Ery A |
0.59 |
1.18 |
0.55 |
| Ery B |
0.66 |
1.04 |
0.61 |
| Ery A–H2Oa |
0.59 |
1.17 |
0.55 |
| Ery A–H2Ob |
1.11 |
0.63 |
1.03 |
| Spi I |
0.62 |
1.12 |
0.05 |
| Spi Ⅲ |
0.64 |
1.08 |
0.05 |
| Tyl A |
2.47 |
0.28 |
0.04 |
| Tyl B |
1.66 |
0.42 |
0.03 |
The quantum efficiencies of azithromycin A and erythromycin A-H2Ob amounted to a value larger than 1. This can only be explained by assuming that the compound was additionally degraded by a mechanism other than photodegradation [53]. Such a mechanism was assumed degradation induced by hydroxyl radicals generated from water by UVC irradiation [5,6].
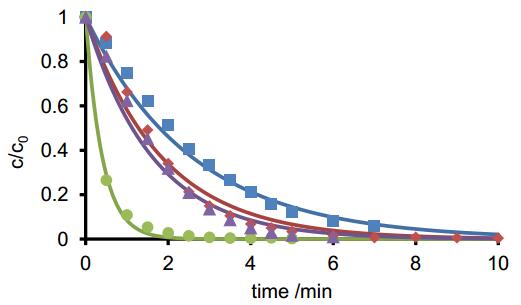
Tylosin generally degraded significantly faster than azithromycin and erythromycin. The degradation curves of azithromycin A, erythromycin A, spiramycin I, and tylosin A are shown in Figure 1. Tylosin A was degraded faster than tylosin B, since tylosin B is formed from tylosin A through elimination of the sugar moiety cladinose. The quantum efficiency of tylosin is lower by a factor of 10 than those of azithromycin and erythromycin, whereas the reaction proceeds much faster or more frequent following the reaction rates.
In general, the photodegradation of azithromycin and erythromycin is assumed to be determined by hydroxyl radicals due to the lack of chromophores that support absorption of photons and hence initiation of photoreactions. As to spiramycin and tylosin on the other hand, degradation is determined by their own photoreactivity since they have conjugated double bonds that absorb photons leading to the photoreaction [9,52].
3.2. Identified photoinduced degradation products
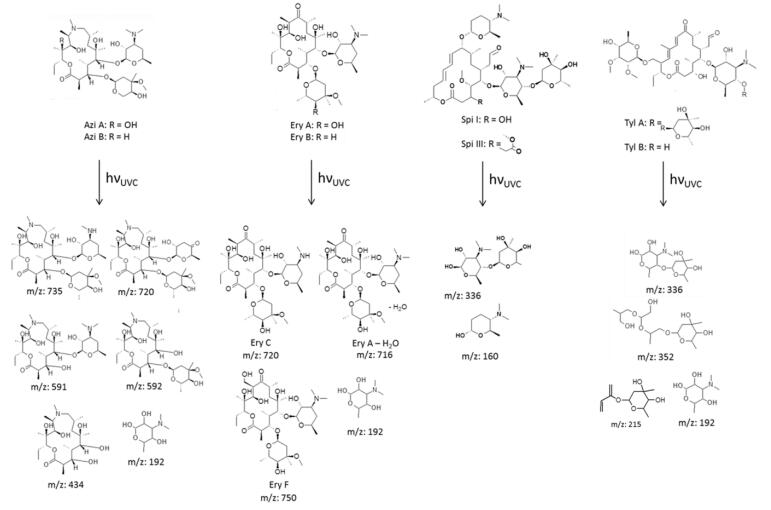
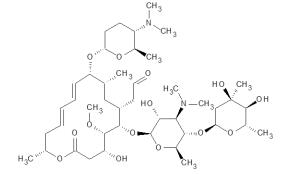
All identified photodegradation products are shown in Table 3. Their proposed structures are shown in Figure 2.
Table 3. Observed degradation products of macrolides together with their fragments derived from MS2 experiments as well as retention times of the products.
| substance |
photo-degradates |
Rt /min |
theoretical [M+H]+ |
observed [M+H]+ |
fragments |
| Azithromycin |
192 |
0.5 |
192.123 |
192.126 |
- |
|
591 |
4.8 |
591.422 |
591.427 |
434.315;
296.217 |
|
434 |
5.2 |
434.312 |
434.315 |
- |
|
735 |
5.4 |
735.500 |
735.506 |
591.426;
368.257 |
|
592 |
8.5 |
592.406 |
592.408 |
300.278;
237.102 |
|
720 |
8.8 |
720.453 |
720.462 |
540.308;
375.266;
250.994 |
| Erythromycin |
192 |
0.6 |
192.123 |
192.123 |
- |
|
720 |
7.5 |
720.452 |
720.457 |
558.366;
460.414;
375.263 |
| Spiramycin |
160 |
0.6 |
160.133 |
160.134 |
142.123 |
|
322 |
3.2 |
322.186 |
322,185 |
118.086 |
|
336 a |
3.7 |
336.202 |
336.204 |
192.122;
174.111;
145.084;
127.074;
101.059 |
|
336 b |
4.4 |
336.202 |
336.204 |
192.122;
174.111;
145.084;
127.074;
101.059 |
| Tylosin |
192 |
1.1 |
192.123 |
192.123 |
- |
|
215 |
1.8 |
215.128 |
215.090 |
- |
|
352 |
3.7 |
|
352.196 |
- |
|
336 |
4.2 |
336.202 |
336.201 |
- |
Photodegradation products for azithromycin with m/z values of the quasi-molecular ions of 735,720,592,591 and 434 were observed and their structures identified. These seven products are consistent with the observations of Tong et al. [54]. In addition, a product with a m/z value of 192 was identified, see Figure 2.
For erythromycin, products with m/z values of the quasi-molecular ions of 750,720, and 192 were found. These products were not reported previously in the literature.
Batchu et al. identified products with m/z values of the quasi-molecular ions of 678,608,590 and 429. The occurence of these products could not be confirmed in this study, cf. Figure 1 [55] During the photodegradation of spiramycin, three products could be identified. The corresponding m/z values of the quasi-molecular ions were 160 and 336. The ion with a m/z value of 336 occurred at two different retention times in the chromatogram. The retention times were 3.8 and 4.2 min. Due to the relative similarity of the retention times, these degradates were assumed to be structurally similar products. An MSn analysis confirmed the hypothesis as the same fragments were obtained (data not shown). With regard to the detected masses and their c-t courses, the degradates represent intermediate photoproducts. The two species could be diastereoisomers, which may have been formed. The isomerism would occur at the position where the lactone ring was attached, i.e. stereoisomers with respect to a resulting hydroxyl group, which could assume R or S configuration, after sugar moiety cleavage from the lactone ring by hydroxyl radical substitution.
The degradation of tylosin under UV irradiation has also been investigated several times [56,57,58]. However, no photodegradation products were described in these studies. In this work, sugar fragments were found as degradation products. The associated m/z values were 352,336,215 and 192, see Figure 1.
3.3. MIC and QSAR
Ecotoxicity was estimated through determination of the MICs against B. subtilis and Ps. fluorescens and through QSAR analysis. The results of both toxicity assessments are shown in Table 4.
Table 4. MIC values of the antibiotics tested against the microorganisms Ps. fluorescens and B. subtilis and QSAR analysis of photodegradation products of macrolides with safer (Italic) and more dangerous (Bold) photoproducts as compared to the starting material. The starting concentrations of efficacy against the organisms were compared with the concentration of the efficacy of the photoproduct.
| compound |
MIC against B. subtilis
/µg mL–1 |
MIC against Ps. fluorescens
/µg mL–1 |
Daphnia magna LC50 (48 h) mg/La |
Fathead minnow LC50 (96 h) mg/La |
Fathead minnow LC50 (96 h) mg/Lb, c |
Branchiopoda LC50 (48 h) mg/Lb, d |
| Azi A |
5.90 |
49.48 |
80.84 |
0.33 |
- |
3.04 |
| Azi B |
|
|
72.43 |
0.87 |
- |
2.22 |
| 735 |
|
|
98.37 |
0.14 |
- |
3.99 |
| 720 |
|
|
202.02 |
- |
- |
28.4 |
| 592 |
|
|
108.58 |
0.04 |
- |
23.4 |
| 591 |
|
|
151.56 |
0.10 |
- |
3.26 |
| 434 |
|
|
97.23 |
4.09 |
695 |
23.3 |
| 192 |
|
|
2067.67 |
4087.53 |
1.58E5 |
1780 |
| Ery A |
0.21 |
96.90 |
135.5 |
- |
- |
8.6 |
| Ery B |
|
|
127.65 |
- |
- |
0.98 |
| Ery C |
|
|
193.84 |
- |
340 |
11.3 |
| Ery F |
|
|
333.08 |
- |
- |
68.4 |
| 716 |
|
|
129.61 |
- |
193 |
6.36 |
| 192 |
|
|
2067.67 |
4087.53 |
1.58E5 |
1780 |
| Spi I |
7.03 |
177.75 |
69.14 |
- |
- |
97 |
| Spi Ⅲ |
|
|
15.00 |
- |
- |
34.2 |
| 336 |
|
|
579.58 |
410.60 |
2.69E5 |
- |
| 322 |
|
|
666.63 |
547.26 |
4E5 |
- |
| 160 |
|
|
367.72 |
1062.61 |
1.88E4 |
- |
| 702 |
|
|
211.54 |
- |
- |
703 |
| Tyl A |
1.26 |
160.80 |
104.55 |
- |
- |
426 |
| Tyl B |
|
|
76.56 |
- |
- |
264 |
| 352 |
|
|
347.51 |
683.37 |
4.39E4 |
- |
| 336 |
|
|
579.58 |
410.60 |
2.69E5 |
- |
| 215 |
|
|
90.11 |
246.51 |
551 |
- |
| 192 |
|
|
2067.67 |
4087.53 |
1.58E5 |
1780 |
a T.E.S.T
b QSAR Toolbox
c Pimephales promelas
d undefined testorganisms |
For the four macrolides, high MIC values were determined on Ps. fluorescens. Growth delay was also observed. This is indicative for the lack of efficiency against Ps. fluorescens, which is in agreement with expectations, since macrolides are administered against gram-positive bacterial infections. Due to the absence of activity against Ps. fluorescens, only B. subtilis was exposed to the drugs. The cleavage of the sugar moieties of macrolides upon irradiation as described above raised the expectation of inactivity of the degradates [43,59]. The ecotoxicity estimation using MIC was hence based on B. subtilis. To this purpose, it was assumed that environmental hazard would be minimal when the solution containing the drug ceased showing antibacterial activity. Using the degradation rate constants k1 from Table 2 and the MIC value, the time tTOX can be calculated according to Equation 4. Here, tTOX is the time when the solution of a compound with an initial concentration c0 is no longer active against the bacteria. The results are given in Table 5.
Table 5. Calculated tTOX values of the four macrolides against B. subtilis.
| Substance |
k /min–1 |
MIC /µg·mL–1 |
tTOX /min |
| Azi A |
0.39 |
5.9 |
3.13 |
| Azi B |
0.31 |
|
3.94 |
| Ery A |
0.59 |
0.21 |
7.72 |
| Ery B |
0.66 |
|
6.90 |
| Ery A–H2Oa |
0.59 |
|
7.72 |
| Ery A–H2Ob |
1.11 |
|
4.10 |
| Spi I |
0.62 |
7.03 |
1.69 |
| Spi Ⅲ |
0.64 |
|
1.63 |
| Tyl A |
2.47 |
1.26 |
1.12 |
| Tyl B |
1.66 |
|
1.67 |
Within eight minutes of irradiation, the MIC values were reached, meaning that all observed macrolides were no longer harmful to B. subtilis. Yet, the calculation does not clarify whether the phototransformation products were more active or ecotoxic than the original drug. The phototransformation products observed were mostly sugar compounds. A more detailed picture of whether a photoproduct would be environmentally hazardous may be provided by QSAR analysis.
The QSAR analysis did not predict values for some of the degradation products and organisms, so that comparison with the parent drug was not possible. Generally, irradiation of the substances had a positive effect. It reduced the efficacy of the substances. The detected sugar fragments were predicted to have higher LC50 values than the intact lactone ring scaffold. This would lead to efficacy against the microorganisms tested and hence eco-toxicology. While these increased LC50 values were computed for some degradates, no values reaching into the lower μg L–1 range were predicted. Therefore, the predicted values would still remain well below concentrations found in surface waters.
A comparison between different programs could be achieved on the basis of fathead minnow, a relevant organism to appear in both programs. Here, the values varied by several orders of magnitude and the toxicity were predicted differently for several photoproducts. This could be explained in terms of distinctive databases and calibration models implemented into the programs. Hence, output parameters but also calculation methods were different. The calculation of T.E.S.T. software was based on the database of EUCAST, while in the QSAR toolbox the calculation relied on the data of the European Chemicals Bureau. A literature search for reference data was unsuccessful. Despite the different absolute values, both predictions were consistent when inspecting the parent drug. Most photoproducts investigated were predicted to be potentially less toxic than the parent.
Yet, QSAR methods rely on databases but the prediction is based on structural similarity. As an alternative to a computational approach, MIC values, i.e. experimental data, might be considered for eco-toxicological assessment [36,60]. Recent studies emphasize that IC50 values might be better suitable since they were assay independent [61]. Nevertheless, MIC values are easier and faster to obtain. Additionally, the quality of IC50 values also depends on the completeness of the sigmoidal curve, which might not be obtained under all circumstances. In this study, tylosin served an example for the other macrolides. A tylosin solution was exposed to UV irradiation and MIC values of the solution were determined at various exposure times, see Table 6. Under UV-irradiation the MIC values were expected to increase.
Table 6. MIC values of aqueous solution of tylosin against B. subtilis depending on irradiation times.
| Irradiation time /min |
MIC against B. subtilis /mg L–1 |
| 0 |
1.05 |
| 1 |
2.1 |
| 2.5 |
4.2 |
| 3.5 |
> 8.41 |
| 5 |
> 8.41 |
| 7 |
> 8.41 |
From Table 6, it can be seen that the longer tylosin was UV irradiated, the higher the MIC value grew. A maximum was reached between 2.5 min and 3.5 min, indicating that the efficacy of tylosin against B. subtilis decreased. With that loss of potency, it can be assumed that the solution provided no more hazard for the organisms and that the degradation products did not possess higher efficacy and hence potential eco-toxicity than the drug itself. Although this finding was exemplarily demonstrated for tylosin, preliminary studies for other antibiotic classes showed similar results.
4. Conclusions
The elimination of pharmaceuticals in water bodies using sustainable methods, as demonstrated in this study by using photolysis, was supported by an estimation of toxicity. The hypothesis that such degradation processes might produce substances even more toxic than the parent drug could not be confirmed. In this respect, MIC values were determined and QSAR analysis was performed. Based on four macrolides the products resulting from UV-C irradiation as well as the corresponding solution mixtures formed during irradiation were shown to be less or not ecotoxic in comparison to the parent antibiotic drugs. From these results, the efficacy of UV irradiation for water purification from antibiotics can be assumed. However, for the future of water purification, it is important to consider that there are other pharmaceuticals and anthropogenic micropollutants in waters that have different properties than macrolides. Their concentrations also depend on seasonal and local influences. In consequence, different exposure times and intensities may be needed to achieve complete degradation.
Acknowledgements
M.V. is grateful for a stipend from the Promotionskolleg of the Niederrhein University of Applied Sciences. The authors thank their institution for further financial support.
Conflict of interest
All authors declare no conflicts of interest in this paper









 DownLoad:
DownLoad: