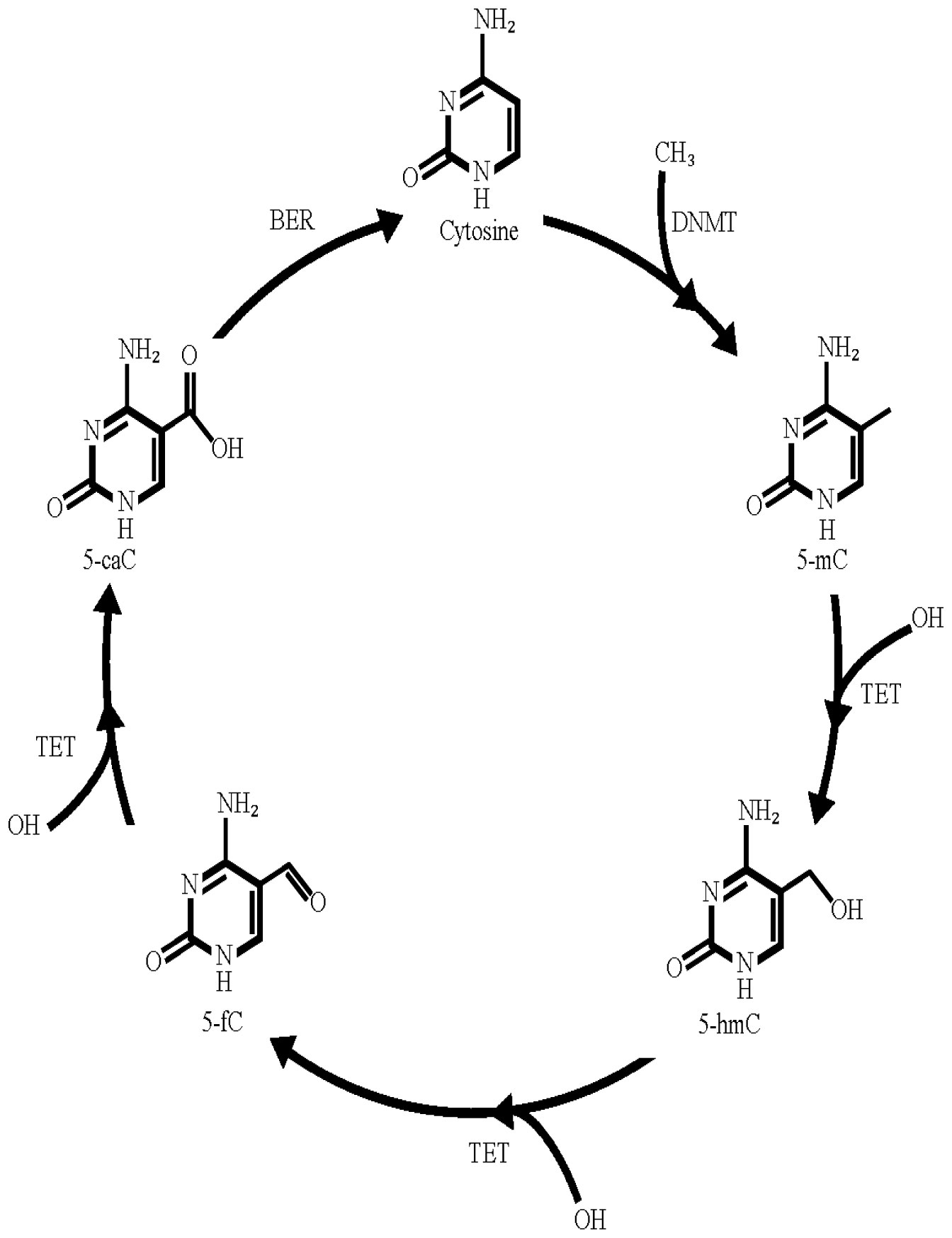
Chromatin is a complex multi-scale structure composed of DNA wrapped around nucleosomes. The compaction state is finely regulated mainly by epigenetic marks present not only on nucleosomes but also on the DNA itself. The most studied DNA post-transcriptional modification is 5-methylcytosine (5-mC). Methylation of the cytosine at CpG islands localized at the promoter is associated with repression of transcription. On the contrary, enrichment of 5-hydroxymethylcytosine (5-hmC), one of the oxidation products of 5-mC by TET (ten-eleven translocation) enzymes, on promoters and enhancers promotes transcription activation. Recently, a new role of 5-hmC has been proposed in the context of DNA repair. 5-hmC was found to be enriched at DNA lesions and knockdown of TET led to impaired repair efficiency. Here, we review our current knowledge regarding the role of the regulation of the 5-mC/5-hmC balance by TET enzymes in the context of transcription modulation as well as DNA repair processes. In a final section, we speculate on the potential involvement of TET proteins in DNA repair mechanisms associated with transcription activation.
1.
Introduction
It has been almost two years since the outbreak of COVID-19. A large number of international research results have given us a certain understanding of the virus. This is a severe respiratory illness caused by the coronavirus [1,2]. The International Committee on Taxonomy of viruses named the virus SARS-CoV-2 is mainly transmitted through respiratory tract. The clinical symptoms of infected people are mostly fever, dry cough and fatigue, and some patients are asymptomatic infected people. When the disease is serious, it will also cause organ failure and even death [3,4].
Currently, the COVID-19 pandemic is still ongoing. According to the latest outbreak of the World Health Organization, as of October 2021, there were more than 70 million newly confirmed cases in Europe [5]. The United Kingdom is one of the worst-affected countries in Europe, with more than 8 million cumulative cases, of which more than 7 million were diagnosed in England alone [6], accounting for 85% of the total cumulative cases reported in the United Kingdom.
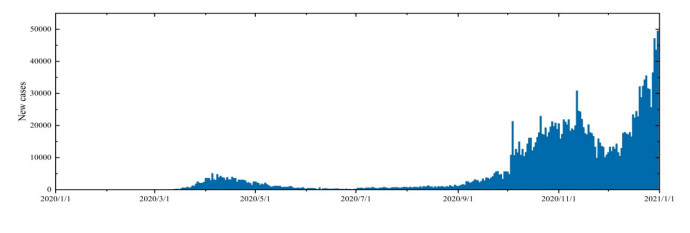
Since more than 80% of confirmed cases in Britain are concentrated in England, we intend to do some theoretical research based on the data of England for the reference of government decision-making. Figure 1 shows the daily new cases data of COVID-19 epidemic in England during 2020 [6]. In early March, due to the obvious increase of new cases, the British government began to implement the first large-scale social blockade at the end of March and gradually unsealed at the beginning of June. This phase corresponds to the phase in which the first small peak appears in Figure 1. In the three months after the first unsealing, the epidemic situation in the region had been relatively gentle. However, since September, the number of new cases per day had increased significantly. By the end of October, the number of new cases per day had reached about 20000.At this time, the British government once again announced that it would implement the second large-scale social blockade on November 5, which lasted until December 2nd. Soon after the second unsealing, the third wave of more large-scale epidemic began, and there were reports that a mutant virus with stronger transmission ability was detected, and the epidemic reached a stage that was difficult to control. On December 20th, Britain ushered in the third social blockade, which lasted until February 2021.
H. Ward et al. based on antibody levels in 365,000 people, showed that at the start of the second wave of infections in England, only 4.4% of adults had IgG antibodies detected using text for lateral flow immunoassay (LFIA) [7]. A study on the antibody positive rate of asymptomatic and symptomatic infected people in Wanzhou District of Chongqing by Quanxin Long et al showed that after 8 weeks of infection, the antibody concentration of more than 90% of the participants decreased by more than 70% [8]. A study on the neutralizing antibody level of SARS-CoV-2 patients within three months after infection found that after analyzing the serum samples of 65 SARS-CoV-2 infected patients, 95% of the cases had seroconversion [9]. Some researchers found that the antibody titers of the two virus strains decreased significantly, and the delta variant virus strain decreased more significantly than the wild strain [10,11,12]. The infectious disease dynamics model is a key tool for studying the spread of infectious diseases. It is generally divided into four compartments, susceptible (S), exposed (E), infected (I) and recovered (R) compartments. It can clearly describe the dynamic relationship between various warehouses in the process of virus transmission, and give relatively accurate predictions on the development trend of infectious diseases. P. Wintachai [13] et al. predicted the change trend of COVID-19 cases over time by establishing SEIR infectious disease dynamics model considering different vaccination rates. A. Fuady [14] et al. established an infectious disease dynamics model considering different vaccination times to explore the inhibitory effect of changes in vaccination time on the spread of covid-19 epidemics. M. Angeli et. al. [15] et al introduced SAIVR mathematical model to forecast the covid-19 epidemic evolution during the vaccination campaign by employing a semi-supervised machine learning process. S. Zhai [16] et al. studied an SEIR-type epidemic model with time delay and vaccination control, the vaccination strategy was expressed as a state delayed feedback which was related to the current and previous state of the epidemic model and investigated the non-negativity and boundedness of the model. J. Medina [17] et al. modeled a trustable and reliable management system based on block chain for vaccine distribution by extending the SEIR model, which included prevention measures such as mask-wearing, social distancing, vaccination rate, and vaccination efficiency. A. Karabay [18] et al. presented a particle-based SEIR epidemic simulator as a tool to assess the impact of different vaccination strategies on viral propagation and to model sterilizing and effective immunization outcomes and the simulator included modules to support contact tracing of the interactions amongst individuals and epidemiological testing of the general population. J. Wieland [19] et al. developed a model for the simulation of the SARS Cov-2 spread in Germany in the context of a complementary course at the Leuphana University. It tried to simulate different scenarios of the number of cases with the help of ODE. Chen [20] et al. used compartmental models to model and analyze the COVID-19 dynamics of different considered populations as susceptible, exposed, infected and rcovered compartments (SEIR). They derived control-oriented compartmental models of the pandemic, together with constructive control laws based on the Lyapunov theory. Antibody levels decrease over time after a person recovers from COVID-19, there will be a chance of re-infection with the virus. In the first model, we explore the impact of declining antibody levels on the spread of the COVID-19 epidemic in the UK, taking into account that a certain proportion of recoveries would become susceptible again. In the optimized model, we add the vaccinated compartment and study the impact of the vaccine's effect on the outbreak.
This study selects the daily new data of the COVID-19 epidemic in England from September 1 to October 31, 2020 as the data for model fitting, that is, the data in the middle and early stages of the second wave of the epidemic in England. Based on these possible factors: 1) The first wave of the epidemic has ended, and the level of antibodies in the infected people began to decline; 2) The British government did not have any intervention policy during this period; 3) There was no vaccination during this period; Therefore we used data for this time period when considering the impact of declining antibody levels on the spread of COVID-19 in this model.
2.
SEIR model for the decline of antibody level in population
Because the spread of COVID-19 has a long incubation period and the incubation period is contagious, in our model, we consider the incubation period and adopt the SEIR model. We divide the total population N into four categories: susceptible (S), exposed (E), infected (I), and recovered (R). $ \beta $ is the rate of disease transmission, $ \sigma $ is the conversion rate from exposed people to infected people, $ \gamma $ is the disease recovery rate, $ \mu $ is the mortality due to disease, and $ P $ is the conversion rate from recovered group to susceptible group. The SEIR infectious disease dynamics model considering the decline of antibody level is shown in Figure 2.
According to the above COVID-19 spread diagram, we establish the infectious disease dynamics model as follows:
2.1. Equilibrium point of the model
We obtain, when $ I = 0 $, the disease-free equilibrium point of model (2.1) is $ E_{01} = (S_0, 0, 0, 0) $.When $ I\neq0 $, the endemic equilibrium point of model (2.1) is
2.2. Basic reproduction number
The basic reproduction number refers to the average number of secondary cases after an infected individual enters the susceptible population [21], the next generation matrix is the most commonly used method to calculate the basic reproduction number.
In order to calculate the basic reproduction number of model (2.1), we take
The Jacobian matrices of F and V are
At disease-free equilibrium, we obtain
The basic reproduction number $ \mathscr{R}_0 $ is the spectral radius of $ {\left. {F{V^{ - 1}}} \right|_{{E_{01}}}} $, so the expression is
2.3. Stability analysis of disease-free equilibrium
Theorem 1. When $ \mathscr{R}_0 < 0 $, model (2.1) is stable at the disease-free equilibrium point, otherwise unstable.
Proof. The Jacobian matrix of model (2.1) at $ E_{01} $ is
The matrix eigenvalue satisfies the following formula:
Obviously $ {\lambda _1} = 0, {\lambda _2} = - P < 0 $, the other two eigenvalues $ {\lambda _3}, \; {\lambda _4} $ satisfy the equation
where
Easy to know
therefore,
So, when $ \mathscr{R}_0 < 1 $, we obrain $ {a_1} > 0 $ and $ {a_2} > 0 $. According to Hurwitz discriminant method, the characteristic roots $ {\lambda _3}, \; {\lambda _4} $ of $ P(\lambda) $ have negative real parts.
To sum up, among the eigenvalues of the Jacobian matrix of model (2.1), the real part of four eigenvalues is negative and one is zero. So, when $ \mathscr{R}_0 < 1 $, model (2.1) is stable at the disease-free equilibrium point, otherwise unstable.
3.
SEIRV model of vaccination
Antibody levels decline over time, and herd immunity approaches that rely on natural immunity become unfeasible. Therefore, on the basis of the above model (2.1), we add the vaccination compartment (people who were successfully vaccinated) to establish the SEIRV model. In this model, we consider daily vaccination of susceptible populations at a fixed vaccination rate and explore the impact of varying injection and failure rates on the outbreak in England. The propagation mechanism of the model is shown in the Figure 3. Here $ \alpha $ refers to the daily proportion of vaccination, $ \omega $ is the vaccine failure rate and refers to the reciprocal of the duration of vaccine effectiveness. The other parameters are the same of model (2.1).
According to the above COVID-19 diagram, the infectious disease dynamics model we established is
3.1. Equilibrium point of the model
Let
When $ I = 0 $, there are
The disease-free equilibrium point of model (3.1) is
When $ I\neq0 $, we obtain
Therefore, the endemic equilibrium point of model (3.1) is
3.2. Control reproduction number
The number of controlled reproduction refers to the number of people who can be infected by an infected person during the infection period under certain prevention and control measures [22]. It is also calculated by the method of next generation matrix.
In order to calculate the control reproduction number of model (3.1), we take
The Jacobian matrices of F and V are
At disease-free equilibrium, there is
The control reproduction number is the spectral radius of $ {\left. {F{V^{ - 1}}} \right|_{{E_{02}}}} $, and the expression is
3.3. Stability analysis of disease-free equilibrium
Theorem 2. When $ {\mathscr{R}_C} < 1 $, the model (3.1) is locally asymptotically stable at the disease-free equilibrium point, otherwise it is unstable.
Proof. The Jacobian matrix of model (3.1) at $ {E_{02}} $ is
The matrix eigenvalue satisfies the following formula:
Obviously $ {\lambda _1} = - P < 0 $, the other eigenvalues $ {\lambda _2}, \; {\lambda _3} $ satisfy the equation
where
We obtain
which means $ {\lambda _2} $ and $ {\lambda _3} $ have negative real parts. The last two eigenvalues $ {\lambda _4}, \; {\lambda _5} $ satisfy the equation
where
So, when $ \mathscr{R}_C < 1 $, we obrain $ {B_1} > 0 $ and $ {B_2} > 0 $. According to Hurwitz discriminant method, the characteristic roots $ {\lambda _4} $ and $ {\lambda _5} $ have negative real parts.
To sum up, all eigenvalues of the Jacobian matrix of model (3.1) have negative real parts, so model (3.1) is locally asymptotically stable at the disease-free equilibrium point, otherwise it is unstable.
4.
Numerical simulation and result
4.1. The parameters in the model
According to model (2.1), the number of new cases per day in England from September 1 to October 31 is fitted by the nonlinear least squares method, and the fitting result is shown in Figure 4. Within the allowable range of error, we set the initial value of the susceptible as $ {S_0} = 55699400 $, the initial value of exposed people as $ {E_0} = 6500 $, the initial value of infected people as $ {I_0} = 1041 $, meaning the number of new cases in England on September 1, and the initial value of recovered people as 200. The conversion rate from exposed people to infected people is $ \sigma = 1/12\; (day^{-1}) $ [23], the recovery rate of disease is $ \gamma = 1/14 \; (day^{-1}) $ [24] and the mortality rate is $ \mu = 0.003 $ [25], which are selected according to the actual transmission of infectious diseases. And we obtain the transmission rate is $ \beta = 1.1295 \times {10^{ - 9}} $ and the conversion rate from the recovered group to susceptible group is $ P = 1.8888 \times 10{}^{ - 6} $ by fitting.
The fitting results of the improved SEIR model are in good agreement with the England data, and can better reflect the growth trend of the COVID-19 epidemic in England.
In the SEIRV model (3.1), $ \alpha $ refers to the daily vaccination rate, which is further explained here. The overall immunization rates corresponding to different daily vaccination rates (60 days after vaccination) is shown in Figure 5. The total population of England is about 50 million, $ \alpha = 0.005 $ means that 250,000 people are vaccinated on the first day. After 60 days of continuous vaccination, the overall immunization rate is 25.9%.
In SEIRV model, the meaning of vaccine failure rate $ \omega $ refers to the reciprocal of the duration of vaccine effectiveness, that is, each corresponds to a duration of vaccine effectiveness. The data details are shown in Table 1.
4.2. Effects of different vaccine failure rates on the epidemic situation in England
In order to evaluate the role of vaccines in epidemic control, we investigate the impact of different vaccination rates and failure rates on the spread of COVID-19 epidemic in England. We change the vaccine failure rate when the fixed vaccination rate is 0.005, and simulate the impact of different failure rates on the spread of COVID-19 epidemic in England. The results are shown in Figures 6–8. In Figure 6, the failure rates are taken from 0 to 0.01 in steps of 0.001; in Figure 7, the failure rate is taken from 0.01 to 0.05 in steps of 0.01; in Figure 8, the failure rate is taken from 0.01 to 0.02 in steps of 0.001. As can be seen from Figures 6–8, with the decrease of vaccine failure rate, the peak of epidemic situation will gradually decrease. When the failure rate is less than 0.01, the peak time will advance with the decrease of failure rate; when the failure rate is greater than 0.01, the peak time will be delayed with the decrease of failure rate. If only Figures 6 and 7 are used to illustrate that 0.01 is the boundary value of peak time trend change, it may be coincidental because the failure rate less than 0.01 is taken as the step of 0.001, and the failure rate greater than 0.01 is taken as the step of 0.01. Therefore, we further take the failure rate from 0.01 to 0.02 in steps of 0.001 for simulation, as shown in Figure 8. It can be seen from Figure 8 that the time of peak value is delayed with the decrease of failure efficiency. In general, when the step of failure rate change is 0.001, the simulation shows that when the fixed vaccination rate is 0.005, the peak of epidemic situation will decrease with the decrease of failure efficiency. When the failure rate is less than 0.01, the peak time will advance with the decrease of failure efficiency; when the failure rate is greater than 0.01, the peak time will be delayed with the decrease of failure efficiency. When the vaccination rate is 0.005, the line chart of the epidemic peak under different vaccine failure rates is shown in Figure 9. When the value of failure rate is large (greater than 0.02), the peak will increase significantly. When the failure rate is 0.001 the peak value is 81.4% lower than the peak value when the failure rate is 0.01, and when the failure rate is 0.01 the peak value is 89.5% lower than the peak value when the failure rate is 0.02. Therefore, the lower the vaccine failure rate, the lower the peak of the epidemic. The peak values under different failure rates are shown in Table 2.
When the vaccination rate is 0.005, the line chart of the peak time of epidemic situation under different vaccine failure rates is shown in Figure 10. It can be seen when the failure rate is less than 0.01, the peak time will advance with the decrease of failure rate; when the failure rate is greater than 0.01, the peak time will be delayed with the decrease of failure rate. When the failure rate is 0.01, the peak time is 528 days later than that when the failure rate is 0.001 and 295 days later than that when the failure rate is 0.05. The peak time under different failure rates is shown in Table 2.
We also discuss the number of new cases per day at 30, 40, 50, 60 and 70 days in England with different failure rates when the vaccination rate is 0.005. The results are shown in Figure 11. It can be seen from the figure that at the same time, the smaller the failure rate, the fewer the number of cases. On the 60th day of vaccination, the vaccine with failure rate of 0.002 is 5.8% lower than the vaccine with failure rate of 0.01; on the 70th day of vaccination, the vaccine with failure rate of 0.002 is 9.1% lower than the vaccine with failure rate of 0.01. Therefore, with the extension of time, the vaccine with low failure rate is more effective in reducing the number of cases than the vaccine with high failure rate. The number of cases is shown in Table 3.
When the vaccination rate is 0.01, we discuss the impact of different vaccine failure rates on the spread of the epidemic in England, the results are shown in Figures 12–15. The simulation results show that the smaller the failure rate is, the lower the peak of epidemic situation is, and 0.019 is the boundary value of failure rate. When the failure rate is less than 0.019, the peak time will advance with the decrease of failure rate; when the failure rate is greater than 0.019, the peak time will be delayed with the decrease of failure rate. Some data are shown in Table 4.
4.3. Effects of different vaccination rates on the epidemic situation in England
When the vaccine failure rate is 0.005, the impact of different vaccination rates on the spread of the epidemic in England is shown in Figure 16. The vaccination rates change from 0.005 to 0.025 in steps of 0.005. According to the simulation, the peak of epidemic situation decreases with the increase of vaccination rate, and the peak time advances with the increase of vaccination rate. When the vaccination rate is 0.025, the peak value decrease by 74.8% and the peak time is 114 days earlier than that when the vaccination rate is 0.005. The result is given in Table 5.
In order to comprehensively evaluate the effects of vaccination rate and failure rate on the peak infection cases and peak time, we add heat-maps for peak infection cases and peak times, the results are shown in Figures 17 and 18. The vaccination rates change from 0.002 to 0.005 in steps of 0.001 and the vaccine failure rates change from 0.001 to 0.01 in steps of 0.001.
5.
Conclusions
The first part of this study is to develop an improved SEIR model of COVID-19 transmission in England taking into account the decline in antibody levels in recovers. In the second part, a SEIRV vaccination model is established on the basis of the decline in antibody levels, taking into account that susceptible populations are vaccinated at a fixed vaccination rate every day. We calculate the basic reproduction number of model (2.1) and the control reproduction number of model (3.1), calculate the disease-free equilibrium point and endemic equilibrium point of the two models, and analyze the stability of the model.
In the numerical simulation part, we further explain the vaccination rate and failure rate: $ \alpha = 0.005 $ means that 250,000 people are vaccinated every day on the basis of 50 million people in England, on the basis of this vaccination rate, the overall immunization rate is 25.9% after 60 days of continuous vaccination. In addition, the meaning of vaccine failure rate $ \omega $ refers to the reciprocal of the duration of vaccine effectiveness, that is, each corresponds to a duration of vaccine effectiveness.
In model (3.1), we investigate the impact of different failure rates on the spread of the epidemic in England when the vaccination rates are 0.005 and 0.01. The results shows that when the fixed vaccination rate is 0.005, when the failure rate is 0.001, the peak value is 81.4% lower than that when the failure rate is 0.01, and when the failure rate is 0.01the peak value is 89.5% lower than that when the failure rate is 0.02. In addition, when the failure rate is 0.01, the peak time is 528 days later than when the failure rate is 0.001 and 295 days later than when the failure rate is 0.05. Therefore, the peak of epidemic situation will decrease with the decrease of failure efficiency. The peak time of the epidemic has two situations. When the failure rate is less than 0.01, the peak time will advance with the decrease of failure efficiency; when the failure rate is greater than 0.01, the peak time will be delayed with the decrease of failure efficiency. On the 60th day of vaccination, the vaccine with failure rate of 0.002 is 5.8% lower than the vaccine with failure rate of 0.01, on the 70th day of vaccination, the vaccine with failure rate of 0.002 is 9.1% lower than the vaccine with failure rate of 0.01. Therefore, with the extension of time, the vaccine with low failure rate is more effective in reducing the number of cases than the vaccine with high failure rate. When the fixed vaccination rate is 0.01, the peak of epidemic situation will decrease with the decrease of failure efficiency. When the failure rate is less than 0.019, the peak time will advance with the decrease of failure efficiency; when the failure rate is greater than 0.019, the peak time will be delayed with the decrease of failure efficiency. We also investigate the impact of different vaccination rates on the spread of the epidemic in England when the fixed vaccine failure rate is 0.005. The peak of epidemic situation decreases with the increase of vaccination rate, and the peak time is advanced with the increase of vaccination rate. When the vaccination rate is 0.025, the peak value decreases by 74.8% and the peak time is 114 days earlier than that when the vaccination rate was 0.005.
6.
Discussion
The rationality of the fitting value of $ P = 1.8888 \times 10{}^{ - 6} $. This fitting value refers to the level of antibody decline in the actual recovered patients, including not only the number of hospitalizations officially counted, but also the number of uncounted patients with moderate and mild symptoms, and the number of confirmed asymptomatic infections. This value is somewhat underestimated. If only the number of recovered patients in hospital is counted according to official data from the UK government, this fitted value may have practical significance. Antibody levels take longer to drop due to higher antibody levels in severely recovered patients [26].
In model (3.1), the meaning of the vaccine failure rate refers to the inverse of the effective duration of the vaccine, that is, the failure rate corresponds to the effective duration of an effective vaccine. The data details are shown in Table 1. Similarly, the vaccination rate corresponds to a time period in which vaccinations are completed, for example $ \alpha = 0.005 $ indicating that it takes 200 days to complete all vaccinations.
In the numerical simulation part, the peak always decreases as the vaccine failure rate decreases. Peak arrival times may be related to boundary values. When the failure rate is less than the boundary value, the peak time will advance as the failure rate decreases; when the failure rate is greater than the boundary value, the peak time will be delayed as the failure rate decreases. In this study, when the vaccination rate was 0.005, the boundary value for the failure rate was 0.01; when the vaccination rate was assumed to be 0.01, the boundary value for the failure rate was 0.019. The boundary values in this paper are based on the failure rate with a step size of 0.001, when we take a smaller step size for simulation, we may get more accurate failure rate boundary values.
Israel has one of the highest vaccination rates in the world [27]. On December 20, 2020, the country took the lead in launching the world's first universal vaccination program for COVID-19. According to the official website of the Israeli Ministry of Health [28], as of March 2, 2020, the proportion of Israel receiving one dose of the vaccine was 51.67%, and the proportion of receiving two doses of the new crown vaccine was 37.53%. By early August 2021, about 62% of Israel's 9.3 million population had received at least one dose of the vaccine, and about 58% had completed two doses. Israel, despite reaching such a high vaccination rate, saw a new peak of cases in early September 2021. According to the World Health Organization, on September 1, 2021, Israel recorded more than 10,000 new cases per day. By the end of August 2021, the vaccination rate in Singapore had reached 80%, and since September 2021, the number of new cases in Singapore has increased significantly, and by the end of October, there were more than 5,000 new cases in a single day.
This article explores the impact of different vaccine failure rates on the spread of the COVID-19 outbreak in the UK, given a certain vaccination rates. Although many countries have achieved high vaccination rates, and even theoretically achieved rates of herd immunity, from the data alone, vaccination does not seem to have a significant inhibitory effect on the epidemic in these countries. The reason may be that the mutated virus is difficult to deal with, or the vaccine is not as effective as expected. In the next article, we will use data from severe cases to assess vaccine efficacy and protection. Vaccination rates can be increased through government policies, but if the protection rate of the vaccine itself is not high, increasing the vaccination rate will not help to fundamentally control the epidemic.
Acknowledgments
This study was funded by Natural Science Foundation of China (NSFC 11901027, 11871093), the China Postdoctoral Science Foundation(2021M703426), Postgraduate Teaching Research and Quality Improvement Project of BUCEA (J2021010), BUCEA Post Graduate Innovation Project (2021098, 2021099). We thank all the individuals who generously shared their time and materials for this study.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: