1.
Introduction
Antibiotic-resistant diseases have been alarmingly expanding over the world in recent years. The World Health Organization (WHO) and other international health organizations are gravely concerned about this phenomenon because of its dire consequences for public health [1]. The World Health Organization estimates that at least 700,000 people die each year from drug-resistant infections, and if action is not taken, this number could rise to 10 million deaths annually by 2050. The main statistical data provided by these organizations serve to highlight the seriousness and scale of this issue. These figures highlight how vital it is to launch coordinated international initiatives to combat the antibiotic resistance crisis. Additionally, the United States' Centers for Disease Control and Prevention (CDC) has shown that the nation experiences over 2.8 million antibiotic-resistant infections annually, which lead to over 35,000 fatalities [2]. The data presented here illustrates the pervasive effects of antibiotic resistance at the national level and serves as a stark warning of the potential consequences if the problem is not effectively addressed. In addition, the European Center for Disease Prevention and Control (ECDC) has drawn attention to the rapid spread of antibiotic-resistant bacteria throughout Europe, with an estimated 33,000 deaths annually resulting from these infections. The data from the ECDC highlights the transnational aspect of the issue and the requirement for a coordinated response on both a regional and international scale. The effectiveness of conventional therapies has been severely impacted by antibiotic resistance, which has turned into a major health concern worldwide. This has increased disease incidence, mortality rates, and healthcare costs. Many factors contribute to this growing issue, such as the overuse of antibiotic prescriptions, the lack of progress in developing novel medicines, and the international spread of resistant bacteria as a result of commerce and travel. The overuse and abuse of antibiotics are some of the major causes of the rise in antibiotic resistance. Antibiotics are frequently taken for viral illnesses in excess or for improper lengths of time in many nations, which causes the emergence of bacterial strains that are resistant to the drug [3]. The slow pace of new antibiotic development is another important factor [4]. Regulatory obstacles and the high expense of research and development have made it difficult for pharmaceutical companies to produce new antibiotics. This has led to a decreasing supply of new antibiotics, which makes it more challenging to successfully tackle bacteria that are becoming resistant to them. Furthermore, international trade and travel contribute to the global spread of resistant microorganisms. Bacteria with resistant strains are easily able to spread across national borders through contaminated food products, ill people, or environmental factors. This interdependence emphasizes the need worldwide collaboration and surveillance to track and manage the emergence of bacteria resistant to antibiotics. Antibiotic resistance has far-reaching effects that affect not just individual individuals but also economies and healthcare systems. A patient's length of sickness, chance of complications, and death rate may rise when the effectiveness of conventional treatments declines. Healthcare expenses and resource use may increase if healthcare practitioners are forced to use more costly and ineffective alternatives. To summarize, the complex issue of antibiotic resistance has a substantial impact on the effectiveness of conventional therapies, which raises the incidence, mortality, and expense of healthcare [5]. The threat posed by antibiotic resistance to world health is growing [6]. It is imperative that practical solutions be found quickly to address this problem.
The current antimicrobial therapy faces multiple limitations, which stem from scientific, regulatory, and economic challenges. The following is an in-depth exploration of these limitations: Traditional antibiotics exert their effects by targeting key functions or structures of bacteria, such as cell wall synthesis, protein synthesis, or DNA replication [7]. However, bacteria can rapidly evolve resistance through various mechanisms, such as mutations, horizontal gene transfer, or the production of enzymes to neutralize antibiotics [8]. The discovery and development process of new antibiotics is lengthy and costly, with a low success rate. Over time, many bacteria have developed resistance to antibiotics, which requires the continuous development of new antibacterial strategies. The clinical trials of new antibiotics require a significant amount of time and resources, and it must be demonstrated that they are superior to existing drugs in terms of safety and efficacy, which increases the complexity of development. Regulatory authorities have strict approval processes for new drugs, requiring a large amount of data to support their safety and effectiveness, which further prolongs the time for new drugs to be launched. Due to the strict control of antibiotic use to slow the development of drug resistance, the market potential of new antibiotics is limited, which reduces the willingness of pharmaceutical companies to invest. The development of antibiotics involves a large amount of upfront investment and a high failure rate, which increases economic risks. Broad-spectrum antibiotics may lack specificity, which means that while they kill pathogenic bacteria, they may also disrupt the beneficial microbial community of the host, leading to microbial imbalance. The use of broad-spectrum antibiotics provides strong selection pressure for bacteria, promoting the survival and proliferation of drug-resistant strains, thereby accelerating the development of drug resistance. Given the limitations of traditional antibiotics, developing alternative antibacterial therapies has become crucial; this includes emerging methods such as bacteriophage therapy [9], antimicrobial peptides [10], nanoparticles, and antisense antimicrobial therapy [11]. The combination of two or more different antibacterial therapies can improve treatment efficacy and reduce the development of drug resistance. Through precision medical methods, antibiotics can be developed by targeting specific mechanisms of specific bacteria, reducing their impact on non-target bacteria. Innovative methods of antimicrobial therapy are crucial for overcoming existing challenges. By exploring new antibacterial mechanisms, developing alternative therapies, and adopting combination therapy strategies, it is possible to more effectively combat drug-resistant bacteria while reducing adverse effects on the host microbiota.
Antimicrobial peptides (AMPs) as a promising class of novel antimicrobial agents with the potential to address the limitations of current therapies. All multicellular organisms create AMPs and proteins, a broad class of naturally occurring chemicals, as their first line of defense. These proteins possess wide-ranging abilities to eradicate bacteria, yeasts, fungus, viruses, and even cancerous cells direct [10]. The innate immune system of many organisms includes antimicrobial peptides, which have a potent inhibitory or lethal effect on invasive infections. However, the organisms are not harmed by these peptides. Antimicrobial peptides have a distinct antibacterial mechanism and AMPs exhibits a lower risk of bacterial resistance evolution compared to most conventional antibiotics [12]. AMPs are generally more difficult to cause resistance, but in some cases, microorganisms may develop resistance mechanisms; for instance, Staphylococcus aureus has developed strains that are resistant to antimicrobial peptides [13]. Short biological molecules that are frequently cationic are known as antimicrobial peptides (AMPs). Thirty of these bioactive peptides were found to be members of the Apidae Cin AMPs, Brevinin-1, Brevinin-2, and Nigrocin-2 AMPs families based on amino acid sequence analysis. These results demonstrate how useful it is to classify and predict the antimicrobial activity of novel AMPs by linking their varied sequences to their predicted peptide structures [14]. In addition, AMPs demonstrated broad-spectrum activity. Their unique mechanisms of action, such as membrane disruption [15] and immunomodulatory effects [16], which may reduce the likelihood of resistance development. Accordingly, AMPs are a viable alternative to traditional antibiotics and are poised to play a crucial role in the next generation of antimicrobial strategies.
Developing new antimicrobial strategies to address the global health crisis caused by antibiotic resistant infections is crucial [17]. Novel techniques such as AMPs have the potential to transform therapeutic strategies in the fight against infectious illnesses. With a variety of antibacterial qualities, AMPs can combat a broad spectrum of infections and present a viable substitute for established antibiotics. Furthermore, the field of treating infectious diseases is also changing because of techniques including phage therapy, immunotherapies, CRISPR-Cas systems, nanotechnology, microbiome modification, and AI integration. Treatments for infectious diseases that are more efficient, focused, and long-lasting can be achieved by utilizing these innovative strategies and welcoming interdisciplinary teamwork. Enhancing the transition of novel treatments from labs to beds, overcoming current obstacles, and fortifying the relationship between industry and government are all crucial. Therefore, to guarantee the availability and efficacy of antimicrobial medications for future generations, we need take action, keep funding the research and development of antimicrobial pharmaceuticals, support policy for antibiotic management, and participate in international collaboration. Although membrane destruction is the main mechanism of AMP, other mechanisms, such as interference with cellular signaling pathways and immune regulation, warrant further exploration. These mechanisms may provide the basis for the development of novel AMP targeting specific pathogens. In this review, we address these gaps by integrating mechanistic insights with advanced strategies for AMP optimization and delivery. A novel aspect of this work is the emphasis on AMP synergies with conventional antibiotics and the actionable recommendations it provides for overcoming translation barriers. By doing so, we aim to bridge the divide between basic research and clinical implementation, offering a comprehensive resource for researchers and clinicians.
2.
Antimicrobial peptides
Antimicrobial [18] peptides (AMPs) are tiny, naturally occurring compounds with a wide range of antimicrobial characteristics that play an important role in practically all living organisms' innate immune response. Antimicrobial peptides (AMPs) can be classified into loop, extended, β-sheet, and α-helical forms. Additionally, they can be identified by the microorganisms they target; examples of these include antiviral, antibacterial, antifungal, and anticancer peptides. This classification highlights the diversity of AMPs and suggests a wide range of viral and neoplastic illnesses for which they may be useful. This classification is crucial for understanding the functional roles and mechanisms of AMPs families [19].
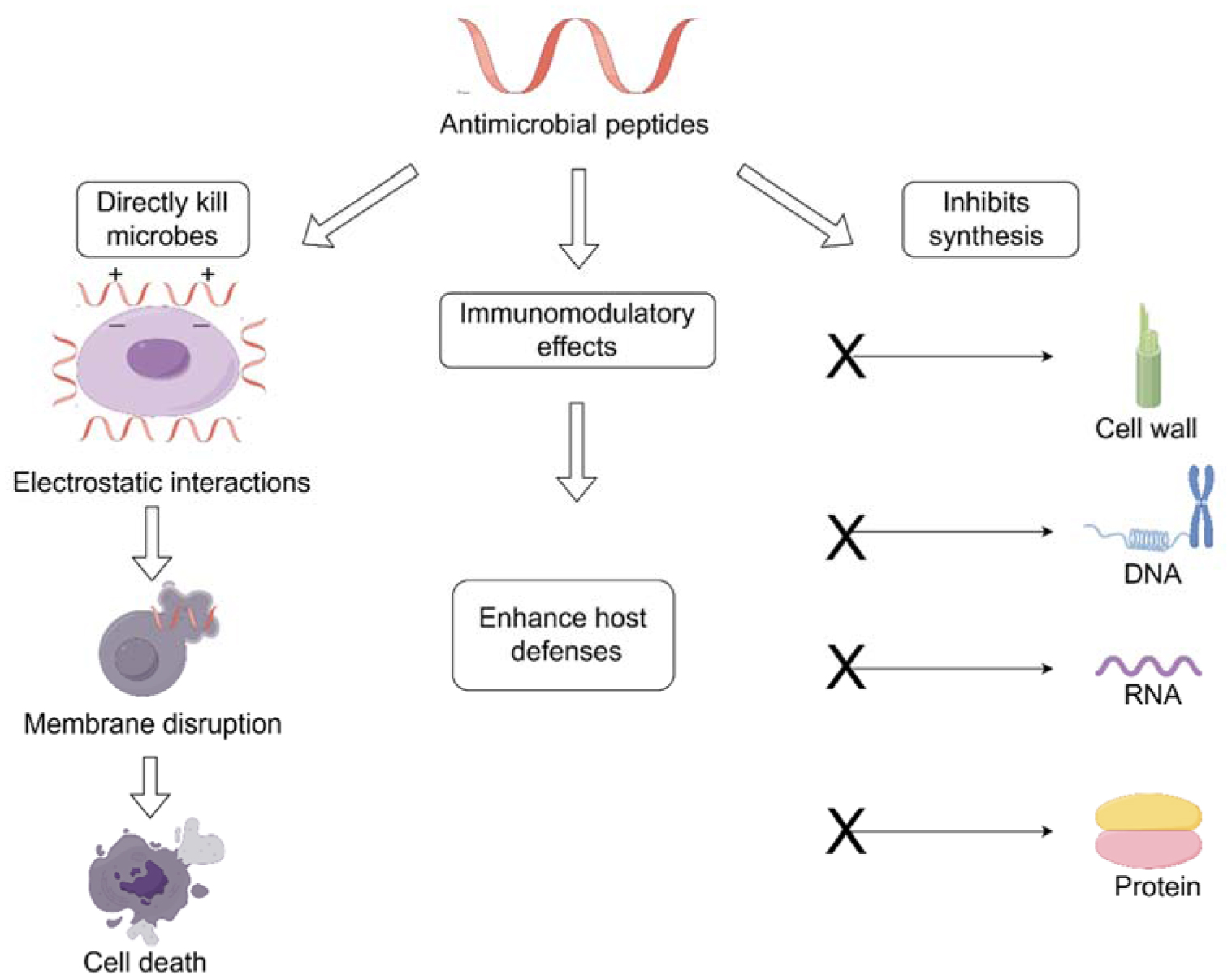
Antibacterial proteins and peptides (AMPs) are an array of naturally occurring chemicals that are created as everyone's first line of defense creatures with several cells. These proteins can engage in widespread activities to kill fungus, viruses, bacteria, yeasts, and cells from cancer. AMPs are used primarily as an antibiotic to defend against potentially harmful bacteria, but bacteria also generate AMPs to protect their ecological specialty. In more advanced eukaryotic creatures, AMPs may also be known as “host” protection peptides, highlighting their extra actions that modulate immunity [20]. Well-researched AMPs are essential to the innate immune response to infections, such as human cathelicidins and defensins [21]. For example, the host's defense against illnesses that occur early in life, including chorioamnionitis, newborn sepsis, or necrotizing enterocolitis (NEC), is mostly dependent on innate immunity, where antimicrobial peptides (AMPs) are important players (Figure 1). The AMPs α and β defensins, cathelicidin LL-37, antiproteases (elafin, SLPI), and hepcidin are critical for the fetus and newborn. The Chori amniotic membranes, the placenta, the fetus or neonate, recruited neutrophils, milk protein intake, or proteolysis can all create them. They are immune-modulating, tissue-repairing, inflammatory-regulating, and antimicrobial. AMPs are detectable as early as week 13, and they gradually grow during pregnancy. Limited studies are available on AMPs' expression and levels in the fetus and neonate. However, the available data supports the involvement of AMPs in the pathophysiology of newborn sepsis, chorioamnionitis, and NEC, as well as their correlation with the severity of the illness. This shows that AMPs may be involved in the diagnosis, treatment, prognosis, and prevention of NEC and sepsis [21]. The development of peptide synthesis and biotechnology has made it possible to produce and modify AMPs in the laboratory. A sophisticated method for the chemical diversity of recombinantly generated antimicrobial peptides (AMPs) is the inclusion of non-canonical amino acids (ncAA). In a number of bacterial production hosts, residue- and site-specific installation techniques show significant potential for producing novel ampicillin-producing microbes and can help combat the ongoing rise of antibiotic resistance in pathogens. Desirable enhancements include pH and protease resistance, solubility, oral availability, and circulatory half-life, particularly from a pharmacological perspective [22]. To overcome natural constraints like poor yield and the requirement for increased potency or stability, which is essential for their development as therapeutic agents, emphasize the significance of synthetic manufacturing.
It is crucial to examine the ways in which AMPs differ from traditional antibiotics in their ability to combat pathogens [23]. Electrostatic interactions enable AMPs to predominantly target microbial membrane. According to research, the primary mechanism by which AMPs cause membrane disruption and intracellular chemical release leads to microbial cell death [24] (Figure 1). AMPs do, however, also display additional mechanisms, including the inhibition of DNA, RNA, protein, and cell wall synthesis, as well as the induction of immunomodulatory effects that strengthen host defenses (Figure 1). Their broad-spectrum activity is enhanced by their complex mode of action, which also lessens the chance that infections may evolve resistance [25]. In order to highlight the adaptability of AMPs as antimicrobial agents, we utilize this section to draw connections between their structural diversity and modes of action [26].
Finally, we address the broad-spectrum activity of AMPs and their therapeutic implications by synthesizing the material from the preceding sections. AMPs' diversity and distinct modes of action make them effective weapons against a variety of pathogens, such as bacteria, viruses, fungi, and cancer cells that are resistant to antibiotics [27]. It is important to consider how AMPs might be able to close important gaps in antimicrobial therapy, especially when it comes to treating infections that are resistant to traditional therapies [28]. Moreover, we emphasize the need for continued research to maximize AMPs' potency, minimize toxicity, and improve delivery techniques to fully realize their therapeutic promise.
The antibacterial effect of antimicrobial peptides is reflected in three aspects. First, they can directly kill microbes and act on microbial membranes through electrostatic interactions, leading to membrane rupture and cell death. Second, they can resist other mechanisms of pathogens, including inhibiting the synthesis of DNA, RNA, proteins, and cell walls. Third, they can induce immune regulatory effects and enhance host defense.
3.
Latest progress in antimicrobial peptides
LL-37 is a peptide consisting of 37 amino acid residues, with the sequence LLGDFFRKSKEKIGKEFKRIVQRKDFLRNLVPRTES. This peptide exhibits broad-spectrum antibacterial, immune regulatory, and wound healing promoting functions through optimized strategies of antibacterial and immune regulation. Its mechanism of action includes the destruction of bacterial membranes, regulation of inflammatory responses, interference with viral infections, and regulation of immune cell function. The sequence of LP21 is C8H15O Trp Lys Lys Lys Leu Leu Lys Trp Trp Leu Lys Lys Phe Lys Leu Asp. This peptide has improved its antibacterial effect through an optimized strategy for the preparation of antimicrobial lipopeptides. However, its specific mechanism of action is not clear. Amanitin is a cationic linear alpha helical antimicrobial peptide composed of 31 to 39 amino acid residues. Through molecular design, its expression level and stability have been improved to adapt to large-scale production. This design has significantly improved the expression level and stability of sericin. Defensins contain 45 to 54 amino acid residues and have a cysteine (Cys) stable alpha beta motif. Its functional improvements include antibacterial, anti-tumor, enzyme activity inhibition, acting as an ion blocker, and increasing tolerance. Its mechanism of action is mainly through electrostatic attraction and binding with bacterial cell membranes, forming pore structures on the surface of the cell membrane, and physical perforation leading to the leakage of bacterial intracellular contents, thereby killing bacteria. Cathelicidins are a diverse class of peptides, taking cathelicidin BF, which contains 30 amino acid residues, as an example. Its sequence is KFFRKLKKKSVKKRAKEFFKPRVIGVSIPF. These peptides not only have antibacterial activity, but also promote wound healing, induce angiogenesis, induce apoptosis of mutant cell lines, and activate lymphocytes. Their mechanisms of action include chemotaxis towards immune cells, induction of mast cell degranulation, and histamine release. Hepcidins are peptides composed of 25 amino acids and contain four disulfide bonds. Its functional improvement mainly lies in regulating iron homeostasis and antibacterial properties. The mechanism of action includes controlling the release and absorption of iron by binding and inactivating ferroportin, as well as increasing production under inflammatory conditions, reducing serum iron levels, and limiting the pathogen's use of the host's iron reserves for growth. Piscidins are a class of histidine rich antimicrobial peptides, the specific sequence of which is not provided. They exhibit antibacterial activity, with mechanisms of action including interaction between amphiphilic alpha helices and lipid bilayers, as well as activity at acidic and alkaline pH values in vivo, making them promising templates for biomedical applications. The sequence of Pexiganan is GIGKFLKKAKKFGKAFVKILKK-NH2. As a synthetic analogue of magainin 2, it exhibits potent and orally active broad-spectrum antibacterial properties. Its mechanism of action includes killing bacteria by disrupting cell membranes or forming channels, as well as synergistic effects with beta lactam antibiotics, which are especially important in the treatment of endotoxic shock. The sequence of Magains is GIGKFLHSAKKFGKAFVGEIMNS, which has broad-spectrum antibacterial activity and inhibitory effects on both Gram positive and Gram negative bacteria, fungi, and protozoa. Its mechanism of action includes exerting cytotoxic effects by preferentially interacting with abundant anionic phospholipids in bacterial membranes, as well as isolation from Xenopus laevis skin, representing a previously unrecognized class of vertebrate antibacterial activity. The Magains sequence is: GIGKFLHGKAFVGEIMNS. Functional improvement: Broad spectrum antibacterial activity, inhibition of Gram positive and Gram negative bacteria, fungi, and protozoa. The mechanism of action is: 1. By specifically interacting with anionic phospholipids on bacterial membranes, it produces cytotoxic effects; 2. It was isolated from the skin of African clawed frogs and represents previously unrecognized vertebrate antibacterial activity. The KR-2-3 sequence is: KRIVKWIKKFLR. Functional improvement: Inhibit tumor cell proliferation. The mechanism of action is: inhibition of biofilm formation and anti-inflammatory effects are associated with low expression of related genes. The Cecropin B sequence is: KWKLFKKIEKVNIRDGLIKVGPAVAVVGQATQIAK. The optimization strategy is to improve the expression level and purity by integrating expression and SUMO tags. For instance, functional improvement enhances antibacterial activity, especially against gram negative bacteria mechanisms of action; and the formation of an alpha helix structure disrupts bacterial cell membrane integrity, leading to leakage of cellular contents (Table 1).
4.
Design and optimization of AMPs
Understanding the basic principles that control antimicrobial peptides' antimicrobial activity and therapeutic potential is essential for their strategic design [39]. The equilibrium between hydrophobicity and charge is essential to these tactics because it promotes contact with microbial membranes while reducing toxicity to mammalian cells [40]. Sequence analysis and structure-activity association studies are used by researchers to pinpoint important motifs and amino acid compositions that are predictive of effectiveness. For example, adding particular amino acids can improve the peptide's antimicrobial activity by strengthening its capacity to damage bacterial membranes [41]. The manufacture of peptide analogs, in which natural AMPs sequences are altered to enhance medicinal qualities, complements this strategy [18]. In order to guarantee that AMPs continue to be a viable choice against emerging microbial threats, these efforts seek to both increase antimicrobial action and limit potential resistance [42].
In order to identify and optimize peptide sequences with desirable properties prior to synthesis and testing, bioinformatics and computer modeling have become essential tools in the AMPs design process [43]. With the use of algorithms, these computational methods examine enormous databases of artificial and natural AMPs to find patterns and characteristics linked to low toxicity and potent antibacterial action. By forecasting novel peptide sequences' activity based on their physicochemical characteristics, machine learning techniques help to further focus the search for viable candidates [44]. AMPs and microbial membranes interact, and molecular dynamics simulations shed light on the mechanisms underpinning AMPs' effectiveness and selectivity [45]. In the pursuit of strong antimicrobials, researchers can save time and money by streamlining the development process and concentrating on peptides with the greatest therapeutic potential by utilizing these technologies. A comprehensive strategy is used to optimize AMPs in order to improve their stability, specificity, and efficacy—all important aspects that dictate whether or not they may be used as a treatment. In the protease-rich environment of the human body, cyclization, the addition of D-amino acids, and the usage of peptidomimetics—which resemble peptides in structure and function but are more resistant to degradation—are some of the tactics that can be used to increase peptide stability [46]. Precise peptide sequence alteration and the investigation of tailored delivery mechanisms are required to increase specificity towards microbial targets and decrease cytotoxicity towards mammalian cells [47]. AMPs can be targeted to particular pathogens using strategies like lipidation or conjugation with targeting moieties, which maximizes effectiveness and reduces off-target effects. A complete understanding of the molecular interactions between AMPs and their targets serves as the foundation for these optimization efforts, guaranteeing that the resulting therapeutic medicines are both safe and efficacious for use in clinical settings [48]. In optimizing AMP, the toxicity-activity balance should be given priority rather than increasing antimicrobial activity and limiting potential resistance. The optimization efficiency can be greatly improved by predicting the optimal sequence through machine learning combined with experimental verification.
The development of AMPs is a complex process. During the development of antimicrobial peptides, sequence design principles are crucial, especially balancing hydrophobicity [49] and charge. Antimicrobial peptides typically need to be amphiphilic, meaning they should contain a combination of hydrophobic and hydrophilic (charged) residues. This structural feature helps antimicrobial peptides attach to the negatively charged bacterial cell surface through electrostatic interactions and interact with the lipid part of the cell membrane through hydrophobic interactions. Hydrophobicity and amphiphilicity are very key to antimicrobial activity. Maintaining a certain level of hydrophobicity and a stable amphiphilic structure is conducive to playing its activity and selectivity. Overly strong hydrophobicity may cause self-aggregation of antimicrobial peptides, reducing their solubility and antimicrobial activity. Charge control: Appropriately increasing the positive charge number of antimicrobial peptides can improve their antimicrobial activity [50]. Antimicrobial peptides are usually cationic at neutral pH, with a positive charge, which attaches to the negatively charged bacterial cell surface through electrostatic interactions. A charge control within+3 to+4 or-9 is more appropriate, which helps balance the charge, and the length can be appropriately extended, with effects being more ideal within 10 to 30 amino acids. Researchers looking at the relationship between structure and function found that there are at least seven physicochemical factors affecting the activity and specificity of amphiphilic α-helical antimicrobial peptides, namely size, sequence, charge, helicity, hydrophobicity [51], amphiphilicity, and the angle between hydrophilic and hydrophobic faces. Through these design principles, we can optimize the structure of antimicrobial peptides to improve their antimicrobial activity and selectivity while reducing toxicity to host cells.
The testing process for the development of antimicrobial peptides, particularly for verifying membrane activity through in vitro and in vivo experiments, typically includes the following steps: Extract and purify the antimicrobial peptide samples and determine their concentration. Communicate with the testing institution to clarify the purpose, requirements, and standards of the testing. Package and label the prepared samples according to the requirements of the testing institution and then send them to the testing facility. Upon receiving the samples, the testing institution will register and conduct a preliminary check to ensure that the samples meet the testing requirements. Antimicrobial Activity Determination: Determine the inhibitory effect of the antimicrobial peptides on specific bacteria using methods such as agar diffusion [52] and microbroth dilution [53]. Determine the purity of the antimicrobial peptides using high-performance liquid chromatography (HPLC) [54], mass spectrometry (MS) [55], and other methods. Determine the molecular weight of the antimicrobial peptides using mass spectrometry or other methods. In Vitro Tests: Use simulated cell membrane chromatography, based on the characteristic that antimicrobial peptides preferentially act on specific phospholipids in the cell membrane, to continuously separate antimicrobial peptides. Additionally, PI staining can be used to observe the impact of antimicrobial peptides on bacterial cell membrane permeability. In Vivo Tests: Conduct animal experiments to study the distribution and metabolism of antimicrobial peptides in the body. After the testing is completed, the testing personnel will analyze the data and prepare a test report. The report should include the testing methods, results, and conclusions. The testing institution will send the test report to the sample provider, explain the results, and answer any related questions. These steps form the basic framework of the testing process in the development of antimicrobial peptides, ensuring their efficacy and safety.
PLGA Nanoparticle Delivery System [56]: Antimicrobial peptides 1-21 and 1-21-1c, derived from esculentin-1 found in frog skin, are encapsulated in poly(lactic-co-glycolic acid)(PLGA) [57] nanoparticles and coated with polyvinyl alcohol(PVA) [58], effectively inhibiting the growth of Pseudomonas aeruginosa (P. aeruginosa) [59] by about 60% for up to 72 hours. PVA adsorbed on the surface of PLGA reduces the adhesion of PLGA to airway mucus. In a mouse model of acute lung infection caused by P. aeruginosa, 1-21-PLGA and 1-21-1c-PLGA conjugates showed stronger antibacterial activity than the control group, approximately 17 times and 4 times, respectively. Biomimetic Magnetic Nanoparticles (BMNPs) [60] and PLGA Nanoassemblies [61]: Antimicrobial peptide AS-48 is combined with BMNPs and PLGA to form PLGA[AS-48-BMNPs] nanoassemblies. PLGA is used to enhance the internalization of BMNPs due to their biocompatibility and biodegradability. Experiments showed that 78% of PLGA[AS-48-BMNPs] were successfully internalized by THP-1 cells within 72 hours. Additionally, the release of AS-48 from the nanoassemblies reached about 45% at 37 °C and pH 7.4, slower than previous nanoformulations. This formulation promoted an 80% increase in THP-1 cell activity compared to the control group and improved the uptake of AS-48 in infected macrophages, reducing cytotoxicity and increasing activity.
These cases demonstrate the potential of antimicrobial peptide delivery systems in enhancing antibacterial effects, reducing cytotoxicity, and increasing bioavailability. Through these advanced delivery systems, antimicrobial peptides can be more effectively applied in clinical treatments.
5.
Challenges in AMP development
A major obstacle in the creation of AMPs is making sure they are selectively poisonous to infections while causing the least amount of damage to host cells [62]. A careful balance is required to prevent harming mammalian cell membranes due to the AMPs' intrinsic method of disrupting cell membranes [63]. Researchers are looking at ways to lower hemolytic activity without sacrificing the effectiveness of antibiotics, such as changing the amino acid sequences [62]. Moreover, another major obstacle is the stability of AMPs under physiological settings. Proteases and other degradative enzymes found in the human body can quickly break down AMPs, reducing their effectiveness. The goal of increasing stability is causing researchers to investigate several methods such as peptidomimetics, adding non-natural amino acids, and protected delivery systems to prolong the half-life of AMPs in vivo while maintaining their therapeutic effects.
Although AMPs are praised for having a lower tendency to cause resistance than conventional antibiotics, it is important to remember that organisms can develop resistance mechanisms [63]. Widespread usage of AMPs may hasten the evolution of resistant strains, particularly in non-medical applications like agriculture. In order to mitigate this, we endeavor to comprehend the molecular underpinnings of plausible resistance strategies, such as alterations in the composition of microbial membranes that diminish AMPs binding or the synthesis of proteases that hydrolyze AMPs. To ensure long-term efficacy, next-generation AMPs are designed with this understanding in mind, circumventing these resistance tactics. Combination treatments using AMPs and additional antimicrobials are also being researched to target bacteria more effectively and lessen the chance that resistance would emerge [64].
A further barrier to the translation of promising laboratory results from AMPs into commercially accessible medicinal treatments is the financial and technological difficulties associated with large-scale manufacture. It can be prohibitively expensive to synthesize AMPs, particularly for those with intricate modifications for improved stability and decreased toxicity, which limits their availability and economic viability [65]. Furthermore, complex production procedures and quality control measures are needed to guarantee the consistency and purity of synthesized AMPs on a wide scale, which drives up expenses even more [66]. To get around these obstacles, researchers are looking at more effective synthetic techniques, recombinant DNA technologies for producing AMPs in yeast or bacterial systems, and creative formulation techniques to increase the affordability of AMPs treatments. It is imperative to tackle the economic and technical obstacles to render AMPs-based treatments a viable alternative in the fight against the worldwide menace of antibiotic-resistant diseases.
6.
Delivery systems for AMPs
Antimicrobial peptides (AMPs) have antibacterial properties, but they are effective therapeutic agents only if they are delivered to the infection site in an efficient and controlled manner Since they have a direct impact on the pharmacokinetics, bioavailability, and therapeutic indices of these compounds, efficient delivery mechanisms are essential for the therapeutic application of AMPs [67]. By preventing enzymatic breakdown and early bodily clearance, an optimal delivery mechanism guarantees that AMPs reach the target location in an active state and at therapeutic concentrations [68]–[70]. Additionally, by reducing off-target effects, targeted delivery methods can reduce possible toxicity and improve the safety profile of AMP based medicines [69]. Additionally, these systems provide the option of controlled release, which permits prolonged antimicrobial activity. This is especially advantageous for treating persistent infections or preventing the formation of biofilms [71]. To overcome the drawbacks of AMPs and turn them into effective clinical treatments, research on the creation of innovative delivery systems is essential (Figure 2).
Hydrogels and nanoparticle carriers are two novel AMP delivery methods made possible by developments in nanotechnology. For the administration of AMPs, nanoparticles such as liposomes, metallic nanoparticles, and polymeric nanoparticles have been thoroughly investigated [72] (Figure 2). By encapsulating AMPs and shielding them from degradation and facilitating targeted distribution to infection sites, these nanocarriers can boost the effectiveness of AMPs and lessen their systemic toxicity [73]. With promising qualities including controlled release, protection of the drug against cleavage and degradation, and the ability to distribute drug molecules to specific areas when using targeted delivery methods, nanocarriers provide a wonderful approach to drug delivery (Figure 2). One of the most promising drug delivery systems is the noisome, which is an aqueous phase containing cholesterol and nonionic surfactants that self-assemble to form a bilayer structure. Noisome are immunogenic, biocompatible, and biodegradable. They are highly stable, have a long shelf life, and enable regulated and/or continuous drug delivery at the target site [74]. Hydrogels, which are made of hydrophilic polymers, offer an additional intriguing avenue for AMP delivery. The stability and activity of AMPs are maintained by their highly hydrated environment, and the controlled release of encapsulated peptides is made possible by their adjustable features (Figure 2). Moreover, further cutting-edge delivery techniques include microneedles [75] and bio adhesive films, which are investigated for particular uses such topical therapies and infections of the mucosa, thus increasing the adaptability of AMP therapies (Figure 2).
Several case studies demonstrate how sophisticated delivery methods may improve the medicinal effectiveness of AMPs. For example, liposomal delivery of the AMPs LL-37 has demonstrated enhanced efficacy and decreased toxicity compared to free peptide treatment in preclinical models of skin infection [76],[77]. Another illustration is the application of polymeric nanoparticles to administer the antibiotic colistin, an AMP, against bacteria resistant to multiple drugs, which led to better treatment outcomes in a lung infection model in mice in September 2021 [78],[79]. Furthermore, regulated release of AMPs greatly sped tissue repair and decreased the microbial burden in wound healing applications where hydrogel-based AMPs delivery has been successfully studied [80],[81]. These case studies demonstrate the viability of using cutting-edge AMP delivery devices and represent a major advancement towards their clinical translation, providing fresh hope in the fight against diseases resistant to antibiotics [82].
Investigating efficient AMP delivery methods is a vibrant and quickly developing topic that tackles important antimicrobial therapy issues [83]. These cutting-edge delivery techniques hold the key to releasing AMPs' full therapeutic potential and bringing in a new era in the treatment of infectious diseases by preserving stability and improving the targeting of AMPs.
To address the limitations of AMPs and transform them into efficacious clinical interventions, inventive delivery system development research is crucial. Recent advancements in nanotechnology have enabled the creation of two unique techniques for delivering ampicillin: Hydrogels and nanoparticle carriers. Through encapsulation, these nanocarriers can protect AMPs from degradation and enable tailored delivery to infection sites, thereby increasing AMP efficacy and reducing systemic toxicity. Hydrogels, which are made of hydrophilic polymers, offer an additional intriguing avenue for AMP delivery. The stability and activity of AMPs are maintained by their highly hydrated environment, and the controlled release of encapsulated peptides is made possible by their adjustable features. To further increase the adaptability of AMPs therapies, further cutting-edge delivery techniques, such as microneedles and bio adhesive films, are investigated for uses such as topical treatments and mucosal infections.
7.
AMPs in combination therapies
One possible tactic to address the growing problem of antibiotic resistance is the incorporation of AMPs into combination therapy with conventional antibiotics [84]–[86]. By utilizing antimicrobial compounds, this strategy may restore the efficacy of medications that have been ineffective against resistant strains of bacteria [87].
Because of their wide range of action and unique modes of action compared to conventional antibiotics, AMPs are great choices for combination therapy [88]. Because of their capacity to damage bacterial cell membranes, they can make germs more susceptible to the effects of other antibiotics, increasing their overall antimicrobial effect [89],[90]. A second method that these peptides can improve the effects of conventional drugs is by strengthening the host's immunological response to infection through the immunomodulatory properties of particular AMPs [91]. Combination therapy incorporating antibiotics and AMPs can decrease the chance of resistance development by attacking many pathways at once, providing a more sustainable method of treating infections [92].
Numerous studies have shown that AMPs and other antimicrobial drugs have synergistic interactions that boost bactericidal effectiveness and reduce resistance rates. For example, studies have demonstrated that specific AMPs can overcome resistance mechanisms in bacteria that normally inactivate beta-lactam antibiotics when coupled with them [93],[94]. Likewise, it has been discovered that AMPs work with aminoglycosides, fluoroquinolones, and non-antibiotic substances like silver nanoparticles to enhance therapy results in infection models [95]. These synergies not only increase the effectiveness of treatment but also make it possible to employ antibiotics at lower dosages, which may lessen the side effects of high-dose antibiotic therapy [96].
The amount of scientific and clinical data showing that AMPs can be used in combination therapy is increasing. Preclinical research has produced encouraging findings, with AMPs-antibiotic combos outperforming monotherapy in terms of their ability to eradicate biofilms and chronic infections. For instance, in a mouse model of cutaneous infection, the combination of the AMPs LL-37 with vancomycin shown increased effectiveness against methicillin-resistant Staphylococcus aureus (MRSA). Additionally, clinical trials are being conducted to assess the efficacy and safety of these combination medicines in human subjects [97]. These investigations are essential for figuring out the best dosage schedules, evaluating possible adverse effects, and verifying the medicinal benefit of AMPs-antibiotic combos over conventional therapies [98].
Utilizing the special qualities of AMPs to increase the effectiveness of conventional antibiotics and other antimicrobial drugs, the strategic use of AMPs in combination therapies is a progressive approach to antimicrobial treatment [99]. It is envisaged that as this field of study develops, novel treatments will offer a potent weapon in the worldwide battle against illnesses resistant to antibiotics, improving patient outcomes and preserving the supply of already available antimicrobial medications.
8.
Regulatory and safety considerations
Antimicrobial peptides (AMPs) have a complicated journey from the lab bench to the patient's bedside, one that is controlled by strict regulatory frameworks intended to guarantee the efficacy and safety of these cutting-edge therapeutic medicines. Researchers and developers must comprehend the regulatory process for AMPs to successfully navigate preclinical studies, clinical trials, and market approval. A number of distinct steps make up the regulatory pathway for AMPs, starting with comprehensive preclinical testing to assess the compounds' pharmacological profile, toxicity, and effectiveness in vitro and in animal models. These investigations are essential for providing a foundation for human trials and for obtaining regulatory agency approval—from the European Medicines Agency (EMA) or the U.S. Food and Drug Administration (FDA)—to move forward with clinical trials. After that, AMPs are clinically developed in three stages: Phase I addresses safety and dosage; Phase II assesses efficacy and side effects; and Phase III contrasts the AMPs with recommended treatments and further evaluates safety and efficacy. Only AMPs that have a positive safety and efficacy profile are allowed to advance to the next stage of research, thanks to stringent review and approval procedures that apply to each phase [100].
Phase I trials, which primarily evaluate the AMPs' safety and pharmacokinetics in a small group of healthy volunteers or patients, are the first step in the clinical development of AMPs [101]. To identify possible side effects and establishing safe dosage ranges, these preliminary trials are essential. Phase II trials widen the focus to include the AMPs' preliminary efficacy against specific conditions while evaluating safety in a larger patient sample [102]. Phase III trials are intended to provide a comprehensive assessment of the safety and efficacy of the AMPs, often in comparison with traditional medicines and often involve a larger patient group. Strict monitoring and adverse effect reporting are maintained during these phases to ensure patient safety. The final step in a successful clinical study is submitting the New Drug Application (NDA) or Biologics License Application (BLA) to regulatory agencies to request permission for commercial usage [103].
Important ethical issues that are representative of the broader difficulties in the study and development of antibiotics are brought up by the synthesis and use of AMPs in therapeutic settings. It is imperative to balance any possible risks to patients with the potential benefits of AMPs, particularly in early-stage trials. Informed consent, which requires full disclosure of all benefits and drawbacks to study participants, is a fundamental element of ethical clinical research. To ensure that their use does not inadvertently contribute to the global increase of resistant diseases [104], antibiotic resistance must also be considered when developing AMPs [105]. Ethical research methodologies also address concerns regarding the availability of these potentially life-saving therapies to all global population segments, regardless of socioeconomic background, by covering the equitable distribution and accessibility of authorized AMPs.
Navigating the legal and ethical landscape is a critical part of producing AMPs, requiring a commitment to rigorous scientific analysis, patient safety, and ethical integrity. By adhering to these recommendations, AMP development can proceed in a way that maximizes its therapeutic potential and safeguards the general welfare of patients and society.
9.
Future directions
AMP research and development are at a critical juncture, offering new hope for infectious disease treatment as the world healthcare landscape struggles with the growing problem of antibiotic resistance [106],[107]. Innovation in AMP research is being driven by emerging trends, which include improving efficacy, reducing toxicity, and addressing resistance-related obstacles [108]. Novel AMPs with optimum features can now be designed because to biotechnology advancements in synthetic biology and nanotechnology, among other areas [109]. Furthermore, the range of antimicrobial drugs that are available is being expanded by the investigation of AMPs obtained from natural sources [110]. These patterns emphasize how AMP research is dynamic and always changing and they show how it has the potential to produce ground-breaking treatments for infectious diseases [111].
AMPs have enormous potential to address global health issues, especially considering the ongoing fight against bacteria that are resistant to antibiotics. The distinct modes of action displayed by AMPs provide a workable substitute, since these resistant bacteria reduce the effectiveness of conventional antibiotics [112]. Their capacity to alter immunological responses and damage bacterial membranes offers a chance to create medications that go by established resistance mechanisms [113]. Additionally, AMPs' broad-spectrum activity against a variety of pathogens, such as bacteria, viruses, and fungi, makes them excellent choices for treating newly emerging infectious diseases [114]. The international medical community understands the role that AMPs play in the broader context of antimicrobial stewardship, which aims to maintain the efficacy of antimicrobial medicines and guarantee a sustained defense against infectious threats.
Innovation and interdisciplinary cooperation are required for the introduction of AMP treatments into clinical practice [115]. It is difficult to create AMP-based therapies that are safe, efficient, and widely available; therefore, knowledge from clinical medicine, chemistry, microbiology, pharmacology, and materials science must be integrated [116]. To effectively negotiate the regulatory framework, acquire financing, and enable the translation of research findings into practical health solutions, collaboration is crucial amongst researchers, physicians, industry stakeholders, and policymakers. Moreover, worldwide collaboration and public-private partnerships can quicken the rate of invention and guarantee that developments in AMP research are used to address pressing public health issues [117]. Our view is that the development of an efficient AMP optimization strategy requires interdisciplinary collaboration, integrating bioinformatics, materials science, and pharmacology. The interdisciplinary character of AMPs development underscores the significance of cultivating surroundings that promote cooperation, ingenuity, and information exchange, propelling the possibilities of AMPs to transform the management of infectious illnesses. The potential of these peptides for science and medicine is highlighted, but so is the collaborative culture needed to fully realize their potential in the field of AMPs research and development [118]. This combination of creativity, teamwork, and dedication to solving global health issues will steer the development of AMPs from the lab to the clinic as the field develops, providing fresh hope in the battle against antibiotic-resistant illnesses.
The first strategy for bioavailability-enhancing or cost-optimized production of specific peptides is terminal modifications: N-terminal acetylation and C-terminal amidation are common terminal modifications to improve the stability of antimicrobial peptide proteases. C-terminal amidation can block the C-terminal carboxyl group of the parental peptide and increase the total charge of the peptide, thereby improving the antimicrobial activity. The second strategy is cyclization: Cyclization is an effective way to improve the stability of antimicrobial peptide proteases. Stabilizing the conformationally restricted structure by cyclization can make the packing of amino acid side chains more tightly and slow the cleavage of proteases. The third strategy is nanotechnology application: Using nanotechnology, antimicrobial peptides can self-assemble into different nanostructures, such as micelles, nanofibers, and twisted bands, which affect the antimicrobial activity of peptide amphiphiles. Micelles have stronger antimicrobial abilities than nanofibers and twisted bands because their disintegrated monomers can insert into the bacterial membrane, causing leakage of the inner and outer membranes of the bacteria. The fourth strategy is pH-responsive nanocarriers: The development of pH-responsive nanocarriers can change the nanostructure according to changes in pH, thereby improving antimicrobial efficiency in specific pH regions. For example, cylindrical nanostructures do not have antimicrobial activity at pH 7, but are converted into micelles at pH 5 and have strong antimicrobial activity against bacteria [117]. These strategies demonstrate the potential to improve the bioavailability of antimicrobial peptides and reduce production costs through chemical modification, nanotechnology, and other methods.
10.
The application of AI in AMP development
In the development of AMPs, the application of artificial intelligence technology is receiving increasing attention. In recent years, artificial intelligence has been applied to the design and optimization of AMPs. Artificial intelligence can analyze and predict various physicochemical parameters such as the antibacterial activity, protease resistance stability, cytotoxicity, and hemolytic activity of AMPs. By analyzing multidimensional parameters such as net charge content, peptide length, amino acid composition, hydrophobicity, and structural orientation, artificial intelligence can accurately and effectively discover new AMPs from a massive potential peptide sequence, accelerating the development process. For example, artificial intelligence technology screens AMPs mainly based on the physicochemical properties of AMPs and non-AMPs in the training dataset, forming a unique discrimination system. Through training on different feature datasets, the model is continuously optimized and improved, and can be used to predict and screen sequences of active AMPs [119].
AI can also predict the antibacterial activity of AMPs; for example, researchers from Stanford University and McMaster University used AI models to design molecules that inhibit the growth of Acinetobacter baumannii, a common drug-resistant bacterium. They synthesized and validated six structurally novel molecules that exhibit antibacterial activity against A. baumannii and other systemically diverse bacterial pathogens in March 2024. In the past two decades, many researchers have discussed the application of artificial intelligence (AI) in the search and design of antimicrobial peptides (AMPs). By using sequence-based features, machine learning (ML) algorithms can discover new peptide scaffolds with good biological activity. To optimize/design AMP, from the perspective of artificial intelligence, evolutionary algorithms are also used to generate peptide libraries rationally. Evolutionary algorithm for generating diversity-oriented peptide libraries and optimizing hit peptides [120].
Researchers at the Max Planck Institute for Land Microbiology in Germany developed a new method for rapidly developing bioactive peptides using deep learning and cell-free protein synthesis (CFPS) techniques. Researchers have developed an algorithm that can generate high potential antimicrobial peptide sequences based on a rich natural protein library. After screening and testing, 30 functional AMPs were identified in November 2023. In vitro, studies have shown that six AMPs exhibit strong antibacterial activity against multiple drug-resistant pathogens, while displaying extremely low resistance and human cytotoxicity [121].
To address emerging drug resistance, the diverse peptide field is the best source of clinically available new AMPs. However, discovering that the new AMP is both complex and expensive is a major issue. The difficulty of identifying antimicrobial peptides from random peptides using discriminative models has increased, but the latest research in artificial intelligence has improved the efficiency of identifying antimicrobial peptides from large libraries. This study successfully screened 12 AMPs from 30000 random peptide libraries using three multi discriminator models. Three potential peptides (P2, P11, and P12) were selected for antibacterial experiments. Further research has shown that these peptides not only possess strong antibacterial activity, but also have extremely low hemolytic activity. Mechanistic studies have shown that these peptides disrupt cell membranes, thereby reducing bacterial resistance. These findings indicate that deep learning based multi discriminator models can identify AMPs from random peptides with potential clinical applications.
Incorporating artificial intelligence for antimicrobial peptide design or synergistic effects of antimicrobial peptides with existing antibiotics is an active area of research in the future. For example, IBM's scientific team has developed an artificial intelligence algorithm that automatically generates antimicrobial peptides, and based on this algorithm, two novel highly active antimicrobial peptides have been designed. The algorithm uses an auto-encoder (VAE) based on variational inference to learn the “chemical space” of the peptide and obtain new highly active antimicrobial peptides through a classifier and hypothesis-reject sampling. Another study showed that novel antimicrobial peptides designed by artificial intelligence could synergistically enhance the effects of aminoglycosides on anticolistin and carbapenem-resistant A. baumannii. The peptide AIG-R5 is effective against drug-resistant strains of A. baumannii, preventing biofilm formation and exhibits synergistic activity with tobramycin. These advances show the potential of AI in antimicrobial peptide design and discovery.
11.
Conclusions
In the fierce fight against antibiotic resistance, the emerging science of AMPs offers promise, underscoring a pivotal shift in our approach to infectious disease management. A century's worth of medical progress is in jeopardy due to a worldwide health problem that AMPs appear to be a promising answer to their distinct modes of action, broad-spectrum activity, and decreased tendency to induce resistance. However, reaching their full potential will require a steadfast dedication to thorough clinical evaluation, careful development, and rigorous research. We have summarized some of the latest research on antimicrobial peptides in tabular form, providing a clearer understanding of the development of antimicrobial peptides. Knowing that antimicrobial peptides are constantly evolving and will need to be explored in the future, more assistance and solutions are needed to overcome more obstacles. There are several scientific, legal, and practical obstacles in the way from bench to bedside that necessitate interdisciplinary cooperation. AMPs herald a future in which innovation, supported by interdisciplinary synergy and persistent investment, opens the way for novel treatments as we stand on the threshold of a new age in antimicrobial medicine. This paradigm change portends the arrival of a more robust healthcare environment in addition to offering the possibility of overcoming present constraints, poised to combat the ever-evolving threat of infectious diseases. To address these barriers, researchers should prioritize the development of AMP engineering techniques that enhance stability and reduce toxicity without compromising efficacy. Additionally, advanced delivery systems, such as nanoparticle-based carriers, warrant further exploration to improve targeted delivery and sustained activity in vivo. Finally, we recommend fostering interdisciplinary collaboration and increasing funding support to bridge the gap between AMP research and clinical application, ensuring these promising molecules can be effectively translated into real-world therapies. Moreover, we suggest combining artificial intelligence to design antimicrobial peptides or synergistic uses of antimicrobial peptides and antibiotics. Designing antimicrobial peptides using artificial intelligence algorithms or enhancing the synergistic effect between antimicrobial peptides and antibiotics is a promising research direction. Researchers should focus on the immunomodulatory effects of AMPs to explore their dual role as antimicrobial agents and immune enhancers. Additionally, the interactions between AMPs and the host microbiota need to be investigated to ensure their long-term safety and efficacy. Advances in synthetic biology and fermentation technology should be leveraged to develop scalable and cost-effective methods for AMP production. Machine learning approaches could also be utilized to optimize AMP sequences, predict antimicrobial activity, and reduce the time required for peptide development.









 DownLoad:
DownLoad:




