Citation: Daniel Calle, Duygu Yilmaz, Sebastian Cerdan, Armagan Kocer. Drug delivery from engineered organisms and nanocarriers as monitored by multimodal imaging technologies[J]. AIMS Bioengineering, 2017, 4(2): 198-222. doi: 10.3934/bioeng.2017.2.198
| [1] | Mujibullah Sheikh, Pranita S. Jirvankar . Harnessing artificial intelligence for enhanced nanoparticle design in precision oncology. AIMS Bioengineering, 2024, 11(4): 574-597. doi: 10.3934/bioeng.2024026 |
| [2] | Masaharu Somiya, Yusuke Yoshioka, Takahiro Ochiya . Drug delivery application of extracellular vesicles; insight into production, drug loading, targeting, and pharmacokinetics. AIMS Bioengineering, 2017, 4(1): 73-92. doi: 10.3934/bioeng.2017.1.73 |
| [3] | P. Mora-Raimundo, M. Manzano, M. Vallet-Regí . Nanoparticles for the treatment of osteoporosis. AIMS Bioengineering, 2017, 4(2): 259-274. doi: 10.3934/bioeng.2017.2.259 |
| [4] | Amin Shakiba, Oussama Zenasni, Maria D. Marquez, T. Randall Lee . Advanced drug delivery via self-assembled monolayer-coated nanoparticles. AIMS Bioengineering, 2017, 4(2): 275-299. doi: 10.3934/bioeng.2017.2.275 |
| [5] | Rachel Emerine, Shih-Feng Chou . Fast delivery of melatonin from electrospun blend polyvinyl alcohol and polyethylene oxide (PVA/PEO) fibers. AIMS Bioengineering, 2022, 9(2): 178-196. doi: 10.3934/bioeng.2022013 |
| [6] | Jianhao Jiang, Muhammet Ceylan, Yi Zheng, Li Yao, Ramazan Asmatulu, Shang-You Yang . Poly-ε-caprolactone electrospun nanofiber mesh as a gene delivery tool. AIMS Bioengineering, 2016, 3(4): 528-537. doi: 10.3934/bioeng.2016.4.528 |
| [7] | Dewmini Mututantri-Bastiyange, James C. L. Chow . Imaging dose of cone-beam computed tomography in nanoparticle-enhanced image-guided radiotherapy: A Monte Carlo phantom study. AIMS Bioengineering, 2020, 7(1): 1-11. doi: 10.3934/bioeng.2020001 |
| [8] | F. Philipp Seib . Silk nanoparticles—an emerging anticancer nanomedicine. AIMS Bioengineering, 2017, 4(2): 239-258. doi: 10.3934/bioeng.2017.2.239 |
| [9] | Leelakrishna Reddy, Segun Akinola . Transforming healthcare with the synergy of biotechnology and information technology. AIMS Bioengineering, 2023, 10(4): 421-439. doi: 10.3934/bioeng.2023025 |
| [10] | Ana Letícia Braz, Ifty Ahmed . Manufacturing processes for polymeric micro and nanoparticles and their biomedical applications. AIMS Bioengineering, 2017, 4(1): 46-72. doi: 10.3934/bioeng.2017.1.46 |
BLI Bioluminiscence imaging
FDG 18F-2-fluordeoxiglucose
FLI Fluorescence imaging
DOTA Tetraazacyclododecane-1, 4, 7, 10-tetraacetic acid
IGDD Image-guided drug delivery
DTPA Diethylen-diamino penta-acetic acid
Gd Gadolinium
MRI Magnetic resonance imaging
NC Nanocarrier
NIRI Near infrared imaging
PET Positron emission tomography
PLGA Poli-(lactic-co-glycolic) acid
SPECT Single photon emission tomography
SPIO Small paramagnetic iron oxide nanoparticle
USI Ultrasound imaging
While investments in drug research have increased exponentially in the last decades, the number of new medicines approved has not changed [1]. Reasons for this unfavorable outcome rely on the fact that many drug candidates, demonstrated to cure the diseases in vitro, fail to accomplish their full therapeutic potential in vivo, hampering a successful translation to the clinic [2,3,4]. In many cases, either the drug candidate results too toxic systemically [5,6,7], it is biodegraded or inactivated inadequately [9], or cannot reach the target site at sufficiently effective concentrations [10]. Moreover, the therapeutic effects of implemented therapies are often realized much later than desired, a circumstance imposing significant economic burdens for the health systems and wasting a precious time to redesign more effective therapeutic approaches for the patient [11]. Finally, therapeutic effects are frequently not the same in different subjects, suggesting that individual patient requirements must be taken into consideration to tailor treatments in a more personalized manner [12]. All these challenges may be overcome by implementing advanced drug delivery systems to carry the drug (s) specifically to the target cells or tissues and release it at the desired concentrations, decreasing undesired toxicity effects and allowing for the rapid evaluation of treatment efficacy in early stages.
Recent nanotechnological formulations and state of the art biomedical imaging technologies are endowed with excellent capabilities to overcome these limitations. Some of the first nanotechnological approaches encapsulated the drug (or drugs) in synthetic nanocarriers (NCs) constructed with solid copolymers, as poly-lactic-co-glycolic acid (PLGA) or with lipid coats, as in liposomes or micelles, for oral or intravenous administrations. This approach involved considerable biotechnological efforts to prepare the nanoparticle with appropriate antigens to overcome the biological barriers and home-in into the target tissue and to decorate it with appropriate imaging probes to allow non-invasive detection. Several excellent review articles have covered advancements in the field of biotechnology [13,14,15,16].
Image-Guided Drug Delivery (IGDD) has already reached considerable interest in recent years, and effective therapies based on this concept are implanted in the clinic. An illustrative example of this progress is provided by Conventional Transarterial Chemo-Embolization (cTACE), a technique commonly used in the treatment of hepatocellular carcinoma. Briefly, relying on X-Ray angiography, cTACE uses hepatic arterial X-ray-guided administration of one, or multiple, cytotoxic drugs formulated in a radiopaque Lipiodol-based formulation to deliver these drug (s) to the tumor. This process is followed by an embolization of the tumor feeding vessels with solid embolic agents [17].Taking advantage of the new nanotechnological developments, cTACE evolved lately, to drug-eluting beads loaded with doxorubicin (DEB)-TACE, and further optimized to treat inoperable hepatocellular carcinoma patients [18].
More recently, the combination of bacterial or viral nanocarriers with molecular biology approaches including, protein and nucleic acid engineering, have permitted to encapsulate drugs or therapeutically modified genetic materials in microorganisms. This advanced strategy allows for the selective delivery of the therapeutic cargo, encapsulated in the microorganism, to specific cells or tissues, taking advantage of the natural targeting abilities of these organisms, thus avoiding extensive and costly biotechnological maneuvers.
In this review, we shall provide a brief overview of recent progress in such drug delivery systems, focusing mainly on those originated from bioengineered organisms and biological building blocks. We complement this perspective with an outline of the most frequently used biomedical imaging methods to evaluate the fate and success of various drug delivery approaches in animal models and humans.
The bioengineered drug delivery systems discussed in this review are shown in Figure 1 and detailed below.
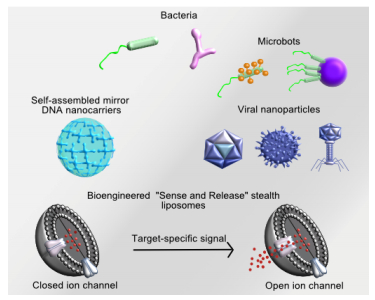 Figure 1. Schematic representation of bioengineered drug delivery systems.
Figure 1. Schematic representation of bioengineered drug delivery systems.The intrinsic properties of bacteria to sense their local environment, active migration and response to external signals make them exciting candidates for drug delivery systems. The idea of using bacteria to treat diseases originates from anecdotal cases was reported as early as two centuries ago, describing tumor regression in patients with severe bacterial infections. Recent studies, indeed, show that some strains of bacteria such as Clostridium beijerinckii, Bifidobacterium bifidum, and Salmonella typhimurium are endowed with a natural tumor targeting ability, and they specifically colonize tumor cells [19]. Upon genetic modifications, these bacteria could also secrete therapeutically active substances such as cytosine deaminase [20], tumor necrosis factor [21], herpes simplex virus thymidine kinase and colicin E3 at the tumor cells [23].
Taking advantage of the anaerobic environment in tumor tissues, Sasaki et al. proposed using nonpathogenic obligate anaerobic Bifidobacterium longum (B. longum) as a vehicle to recognize and target the solid cancer tissues selectively. In this work, the cytosine deaminase gene of Escherichia coli (E. coli) (e-CD) was inserted under the promoter region of the plasmid (pBLES100), which converts a commercially available antifungal reagent 5-fluorocytosine (5FC), to active 5-fluorouracil (5FU), a popular anticancer drug. When rats bearing autochthonous mammary tumors injected with the transfected B. longum directly or intravenously, suppression of tumor growth was demonstrated [24].
Panteli et al. explored the chemotaxis behavior of bacteria. Genetically modified tumor-targeting bacteria were engineered to sense glucose concentration and, as a response, trigger recombinant protein expression within tumors. In this study, a K-12 strain of E. coli was engineered with a hybrid receptor system, to produce a chemotaxis-osmoporin fusion protein, Trz1, to sense glucose and produce green fluorescence protein (GFP). Glucose-dependent GFP expression was observed in aqueous solution as well as in the solid tumor cell masses [25]. These results demonstrated both the capabilities of bacteria to sense metabolic activity and growth characteristics of tumors and their potential to improve cancer therapies by directly targeting viable tumor regions. In addition, the potential of bacteria to selectively colonize hypoxic areas of tumors that cannot be reached by chemotherapeutic drugs offers an exciting therapeutic opportunity. Many such cases are reaching various phases of clinical trials [26].
Flagellar bacterial cells have also been used as onboard actuators and sensors in biohybrid systems due to their high mobility, versatile sensing abilities, ease of genetic manipulations, and strong viability. In these so-called microbots, motile microorganisms, are integrated with engineered functional synthetic materials for targeted drug delivery. Akin et al. designed microbots, using an attenuated form of the intracellular bacteria Listeria monocytogene [27]. In their approach, cargo (a fluorescent or a bioluminescent gene) is loaded onto the streptavidin-coated polystyrene nanoparticles, which are conjugated to the L. monocytogene surface via biotin-streptavidin interactions. When incubated with cultivated cells, these internalized the cargo-carrying microbots. Moreover, genes released from the microbots were satisfactorily expressed in the cells. Furthermore, microbots proved to be functional also in vivo. Mice injected with microbots expressed the transported genes tagged with luciferase promoters, as revealed by the bioluminescence emitted by different organs [27].
In a recent study, Zhuang et al. attached the bacteria to the cargo. They gained control over the tactic motion of multi-bacteria propelled polystyrene bead microbots. They choose Serratia marcescens for its high mobility, sensing ambient pH, tactic behavior, and natural adhesion to defined surfaces [28]. S. marcescens cells were attached to 3 μm fluorescent polystyrene beads. Researchers showed that depending on the applied pH-gradient profile, the microrobots exhibit either unidirectional or bidirectional pH-tactic motions, which are also observed in free-swimming bacteria [29]. If the pH-sensitivity of S. marcescens can be tuned to the desired pH, these bacteria-propelled microbots could transport the cargo specifically to tumors, which intrinsically have a lower extracellular pH than the periphery of normal tissue.
Microsponges are porous spherical microparticles with an ability to entrap a broad range of active ingredients. Their pores form a continuous arrangement open to the exterior surface of particles, permitting the outward diffusion of the trapped drug molecule at a controlled rate, depending on the pore size.
Microsponge technology was first introduced for topical drug products to facilitate the controlled release of the active drug into the skin to reduce systemic exposure and minimize local cutaneous reactions to active drugs. Lee et al. engineered a self-assembled microsponge system out of RNA molecules. The delivery vehicle comprised of RNA interference (RNAi) polymers, which self-assemble into nanoscale pleated sheets of hairpin RNA, forming sponge-like microspheres consisting entirely of cleavable RNA strands. The cell's RNA machinery processes the microsponges and converts the stable hairpin RNA to siRNA only after cellular uptake. Therefore, the delivery system inherently provides protection for siRNA during delivery and transport to the cytoplasm. They also observed an improved stability of RNA and the relatively efficient encapsulation process of siRNA [30].
The ability to hold the active ingredients in a protected environment and release them in a time mode makes microsponges an attractive drug delivery system.
The natural function of viruses to deliver nucleic acids, replicate in and kill human cells inspired researchers to engineer viruses, or use viral portions, to deliver drugs and imaging reagents to appropriate target sites [31]. From the material science and engineering point of view, viral nanoparticles are very attractive nanocarriers. They have regular geometric shapes and sizes and can dynamically self-assemble in vitro. They present structural building blocks for chemical or genetic modifications and able to carry diverse type of cargo from inorganic metals to exogenous DNA to proteins. Furthermore, the cost of manufacturing is low [32,33,34].
Esfandiarie et al. took advantage of filamentous plant viruses to implement a targeted drug delivery system for breast cancer. It has been shown that due to their larger surface and more potential binding sites, filamentous plant viral nanoparticles (VNPs) have enhanced tumor homing and tissue penetration compared to isometric VNPs [35]. Esfandiarie et al. successfully conjugated potato virus X (PVX) with Herceptin (Trastuzumab) monoclonal antibody for the treatment of breast cancer cells [33]. Indeed, they could show that at two dosages of these PVX-HER nanoparticles, HER2-positive SK-OV-3, and SK-BR-3 cells were effectively killed.
Another plant virus, Cowpea mosaic virus (CPMV), was developed as a carrier of doxorubicin (DOX). CPMV-DOX viral nanoparticles, carrying eighty DOX molecules attached to its external surface carboxylates, showed greater cytotoxicity than free DOX toward HeLa cells [36]. Cell imaging data revealed that the CPMV-conjugate is targeted to the endolysosomal compartment of the cells. Here, the proteinaceous drug carrier is degraded and the drug released, inducing cell death [36].
The use of engineered virus-based capsids has been reported to deliver payloads of siRNAs to cancer cells in vitro and in vivo. In one study, virus-like particles (VLPs) were reassembled in vitro with the RNA bacteriophage MS2 coat protein and an RNA-conjugate encompassing a siRNA to target a siRNA against a known tumor target, the bcl oncogene transcript. The conjugation of human holotransferrin targeted these nanoparticles to HeLa cells. The particles entered cells via receptor-mediated endocytosis and elicited siRNA effects. These authors showed that the virus-based system was more effective than commercial cationic lipid preparations to deliver more efficiently siRNAs to cells. Indeed, this advantage can be attributed to the more efficient intracellular trafficking of the natural virus-based carrier system as compared to the artificial carrier system [37].
Choi et al. reported that the chimeric capsid protein composed of a hepatitis B virus capsid shell, p19 RNA binding protein, and integrin-binding peptide (RGD peptide), assembled into a macro container-like structure with capsid shell had the potential as an efficient siRNA nanocarrier in cell culture [38]. Later, to extend RNAi to the in vivo applications, the authors investigated the siRNA delivery efficacy of these siRNA/capsid nanocarrier complexes using mice bearing lateral B16F10/RFP tumors. When systemically administered, siRNA/capsid nanocarrier complexes delivered siRNA to tumor tissues and efficiently suppressed red fluorescent protein (RFP) gene expression in these mice. The encapsulated siRNAs are protected from nucleases in plasma by shielding effect derived from the capsid shell, which in turn enhanced the longevity of siRNA. The multivalent RGD peptides on shell surface mediated binding to integrin receptors overexpressed on tumor cells thereby showed efficient delivery of siRNA to the tumor tissues in vivo. These results present an alternative approach to the systemic delivery of siRNA to the tumor sites while enhancing the stability of siRNA in vivo [39].
Cheng et al. explored enveloped viruses as nanocarriers for different cargo molecules[34]. To combine the advantages of plant viruses and oncogenic animal viruses (Table 1), they developed alphavirus-like viral nanoparticles. These VNPs can carry various cargo and able to enter cells.
| Delivery vehicle | Advantages | Disadvantages |
| Bacterial | *Direct expression of therapeutic proteins at the target site *On-site production of therapeutic molecules *Lower therapeutic dose compared to systemic treatment *Protection of drug from biodegradation *Minimal side effects |
*Limited expression of eukaryotic proteins due to the lack of efficient posttranslational modifications *Potential risk of losing the engineered behavior and functionality in genetically modified bacteria |
| Microbots | *Steering bacteria towards a specific location inside the body via taxis *Reaching the target site at a faster rate before they are cleared away by the reticuloendothelial system |
*Dose-limiting toxicity of bacterial cells may restrict efficacy |
| Viral nanoparticles originating from: *Plant viruses *Oncolytic animal viruses *Enveloped viruses |
*Efficient internalization by animal cells, visualize tumor vasculature, targets areas of inflammation, monitor angiogenesis over time in mice [61,62,63,64]. *Cellular selectability: ability to discriminate human tumor cells from healthy cells, genetic modifications *Systemic tumor targeting *In vitro self-assembly allowing incorporation of nonviral genome and nanoparticles *Devoid of viral genome *Can target new cells *Undergo fusion *Easy surface modifications |
*The absence of envelop might necessitate surface modifications for targeting and potential immune reaction *Difficulty to load chemical or inorganic cargo, potential for introducing a modified virus into host genome *Low efficiency in introducing the core-like particles into viral glycoprotein-expressing cells |
| Microsponges | *Improved physical and chemical stability *Greater available concentrations *Controlled release of the active ingredients, *Reduced skin irritation and sensitization |
*Potential toxicity of traces of residual monomers |
| Ion channels in stealth liposomes | *High sensitivity to environmental cues *Efficient release *Biocompatible *Ability to encapsulate hydrophobic and/or hydrophilic drugs *Allowing chemical modifications to sense different environmental signals |
*Added costs of ion channel production and modification *Potential risk of immunogenicity |
DNA has received attention as an emerging material to generate drug delivery systems. Especially its biocompatibility, programmable self-assembly, and precision over the size and shape of nanostructures are very attractive [40,41,42]. Recent reviews on DNA in drug delivery can be found in Kumar et al. and Angell et al. [44]. It has been shown that the simplest three-dimensional DNA tetrahedron could pass through the cellular membrane with no additional modifications. However, the material was not stable in vivo, due to degradation by serum nucleases [45]. To address poor serum stability, Kim et al. used enantiomeric DNA, i.e. L-DNA, as their building block in place of the natural D-DNA [46]. While L-DNA can hybridize to the complementary DNA as natural D-DNA, it could be recognized much more weakly by serum nucleases than D-DNA (Hayashi). They first designed L-DNA tetrahedron nanoparticles and saw that these new vehicles have significantly higher cell penetration rates than their natural counterpart [47]. Next, they tested the in vivo stability, distribution, and efficacy of D-DNA tetrahedron carriers for in vivo tumor-targeted delivery of doxorubicin. Due to higher serum stability, enhanced intracellular uptake, systemic injection of doxorubicin-containing L-DNA tetrahedrons elicited highly improved DOX potency [46].
Liposomes are the first nanomedicine delivery systems to make the transition from the bench to the market. Liposomes consist mainly of phospholipids, which spontaneously form a lipid bilayer surrounding an aqueous core via non-covalent interactions when dispersed in water [48]. Since their discovery about five decades ago, liposomes have been widely investigated in drug delivery and imaging. A number of these have been clinically approved as nanocarriers for various diseases [49,50].
The delivery was, however, suboptimal for most nanoparticles. The slow rate of drug release from the liposomes limits their bioavailability. There are two major factors which can affect the effectiveness of the drug release: ⅰ) the sensitivity of the nanocarrier towards the stimuli, and ⅱ) the release kinetics of the drug from the nanocarrier. Therefore, stimuli-responsive liposomal drug release systems were developed to increase and control the drug concentration in the tumor. An ideal drug release system senses a target-specific signal and releases the drug at a rate that corresponds to the magnitude of the signal. Several methods based on triggered release of drugs have been described including temperature, pH, light, and ultrasound [51,52,53]. The first generation of temperature sensitive liposomes did not meet the optimal release requirements. The release rate was too slow, and the temperature at which the release occurs was too high (43-45 ℃) for clinical applications [54]. Later, more sensitive systems were developed to respond to 41 ℃. However, only 20% of the drug could be released at 37 ℃ when incubated in serum rich medium for 15 min [54], limiting the amount of the drug delivered to the tumor tissue and inducing exposure of healthy tissue to the drug. Similarly, pH-sensitive liposomes were developed to respond to the acidic pH in tumors, ranging from 5.7 to 7.1, due to an increased glycolysis, which stimulates the production of lactic acid [55]. Zhang et al. reported PEG-b-poly (L-histidine)-poly (lactic-co-glycolic acid) micelles with a size of 125 nm at pH 7.4. When incubated at pH 6, the size of the micelles increased till almost 500 nm due to the swelling and collapse of the micelle structure after protonation of the histidine units. While around 20% of the encapsulated drug was released at pH 7.4 after 72 h, 70% was released at pH 5 during the same period [56]. Despite these efforts, there is still need for drug carriers with a sensitive and efficient triggered-release. To address this challenge, our group developed "Sense and Release" (SR) liposomes. These are stealth liposomes decorated with ion channels on their surface (Figure 1). Ion channels are membrane-embedded proteins, which sense physical and chemical cues and as a response, generate transient pores in the lipid membranes. Specific ions or molecules go through these pores. To generate SR liposomes, we modified an ion channel to detect the subtle pH differences between the healthy and diseased cells [58], or to detect an external signal, such as light [59]. After embedding these ion channels in liposomes and showing the pH-or light-induced liposomal release in vitro [46], we tested pH-responsive release also in vivo using a glioblastoma mouse model. After non-invasively determining the pH-map of the tumors using ISUCA and MRSI, we injected the animals with Gd-DTPA-loaded pH-sensitive SR liposomes to evaluate the release of Gd in acidic pH. As seen in Figure 3, the engineered ion channel in liposomes could discriminate physiologically relevant minor pH changes with an unprecedented precision of 0.2 pH unit, and release the drug accordingly [60]. In parallel to efforts to develop synthetic, responsive system, the ability to engineer and fine-tune ion channels offers unique opportunities for sensing signals specific to different disease situations and releasing nanocarrier payload accordingly.
Image-guided drug delivery (IGDD) strategies implement molecular imaging methodologies to evaluate, in vivo and non-invasively, targeting and release of drugs from bioengineered organisms or NC formulations in vivo [67,68]. Additionally, IGDD methodologies may provide drug pharmacokinetics and biodistribution profiles in vivo, improving therapeutic efficacy, decreasing toxicity and helping to develop more personalized medicine approaches [69].
Several aspects merit consideration when developing IGDD approaches into successful diagnostic methods and therapies. First, a judicious choice of the optimal drug (or a combination of drugs) to interfere, stop or reverse the progression of the disease is needed [70,71,72]. Drugs that are effective, but relatively toxic upon free administration, as in oncologic or neurodegenerative therapies [73,74], are best suited for this purpose, since bioengineered organisms and nanoformulations may improve the therapeutic window considerably [75]. Second, these nanocarriers must be decorated with appropriate imaging agents that are suitable for one (or more) imaging modalities. Furthermore, the passage of the carriers through the biological barriers between the site of administration and the site of action should be optimized [14,76,77]. This may require additional surface modifications of the carriers with specific directional agents, targeting physiological or pathological transport or receptor systems of the imaged tissue (Figure 2) [78,79]. In this respect, overcoming the blood-brain barrier permeability restrictions, entail particular relevance in the treatment of neurologic disorders [79]. Finally, different therapeutic strategies may need to be implemented to fulfill individual patient needs, requiring very versatile platforms; (ⅰ) to include different drugs, engineered nucleic acids or proteins (or their combinations), (ⅱ) to adapt to available imaging modalities and (ⅲ) to incorporate adequate targeting systems depending on the biological barriers to cross and the cellular targets to reach [80]. The following sections provide an overview on these aspects.
Biomedical images are produced by the interaction between an electromagnetic radiation and the biological specimen [81]. The electromagnetic spectrum spans from the shortest wavelengths and highest energies associated with the cosmic rays to the longest wavelengths and lowest energies associated with the heating radiation (Figure 2). The γ-radiation, X-rays, ultraviolet, visible and infrared lights, micro-or radio frequency waves, lay in between these two extremes. Nuclear medicine involves the use of highly penetrating γ-or positron radiations, generating high sensitivity (10-12M) images with limited resolution (mm). Optical radiations may become very sensitive (10-15M) and resolutive, as in microscopy, but their penetration capacity within the biological specimen is limited in vivo (mm) and, only very thin objects or highly superficial processes, can be imaged. Penetration within the specimen increases from ultraviolet to near-infrared (NIR) radiations.
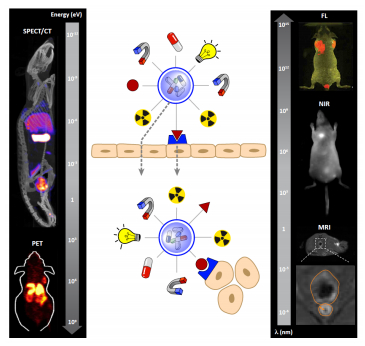 Figure 2. Overview of image-guided drug delivery. Different imaging probes active through the electromagnetic spectrum may be attached the surface of an engineered organism, biological building block, or NC. The electromagnetic spectrum is indicated by the gray arrows of ascending wavelength (right arrow, nm) or descending energy (left arrow, eV). After administration, passive targeting to the site of action may occur to overcome, at least partially, the interposed permeability barriers. Immune directed reagents to receptors or transporter molecules present in the barrier may also be attached to overcome the barrier in active targeting strategies. Finally, engineered microorganisms or synthetic NCs may include additional ligand (s) to bind selectively to specific surface receptors of the target cell or tissue. Representative SPECT (bottom left), PET (top left), fluorescent (FL, top right), near-infrared (NIR, center right) or MRI (bottom right) images of drug delivery. Adapted from [86,87,88,89,90]. Reproduced with permission of the publisher.
Figure 2. Overview of image-guided drug delivery. Different imaging probes active through the electromagnetic spectrum may be attached the surface of an engineered organism, biological building block, or NC. The electromagnetic spectrum is indicated by the gray arrows of ascending wavelength (right arrow, nm) or descending energy (left arrow, eV). After administration, passive targeting to the site of action may occur to overcome, at least partially, the interposed permeability barriers. Immune directed reagents to receptors or transporter molecules present in the barrier may also be attached to overcome the barrier in active targeting strategies. Finally, engineered microorganisms or synthetic NCs may include additional ligand (s) to bind selectively to specific surface receptors of the target cell or tissue. Representative SPECT (bottom left), PET (top left), fluorescent (FL, top right), near-infrared (NIR, center right) or MRI (bottom right) images of drug delivery. Adapted from [86,87,88,89,90]. Reproduced with permission of the publisher.Finally, ultrasound and radiofrequency imaging methods provide excellent penetration capacity and resolution (μm), at the expense of limited sensitivity (10-3M). Table 2 summarizes types, merits, and drawbacks of these imaging modalities. A more detailed description of the fundamentals of each imaging modality is not within the scope of this section, but interested readers may find adequate descriptions in the monography of ref. [82].
| Imaging techniques | Advantages | Disadvantages |
| MRI | *Excellent anatomic contrast *High spatial resolution (30-500 mm) *High penetration (whole body) *Excellent patient safety *High intrinsic contrast |
*Long acquisitions (sec-min) *Poor sensitivity (mM) *Expensive instrumentation |
| PET | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use external positron emitters *Very expensive instrumentation and probes |
| SPECT | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Long acquisitions (min) *Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use-emitters *Expensive instrumentation and probes |
| CT | *Short time acquisition *High spatial resolution (10-500 mm) *High penetration (whole body) *High intrinsic contrast between bones and soft tissues |
*Poor functional/molecular contrast *Ionizing radiation *Poor sensitivity to contrast agents (mM) |
| Ultrasound | *Short time acquisition *High patient security *High intrinsic contrast *Economic |
*Higher resolution involves lower penetration and vice versa *Poor sensitivity to contrast agent (mM) |
| Luminescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (0.2-10 mm) *Poor penetration *Without intrinsic contrast, it is necessary luminescent agents |
| Fluorescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (1-2 mm) *Poor penetration *Without intrinsic contrast, it is necessary fluorescent agents |
Imaging methodologies are a necessary, but not sufficient for IGDD. Imaging probes are equally important since they enable the detection of the decorated organism or nanocarrier by one (or more) imaging methods.
Early imaging probes were chemicals with sub-nanometric dimensions active in the different regions of the electromagnetic spectrum. Briefly, periodinated benzenes, Gadolinium chelates, and 99mTc derivatives were among the first contrast agents used in X-ray, MRI, and nuclear medicine, respectively [83,84,85].
A large variety of SPECT probes have become commercially available later to monitor non-invasively tissue perfusion [91], hypoxia [92], inflammation [93], thyroid function or even cerebral activation [95]. Their main advantage is the possibility to use relatively low-cost gamma cameras for detection and relatively long half-lives (in the hours range) SPECT emitters, while their main limitation is the reduced resolution of SPECT imaging [96,97]. The latter limitation has been overcome using PET probes, offering increased spatial and temporal resolution, at the expense of the more expensive PET equipment and the reduced half-life (in the min. range) of the positron emitters. A large array of PET probes has become available, including neurotransmitter analogs [98], antibodies against physiological or pathological receptor or transport molecules as Integrins, Cadherins, Vascular Endothelial Growth Factor and its receptors, or matrix metalloproteinases, involved in tumor invasion, metastasis, angiogenesis [99,100,101,102] and inflammation [103,104], among others.
The first generation of imaging agents for MRI, involved mainly Gd (Ⅲ) chelates, able to enhance water relaxation rates in those tissues where they accumulated [83,105,106]. Gd (Ⅲ) is used because it has seven unpaired, slow relaxing electrons, and depicts the largest magnetic moment among the rare-earth series. The ligands most frequently used are either linear, derived from diethylendiamino pentaacetic acid (DTPA), or cyclic, derived from the tetraazacyclododecane-1, 4, 7, 10-tetraacetic acid (DOTA). In all these cases, the ligand provides eight binding sites anchoring the Gd (Ⅲ) within the chelate, leaving free one the nine chelating sites of the metal, for water contact. The contact between water in the solution or tissue with the Gd (Ⅲ), and the fast exchange of this water molecule with the bulk solution reduces very significantly the relaxation times of tissue water, resulting in clearly enhanced image intensity in those regions containing the chelate [83].
Superparamagnetic iron oxide nanoparticles were among the first contrast agents with nanometric sizes proposed to increase the relaxing capacity of the paramagnetic chelates [107,108,109,110]. These nanoparticles contain a magnetite core (Fe3O4), covered most frequently by a derivatized dextran, acrylic acid polymer or even lipid coat. The particles are prepared by alkaline precipitation of mixtures of Fe3+ and Fe2+ in the presence of stabilizing agents as dextran or oleic acid. These depict improved molecular relaxivity values, as compared to paramagnetic the Gd (Ⅲ) chelates, allowing for a significant increase in the sensitivity for MRI detection. This is because the cooperative alignment of the magnetic moments from the iron ions in the superparamagnetic nanoparticles results in significantly larger magnetic moments than the additive alignment of the paramagnetic Gd (Ⅲ) moments. Superparamagnetic behavior results mainly in T2 and T2* enhancement, in contrast with the paramagnetic T1 enhancement, of the Gd (Ⅲ) chelates. However, the fact that the contrast induced by superparamagnetic nanoparticles results in a decrease in MRI signal intensity and darker image areas limited their further development.
Nuclear imaging offers a vast range of possibilities to image in vivo the fate and effects of drugs, by attaching radionuclides to nanocarriers, or biologically active molecules that are targeted to specific transport systems or receptors present in physiological or pathological tissues[67]. Single Photon Emission Computed Tomography (SPECT) and Positron Emission Tomography (PET) have been most widely used. Notably, the drug can be labeled directly with an active SPECT or PET radionuclide and, therefore, direct imaging by SPECT or PET of the subject, may reveal unambiguously if the labeled drug has reached the damaged tissue. Different approaches have been implemented to optimize the half-life of the radionuclide and the pharmacokinetics of the platform containing the drug [86]. 18F-2-deoxi-glucose (FDG) is one of the most used PET biomarkers in this category, generally used to mimic glucose transport and intracellular glucose accumulation in inflamed and tumoral tissues [111]. Similarly, 18F labeled antibodies have been commonly used to target a variety of physiological or pathological receptors or proteins [112].
In addition, the radio nucleus may be coupled to the nanocarrier surface, as it has been done to explore the capacity of encapsulated drugs to cross external barriers. Gupta et al. used sparfloxacin-loaded PLGA nanoparticles labeled with radionuclide Tc-99m as drug platform to cross eyes barriers and reach lesions inside the eye in an albino rabbit model. Using a gamma camera, they could monitor how this nanocarrier crossed the cornea and was distributed over the whole body. A similar approach was implemented by Luo et al. using a nanostructured lipid carrier coated with chitosan oligosaccharides. Möller et al. used 99mTc-DTPA to evaluate the difference between pulsating aerosols and nasal pumps, finding that pulsating aerosols can distribute better the drug in the upper airways.
Nuclear imaging has also become a robust tool in cancer diagnosis and treatment [116]. Xiao et al. developed a platform based in multifunctional unimolecular micelles made of hyperbranched amphiphilic block copolymers conjugated with cRGD peptide and NOTA which were labeled with 64Cu for PET imaging and were sensitive to pH. They could show that the NC released the anticancer drug doxorubicin in the acid microenvironment of gliomas implanted in the flank. Guo et al. also implemented multifunctional unimolecular micelles, based on a novel brush-shaped amphiphilic block copolymer, proving acidic pH-triggered release in a murine breast tumor model.
Graphene structures have also been investigated as drug nanocarriers valid for nuclear imaging drug delivery. Hong et al. have studied the efficacy of nano-graphene radiolabeled with 66Ga and antibody TRC105 in the targeting of a murine breast cancer, being a perfect platform to transport a specific drug to the tumor. Carbon nanotubes also provide valuable platforms for nuclear imaging drug delivery. Liu et al. investigated the accumulation in tumor cells of single-walled carbon nanotubes functionalized with phospholipids bearing polyethylene-glycol radiolabeled with 64Cu. They showed a high accumulation in glioblastoma cells implanted in mice, with the possible addition of the drug to the nanotube scaffold to target the tumor cells.
Visible light imaging methods depict high sensitivity (10-15 M), are low-cost and easy to use. The field applications cover rodent models, superficial imaging of larger animals or humans in vitro. Despite these advantages, optical imaging remains limited by high absorbance of tissue to visible frequencies, making this technique not very useful in the clinic. However, spectacular advances have been derived by combining optical detection with genetic engineering. This approach normally involves the coupling of a luciferase or green fluorescent protein (GFP) promoter to the transgene investigated, visualizing the co-expression of the luciferase or GFP genes through luminescence or fluorescent imaging [121,122,123].
Wang et al. investigated the pH-controlled release of a chemotherapy molecule delivered with PEGylated nanoparticles. They could follow the drug release in cancer cells (KB and HeLa cell) conjugating the nanoparticles with folic acid to target the folate receptors expressed on tumor cells, using in vitro luminescence. Yuan et al. followed the same strategy using self-assembled nanoparticles based on PEGylated conjugated polyelectrolyte with glioblastoma and breast cancer cells. These platforms were also endowed with the possibility to deliver photosensitizer agents for photodynamic therapy. Usually, drug platforms are attached to a molecule which emits light on the visible or infrared as indocyanine green or green fluorescent protein (GFP). Cool et al. [126], followed the drug release of indocyanine green contained in liposomes using ultrasound applied to the leg of a mouse.
Recent nanotechnological platforms as quantum dots have been successfully implemented in preclinical cancer models. Gao et al. encapsulated luminescent quantum dots with an amphiphilic triblock copolymer with targeting ligands and drug-delivery functionalities. By fluorescence imaging, they followed the accumulation of the quantum dots in prostate tumor cells implanted in a mouse.
Graphene structures have been investigated as drug carriers for optical image-guided drug delivery in vitro. Chen et al. developed a Fe3O4-filled carbon nanotube conjugated with quantum dots and doxorubicin to follow by fluorescence the release of the drug in cancer cells delivered by externally applied magnetic fields. Sun et al. synthesized biocompatible nano-graphene oxides which present intrinsic photoluminescence for optical imaging. They also attached doxorubicin and a specific antibody Rituxan to selective recognize and kill lymphoma cells in vitro.
Most of the imaging probes used for MRI are based on gadolinium chelates or ferromagnetic nanoparticles [129,130]. Several groups have designed platforms to combine these agents with drug delivery. Pacheco-Torres et al. developed pH-sensitive Ion channel-functionalized stealth liposomes to use them in a cerebral glioma rodent model. The amount of gadolinium released in the tumor depends on the pH of the medium, being possible to establish a pH map of the tumor (Figure 3).
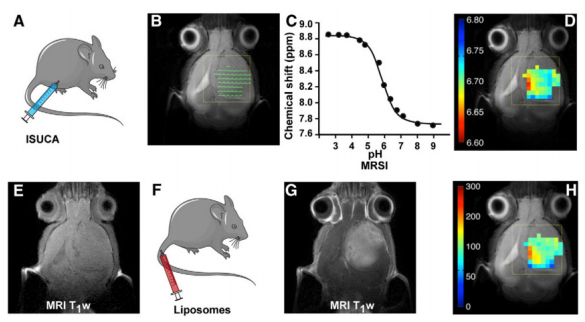 Figure 3. pH-triggered release of Gd (Ⅲ) DTPA from pH-sensitive liposomes into an in vivo glioblastoma model.A spectroscopic pH probe is injected intraperitoneally (A), allowing for the acquisition of a spectroscopic grid (B) and the preparation of an extracellular pH map of the tumor (D), based on the chemical shift dependence of pH sensitive resonance from the probe. A basal T1w image from the glioblastoma is acquired (E) before the injection of Gd (Ⅲ) DTPA loaded liposomes containing the pH sensitive nanovalve engineered from the mechanosensitive channel protein (MsCL) (F). Successive T1wimages may be acquired after injection revealing the kinetics of Gd (Ⅲ) DTPA release (G). Decreased intensity regions in the T1 map reveal that Gd (Ⅲ) DTPA has been released from the pH sensitive liposomes as a response to the acidic pH environment of the tumor. Reproduced from ref. [60]with permission of the publisher.
Figure 3. pH-triggered release of Gd (Ⅲ) DTPA from pH-sensitive liposomes into an in vivo glioblastoma model.A spectroscopic pH probe is injected intraperitoneally (A), allowing for the acquisition of a spectroscopic grid (B) and the preparation of an extracellular pH map of the tumor (D), based on the chemical shift dependence of pH sensitive resonance from the probe. A basal T1w image from the glioblastoma is acquired (E) before the injection of Gd (Ⅲ) DTPA loaded liposomes containing the pH sensitive nanovalve engineered from the mechanosensitive channel protein (MsCL) (F). Successive T1wimages may be acquired after injection revealing the kinetics of Gd (Ⅲ) DTPA release (G). Decreased intensity regions in the T1 map reveal that Gd (Ⅲ) DTPA has been released from the pH sensitive liposomes as a response to the acidic pH environment of the tumor. Reproduced from ref. [60]with permission of the publisher.Kaida et al. developed polymeric micellar nanocarriers containing gadolinium and platinum anticancer drugs to follow the accumulation of the drug in a rodent model of pancreatic cancer. Several groups have developed thermal sensitive liposomes (TSL) as drug carriers. De Smet et al. and Negussie et al. developed independently TSL loaded with doxorubicin and the MRI contrast agent (Gd-HP-DO3A) for MRI-guided drug delivery in a gliosarcoma tumor model and a VX2 tumor model, respectively. MR also allowed also in these cases to obtain a temperature map of the tumor, which corresponds to gadolinium release. Tagami et al. developed TLS loaded with Gd-DTPA and doxorubicin, which were investigated in a mouse mammary carcinoma model. In this case, the thermal release was induced introducing the leg-implanted tumor in a water bath with controlled temperature.
Graphene compounds have also been used as platforms for MRI-guided drug delivery. Ma et al. synthesized a superparamagnetic graphene oxide-iron oxide hybrid nanocomposite functionalized by a biocompatible polyethylene glycol (PEG) to be biologically stable. Doxorubicin was loaded and, because of the iron oxide effect on transversal magnetization, it became possible to visualize the biodistribution in a murine breast cancer mouse model using MRI.
All imaging techniques implemented above depict advantages and disadvantages. Nuclear imaging as gamma cameras, SPECT or PET, and optical imaging are endowed with high sensitivity, making them very suitable to study metabolism and drug biodistribution. However, their spatial resolution may be considered poor, making it recommendable to complement them with additional imaging approaches with higher spatial resolution as X-Rays, Computed Tomography or Magnetic Resonance Imaging. In this respect, the implementation of multimodal Image-guided drug delivery platforms has improved IGDD considerably [15,135].
Calle et al. developed liposomes containing ferromagnetic nanoparticles and Rhodamine-100 to use them as multimodal probes for MRI and optical imaging (Figure 4). The liposomes were also loaded with polyunsaturated fatty acids as an anti-inflammatory formulation and probe them in a glioma mouse model, visualizing the accumulation of the liposomes in the tumor area. Mikhaylov et al. synthetized ferri-liposomes loaded with the fluorescent marker Alexa Fluor 546 to visualize the NC using MRI and optical imaging. The ferri-liposomes delivered JPM-565, an inhibitor of cysteine cathepsins to reduce tumor and its microenvironment progression in a mouse breast cancer model. Xu et al. encapsulated hydrophobic upconversion nanoparticles with iron oxide nanoparticles using an amphiphilic block copolymer to be used as contrast agents in luminescence and magnetic resonance imaging. The nanocomposite was also loaded with doxorubicin as an anticancer drug and tested in a mammary mouse carcinoma model. Similarly, Yang et al. developed superparamagnetic iron oxide nanoparticles as platforms to anticancer drugs (DOX), a PET radionuclide (64Cu) and an active tumor targeting ligand (cRGD). They followed the biodistribution of the drug in a glioblastoma mouse model using PET and MRI techniques.
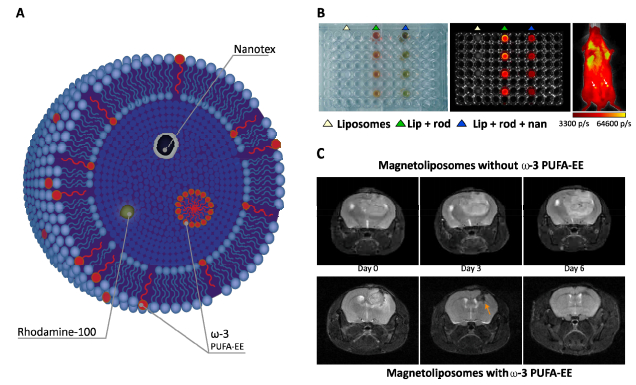 Figure 4. Multimodal theranostic magnetoliposomes. A: Representative liposomal preparation containing ω-3 poly-unsaturated fatty acids ethyl esthers (PUFA-EE) activated for multimodal MRI and fluorescence imaging. B: Optical (left panel) or fluorescence (center panel) imaging of empty liposomes, liposomes containing rodhamine-100 only or rhodamine-100 and the superparamagnetic nanoparticle Nanotex at increasing concentrations in a 96 well microplate. In vivo fluorescence imaging of liposomal preparations containing Nanotex (left arrow) or not (right arrow) injected subcutaneously in a mouse. C: Effect of the administration of magnetoliposomes loaded with PUFA-EE on the development of C6 cell glioma at days 0, 3 and 6 after implantation. Upper panels: Magnetoliposomes without ω-3 PUFA-EE: Lower panels: Magnetoliposomes with ω-3 PUFA-EE. Reproduced from ref. with permission of the publisher.
Figure 4. Multimodal theranostic magnetoliposomes. A: Representative liposomal preparation containing ω-3 poly-unsaturated fatty acids ethyl esthers (PUFA-EE) activated for multimodal MRI and fluorescence imaging. B: Optical (left panel) or fluorescence (center panel) imaging of empty liposomes, liposomes containing rodhamine-100 only or rhodamine-100 and the superparamagnetic nanoparticle Nanotex at increasing concentrations in a 96 well microplate. In vivo fluorescence imaging of liposomal preparations containing Nanotex (left arrow) or not (right arrow) injected subcutaneously in a mouse. C: Effect of the administration of magnetoliposomes loaded with PUFA-EE on the development of C6 cell glioma at days 0, 3 and 6 after implantation. Upper panels: Magnetoliposomes without ω-3 PUFA-EE: Lower panels: Magnetoliposomes with ω-3 PUFA-EE. Reproduced from ref. with permission of the publisher.In summary, we presented some of the most promising, emerging, bioengineered systems used in drug delivery, and we elaborated on the recent developments and importance of biomedical imaging methods for evaluating drug delivery and its effects.
While the most established nanocarrier liposomes are already in the market, soon, we might see multifunctional and sensory liposomes that, once reaching their target, could report the location and the status of the sick cell by appropriate imaging biomarkers while releasing an adjusted-dose drug according to the demands of the target cell.
In the meantime, DNA-based systems would offer shapes that would enhance the cellular uptake in cells other than the cancer cells, for delivering various cargos. While microbes would be functionalized to carry different loads, a patterned attachment of flagellar bacteria to a cargo might allow its controlled and directional travel inside the body. Viral nanoparticles promise cell-specific delivery of various cargos. Moreover, maybe we will see the first microbe physician as envisioned by Claesen and Fischbach within the coming ten years [139]. The microbe would sense the environment around an infected cell, decide on the therapeutic compound, and genetically produce it and release to the environment of the diseased cell. Following the signals of the cell, the microbe would monitor if the cell were cured. Once this job is completed, with a normal cell signal, the microbe would eliminate itself. Further understanding of the dynamics of the microbiota of our body and its relation to the immune system, would facilitate the realization of this approach [139].
While developing new delivery systems, the imaging technology will grow in parallel. Initial approaches using single imaging methods may evolve into hybrid imaging systems, complementing the weaknesses of some technologies with the strengths of others. In this sense, multimodal combinations as PET/MRI are already in operation, and optical expansions to fluorescence or bioluminescence imaging are not difficult to envision [140,141,142]. Together, improvements in drug delivery and imaging methods promise to open a new era in the personalized treatment of both common and rare pathologies. However, before reaching to that point, safety, cost-effectiveness, scaling up, and regulatory aspects of the bioengineered drug delivery and imaging systems will need to be addressed.
This work was supported in part by grants SAF2014-53739-R and S2010/BMD-2349 to SC. Funding sources were not involved in the design of the study, in the collection, analysis and interpretation of data, in the writing of the report nor in the decision to submit the article for publication.
Authors are indebted to Mr. Javier Perez CSIC for the professional drafting of the illustrations and to Profs. Paloma Ballesteros UNED and Pilar Lopez-Larrubia CSIC for helpful suggestions and critical reading of the manuscript.
Authors declare no conflict of interest in this paper.
| [1] |
Bunker A, Magarkar A, Viitala T (2016) Rational design of liposomal drug delivery systems, a review: combined experimental and computational studies of lipid membranes, liposomes and their PEGylation. BBA Biomembranes 1858: 2334–2352. doi: 10.1016/j.bbamem.2016.02.025

|
| [2] | Mak IW, Evaniew N, Ghert M (2014) Lost in translation: animal models and clinical trials in cancer treatment. Am J Transl Res 6: 114–118. |
| [3] |
Kopecek J (2010) Biomaterials and drug delivery: past, present, and future. Mol Pharm 7: 922–925. doi: 10.1021/mp1001813

|
| [4] |
Goldstein DB (2003) Pharmacogenetics in the laboratory and the clinic. N Engl J Med 348: 553–556. doi: 10.1056/NEJMe020173

|
| [5] |
Uetrecht J (2003) Screening for the potential of a drug candidate to cause idiosyncratic drug reactions. Drug Discov Today 8: 832–837. doi: 10.1016/S1359-6446(03)02816-2

|
| [6] | Lindon JC, Nicholson JK, Holmes E, et al. (2003) Contemporary issues in toxicology the role of metabonomics in toxicology and its evaluation by the COMET project. Toxicol Appl Pharm 187: 137–146. |
| [7] | Shaw LM, Kaplan B, Kaufman D (1996) Toxic effects of immunosuppressive drugs: mechanisms and strategies for controlling them. Clin Chem 42: 1316–1321. |
| [8] |
Serajuddin A (1999) Solid dispersion of poorly water-soluble drugs: early promises, subsequent problems, and recent breakthroughs. J Pharm Sci 88: 1058–1066. doi: 10.1021/js980403l

|
| [9] |
Brodie BB (1962) Difficulties in extrapolating data on metabolism of drugs from animal to man. Clin Pharm Th 3: 374–380. doi: 10.1002/cpt196233374

|
| [10] | Dedrick RL, Flessner MF (1997) Pharmacokinetic problems in peritoneal drug administration: tissue penetration and surface exposure. J Natl Cancer I 89: 480–487. |
| [11] |
Bach PB (2009) Limits on medicare's ability to control rising spending on cancer drugs. N Engl J Med 360: 626–633. doi: 10.1056/NEJMhpr0807774

|
| [12] |
Vermeire E, Hearnshaw H, Van Royen P, et al. (2001) Patient adherence to treatment: three decades of research: a comprehensive review. J Clin Pharm Ther 26: 331–342. doi: 10.1046/j.1365-2710.2001.00363.x

|
| [13] |
Cho EC, Glaus C, Chen J, et al. (2010) Inorganic nanoparticle-based contrast agents for molecular imaging. Trends Mol Med 16: 561–573. doi: 10.1016/j.molmed.2010.09.004

|
| [14] |
Dobrucki LW, Pan D, Smith AM (2015) Multiscale imaging of nanoparticle drug delivery. Curr Drug Targets 16: 560–570. doi: 10.2174/1389450116666150202163022

|
| [15] |
Garcia J, Tang T, Louie AY (2015) Nanoparticle-based multimodal PET/MRI probes. Nanomedicine 10: 1343–1359. doi: 10.2217/nnm.14.224

|
| [16] |
Janib SM, Moses AS, MacKay JA (2010) Imaging and drug delivery using theranostic nanoparticles. Adv Drug Deliver Rev 62: 1052–1063. doi: 10.1016/j.addr.2010.08.004

|
| [17] |
Llovet JM, Real MI, Montaña X, et al. (2002) Arterial embolisation or chemoembolisation versus symptomatic treatment in patients with unresectable hepatocellular carcinoma: a randomised controlled trial. Lancet 359: 1734–1739. doi: 10.1016/S0140-6736(02)08649-X

|
| [18] | Zhou X, Tang Z, Wang J, et al. (2014) Doxorubicin-eluting beads versus conventional transarterialchemoembolization for the treatment of hepatocellular carcinoma: a meta-analysis. Int J Clin Exp Med 7: 3892–3903. |
| [19] |
Pawelek JM, Low KB, Bermudes D (2003) Bacteria as tumour-targeting vectors. Lancet Oncol 4: 548–556. doi: 10.1016/S1470-2045(03)01194-X

|
| [20] | King I, Bermudes D, Lin S, et al. (2004) Tumor-targeted salmonella expressing cytosine deaminase as an anticancer agent. Hum Gene Ther 13: 1225–1233. |
| [21] | Low KB, Ittensohn M, Le T, et al. (1999) Lipid a mutant salmonella with suppressed virulence and TNF-α induction retain tumor-targeting in vivo. Nat Biotechnol 17: 37–41. |
| [22] | Pawelek JM, Low KB, Bermudes D (1997) Tumor-targeted salmonella as a novel anticancer vector. Cancer Res 57: 4537–4544. |
| [23] | Schlechte H, Elbe B (1988) Recombinant plasmid DNA variation of clostridium oncolyticum- model experiments of cancerostatic gene transfer. Cent Sheet Bacteriol Microbiol Hyg Ser A 268: 347–356. |
| [24] |
Sasaki T, Fujimori M, Hamaji Y, et al. (2006) Genetically engineered bifidobacterium longum for tumor-targeting enzyme-prodrug therapy of autochthonous mammary tumors in rats. Cancer Sci 97: 649–657. doi: 10.1111/j.1349-7006.2006.00221.x

|
| [25] |
Panteli JT, Forbes NS (2016) Engineered bacteria detect spatial profiles in glucose concentration within solid tumor cell masses. Biotechnol Bioeng 113: 2474–2484. doi: 10.1002/bit.26006

|
| [26] |
Hosseinidoust Z, Mostaghaci B, Yasa O, et al. (2016) Bioengineered and biohybrid bacteria-based systems for drug delivery. Adv Drug Deliver Rev 106: 27–44. doi: 10.1016/j.addr.2016.09.007

|
| [27] |
Akin D, Sturgis J, Ragheb K, et al. (2007) Bacteria-mediated delivery of nanoparticles and cargo into cells. Nat Nanotechnol 2: 441–449. doi: 10.1038/nnano.2007.149

|
| [28] |
Edwards MR, Carlsen RW, Zhuang J, et al. (2014) Swimming characterization of serratia marcescens for bio-hybrid micro-robotics. J MicroBio Robot 9: 47–60. doi: 10.1007/s12213-014-0072-1

|
| [29] |
Zhuang J, Carlsen RW, Sitti M (2015) pH-taxis of biohybrid microsystems. Sci Rep 5: 11403–11415. doi: 10.1038/srep11403

|
| [30] |
Lee JB, Hong J, Bonner DK, et al. (2012) Self-assembled RNA interference microsponges for efficient siRNA delivery. Nat Mater 11: 316–322. doi: 10.1038/nmat3253

|
| [31] |
Koudelka KJ, Pitek AS, Manchester M, et al. (2015) Virus-based nanoparticles as versatile nanomachines. Annu Rev Virol 2: 379–401. doi: 10.1146/annurev-virology-100114-055141

|
| [32] |
Douglas T, Young M (2006) Viruses: making friends with old foes. Science 312: 873–875. doi: 10.1126/science.1123223

|
| [33] | Esfandiari N, Arzanani MK, Soleimani M, et al. (2015) A new application of plant virus nanoparticles as drug delivery in breast cancer. Tumor Biol 37: 1229–1236. |
| [34] |
Cheng F, Tsvetkova IB, Khuong YL, et al. (2013) The packaging of different cargo into enveloped viral nanoparticles. Mol Pharm 10: 51–58. doi: 10.1021/mp3002667

|
| [35] |
Steinmetz NF, Mertens ME, Taurog RE, et al. (2010) Potato virus x as a novel platform for potential biomedical applications. Nano Lett 10: 305–312. doi: 10.1021/nl9035753

|
| [36] |
Aljabali AAA, Shukla S, Lomonossoff GP, et al. (2013) CPMV-DOX delivers. Mol Pharm 10: 3–10. doi: 10.1021/mp3002057

|
| [37] |
Galaway FA, Stockley PG (2013) MS2 viruslike particles: a robust, semisynthetic targeted drug delivery platform. Mol Pharm 10: 59–68. doi: 10.1021/mp3003368

|
| [38] |
Choi KM, Choi SH, Jeon H, et al. (2011) Chimeric capsid protein as a nanocarrier for siRNA delivery: stability and cellular uptake of encapsulated siRNA. Acs Nano 5: 8690–8699. doi: 10.1021/nn202597c

|
| [39] |
Choi KM, Kim K, Kwon IC, et al. (2013) Systemic delivery of siRNA by chimeric capsid protein: tumor targeting and RNAi activity in vivo. Mol Pharm 10: 18–25. doi: 10.1021/mp300211a

|
| [40] |
Kim KR, Kim DR, Lee T, et al. (2013) Drug delivery by a self-assembled DNA tetrahedron for overcoming drug resistance in breast cancer cells. Chem Commun 49: 2010–2012. doi: 10.1039/c3cc38693g

|
| [41] |
Jiang Q, Song C, Nangreave J, et al. (2012) DNA origami as a carrier for circumvention of drug resistance. J Am Chem Soc 134: 13396–13403. doi: 10.1021/ja304263n

|
| [42] | Charoenphol P, Bermudez H (2014) Design and application of multifunctional DNA nanocarriers for therapeutic delivery. Acta Biomater 10: 1683–1691. |
| [43] |
Kumar V, Palazzolo S, Bayda S, et al. (2016) DNA nanotechnology for cancer therapy. Theranostics 6: 710–725. doi: 10.7150/thno.14203

|
| [44] |
Angell C, Xie S, Zhang L, et al. (2016) DNA nanotechnology for precise control over drug delivery and gene therapy. Small 12: 1117–1132. doi: 10.1002/smll.201502167

|
| [45] |
Taylor AI, Beuron F, Peak CSY, et al. (2016) Nanostructures from synthetic genetic polymers. Chembiochem 17: 1107–1110. doi: 10.1002/cbic.201600136

|
| [46] |
Kim KR, Kim HY, Lee YD, et al. (2016) Self-assembled mirror DNA nanostructures for tumor-specific delivery of anticancer drugs. J Control Release 243: 121–131. doi: 10.1016/j.jconrel.2016.10.015

|
| [47] |
Kim KR, Lee T, Kim BS, et al. (2014) Utilizing the bioorthogonal base-pairing system of l-DNA to design ideal DNA nanocarriers for enhanced delivery of nucleic acid cargos. Chem Sci 5: 1533–1537. doi: 10.1039/C3SC52601A

|
| [48] |
Bangham AD, Standish MM, Watkins JC (1965) Diffusion of univalent ions across the lamellae of swollen phospholipids. J Mol Biol 13: 238–IN27. doi: 10.1016/S0022-2836(65)80093-6

|
| [49] |
Allen TM, Cullis PR (2004) Drug delivery systems: entering the mainstream. Science 303: 1818–1822. doi: 10.1126/science.1095833

|
| [50] |
Pattni BS, Chupin VV, Torchilin VP (2015) New developments in liposomal drug delivery. Chem Rev 115: 10938–10966. doi: 10.1021/acs.chemrev.5b00046

|
| [51] |
Leung SJ, Romanowski M (2012) Light-activated content release from liposomes. Theranostics 2: 1020–1036. doi: 10.7150/thno.4847

|
| [52] |
Ng LT, Yuba E, Kono K (2009) Modification of liposome surface with pH-responsive polyampholytes for the controlled-release of drugs. Res Chem Intermediat 35: 1015–1025. doi: 10.1007/s11164-009-0089-6

|
| [53] |
Obata Y, Tajima S, Takeoka S (2010) Evaluation of pH-responsive liposomes containing amino acid-based zwitterionic lipids for improving intracellular drug delivery in vitro and in vivo. J Control Release 142: 267–276. doi: 10.1016/j.jconrel.2009.10.023

|
| [54] | Landon CD, Park JY, Needham D, et al. (2011) Nanoscale drug delivery and hyperthermia: the materials design and preclinical and clinical testing of low temperature-sensitive liposomes used in combination with mild hyperthermia in the treatment of local cancer. Open Nanomed J 3: 38–64. |
| [55] |
Stubbs M, McSheehy PM, Griffiths JR (1999) Causes and consequences of acidic pH in tumors: a magnetic resonance study. Adv Enzyme Regul 39: 13–30. doi: 10.1016/S0065-2571(98)00018-1

|
| [56] |
Zhang J, Tao W, Chen Y, et al. (2015) Doxorubicin-loaded star-shaped copolymer PLGA-vitamin E tpgs nanoparticles for lung cancer therapy. J Mater Sci Mater M 26: 165. doi: 10.1007/s10856-015-5498-z

|
| [57] |
Kocer A (2007) A remote controlled valve in liposomes for triggered liposomal release. J Liposome Res 17: 219–225. doi: 10.1080/08982100701528203

|
| [58] |
Kocer A, Walko M, Bulten E, et al. (2006) Rationally designed chemical modulators convert a bacterial channel protein into a pH-sensory valve. Angew Chem Int Edit 45: 3126–3130. doi: 10.1002/anie.200503403

|
| [59] |
Kocer A, Walko M, Meijberg W, et al. (2005) A light-actuated nanovalve derived from a channel protein. Science 309: 755–758. doi: 10.1126/science.1114760

|
| [60] | Pacheco TJ, Mukherjee N, Walko M, et al. (2015) Image guided drug release from pH-sensitive Ion channel-functionalized stealth liposomes into an in vivo glioblastoma model. Nanomedicine 11: 1345–1354. |
| [61] |
Shriver LP, Koudelka KJ, Manchester M (2009) Viral nanoparticles associate with regions of inflammation and blood brain barrier disruption during CNS infection. J Neuroimmunol 211: 66–72. doi: 10.1016/j.jneuroim.2009.03.015

|
| [62] |
Rae CS, Khor IW, Wang Q, et al. (2005) Systemic trafficking of plant virus nanoparticles in mice via the oral route. Virology 343: 224–235. doi: 10.1016/j.virol.2005.08.017

|
| [63] |
Lewis JD, Destito G, Zijlstra A, et al. (2006) Viral nanoparticles as tools for intravital vascular imaging. Nat Med 12: 354–360. doi: 10.1038/nm1368

|
| [64] |
Leong HS, Steinmetz NF, Ablack A, et al. (2010) Intravital imaging of embryonic and tumor neovasculature using viral nanoparticles. Nat Protoc 5: 1406–1417. doi: 10.1038/nprot.2010.103

|
| [65] |
Manchester M, Singh P (2006) Virus-based nanoparticles (VNPs): platform technologies for diagnostic imaging. Adv Drug Deliver Rev 58: 1505–1522. doi: 10.1016/j.addr.2006.09.014

|
| [66] |
Cheng F, Mukhopadhyay S (2011) Generating enveloped virus-like particles with in vitro assembled cores. Virology 413: 153–160. doi: 10.1016/j.virol.2011.02.001

|
| [67] |
Weissleder R, Mahmood U (2001) Molecular imaging. Radiology 219: 316–333. doi: 10.1148/radiology.219.2.r01ma19316

|
| [68] |
Bao G, Mitragotri S, Tong S (2013) Multifunctional nanoparticles for drug delivery and molecular imaging. Annu Rev Biomed Eng 15: 253–282. doi: 10.1146/annurev-bioeng-071812-152409

|
| [69] |
Ding H, Wu F (2012) Image guided biodistribution of drugs and drug delivery. Theranostics 2: 1037–1039. doi: 10.7150/thno.5321

|
| [70] |
Brys AK, Gowda R, Loriaux DB, et al. (2016) Nanotechnology-based strategies for combating toxicity and resistance in melanoma therapy. Biotechnol Adv 34: 565–577. doi: 10.1016/j.biotechadv.2016.01.004

|
| [71] | Gowda R, Jones NR, Banerjee S, et al. (2013) Use of nanotechnology to develop multi-drug inhibitors for cancer therapy. J Nanomed Nanotechnol 4: 184. |
| [72] |
Medina FJL, Giulianotti MA, Welmaker GS, et al. (2013) Shifting from the single to the multitarget paradigm in drug discovery. Drug Discov Today 18: 495–501. doi: 10.1016/j.drudis.2013.01.008

|
| [73] |
Yuan Y, Cai T, Xia X, et al. (2016) Nanoparticle delivery of anticancer drugs overcomes multidrug resistance in breast cancer. Drug Deliv 23: 3350–3357. doi: 10.1080/10717544.2016.1178825

|
| [74] |
Zheng H, Fridkin M, Youdim M (2014) From single target to multitarget/network therapeutics in Alzheimer's therapy. Pharmaceuticals 7: 113–135. doi: 10.3390/ph7020113

|
| [75] | Pawar S, Shevalkar G, Vavia P (2016) Glucosamine-anchored doxorubicin-loaded targeted nano-niosomes: pharmacokinetic, toxicity and pharmacodynamic evaluation. J Drug Target 24: 730–743. |
| [76] |
Blanco E, Shen H, Ferrari M (2015) Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat Biotechnol 33: 941–951. doi: 10.1038/nbt.3330

|
| [77] |
Shin TH, Choi Y, Kim S, et al. (2015) Recent advances in magnetic nanoparticle-based multi-modal imaging. Chem Soc Rev 44: 4501–4516. doi: 10.1039/C4CS00345D

|
| [78] |
Johnsen KB, Moos T (2016) Revisiting nanoparticle technology for blood-brain barrier transport: unfolding at the endothelial gate improves the fate of transferrin receptor-targeted liposomes. J Control Release 222: 32–46. doi: 10.1016/j.jconrel.2015.11.032

|
| [79] |
Grabrucker AM, Ruozi B, Belletti D, et al. (2016) Nanoparticle transport across the blood brain barrier. Tissue Barriers 4: e1153568–e1153571. doi: 10.1080/21688370.2016.1153568

|
| [80] | Ho D, Wang C-HK, Chow EKH (2015) Nanodiamonds: the intersection of nanotechnology, drug development, and personalized medicine. Sci Adv 1: e1500439–e1500439. |
| [81] | Webb S (1988) The physics of medical imaging, CRC Press. |
| [82] | Farncombe T, Iniewsky K (2013) Medical imaging: technology ad applications, CRC Press, 732. |
| [83] |
Caravan P, Ellison JJ, McMurry TJ, et al. (1999) Gadolinium(III) chelates as MRI contrast agents: structure, dynamics, and applications. Chem Rev 99: 2293–2352. doi: 10.1021/cr980440x

|
| [84] | Pavel DG, Zimmer M, Patterson VN (1977) In vivo labeling of red blood cells with 99mTc: a new approach to blood pool visualization. J Nucl Med 18: 305–308. |
| [85] |
Hahn MA, Singh AK, Sharma P, et al. (2011) Nanoparticles as contrast agents for in-vivo bioimaging: current status and future perspectives. Anal Bioanal Chem 399: 3–27. doi: 10.1007/s00216-010-4207-5

|
| [86] |
Chakravarty R, Hong H, Cai W (2014) Positron emission tomography image-guided drug delivery: current status and future perspectives. Mol Pharm 11: 3777–3797. doi: 10.1021/mp500173s

|
| [87] | de Smet M, Langereis S, van den Bosch S et al. (2013) SPECT/CT imaging of temperature-sensitive liposomes for MR-image guided drug delivery with high intensity focused ultrasound. J Control Release 169: 82–90. |
| [88] |
Gao X, Cui Y, Levenson RM, et al. (2004) In vivo cancer targeting and imaging with semiconductor quantum dots. Nat Biotechnol 22: 969–976. doi: 10.1038/nbt994

|
| [89] |
Weissleder R, Tung CH, Mahmood U, et al. (1999) In vivo imaging of tumors with protease-activated near-infrared fluorescent probes. Nat Biotechnol 17: 375–378. doi: 10.1038/7933

|
| [90] |
Calle D, Negri V, Ballesteros P, et al. (2015) Magnetoliposomes loaded with poly-unsaturated fatty acids as novel theranostic anti-inflammatory formulations. Theranostics 5: 489–503. doi: 10.7150/thno.10069

|
| [91] |
Heinle SK, Noblin J, Goree BP, et al. (2000) Assessment of myocardial perfusion by harmonic power doppler imaging at rest and during adenosine stress: comparison with (99 m) Tc-sestamibi SPECT imaging. Circulation 102: 55–60. doi: 10.1161/01.CIR.102.1.55

|
| [92] | Urtasun RC, Parliament MB, McEwan AJ, et al. (1996) Measurement of hypoxia in human tumours by non-invasive spect imaging of iodoazomycin arabinoside. Brit J Cancer Suppl 27: S209–S212. |
| [93] | Leitha T, Glaser C, Pruckmayer M, et al. (1998) Technetium-99m-MIBI in primary and recurrent head and neck tumors: contribution of bone SPECT image fusion. J Nucl Med 39: 1166–1171. |
| [94] | Tharp K, Israel O, Hausmann J, et al. (2004) Impact of 131I-SPECT/CT images obtained with an integrated system in the follow-up of patients with thyroid carcinoma. Eur J Nucl Med Mol I 31: 1435–1442. |
| [95] |
Fukuyama H, Ouchi Y, Matsuzaki S, et al. (1997) Brain functional activity during gait in normal subjects: a SPECT study. Neurosci Lett 228: 183–186. doi: 10.1016/S0304-3940(97)00381-9

|
| [96] |
Rudin M, Weissleder R (2003) Molecular imaging in drug discovery and development. Nat Rev Drug Discov 2: 123–131. doi: 10.1038/nrd1007

|
| [97] | Bushberg JT, Boone JM (2011) The essential physics of medical imaging, Lippincott Williams & Wilkins. |
| [98] |
Finnema SJ, Scheinin M, Shahid M, et al. (2015) Application of cross-species PET imaging to assess neurotransmitter release in brain. Psychopharmacology 232: 4129–4157. doi: 10.1007/s00213-015-3938-6

|
| [99] | Haubner R, Maschauer S, Prante O (2014) PET radiopharmaceuticals for imaging integrin expression: tracers in clinical studies and recent developments. Biomed Res Int 2014: 871609–871617. |
| [100] |
Tateishi U, Oka T, Inoue T (2012) Radiolabeled RGD peptides as integrin alpha(v)beta3-targeted PET tracers. Curr Med Chem 19: 3301–3309. doi: 10.2174/092986712801215937

|
| [101] |
Wagner S, Breyholz HJ, Law MP, et al. (2007) Novel fluorinated derivatives of the broad-spectrum MMP inhibitors N-hydroxy-2(R)-[[(4-methoxyphenyl)sulfonyl](benzyl)- and (3-picolyl)-amino]-3-methyl-butanamide as potential tools for the molecular imaging of activated MMPs with PET. J Med Chem 50: 5752–5764. doi: 10.1021/jm0708533

|
| [102] | Stacy MR, Maxfield MW, Sinusas AJ (2012) Targeted molecular imaging of angiogenesis in PET and SPECT: a review. Yale J Biol Med 85: 75–86. |
| [103] | Ripa RS, Pedersen SF, Kjaer A (2016) PET/MR imaging in vascular disease atheroscleroaia and inflammation. Positron Emission Tomo 11: 479–488. |
| [104] |
Wu C, Li F, Niu G, et al. (2013) PET imaging of inflammation biomarkers. Theranostics 3: 448–466. doi: 10.7150/thno.6592

|
| [105] |
Pacheco TJ, Calle D, Lizarbe B, et al. (2011) Environmentally sensitive paramagnetic and diamagnetic contrast agents for nuclear magnetic resonance imaging and spectroscopy. Curr Top Med Chem 11: 115–130. doi: 10.2174/156802611793611904

|
| [106] | Lanza GM, Moonen C, Baker JR, et al. (2013) Assessing the barriers to image-guided drug delivery. WIRE Nanomed Nanobiotechnol 6: 1–14. |
| [107] | Na HB, Song IC, Hyeon T (2009) Inorganic nanoparticles for MRI contrast agents. Adv Mater 21: 2133–2148. |
| [108] |
Bonnemain B (1998) Superparamagnetic agents in magnetic resonance imaging: physicochemical characteristics and clinical applications: a review. J Drug Target 6: 167–174. doi: 10.3109/10611869808997890

|
| [109] |
Yu Y, Sun D (2010) Superparamagnetic iron oxide nanoparticle "theranostics" for multimodality tumor imaging, gene delivery, targeted drug and prodrug delivery. Expert Rev Clin Pharmaco 3: 117–130. doi: 10.1586/ecp.09.39

|
| [110] |
Liu F, Laurent S, Fattahi H, et al. (2011) Superparamagnetic nanosystems based on iron oxide nanoparticles for biomedical imaging. Nanomedicine 6: 519–528. doi: 10.2217/nnm.11.16

|
| [111] | Al-Nahhas A, Win Z, Singh Q, et al. (2006) The role of 18F-FDG PET in oncology: clinical and resource implications. Nucl Med Rev Cent East Eur 9: 1–5. |
| [112] | Chopra A (2004) 18F-Labeled N-succinimidyl-4-fluorobenzoate-conjugated rat anti-mouse vascular endothelial growth factor receptor 2 monoclonal antibody linked to microbubbles, MICAD. |
| [113] | Gupta H, Aqil M, Khar RK, et al. (2010) Sparfloxacin-loaded PLGA nanoparticles for sustained ocular drug delivery. Nanomedicine 6: 324–333. |
| [114] |
Luo Q, Zhao J, Zhang X, et al. (2011) Nanostructured lipid carrier (NLC) coated with chitosan oligosaccharides and its potential use in ocular drug delivery system. Int J Pharm 403: 185–191. doi: 10.1016/j.ijpharm.2010.10.013

|
| [115] |
Möller W, Schuschnig U, Celik G, et al. (2013) Topical drug delivery in chronic rhinosinusitis patients before and after sinus surgery using pulsating aerosols. Plos One 8: e74991. doi: 10.1371/journal.pone.0074991

|
| [116] |
Gallamini A, Zwarthoed C, Borra A (2014) Positron emission tomography (PET) in oncology. Cancers 6: 1821–1889. doi: 10.3390/cancers6041821

|
| [117] |
Xiao Y, Hong H, Javadi A, et al. (2012) Multifunctional unimolecular micelles for cancer-targeted drug delivery and positron emission tomography imaging. Biomaterials 33: 3071–3082. doi: 10.1016/j.biomaterials.2011.12.030

|
| [118] |
Guo J, Hong H, Chen G, et al. (2014) Theranostic unimolecular micelles based on brush-shaped amphiphilic block copolymers for tumor-targeted drug delivery and positron emission tomography imaging. Acs Appl Mater Interface 6: 21769–21779. doi: 10.1021/am5002585

|
| [119] |
Hong H, Zhang Y, Engle JW, et al. (2012) In vivo targeting and positron emission tomography imaging of tumor vasculature with (66)Ga-labeled nano-graphene. Biomaterials 33: 4147–4156. doi: 10.1016/j.biomaterials.2012.02.031

|
| [120] |
Liu Z, Cal W, He L, et al. (2007) In vivo biodistribution and highly efficient tumour targeting of carbon nanotubes in mice. Nat Nanotechnol 2: 47–52. doi: 10.1038/nnano.2006.170

|
| [121] |
Blasberg RG (2003) In vivo molecular-genetic imaging: multi-modality nuclear and optical combinations. Nucl Med Biol 30: 879–888. doi: 10.1016/S0969-8051(03)00115-X

|
| [122] |
Hoffman RM (2015) Application of GFP imaging in cancer. Lab Invest 95: 432–452. doi: 10.1038/labinvest.2014.154

|
| [123] | Kocher B, Piwnica WD (2013) Illuminating cancer systems with genetically engineered mouse models and coupled luciferase reporters in vivo. Cancer Discov 3: 616–629. |
| [124] |
Wang C, Cheng L, Liu Z (2011) Drug delivery with upconversion nanoparticles for multi-functional targeted cancer cell imaging and therapy. Biomaterials 32: 1110–1120. doi: 10.1016/j.biomaterials.2010.09.069

|
| [125] |
Yuan Y, Liu B (2014) Self-assembled nanoparticles based on PEGylated conjugated polyelectrolyte and drug molecules for image-guided drug delivery and photodynamic therapy. Acs Appl Mater Interface 6: 14903–14910. doi: 10.1021/am5020925

|
| [126] | Cool SK, Geers B, Roels S, et al. (2013) Coupling of drug containing liposomes to microbubbles improves ultrasound triggered drug delivery in mice. J Control Release 172: 885–893. |
| [127] | Chen ML, He YJ, Chen XW, et al. (2012) Quantum dots conjugated with Fe3O4-filled carbon nanotubes for cancer-targeted imaging and magnetically guided drug delivery. Langmuir 28: 16469–16476. |
| [128] |
Sun X, Liu Z, Welsher K, et al. (2008) Nano-graphene oxide for cellular imaging and drug delivery. Nano Res 1: 203–212. doi: 10.1007/s12274-008-8021-8

|
| [129] | Shen Z, Wu A, Chen X (2016) Iron oxide nanoparticle based contrast agents for magnetic resonance imaging. Mol Pharm, DOI: 10.1021/acs.molpharmaceut.6b00839. |
| [130] | Hermann P, Kotek J, Kubíček V, et al. (2008) Gadolinium(III) complexes as MRI contrast agents : ligand design and properties of the complexes. Dalton Trans 23: 3027–3047. |
| [131] |
Kaida S, Cabral H, Kumagai M, et al. (2010) Visible drug delivery by supramolecular nanocarriers directing to single-platformed diagnosis and therapy of pancreatic tumor model. Cancer Res 70: 7031–7041. doi: 10.1158/0008-5472.CAN-10-0303

|
| [132] |
Negussie AH, Yarmolenko PS, Partanen A, et al. (2011) Formulation and characterisation of magnetic resonance imageable thermally sensitive liposomes for use with magnetic resonance-guided high intensity focused ultrasound. Int J Hyperther 27: 140–155. doi: 10.3109/02656736.2010.528140

|
| [133] |
Tagami T, Foltz WD, Ernsting MJ, et al. (2011) MRI monitoring of intratumoral drug delivery and prediction of the therapeutic effect with a multifunctional thermosensitive liposome. Biomaterials 32: 6570–6578. doi: 10.1016/j.biomaterials.2011.05.029

|
| [134] |
Ma X, Tao H, Yang K, et al. (2012) A functionalized graphene oxide-iron oxide nanocomposite for magnetically targeted drug delivery, photothermal therapy, and magnetic resonance imaging. Nano Res 5: 199–212. doi: 10.1007/s12274-012-0200-y

|
| [135] |
Al-Jamal WT, Kostarelos K (2007) Liposome-nanoparticle hybrids for multimodal diagnostic and therapeutic applications. Nanomedicine 2: 85–98. doi: 10.2217/17435889.2.1.85

|
| [136] |
Mikhaylov G, Mikac U, Magaeva AA, et al. (2011) Ferri-liposomes as an MRI-visible drug-delivery system for targeting tumours and their microenvironment. Nat Nanotechnol 6: 594–602. doi: 10.1038/nnano.2011.112

|
| [137] |
Xu H, Cheng L, Wang C, et al. (2011) Polymer encapsulated upconversion nanoparticle/iron oxide nanocomposites for multimodal imaging and magnetic targeted drug delivery. Biomaterials 32: 9364–9373. doi: 10.1016/j.biomaterials.2011.08.053

|
| [138] |
Yang X, Hong H, Grailer JJ, et al. (2011) cRGD-functionalized, DOX-conjugated, and ⁶⁴Cu-labeled superparamagnetic iron oxide nanoparticles for targeted anticancer drug delivery and PET/MR imaging. Biomaterials 32: 4151–4160. doi: 10.1016/j.biomaterials.2011.02.006

|
| [139] |
Claesen J, Fischbach MA (2015) Synthetic microbes as drug delivery systems. Acs Synth Biol 4: 358–364. doi: 10.1021/sb500258b

|
| [140] |
Sotoudeh H, Sharma A, Fowler KJ, et al. (2016) Clinical application of PET/MRI in oncology. J Magn Reson Imaging 44: 265–276. doi: 10.1002/jmri.25161

|
| [141] |
Pan D, Caruthers SD, Chen J, et al. (2010) Nanomedicine strategies for molecular targets with MRI and optical imaging. Future Med Chem 2: 471–490. doi: 10.4155/fmc.10.5

|
| [142] |
Culver J, Akers W, Achilefu S (2008) Multimodality molecular imaging with combined optical and SPECT/PET modalities. J Nucl Med 49: 169–172. doi: 10.2967/jnumed.107.043331

|
| 1. | Denisa Lizoňová, Samuel Frei, Martin Balouch, Aleš Zadražil, František Štěpánek, Multilobed Magnetic Liposomes Enable Remotely Controlled Collection, Transport, and Delivery of Membrane-Soluble Cargos to Vesicles and Cells, 2021, 2576-6422, 10.1021/acsabm.1c00106 | |
| 2. | Charles D. Cox, Navid Bavi, Boris Martinac, Bacterial Mechanosensors, 2018, 80, 0066-4278, 71, 10.1146/annurev-physiol-021317-121351 | |
| 3. | M.D. Figueroa-Pizano, E. Carvajal-Millan, 2022, 9780323918640, 419, 10.1016/B978-0-323-91864-0.00008-5 | |
| 4. | Ahmad Zaid, Amiram Ariel, Harnessing anti-inflammatory pathways and macrophage nano delivery to treat inflammatory and fibrotic disorders, 2024, 0169409X, 115204, 10.1016/j.addr.2024.115204 |
| Delivery vehicle | Advantages | Disadvantages |
| Bacterial | *Direct expression of therapeutic proteins at the target site *On-site production of therapeutic molecules *Lower therapeutic dose compared to systemic treatment *Protection of drug from biodegradation *Minimal side effects |
*Limited expression of eukaryotic proteins due to the lack of efficient posttranslational modifications *Potential risk of losing the engineered behavior and functionality in genetically modified bacteria |
| Microbots | *Steering bacteria towards a specific location inside the body via taxis *Reaching the target site at a faster rate before they are cleared away by the reticuloendothelial system |
*Dose-limiting toxicity of bacterial cells may restrict efficacy |
| Viral nanoparticles originating from: *Plant viruses *Oncolytic animal viruses *Enveloped viruses |
*Efficient internalization by animal cells, visualize tumor vasculature, targets areas of inflammation, monitor angiogenesis over time in mice [61,62,63,64]. *Cellular selectability: ability to discriminate human tumor cells from healthy cells, genetic modifications *Systemic tumor targeting *In vitro self-assembly allowing incorporation of nonviral genome and nanoparticles *Devoid of viral genome *Can target new cells *Undergo fusion *Easy surface modifications |
*The absence of envelop might necessitate surface modifications for targeting and potential immune reaction *Difficulty to load chemical or inorganic cargo, potential for introducing a modified virus into host genome *Low efficiency in introducing the core-like particles into viral glycoprotein-expressing cells |
| Microsponges | *Improved physical and chemical stability *Greater available concentrations *Controlled release of the active ingredients, *Reduced skin irritation and sensitization |
*Potential toxicity of traces of residual monomers |
| Ion channels in stealth liposomes | *High sensitivity to environmental cues *Efficient release *Biocompatible *Ability to encapsulate hydrophobic and/or hydrophilic drugs *Allowing chemical modifications to sense different environmental signals |
*Added costs of ion channel production and modification *Potential risk of immunogenicity |
| Imaging techniques | Advantages | Disadvantages |
| MRI | *Excellent anatomic contrast *High spatial resolution (30-500 mm) *High penetration (whole body) *Excellent patient safety *High intrinsic contrast |
*Long acquisitions (sec-min) *Poor sensitivity (mM) *Expensive instrumentation |
| PET | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use external positron emitters *Very expensive instrumentation and probes |
| SPECT | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Long acquisitions (min) *Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use-emitters *Expensive instrumentation and probes |
| CT | *Short time acquisition *High spatial resolution (10-500 mm) *High penetration (whole body) *High intrinsic contrast between bones and soft tissues |
*Poor functional/molecular contrast *Ionizing radiation *Poor sensitivity to contrast agents (mM) |
| Ultrasound | *Short time acquisition *High patient security *High intrinsic contrast *Economic |
*Higher resolution involves lower penetration and vice versa *Poor sensitivity to contrast agent (mM) |
| Luminescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (0.2-10 mm) *Poor penetration *Without intrinsic contrast, it is necessary luminescent agents |
| Fluorescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (1-2 mm) *Poor penetration *Without intrinsic contrast, it is necessary fluorescent agents |
| Delivery vehicle | Advantages | Disadvantages |
| Bacterial | *Direct expression of therapeutic proteins at the target site *On-site production of therapeutic molecules *Lower therapeutic dose compared to systemic treatment *Protection of drug from biodegradation *Minimal side effects |
*Limited expression of eukaryotic proteins due to the lack of efficient posttranslational modifications *Potential risk of losing the engineered behavior and functionality in genetically modified bacteria |
| Microbots | *Steering bacteria towards a specific location inside the body via taxis *Reaching the target site at a faster rate before they are cleared away by the reticuloendothelial system |
*Dose-limiting toxicity of bacterial cells may restrict efficacy |
| Viral nanoparticles originating from: *Plant viruses *Oncolytic animal viruses *Enveloped viruses |
*Efficient internalization by animal cells, visualize tumor vasculature, targets areas of inflammation, monitor angiogenesis over time in mice [61,62,63,64]. *Cellular selectability: ability to discriminate human tumor cells from healthy cells, genetic modifications *Systemic tumor targeting *In vitro self-assembly allowing incorporation of nonviral genome and nanoparticles *Devoid of viral genome *Can target new cells *Undergo fusion *Easy surface modifications |
*The absence of envelop might necessitate surface modifications for targeting and potential immune reaction *Difficulty to load chemical or inorganic cargo, potential for introducing a modified virus into host genome *Low efficiency in introducing the core-like particles into viral glycoprotein-expressing cells |
| Microsponges | *Improved physical and chemical stability *Greater available concentrations *Controlled release of the active ingredients, *Reduced skin irritation and sensitization |
*Potential toxicity of traces of residual monomers |
| Ion channels in stealth liposomes | *High sensitivity to environmental cues *Efficient release *Biocompatible *Ability to encapsulate hydrophobic and/or hydrophilic drugs *Allowing chemical modifications to sense different environmental signals |
*Added costs of ion channel production and modification *Potential risk of immunogenicity |
| Imaging techniques | Advantages | Disadvantages |
| MRI | *Excellent anatomic contrast *High spatial resolution (30-500 mm) *High penetration (whole body) *Excellent patient safety *High intrinsic contrast |
*Long acquisitions (sec-min) *Poor sensitivity (mM) *Expensive instrumentation |
| PET | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use external positron emitters *Very expensive instrumentation and probes |
| SPECT | *Good functional/molecular contrast *High penetration (whole body) *High sensitivity (pM) |
*Long acquisitions (min) *Poor anatomic contrast (1-5 mm) *Ionizing radiation *Without intrinsic contrast, it is necessary to use-emitters *Expensive instrumentation and probes |
| CT | *Short time acquisition *High spatial resolution (10-500 mm) *High penetration (whole body) *High intrinsic contrast between bones and soft tissues |
*Poor functional/molecular contrast *Ionizing radiation *Poor sensitivity to contrast agents (mM) |
| Ultrasound | *Short time acquisition *High patient security *High intrinsic contrast *Economic |
*Higher resolution involves lower penetration and vice versa *Poor sensitivity to contrast agent (mM) |
| Luminescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (0.2-10 mm) *Poor penetration *Without intrinsic contrast, it is necessary luminescent agents |
| Fluorescence | *Short time acquisition *Good functional/molecular contrast *High patient security *High sensitivity to contrast agent (nM) |
*Poor anatomic contrast *Poor spatial resolution (1-2 mm) *Poor penetration *Without intrinsic contrast, it is necessary fluorescent agents |