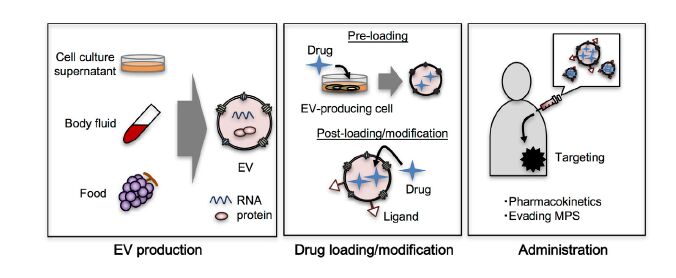
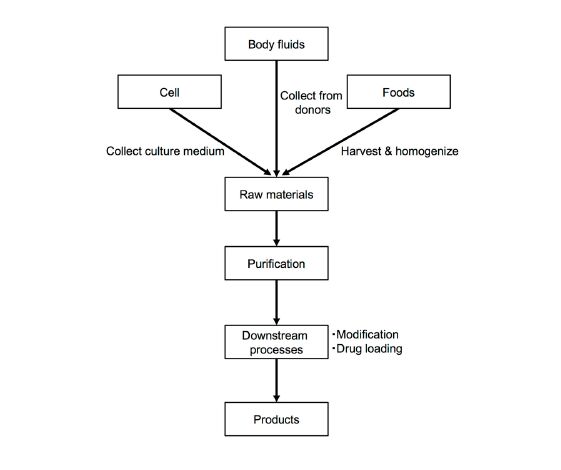
Extracellular vesicles (EVs) are secreted from any types of cells and shuttle between donor cells and recipient cells. Since EVs deliver their cargos such as proteins, nucleic acids, and other molecules for intercellular communication, they are considered as novel mode of drug delivery vesicles. EVs possess advantages such as inherent targeting ability and non-toxicity over conventional nanocarriers. Much efforts have so far been made for the application of EVs as a drug delivery carrier, however, basic techniques, such as mass-scale production, drug loading, and engineering of EVs are still limited. In this review, we summarize following four points. First, recent progress on the production method for EVs is described. Second, current techniques of drug loading methods are summarized. Third, targeting approach to specifically deliver cargo molecules for diseased sites by engineered EVs is discussed. Lastly, strategies to control pharmacokinetics and improve biodistribution are discussed.
1.
Introduction
The security of sensitive information has become a significant concern in the age of 5G networks. digital images, including agreements, paintings, medical reports, agreements, and other scanned documents, are a primary source of information requiring the highest sensitivity level. Protecting the privacy of digital images when shared between authorized parties in systems such as the cloud is of utmost importance [1]. There have been advancements in developing multiple effective encryption algorithms to protect multimedia data's security and privacy. These algorithms rely on two distinct principles: symmetric and asymmetric key algorithms. Confusion and diffusion modules are the major techniques used for symmetric algorithms [2,3]. The confusion module is usually applied after the diffusion operation has successfully severed the relationship between the ciphered data and the keys employed in image, audio and video encryption [2,4,5,6,7]. The data used in both modules are obtained from a range of numbers generated by a pseudo-random number generator (PRNG). Modern image cryptography relies heavily on well-designed PRNGs that utilize mathematical mechanisms [3,8,9]. As a result, numerous effective algorithms have been created to produce substitution boxes (S-boxes) and pseudo-random number (PRN) sequences [10,11,12,13]. In [14,15], the authors introduced a comprehensive scheme for securing images, employing a combination of chaos-based block permutation and weighted bit plane chain diffusion. Furthermore, the authors proposed a face image privacy protection scheme that relies on chaos and DNA cryptography. This dual approach addresses image security through advanced encryption techniques and the emerging need for robust privacy protection in the context of face images. In [16,17], the authors give an idea of an Image encryption algorithm based on plane-level image filtering, discrete logarithmic transform, and RNA-encoded color image encryption scheme based on a chain feedback structure. There are two types of S-boxes available: static and dynamic. Static S-boxes operate and generate outputs in fixed modes, whereas dynamic S-boxes possess multiple operating modes. Dynamic S-box algorithms are preferred because they increase computational costs for cryptanalysts. Recent studies have proposed several techniques to enhance the security of cryptographic systems. For example, Ibrahim et al. [3] introduced a method that utilizes permuted elliptic curves (ECs) to generate key-dependent dynamic S-boxes, aiming to minimize computational expenses. Alhandawi et al. [18] suggested an S-box configuration based on a modified Firefly algorithm, claiming to exhibit satisfactory cryptographic characteristics. In addition, a new algorithm utilizing a group structure was introduced in [19], which provides high nonlinearity for secure S-box generation. Furthermore, Toughi et al. [20] presented an image encryption scheme utilizing PRNG and advanced encryption standard (AES) modules, while [21] designed an image encryption method using a chaotic model with sufficient pseudo-creation capability. Recently, chaotic systems and error-correcting codes have gained popularity for generating PRNS and constructing S-boxes for image encryption algorithms.
These approaches have received recognition for their characteristics, such as non-periodicity, responsiveness to input parameters, ergodicity, key sensitivity, and chaotic properties, as mentioned in references [3,18,22,23,24,25]. In [26], the authors devised a secure algorithm capable of operating in digital and optical environments. Wang et al. [27] introduced a cryptosystem that leverages diverse techniques like chaotic maps, Fisher-Yates shuffling, and DNA sequence encoding to deliver precise encryption and rapid convergence. Although chaotic maps can generate random sequences quickly, EC structures are more suitable for generating random sequences due to their computational precision [28]. Reyad et al. [29] developed an idea based on ECs to obtain PRNs that operate effectively in image encryption. Moreover, El-Latif et al. [30] used cyclic ECs and hybrid-chaotic systems to develop an effective image encryption scheme. To generate PRNs, the authors in [3,20] employed an ECs group law operating tool in conjunction with a large prime field, while [2,23] utilized a recursive approach and group law operating tool to identify all points on ECs and generate both S-box and PRNs using algebraic arithmetic operations. However, these techniques can be computationally expensive when working with large prime fields. Using a small fixed prime field may not be effective for generating enough data with strong cryptographic features. Despite attempts to address these challenges, [2] could only produce two strong dynamic S-boxes using a minimum fixed odd prime field. Recently, Farwa et al. [31] proposed constructing the nonlinear component of block cipher by employing EC over binary extension field (BEF) and utilizing the group structure of EC. In [25,26,32,33], the author extended this idea using EC over the Galois field with n equals 8, 9 and odd n greater than 9 and utilized the operations of the corresponding Galois field. All the EC-based schemes discussed above use finite fields to achieve the desired level of security. The security of these cryptographic systems, which rely on EC over finite fields, is primarily determined by the computational resources required to solve the discrete logarithm problem. Computers typically perform mathematical operations with binary digits (bits), which can only have two possible values (0 or 1). In the context of cryptography, cryptographic algorithms must be designed to operate on binary data. By performing computations in a BEF, the computational complexity of cryptographic algorithms can be reduced, increasing their efficiency and security.
In this context, we explain two distinct mechanisms that utilize the indexing technique: the S-box method and a collection of PRN streams, each with its unique approach. It is worth mentioning that the S-box construction technique (SCT) generates multiple dynamic S-boxes in 16×16 standard format employing features of BEF. The core sentiment behind SCT is that EC points and operations of the corresponding Galois field jointly equip it. This way, we reduce the time complexity and increase the proposed algorithm's security strength as the computer works in a binary field. Moreover, BEF enables a high degree of parallelism, essential in modern computer architectures. Parallelism allows multiple arithmetic operations to be performed simultaneously, leading to faster computation times. Moreover, the PRN technique is partly utilized by both EC points and basic algebraic operations in a BEF. Due to this, the PRN scheme produces numerous random patterns while ensuring that these patterns are non-repeating and verified. As a result, it is an effective method for achieving diffusion in large-scale multimedia data. Moreover, the findings obtained from implementing both modules confirm the suitability of utilizing SCT and PRN techniques and indexing techniques in various cryptographic protocols.
The rest of the study is structured as follows: Section 2 presents the fundamental principles and discoveries of EC and BEF. Section 3 elucidates the suggested S-box and PRN mechanisms. Section 4 centers on the proposed encryption scheme. Consequently, Section 5 presents the results of simulations conducted on the SCT and proposed encryption scheme. Finally, Section 6 concludes the discussion.
2.
Preliminaries
This section covers important concepts such as ECs, Galois fields, Euler's phi function, and primitive polynomials, which are essential and foundational.
2.1. Elliptic curve
For any given prime field Fp, an EC of the form
where a and b are non-zero elements of the corresponding prime field are called weierstrass form of an EC. Also, when we take a=0, then the obtained EC of the form
where b≠0 is called Mordell elliptic curve (MEC). The specialty of this curve is that it has p+1 points lying on that EC if we take prime field of the form
where each integer in the field Fp appear once as y-coordinates [34].
2.2. Galois field GF(2n)
Let R be a commutative ring with identity, with binary operation addition and multiplication. Then I⊆R is called an ideal of R if
and 𝒶I⊆I for every 𝒶∈R. An ideal in a ring R denoted as A≠R, is considered maximal ideal when no other proper ideal of R exists that contains A. A commutative ring with an identity whose nonzero elements forms a group under multiplication is called field F. The polynomial ring, denoted by Zp[x] is a set of polynomials whose coefficients are from the field Zp. A polynomial f(x) in Zp[x] is an irreducible polynomial, if it cannot be reduced into the product of lower-degree polynomials in Zp[x], and the ideal generated by f(x) will be the maximal ideal of the ring Zp[x] represented as
The quotient Zp[x]<f(x)> is known as Galois field GF(pm) having pm elements, where m is the degree of PIP f(x) and p is any prime number. A polynomial
is said to have a PIP of degree m if all its roots are also primitive elements in the corresponding Galois field. Also, addition and subtraction are performed using the corresponding field Zp. The product of two polynomials in Zp[x] is equivalent to the remainder obtained from the Euclidean division by p. The extended Euclidean algorithm can compute the multiplicative inverse of any nonzero element. The total number of PIPs of degree n in the binary field is φ(2n−1)n, where φ denotes Euler's phi function.
3.
Proposed technique for S-boxes and pseudo-random numbers
In this segment, we suggest a cryptographic algorithm that relies primarily on two distinct methods of generating random data with a specific length. The precise instructions for each approach are described in subsequent sub-sections.
3.1. S-box construction technique (SCT)
Generating robust and adaptable S-boxes is a critical factor in developing effective cryptographic systems, as they are instrumental in performing nonlinear transformations that evaluate the strength of well-designed crypto-algorithms [35]. Consequently, generating dynamic S-boxes with optimal cryptographic properties is highly desirable in contemporary cryptography. To address the limitations of current S-box constructions and obtain multiple S-boxes, we suggest a rapid technique that employs ECs over the Galois field and their algebraic operations. The subsequent explanation illustrates how the proposed SCT operates.
1) Choose PIP of degree 8 over the binary field
Since the number of PIP of degree 8 over the binary field is 16, one can independently choose any other PIP of degree 8.
2) Select an EC E(b,2,8) of the form
3) Generate EC points (𝓍,𝓎) by utilizing above equation over the PIP.
4) Apply a bijective map on the points of EC (𝓍,𝓎), such that
Defined by
where (𝓍,𝓎)∈E(b,2,8)𝓍,𝓎.
5) Apply an inverse map under the corresponding BEF
Defined as
where h be any fixed element of 𝓍-coordinates and 𝓍∈E(b,2,8)𝓍. Also, inverse is taken under the BEF of order 256 and PIP is taken as mentioned above.
6) For the construction of S-box, further apply a map
defined as
where r∈F256 be any non-zero element fixed element and 𝓏r∈F256. Here + presents addition over the Galois field GF(28).
Since the number of PIP of degree 8 over the binary field is 16, given in Table 1. So, the scheme is capable to generating 16×255×255 different number of 8×8 S-boxes corresponding to the BEF of degree 8 having optimal NL 112 of each which are given in Table 6. The S-boxes constructed through proposed SCT are depicted in Tables 2–5.
3.2. PRN generation scheme
PRNs that have been verified are crucial in numerous cryptographic uses, such as data encryption and gambling. To ensure a strong masking effect in data encryption, PRNs are generated using various mathematical structures, including ECs. In this part, instead of using large prime field dependent schemes, we engaged BEF of order n to generate PRNs. The following lines define the proposed algorithm:
1) Choose primitive irreducible polynomials (PIP) P(𝓉) of degree n over the binary field. Since the number of PIP of degree n over the binary field is φ(2n−1)n, one can independently choose any other PIP of degree n.
2) Select an EC E(b,2,n) of the form
here b be any element of the corresponding Galois field excluding zero.
3) Generate EC points E(b,2,n)𝓍,𝓎 by employing equation over given P(𝓉).
4) Apply a map on the points of EC points such that
defined by
where (𝓍,𝓎)∈E(b,2,n)𝓍,𝓎.
5) For the generation of PRN, further apply an inverse map under the corresponding BEF
defined as
where 𝓌∈GF(2n)∖{0} be any fixed element. Also, inverse is taken under the GF(2n) and corresponding PIP is utilized.
Since, the irreducible polynomials of degree n that are binary primitives are φ(2n−1)n, where ϕ represents Euler's phi function. So, one can generate φ(2n−1)n×(2n−1) different number of PRN sequences corresponding to the BEF of degree n using the proposed mechanism.
4.
Proposed encryption decryption algorithm
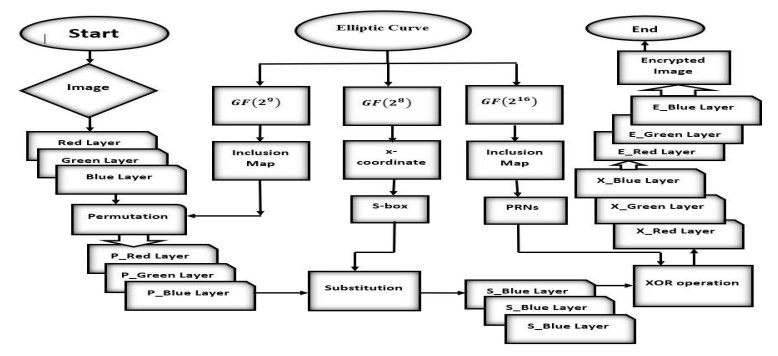
In domains like military, commercial, and medical, images are a form of visual content that requires cautious handling during transmission. Various mathematical frameworks are employed to establish standardized techniques for encrypting images to ensure reliability and safety. Typically, these encryption methods use chaotic and EC systems to create PRNs and S-boxes. This section introduces a novel approach to image encryption that assesses the appropriateness of prospective S-boxes and PRNs for facilitating secure image storage and communication over an insecure channel. Specifically, the proposed method involves encrypting an image I with dimensions of M×N×3, where M represents rows and N represents columns. Also, we use the symbols R, G and B to represent the color components red, green, and blue in an M×N image. When encrypting the image, all three channels are treated as a grayscale image, and each component is encrypted separately. The level of distortion introduced to the image defines the significance of the encryption scheme.
4.1. Encryption scheme
The encryption process involves several steps.
1) Let I denote the color image of pixels M×N×3, where M denotes rows and N denotes columns of the image. Here, 3 denotes the intensities of RGB layers. We work separately on these channels.
2) Since, any two adjacent pixels in the digital image data have strong relationships with one another. To scramble image elements, we take n=9 and the corresponding PIP of the form
to generate points (x,y) of EC by employing proposed technique (described in Section 3.2). Then use the inclusion map on each both the coordinates of EC points, which is defined as follows:
So, after applying this inclusion map, the obtained positive values of 𝓍, 𝓎 coordinates of EC are employed to original image I such that
where (i,j) denotes the integer position in the shuffling matrix Ip. Each color component of the image undergoes the permutation process to shuffle the pixels' positions. Consequently, one can get new layers denoted by Rp,Gp and Bp. By applying this process, we get the scrambled image.
3) To enhance the security against chosen plain-text attacks, the substitution step is a crucial component of any cryptographic algorithm. To achieve this, the proposed method incorporates the use of S-boxes generated through the suggested S-box methodology described in Section 3.1. One of the suggested S-boxes is selected for implementation. These S-boxes possess strong cryptographic properties and contribute to the overall strength of the scheme. Following that, the acquired S-boxes are utilized to substitute the scrambled components Rp,Gp and Bp of the image using a technique identical to AES substitution. Consequently, the substituted components Rs,Gs and Bs can be obtained.
4) The generation of PRNs holds great significance in multiple multimedia data protection applications. Numerous schemes for generating random numbers have been investigated in the research. Among them, EC is commonly employed for random number generation. In this section, a sequence of random numbers ψ is generated by selecting an appropriate value for n such that 2n≥M×W, ensuring the diffusion of encrypted data through the proposed technique (explained in Section 3.2). Consequently, take M×W number of elements ψr from that sequence and reduce the size of elements of that sequence in the range of image bits. In this part, we take n=16 and the corresponding PIP of the form
to generate PRNs sequence ψ by employing proposed technique (described in Section 3.2). Further, apply mode operation to the elements of sequence ψ and covert them in the range of 256 order Galois field
defined as
where s∈ψ. The reduced sequence ψr are then utilized for the diffusion phase using the below equations
where RE, GE, and BE are the encrypted pixel values for the red, green, and blue channels, respectively, and ψr(i) is the ith-byte in PRNs stream ψr.Rs(i),Gs(i) and Bs(i) is the ith-byte in RGB channels Rs,Gs, and Bs respectively. Eventually, blend these components of the image, which is required ciphered image.
In this study, we tested the color image of women, house, jellybeans, and couple of dimensions 256×256. The decryption process of the proposed algorithm is same as the encryption process but with the inverse order of operations. The flowchart of proposed algorithm is also depicted in Figure 1. Further, the outcomes and analyses are presented in the subsequent section.
4.2. Decryption scheme
In this subsection, we discussed the process of image decryption in detail. First, we take the cipher image obtained from the encryption process defined in the previous subsection. Then, we divide the image into RGB channels and XORed with the generated sequence, which each channel is applied in the encryption scheme. Further, substitute inverse S-boxes with each channel as we did in the encryption scheme. Moreover, an inverse permutation on each coordinate of 2) in Section 4.1 is applied to the obtained image to get the plain image.
5.
Security and performance analyses
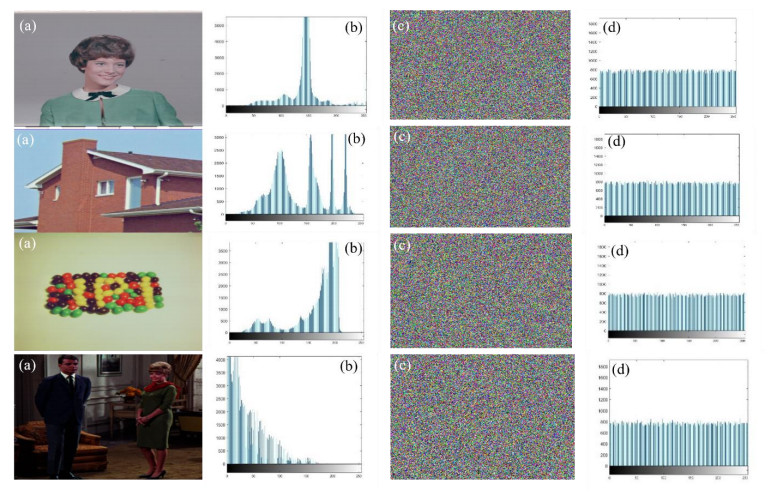
If an encryption algorithm passes several security tests and meets specific standards, it is deemed suitable for practical use. In this research, we evaluated the effectiveness of a proposed cryptosystem by encrypting different color images, such as women, house, jellybeans, and couple, shown in Figure 2. Following the encryption process, the encrypted images underwent several performance tests. These tests, which will be elaborated on in the upcoming subsection, strived to evaluate their stability against assorted attacks.
5.1. Performance analysis of the generated S-box
The cryptographic strength of the S-boxes developed for the encryption procedure is evaluated using established metrics such as nonlinearity (NL), strict avalanche criteria (SAC), linear branch number (LBN), differential branch number (DBN), bit independence criteria (BIC), linear approximation probability (LP), differential approximation probability (DP), balance, and linear structure (LS). These assessments are commonly employed to gauge the effectiveness of S-boxes. The ensuing results present the performance index of the generated S-boxes.
5.1.1. NL
The NL of a Boolean function f refers to the minimum Hamming distance between the set of all affine Boolean functions and f. We denoted the nonlinearity off f by Nf and mathematically it can be defined as
where A is the set of all affine Boolean functions and Nf denotes the hamming distance between f and h. The maximum NL score of n×n S-box can have 2n−1−2n2−1.
Thus, in the case for n=8, the maximum possible NL score is 120. Also, the proposed S-boxes have an optimal NL score of 112 depicted in Table 6.
5.1.2. SAC
The notions of completeness and avalanche were created by Webster and Tavares in 1985, who also detailed the analysis of the SAC. This criterion was investigated to see how the output bits performed when the input bits underwent alterations. Also, one can claim that the SAC criterion is satisfied if all SAC matrix entries are located within a small neighborhood of 0.5. Table 6 displays the SAC outcome of the suggested S-boxes and their comparison to various existing schemes. As a result, the proposed S-boxes met the requirements of the sac test.
5.1.3. BIC
In 1985, Webster and Tavares also provided the significant Boolean function property known as the BIC. The individual bits generated by the eight-constitution function are compared using the BIC. This criterion assesses the correlation between the nth and mth output bits if the ith input bit undergoes a little change. An S-box is deemed to meet the BIC requirements if the entries of its BIC matrix are near 0.5. The different proposed and existing S-boxes are put to the BIC test. The BIC result of the proposed S-boxes and some existing S-boxes is shown in Table 6.
5.1.4. LP
The LP analysis is used to determine the scheme's maximum imbalance value. We assign Bi and Bo to the input and output masks, respectively. The sequence of equal output bits chosen by mask Bo is comparable to the equality of the input bits selected by mask Bi, according to Matsui's definition of LP, defined mathematically as follows:
where Y stands for the set input bits of order 2n. The performance results of the LP analysis are shown in Table 6, indicating that the suggested S-boxes successfully resist linear cryptanalysis.
5.1.5. DP
The value of DP is calculated using the differential uniformity of the S-box, which is defined as:
This indicates that each input differential δu corresponds to a unique output differential δv, ensuring a uniform probability mapping for each i. The DP analysis of the S-boxes produced using the proposed construction approach indicates that the resulting values are close to the ideal value, as presented in Table 6.
5.1.6. Balance
The Boolean function is said to be balanced when there is an equal chance of both 0 and 1 appearing as the output of the Boolean function after all input variable possibilities have been considered. Table 7 depicts that every S-box of the proposed scheme has that property.
5.1.7. Differential and linear branch number
The DBN of an n×n matrix M is a mapping φ:({0,1}m)n⟶({0,1}m)n defined as
The S-box has an input and output size of m-bits each, and the number of S-boxes in a diffusion layer is represented by n arranged in a matrix M. Furthermore, wt denotes the hamming weight of a codeword which gives us the nonzero vectors in that codeword [16]. On the other hand, in LBN, instead of using matrix M, the transpose of that matrix is engaged as defined below
where cc(g,g') presents the coefficient of auto correlation. Additionally, DBN is associated with the difference distribution table, whereas LBN is related to the correlation matrix. The proposed S-boxes LBN and DBN values are presented in Table 7.
5.1.8. LS
The cryptographic significance of the S-boxes LS is examined to ensure its robustness against attacks. It has been observed that block ciphers with linear techniques can be vulnerable to attacks that are faster than an exhaustive key search. Therefore, the confusion phase of the block cipher must avoid any LSs. The LS of an S-box is determined by the following mathematical expression
where
and for some 𝒶∈F2n and C∈F2. The LS of an S-box is defined by its Boolean function C. If C is equal to zero, the LS is known as an invariant LS. If C is equal to one, the LS is known as a complementary LS. Table 7 demonstrates that the proposed S-boxes possess no LS, making them suitable for cryptographic purposes.
5.2. Security performance of the proposed image encryption technique
In this part, several well-known security tests are used to evaluate the proposed encryption system's level of security. We used images of women, house, jellybeans, and couple for encryption.
5.2.1. Histogram analysis
An image histogram visualizes the distribution of grayscale frequencies within an image, offering insights into its tonal distribution. When applying the suggested technique for image encryption, the frequency of occurrence for each grayscale value in the encrypted image tends to become more uniform, resulting in a flatter histogram. This indicates that the encryption method is highly resistant to traditional statistical attacks. The corresponding images and their histograms are illustrated in Figure 3, the findings indicate that the histograms of the encrypted images exhibit a nearly uniform distribution and differ significantly from those of the original images. This observation suggests that the proposed scheme demonstrates high resilience against statistical attacks.
5.2.2. Information entropy
The amount of unpredictability and uncertainty of the gray-scale values in the encrypted image is calculated using information entropy. The appropriate entropy score is 8 bits because the encrypted image data's numeric range is 0 to 255. As a result, the encrypted image is increasingly resistant to popular statistical attacks, the closer it comes to 8 bits. The higher entropy value of the proposed scheme can be attributed to its ability to generate more random encrypted data. This randomness makes it difficult for an attacker to determine the original image from the encrypted data. As a result, the proposed scheme can efficiently resist statistical analysis, making it a suitable choice for various security applications. Overall, the results presented in Table 8 indicate that the proposed scheme has higher entropy.
5.2.3. Contrast
The contrast ratio, which helps the viewer recognize the object in the image, is one of the key aspects of image quality. Contrast analysis determines how much contrast there is between adjacent pixels over the entire image. The encryption method is deemed to pass the contrast test if the contrast ratio in the ciphered image is increased. The following is a list of the contrast coefficient's mathematical representations:
where Q(i,j) denotes the number of gray level co-occurrence matrices of the image. Also, the constant image has a contrast value of zero. The contrast score of the encrypted image is approximately 10.49 presented in Table 9, indicating a significant variation in pixel intensity and its adjacent pixels throughout the entire image.
5.2.4. Energy
The gray level co-occurrence matrices of the encrypted image are required for analyzing the images energy. The square root of the angular second moment is used in energy analysis to determine the uniformity of pixel intensities. The energy is calculated using the mathematical equation provided below:
whereas Q(i,j) represents GLCM. The low homogeneity score of the encrypted images indicates a higher difference in the GLCM.
5.2.5. Homogeneity
We focus on assessing the GLCM, which is also known as a grey-tone spatial dependency matrix, to determine the proximity of dispersed elements in images to the GLCM diagonal. This is because images inherently contain dispersed contents when captured. The equation utilized for analyzing homogeneity is expressed mathematically as
The homogeneity score for the encrypted images is very low, which suggests that the difference in the GLCM is higher.
5.2.6. Correlation
There is a strong correlation between adjacent pixels in color images due to their close values. The correlation coefficient measures the linearity between neighboring pixel values in the vicinity. The primary objective of the encryption method is to distort the pixels to minimize the correlation among adjacent pixels in the image. For an image encryption algorithm to be considered robust and suitable for security purposes, the correlation coefficient of the encrypted image should approach zero. The experimental results of the correlation test, conducted on various plain and encrypted images for each color channel, are presented in Table 10. The correlation coefficient values obtained from the test indicate that the proposed encryption scheme is highly effective and resilient against statistical attacks. Additionally, the correlation plots depicted in Figure 4 provide evidence of the effectiveness of the proposed approach.
5.2.7. Differential attacks
Attackers commonly employ the differential attack method, where they seek to detect patterns in the encrypted data generated by two nearly identical plain inputs. If such a pattern exists, the attacker may exploit it to uncover the precise key or exploit a vulnerability in the encryption algorithm's security A secure encryption technique creates encrypted data that appears almost random, even when there is a minor change in the input data, as a barrier against differential assaults. The unified average changing intensity (UACI) and the number of pixels change rates (NPCR) are the relevant metrics to assess the encryption scheme's susceptibility to differential attacks. These findings illustrate the strong correlation between the suggested encryption method and the original image data, which could enhance its resilience to differential attacks. Table 11 assesses various color images with their respective NPCR and UACI scores measured. The proposed encryption approach scored higher than the optimal value of 99.58% for NPCR, while the UACI scores were within the optimal range of [33.3% to 33.5%]. These results imply that the proposed encryption method relies heavily on the original image data and has the potential to be more effective against differential attacks.
5.2.8. Mean square error (MSE)
The MSE stands out as a widely used metric for quantifying the discrepancy between the original and encrypted images, thereby evaluating the efficacy between the pixels of the plain image and the corresponding pixel in the encrypted image for all pixels in the image. The resulting squared errors are summed and divided by the total number of pixels. Notably, greater MSE values indicate increased robustness of an encryption algorithm against statistical attacks.
5.2.9. Peak signal to noise ratio (PSNR)
Utilizing the MSE as a foundation, the PSNR emerges as an additional performance measure for assessing encryption algorithms. As given by the following equation, PSNR is determined by taking the logarithm of the ratio between the square of the maximum pixel value (typically 255) and the MSE. As PSNR and MSE display an inverse relationship, diminished PSNR values signify enhanced robustness of an encryption algorithm
Presented in Table 12 are the outcomes for both MSE and PSNR achieved through our newly proposed encryption algorithm across various images. Furthermore, we provide a comparison with the latest literature in Table 12, focusing on MSE and PSNR, respectively. Notably, the findings indicate that our proposed algorithm exhibits superior MSE and PSNR values when compared to [48,49].
5.2.10. Resistant to cryptographic attacks
In the proposed scheme, an algorithm for image encryption is designed to combine an elliptic curve and arithmetic operations of a BEF and an invertible function under the Galois field. This algorithm has been designed to resist various attacks, including chosen-plaintext and chosen-ciphertext attacks. Since a robust encryption algorithm integrates confusion and diffusion properties to fortify its security measures. In the proposed algorithm, we employed permutation to disperse the pixels of images. Further, we generate the nonlinear component by utilizing EC over BEF and inverse function, introducing complexity and preventing simple algebraic relationships between the plain and obtained image. Further, the invertible function under the Galois field provides diffusion to ensure that any changes made to the ciphertext will significantly impact the decrypted image. Additionally, the key stream is generated by utilizing the points of EC and operations of the Galois field; the generated key stream is then XORed with the image entries. The randomness of the key stream ensures that the XOR operation is not easily predictable, enhancing the security of the encryption. The pseudo-randomness of PRNs helps prevent attackers from exploiting regularities or biases in the encryption process. Using these three cryptographic primitives in combination provides a high level of security and makes it difficult for an attacker to break the encryption.
Additionally, using the complex structure of EC and operations of BEF ensures that the algorithm resists attacks. Collectively, these inherent properties impose significant challenges for potential attackers attempting to deduce information about the encryption key or plaintext from the ciphertext. Overall, this proposed algorithm is a robust and effective method for image encryption that provides resistance to various attacks. With the increasing importance of secure image transmission in today's digital world, this algorithm is an essential contribution to the field of cryptography.
5.2.11. Complexity analysis
The complexity analysis involves assessing the resources, such as time and memory, required for execution. Various methods exist to determine algorithmic complexity, the most common being big "O" notation. In this section, we evaluated the proposed scheme using big O. Given that the scheme functions as a substitution permutation network, it initially generates S-boxes, employing them for substitution in the encryption process. Subsequently, the generated numbers are utilized in the permutation module, which linearly shuffles image data. Consequently, the permutation module's time complexity for data permutation is O(3×M×N). Similarly, substituting fixed pixels within the permutation module also requires constant time. In summary, the overall time complexity of the proposed algorithm is O(3×M×N).
6.
Conclusions
EC structure is commonly employed in image encryption applications. In this article, we designed a technique to protect RGB images while transmitting them through insecure channels. The proposed scheme employs a three-phase mechanism to encrypt data. In the first phase, each pixel value is dispersed using a piecewise function on EC points, while in the second phase, the proposed S-box is utilized to create confusion in the image. Subsequently, a PRNS is generated and applied to the confused image to achieve the desired diffusion. The key elements of this proposed image encryption technique include the following: Both SCT and PRNS are designed by utilizing the properties of BEF on EC points. Instead of using large primes, a novel technique is employed for both SCT and PRNS. BEF can resist side-channel attacks, a security attack that exploits information leaked during a cryptographic operation. Because BEF has a uniform distribution of values, which makes it difficult for attackers to obtain sensitive information, BEF can designate large numbers compactly, which is helpful in applications requiring efficient data storage and transmission.
Regarding security analysis, the proposed scheme is up to the mark. Using various testing tools, we assessed the effectiveness of the proposed SCT and determined that it exhibits greater efficiency relative to its respective features. Moreover, standardized tests are performed on the encrypted image data to evaluate the encryption performance. The results of the simulations indicate that the proposed modules generate encrypted data that is highly resistant to typical attacks. Furthermore, a comparative analysis between our scheme and recent research demonstrates that our approach requires fewer operations than existing schemes. From a futuristic point of view, we can also extend this algorithm to the general algorithm.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their gratitude to the deanship of Scientific research at King Khalid University for funding this work through the research group's program under grant number R.G.P.2/5/44.
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad: