Enhancing the robustness of block ciphers through a graphical S-box evolution scheme for secure multimedia applications

1.   Introduction

Data security includes methods that prevent unauthorized entry, disclosure, alteration, tampering, and interruption of sensitive information ^[1,2]. In cryptography, we implement procedures to safeguard data, referred to as cryptosystems or ciphers. There are two principal categories of cryptography: Asymmetric cryptography and symmetric cryptography. Asymmetric cryptography utilizes a pair of keys for its operations, whereas symmetric cryptography employs just one key for both encryption and decryption. We categorize symmetric ciphers into two branches: block ciphers and stream ciphers ^[3]. Sun et al. ^[4] proposed a full mesh aggregation approach, emphasizing the robustness required for securing cryptographic operations.

The stream cipher operates on a byte-by-byte basis to transform plaintext into ciphertext. In the block cipher, a cryptographic key and algorithm encrypt the secret data into blocks to produce ciphertext. The block cipher's substitution box (S-box) is a fundamental and distinctive feature that is essential for the purpose of concealing the connections between the ciphertext and the key. S-boxes are used in conventional block ciphers, such as the advanced encryption standard (AES) ^[5] and data encryption standard (DES) ^[6], to provide cryptosystems with the obfuscation property described by Shannon ^[7]. In general, the protection of a cryptosystem is contingent upon the grade of the S-box that is employed. The competency of block ciphers is guaranteed by the robust S-box. The significance of the S-box in encryption techniques can be illustrated. By investigating its capacity to induce confusion and perplexity in plaintext and by conducting a variety of analyses, we can illustrate its importance.

The S-box in DES is compromised and should no longer be utilized in critical systems. Consequently, inadequate S-boxes diminish the reliability of cryptosystems, making robust S-boxes essential for the creation of dependable cryptosystems. This prompted the cryptographer to embark on a deeper study to create cryptographically secure S-boxes. The AES block cipher has efficiently employed the 8-bit S-box. As a result of the advantageous implementation of the 8-bit S-box, cryptographers globally concentrated on developing resilient S-boxes of the dimensions 8×8. Siddiqui et al. ^[8] employed an elliptic curve to form a secure S-box. In ^[9], the authors introduced a novel method based on the chaotic function firefly algorithm to construct a reliable S-box. In ^[10], DNA-based computing was employed alongside a chaotic dynamical framework to generate a robust S-box. In ^[11], a certain type of algebraic structure was employed to compose more than 2 million copies of AES-like S-boxes. In ^[12], the authors provided an innovative S-box design method. To construct an S-box with elevated nonlinearity, the authors used graphs for a certain triangle group and a permutation group of large order. In ^[13], the authors introduced a resilient S-box utilizing the stochastic fractal search technique. Artuger and Ozkaynak ^[14] proposed a novel method for constructing safe S-boxes utilizing chaos theory and genetic algorithms. Fadhil et al. ^[15] employed a one-dimensional logistic chaotic map to generate an S-box with satisfactory cryptographic attributes. In ^[16], we present an efficient S-box construction methodology utilizing algebraic rings and symmetric groups. Ullah et al. devised a systematic methodology for the creation of extremely nonlinear S-boxes ^[17]. The authors utilized the concept of Mordell elliptic curves in the proposed strategy. In ^[18], a robust S-box design was introduced, incorporating a chaotic sequence and a complete Latin square. In ^[19], the suggested S-box was developed using a chaotic dynamical oscillator. In ^[20], researchers developed a novel mechanism of S-box formation that makes use of coset diagrams and a newly defined matrix operation. Khan et al. introduced an S-box derived from a chaotic map exhibiting minimal differential uniformity ^[21]. Artuger and Özkaynak ^[22] offered an innovative method to improve the quality of chaos-based substitution boxes. The technique was successfully evaluated on many S-boxes. In ^[23], a novel external parameter-independent cost mapping was utilized in the development of robust S-boxes.

Recent advances in data security include DNA storage encryption methods, hybridization techniques, and chaotic semi-tensor product theory applications ^[24,25,26]. Video encryption innovations leverage temporal action segmentation and 2D memristive cubic maps for enhanced security ^[27,28]. Innovative approaches to data security include the construction of non-degenerate hyperchaotic systems ^[29], video encryption algorithms leveraging 2D extended Schaffer function maps and neural networks ^[30], and the application of 2D-HELS hyperchaotic maps for secure image encryption through RNA operations and dynamic confusion ^[31].

The growth of algebraic frameworks and their automorphism features are essential concerns. Furthermore, AES proved to be susceptible to several linear cryptanalysis attacks, and numerous loops were deciphered. These issues necessitate the development of new, complex, and robust methods for constructing secure S-boxes. The goal of this research is to develop a novel S-box design scheme based on the combination of two group theoretic graphs whose sum of vertices is 256. We generate a sequence with the vertices of these graphs that possess enough randomness, which is necessary for a reliable S-box. We organize the remaining content of this study as follows: In Section 2, we present some basic knowledge about the Galois field of prime power order and coset graphs. Section 3 provides the construction scheme of the proposed S-box. Section 4 focuses on evaluating the generated S-box's performance using various algebraic analyses. We conduct several statistical analyses in Section 5 to assess the suitability of the generated S-box for image encryption applications through MLC. This section also contains differential analysis, and histogram test. Section 6 presents the conclusion of this research.

2.   Mathematical preliminaries

Prior to detailing the suggested strategy, it is essential to explain certain details regarding the modular group $\boldsymbol{M}$, Galois fields $\boldsymbol{G}\boldsymbol{F}\left({\mathbf{2}}^{\boldsymbol{n}}\right)$, and the associated coset graphs.

2.1.   Coset graphs of the modular group over Galois fields

Until 1830, algebraists believed that a finite field has always prime order. For each prime $p$ and $n\in \mathbb{N},$ Évariste Galois constructed a field having ${p}^{n}$ number of elements. It is referred to as Galois field, symbolized by $GF\left({p}^{n}\right).$ Galois proved that $GF\left({p}^{n}\right) = {\mathbb{Z}}_{p}\left[X\right]/f\left({\varUpsilon}\right) = \left\{{\varUpsilon}, {{\varUpsilon}}^{2}, {{\varUpsilon}}^{3}, \dots, {{\varUpsilon}}^{n-1} = 1\right\}$, where ${\mathbb{Z}}_{p}\left[X\right]$ represents the field extension of ${\mathbb{Z}}_{p}$ and $f\left({\varUpsilon}\right)$ is an nth degree irreducible polynomial over ${\mathbb{Z}}_{p}$ ^[32]. In other words, a Galois field $GF\left({p}^{n}\right)$ can be built using an irreducible polynomial of degree $n$ over ${\mathbb{Z}}_{p}$. It is essential to note that, for fixed values of $p$ and $n$, many irreducible polynomials of degree $n$ exist over ${\mathbb{Z}}_{p}$; hence, several Galois fields $GF\left({p}^{n}\right)$ of a given order ${p}^{n}$ can be generated.

The modular group $M$ ^[33] is generated by $x:\gamma ⟶\frac{-1}{\gamma }$ and $y:\gamma ⟶\frac{\gamma -1}{\gamma }$, with the finite presentation $\left\langle{x, y:{x}^{2} = {y}^{3} = 1}\right\rangle$. The coset graphs for M were developed in 1983 by Q. Mushtaq ^[34]. These graphs result from the action of M on $GF\left({p}^{n}\right)$∪ {∞}. The generators $x:\gamma ⟶\frac{-1}{\gamma }$ and $y:\gamma ⟶\frac{\gamma -1}{\gamma }$ of $M$ are applied to each element of $GF\left({p}^{n}\right)$. Consequently, we obtain permutation representations of $x$ and $y$. Since $x$ has order two, then, the permutation representation of $x$ is the product of disjoint transpositions. Similarly, the permutation representation of $y$ is the product of disjoint cycles of length three. In a coset graph, each cycle $\left(a, b, c\right)$ of $y$ gives rise to a triangle $\mathrm{\Delta }abc$ and each cycle $(r, s)$ of $x$ represents a line joining $r$ and $s$ called the $x$-edge. Note that if $r$ and $s$ are in different cycles of $y$, then $(r, s)$ is a line joining vertices of two different triangles; otherwise, $(r, s)$ is a loop, that is, a line joining two vertices of the same triangle. The elements of $GF\left({p}^{n}\right)$ ∪ {∞} that are fixed points of $x$ and $y$ are presented by small circles. A coset graph is composed of triangles, where each vertex of the triangle is linked to just one vertex of the triangle via an x-edge. For further elucidation on the coset graphs of M, we suggest consulting references ^[35,36,37].

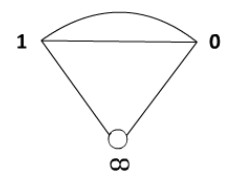
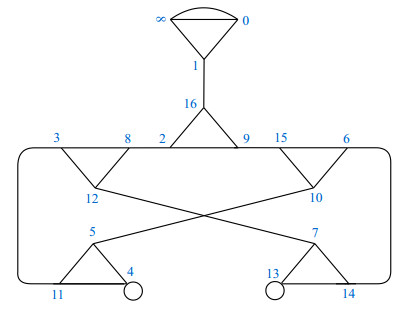
In the subsequent example, we construct a coset graph of M over $GF\left(17\right)\cup \left\{\infty \right\}.$

Example 2.1 In order to draw the coset graph of $M$ on $GF\left(17\right)$ ∪ {∞}, we first apply $x:\gamma ⟶\frac{-1}{\gamma }$ and $y:\gamma ⟶\frac{\gamma -1}{\gamma }$ on each element of $GF\left(17\right)$ ∪ {∞}. It is important to mention that, for every $\gamma \in GF\left(17\right)$ ∪ {∞}, both $\left(\gamma \right)x$ and $\left(\gamma \right)y$ are fractions. Since $17$ is zero in $GF\left(17\right)$, we continue to add $17$ to the numerator until we reach an integral value. This method allows us to derive the permutation forms of $x$ and $y$:

The coset graph in Figure 1 is the result of the aforementioned permutation forms of $x$ and $y$.

2.2.   Galois fields involved in the proposed method

An $8$-bit S-box has 256 distinct entries and ${2}^{8} = 256$, therefore Galois field $GF\left({2}^{8}\right)$ plays a vital role in the $8$-bit S-box construction scheme. In the literature, many S-box design proposals involving $GF\left({2}^{8}\right)$ have been suggested. The S-box used in AES ^[5] is generated by the irreducible polynomial $1+{\varUpsilon}+{{\varUpsilon}}^{3}+{{\varUpsilon}}^{4}+{{\varUpsilon}}^{8}$. In ^[38,39], the authors proposed the method of S-box design based on $1+{\varUpsilon}+{{\varUpsilon}}^{2}+{{\varUpsilon}}^{3}+{{\varUpsilon}}^{4}+{{\varUpsilon}}^{8}$. Farwa et al. ^[40] generated an S-box by using $1+{{\varUpsilon}}^{4}+{{\varUpsilon}}^{5}+{{\varUpsilon}}^{6}+{{\varUpsilon}}^{8}$. In this work, instead of using the Galois field $GF\left({2}^{8}\right)$ of 256 elements, we first involve $G{F}_{1}\left({2}^{7}\right)$ and $G{F}_{2}\left({2}^{7}\right)$ both having 128 elements, write their elements in a $16\times 16$ matrix with the help of the vertices of their coset graphs, and then define a function $f:G{F}_{1}\left({2}^{7}\right)\cup G{F}_{2}\left({2}^{7}\right)⟶GF\left({2}^{8}\right)$ to generate our initial S-box of reasonable strength. Furthermore, we increase complexity by reshuffling the initial S-box columns. The irreducible polynomials $f\left({\varUpsilon}\right) = 1+{{\varUpsilon}}^{4}+{{\varUpsilon}}^{7}$, $g\left({ T}\right) = 1+{ T}+{{ T}}^{2}+{{ T}}^{3}+{{ T}}^{5}+{{ T}}^{6}+{{ T}}^{7},$ and $h\left(\delta \right) = 1+{\delta }^{4}+{\delta }^{5}+{\delta }^{6}+{\delta }^{8}$ are used to generate the elements of $G{F}_{1}({2}^{7}$), $G{F}_{2}\left({2}^{7}\right)$, and $GF\left({2}^{8}\right),$ respectively (see Tables 1–3).

3.   Proposed S-box construction method

The construction process of the generated S-box is based on coset graphs for $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$ and $G{F}_{2}\left({2}^{7}\right)\cup \left\{\infty \right\}$ along with a certain column reshuffling pattern. This section is devoted to narrating the process used to complete the task.

3.1.   Coset graphs used in the method

We designed the proposed S-box using two coset graphs ${D}_{1}$ and ${D}_{2}$ evolved through the action of $M$ on $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$ and $G{F}_{2}\left({2}^{7}\right)\cup \left\{\infty \right\},$ respectively.

In this section, we propose our S-box construction method based on the concepts described in the previous section.

3.1.1.   Coset graphs of $M$ for $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$

In order to form coset graphs of $M$ for $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$, we first apply the generators $x:\gamma ⟶\frac{-1}{\gamma }$ and $y:\gamma ⟶\frac{\gamma -1}{\gamma }$ of $M$ on each element of $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$ and obtain permutation representations of $x$ and $y$, respectively. For instance,

$\left({{\varUpsilon}}^{1}\right)x = \frac{-1}{{{\varUpsilon}}^{1}} = \frac{1}{{{\varUpsilon}}^{1}} = \frac{{{\varUpsilon}}^{127}}{{{\varUpsilon}}^{1}} = {{\varUpsilon}}^{126}$ and $\left({{\varUpsilon}}^{126}\right)x = \frac{-1}{{{\varUpsilon}}^{126}} = \frac{1}{{{\varUpsilon}}^{126}} = \frac{{{\varUpsilon}}^{127}}{{{\varUpsilon}}^{126}} = {{\varUpsilon}}^{1}$, that is, $\left({{\varUpsilon}}^{1}, {{\varUpsilon}}^{126}\right)$.

Also, $\left({{\varUpsilon}}^{1}\right)y = \frac{{{\varUpsilon}}^{1}-1}{{{\varUpsilon}}^{1}} = \frac{{{\varUpsilon}}^{97}}{{{\varUpsilon}}^{1}} = {{\varUpsilon}}^{96}$, $\left({{\varUpsilon}}^{96}\right)y = \frac{{{\varUpsilon}}^{96}-1}{{{\varUpsilon}}^{96}} = \frac{{{\varUpsilon}}^{126}}{{{\varUpsilon}}^{96}} = {{\varUpsilon}}^{30}$, and $\left({{\varUpsilon}}^{30}\right)y = \frac{{{\varUpsilon}}^{30}-1}{{{\varUpsilon}}^{30}} = \frac{{{\varUpsilon}}^{31}}{{{\varUpsilon}}^{30}} = {{\varUpsilon}}^{1}$, that is, $\left({{\varUpsilon}}^{1}, {{\varUpsilon}}^{96}, {{\varUpsilon}}^{30}\right).$

In a similar way, we find all remaining cycles of the permutations $x$ and $y$ which are given as:

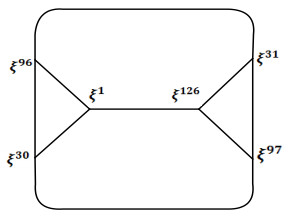
These permutations of $x$ and $y$ give rise to a disconnected coset diagram ${D}_{1}$, consisting of a total of 22 patches. It is worth mentioning that out of these 22 patches, 21 are of similar type, denoted by ${D}_{1}\left({\mathrm{\Gamma }}_{i}\right)$, where $i = \mathrm{1, 2}, 3, \dots, 21$, and the 22^nd patch, which is a straight line connecting 1 and 0 through $x$, is denoted by ${D}_{1}\left(\mathrm{\Pi }\right)$. Figures 2 and 3 show ${D}_{1}\left(\mathrm{\Pi }\right)$ and one of the copies of ${D}_{1}\left({\mathrm{\Gamma }}_{i}\right)$, respectively.

3.1.2.   Coset graphs of $M$ for $G{F}_{2}\left({2}^{7}\right)\cup \left\{\infty \right\}$

We denote this coset diagram by ${D}_{2}$, obtained as a result of the action of $M$ on $G{F}_{2}\left({2}^{7}\right)\cup \left\{\infty \right\}$. The permutation representations of $x$ and $y$ are given below:

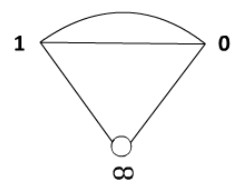
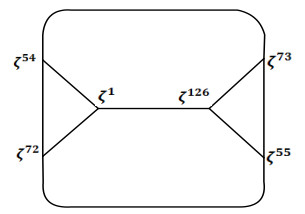
The coset diagrams ${D}_{1}$ and ${D}_{2}$ are similar except in the labeling of the vertices. In ${D}_{2}$, the 21 similar types of patches are denoted by ${D}_{2}\left({\mathrm{\Gamma }}_{i}\right)$, and the 22^nd patch is represented by ${D}_{2}\left(\mathrm{\Pi }\right)$. In Figures 4 and 5, ${D}_{2}\left(\mathrm{\Pi }\right)$ and one of the copies of ${D}_{2}\left({\mathrm{\Gamma }}_{i}\right)$ are shown, respectively.

3.2.   Proposed method

The suggested S-box construction scheme involves three steps. The explanation of all three steps is provided below.

Step 1. In this step, we construct a square matrix of 256 elements by the above-mentioned two coset graphs, that is, coset graphs for $G{F}_{1}\left({2}^{7}\right)$ and $G{F}_{2}\left({2}^{7}\right)$. We pick one copy of fragments ${D}_{1}\left({\mathrm{\Gamma }}_{i}\right):i = \mathrm{1, 2}, 3, \dots, 21,$ which has a vertex with the least power of ${\varUpsilon}$, that is, ${{\varUpsilon}}^{1}$. Call it ${D}_{1}\left({\mathrm{\Gamma }}_{1}\right)$, and apply $xyx{y}^{-1}xy$ on ${{\varUpsilon}}^{1}\in {D}_{1}\left({\mathrm{\Gamma }}_{1}\right)$ such that we reach ${{\varUpsilon}}^{126}$ by following the path:

${{\varUpsilon}}^{1}\stackrel{x}{\to }{{\varUpsilon}}^{126}\stackrel{y}{\to }{{\varUpsilon}}^{97}\stackrel{x}{\to }{{\varUpsilon}}^{30}\stackrel{{y}^{-1}}{\to }{{\varUpsilon}}^{96}\stackrel{x}{\to }{{\varUpsilon}}^{31}$ (see Figure 3). Insert ${{\varUpsilon}}^{1}, {{\varUpsilon}}^{126}, {{\varUpsilon}}^{97}, {{\varUpsilon}}^{30}, {{\varUpsilon}}^{96}$, and ${{\varUpsilon}}^{31}$ at the 1^st, 2^nd, 3^rd, 4^th, 5^th and 6^th places of the first row, respectively. Next, we choose a copy from the fragments ${D}_{2}\left({\mathrm{\Gamma }}_{i}\right):i = \mathrm{1, 2}, 3, \dots, 21$ that contains a vertex with the least power of ${ T},$ that is, ${{ T}}^{1}.\mathrm{N}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{ }\mathrm{i}\mathrm{t}{D}_{2}\left({\mathrm{\Gamma }}_{1}\right)\left(\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{ }\mathrm{F}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }5\right)$ and write all the vertices of ${D}_{2}\left({\mathrm{\Gamma }}_{1}\right)$ at the 7^th, 8^th, 9^th, 10^th, 11^th, and 12^th positions of the 1^st row in a similar way as written in the case of ${D}_{1}\left({\mathrm{\Gamma }}_{1}\right)$. After that, select a copy from $\left\{{D}_{1}\left({\mathrm{\Gamma }}_{i}\right):i = \mathrm{1, 2}, 3, \dots, 21\right\}-\left\{{D}_{1}\left({\mathrm{\Gamma }}_{1}\right)\right\}$ that has the least power of ${ T}$ (it is important to mention here that the vertex with the least power of ${ T}$ does not have to be ${{ T}}^{2},$ because ${{ T}}^{2}$ could be one of the vertices of ${D}_{1}\left({\mathrm{\Gamma }}_{1}\right)$. Name this copy ${D}_{1}\left({\mathrm{\Gamma }}_{2}\right)$, and write the six vertices of ${D}_{1}\left({\mathrm{\Gamma }}_{2}\right)$ as the next six elements (13^th, 14^th, 15^th and 16^th elements of the 1^st row and the 1^st and 2^nd elements of the 2^nd row) of the matrix in a similar order mentioned in the case of ${D}_{1}({\mathrm{\Gamma }}_{1}$). Then, we use a copy from $\left\{{D}_{2}\left({\mathrm{\Gamma }}_{i}\right):i = \mathrm{1, 2}, 3, \dots, 21\right\}-\left\{{D}_{2}\left({\mathrm{\Gamma }}_{1}\right)\right\}$ to write 6 more elements, and this process continues until all the copies of ${D}_{1}\left({\mathrm{\Gamma }}_{i}\right)$ and ${D}_{2}\left({\mathrm{\Gamma }}_{i}\right)$ are exhausted. In this way, we have filled the matrix with the elements of $G{F}_{1}\left({2}^{7}\right)$ and $G{F}_{2}\left({2}^{7}\right)$ up to the 12^th element of the 16^th row. Lastly, place 1, 0 from fragment ${D}_{1}\left(\mathrm{\Pi }\right)$ and 1, 0 from fragment ${D}_{2}\left(\mathrm{\Pi }\right)$ at the 13^th, 14^th, 15^th, and 16^th positions of the last row. Thus, we were able to develop a square matrix (see Table 4) with $256$ points from $G{F}_{1}\left({2}^{7}\right)$ and $G{F}_{2}\left({2}^{7}\right)$.

Step 2. In Step 1, we created a matrix with 128 distinct entries at 256 positions, ensuring each entry occupies two positions. In this step, we construct our initial S-box, that is, a square matrix of order 16 with distinct entries (see Table 5) by defining a bijective map $f:G{F}_{1}\left({2}^{7}\right)\cup G{F}_{2}\left({2}^{7}\right)⟶GF\left({2}^{8}\right)$ by

The constructed initial S-box possesses satisfactory qualities to secure sensitive information. Its nonlinearity value is 104.50. In the next step, we further strengthen its security capabilities.

Step 3. In this step, we apply the action of a permutation group G with four generators on the initial S-box to generate our proposed S-box. The group G is generated by the elements a, b, c, and d, where the generators are given as:

$a =$(1,148,162, 24, 38, 93,152, 90, 78, 41, 13, 54, 35,213,155, 89, 98,127,192,211, 5,200,186,117, 96, 99,206, 37,208,229,250,109,203,181, 25,107,170,246, 14, 33,207,150, 77,232, 97,240,112,231, 95,122,182,252, 74, 57, 66,129, 6, 30,102,251, 23,165, 9,151,120,134,234, 55, 12,184,256,239,218,188,244,104,216,233,131,177,224,164,214,220,195, 15, 42,227, 48,198, 50, 31,118, 83,156, 88,147,124,179, 47, 80,222, 19,111,169, 32,221, 76,139, 67,140,245,110,238,132,103, 56,115, 63,125,161,201, 86,194,167, 20, 39,199,128, 79,126, 84,176,226, 58,119, 28, 49).

$b =$ (2,149, 65,193, 73, 52, 8).

$c =$(3,105,254, 43,174,175,166,137, 7, 17,173,133,145,144, 51,138, 75,249,253, 64,146,197,159,235,191,121, 94,172,114,236,142,160, 92,189, 85,255,153, 27,196,141, 91,100,187,185,204,183,180, 59, 26, 68, 53,219, 36, 82, 71,178, 60, 10,157, 11, 44, 4,248, 45,202,106, 61, 72,243,168, 87, 22,225,136,101,163,209, 21,190,116,247,158,242, 18, 70,210,143,212,113,205,237, 62,130, 29,228,123, 40,215,171,108,154, 46, 16).

$d =$(34, 81,241,230, 69,217,135).

With the help of GAP software, we determine that $G$ has the finite presentation of the form:

and the order of $G$ is $696486$. The actions of all these 696486 elements (permutations) on the initial S-box produce a new S-box. After exhaustive enumeration, we identify that the S-box resulting from the application of the element ${a}^{83}{b}^{5}{c}^{13}{d}^{4}$ achieves the highest nonlinearity score of 111.75. Thus, we select this S-box as our proposed S-box (see Table 6) for its enhanced security properties.

4.   Algebraic analyses

In this section, we undertake an assessment of the security characteristics of the newly created S-box. The evaluation of the properties of the proposed S-box is critical in determining its potential use in various encryption techniques and security contexts. To accomplish this objective, we apply five security performance tests. We then compare the results obtained from the proposed S-box to those of widely recognized S-boxes. The subsequent sections present a comprehensive explanation of the security tests employed on these S-boxes.

4.1.   Bijection test

The bijection test assesses the distinctiveness of the output generated by an S-box. When an S-box meets the bijection criterion, the output values are distinct and are not repeated within the range of $\left[\mathrm{0,255}\right].$ Additionally, a one-to-one correspondence exists between each input and output value. The suggested S-box has been found to meet the criteria for the bijection test. It generates distinct output values within the range of $[0,255]$, establishing a one-to-one correspondence between each input and its corresponding output.

4.2.   Nonlinearity

A Boolean mapping $\theta :{Z}_{2}^{k}⟶{Z}_{2}$ is nonlinear if it is at least as far away from the set of affine mappings as possible. This makes sure that the input vectors are not linearly mapped to the output vectors ^[41]. Its mathematical calculation is as follows:

where ${\mathcal{S}}_{\theta }\left(v\right) = {\sum }_{u\in {Z}_{2}^{k}}{\left(-1\right)}^{\theta \left(u\right)}{\left(-1\right)}^{u.v}$ is the Walsh spectrum of $\theta \left(u\right)$ and $u.v$ represents the scalar product of $u$ and $v,$ respectively. Table 7 shows that the average nonlinearity of all eight Boolean mappings in the proposed S-box is 111.75. Table 12 presents a comparison of our S-box with other S-boxes in terms of nonlinearity analysis, demonstrating the proficiency of our S-box.

4.3.   Strict avalanche criteria

The assessment of the quality of an S-box also encompasses the use of the strict avalanche criterion (SAC), which was introduced in 1985 ^[42]. This method assesses whether altering a single input bit results in a probability of half of the output bits changing. This analysis is characterized by the determination of the S-box's dependency matrix. A desirable S-box should have an average value for all dependency matrix elements that is closer to 0.50. Table 8 shows the dependency matrix of the developed S-box, with an SAC average value of 0.5007, which is nearly equal to the ideal value. Therefore, the developed S-box meets the SAC requirements.

4.4.   Bits independence criteria

The bit independence criteria (BIC) is a set of strict rules for checking how well the output bits work and how changes affect the next encryption cycles. This scrutiny involves pairwise comparison of the variables to ascertain their level of independence. For intricate and dependable systems, a high degree of BIC-nonlinearity is essential. Table 9 illustrates the BIC-nonlinearity dependency matrix. Additionally, we apply the SAC to BIC. Table 10 showcases the dependency matrix for BIC-SAC. The findings indicate that the proposed S-box meets the BIC requirements.

4.5.   Linear probability

To ensure data privacy, modern block ciphers aim to increase the degree of indeterminacy and complexity in the encrypted data bits. This mechanism provides a shield against various techniques utilized by cryptanalysts to decipher the encrypted text. The primary way to achieve this is by deploying S-boxes. An S-box with a lower linear probability (LP) score is generally considered to be an effective countermeasure against linear cryptanalysis attacks. A mathematical formula ^[43] determines the LP of a substitution box, as shown below:

where ${f}_{u}$ and ${g}_{u}$ represent input and output masks, respectively. The proposed S-box has an LP score of 0.0703.

4.6.   Differential uniformity

A fundamental measure of an S-box's performance, differential uniformity (DU) ^[43], evaluates its resistance against differential attacks. We compute DU as the number of identical mappings from an input differential $\Delta \mathcal{r}$ to an output differential $\Delta \mathcal{s}$. The S-box is considered efficient in countering differential attacks when it has a low DU value. The mathematical formula to calculate the DU value is as follows;

Table 11 shows the differential distribution for the proposed S-box. Our S-box has a maximum DU value of 6, which indicates that it is sufficiently strong to resist the effects of differential attacks.

4.7.   Comparison analysis discussion

The suggested S-box shows remarkable cryptographic properties, therefore stressing the strength of its developing technique in comparison to current S-boxes. By means of a thorough investigation of important performance measures in Table 12, the S-box exhibits robustness against several cryptographic assaults, surpassing many previously developed S-boxes using optimization, algebraic, and chaotic approaches. Significant findings on the strength of the suggested S-box architecture are presented below.

i. To withstand linear assaults, the S-box must have a large NL value. It is critical for defending against linear cryptanalysis by increasing the S-box's complexity and confusion. The proposed S-box achieves an average NL value of 111.75, which is significantly higher than S-boxes listed in Table 12. Therefore, the proposed S-box has a significant level of complexity and confusion, rendering it resistant to all available linear cryptanalysis techniques.

ii. A SAC value close to 0.5 shows that each output bit depends equally on each input bit. This way, an optimal diffusion effect can be achieved. The SAC value of the proposed S-box (0.5007) is approximately equal to 0.5 outperforming many S-boxes listed in Table 12. This shows the S-box's strong compliance with the SAC requirement, ensuring a robust spread of bit changes across output.

iii. In terms of BIC, both for SAC and NL, the proposed S-box exhibits superior performance. A high BIC score ensures that changes in individual bits are independent and propagate effectively, a critical feature for strong encryption. The proposed S-box achieves BIC-NL and BIC-SAC values that surpass most of the existing S-boxes, ensuring optimal bit independence.

iv. An efficacious S-box has a lower DU value. As shown in Table 12, the DU value of the proposed S-box is either less than or equal to the DU values of the S-boxes listed in Table 12.

v. An S-box with a low LP score is less susceptible to linear cryptanalysis. Our S-box has an LP score of 0.0703, which is lower or equal to the LP values of the S-boxes listed in Table 12.

5.   Majority logic criterion for encryption analysis

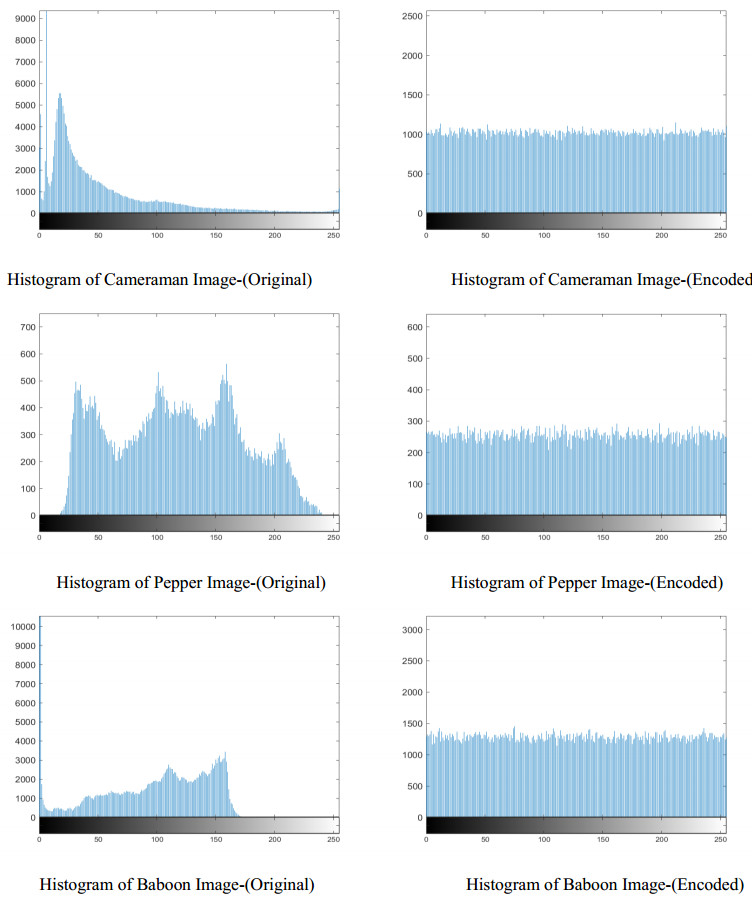
The MLC ^[61] comprises a collection of evaluations, including contrast, correlation, energy, homogeneity, and entropy. The results of these tests assist in selecting the most suitable S-box for the encryption procedure. We assess the statistical competence of the S-box using the MLC for various encryption techniques. The available research describes a variety of statistical and analytical techniques for determining the S-box's potential to generate perplexity. Since the encryption process distorts the image, it is essential to understand the impact of statistical characteristics. A correlation test examines the relationship between plaintext and ciphertext. The entropy value depicts the level of randomness in the ciphertext image. Contrast analysis evaluates the brightness loss in the plaintext image during the encryption process. We can examine more features of the ciphertext by employing homogeneity and energy analyses. In light of the significance of these analyses' findings, we used our S-boxes to encrypt plaintext images and conduct MLC tests. For this purpose, we choose three 256×256 grayscale images of pepper, cameraman, and baboon. Figure 6 displays all images before and after encryption, while Table 13 lists the MLC outcomes. These results demonstrate the effectiveness of the developed substitution box for image encryption and its strong cryptographic attributes, making it suitable for use in safe data transmission algorithms.

5.1.   Differential analysis

The two major criteria, unified average changing intensity (UACI) and number of pixel change rate (NPCR), are employed for quantifying the impact of a single pixel alteration on the image encoded. The disparity in pixel counts between the two encoded images is quantified by NPCR, while the mean intensity variance is assessed using UACI. The pixel variation between two initial images is merely one, with their associated encoded images represented as ${C}_{1}\left(i, j\right)$ and ${C}_{2}\left(i, j\right)$. The NPCR and UACI scores are computed using the subsequent equations:

where $D\left(i, j\right) = 0$ if ${C}_{1}\left(i, j\right){ = C}_{2}\left(i, j\right)$ and otherwise, $D\left(i, j\right) = 1$. Also, $M$ is the width and $N$ is the height of the image. Table 14 provides a comprehensive overview of the UACI and NPCR measures.

5.2.   Histogram analysis

Histograms depict the distribution of pixel grey level intensities within an image. A cryptanalyst may employ the provided information to execute histogram attacks if the distribution is non-uniform. Nonetheless, the methodology has been developed to withstand histogram assaults, rendering data unidentifiable if the histogram is homogeneous and flattening. Analysing the histograms of the encoded and initial images reveals the disparities in colour intensity between the two. We performed analyses on the histograms of both the original and encrypted images and discovered that the histogram distribution of the encoded image, produced using the suggested S-box, markedly diverges from that of the original image. Figure 7 displays the histograms of both the original and encrypted versions of selected photographs for encryption. The histogram of the encrypted image has a notably uniform distribution, validating the efficacy of the suggested technique.

6.   Conclusions

This article introduces an innovative strategy for constructing dependable and resilient S-boxes with significant nonlinearity. The approach investigates the principles underlying coset graphs, which are derived from $G{F}_{1}\left({2}^{7}\right)\cup \left\{\infty \right\}$ and $G{F}_{2}\left({2}^{7}\right)\cup \left\{\infty \right\}$, in addition to a particular type of column rearrangement. Initially, an S-box is constructed by selecting vertices from two distinct graphs and placing them at predetermined positions within the matrix representing the S-box. Following the initial step, a permutation group of large order enhances the robustness of the initial S-box, ensuring its resistance against various cryptanalytic attacks. An execution evaluation quantifies the cryptographic quality of the generated S-box. When comparing the created S-box with other contemporary S-boxes, we see that it possesses superior cryptographic characteristics. Furthermore, the constructed S-box is applied to encrypt digital images, and the results obtained through the MLC indicate that the encrypted content exhibits favorable encryption quality. Therefore, the utilization of the suggested S-box in the domain of image encryption indicates its appropriateness for safeguarding data while it is being transmitted over an unsecured channel.

Author contributions

Abdul Razaq: Conceptualized the study, developed the methodology, and conducted the analysis. Muhammad Mahboob Ahsan: contributed to algorithm development, data validation, and manuscript review. Hanan Alolaiyan: Secured funding, contributed to mathematical framework design, and assisted in interpretation and revisions. Musheer Ahmad: Reviewed literature, linked to prior research, and refined the manuscript. Qin Xin: Supported computational implementation and manuscript preparation. All authors reviewed and approved the published version.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This project is supported by the Researchers Supporting Project Number (RSP2024R317) King Saud University, Riyadh, Saudi Arabia.

Conflicts of interest

The authors declare no conflict of interest.

Supplementary

Illustration and implementation details of step III in S-box construction

In Step III of the proposed method for S-box construction, we demonstrate that applying the element ${a}^{83}{b}^{5}{c}^{13}{d}^{4}$ to the initial S-box transforms it into the proposed S-box, achieving a nonlinearity score of 111.75. Here, we illustrate the process in detail. Since

$a =$(1,148,162, 24, 38, 93,152, 90, 78, 41, 13, 54, 35,213,155, 89, 98,127,192,211, 5,200,186,117, 96, 99,206, 37,208,229,250,109,203,181, 25,107,170,246, 14, 33,207,150, 77,232, 97,240,112,231, 95,122,182,252, 74, 57, 66,129, 6, 30,102,251, 23,165, 9,151,120,134,234, 55, 12,184,256,239,218,188,244,104,216,233,131,177,224,164,214,220,195, 15, 42,227, 48,198, 50, 31,118, 83,156, 88,147,124,179, 47, 80,222, 19,111,169, 32,221, 76,139, 67,140,245,110,238,132,103, 56,115, 63,125,161,201, 86,194,167, 20, 39,199,128, 79,126, 84,176,226, 58,119, 28, 49),

$b =$(2,149, 65,193, 73, 52, 8),

$c =$(3,105,254, 43,174,175,166,137, 7, 17,173,133,145,144, 51,138, 75,249,253, 64,146,197,159,235,191,121, 94,172,114,236,142,160, 92,189, 85,255,153, 27,196,141, 91,100,187,185,204,183,180, 59, 26, 68, 53,219, 36, 82, 71,178, 60, 10,157, 11, 44, 4,248, 45,202,106, 61, 72,243,168, 87, 22,225,136,101,163,209, 21,190,116,247,158,242, 18, 70,210,143,212,113,205,237, 62,130, 29,228,123, 40,215,171,108,154, 46, 16),

$d =$(34, 81,241,230, 69,217,135).

Therefore,

a⁸³b⁵c¹³d⁴ = (1,220,208,245, 6,148,195,229,110, 30,162, 15,250,238,102, 24, 42,109,132,251, 38,227,203,103, 23, 93, 48,181, 56,165,152,198, 25,115, 9, 90, 50,107, 63,151, 78, 31,170,125,120, 41,118,246,161,134, 13, 83, 14,201,234, 54,156, 33, 86, 55, 35, 88,207,194, 12,213,147,150,167,184,155,124, 77, 20,256, 89,179,232, 39,239, 98, 47, 97,199,218,127, 80,240,128,188,192,222,112, 79,244,211, 19,231,126,104, 5,111, 95, 84,216,200,169,122,176,233,186, 32,182,226,131,117,221,252, 58,177, 96, 76, 74,119,224, 99,139, 57, 28,164,206, 67, 66, 49,214, 37,140,129)(2, 52,193,149, 8, 73, 65)(3,144, 94,141, 36,106,190, 62,105, 51,172, 91, 82, 61,116,130,254,138,114,100, 71, 72,247, 29, 43, 75,236,187,178,243,158,228,174,249,142,185, 60,168,242,123,175,253,160,204, 10, 87, 18, 40,166, 64, 92,183,157, 22, 70,215,137,146,189,180, 11,225,210,171, 7,197, 85, 59, 44,136,143,108, 17,159,255, 26, 4,101,212,154,173,235,153, 68,248,163,113, 46,133,191, 27, 53, 45,209,205, 16,145,121,196,219,202, 21,237)(34, 69, 81,217,241,135,230).

To illustrate the application of a⁸³b⁵c¹³d⁴ on the initial S-box to generate the proposed S-box:

● Since 1 is mapped to 220, we shift the 1st element (which is 2) of the initial S-box to the 220th position (12th element in the 14th row, calculated as 13 × 16 + 12 = 220).

● Since 220 is mapped to 208, we shift the 220th element (207) of the initial S-box to the 208th position (16th element in the 13th row, 13 × 16 = 208).

● Continuing in this manner, 135 is mapped to 230, so we shift the 135th element (59) to the 230th position (6th element in the 15th row, 14 × 16 + 6 = 230).

● Finally, since 230 is mapped to 34, we shift the 230th element (86) to the 34th position (2nd element in the 3rd row, 2 × 16 + 2 = 34).

This iterative process continues for all mappings, thereby constructing the proposed S-box.