1. Introduction

There exist biotechnological processes characterizing with production and consumption of intermediate metabolite. When the considered metabolite is accumulated in the reactor up to definite concentration, the physiological state, corresponding to maximal productivity of the target product, is reached. The difference between production and consumption rates of the metabolite is accepted as key parameter for recognizing of this physiological state. Depending on the process target product, the role of intermediate metabolite could be different. As examples: i) in well known recombinant protein production by cultivation of Saccharomyces cerevisiae (or E. coli), during the fermentative growth of biomass on glucose, ethanol (and/or acetate) is produced and during the following phase, this product is used as substrate for oxidative growth of biomass on ethanol (and/or acetate); ii) the process of gluconic acid production by Aspergillus niger, the gluconic acid is produced at the beginning of the process and when the main carbon source is exhausted, the gluconic acid is used for biomass growth. In general, the bioprocesses mentioned above could be summarised according to the role of the intermediate metabolite in the bioprocess: i) as main substrate for target product production: recombinant protein ^{[1,2,3,4,5,6,7,8]} etc. ii) as target product: ethanol ^[9,10,11,12]; gluconic acid ^{[13,14,15,16]} etc. Those bioprocesses are carried out as fed-batch or continuous. The information about intermediate metabolite production and consumption rates could be used for on-line recognitions of process physiological states and applied for their monitoring and control. Special interests provoke mixed culture processes ^[17]. They are widely used in food industry (wine, beer, milk) as well as in wastewater treatment processes ^[18,19]. As a rule, one microorganism produces an intermediate metabolite that is used as main substrate for other microorganism growth. The target process product depends of second biomass concentration in the reactor. Moreover, the growth of each microorganism needs different cultivation conditions (dissolved oxygen, pH, T°C) that have to be changed for optimal control. In this way the growth of both biomasses will be stimulated separately. So, software sensors for intermediate metabolite production and consumption rates could plays a key role in these cases. As an example, the microbial production of poly-b-hydroxybutyric acid (PHB) by mixed culture of Lactobacillus delbrulckii and Ralstonia eutropha is considered ^{[20,21,22,23,24,25]}.

In this paper, an approach for monitoring of physiological states for two classes of bioprocesses mentioned above is proposed. It is based on a general cascade software sensor of process kinetics. The sensor' input information is on-line measurements of main carbon source and intermediate metabolite. The derived software sensors are investigated by simulations using data of two real processes and applied in algorithms for process adaptive control.

---

2. Monitoring of Intermediate Metabolites Production and Consumption Rates

---

2.1. Problem formulation and structure of casade software sensor

A class of biotechnological processes is considered, characterized with production and consumption rates of intermediate metabolite, which is directly related to target product synthesis. It is assumed that the input information consists of on-line measurements of main carbon source and intermediate metabolite. The yield coefficients related to intermediate metabolite production are known a priory. The main task is to receive on-line information about production and consumption rates of intermediate metabolite.

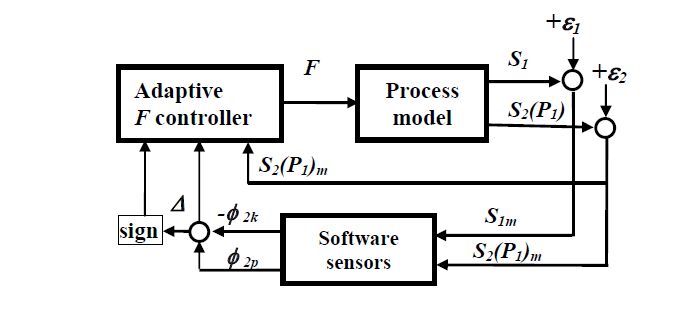
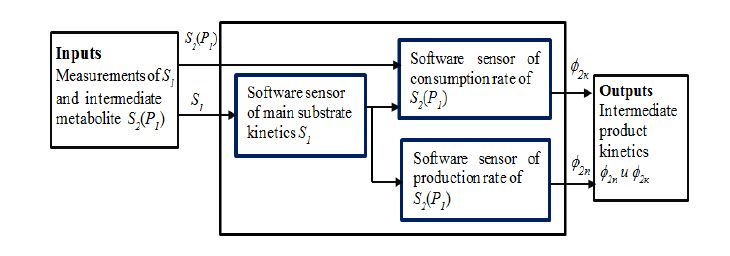
To resolve this problem, a cascade structure of software sensor for these parameters is proposed. In the first step, the kinetics of the main carbon source and the consumption rate of the intermediate metabolite are estimated. In the second step, software sensor of production rate of the metabolite is derived using the information from the first one. The tuning procedure proposed in ^[16] is used for the design of software sensors included in the scheme shown in Figure 1.

In the next sections, applications of this structure to two types of processes will be done.

---

2.2. Application of the cascade software sensor for monitoring and control of bioprocesses characterizing with growth of one microorganism

A class processes characterizing with one microorganism, X, growth is considered. The intermediate metabolite, S₂ (P₁), is produced by main carbon source, S₁, and consumed for target product, P_n, synthesis.

The proposed below cascade software sensor has the structure given in Figure 1. As case study, fed-batch process simultaneous saccharification and fermentation of starch to ethanol will be considered.

---

2.2.1. Case study: fed-batch process of simultaneous saccharification and fermentation of starch to ethanol (SSFSE) by Saccharomyces cerevisiae

Unstructured model

The unstructured model of the one-step process for the simultaneous saccharification and fermentation of starch to ethanol by recombinant yeast is based on the hierarchical unstructured model of ^[26], and is described in detail in ^[27]. For the sake of completeness, the unstructured model is presented. The mass balance for the susceptible and resistant starch fractions is:

$\frac{d{{S}_{Sus}}}{dt}=-{{R}_{Sus}}{{S}_{Sus}}$

(1a)

$\frac{d{{S}_{res}}}{dt}=-{{R}_{res}}{{S}_{res}}$

(1b)

Therefore the balance of total starch degradation is:

$\frac{dS}{dt}=-{{R}_{Sus}}{{S}_{Sus}}-{{R}_{res}}{{S}_{res}}$

(1c)

where:

${{R}_{Sus}}=\frac{{{k}_{sus}}Enz}{{{K}_{m}}\left( 1+\frac{G}{{{K}_{G}}} \right)+\frac{{{S}_{Sus}}^{2}}{{{K}_{Starch}}}+{{S}_{Sus}}+{{S}_{res}}}$

(1d)

${{R}_{res}}=\frac{{{k}_{res}}Enz}{{{K}_{m}}\left( 1+\frac{G}{{{K}_{G}}} \right)+\frac{{{S}_{res}}^{2}}{{{K}_{Starch}}}+{{S}_{Sus}}+{{S}_{res}}}$

(1e)

The Enzyme balance is:

$\frac{dEnz}{dt}={{R}_{Enz}}-\left( \mu +\beta \right)Enz$

(1f)

where:

${{R}_{enz}}=\frac{({{\mu }_{\max }}+\beta )({{S}_{Sus}}+{{S}_{res}})En{{z}_{\max }}}{{{K}_{enz}}+{{S}_{Sus}}+{{S}_{res}}}$

(1g)

For the Cells balance, both cells growth and dead are considered:

$\frac{dX}{dt}=\mu X\,\,-{{K}_{d}}X$

(1h)

where

$\mu ={{\mu }_{\max }}\left( \frac{G}{{{k}_{s}}+G+\frac{{{G}^{2}}}{{{K}_{ss}}}} \right)\left( 1-\frac{E}{{{E}_{m}}} \right)$

(1i)

The Glucose balance considers the glucose produced from starch, and the glucose consumed for both growing of cells and ethanol production:

$\frac{dG}{dt}=1.111\,\,({{R}_{Sus}}{{S}_{Sus}}+{{R}_{Res}}{{S}_{Res}})\,\,\,\,-\left( \frac{\mu X}{{{Y}_{X/G}}} \right)-\left( \frac{\nu X}{{{Y}_{E/G}}} \right)$

(1j)

Finally, the ethanol balance is:

$\frac{dE}{dt}=\nu X$

(1k)

where:

$\nu ={{\nu }_{\max }}\left( \frac{G}{{{k}_{sp}}+G+\frac{{{G}^{2}}}{{{K}_{ssp}}}} \right)\left( 1-\frac{E}{{{E}_{mp}}} \right)$

(1l)

Parameter values of the unstructured model (1) were obtained by a stochastic optimization procedure described in ^[27] using experimental data reported by ^[9].

Model for control

According to the General Dynamical Model Approach ^[28], the model for control is derived on the basis of a process reaction scheme given below. The mechanism of ethanol, P₃, production by Saccharomyces cerevisiae from starch, S₁, is presented as follows:

$\begin{align} & {{S}_{1}}\xrightarrow{{{\phi }_{1}}}{{S}_{2}}({{P}_{1}}) \\ & {{S}_{2}}({{P}_{1}})\xrightarrow{{{\phi }_{2}}}X+{{P}_{2}} \\ & {{S}_{2}}({{P}_{1}})\xrightarrow{{{\phi }_{3}}}{{P}_{3}} \\ \end{align}$

(2)

where φ₁ represents the rate of enzymatic hydrolysis, that is, the conversion of starch, S₁, into glucose, S₂ (P₁) . The glucose is consumed in the second reaction at a rate φ₂ for biomass growth and enzyme, P₂, secretion and in the third reaction for ethanol production, P₃, at a rate φ₃.

The model for control for the considered fed-batch process is presented as follows:

$\frac{d{{S}_{1}}}{dt}=-{{\phi }_{1}}-\frac{F}{V}{{S}_{1}}+\frac{F}{V}{{S}_{in}}$

(3a)

$\frac{d{{S}_{2}}({{P}_{1}})}{dt}={{k}_{1}}{{\phi }_{1}}-{{k}_{2}}{{\phi }_{2}}-{{k}_{3}}{{\phi }_{3}}-\frac{F}{V}{{S}_{2}}({{P}_{1}})$

(3b)

$\frac{dX}{dt}={{\phi }_{2}}-\frac{F}{V}X$

(3c)

$\frac{d{{P}_{3}}}{dt}={{\phi }_{3}}-\frac{F}{V}{{P}_{3}}$

(3d)

$\frac{d{{P}_{2}}}{dt}={{k}_{4}}{{\phi }_{2}}-\frac{F}{V}{{P}_{2}}$

(3e)

$\frac{dV}{dt}=F$

(3f)

where F is the starch feed rate; V is the reactor volume; S _in is the starch concentration in the feed;

${{\phi }_{1}}={{R}_{Sus}}{{S}_{Sus}}+{{R}_{res}}{{S}_{res}}$

(3g)

${{\phi }_{2}}=\mu X\,\,$

(3h)

${{\phi }_{3}}=\nu X$

(3i)

k₁-k₄ are yield coefficients.

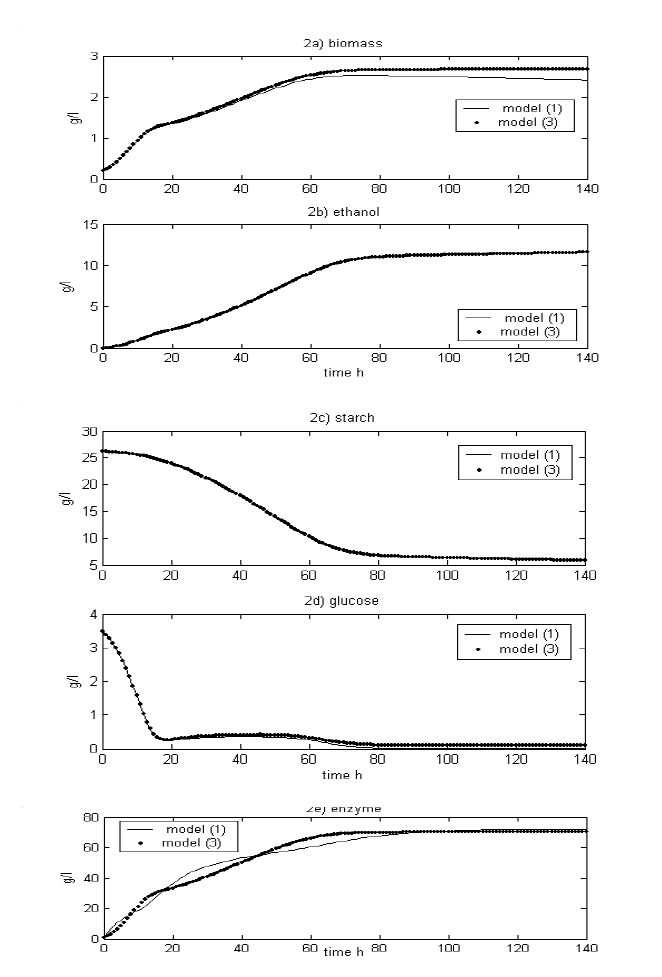
Since the model for control has described the dynamics of the main variables as well as the unstructured one, the next step is the identification of the parameters for model (3). This is done using the batch phase of the process, applying an optimization procedure proposed in ^[2,14,15]. The optimization criterion is the minimization of the mean square error between the state variables of model (1) and model (3). The obtained optimal values of the parameters are: k₁ = 1.086, k₂ = 1.1151, k₃ = 2.0226, k₄ = 28.1748.

In figure 2, simulations of the model for control (3) are cross-validated with model (1) data for the batch condition. As can be seen in the figures, the model (3) (points) describes the dynamics of the main process variables as well as the unstructured model (1) (lines). However, some differences can be noticed in figure 2a due to the effect of the cell death constant, k_d, included in the equation (1 hour). It is important to remark that for the batch conditions at around 20-60 hours the process reaches an equilibrium state for the glucose concentration (figure 2d), which is characterized by a constant biomass growth rate (figure 2a), a constant ethanol production rate (figure 2b) and constant starch degradation rate (figure 2c). However, after 60 hours, this equilibrium state cannot be maintained because of the low level of starch concentration in the fermentor. Therefore, in order to keep the equilibrium condition and obtain high ethanol production rates for longer times, it is necessary to feed additional starch into the reactor, which means to operate under fed batch conditions. For maintaining the process at that equilibrium state for glucose concentration under fed batch conditions, it is necessary to estimate first the glucose production and consumption rates, which is done in the next section through the use of software sensors.

Software sensors of glucose production and consumption reaction rates

Software sensors design is done applying the method proposed in ^[16]. It is assumed that starch and glucose concentrations are measured on-line by industrially available hardware sensors ^[29]. The first step is on-line estimation of starch consumption rate, ${{\phi }_{1}}$, using on-line measurement of starch concentration. The software sensor of is an observer-based estimator with structure:

$\frac{d{{{\hat{S}}}_{1}}}{dt}=-{{\hat{\varphi }}_{1}}-\frac{F}{V}{{S}_{1m}}+\frac{F}{V}{{S}_{in}}+{{\omega }_{1s}}\left( {{S}_{1m}}-{{{\hat{S}}}_{1}} \right)$

(4a)

$\frac{d{{{\hat{\varphi }}}_{1}}}{dt}={{\gamma }_{1s}}\left( {{S}_{1m}}-{{{\hat{S}}}_{1}} \right)$

(4b)

where ω_1s and γ_1s are estimator parameters, S_1m = S₁ + ε, ε is measurement noise.

The design parameters of estimator (4) are derived using an optimal tuning procedure, proposed in ^[16]. For the considered case, the following expressions are obtained:

$\begin{align} & {{\omega }_{1sopt}}=2\xi \sqrt{\frac{{{m}_{11s}}}{2{{m}_{21s}}}} \\ & {{\gamma }_{1sopt}}=\frac{{{\left( {{\omega }_{1sopt}} \right)}^{2}}}{4{{\xi }^{2}}} \\ \end{align}$

(5)

where: m_11s is the upper bound of $d{{\varphi }_{1}}/dt$; m_21s is the upper bound of additive noise of starch; $\xi$ = damping coefficient, a usual value is 0.99.

Glucose production rate is estimated using the first term of the right hand side of equation (3b), where φ₁ is substituted by its estimates from (4b):

${{\hat{\varphi }}_{2p}}={{k}_{1}}{{\hat{\varphi }}_{1}}$

(6)

The next step is to design of the glucose consumption rate estimator. The second and third terms of right hand side of the eq. (3b) are presented as an unknown time-varying parameter:

${{\varphi }_{2k}}={{k}_{2}}{{\phi }_{2}}+{{k}_{3}}{{\phi }_{3}}$

(7)

An estimator of φ_2k can be derived as follows:

$\frac{d{{{\hat{S}}}_{2}}({{P}_{1}})}{dt}={{\hat{\varphi }}_{2p}}-{{\hat{\varphi }}_{2k}}-\frac{F}{V}{{S}_{2}}{{({{P}_{1}})}_{m}}+{{\omega }_{2s}}\left( {{S}_{2}}{{({{P}_{1}})}_{m}}-{{{\hat{S}}}_{2}}({{P}_{1}}) \right)$

(8a)

$\frac{d{{{\hat{\varphi }}}_{2k}}}{dt}={{\gamma }_{2s}}\left( {{S}_{2}}{{({{P}_{1}})}_{m}}-{{{\hat{S}}}_{2}}({{P}_{1}}) \right)$

(8b)

The design parameters of estimator (8) are derived using the tuning procedure proposed in ^[16]. For the considered case, the following expressions are obtained:

$\begin{align} & {{\omega }_{2sopt}}=2\xi \sqrt{\frac{{{m}_{12s}}}{2{{m}_{22s}}}} \\ & {{\gamma }_{2sopt}}=\frac{{{\left( {{\omega }_{2sopt}} \right)}^{2}}}{4{{\xi }^{2}}} \\ \end{align}$

(9)

where: m_12s is the upper bound of $d{{\varphi }_{2k}}/dt$; m_22s is the upper bound of additive noise of glucose.

Simulations are carried out using the values of the design parameters ω_1s, γ_1s, ω_2s, γ_2s, calculated by eqs. (5) and (9) for estimators (4) and (8), respectively, where m_11s = 0.35, and m_21s = 1.3, m_12s = 0.45, and m_22s = 0.1. The white noise signals, e, simulate measurement noises at standard deviation 5% of the mean values of starch and glucose concentrations. Therefore, the optimal values of the design parameters are: ω_{1s opt} = 1.23, γ_1sopt = 0.386, ω_{2s opt} = 4.427, γ_2sopt = 5.

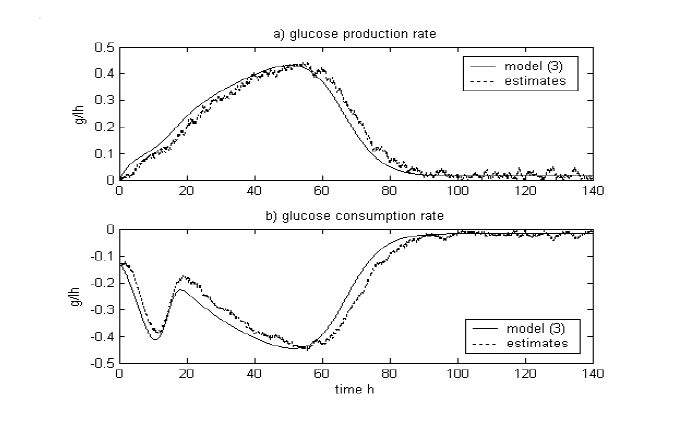
In figures 3a and 3b, comparisons between simulation of model (1) and estimators (4) and (8) are shown respectively. In figure 3, a good tracking of glucose production and consumption rates can be observed, following adequately the trends of the "true" values obtained from model (1).

Adaptive control design

The adaptive control scheme proposed here for the SSFSE process is shown in figure 4, where the manipulated variable is starch feed rate (F) and the controlled variable is glucose concentration S₂ (P₁). It is important to remark that although glucose is the "explicit" controlled variable, the real purpose of the adaptive control scheme is to obtain a high ethanol concentration (and at the same time a high productivity value), by maintaining a proper value for the glucose concentration.

For increasing the productivity of the process operating under fed batch conditions, the main purpose of the control strategy proposed in this work, is to stabilize the glucose concentration in the equilibrium state observed during batch conditions as long as possible. In this way, the process control comes down to stabilize the glucose concentration using the starch feeding as manipulated variable. Software sensors of glucose production and consumption rates are used for recognition of this equilibrium state. The difference between software sensor's measurements is defined as a marker Δ for recognizing the equilibrium state:

$\Delta ={{\hat{\varphi }}_{2p}}-{{\hat{\varphi }}_{2k}}$

(10)

When the sign of the marker Δ is positive, the glucose production is higher than the glucose consumption. The negative sign shows the opposite situation. The main purpose is to observe the sign of the marker and to stimulate the glucose production by starch feeding when the consumption is higher. Therefore, the starch has to be added when the marker is negative only. The amplitude of the starch feed impulses could be calculated by the dynamical equation of glucose concentration eq. (8a) (without the last term), assuming zero dynamics of the glucose concentration:

$F=-({{\hat{\varphi }}_{2p}}-{{\hat{\varphi }}_{2k}})V/{{S}_{2}}{{({{P}_{1}})}_{m}}$

(11a)

The control law (11a) will be applied only when the marker is negative; therefore, the control algorithm block is expressed as follows:

$F=\left\{ \begin{matrix} 0 & if\,\,\,\,\Delta \ge 0 \\ -({{{\hat{\varphi }}}_{2p}}-{{{\hat{\varphi }}}_{2k}})V/{{S}_{2}}{{({{P}_{1}})}_{m}} & if\,\,\,\Delta ＜0 \\ \end{matrix} \right.$

(11b)

Investigations of the control scheme (figure 4) are realized by simulations. Model (1) is used as the object for control. Simulations of starch and glucose concentrations are corrupted by additive noise e. These white noise signals, ε, simulate measurement noises at standard deviation 5% of the mean starch and glucose concentrations. The ‘estimator' block realizes two tasks: i) it calculates the ${{\hat{\varphi }}_{2p}},{{\hat{\varphi }}_{2k}}$ values and ii), it estimates the sign of the marker Δ, then the information is used for calculation of the control law (11).

Results and discussions

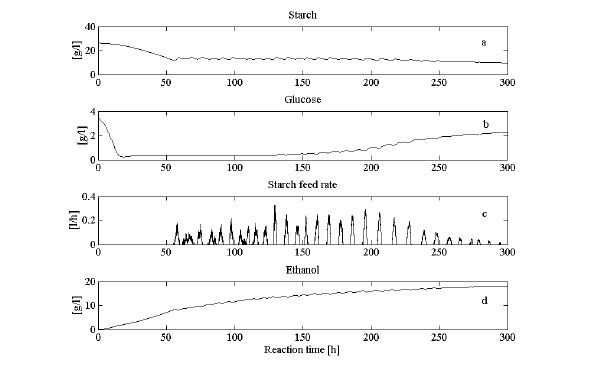
The simulation results are shown in figures 5 and 6. In figures 5a and 5b, the control outputs are presented, in figures 5c and 5dstarch feed rate and ethanol concentration are shown respectively. The process starts in batch phase and the control is switched on only when the glucose production rate starts to decrease, which occurs around 50 hours of fermentation as can be seen in figure (3a). As it is shown in figure 5c, the real starch feeding impulses appear with delay because of the estimator error shown in figures 3a and 3b.

The control input shown in figure 5c keeps the glucose concentration close to the equilibrium state for more than 100 hours. After that, glucose concentration increases as can be seen in figure 5b.

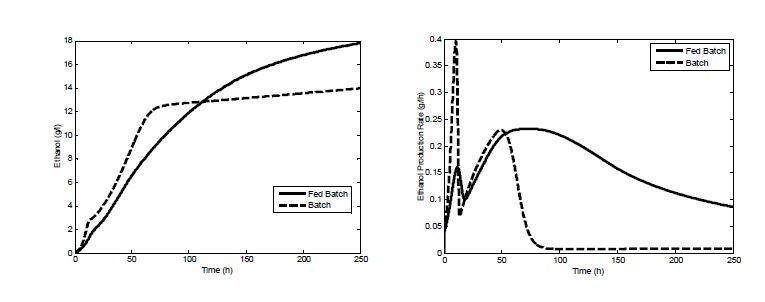
In Figure 6 are shown the simulation results for the ethanol concentration and the ethanol growth rate as fed batch results are compared to those for the batch process, which was open loop simulated using the model given in ^[27]. It can be seen that the ethanol concentration (and therefore the productivity) for the controlled fed batch process is higher than the ethanol concentration reached under batch operation. Furthermore, it is important to remark that the ethanol production rate in the fed batch process can be kept at higher values than for the batch, assuring a more productive process.

The observed high values of the ethanol production rate in the period 50-100 hours during fed-batch process (Figure 6 right side) correspond with the maintained set-point of glucose concentration in this period confirming the appropriate choice of control. After this period a deviationfrom this set-point is observed that could be explained by different factors: for example by the offset due to the fact that an integral action is not taken into account as part of the control calculations or by the fact that the yield coefficients related to the estimation of glucose production and consumption rates even in a low degree in practice are time-varying ones. The idea is to present a simple and easy way to implement the control law that could be object of improvement as a future task.

---

2.3 Application of the casade software sensor for monitoring and control of bioprocesses characterizing with growth of two microorganisms

During considered processes the first microorganism transforms the main substrate to intermediate metabolite, which is substrate of the second microorganism growth and target product synthesis. The reaction scheme according the General Dynamical Model approach ^[28] is consists of the following three reactions φ₁, φ₂ and φ₃:

$\begin{align} & \begin{matrix} {{S}_{1}}+{{O}_{2}} & \xrightarrow{{{\phi }_{1}}} & {{X}_{1}}+{{S}_{2}}({{P}_{1}} \\ \end{matrix}) \\ & \begin{matrix} {{S}_{2}}({{P}_{1}})+{{S}_{3}}+{{O}_{2}} & \xrightarrow{{{\phi }_{2}}} & {{X}_{2}}+ \\ \end{matrix}{{P}_{2}} \\ & \begin{matrix} {{S}_{2}}({{P}_{1}})+{{O}_{2}} & \xrightarrow{{{\phi }_{3}}} & {{P}_{2}} \\ \end{matrix} \\ \end{align}$

(12)

The first one is related to the growth of the microorganism X₁, and intermediate metabolite, S₂ (P₁) production on the main carbon source and the oxygen. The second reaction describes the second microorganism, X₂, related with the target product, P₂, synthesis on the intermediate metabolite, oxygen and substrate, S₃. The third reaction represents non-growth associated production of P₂, where the biomass plays simply the role of catalyst.

To be reached maximal production of the target product, the consumption and production of the intermediate metabolite have to be maintained in optimal balance. For this purpose, software sensors of the intermediate metabolite' kinetics using available on-line measurements have to be derived. The kinetics estimates will be a basis for monitoring of physiological state of the culture as well as will allow to be recognized the optimal state.

The proposed below cascade software sensor has the structure given in Figure 1. As case study, fed-batch process for biopolymers (PHB) production using mixed culture L. delbrueckii and R. Eutropha will be considered.

---

2.3.1 Case study: fed-batch process of PHB production by mixed culture L. delbrueckii and R. eutropha

Unstructured process model

A lot of experiments ^[25] are done to investigate the fermentation of mixed culture of L. delbrulckii and R. eutropha. Each experiment starts as mono batch aerobic fermentation of L. delbrulckii where glucose is the main carbon source. After 4 hours, R. eutropha, is inoculated and lactate that is produced by L. delbrulcki converts to PHB by R. eutropha in the oxygen and ammonium presence.

The following unstructured model is proposed in ^[25]. It describes the dynamics of L. delbrulckii and R. eutropha based on mass balances with appropriate kinetic expression:

$\frac{d{{X}_{1}}}{dt}={{\mu }_{1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}}){{X}_{1}}-\frac{F}{V}{{X}_{1}};$

(13a)

$\frac{d{{S}_{1}}}{dt}=-{{\rho }_{s1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}}){{X}_{1}}+\frac{F({{S}_{in}}-{{S}_{1}})}{V};$

(13b)

$\frac{d{{S}_{2}}({{P}_{1}})}{dt}={{\rho }_{p1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}}){{X}_{1}}-{{\rho }_{s2}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}}){{X}_{2}}-\frac{F}{V}{{S}_{2}}({{P}_{1}});$

(13c)

$\frac{d{{X}_{2}}}{dt}={{\mu }_{2}}({{S}_{2}}({{P}_{1}}),{{O}_{2}},{{S}_{3}}){{X}_{2}}-\frac{F}{V}{{X}_{2}};$

(13d)

$\frac{d{{S}_{3}}}{dt}=-{{\rho }_{s3}}({{S}_{2}}({{P}_{1}}),{{O}_{2}},{{S}_{3}}){{X}_{2}}-\frac{F}{V}{{S}_{3}};$

(13e)

$\frac{d{{P}_{2}}}{dt}={{\rho }_{p2}}({{S}_{3}}){{X}_{2}}-\frac{F}{V}{{P}_{2}};$

(13g)

where X₁ is cell concentration of L. delbrueckii; X₂ is cell concentration of R. eutropha; S₁ is glucose concentration; S_in is glucose concentration in the feed; V is broth volume; S₂ (P₁) is lactose concentration; S₃ is ammonium concentration; P₂ is PHB concentration; O₂ is dissolved oxygen concentration.

The specific growth rates, μ₁ and μ₂, respectively to L. delbrueckii and R. eutropha respectively, ρ_s1 is glucose consumption; ρ_s2 is lactose consumption; ρ_s3 is ammoniumconsumption; ρ_p1 is lactose production;ρ_p2 is PHB production are given by the following expressions:

${{\mu }_{1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})=\frac{{{\mu }_{m1}}({{O}_{2}}){{S}_{1}}}{{{K}_{s}}+{{S}_{1}}}{{(1-\frac{{{S}_{2}}({{P}_{1}})}{{{S}_{2}}{{({{P}_{1}})}_{m}}})}^{n}}$${{\mu }_{m1}}={{a}_{1}}{{e}^{-{{a}_{2}}{{O}_{2}}}}+{{a}_{3}}$и${{\mu }_{m2}}={{d}_{1}}{{e}^{-{{d}_{2}}{{O}_{2}}}}+{{d}_{3}}$

${{\rho }_{s1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})=\frac{{{\mu }_{1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})}{{{Y}_{{{X}_{1}}/{{S}_{1}}}}({{O}_{2}})}+\frac{{{\rho }_{p1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})}{{{Y}_{{{S}_{2}}({{P}_{1}})/{{S}_{1}}}}({{O}_{2}})}$

${{\rho }_{p1}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})=\alpha {{\mu }_{1}}+\beta ({{S}_{1}},{{O}_{2}})$;

$\beta ({{S}_{1}},{{O}_{2}})=\frac{{{\beta }_{m}}({{O}_{2}}){{S}_{1}}}{{{K}_{S}}+{{S}_{1}}}$ and ${{\beta }_{m}}({{O}_{2}})={{c}_{1}}{{e}^{-{{c}_{2}}{{O}_{2}}}}+{{c}_{3}}$, ${{Y}_{{{S}_{2}}({{P}_{1}})/{{S}_{1}}}}({{O}_{2}})={{b}_{1}}{{e}^{-{{b}_{2}}{{O}_{2}}}}+{{b}_{3}}$

${{\rho }_{s2}}({{S}_{1}},{{S}_{2}}({{P}_{1}}),{{O}_{2}})=\frac{{{\mu }_{2}}({{S}_{2}}({{P}_{1}}),{{O}_{2}},{{S}_{3}})}{{{Y}_{X2}}{{_{/}}_{{{S}_{2}}({{P}_{1}})}}({{O}_{2}})}$ , ${{Y}_{X2}}{{_{/}}_{{{S}_{2}}({{P}_{1}})}}({{O}_{2}})={{f}_{1}}{{e}^{-{{f}_{2}}{{O}_{2}}}}+{{f}_{3}}$

${{\rho }_{s3}}({{S}_{2}}({{P}_{1}}),{{O}_{2}},{{S}_{3}})=\frac{{{\mu }_{2}}({{S}_{2}}({{P}_{1}}),{{O}_{2}},{{S}_{3}})}{{{Y}_{{{X}_{2}}/{{S}_{3}}}}({{O}_{2}})}$ ; ${{\rho }_{p2}}({{S}_{3}})={{q}_{m}}\left( \frac{{{k}_{N}}}{{{k}_{N}}+{{S}_{3}}} \right)$

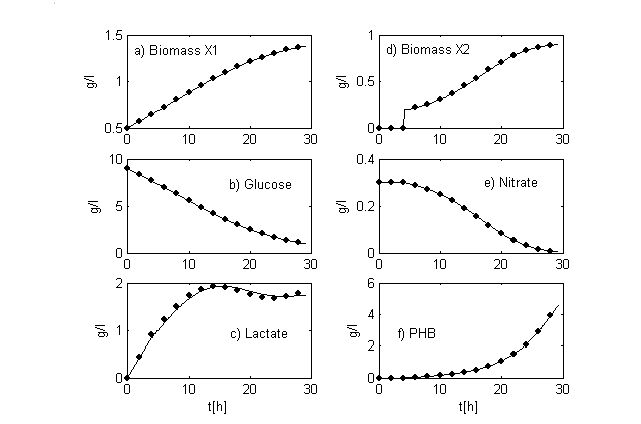
Parameter values of the unstructured model (13) are obtained in experimental way and they are given in ^[25]. In figure 7 (a-f), the batch phase of the model is shown with points. In figure 7d, the inoculation of R. eutropha at 4h of fermentation can be observed.

Model for control derivation

The mechanism of PHB production by mixed culture of L. delbrulckii and R. eutropha could be presented by the following reaction scheme (12). Itconsists of three reactions: φ₁, φ₂ and φ₃. The first one represents growth associated production of lactose, S₂ (P₁). The glucose, S₁, in the oxygen, presence is converted to lactose by L delbrulckii, X₁. The second reaction represents growth associated production of PHB. The lactose in the oxygen and ammonium presence is converted to PHB by R. eutropha, X₂. The third reaction represents non-growth associated production of PHB where the biomass plays simply the role of catalyst.

Following the rules proposed in ^[28], the model for control is derived on the basis of reaction scheme (2) and it is presented as follows:

$\left| \begin{matrix} \frac{d{{X}_{1}}}{dt} \\ \frac{d{{S}_{1}}}{dt} \\ \frac{d{{S}_{2}}({{P}_{1}})}{dt} \\ \begin{align} & \frac{d{{X}_{2}}}{dt} \\ & \frac{d{{S}_{3}}}{dt} \\ \end{align} \\ \frac{d{{P}_{2}}}{dt} \\ \end{matrix} \right|=\left| \begin{matrix} 1 & 0 & 0 \\ -{{k}_{1}} & 0 & 0 \\ {{k}_{2}} & -{{k}_{3}} & -{{k}_{4}} \\ 0 & 1 & 0 \\ 0 & -{{k}_{5}} & 0 \\ 0 & {{k}_{6}} & 1 \\ \end{matrix} \right|\left[ \begin{matrix} {{\phi }_{\text{1}}} \\ {{\phi }_{2}} \\ {{\phi }_{3}} \\ \end{matrix} \right]-\frac{F}{V}\left| \begin{matrix} {{X}_{1}} \\ {{S}_{1}}-{{S}_{in}} \\ {{S}_{2}}({{P}_{1}}) \\ {{X}_{2}} \\ {{S}_{3}} \\ {{P}_{2}} \\ \end{matrix} \right|$

(14)

The model for control (14) has to describe the dynamics of the main process variable as well as the unstructured model (13). Comparing both models, they have different structures. Hence, the next step is model (14) parameters identification.

Identification of the model for control

Identification of the model (14) parameters is realized using the batch phase of both process models applying an optimization procedure proposed in ^[2,14,15]. The optimization criterion is the minimal mean square error between state variables of model (13) and model (14). The obtained optimal values of model (14) parameters are: k₁ = 9.1496, k ₂ = 5.7282, k₃ = 4.2169, k₄ = 0.0715, k₅ = 0.4151, k₆ = 0.0785

In figure 7a-f, simulations of model for control (14) are cross-validated with model (13) data. As can be seen in the figures, the model (14) (lines) describes the dynamics of the main process variables as well as the unstructured model (13) (points). A model with a structure (14) and parameters listed above could be used for process monitoring and control design.

Design of substrate consumption rates estimators

As only two variables are available [S₁ and S₂ (P₁)]on-line, only two parameters could be estimated according necessary conditions for the process (14) observability. We define two new kinetic parameters, φ₁ and φ₂. They are consumption rates of glucose and lactose given in (14) and which are considered as unknown time-varying parameters.

${{\varphi }_{1}}=-{{k}_{1}}{{\phi }_{1}}$

(15)

${{\varphi }_{2}}=-{{k}_{3}}{{\phi }_{2}}-{{k}_{4}}{{\phi }_{3}}$

(16)

The first step of the procedure is the estimation of consumption rate φ₁ (as well as estimation of reaction rate φ₁) using on-line measurements of glucose. The estimator of φ₁ is an observer-based estimator as follows:

$\frac{d{{{\hat{S}}}_{1}}}{dt}={{\hat{\varphi }}_{1}}-\frac{F({{S}_{1m}}-{{S}_{f}})}{V}+{{\omega }_{1}}({{S}_{1m}}-\hat{S})$

(17)

$\frac{d{{{\hat{\varphi }}}_{1}}}{dt}={{\gamma }_{1}}({{S}_{1m}}-\hat{S})$

(18)

where ω1 and γ1 are estimator design parameters, S_1m = S₁ + ε₁; ε₁ is a measurement noise.

The design parameters of estimators (17,18) are derived using an optimal tuning procedure, proposed in ^[16]. In a result, the following expressions are obtained:

$\begin{align} & {{\omega }_{1opt}}=2\zeta \sqrt{\frac{{{m}_{11}}}{2{{m}_{21}}}} \\ & {{\gamma }_{1opt}}=\frac{\omega _{1opt}^{2}}{4{{\zeta }^{2}}} \\ \end{align}$

(19)

where m11 is upper bound vector of time-derivative of ${{\varphi }_{1}}$; m₂₁ is upper bound of additive noise of glucose measurement; ζ is a damping coefficient which value is fixed close to 1.

The estimates of reaction rate φ₁ can be calculated using the kinetic relationship (15):

${{\hat{\phi }}_{1}}=-{{\hat{\varphi }}_{1}}/{{k}_{1}}$

(20)

The next step is the estimation of φ₂ - consumption rate of lactate, using the on-line measurements of this metabolite and the estimates of φ₁ (20). The estimator of φ₂ is as follows:

$\frac{d{{{\hat{S}}}_{2}}({{P}_{1}})}{dt}={{k}_{2}}{{\hat{\phi }}_{1}}+{{\hat{\varphi }}_{2}}-\frac{F}{V}{{S}_{2}}{{({{P}_{1}})}_{m}}+{{\omega }_{2}}({{S}_{2}}{{({{P}_{1}})}_{m}}-{{\hat{S}}_{2}}({{P}_{1}}))$

(21)

$\frac{d{{{\hat{\varphi }}}_{2}}}{dt}={{\gamma }_{2}}({{S}_{2}}{{({{P}_{1}})}_{m}}-{{\hat{S}}_{2}}({{P}_{1}}))$

(22)

where ω2 and γ2 are design parameters, S₂ (P₁)_m = S₂ (P₁) + ε₂ , ε₂ is measurement noise.

Applying the procedure mentioned above, the following expressions are obtained:

$\begin{align} & {{\omega }_{2opt}}=2\zeta \sqrt{{{m}_{12}}/2{{m}_{22}}} \\ & {{\gamma }_{2opt}}=\omega _{2opt}^{2}/4{{\zeta }^{2}} \\ \end{align}$

(23)

where m₁₂ is upper bound of the time-derivative of ${{\varphi }_{2}}$ (t) and m₂₂ is upper bound of ε₂.

According the model (21), lactose production rate can be calculated by the following equation:

${{\varphi }_{3}}={{k}_{2}}{{\hat{\phi }}_{1}}$

Define the difference between production and consumption rates of lactose as follows:

${{\varphi }_{3}}={{k}_{2}}{{\hat{\phi }}_{1}}$

(24)

This difference could be considered as marker of physiological state of culture and applied for adaptive control of process as is shown in the next section.

Adaptive control design

The aim at process control is to receive more target product PHB using an optimal amount of glucose. For this purpose, the lactate concentration has to be kept at an optimal value during the process. In such a way, the concentration of X₂ and the production of PHB will be increase. So, the optimal process control is came down to stabilization of lactate concentration at an optimal value in the reactor. Hence, software sensors of lactate production and consumption rates have to be designed. Analyzing the model (14) and using information from the experimental investigations realized in ^[25], the following conclusions could be formulated: i) parameter φ3 is proportional to X₁ growth rate and parameter φ₂ is to X₂ growth rate. Hence, each software sensor gives information for the growth rate of one microorganism. Using this information as control inputs, we can stimulate the growth of both microorganisms separately. ii) The growth of X₁ requires low O₂ value, but the growth of X₂ is stimulated by keeping a high O₂ value according the investigations in ^[25]. The high and low level of the dissolved oxygen, 3 ppm and 0.5 ppm, are derived on the bases of experiments by the same authors. These levels could be set-points in the control scheme for physical-chemical parameters control (including dissolved oxygen) usually available in laboratories. The idea is these set-points to be switched on depending on the marker' sign to stimulate separately either the growth of X₁ or X₂ iv) High lactose concentration inhibits the X₂ growth (see eq.13c). An optimal value of lactose concentration in the reactor can be calculated theoretically by the expression ${{S}_{2}}{{({{P}_{1}})}_{opt}}=\sqrt{{{K}_{i}}{{K}_{p}}}$; iv) the growth of X₁ depends also on glucose concentration in the reactor. v) For optimal control of the considered process, S₂ (P₁) opt has to be reached and kept during the fermentation.

An idea for such control of lactose production and consumption is proposed on the basis of the marker $\Delta ={{\hat{\varphi }}_{3}}-{{\hat{\varphi }}_{2}}$ leading the process to the target S₂ (P₁)_opt.

When Δ is negative, there is superiority to S₂ (P₁) consumption and the growth of X₁ has to be stimulated. When Δ is positive, there is superiority to lactose production and the growth of X₂ has to be provoked.

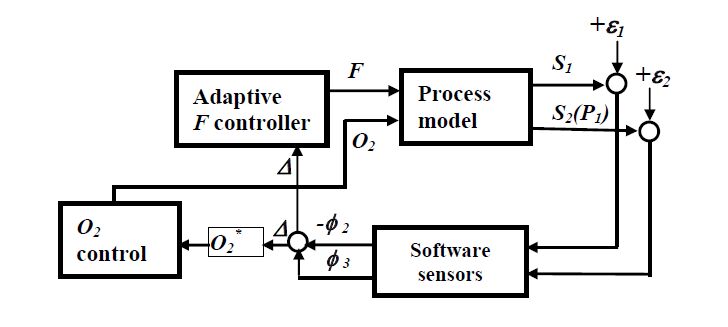
This idea is developed as a control scheme shown in figure. 8. This is a MIMO adaptive control scheme that consists of two control input - glucose feed rate (F) and dissolved oxygen (O₂) and two outputs glucose and lactose concentrations in the reactor. For simulations, the process is presented with unstructured model (13). The two outputs are corrupted by additive white noises (ε) and they are used for estimation of production (φ₃) and consumption (φ₂) rates of lactose. The marker, Δ, is used to change the set value (O₂^*) of dissolved oxygen controller from high to low level according the sign of Δ. Simultaneously, the same information is used for adaptive control design of glucose feed rate.

---

3. Results and Disscussions

Simulations are carried out with Δ calculated from equation (24). The design parameters g and w of estimators φ₁ (t) and φ₂ (t) are obtained by eqs. (19) and (23), respectively, where m₁₁ and m₁₂, are set to 0.1. The white noise signals, e, simulate measurement noises at standard deviation 5% of the mean S₁ and S₂ (P₁) concentrations. The values of m₂₁ and m₂₂ are 0.07 and 0.119 respectively. Therefore, the optimal values of the design parameters are: ω_1opt = 1.685, γ_1opt = 0.724, ω_2opt = 0.83, γ_2opt = 0.175.

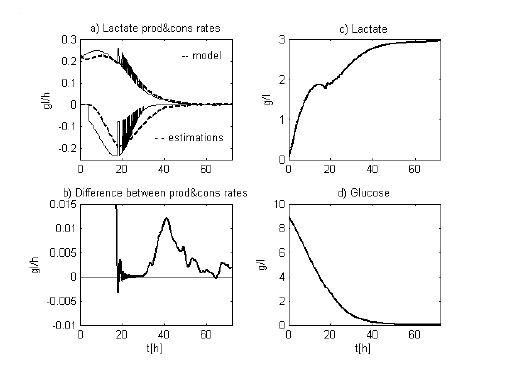
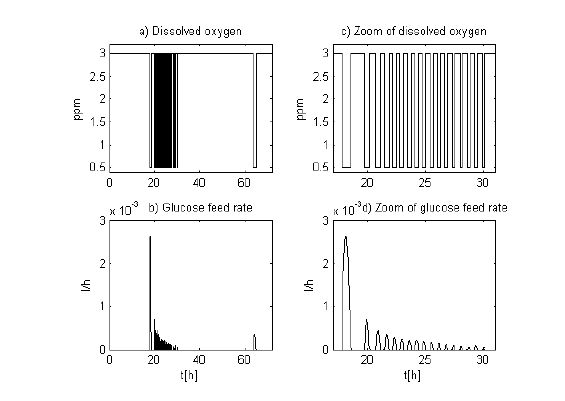
The simulation results are shown in figures 9 and 10. In figure 9a, a good tracking elapse of ${{\hat{\varphi }}_{3}}$ and ${{\hat{\varphi }}_{2}}$ can be observed. They follow the trends of "true" values obtained from model (14). In figure 9b, a zoom of Δ is shown. In figures 10a, b, control inputs are shown, and in figures 10c, d, the zooms of these signals are presented.

The switching over of the low level of the O₂, as well as the inclusion of the glucose feed, is realized, when Δ becomes negative, i.e. when is necessary to stimulate the growth of L. delbrulckii. The levels of the glucose feed impulses are determined by the dynamical equation of lactate concentration (eq. 21 without the last term), accepting zero dynamics, known kinetics (24) and optimal value of the lactose concentration, S₂ (P₁)_opt, calculated around 3 g/l using the expression with the parameters values proposed in ^[25]:

${{F}_{opt}}=-({{\hat{\varphi }}_{3}}-{{\hat{\varphi }}_{2}})V/{{S}_{2}}{{({{P}_{1}})}_{opt}}$

(25a)

The control law (25a) will be applied only when the marker is negative; therefore, the control algorithm block for glucose feed is expressed as follows:

$F=\left\{ \begin{matrix} 0 & if\,\,\,\,\Delta \ge 0 \\ -({{{\hat{\varphi }}}_{3}}-{{{\hat{\varphi }}}_{2}})V/{{S}_{2}}{{({{P}_{1}})}_{opt}} & if\,\,\,\Delta ＜0 \\ \end{matrix} \right.$

(25b)

In the case of positive Δ, the O₂ switches to high level, and there is not S₁ feed, i.e. the accumulated lactose is consumpted by R. eutropha. In a result, the lactose concentration tends to its optimal value as is shown in figure 9c. In figure 9d, the elapse of glucose is shown.

Simulation results show the good performance of the proposed control algorithm. This gives reasons the control scheme in figure 8 to be applied in real life experiments. Moreover, the same idea could be used for control of other mixed cultures processes.

---

4. Conclusion

A new approach for estimation of physiological states is investigated. It is applied for monitoring and control algorithms design for two groups of processes. They are biotechnological processes which are characterized with balance between the production and consumption rates of key intermediate metabolite which determines optimal physiological process state with respect the target product.

The proposed general cascade scheme for monitoring is adapted and included in the control algorithms of processes of simultaneous saccharification and fermentation of starch to ethanol and biopolymer production by mixed culture. The simulation investigations show the good properties of the proposed monitoring approach and its potential to be used in control of real processes.

---

Conflict of Interest

All authors declare no conflicts of interest in this paper.

---