1.
Introduction
Regarding the dynamic evolution of modern healthcare that is driven by an uninterrupted flow of technological innovations, which are redefined with each innovation, the boundaries are associated with medical science. Among these devices, biomedical implants take a front and center position given their extraordinary ability to replicate, support, or enhance varying biological functions within the human body [1]. From the artificial joints, which provide a range to a limb's mobility, creating surgical symphony and cardiac rhythms of human life when coupled with pacemakers, have gone beyond their mechanical roots in 2017. It is not only in addressing specific medical conditions that these are so meaningful but the improvement they bring to health and quality of life for those who have experienced illness. The combination of efforts from biomaterials research, engineering, and medical sciences have made it possible to produce ‘miraculous’ examples of biomedical implants that manifest the highest advancements up to our days in enhancing patient outcomes.
Increasing demand for next-generation and high-end biocompatible implants has promulgated nanoparticles as the avant-garde of biomedical implant technology development. These multifunctional nanoparticles, due to their small size and properties of interest, will revolutionize the enhancement of these implants. The incorporation of nanoparticles is expected to revolutionize the fundamental nature of biomedical implants by providing solutions for perpetually encountered issues such as increased biocompatibility and efficient therapeutic functionalities besides limiting side effects. In particular, nanoparticles have been the subject of considerable research as a potential drug delivery system for treating various diseases, and several researchers have reported that using Nano carriers to deliver drugs enhance targeted therapy without causing damaging side effects or reducing bioavailability.
Nanoparticles are not just a new tool to the toolkit of healthcare but an epoch in their own challenge having adding these tiny robots will turn each barrier obstructing treatment into memory. The following exploration uncovers the complex interrelations between nanoparticles and biomedical implants, revealing for us what synergies like these might bring to rewrite healthcare as we know it [2].
Mechanics have described the biomedical implants as mechanical or electronic devices that replace, support, or enhance physiological functions in human body. Biomedical implants are installed in some way to aid with treating various medical conditions from cardiovascular diseases to musculoskeletal issues [3]. These implants may take the form of orthopedic implants, cardiovascular devices, or neurological prostheses—the goal is to normalize physiological function (such as under active thyroid), alleviate symptoms of a disease state (such as an implanted cochlear device for hearing loss), and in some cases replace organ tissue entirely (orthotropic heart transplantation). Biomedical implants have followed a long evolutionary path, and much progress has been made in various disciplines, such as materials science, engineering, and clinical medicine [4]. That is not all, however: Implants can be made to last longer and are surgically placed with a view toward their ‘assimilation’ in the body. Nevertheless, obstacles from immune response and inflammation to the lack of therapeutic functionalities are crucial issues that further drives scientists towards innovative strategies. Due to their distinct physical and chemical properties, nanoparticles have been widely recognized as beneficial agents in the innovation of biomedical grafts. Size typically on λ ranging from 1 to 100 nm providing a dense surface area-to-volume, and tunable (chemically modifiable) particle interface is used due to them being the smallest division of bulk form, with characteristics such as mass transferential. These are features that allow nanoparticles to be designed for performance-enhancing functions in biomedical implants [5].
Consequently, targeting drug delivery with nanoparticles is an excellent option for anti-cancer therapy due to the potential benefit of a more precise and effective therapeutic way. Furthermore, they promote bio-compatibility through their integration into the implant surfaces, lowering potential of rejection and inflammation. Its uses span from controlled drug release with the help of magnetic nanoparticles to being an effective means for improved imaging in diagnostic applications as contrast agents. These properties are exploited by researchers to fabricate implants with additional functions and benefits for the general well-being of a patient [1].
We aim to present a peek overview of the intricate, dynamic interplay between nanoparticles with biomedical implants that illustrate very lucidly how Nano technological intervention modifies each segment in which one intervenes. In this review, we aim to present the current state-of-the-art in research findings and advances that synthesize nanoparticles to perform versatile functions used as hybrids with biomedical implants for enhanced performance.
This is not meant to be simply a review of the advancements made. The report is aimed at researchers, clinicians, and other stakeholders within the healthcare landscape providing an overview of the developments in this field as well as indicating further areas for exploration. A unique advantage of these findings is the ability to fill gaps in our current understanding, drive new lines of questioning, and lead to improved safety, efficacy, and technology related with biomedical implants for significantly better patient outcomes. We uncover the pathway into the future where nanotechnology in bio imaging can revolutionize healthcare by navigating through the complex world of nanoparticles in biomedical implants.
2.
Types of biomedical implants
Biomedical implants are devices that are carefully developed and made from biocompatible materials like metals, ceramics, polymers, or biological tissues. They represent the fusion of state-of-the-art medical technology and precise engineering. These implants serve a variety of therapeutic purposes in the human body and are the result of interdisciplinary collaboration between biomedical engineers, materials scientists, doctors, and regulatory agencies. They are essential to modern healthcare because they can do everything from regulate physiological processes, like heart rhythm with pacemakers, to restore structural integrity and function, as demonstrated by orthopedic implants for joint replacements. Biomedical implants are surgically inserted with extreme accuracy, according to strict safety and quality requirements while greatly improving patient outcomes, quality of life, and pushing the frontiers of medical innovation.
2.1. Orthopedic implants
Orthopedic implants encompass crucial solutions for joint and bone-related issues. Hip replacements involve artificial components like the femoral stem, acetabular cup, and ball-and-socket structure, alleviating hip joint issues. Knee replacements consist of femoral and tibia components with a plastic spacer, mimicking natural knee motion to restore functionality. Spinal implants, including rods, screws, and plates, stabilize the spine, addressing conditions like fractures or spinal deformities [2]. Figure 1 visually encapsulates these orthopedic implants, outlining their key components and their pivotal roles in restoring mobility and alleviating discomfort associated with joint and spinal issues [3].
2.2. Cardiovascular implants
Cardiovascular implants are medical devices used to treat a variety of heart and blood vessel conditions. They are surgically implanted into the body to restore or improve blood flow, regulate heart rhythm, or replace damaged valves. Common types of cardiovascular implants include stents, pacemakers, and artificial heart valves [4]. Stents are expandable tubes used to prop open narrowed arteries, while pacemakers are battery-powered devices that regulate heart rate [5]. Artificial heart valves are surgically inserted to replace damaged or diseased valves that control blood flow through the heart. These implants have significantly improved the quality of life for millions of people worldwide [6],[7].
Figure 2 shows an implanted medical device known as an artificial cardiac pacemaker, or just a pacemaker, which creates electrical pulses that are supplied to one or more of the heart's chambers via electrodes. Every pulse controls the heart's electrical conduction system by causing the targeted chamber or chambers to contract and pump blood.
2.3. Dental implants
Dental implants are essential solutions for tooth loss, providing functional and aesthetic benefits. These implants include components like crowns, bridges, and implant-supported dentures. Crowns and custom-made caps replace damaged or missing teeth, restoring their shape and function [9]. Bridges span the gap created by missing teeth, anchored by neighboring natural teeth or implants, improving both appearance and chewing ability [10]. Implant-supported dentures offer stable, secure prosthetic devices attached to dental implants, enhancing comfort and functionality compared to traditional removable dentures. These dental implants address tooth-related concerns, promoting oral health, and significantly improving the quality of life for individuals with missing teeth [1].
Figure 3 shows how dental implants are precisely positioned inside a model of a human jaw. The implants, which are two metal screws inserted into the lower jawbone, serve as a representation of the sophisticated methods utilized in contemporary dentistry to restore lost teeth. Restored functionality and aesthetics are guaranteed by the exposed upper portions of the screws above the gum line, which are prepared to hold dental crowns. This intricate illustration demonstrates the painstaking steps required in dental implantology and how biocompatible materials are integrated with natural bone to produce the best possible outcomes for tooth replacement therapy.
2.4. Neurological implants
Neurological implants are sophisticated devices designed to interact with the nervous system, including the brain, spinal cord, and peripheral nerves [12]. These implants are utilized to modulate or restore neural function, often through the delivery of electrical impulses or the monitoring of neural activity. They encompass a range of technologies, including deep brain stimulators for conditions like Parkinson's disease, neuroprosthetics for restoring limb function in paralysis, and devices for treating epilepsy, chronic pain, and other neurological disorders. Neurological implants aim to alleviate symptoms, restore lost functions, or improve the overall quality of life for individuals affected by neurological conditions [13].
Figure 4 depicts an image of a spinal cord stimulation (SCS) system, which are implants used to alleviate chronic pain in the neurological field. This image shows the implant, as it rests on what appears to be a partially exposed spinal column with electrodes perfectly aligned along the center. The electrodes that connect to the spinal cord are linked to an external controller, which permits adjustments in electrical signals sent into a person's spine by both the patient and health care provider. SCS therapy aims to block/alter the arrival of pain signals to the brainstem before going into full force, working well in conditions like neuropathic or spinal cord injury. Visible in the image is also an external controller interface, which is used for programming and controlling stimulation parameters ensuring individualized treatment.
2.5. Ophthalmic implants
Ophthalmic implants are specialized devices designed for the eyes to address various vision-related issues or eye conditions. These implants are used in ophthalmology to either replace damaged eye structures or to enhance visual function [14]. They encompass a range of devices such as intraocular lenses (IOLs) used in cataract surgery to replace the eye's natural lens, corneal implants for addressing corneal irregularities, retinal implants for restoring vision in certain types of blindness, and orbital implants used in reconstructive surgeries after eye removal (enucleation). Ophthalmic implants play a crucial role in restoring or improving vision, supporting eye health, and addressing a spectrum of eye-related conditions to enhance visual acuity and overall quality of life for patients [15].
Figure 5 depicts the Image of a three-piece intraocular IOL, the artificial lens used to replace the natural lens in an eye that has gotten cloudy as it does with cataracts. The sandwich made of these transparent, disc-shaped devices has a central optical portion designed to concentrate light on the retina and is surrounded by thin loops called haptics that keep the lens in place within the eye. The meticulous surgical architecture and high-definition vision characteristics of these IOLs demonstrate their relevance in visual restoration with possible superiorities to natural lens functions. This image is especially ideal for showcasing innovative technology advancements in ophthalmology and the updated materials and design technologies that result in better patient results after cataract surgery.
2.6. Drug delivery implants
Drug-eluting stents, used in cardiovascular procedures, are examples of real-time uses of drug delivery implants, which provide a sophisticated approach to therapeutic intervention. Usually made of biocompatible materials, these implants act as reservoirs for medicinal substances, releasing them gradually to target particular tissues or organs. Drug-eluting stents, for example, use anti-proliferative medications to prevent restenosis after angioplasty, which greatly enhances patient outcomes. Comparably, hormones are released gradually via contraceptive implants, allowing for long-term contraception with little to no user involvement.
Drug delivery implants have potential applications beyond cardiovascular and reproductive health. These include the treatment of chronic illnesses such as diabetes and cancer, where accurate and targeted drug administration is critical to successful management. Their creation reflects the cooperative efforts of researchers, physicians, and industry stakeholders to increase therapeutic precision and patient care in modern medicine. These factors include complex considerations of drug release kinetics, biocompatibility, and regulatory compliance.
Figure 6 is a detailed image of an expanded drug-eluting coronary stent. The metallic grey stent is releasing anti-restenosis medication. This illustration shows the mesh design of the stent, which is intended to hold up arteries while delivering a drug at specific points along an artery. Arterial tissues in the vicinity are shown as a transparent pink, making it easy to differentiate between medical devices and biological structures. The image helps to illustrate the importance of real heart surgeries in challenging heart disease and combines both engineering and medicine to endeavor better patient outcomes.
3.
Need for improvements and innovations in implant technology
3.1. Biocompatibility enhancements
Biomedical implants must seamlessly integrate with the body without causing adverse reactions. Research and innovation in this area focus on developing biomaterials that closely mimic natural tissues [26]. This involves exploring biodegradable materials or surface coatings that reduce the body's immune response, promoting better integration of implants. Improvements in materials science aim to create surfaces that encourage tissue growth while minimizing the risk of rejection or adverse reactions.
3.2. Longevity and durability
Enhancing the lifespan and durability of implants is crucial to reduce the frequency of replacements or revisions. Advanced materials research is a primary focus, aiming to discover materials that are not only biocompatible but also exhibit superior mechanical strength and resistance to wear and corrosion [27]. Here is a significant emphasis on improved testing methods and simulations to predict the long-term behavior of materials within the body, aiding in the selection and design of longer-lasting implants [28].
3.3. Minimally invasive techniques
Advancements in surgical procedures are moving toward minimally invasive techniques. Robotic-assisted surgeries are becoming more prevalent, allowing surgeons to perform intricate procedures through smaller incisions, minimizing trauma, and accelerating recovery. Imaging technologies also play a pivotal role, enabling surgeons to visualize anatomy more accurately and guide precise placement of implants with minimal disruption to surrounding tissues [29].
3.4. Customization and personalization
Advances in imaging technologies, coupled with the capabilities of 3D printing, allow for the creation of patient-specific implants tailored to individual anatomy Customization improves fit and reduces the risk of complications, while the integration of patient-specific data, such as genetics and lifestyle factors, further enhances the efficacy of implants [30],[31].
3.5. Reducing infection risks
Preventing infections associated with implants is a critical concern. Research focuses on developing coatings with inherent antimicrobial properties to prevent bacterial adhesion and reduce the risk of infection around the implant site. Drug-eluting implants that release antimicrobial agents or antibiotics locally aim to prevent infections during the post-implantation period [32].
3.6. Biodegradable implants
Temporary implants that gradually degrade within the body over time eliminate the need for subsequent surgeries to remove them. These biodegradable implants offer benefits by reducing patient discomfort, healthcare costs, and potential complications associated with additional surgical procedures [33].
4.
Nanoparticles in biomedical implants
Nanoparticles are submicroscopic particles that range in size from 1 to 100 nanometers. At this scale, they exhibit unique physical, chemical, and biological properties that distinguish them from bulk materials. Nanoparticles, typically ranging from 1 to 100 nanometers, offer a unique advantage in biomedical implants due to their size similarity to biological structures and molecules. This size range enables nanoparticles to penetrate biological barriers, including cell membranes and tissues, facilitating targeted drug delivery and interactions at the cellular level [34]. In implant applications, their small size allows for precise localization and controlled release of therapeutic agents, minimizing off-target effects and enhancing treatment efficacy.
4.1. Methods of incorporating nanoparticles into implants
4.1.1. Surface coating
Nanoparticles are coated onto the surface of the implant. Surface coating involves depositing a layer of nanoparticles onto the outer surface of the implant. This can be achieved through techniques such as physical vapor deposition, chemical vapor deposition, or dip coating. The coated nanoparticles enhance the implant's surface properties, providing benefits such as improved biocompatibility, reduced friction, and controlled release of substances like drugs or growth factors [35].
4.1.2. Encapsulation
Nanoparticles encapsulate drugs or therapeutic agents within the implant.
In this method, nanoparticles are loaded with drugs or therapeutic agents and then encapsulated within the implant material. This encapsulation protects the loaded substances from degradation and controls their release over time. This is particularly useful in drug delivery applications, ensuring a sustained and targeted release of therapeutic compounds [36],[37].
4.1.3. Bulk incorporation
Nanoparticles are integrated into the bulk structure of the implant material.
Nanoparticles, typically metallic or ceramic in nature, are mixed with the implant material during its fabrication. This process occurs at the bulk level, providing enhanced mechanical and functional properties to the entire implant. Bulk incorporation is commonly used in the synthesis of nanocomposite materials, contributing to improved strength, wear resistance, and other desired characteristics [38].
4.1.4. Hydrogel nanocomposites
Nanoparticles are embedded within hydrogel matrices.
Hydrogels, which are water-absorbing polymers, can be infused with nanoparticles to form nanocomposites. This method is particularly relevant for soft tissue implants or drug delivery systems [39]. The hydrogel provides a flexible and biocompatible matrix, while the nanoparticles enhance the mechanical properties and drug-loading capacity of the composite [40].
4.1.5. Electrospinning
Nanoparticles are incorporated into polymer fibers through electrospinning.
Electrospinning is a technique that involves creating ultrafine fibers by applying an electric field to a polymer solution or melt. During the electrospinning process, nanoparticles can be introduced into the polymer solution, leading to the formation of nanofibrous structures. This method is advantageous for creating implantable materials with high surface area, porosity, and controlled drug release [41].
4.1.6. Layer-by-layer assembly
Nanoparticles are alternately deposited on the implant surface.
In layer-by-layer assembly, nanoparticles with opposite charges are sequentially deposited onto the implant surface. This method allows precise control over the thickness and composition of the coating. It is commonly used for creating thin films on implant surfaces, providing functionalities such as improved biocompatibility, drug release, or antibacterial properties [42]. Table 2 shows the methods of incorporating nanoparticles into biomedical implants.
4.2. Benefits of using nanoparticles in implants
4.2.1. Enhanced properties
Nanoparticles contribute to enhanced mechanical, electrical, and thermal properties of implant materials. The incorporation of nanoparticles, especially metallic ones like gold or titanium, into implant materials can significantly enhance their mechanical strength and conductivity. This is particularly crucial in orthopedic implants where mechanical stability is paramount [43].
4.2.2. Drug delivery
Controlled release of therapeutic agents from nanoparticles allows for targeted and sustained drug delivery, reducing side effects. Nanoparticles provide an efficient platform for drug delivery. By encapsulating drugs within nanoparticles, controlled release profiles can be achieved. This is advantageous in managing chronic conditions, where a steady concentration of medication is required over an extended period. The controlled release also minimizes potential side effects associated with sudden peaks in drug concentration [44].
4.2.3. Biocompatibility
Surface modification with nanoparticles enhances biocompatibility, reducing the risk of implant rejection. Nanoparticles can be engineered to improve the biocompatibility of implant materials. Surface modifications with biocompatible nanoparticles, such as polymeric nanoparticles or hydroxyapatite, can create a more favorable interface between the implant and surrounding biological tissues. This helps to mitigate immune responses and reduce the risk of implant rejection [45].
Nanoparticles are instrumental in improving the biocompatibility of biomedical implants through surface modifications, controlled drug delivery mechanisms, and by influencing optimum tissue-selectivity. For instance, silver nanoparticles (AgNPs) are famous for their antibacterial activities that can help reduce infections related to implants. As Burdușel et al. found, silver nanoparticles are one of the well-known effective antibacterial materials that, as highlighted by Fortunati et al. (2018), “have received great attention because they provide excellent antimicrobial activities and infections control within biomedical implants.” The subcellular size of AgNPs also means more efficient interactions with cellular components to help integrate into tissue environments, leading to improved biocompatibility. Overall, a characteristic of silver nanoparticles in relation to biomedical implants is their lowest level of bacterial colonization while remaining compatible with tissue healing [46].
Nanoparticles also play a substantial role in implants through bone tissue engineering wherein it enhances the mechanical properties and bioactivity. Vieira et al. [47] demonstrated that incorporation with nanoparticles including nano-hydroxyapatite or silica to scaffolds could improve bioactivity and osteoconductivity of the scaffold. According to the researchers, “Incorporating nanoparticles into scaffolds can enhance bioactivity and osteoconductivity of bone implants by controlled releasing therapeutic components.” Such a controlled release of the therapeutic agents is helpful during tissue regeneration and provides long term interaction between implant and surrounding bone, taking part in enhanced integration coupled with minimum rejection caused due to implant. These combined capabilities will make it possible to improve the mechanical and biological behavior of implants, key aspects for orthopaedic implantology, and variation on bone tissue engineering field to ensure long-term success in biomedical methods [47].
4.2.4. Antibacterial properties
Metallic nanoparticles, such as silver, exhibit inherent antibacterial properties, reducing the risk of infections. Incorporating metallic nanoparticles with inherent antibacterial properties, like silver nanoparticles, into implant surfaces can create a protective barrier against bacterial colonization. This is particularly crucial in preventing infections associated with implantation, which can lead to implant failure and complications [48].
4.2.5. Tissue regeneration
Ceramic nanoparticles, such as hydroxyapatite, mimic the composition of natural bone. Incorporating these nanoparticles into implants, especially in orthopedics, can enhance the integration of the implant with surrounding bone tissue, promoting faster healing and reducing the risk of implant loosening [49].
4.2.6. Diagnostic applications
Quantum dots and other nanoparticles serve in diagnostic applications, enabling imaging and sensing for better monitoring of implant performance. Nanoparticles with unique optical properties, like quantum dots, can be used for imaging and diagnostic purposes. They enable non-invasive monitoring of the implant's condition, allowing healthcare professionals to assess its functionality and detect any abnormalities. This contributes to early intervention and improved patient outcomes [50].
4.2.7. Enhanced personalized medicine
Nanoparticles used as part of biomedical implants will provide highly individualized treatment and have promise for a breakthrough in Personalized Medicine. They contribute most importantly by providing a means to deliver therapeutic agents locally, with high precision directly onto the implant site. By functionalizing nanoparticles, one can also engineer the particles to package and release drugs, be used as growth factors, or as other bioactive molecules in a non-resolving manner to specific physiological triggers. Because the cargo reaches its destination precisely and within hours or days of when it started on board, this type of targeted delivery minimizes side effects in every major organ system while enhancing therapeutic impact. For instance, the release of drugs using nanoparticles can be customized to modify their profile based on the genetic make-up or disease state of patients deploying a patient-centric therapeutic strategy [51].
Nanomaterials are also be made to interact exclusively with the surface of some cell types or molecular markers, having implants developed that would be more compatible with the tissue and immune system. Another important feature of these surfaces includes providing the implant surface specifically, which is carried out with cells and no other proteins or foreign materials, causing less probability for rejection and enabling more incorporation of implant into the body. Moreover, the surface of nanoparticles can be altered to reflect particular biological traits such as tissue composition and blood chemistry unique to an individual patient for a highly-personalized implant. Through these targeted interactions and responses, nanoparticles can make for biomedical implants that are more accurate in treatment performance but moreover tailored to the individual patient's needs, thereby opening up personalization of healthcare [52].
5.
Biocompatibility and safety
5.1. The importance of biocompatibility in implant materials
Understanding the host's reaction to implants and biomaterials requires a grasp of biocompatibility. Developing medical implants and enhancing their functionality also depends on biocompatibility. Given that biomaterials are placed in close proximity to human tissues and are anticipated to stay there for an extended amount of time, it is crucial to properly evaluate their safety. Thorough safety assessments are also being conducted on biodegradable polymers. Studies on their biodegradability and biocompatibility are required. “Biocompatibility” refers to a compound's ability to coexist with live tissue or a living system by not being harmful, poisonous, or immune-7yhsuppressive. Furthermore, the substance can facilitate a cell-biomaterial interaction within the tissue where it is inserted [53].
Both internal and environmental factors unique to the host and implant site affect the biocompatibility of biomaterials. The intrinsic factors determining biocompatibility are many and include shape, size, surface chemistry and roughness, design, morphology and porosity, composition, sterility, duration of contact, and degradation. The extrinsic variables are the host species, genetic inheritance, implantation place, and microenvironment. The quality of the implanted material's biocompatibility is determined by the interaction of these variables [54]. A variety of in vitro and in vivo tests are used in the intricate process of biocompatibility assessment to measure cytotoxicity, allergic reactions, irritation, inflammation, and systemic and chronic toxicity. The International Organization of Standardization (ISO) 10993 provides a detailed description of the standards for the assessment of medical device biocompatibility [55].
In the early years of the clinical applications of biomaterials and implantable medical devices, there was only a poor understanding of biocompatibility. More or less by default, the host response came to be considered as a combination of a perturbation of classical wound healing and the degree of ‘biomaterial toxicity’ that, whatever precise mechanism was involved, influenced the host systemically and locally. The initial euphoria of being able to place a wide variety of materials, including metals and alloys, glasses and ceramics, natural and synthetic polymers and composites, into the body for the treatment of patients, with at least some success, gradually subsided as it was realized that this material selection process should be somewhat more refined [26].
As a result, titanium, cobalt, and stainless-steel alloys replaced easily accessible alloys like bronze and vanadium steel. Engineering plastics like nylon and polyacetals have been replaced by acrylics, polyolefins, silicone elastomers, and fluorocarbon polymers [56]. The primary requirement for the material to be as “inert” as possible served as the guide for this selection process, regardless of the type of content. This was a controversial topic since, in a scientific sense, it could be said that no substance is completely inert within the body; there must always be some interaction, particularly near the interface [57].
However, since the response has to be “appropriate” and appropriateness has to do with the host not experiencing any detrimental effects that are clinically meaningful, the idea of biomaterial inertness was translated into the implications of the biocompatibility definition [58]. Consequently, the enhancement of corrosion resistance using alloys was linked to the asymptotic curve of adequate inertness by reducing the release of metal ions or particle products. Improved inertness in polymers resulted from molecular design that reduced water absorption, hydrolysis, oxidation, and the release of impurities and additives. For many implanted devices and extracorporeal systems, inertness-controlled biocompatibility is the first step towards clinical success. Of course, this is not the only important factor; mechanobiological processes, particularly the effects of mechano transduction resulting from the interaction of forces between biomaterial and tissues, as well as the peculiar effects of patient-derived factors and the implications of clinical skill variables, need to be taken into account. The selection of biomaterials for joint prostheses, cardiovascular devices, dental and maxillofacial implants, surgical meshes, ophthalmological goods, and other applications is governed by inertness in addition to functionality [59].
Determining biocompatibility requires consideration of numerous internal and external factors specific to the host and implant site. These variables include things like surface chemistry, size, form, content, design, and other elements. The degree of implanted material's biocompatibility is influenced by a multitude of extrinsic factors that interact with these intrinsic features. The host species, implantation site, genetic inheritance, and microenvironment are a few of the variables. Many investigations evaluate different aspects, both in vivo and in vitro, such as cytotoxicity, allergic reactions, inflammatory responses, irritation, and systemic and chronic toxicity [60].
It becomes essential to address issues regarding the inertness of biomaterials in this intricate assessment procedure.
The objective of researchers is to reduce any potential adverse effects, despite the fact that no substance in the body can be completely inactive. For example, in order to promote inertness, advances in polymer design attempt to limit hydrolysis, oxidation, water absorption, and the release of contaminants and additives. It is critical to understand that the host response is influenced by both material qualities and mechanobiological processes, as well as patient-derived factors including genetics and general health [61].
Thus, inertness and usefulness must be balanced when choosing biomaterials for a variety of applications, such as joint prosthesis, cardiovascular devices, dental implants, surgical meshes, and ophthalmological products. In line with the ultimate objective of returning the human body to its natural form following physical trauma, disease, or genetic anomalies, this nuanced strategy guarantees the long-term success of biomedical implants. Table 3 summarizes systematically the kind of biocompatibility assessments conducted for the various types of nanoparticles incorporated within biomedical implants. It categorizes, in an ordered manner, the various types of implant materials, the corresponding methods by which their biocompatibility is evaluated, key findings of the study, and associated considerations of safety. This structured overview emphasizes the diversity in nanoparticle applications in implant types and the spectrum of methods employed to analyze their interaction with biological tissues. Here the evidence and safety insights drawn together highlight the requirement of right biocompatibility assessment if there is a likely high usage of nanoparticles in implanted devices in medical application areas.
5.2. Evaluating the biocompatibility of nanoparticle-enhanced implants
Many types of materials, shapes, and sizes have been made possible by developments in nanotechnology and nanofabrication. “A material with any external dimension in the nanoscale or having internal structure or surface structure in the nano-scale” is how International Organization for Standardization/Technical Specification (ISO/TS) 80004 defines nanomaterials (NM). Due to size-dependent characteristics such as high surface-to-volume ratio, high reactivity, prominent quantum effects, etc., many material traits are unique at this scale. Furthermore, because they can be handled at the nanoscale, NMs or materials with Nano characteristics can be developed and optimized for maximum performance. One area where NMs have been used is in biomedical applications, where their adaptability in producing unlimited geometries and hierarchical architectures has enabled amazing and quick progress [71]. Intentional or unintentional exposure to NMs naturally causes complex interactions in living systems, including the foreign body response (FBR). Depending on the kind of NMs present as well as the tissues and cells involved, these interactions can differ greatly. Certain natural products (NMs) exhibit advantageous relationships with the immune system and are designed for medicinal objectives. Others cause unfavorable reactions that could worsen health issues. Furthermore, because of their unusual size, NMs could be dangerous for people who produce them [72].
Even with the significant advancement in the engineering of NMs for biological applications, there are particular difficulties with the NM design parameter and the possible tissue- and cell-specific reactions they may cause. For instance, the surface characteristics of a particular NM play a major role in determining its biocompatibility [26]. The consequence of the FBR is nearly invariably the presence of acute or chronic inflammation in addition to the desired features like medication release, bio integration, etc. By itself, encapsulation and inflammation are not always bad things; in fact, in some situations, like with intrauterine contraception, they can be advantageous. Perhaps a better objective for bioengineers would be to modulate the inflammatory response because of its widespread nature. There have been proposals for the integration of biomaterials with biological regulators, such as immunomodulatory drugs.
Biocompatibility is the capacity of a biomaterial to carry out its intended role in relation to a medical therapy, generating the most appropriate beneficial cellular or tissue response in that particular scenario and optimizing the clinically relevant performance of that therapy without inducing any undesired local or systemic effects in the recipient or beneficiary of that therapy. Furthermore, his definition is acknowledged. The ability of the particles to directly disrupt the normal structure of human and animal organs and tissues, as well as to negatively impact normal physiology, is referred to in this context as NP toxicity [73]. It is commonly acknowledged that physiochemical factors, including particle size, shape, composition, surface charge and chemistry, and ensuing stability of nanoparticles influence toxicity. NPs are no larger than 100 nm in size. There are numerous methods to obtain them, including vacuum deposition, gas phase synthesis, mechanical processing (milling and grinding technologies), and wet chemical treatment (chemical reactions in solution). It can take the shape of a polymer, latex body, carbon particles, ceramic particles, or metal particles. These nanoparticles (NPs) can vary in size, shape, and chemical content depending on the preparation technique used [68].
They can also have a surface coating or not. The interactions of the nanomaterials with the cells or tissues can be influenced by each of these elements. NPs have the ability to penetrate membrane cells and travel through lymphatic, blood, and synaptic arteries in nerve cells. In addition, NPs preferentially gather in particular cellular structures and types of cells. Strong permeability NPs pose a risk to human health in addition to being effective in facilitating drug delivery. There is a significant surge in the creation of NPs for biomedical applications, such as gene or medication delivery, magnetic hyperthermia, and medical imaging [74].
New nanostructures must pass rigorous assessments to ensure their biological security before being used in biomedical applications. NPs show promise in several different types for use in biomedicine. Nanotubes' distinct size, shape, and structure have drawn a lot of attention to their analysis for biomedical applications. Currently, carbon nanotubes are the most extensively utilized type of nanotube used in biomedical applications. Other nanotubes used in biomedical applications include silicon dioxide, boron nitride, titanium dioxide, and organic nanotubes. The unique structure, size, and form of nanotubes have attracted a lot of interest in their investigation for use in biomedical applications. The most often employed kind of nanotube in biomedical applications is carbon nanotubes. In addition to silicon dioxide, boron nitride, titanium dioxide, and organic nanotubes, other nanotubes are employed in biomedical applications [75].
Biomaterials should normally provoke minimal unfavorable tissue response and be able to be integrated into the biological system. Because titanium (Ti) and its alloys have less immunogenic potential in vivo and are more biostable and biocompatible than allogenic grafts and other biomaterials, they are frequently employed in medicine and dentistry. Ti, on the other hand, does not cause the first biological reactions necessary to establish biocompatibility because it is a bio-inert metal [71].
Implant failure could then follow from this, interfering with bone healing at the tissue–implant contact. The use of NPs has shown to be a successful intervention for enhancing the biological principles of titanium implants [38]. Using foreign material with characteristics similar to those of innate tissue, bio-integration can occur synergistically without inducing an immune response. Particles that are nanoscale structurally resemble ligands, receptors, and deoxyribonucleic acid (DNA) in different body proteins. Additionally, it has been demonstrated that Nano biomaterials can absorb living cells. As a result, they can be used to conjugate with organic material and transfer nucleic acids, both of which are important steps towards bio integration. NPs are made of any kind of biocompatible material and have diameters that are ultrafine, with dimensions inside the nanoscale. It is commonly known that implant materials' biocompatibility and bioactivity are enhanced more effectively when nanoparticles are added than when comparable bulk materials are used [65].
Coating Ti-based implants with a material that demonstrates both biocompatibility and antimicrobial activity may increase the likelihood of implant success even further. This is because Ti surfaces not only encourage bacterial adhesion, which leads to infection and inflammatory processes, but also encourage cell adhesion, which is followed by Osseo integration. Inorganic NPs exhibit hydrophilicity, biocompatibility, remarkable stability, minimal toxicity, and resistance to microbial degradation. By adding NPs like copper, silver, and zinc to Ti implants, antibacterial activity and no cytotoxicity against human cells are possible [38]. Due to their enhanced antibacterial qualities, metal NPs provide additional advantageous clinical therapies by impeding bacterial attachment and potentially preventing infection during the process of bone mending. With the goal of being used in the therapeutic setting, technologies utilizing nanoparticle-based methods for improving cellular survival and biocompatibility, as well as delivering bioactive compounds, are constantly evolving. According to the established protocol for biological research, the implant material must first go through in vitro cytotoxicity testing protocols. This is followed by in vivo testing to evaluate the biocompatibility of these devices and characterize their interaction with soft tissue [73]. The precise process of NPs' interaction with various cells in a biological medium, as well as the intricate cellular mechanisms at the bone-implant interface during osteogenesis, remain mostly unclear. Moreover, there is a lack of documentation about the degree to which Ti implants modified with NPs improve biocompatibility.
5.3. Potential safety concerns and risk assessment
While nanoparticles have shown considerable promise in the development of biomedical implant technologies, to ensure the smooth integration of these materials into medical procedures, a thorough examination of any possible safety concerns is required. A detailed evaluation of any potential safety issues pertaining to the use of nanoparticles in biomedical implants is a crucial part of this research. Recent research has highlighted the range of nanoparticles employed in different applications, from metallic to polymeric nanoparticles. The interactions between these nanoparticles and biological systems are complex and multifaceted. Anticipating potential safety hazards requires an understanding of immunological reactions, cellular reactivity, and overall biocompatibility [76]. Concerns over the consequences of chronic exposure have also been raised by studies on the long-term effects of nanoparticle exposure that have concentrated on whether these materials accumulate with time.
The biodegradability and clearance mechanisms of nanoparticles further improve their overall safety profile. While some nanoparticles biodegrade in a way that is advantageous, others may cause problems with durability. Thorough toxicity investigations that focus on the specific nanoparticles utilized in biological applications are crucial. These researchers should address a wide range of toxicity-related topics, including genotoxicity, cytotoxicity, and possible effects on certain organs [77].
Effective risk assessment approaches must be used to evaluate the safety of biomedical implants, including nanoparticles. However, there is an issue with these protocols' standardization. Because regulatory bodies play a crucial role in keeping an eye on the security of these systems, a standardized approach to risk assessment is necessary [54]. To summarize, it is critical that all safety issues be addressed and comprehensive risk assessments be finished prior to developing and implementing nanoparticle-based biomedical implants. The successful and secure incorporation of these state-of-the-art technologies into healthcare will depend on multidisciplinary research being conducted in the future, legal requirements being met, and risk assessment protocols being continuously improved.
6.
Enhanced mechanical and functional properties
6.1. Impact of nanoparticles on the mechanical properties of implants
Medical implants are essential instruments for treating chronic illnesses, restoring physical function, and improving the overall quality of life for millions of individuals worldwide. However, implant failures due to infection, mechanical wear, corrosion, and tissue rejection continue to be a major issue [27]. Nanocomposites, which are composed of nanoparticles or Nano fillers dispersed throughout a matrix material, have shown promising results in terms of enhancing implant performance [53]. Because they offer efficient, less invasive treatments for a variety of medical ailments, medical implants have completely changed the face of modern healthcare. These days, they are vital instruments for the restoration of physiological functions, the management of long-term ailments, and the enhancement of millions of patients' lives across the globe. Medical implants do have disadvantages, despite all their benefits, and they present a number of application, design, and manufacturing challenges. One of the many difficulties presented by medical implants is their vulnerability to malfunction or failure, which may cause issues and have a negative impact on health.
Implant failures can be caused by a variety of causes, such as tissue rejection, infection, mechanical wear, and corrosion. These problems can occur even with the most advanced implant designs and materials, requiring recurrent procedures and implant replacements. To address these issues, researchers are looking into how nanocomposites might enhance the performance of medical implants [20].
The basic building blocks of materials referred to as nanocomposites are nanoparticles or Nano fillers dispersed within a matrix material, such as polymer or metal. These materials are perfect for use in medical implant applications because of their unique properties, which include high strength, flexibility, and biocompatibility. Though in its infancy, the use of nanocomposites in medical implants has progressed significantly. Researchers have developed a wide range of nanocomposites for use in dental, orthopedic, and cardiovascular stent applications, as well as in medical implants [78]. These materials, which improve mechanical strength, wear resistance, and biocompatibility, have the potential to reduce implant failure rates and increase patient satisfaction. Although the application of nanocomposites in medical implants holds considerable potential, several concerns remain to be resolved. Ensuring the materials' long-term safety and biocompatibility is a major challenge because of their small size and high surface area, which may make them more susceptible to interactions with biological systems [68]. Furthermore, before these materials are widely employed in clinical settings, trustworthy and affordable production procedures need to be established.
Surface modification with nanocomposites is a powerful technique to improve implant performance. This technique modifies the surface properties of the implant material to enhance biocompatibility, promote Osseo integration, or introduce bioactive components [75]. The surface can be altered by a variety of techniques, including coating, chemical functionalization, and Nano patterning. For implant materials that are nanocomposite, it is possible to tailor the unique properties of nanoparticles to maximize their efficacy. By adjusting the size, shape, chemical composition, and surface properties of nanoparticles, researchers can create implant materials with enhanced bioactivity, biocompatibility, and mechanical resilience. Wear and corrosion greatly affect implant materials' lifetime and effectiveness. Extended exposure to mechanical forces and physiological conditions can lead to material degradation and the production of wear debris, which can cause issues such as implant failure, inflammation, and osteolytic [59]. Using nanocomposites is a feasible way to reduce implant material corrosion and wear.
6.2. Improved functional performance of implants through nanoparticles
The way biomedical implants achieve functional performance has been profoundly altered by the introduction of nanoparticles, creating new opportunities for enhanced tissue integration, more efficient medication administration, and cutting-edge imaging. Scholars have endeavored to comprehend how the distinct characteristics of nanoparticles, like their size and surface roughness, contribute to optimizing the intended applications of these implants. For example, in drug delivery systems, the kinetics of release and cellular absorption are significantly influenced by the size and structure of the nanoparticles. To enable these nanoparticles to carry out the required functions, certain chemical groups or proteins can be added to their surfaces [78].
This field of study examines the technical characteristics of nanoparticles as well as their applications in terms of implant efficacy and patient outcomes. The purpose is to determine whether employing nanoparticles may significantly improve functional performance and have positive impacts on patients. For example, in the field of drug delivery, Nano composites allow for the precise and regulated release of medications, which may reduce adverse effects and boost therapeutic effectiveness [79]. Similar to this, nanoparticle-enabled breakthroughs in imaging capabilities help doctors make more accurate diagnoses by providing them with vital information about the condition of the implant and the surrounding tissues [80].
As research continues, the integration of nanoparticles to improve functional performance remains at the forefront of biomedical innovation. The objective is not only to enhance the technical aspects of implants but also to translate these advancements into significant improvements in patient care so as to guarantee that the promise of nanotechnology in biomedical applications translates into real benefits for those in need of cutting-edge medical interventions.
6.3. Case studies demonstrating enhanced properties
The performance and characteristics of various implants have been improved as a result of the integration of nanoparticles. To improve the osseointegration and wear resistance of titanium dioxide (TiO2) implants, hydroxyapatite (HA) nanoparticles were introduced. The improved osteoconductivity and bioactivity of HA nanoparticles, which support implant integration and bone development, are responsible for this improvement. On the other hand, biocompatibility and the risk of implant-associated infection were improved, and bacterial adhesion and biofilm formation were successfully reduced in orthopedic stainless-steel implants treated with silver nanoparticles (AgNPs). The silver ions that AgNPs release are thought to possess antibacterial qualities, which accounts for their potent antimicrobial activity. Moreover, polymeric nanoparticles added to drug-eluting stents allowed for targeted and prolonged drug release, improving the safety and effectiveness of stent implantation [18]. Nanoparticles can limit potential adverse effects and reduce systemic drug exposure by encapsulating various drugs and releasing them at the implant site in a regulated manner. This customized drug delivery approach has shown promising results in the treatment of coronary artery disease and other cardiovascular illnesses [81].
Table 4 lists the classification of the different types of nanoparticles and describes the contribution of each nanoparticle to improving the durability, biocompatibility and functionality of the implant. In this mapping, it depicts the application of nanoparticle enhancement on different implant categories, further underlining its versatility for improving implant performance. This summary provides insight into the modifications that can be implemented in nanoparticle integration specific to various implant types that ensure proper realization of any innovative biomedical engineering activity.
7.
Controlled drug delivery
One of the most advanced methods in pharmaceutical science is controlled drug delivery, which precisely regulates the release kinetics of therapeutic substances in the body to maximize benefits and reduce side effects. Using mechanisms like diffusion, erosion, or stimuli-responsive materials, these systems allow customized release profiles over long periods of time, defying traditional approaches [40]. Controlled drug delivery has a wide range of therapeutic applications, from cardiovascular disease care to oncology, and it offers the promise of better patient adherence and treatment outcomes. However, to guarantee stability and repeatability, careful consideration of medication characteristics, carrier materials, and regulatory requirements is required throughout the creation of these systems. Future developments in controlled medication delivery have the potential to completely transform patient care by providing individualized therapeutic interventions that are tailored to each patient's needs through interdisciplinary collaboration [39].
7.1. Roles of nanoparticles in drug delivery from implants
Controlled drug delivery and its significance in biomedical implants
Controlled drug delivery (CDD) is a technique for administering therapeutic agents at a predetermined rate over a specified period [94]. It offers several advantages over conventional drug delivery methods and is a technique for administering therapeutic agents at a predetermined rate over a specified period. It offers several advantages over conventional drug delivery methods [79].
7.1.1. Improved drug efficacy
The controlled and sustained release of therapeutic chemicals from implants is made possible by nanoparticles, which are essential for improving treatment efficacy. Long-term drug release patterns can be achieved by implants by encasing medications inside nanoparticles, which keeps therapeutic concentrations within the intended range for longer. To further increase the pharmacological effects of medications, nanoparticles can also prevent drug degradation and improve solubility, bioavailability, and cellular uptake. By precisely regulating the kinetics of medication administration, therapy efficacy is eventually increased while systemic side effects are kept to a minimum [95].
Studies have demonstrated that nanoparticle-based drug delivery systems significantly enhance drug efficacy compared to conventional methods. For instance, a 2022 study reported a 40% increase in tumor volume reduction in a cancer therapy model using nanoparticle-based delivery [79].
7.1.2. Reduced dosing frequency
One important aspect of patient adherence and treatment compliance is the ability to reduce dose frequency, which is made possible using nanoparticles in drug delivery from implants. Implants containing nanoparticles can produce sustained therapeutic levels in the body, eliminating the need for repeated dosage intervals by prolonging the period of drug release. In addition to increasing patient comfort and convenience, this reduces variations in drug plasma concentrations, maximizing treatment efficacy and reducing the possibility of negative effects from peak-and-trough dosing schedules. Reduced dosing frequency hence contributes to better patient outcomes and increased adherence to treatment [38].
Nanoparticle-based drug delivery systems can reduce dosing frequency, improving patient compliance and convenience. A 2022 study reported a reduction in dosing frequency from daily injections to once-monthly injections for rheumatoid arthritis treatment using a nanoparticle-based system.
7.1.3. Targeted drug delivery
With the use of nanoparticles, implants can carry drugs to specific tissues or cells in the body with precision, making them an effective tool for targeted drug delivery. Nanoparticles can be made to display affinity for certain biological targets by means of surface modification or functionalization [74]. This allows for the selective accumulation and retention of medicines at the site of action. By maximizing therapeutic advantages and reducing unpleasant reactions, this focused approach maximizes drug efficacy while minimizing off-target effects and systemic exposure. Targeted medication administration via implants also presents potential for personalized medicine techniques, which adjust treatment plans based on the unique characteristics of each patient and their disease profile to provide the best possible results [74].
Nanoparticle-mediated targeted drug delivery can minimize exposure to healthy tissues and reduce systemic toxicity. A 2021 study demonstrated a 75% reduction in tumor size and a 50% increase in overall survival in a cancer therapy model using nanoparticle-mediated targeted drug delivery.
7.2. Advantages of using nanoparticles for controlled drug release
Nanoparticles, with their unique size and properties, offer several advantages for CDD from implants; high drug loading capacity, Tailorable surface properties, Versatility, Increased bioavailability, reduced systemic exposure etc.
7.2.1. High drug loading capacity
The ability of nanoparticles to contain and transport large therapeutic payloads within their nanoscale geometries is truly astounding. This is explained by their enormous surface area to volume ratio, which makes drug loading and encapsulation effective. From a technological perspective, through different encapsulation techniques, including physical entrapment, chemical conjugation, or electrostatic interactions, nanoparticles can be created to accommodate a wide range of medicinal molecules, including hydrophilic and hydrophobic substances. Professionally speaking, this benefit translates into the capacity to deliver therapeutically relevant drug doses using fewer carrier quantities, enabling more compact and effective drug delivery systems [36].
Drug molecules can be encapsulated in large quantities by nanoparticles, allowing for long-term continuous release. According to a study, poly lactic-co-glycolic acid (PLGA) nanoparticles had an 80% drug-loading capacity.
7.2.2. Tailorable surface properties
Nanoparticles provide the flexibility to modify their surface characteristics to fulfill certain therapeutic needs. Nanoparticles can possess desired properties like increased biocompatibility, extended circulation time, or specific binding to biological receptors by means of surface modification or functionalization procedures. In theory, precise control over surface chemistry and functionality is possible using surface engineering techniques, including covalent conjugation, adsorption, and layer-by-layer assembly. Experts in the field can use this capacity to create nanoparticles with customized surface characteristics that maximize therapeutic benefits by improving tissue targeting, minimizing off-target effects, and optimizing drug delivery efficiency [96].
Implant performance can be improved by customizing the surface characteristics of nanoparticles to decrease protein adsorption and increase biocompatibility. The biocompatibility of nanoparticles was greatly improved by polyethylene glycol (PEG) treatment.
7.2.3. Versatility
With respect to content, size, shape, and structure, nanoparticles are remarkably versatile and have a wide range of uses in controlled drug release. In theory, a broad variety of materials, such as polymers, lipids, metals, and inorganic compounds, can be synthesized into nanoparticles by a variety of techniques, including emulsion, self-assembly, and nanoprecipitation. Professionally speaking, this adaptability allows for the creation of nanoparticles with unique characteristics to tackle certain therapeutic difficulties, such as stimuli-responsive drug carriers or prolonged release formulations. Additionally, nanoparticles can be designed to facilitate parenteral, topical, and oral distribution, hence increasing their usefulness in drug delivery applications [50].
Numerous materials can be used to create nanoparticles, which enables the delivery of a large range of medications with various characteristics. The adaptability of nanoparticles in controlled drug delivery (CDD), including different kinds of drugs.
7.2.4. Increased bioavailability
The therapeutic efficacy of medications that are poorly soluble or permeable may be improved by the use of nanoparticles, which can increase their bioavailability. In theory, hydrophobic medications can be dissolved in water by nanoparticles, shielded from enzymatic breakdown, and allowed to pass across biological barriers like the blood-brain barrier and the gastrointestinal system. Professionally speaking, this benefit translates into better drug distribution, absorption, and retention in target tissues, improving therapeutic results and decreasing patient variability in drug response [97].
Drugs, particularly those with low permeability or solubility, can have their bioavailability increased by nanoparticles. The medicine can be better absorbed into the bloodstream and kept from degrading by being encapsulated within the nanoparticle structure.
7.2.5. Reduced systemic exposure
By delivering drugs to particular tissues or cells with precision, nanoparticles reduce systemic exposure and off-target effects. It is technically possible to modify the surface of nanoparticles with targeting ligands or antibodies to give them a preferential affinity for sick tissues or cells. From a professional standpoint, this benefit presents the possibility of improving the therapeutic index of medications by increasing their concentration at the site of action and reducing their exposure to healthy tissues [80]. By lowering systemic exposure, nanoparticles improve the safety profile of drug formulations and improve patient outcomes by reducing the likelihood of systemic toxicity and adverse events.
Nanoparticles can minimize systemic exposure to medications and lower the chance of side effects by directing them to specific areas. This is especially advantageous for medications with limited therapeutic windows, in which there is little difference between hazardous and useful doses [98].
7.3. Mechanisms of nanoparticle-mediated drug delivery from implants
Multiple methods are involved in medication delivery from implants mediated by nanoparticles, including:
7.3.1. Diffusion
Drugs involved in nanoparticles diffuse or slowly pass through the carrier matrix or the surface of the nanoparticle into the surrounding tissues or bloodstream. Particle size, carrier material structure, and concentration variations are some of the variables that affect this movement. Researchers may manage the rate at which medications are released from implants by adjusting these variables, which enables consistent and regulated drug administration over an extended period of time. For the delivery of small molecule medications with modest permeability and solubility, diffusion is especially helpful [31].
Medication diffuses into the surrounding tissue passively from the nanoparticles. A two-month study investigating the diffusion process of PLGA implant nanoparticles revealed continued release.
7.3.2. Erosion
Drugs that have been encapsulated are released by the slow disintegration or dissolution of the implant matrix or nanoparticle carrier, which is known as erosion. Environmental variables, including pH, temperature, and the composition and degradation capacity of the material, impact this process [96]. With erosion-based drug release, the rate of release is controlled by the carrier material's rate of deterioration, enabling prolonged and adjustable delivery. It works well for delivering medications that have stability problems or require a longer release [99].
When the biodegradable polymer matrix of the nanoparticles degrades, the medication inside is liberated. A study suggests that adjusting the molecular weight of the polymer could control the rate at which PCL nanoparticles disintegrate, providing tailored drug release kinetics.
7.3.3. Stimuli-responsive release
Under the latest strategy termed “stimulus-responsive release”, medications are released by nanoparticles in response to particular environmental cues or external triggers. These can be temperature variations, pH shifts, or the presence of certain chemicals. Researchers may precisely control the release of medications at certain times and locations by inserting sensitive components into the design of nanoparticles, thus enabling customized therapeutic treatments. With this technique, drug administration is flexible and can be tailored to the specific needs and conditions of each patient through targeted and triggered release profiles [43].
The drug is released in response to specific stimuli, such as changes in pH, temperature, or an external magnetic field. Different systems of stimuli-responsive nanoparticles allow for controlled release in response to specific physiological cues. Table 5 exemplifies the possibility of targeted and sustained release from an enhanced nanoparticle implant. Thus, it gives some idea of which specific nanoparticles are mixed with other elements to obtain desirable drug release profiles and in order to retain therapy efficacy at the site of action for as long as possible and delivery can be targeted to target tissue or sites. As an organized summary of advancement towards mechanisms of drug release highlights contributions of nanoparticles in achieving more efficient, better localized, treatment regimens via implantable devices. The table emphasizes the possibility of these innovations to reduce side effects, improve patient results, and thus support the general therapeutic efficacy of implants.
7.4. Applications in drug-eluting stents and other implantable devices
Nanoparticles have emerged as key facilitators in the creation of controlled drug delivery systems, particularly in the field of implanted medical devices. Nanoparticles are an excellent choice for optimizing the therapeutic potential of implants due to their unique properties, including size, surface characteristics, and biocompatibility. For the diverse uses of nanoparticles in drug-eluting stents and other implanted devices discussed in this section, targeted, prolonged, and controlled drug release is crucial. The future of implanted medical devices is being shaped by nanoparticle-enabled technologies, which provide improved patient outcomes and more options in tailored medicine, from cardiovascular therapy to orthopedic modifications.
7.4.1. Drug-eluting stents
It is largely thanks to the discovery of nanoparticles that drug-eluting stent technologies have reduced rates of restenosis much lower than that of a traditional bare-metal stent. Therefore, with the application of nanoparticles into the drug-eluting stent, long-term effectiveness in vascular therapy is ensured due to controlled and time-release delivery of anti-proliferative medication.[105]. Figure 7 illustrates the placement of a drug-eluting stent within a coronary artery, showing how it adheres to the artery wall to prevent restenosis and maintain blood flow.
7.4.2. Implantable drug reservoirs
In order to create implantable drug reservoirs that allow for targeted and sustained drug release for a range of therapeutic purposes, nanoparticles are essential. Research from the past shows that nanoparticle-enhanced reservoirs can be used to treat long-term medical diseases, including hormone replacement therapy and chronic pain management with little to no patient involvement [81]. In recent years, several designs of drug-eluting implants have been developed to enhance therapeutic outcomes and usability. Figure 8 illustrates the different types of implant structures including polymer-coated drug cores (a), cylindrical implants for localized therapy (b), and miniaturized designs for discrete delivery (c–f). The designed structure is expected to improve controlled drug release and ensure versatility across medical applications:
7.4.3. Integration with orthopedic implants
Orthopedic implant-integrated nanoparticles have the potential to improve bone regeneration and lower infection rates. Researchers have looked into using nanoparticles to provide growth factors or antibacterial compounds locally in orthopedic implants. This method enhances the integration of orthopedic implants with surrounding tissues and overall biocompatibility while aiding in the healing process [43]. Figure 9 Shows the same idea for dental implants: Titanium dental implant with surface modifications (a); and how this is inserted in the jawbone (b); and their corresponding molecular interactions with enhancement on integration and healing.
7.4.4. Controlled drug delivery
Controlled drug release from implants using nanoparticles has created new possibilities in the effective and side-effect reduced treatment of diseases along with their implantation. In ophthalmology, ocular implants utilizing nanoparticles have been.
for the treatment of glaucoma and macular degeneration to permit sustained delivery rates directly to the eye, resulting in increased patient compliance with a decreased frequency between medication administrations. In addition, studies are underway to determine if the controlled release of microbicides (e.g., through cervical inserts or vaginal and subcutaneous skin implants) reduces systemic absorption. For the purpose of treating diseases such as cervical cancer or infections, sub-mucosal route targeting delivers medications straight to the cervix and can offer a controlled method with sustained release while reducing systemic side effects associated with oral administration. Bacterial vaginosis, routine antibiotic treatment of sexually transmitted infections, and hormone therapy may enhance patient compliance and obviate the need for multiple doses, as with orally administered products. These types of implants are installed under the skin and release drugs in a steady state over time, which makes them efficient for long-term therapies (e.g., hormone replacement therapy [10], pain relief management, or treatments regarding chronic diseases). Nanoparticles improve drug release rate and duration, enabling more effective treatments with greater patient comfort and compliance in a variety of medical applications [109],[110]. Figure 10 Shows a variety of medical implants for drug delivery and contraceptive applications, including ocular inserts, subcutaneous skin implants, intrauterine devices, and vaginal inserts. These implants represent an application of nanoparticle technology which enables drugs to be directly released at the point of treatment site in an effort to help minimize systemic side effects while maximizing patient compliance. For instance, ocular inserts deliver drugs directly into the eye to be used for the treatment of glaucoma; subcutaneous implants are utilized as long-term contraceptives through the slow release of birth-control agents. Intrauterine devices and vaginal inserts also provide localized hormone delivery that tends to reduce as much as possible the frequent dosing needed in the resultant therapeutic outcome.
7.4.5. Gastrointestinal implants
In recent years, the use of nanoparticles in gastrointestinal implants has become more popular. The use of nanoparticles in medical devices such as drug-eluting stents for gastrointestinal applications has been studied in the past. For diseases like inflammatory bowel disease, customized medication administration can be achieved through gastrointestinal tract implants reinforced with nanoparticles, avoiding systemic side effects while producing a localized therapeutic impact. To sum up, there has been a lot of advancement in the use of nanoparticles in drug-eluting stents and other implanted devices, providing regulated, sustained, and targeted drug delivery. These developments usher in a revolutionary era in medical interventions, influencing the effectiveness and prosperity of several therapeutic uses.
8.
Infection control (biofilms formations) and anti-inflammatory effects
8.1. Biofilm formation
Biofilm production is a major obstacle to infection management, which is crucial for the healthcare industry as well as other sectors. Complex populations of bacteria known as biofilms form a slimy, protective matrix on surfaces. These formations are present in tissues, medical devices, and a variety of surfaces [112]. They can cause chronic infections that are repeatedly unresponsive to standard antibiotic therapies. Multiple bacterial species are involved in the intricate, multi-step process of biofilm development, which is often cyclic. Extracellular polymeric material, or EPS, combines polysaccharides, proteins (composed primarily of D-amino acids), fatty acids, and various nucleic acids secreted by bacterial biofilms. Although EPS is thought to make up over 80% of biofilms and is crucial to the production of biofilms, most biofilms lack adequate EPS characterization [113].
The extracellular polymer shell (EPS) is a dense matrix mostly made up of water channels that facilitate the transfer of nutrients and oxygen. Apart from shielding the bacteria against drugs and the host's immune system (white blood cells, monocytes, and antibodies), the extracellular polymeric substance (EPS) provides a fundamental surface attachment platform. Microorganisms adhere, colonize, and mature on surfaces during biofilm development's intricate and dynamic process. This phenomenon significantly impacts several disciplines, including environmental research, industry, and health. It is pervasive in both natural and artificial contexts. Table 6 highlights Key features of biofilm formation [114]. The features of the formation of a biofilm on biomedical implants are discussed, which in turn imply a loss in function of a device and even patient's health. On the whole, these features translate to the clinic. Features contributing to biofilm formation, as well as all associated challenges—infection and implant degradation, are illustrated in Table 6. It underlines the critical aspects above highlighted, making the table focus on the importance of controlling biofilm in the design and maintenance of implants. It, thereby, draws light to innovation towards solutions that would mitigate such effects and improve the long-term efficacy of an implant.
8.2. Using nanoparticles to prevent implant infections
Nanoparticles' distinct physical and chemical characteristics have demonstrated tremendous promise in preventing implant-related infections. The utilization of nanoparticles to avoid infections in implants is a rapidly evolving field that draws upon nanotechnology, materials science, and medicine. There are several applications for nanoparticles in this regard.
Table 7 summarises a few of the various nanoparticles used within biomedical implants to prevent infection, including mechanisms, main function, advantages and associated problems. Organized in such a manner the table explains how specific nanoparticle works in the contribution to prevent infection through antibiotic action, resistance to biofilms, and immune modulation among others. It further describes the advantages and potential drawbacks of each nanoparticle type, thus giving an unbiased view of their utility in practical applications. All these references are provided as evidence to these perceptions that reflect the present scenario in infection-resistant implant technologies in terms of research and development.
9.
Extended case study of nanoparticles for diagnosis
9.1. Nanoparticles in cancer treatment
The treatment of cancer is one of the most challenging medical problems, and there is an urgent need for more focused and efficient therapeutic techniques. Because of their unique physicochemical characteristics, nanoparticles have become ground-breaking weapons in the battle against cancer. The only options for traditional cancer therapies are radiation, chemotherapy, and surgery, all of which run the risk of causing harm to healthy tissues or not completely curing the disease. Nanotechnology provides tools to guide tumor resection surgery, target medicines directly and selectively for malignant cells and neoplasms, and improve the therapeutic efficacy of radiation-based treatments. When taken as a whole, these developments may result in a lower risk for the patient and a higher chance of a successful outcome [127]. This lengthy case study explores the complex uses of nanoparticles in cancer therapy, providing a thorough synopsis of research results and their potential to revolutionize the field of oncology.
Beyond just delivering drugs, researchers looking at nanotechnology in cancer therapy also aim to develop novel medicines that can be obtained only by utilizing the unique features of nanomaterials.
First, as demonstrated by laser ablation and hyperthermia applications, certain physical characteristics of nanoparticles, such as energy absorption and reradiation, may be utilized to disturb sick tissue.
Second, while nanoparticles are big enough to contain various therapeutic materials, such as radionuclides and active pharmaceutical components, they are tiny enough to concentrate at the tumor sites.
Third, their large surface area can be functionalized by ligands that actively direct their direction in vivo, such as peptides, aptamers, antibodies, or DNA or RNA strands. Moreover, artificial antigen-presenting cells and in vivo depots of immunostimulatory substances for long-term anti-tumor efficacy are creatively designed using nanostructured architectures. These apps support effective medication administration, multimodal therapy, and theragnostic. Chemotherapy and radiation therapy are examples of traditional cancer therapies that frequently lack specificity, which can have serious side effects and reduce their therapeutic efficacy. Because of their diameters in the nanoscale range, nanoparticles provide a viable path for using precision medicine to treat cancer. Their size, surface properties, and capacity for functional engineering make them the perfect choice for targeted drug administration, imaging, and treatment.
9.2. Research findings
9.2.1. Targeted delivery of drugs
Discovery: Nanoparticles may be engineered to deliver drugs specifically to cancer cells. Selective delivery of therapeutic medicines is made possible by surface modifications using ligands or antibodies, which enable precise recognition and binding to cancer cell receptors. By decreasing systemic adverse effects and enhancing medication accumulation at the tumor site, this focused method improves treatment results overall.
9.2.2. Enhanced permeability and retention (EPR) effect
Discovery: Nanoparticles utilize the EPR effect to take advantage of the distinct physiology of tumor vasculature. Because of the leaking blood vessels, this mechanism permits nanoparticles to passively collect in tumor tissues. The EPR effect, which capitalizes on the variations in vascular permeability between healthy and malignant tissues, improves medicine delivery to the tumor location.
9.2.3. Photothermal and photodynamic therapy
Discovered: Certain nanoparticles possess photothermal characteristics, including gold nanoparticles. These nanoparticles emit heat in response to near-infrared light, causing localized hyperthermia that has the ability to specifically destroy cancer cells. Furthermore, nanoparticles can be engineered for photodynamic treatment, which produces reactive oxygen species in response to light exposure and specifically destroys cells.
9.2.4. Imaging using many modalities
Discovering: Nanoparticles function as adaptable contrasts for a range of imaging techniques. They can improve fluorescence imaging, computed tomography (CT), and magnetic resonance imaging (MRI). With the capacity to visualize tumors precisely, this multimodal imaging technology makes image-guided medication administration and therapy possible.
9.2.5. Overcoming drug resistance
Discovering: Nanoparticles offer a means of assisting cancer cells in overcoming drug resistance. Through the co-administration of various therapeutic drugs with unique modes of action, nanoparticles can effectively target diverse populations of cancer cells and counteract resistance, enhancing the effectiveness of treatment.
10.
Challenges and ethical consideration in integrating nanoparticles with biomedical implants
10.1. Challenges in integrating nanoparticles with biomedical implants
10.1.1. Targeted drug delivery and controlled release
Nanoparticle integration into biomedical implants is complex given the need for targeted drug delivery and effective control over release. A major challenge is to ensure nanoparticles specifically target certain cells or tissues with minimal off-target effects. However, the design of nanoparticles with optimal surface properties presents a challenge because it is difficult to tailor their surfaces in order to achieve maximal targeting capabilities while ensuring stability and biocompatibility. This could also complicate the manufacturing process and influence nanoparticle release profiles; researchers have suggested that although targeting of nanoparticles using ligands can blunt some specificity, it may result to too target a nanomaterial with poor therapeutic outcomes [128]. Indeed, for example, a controlled release of therapeutics over months or years is notoriously difficult to achieve in vivo due to the fact that one has no control other than at the manufacturing stage and maybe not even then and also because the human body is extraordinarily complex [129]. These hurdles highlight the essential for new design methods and more elaborate delivery technologies.
10.1.2. Integration with advanced materials and technologies
There are also a lot of difficulties in combining with advanced materials and technologies; one of the problems that have to be faced when working with nanoparticles and smart materials is compatibility and stability in processability/performance. Even though the recent progress in nanoparticles has contributed to enhancing flexible electronics and 3D-printed materials; it also demonstrates challenges of durability and maintenance issues during a long-term utilization period for these hybrid systems [130]. For example, even if nanoparticle-enhanced smart materials can exhibit an adaptable environmental response, it is not guaranteed this functionality will be reliable and that the material services over time [131]. The coffin is in developing materials that are mechanically superior and biocompatible, which requires Research and Development (R&D).
10.1.3. Regulatory and ethical considerations
It is important to consider regulatory and ethical aspects in the development of biomedical implants using nanoparticles. Nanomedicine cannot be standardized, and the current regulatory landscape is far behind what technologically already seems possible. One impediment to this goal is the absence of standard protocols for evaluating nanoparticle-based implants, which in some instances result in discrepancies between regulatory practices and a lag time from bench to bedside. There is also the ethical question of nanoparticle long term effects on human and environmental health. Nanoparticles, for example, offer tremendous therapeutic benefits but their unintended biological interactions and environmental accumulation create apprehensions about safety [132]. A strong case exists for comprehensive guidelines and ethical considerations to tackle these issues, which is crucial if nanoparticle implants are expected to be safe and effective.
10.1.4. Long-term stability and degradation
For many biomedical implants, a major challenge is to control the degradation of nanoparticles long-term. Additionally, nanoparticles need to remain intact and effective for long periods in the body, which is a hostile place for these delicate constructs. Current research interests include degradation and time-related nanoparticle-induced disorders in biological systems. Thus, the challenge is to design nanoparticles that can hold up under biological conditions, all while delivering reliable performance for decades of implant life. For example, researchers have brought up issues in the release of degradation products that might cause toxicities or disturb the function of implants [133]. This underscores the importance of designing nanoparticles with tailored degradation profiles that minimize toxicity, which is essential for bio integration into biomedical implants.
10.1.5. Manufacturing and scalability
Manufacturing and scalability are major bottlenecks to translating innovations in nanotechnology into practical nanoparticle-enhanced biomedical implants. The synthesis of nanoparticles may vary depending on various synthesis methods leading to a diversity in quality and application performance, making it difficult to produce the same type of nanoparticle at a large scale. Furthermore, the homogeneous introduction of nanoparticles into bio medically-used implants without deterioration in their properties or safety needs accurate manufacturing procedures [134]. Solving these challenges requires establishing robust production methods that will provide nanoparticle-based implants practical as well as reliable for clinical use.
10.2. Ethical considerations and potential risks
10.2.1. Long-Term health effects of nanoparticle implants
The nanoparticles in an implantable device raise ethical and long-term health risk concerns. Owing to the small size, nanoparticles can easily cross cellular membranes, and targeting different tissues could bring unforeseen consequences in biology. Furthermore, scientists are sometimes ill-equipped to predict long-term effects of nanoparticles on our body that directly connect with its use for implants. This demonstrates potential health risks due to nanoparticle accumulation and interactions within the body that may not always be detected through tests. These concerns challenge the ethics of this context, stressing the appropriate need for an increase in careful and continuous safety assessments to prevent patients being met these unknown health risks [43].
10.2.2. Environmental impact of nanoparticle disposal and degradation
Beyond health issues, there are ethical considerations of environmental impacts presented by nanoparticles. The nanoparticles that are disposed of as medical waste or released from implants can have adverse effects on ecosystems and wildlife. The small size, reactivity, and high surface area of nanoparticles may lead to their release into the environment, where they might disperse broadly within ecosystems, eventually becoming toxic to more than one form of life. Knowing how nanoparticles degrade and act within the environment is essential to mitigate such risks. This includes creating proper techniques for removal and reducing their air pollution to decrease their deplorable consequences [43].
10.2.3. Equity and accessibility in nanoparticle-based healthcare technologies
Another urgent ethical concern is the equity in access to nanoparticle-based implants. While this cutting-edge technology comprises the future in transforming healthcare by delivering novel therapies, attention to ensuring equitable availability for all populations is a concern. However, there is a danger that by focusing on these approaches, regions of poverty may be left behind and perpetuate current healthcare inequities. For the future, it is imperative that all patients be granted access to nanoparticle-based implants irrespective of their financial or social background in order not only to avoid further expanding existing healthcare disparities but also to guarantee equal availability throughout hospitals and medical centers. This requires policies and practices to ensure equity (fairness) as well as inclusivity in accessing novel medical tools [135].
11.
Future directions of nanoparticles in biomedical implants
When we consider where nanoparticles in biomedical implants will go in the future, it is clear that a revolution in healthcare innovation is about to occur. The intersection of biomedical engineering and nanotechnology presents significant opportunities for groundbreaking advancements in the creation and utilization of implantable medical devices. Several important paths become apparent as areas of focus for research and development as we move forward. Future research in this field should concentrate on a few important areas to improve the efficacy and safety of nanoparticle-based implants.
11.1. Enhanced biocompatibility and safety
The most frequent research field with regard to the use of nanoparticles in biomedical implants is concerned with improving their biocompatibility and security. In some cases, nanoparticles can induce an immune response or prove toxic, triggering inflammation and implant rejection. Avenues for future research include refining surface modifications to reduce some of these associated effects. One potential example may be to coat nanoparticles with biocompatible polymers or hydrogels for better tissue integration. Finally, long-term in vivo stability and breakdown of nanoparticles should be further pursued. Creating biodegradable nanoparticles that degrade into non-toxic metabolites is a way to address these responses. Improved in vivo model systems, which more accurately reproduce human responses, will also be critical for determining the chronic effect of particles on health [136].
11.2. Targeted drug delivery and controlled release
Another potential area of research is the development of improved drug delivery systems like targeted and controlled release with nanoparticles. Drug delivery systems (DDS) are an approach to delivering drugs for the treatment of localized diseases with limited systemic side effects. Recent trends project toward the development of nanoparticles that possess cell or tissue type targeting specificity, which will form an important direction for future investigations and therapeutic use designed with the artificial conjugation strategy. For example, nanoparticles could be designed to uniquely target a type of cancer cell or an inflamed tissue. Responsive drug delivery systems can release therapeutic agents in response to specific stimuli, such as pH shifts or temperature changes, which serve as another level of control that enables the improvement of treatment selectivity. Further, the investigation of nanoparticles for co-delivery can deliver therapeutics from designing a single nanoparticle as a solution to realize a combination regimen should enhance thermodynamics in disease treatment [137].
11.3. Personalized nanomedicine
Nanoparticles are an important part of personalized cancer therapy, with a focus on treatments that can be tailored to the molecular and genetic features of individual patients. Researchers should now concentrate on the development of nanoparticles that can be tailored to individual genetic profiles or path biochemical markers. Augmenting nanoparticles that change their behavior to the diverse biological host environment will lead to more personalized treatments. Nanoparticles might be programmed, for example, to tailor release profiles or target development based on continuous feedback from the patients. The combination of nanoparticle technologies with genomics and other personalized medicine approaches is expected to result in better-targeted therapies, increase the options for personalization of therapy that will mitigate toxicity effects associated usually with non-specific treatments from untargeted drugs [138].
11.4. Integration with advanced materials and technologies
Combining nanoparticles with breakthrough materials and technologies is an overlapping issue of great interest that will enable us to achieve higher standards in biomedical implants design. Nanoparticles can also be conjugated with ‘high performance’ smart material that respond to environmental stimuli (e.g., temperature or pH) and a pre-requisite of a dynamic implant in which these particles are incorporated into the matrix of the designed device so that real time changes may need to be exogenous. Some researchers employ nanoparticles not only to circumvent implant-induced inflammation and fibrosis but also to merge nanotechnology with flexible electronics into physiological signal tracking, feedback-active (hard-soft) systems that will potentially enable adaptive response treatments. This area of research would help catalyze the next generation towards more sophisticated implant structures with complementary functions and further push medical technologies to see manifold enhancements in human health monitoring [139].
11.5. Regulatory and ethical considerations
The more nanoparticle technologies develop, the greater regulatory and ethical questions arise. Therefore, establishment of extensive guidelines and standards for nanoparticle use in biomedical implants are necessary to validate their safety profile. The framework should also support the development of methodologies that facilitate long-term toxicological endpoint evaluation for human health assessment. In addition, consideration should be given to ethical issues related to the environmental effects of potential interventions and equitable distribution of advanced treatments. Researchers must engage alongside regulators for a development path that enables robust and timely approval of nanoparticle-based implants compatible with regulatory standards; it is also important to anticipate societal implications [132].
12.
Conclusion
The encapsulation of nanoparticles in biomedical implants represents a major step in improving healthcare. The power of these micron-scale objects is in the macro-level opportunities they provide: Targeted drug delivery mechanisms, better tissue regeneration pathways, and real-time feedback for implant performance. Nanoparticles similarly boost the performance of biomedical implants and pave a way to personalized medical treatment, where therapeutic approaches can be geared towards different patient groups based on their particular disease manifestations. Nevertheless, while nanoparticles are an important new frontier of progress, they also present challenges. These include addressing critical issues like long-term biocompatibility, preventing unintended consequences of biological interactions, and understanding the complete effect nanoparticles will have on both human health as well as the ecosystem. These hurdles further emphasize the need for continuing advancement and discovery in this quickly changing world.
On the other hand, if nanoparticles fulfill their promise in biomedical implants, a balance is needed between that high-flying image and ethical behavior and fair access to them. Now that these technologies are moving ahead, it has led to a critical need for the development of standardized methods by which/where they can be evaluated in terms of safety and long-term impacts. Moreover, the environmental impact of nanoparticle waste and degradation must be adequately controlled to avoid adverse ecological consequences. This will help address concerns that only a few patients can afford the advantages of nanoparticle-enhanced implants and prevent widening healthcare disparities. Human-like style, the complexities of moving forward will require continued collaboration between researchers, clinicians, and regulatory bodies as well as policymakers. Addressing these critical considerations will enable the nanomedicine field to realize its tremendous potential and bring us closer to developing efficacious Nano-enabled healthcare solutions in a scientifically rigorous and ethically grounded manner.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
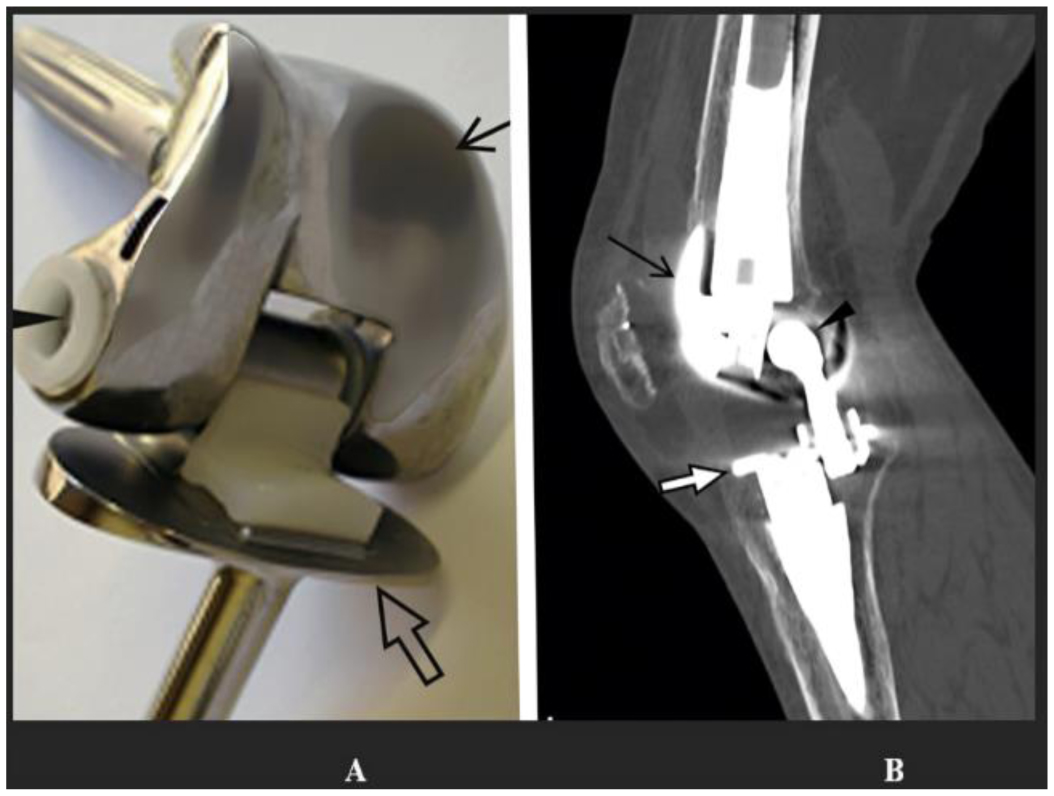









 DownLoad:
DownLoad:












