1. Introduction

Biomass gasification-fermentation is a two-step thermochemical-biological conversion process that can be used to produce fuels and chemicals from renewable feedstocks. In the first step, renewable feedstocks such as dedicated energy crops, crop residues, wood, and municipal solid waste are converted to primarily carbon monoxide (CO), hydrogen (H₂) and carbon dioxide (CO₂) through gasification using a limited amount of oxidizing agent (such as air, oxygen and/or steam) at high temperatures that typically range from 600 to 1,000 °C ^[1,2,3,4]. The extreme gasification environment breaks down organic compounds into a stable gaseous mixture commonly referred as synthesis gas (syngas). Syngas is composed of CO, H₂, and CO₂ as well as impurities, such as nitrogen (N₂), methane (CH₄), ethane (C₂H₆), ethylene (C₂H₄) and acetylene (C₂H₂), tars, ammonia (NH₃) and hydrogen sulfide (H₂S), and particulates. In the second step, syngas is fermented by anaerobic microbes, i.e., acetogens, such as Clostridium ljungdahlii, Clostridium autoethanolgenum, Eubacterium limosum (aka Butryibacterium methylotrophicum), Clostridium carboxidivorans, Clostridium ragsdalei, Clostridium species MAceT113 and Alkalibaculum bacchi to form acids (acetic acid, butyric acid, hexanoic acid), alcohols (ethanol, isopropanol, butanol, hexanol), and specialty chemicals (2, 3-butanediol, acetone, fatty acids, fatty alcohols) ^{[5,6,7,8,9,10,11,12,13,14]}. This process is referred to as syngas fermentation.

Biomass gasification-fermentation offers several major advantages compared to other processes that have been proposed for production of fuels and chemicals from renewable feedstocks.

1. Gasification utilizes lignin and all other organic molecules present in the process feedstock to produce syngas; hence, theoretically, all organic parts of the feedstock can be converted into fuels and chemicals during fermentation. Other processes that use renewable feedstocks, such fermentations of sugars from either sugar crops (e.g., sugar cane, sugar beets and sweet sorghum) or enzymatic hydrolysis of starch, cellulose and/or hemicellulose, can only use the carbohydrates in the feedstock for fuel and chemical production. Lignin makes up between 17 and 30% of the organic portion of biomass ^[15].

2. Conversion of syngas through fermentation takes place at lower temperatures and pressures than chemical catalytic conversions of syngas; thus, specially designed reactors that are resistant to high temperatures and pressures are not required to conduct syngas fermentation ^[12]. This reduces capital and operational costs.

3. Microbial fermentations produce fewer by-products than chemical catalyst conversion; hence, fermentation has higher product specificities ^[16].

4. Acetogens involved in syngas fermentation are able to operate under flexible CO:H₂:CO₂ ratios; thus, syngas reforming is not required to match fermentation conditions

5. Gaseous substrates, such as CO and H₂, allow uncoupling of hydraulic retention time with the supply of substrate, thus offering a better control of substrate and product inhibition ^[12].

6. Hazardous or xenobiotic products are not formed in the fermentation process ^[16].

7. The mesophilic incubation temperatures, low media carbohydrate levels, low operating pH and high CO concentrations are inhibitory to many classes of contaminating microorganisms, including methanogens ^[4].

Despite these advantages, several challenges emerge while integrating biomass gasification with syngas fermentation. These include high temperatures (600-1000 °C) for gasification and the accompanying costs to achieve these temperatures, gas-liquid mass transfer, reactor design, low cell mass concentrations, low product yields, slow conversion rates, low stability of microbial catalysts, high cost of fermentation media, and inhibitory effects of gas impurities ^{[17,18,19,20]}. Several studies have focused on understanding the microbial physiology of syngas fermenting microbes, and optimizing and maximizing syngas fermentation ^{[21,22,23,24]}. However, few studies have focused on the integrating of the two technologies. The following review identifies and addresses the underlying research gaps and challenges, thus enabling a holistic approach for designing and commercializing biomass gasification-fermentation process.

---

2. Biomass Gasification

The conversion of biomass to syngas occurs through four steps, namely: drying, devolatilization, oxidation and reduction. Drying releases moisture from biomass that further reacts to form H₂. Devolatilization occurs at temperatures between 225 and 500°C and releases volatile compounds from biomass ^[25]. Oxidation is the next step wherein the devolatilized products (i.e., char, tar and gases) react with an oxidizing agent yielding essential heat for endothermic reactions. Reduction is the final gasification step, which reduces the hot combustion products (produced during oxidation) mainly to CO and H₂.

Gasifiers are classified based on the availability of heat to drive the reactions (direct or indirect) and on the type of bed. Direct gasification involves use of air and/or oxygen (O₂) as an oxidizing agent, which reacts with biomass within the gasifier and produces heat energy needed to drive endothermic gasification reactions. In indirect gasification, the gasifier is externally heated to supply essential heat for gasification reactions. Direct gasification using air (i.e., air-gasification) results in N₂ diluted (50-65%) syngas with low H₂ and CO concentrations while indirect gasification, which typically uses steam or oxygen as an oxidizing agent, yields syngas with higher H₂ and CO concentrations. Detailed discussion on gasifier types based on the bed configuration can be found in other literature ^[2,3].

---

2.1. Gasifier biomass feedstocks

Biomass, such as dedicated energy crops, agricultural and forestry residues, and municipal solid waste, can be gasified to generate syngas. Biomass exhibits higher reactivity and require a lower gasification temperature than coal, which historically has been used as a gasifier feedstock to generate syngas ^[2]. However, biomass generally contains less carbon (39-52%) than coal (68-92%) ^[25,26], consequently, less carbon is available for conversion into carbon-based gaseous products in the syngas.

---

2.2. Parameters influencing biomass gasification

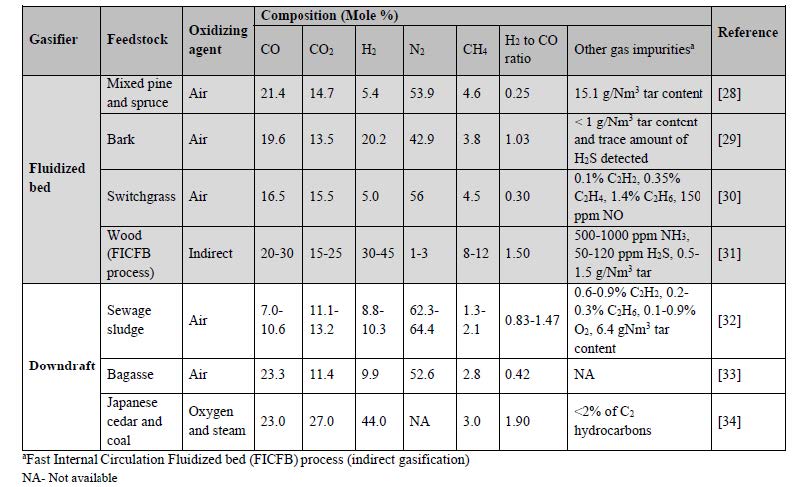
Feedstock properties(such as size, shape, density, chemical composition, energy content and reactivity) and gasification conditions (such as reactor type, temperature, pressure, type and flow of oxidizing agent, biomass flow, and catalyst used) have considerable influence on syngas composition and impurities ^[3,27]. Table 1 lists syngas composition and impurities from gasification of a variety of feedstocks as a function of gasifier reactor type, biomass feedstock and oxidizing agent.

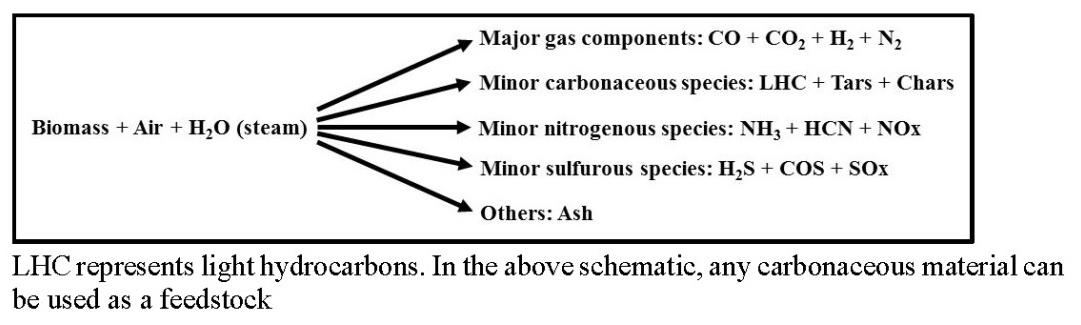
The overall gasification reaction using air and/or steam is represented in Figure 1. The formations of char and tar are usually due to incomplete conversion of biomass into syngas ^[3].

---

2.2.1. Syngas impurities and clean up

Syngas contains several undesirable impurities such as tars (defined as benzene and other condensable aromatic hydrocarbons of molecular weight higher than benzene), particulate matter (pure carbon and ash), inorganic compounds (ammonia, hydrogen cyanide, hydrogen sulfide, carbonyl sulfide, and nitric oxides), and light hydrocarbons (methane, acetylene, ethylene, and ethane) ^[25]. Syngas impurities can profoundly affect gas utilization technology downstream of the gasifier ^[3,25]. Handling and removal of tars have been one of the major challenges during process scale-up, as tars tend to condense at low temperature and/or form aerosols that affect engine and turbine performance ^[3,25]. The condensed tars easily mix with particulates and accumulate on inside surfaces resulting in the clogging and fouling of pipes and equipment ^[3,25]. Cleaning and reforming raw syngas is a major downstream process for effective utilization of syngas by subsequent processes ^[2,3]. Tar content in syngas varies depending on gasifier type, gasification time-temperature combination, bed geometry and type of oxidizing agent used ^[3,25].

---

3. Factors in Gasification That Influence Fermentation

For successful integration of biomass gasification and syngas fermentation processes, it is important to identify the key factors in gasification that can have a potential impact on fermentation. Some of these factors are the carbon conversion efficiency, syngas impurities, H₂/CO ratio and usability of CO₂ in the presence of CO.

---

3.1. Carbon conversion efficiency

Carbon conversion efficiency (CCE_G) quantifies the effectiveness of a gasification process and is defined as the ratio between the mass flow rate of carbon in the syngas to mass flow rate of carbon in the feedstock ^[25]. In general, the CCE_G for a gasifier can vary between 60 and 99% ^[25], which means that 60-99% of the carbon present in the feedstock can be converted into carbon-containing gases. Carbon loss is mostly in the form of tars, char and volatile hydrocarbons. These compounds that represent carbon that is unavailable for subsequent conversion to alcohols during fermentation; therefore, conversion of these impurities to syngas CO and H₂ is desirable so that they are available for fermentation. Normally, carbon in the form of volatile hydrocarbons, such as CH₄ and C₂H₂, are accounted for in the calculation of CCE_G along with CO and CO₂; however, volatile hydrocarbons are not fermentable by syngas fermenting microorganisms. Hence, a modified CCE_G that accounts for CO and CO₂ as the only fermentable carbon is more appropriate for carbon balance calculations involving syngas fermentation. In one study, a lab scale fluidized bed air gasification system achieved a CCE_G of 89% while the modified CCE_G for syngas fermentation was 72% ^[27].

Increasing the gasifier operating temperature converts tars into CO, CO₂ and H₂, thereby, increasing the CCE_G ^[3]. However, the operating costs also increase as temperature increases. An effect similar to increasing temperature can be obtained by reducing tar content with an in-bed catalyst such as dolomite and limestone used during fluidized bed gasification ^[3]. CCE_G can also be controlled by the equivalence ratio (ER) ^[35], which is the ratio of actual air supplied to the stoichiometric air required for complete combustion of biomass. Higher ERs result in higher operating temperatures, which in turn increases the degree of oxidation of available carbon and thus increases CCE_G ^[27]. However, higher ERs also result in more CO₂; hence, optimum ER, which results in more CO and H₂ ^[27], is more suitable for producing syngas for fermentation. Lv et al. ^[36] showed that an increase in ER from 0.19 to 0.23 in an air-steam gasification system increased CCE_G by 19%. Decrease in the size of biomass particles can also result in a higher CCE_G because heating rates increased with an increase in the surface area of biomass particles ^[36].

Cold gas efficiency (CGE) is another energy efficiency calculated for gasifiers. CGE is defined as the ratio of chemical energy of syngas to the total energy throughput to the gasifier ^[25]. Higher CGE results in a higher chemical energy, also called heating value, of the syngas. Higher CGE represents higher CO and H₂ concentrations in the syngas, which are desirable for fermentation.

---

3.2. Effect of syngas impurities

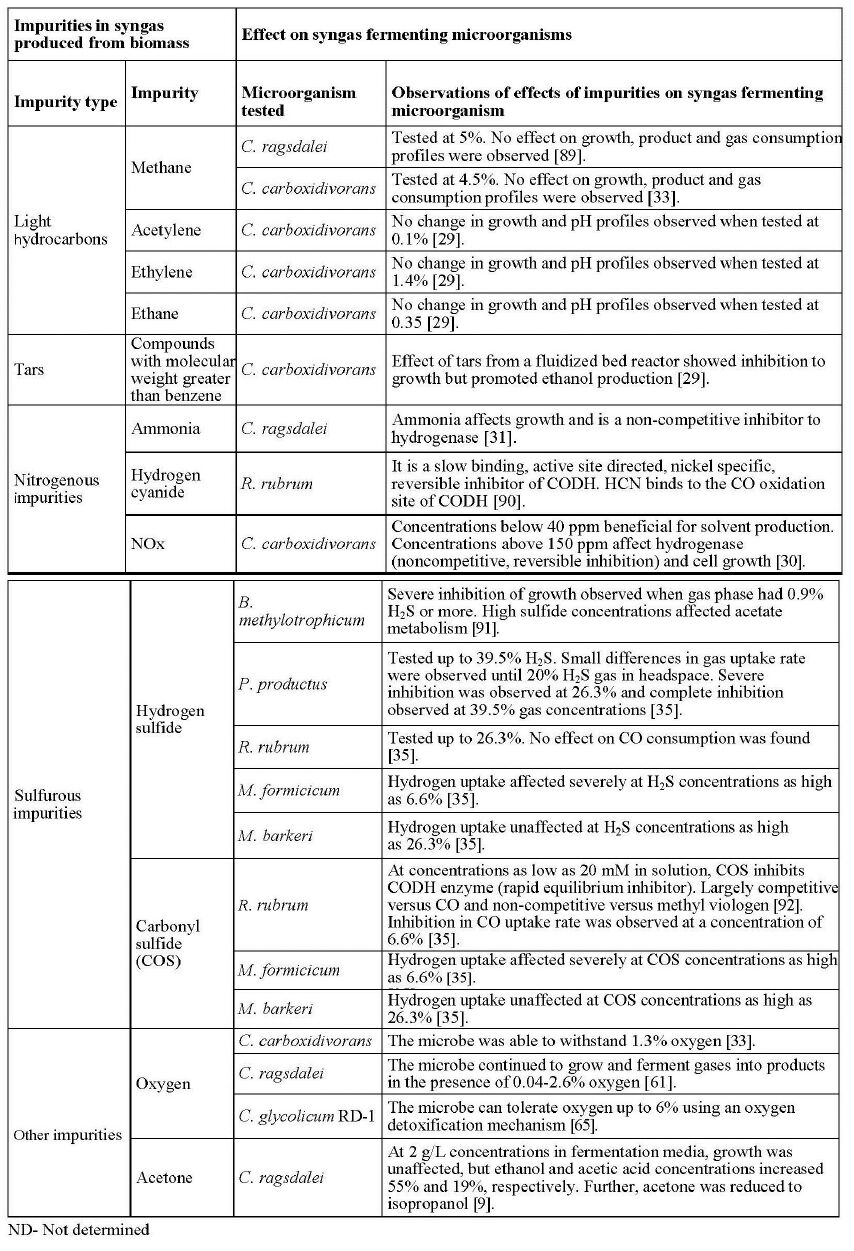
Although CCE_G is generally high in gasification, the presence of impurities (compounds other than CO, CO₂ and H₂), such as tars, inorganic impurities and light hydrocarbons, can reduce fermentability of syngas ^[30,37,38]. These species can affect growth, enzyme kinetics and/or alter growth media by changing the osmolarity, pH and/or redox potential ^[38]. Microbial catalysts can tolerate sulfides (such as carbonyl sulfide, hydrogen sulfide and sulfur dioxide), chlorine compounds and tars ^[4,39]; however, the effects of these contaminants on alcohol production and cell growth have not been thoroughly studied. Understanding of gasification parameters that cause production of these contaminants and effects of these contaminants on fermentation are critical for design and development of an economically viable gasification-fermentation process. A limited number of studies have examined the effects of syngas impurities on syngas fermentation microorganisms and have shown both positive and negative effects of various impurities on growth and product distribution ^{[30,40,41,42]}. Metabolically, many syngas impurities deactivate key enzymes involved in the Wood-Ljungdahl pathway such as carbon monoxide dehydrogenase (CODH), hydrogenase, and alcohol dehydrogenase ^[37,38,43]. Table 2 lists the highest concentrations of various impurities reported in syngas in conjunction with microbial catalysts and their tolerance ceiling. Microbes demonstrate varied responses to impurities, so generalization of such responses is not warranted.

Several studies have compared the effects of syngas produced from biomass gasification and syngas produced from mixing pure gases on cell growth and ethanol and acetic acid production. Datar et al. ^[40] fermented biomass-generated syngas from a fluidized bed gasifier. Researchers observed growth inhibition of C. carboxidivorans in a bioreactor. Growth resumed when biomass-generated syngas was substituted by clean bottled gas. Another study observed that C. ragsdalei adapted to biomass-generated syngas exhibited a 133% increase in ethanol concentration and 500% decrease in acetic acid concentration in comparison to cells that were grown on pure gas mixes ^[41]. Cultural adaptation to impurities prior to large scale cultivations has been shown to increase ethanol to acetic acid ratios.

---

3.2.1. Effect of carbonaceous impurities

Carbonaceous impurities originate from carbon, hydrogen and oxygen in the feedstock that could not be converted into CO, CO₂ and H₂ during gasification and include lighter hydrocarbons, such as CH₄, acetylene (C₂H₂), ethylene (C₂H₄), and ethane (C₂H₆), and tars. CH₄ is a major component of syngas, which is formed through the methanation reaction during gasification.

---

3.2.1.1. Effect of volatile hydrocarbons

The formation of CH₄ could be important for the overall gasification process and cannot be completely avoided as it is an exothermic process and the heat evolved by this reaction supports other endothermic reactions. The highest concentration of CH₄ in syngas reported in literature is 14.9% using air-steam co-gasification of coal and plastic waste mixtures in a fluidized bed gasifier ^[50]. In a previous study, syngas with a CH₄ concentration of 4.5% was fed to C. carboxidivorans ^[40]. CH₄ did not affect gas utilization or growth, which confirmed the inert nature of CH₄ in syngas fermentation. Ahmed et al. ^[30] reported that syngas containing C₂H₂ (0.1% v/v), C₂H₄ (1.4% v/v) and C₂H₆ (0.35% v/v) did not affect growth during syngas fermentations with C. carboxidivorans.

In general, syngas-fermenting microbes have many enzymes similar to nitrogen fixing bacteria and methanogens ^[51,52] and are also found in close connection to methanogens and sulfate reducing bacteria in their natural environment ^[53]. Therefore, some understanding of how syngas-fermenting microbes could respond to volatile hydrocarbons in syngas can be obtained by reviewing literature that investigated the effects of volatile hydrocarbons on these similar microbes. For instance, in Azotobacter vinelandii, C₂H₂ was found to be a slow binding, active site directed reversible inhibitor of nickel-ferrous hydrogenase involved in catalyzing the oxidation of H₂ ^[52]. C₂H₂ also inhibits many methanogenic microorganisms by interfering with membrane linked proton movement and ATP synthesis ^[54]. However, C₂H₂ fermenting anaerobic microorganisms have been discovered ^[55]. Pelobacter acetylenicus, a C₂H₂ fermenting microbe has a tungsten-iron-sulfur protein called acetylene hydratase that catalyzes a net hydration reaction rather than a redox reaction producing ethanol and acetate as major fermentation products through acetaldehyde as a metabolic intermediate ^[55].

${C_2}{H_2} + {\rm{ }}{H_2}O \to C{H_3}CHO \Delta G{\rm{ }} = {\rm{ }} - 111.9{\rm{ }}KJ/mole$

(1)

Like C₂H₂, C₂H₄ also has an inhibitory effect on methanogens ^[54]. About 50% of CH₄ formation was inhibited at 0.07% C₂H₄ and as C₂H₄ concentration increased to 0.5%, more than 94% CH₄ formation was inhibited, but these inhibitions were found to be reversible ^[56]. In a different study, Oremland and Taylor ^[57] showed inhibition of CH₄ formation by C₂H₂ and C₂H₄, but, C₂H₆ was found to be an inert gas for fermentation.

---

3.2.1.2. Effect of tars

A review by Rabou et al. ^[58] classified tars based on physical properties into five classes: 1) GC undetectable, which are 7 carbon and higher ring compounds, 2) heterocyclic such as phenol, cresol and pyridine, 3) light aromatic such as toluene, styrene and xylene, 4) light poly-aromatic such as naphthalene, phenanthrene and anthracene, and 5) heavy poly-aromatic such as fluoroanthene, pyrene, chrysene, perylene and benzoperylene. Usually, the concentration of individual components in tars is of less practical use ^[58]; thus, the total tar content produced during gasification is usually determined gravimetrically by dissolving tar in acetone solution at low temperatures. Benzene and toluene have been found to be two predominant tar compounds in syngas produced from gasification of switchgrass ^[59]. Xu et al. ^[38] reported Henry’s Law constants for common syngas impurities. Henry’s Law constants give an idea about the solubility of gaseous components in aqueous media. Henry’s Law constants for naphthalene and benzene were observed to be 1,000 and 10,000 fold higher than those for CO and H₂, respectively. Due to such high solubilities in aqueous media, these compounds could impart a significant impact during fermentations despite their low concentrations in syngas ^[38].

Ahmed et al. ^[30] used a 0.025 m filter to remove particulate matter and some tars from biomass-generated syngas to overcome cell dormancy. The filter removed the nitric oxide (NO) which was observed to be the potential inhibitor of hydrogenase activity responsible for reducing the amount of carbon and H₂ available for product formation. The study further tested the effect of supplementing fermentation media with 1 ml of acetone solution containing tars. Initial cell growth was inhibited by the addition of tars; however, eventually the cells did grow, possibly due to microbial adaptation. This study corroborated previous observations and showed that tars inhibited cellular growth, but did not cause cell death. Also, tars promoted ethanol production and inhibited acetic acid production, thus increasing the ethanol to acetate ratio ^[30].

---

3.2.1.3. Methods to reduce tars and light hydrocarbons

Thermal cracking of tars and light hydrocarbons into permanent gases such as CO and H₂, normally occurs at temperatures above 1,000 °C, but biomass gasification generally occurs at lower temperatures ^[2]. Several syngas tar and light hydrocarbon removal technologies such as wet scrubbing, dry scrubbing, dry-wet scrubbing and hot gas catalytic conditioning have been commercialized ^[2]. Scrubbing techniques are cost effective, but often generate a stream of contaminated water that may require extensive biological or thermal treatments ^[3]. Catalytic conversions convert tars into CO and H₂, thereby improving the overall yield of syngas in gasification ^[3]. Nickel, dolomite, and limestone based catalysts can also be used in fixed-bed applications (downdraft and updraft), but are not robust for fluidized bed reactor systems ^[25]. Commercial steam reforming and naptha cracking catalysts have been shown to successfully crack tars in a secondary reactor downstream from the gasifier; however, challenges with coking and economic viability due to their high costs still remain ^[60,61]. Biochar (byproduct of biomass gasification) and biochar-supported catalysts have also shown to reduce significantly syngas tars ^[62,63,64]. Hydrocarbons can also be removed by Rectisol wash (acid-gas removal process) that employs methanol as solvent and removes a number of species such as H₂S, NH₃ and HCN with concomitant separation of CO₂ ^[26]. Removal technologies for hydrocarbons and tars have been reviewed elsewhere ^[3,25,58].

---

3.2.2. Effect of nitrogenous species

Nitrogenous species such as ammonia (NH₃), hydrogen cyanide (HCN) and nitric oxides (NOx) are commonly present in syngas. These species are formed predominantly from the nitrogen contained in the biomass ^[26] and/or from nitrogen in char produced during gasification ^[65]. The environment in a gasifier can have both reduction zones and oxidation zones. Under reduced condition in the pyrolytic zone of the gasifier, N-H and N-C bonds in the biomass structure are converted into HCN, which is subsequently reduced to ammonia ^[26,65]. The proportions of these two intermediates formed depend on the type of gasifier and gasifer conditions ^[65]. For example, when H₂ concentrations are available in surplus, nitrogen that is predominantly available as NH₃ and HCN does not undergo further decompositon. Further, it has been noted that concentrations of NH₃ and HCN depend on feedstock nitrogen compositon ^[25]. When a gasifier has excess O₂ in the oxidation zone, a part of ammonia gets transformed to nitric oxide (NO) or nitrous oxide (N₂O). The oxidation of ammonia to N₂O is more favorable, but is not a common occurrence in gasification because N₂O gets reduced to NO by the time it exits the gasifier ^[65].

$Nitrogeninbiomass \to HCN\mathop \to \limits^{{H_2}O} NH3\matrix{ {\mathop \to \limits^{NO} } \cr {\mathop \to \limits_{{O_2}} } \cr } \matrix{ {{N_2}} \cr {NO} \cr }$

(2)

The presence of chlorine compounds in gas, such as HCl, can result in the formation of ammonium chloride (NH₄Cl), increase osmolarity of fermentation media and inhibit hydrogenase in enzymatic systems above certain levels ^[43].

---

3.2.2.1. Effect of ammonia (NH3)

NH₃ concentrations ranging from 0.5 to 1% in syngas have been reported ^[31]. NH₃ is highly soluble in water forming ammonium ions (NH₄⁺). NH₄⁺ can serve as a nitrogen source, but excess NH₄⁺ is inhibitory to many syngas fermenting bacteria ^[38]. A very strong inhibition has been observed above 2.7 gL^-1 NH₄⁺in C. ragsdalei ^[38] which was due to non-competitive inhibition of hydrogenase enzymes ^[43].

---

3.2.2.2. Effect of nitric oxide (NO)

Effect of NO on C. carboxidivorans was studied by Ahmed and Lewis ^[37]. They observed that concentrations of NO above 40 ppm acted as a non-competitive, reversible inhibitor to hydrogenase. At these concentrations, 5-7 times increase in ethanol production was also observed due to the increased activity of alcohol dehydrogenase. However, at NO concentrations of 140-150 ppm, H₂ consumption was completely shut down. A similar metabolic shift was also observed with C. ragsdalei when biomass-generated syngas from a fluidized bed gasifier with a NO concentration of 44.5 ppm was used as a fermentation substrate ^[41]. In comparison to pure bottled syngas, a 133% increase in ethanol and a 200% decrease in acetic acid concentrations were observed.

---

3.2.2.3. Methods to reduce nitrogenous impurities

NH₃ and HCN have high solubility in water and can be removed by water wash systems, such as Rectisol wash that employs methanol as a solvent at low temperatures ^[26]. NO_x and N₂O gases can be removed by non-selective catalytic reduction (NSCR), selective catalytic reduction and catalytic decomposition of N₂O into N₂ and O₂ ^[66,67,68].

---

3.2.3. Effect of sulfurous species

Sulfur compounds such as hydrogen sulfide (H₂S), carbonyl sulfide (COS) originate from sulfur in the feedstock. Gasification of coal generally results in higher sulfur gas concentration compared to biomass gasification due to higher sulfur content of coal (0.4-4.9%) versus biomass such as switchgrass (0.2%) ^[26,69]. Among all sulfur gases, H₂S is the dominating species and can account for 93-96% of the total sulfur content in syngas with the balance accounted for by COS ^[26,70].

---

3.2.3.1. Effect of hydrogen sulfide and COS

Chemical catalysts are less tolerant to sulfur than are microbial catalysts as certain chemical catalysts are inactivated at 0.1 ppm of sulfur in the producer gas ^[4]. Methanogens, hydrogenic bacteria (bacteria that perform the water gas shift reaction, which includes syngas fermentation bacteria) and acetogens have demonstrated tolerances of up to 20% sulfur in feed gases (Table 2) ^[42]. P. productus, E. limosum and R. rubrum were shown to degrade COS into H₂S using the following reaction scheme, while C. ljungdahlii cells were unable to metabolize or degrade COS using the following reaction ^[71]:

$COS{\rm{ }} + {\rm{ }}{H_2}O \to {H_2}S{\rm{ }} + {\rm{ }}C{O_2}$

(3)

Sulfides also serve to control redox potential, remove residual O₂ and act as a sulfur source for microbial metabolism ^[72]. Hu et al. ^[72] observed that mass transfer played an important role in sulfide loss from continuous bioreactors while equilibrium between the sulfide level in gaseous phase and aqueous phase played an essential role in small scale reactors. Researchers also observed that increasing sulfide concentrations from 0 to 1.9 mM in small scale batch cultivations of C. ragsdalei increased ethanol concentration from 0.9 to 2.1 g/L and decreased acetic acid concentration from 5.2 to 3.6 g/L.

---

3.2.3.2. Methods to reduce sulfurous species

Even though microbes show a higher tolerance to sulfur gases compared to chemical catalysts, it is recommended to test the effect of sulfur gases before drawing any broad conclusions from the limited studies. Removal of sulfur compounds (desulfurization or acid gas removal) can be achieved by adsorption, absorption, diffusion or chemical conversion ^[26]. The technique selected will depend on gas purity requirements, raw gas composition, selectivity of the process and economic considerations ^[26]. It is also important to note that amine absorption systems commonly used for desulfurization of gas also remove CO₂, which can be used as a carbon source by syngas fermentation bacteria.

---

3.2.4. Effect of other compounds

The presence of O₂ and acetone in syngas has been reported in literature ^[9,48]. O₂ is usually completely consumed during gasification; thus, its presence is usually due to downstream operations such as compressors and wash water ^[26]. Likewise, acetone is introduced into the syngas during wet scrubbing of gases to remove tar species ^[9,30,40].

---

3.2.4.1. Effect of oxygen

O₂ is one of the most toxic gases during syngas fermentation as it inhibits several enzymes such as pyruvate-ferredoxin oxidoreductase hydrogenases (including Ni- and Fe- containing) present in the Wood-Ljungdahl pathway. Its presence in fermentation media can also increase redox potential ^[22,73]. However, some acetogens, like A. woodii, C. magnum, C. glycolicum RD-1 and M. thermoacetica, are tolerant to O₂ concentrations ranging from 0.5% to 6% ^[74,75]. C. glycolicum RD-1 is one of the most interesting acetogens because it can withstand up to 6% O₂ and produce ethanol, lactate and H₂ as end products ^[49]. Under anoxic conditions, acetogenic metabolism shifts towards enzyme pathways that are less sensitive to O₂, resulting in production of acetic acid and ethanol ^[49,74]. Furthermore, a few acetogens, such as A. woodii, C. magnum, S. silvatica, M. thermoacetica andC. glycolicum RD-1, contain enzymes, such as reduced NADH-oxidase, superoxide dismutase, rubredoxin oxidoreductase (superoxide reductase), rubrerythrin (a peroxidase), catalase and cytochrome ba oxidase, that are involved in the removal of O₂ or its toxic products ^[49,74,75].

C. carboxidivorans has been shown to tolerate O₂ concentrations up to 1,900 ppm (or 0.19%) without any impact on CO and H₂ utilization, growth or product formation ^[40]. Kundiyana et al. ^[48] showed that pilot scale fermentation of syngas using C. ragsdalei was unaltered when O₂ concentrations between 0.04 to 2.6% were observed in syngas from a downdraft gasifier. For the integration of the gasification-syngas fermentation process, it is essential that the level of tolerance to O₂ be determined for different syngas fermenting microbes.

---

3.2.4.2. Effect of acetone

Acetone is another compound whose presence in syngas is reported in literature. Ramachandriya et al. ^[9] reported that acetone concentration of 0.4% in syngas did not affect C. ragsdalei growth, but product formation was redistributed to produce isopropanol as one of the end products. Production of isopropanol is unique to the acetogenic fermentation systems and alludes further to the presence of a secondary alcohol dehydrogenase enzyme ^[9].

---

3.2.4.3. Methods to remove oxygen and acetone from syngas

Due to the high solubility of acetone in water, any carryover of acetone from a water-acetone scrubbing system will result in its accumulation in fermentation broth; thus, the scrubbing system for tars must be carefully designed so that it does not affect the fermentation process. Any wash system must use de-aerated water to eliminate introduction of O₂ in syngas ^[26]. O₂ can be removed from syngas by installing copper scrubbers, but care has to be taken due to the presence of C₂H₂ in syngas as it reacts with copper to form the explosive copper acetylide ^[76]. Oxygen from gas streams can also be removed by using other metal based catalysts such as platinum and palladium catalysts supported on alumina ^[77].

From the above discussion, it is clear that that many minor gaseous components introduced during gasification and syngas processing can have both positive and negative effects on syngas fermenting bacteria. In general, the tolerance level of microbes to sulfur compounds is better than chemical catalysts and microbial adaptation to gaseous components is an important strategy to overcome any inhibitory effects. However, it is important to underscore that different microbes behave differently in the presence of these gaseous components. Understanding how each of these gaseous components interacts with the microbial system will help identify problems and better optimize a gasification-syngas fermentation process.

---

3.3. H₂:CO requirements

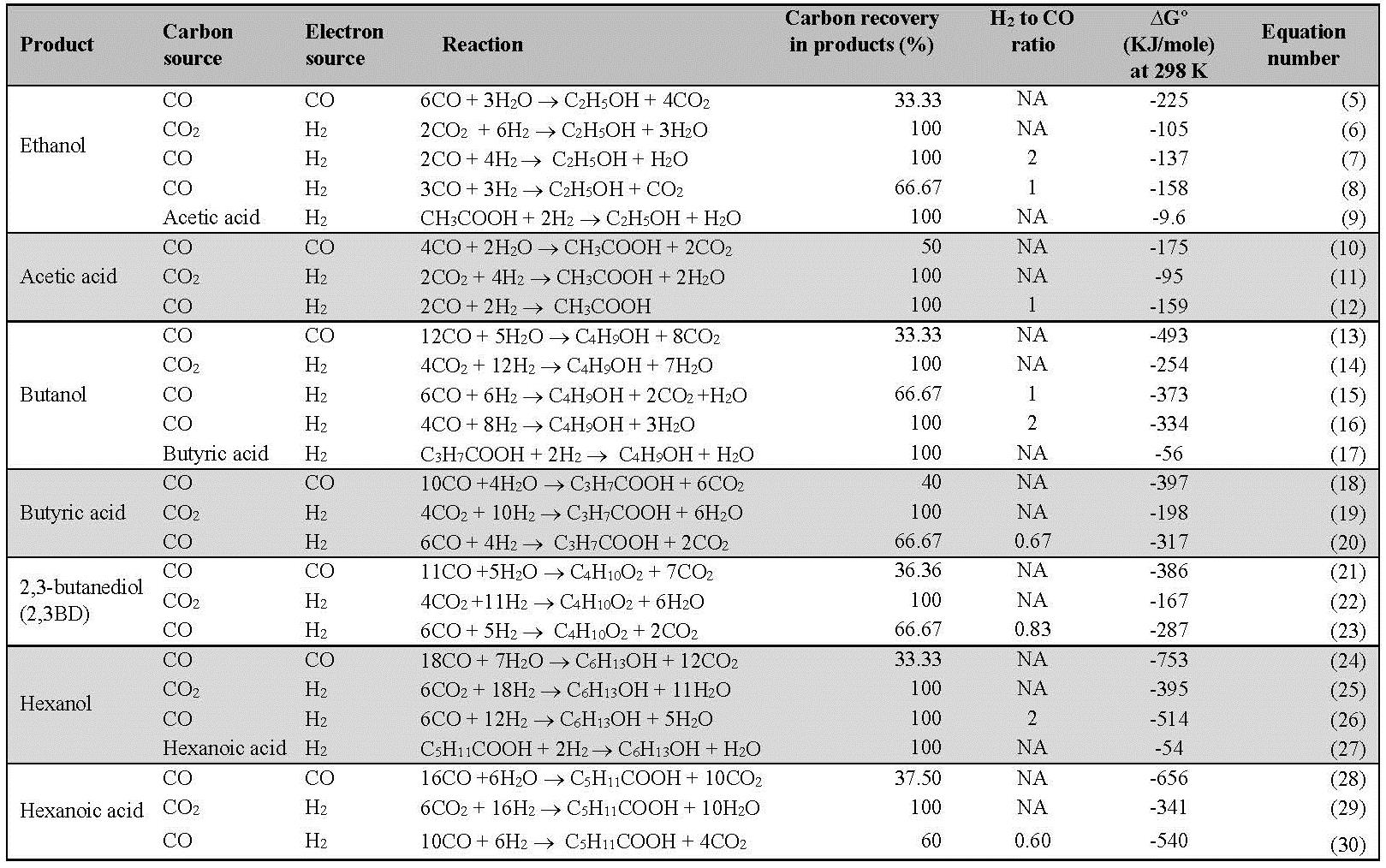
One of the major challenges developing syngas thermochemical conversion processes is producing syngas with fixed H₂ to CO ratios for a process utilizing syngas as a substrate. For instance, catalytic synthesis of methanol, mixed alcohol synthesis and hydrocarbon fuel synthesis by the Fisher-Tropsch process require the H₂ to CO ratio to be around 2, 1.1 and 0.6, respectively ^[29,78], which imposes additional reforming steps and increases overall process cost. On the contrary, microbial fermentations of syngas utilize different ratios of CO, H₂ and CO₂. Reactions for formation of ethanol and acetate with corresponding Gibbs free energies (ΔG) at 298 K can be found in Table 3.

For syngas fermentations, efficiency is measured as a ratio between experimental yields (moles or grams of product that has been produced per mole or gram of substrate consumed) and the theoretical yield (moles or grams of product that can be produced theoretically per mole or gram of substrate consumed). This ratio is commonly referred as the % of theoretical yield of gaseous substrate into products. This is different from percentage gas utilization, which is simply the ratio between the amount of gas consumed by the microbe to the amount of gas supplied. Gas utilization can be improved with better reactor designs and/or by recycling unused gases; however, fermentation efficiency is increased if the microbial catalyst is highly specific to one product.

The fermentation efficiencies of various syngas fermenting microbes for ethanol production have not been widely reported. The fermentation efficiency for ethanol production using C. ragsdalei at a H₂ to CO ratio of 0.25 ranged from 12.9 to 60% ^[8,9], while that for C. carboxidivorans ranged from 45.1 to 54.9% ^[9]. Generally, direct gasification of biomass using a fluidized bed gasifier provides a H₂ to CO ratio between 0.25 and 0.53 (Table 1). Rajagopalan et al. ^[79] reported 55% fermentation efficiency for ethanol production with C. carboxidivorans grown on 25% CO, 15% CO₂ and 60% N₂ mixtures. C. ljungdahlii when grown on 80% CO, 20% CO₂ gas mix showed a fermentation efficiency of 71.9% for ethanol production ^[80]. A patent from BRI Energy (now INEOS Bio) reported production of 30 g/L ethanol with 96% conversion of CO and 60% conversion of H₂ to ethanol and a productivity of 38 g/L*d using a 2 stage continuous stirred tank reactor (CSTR) ^[81].

Gasification canproduce different H₂ to CO ratios (Table 1) depending on the feedstock, type and design of the gasifier, operating conditions, and the type of catalyst used. An equimolar concentration of CO and H₂, if available, during fermentation will theoretically yield 0.67 moles of ethanol, i.e. two thirds of the carbon in CO can be converted into ethanol, which is the same as the theoretical yield of ethanol from glucose. Some Clostridium species can produce ethanol following stoichiometric equation 4, which requires a H₂ to CO ratio of 2. This ratio can be produced through indirect gasification using steam. Syngas fermentation can also occur in the absence of CO with a CO₂ to H₂ ratio of 1:3 (equation 6, Table 3) conserving all the carbon in CO₂ to ethanol. However, this molar ratio is attainable only when a reforming step such as a water gas shift reactor is added to the downstream gasification process. Such additional unit processes will increase the cost of the overall process at the expense of obtaining complete carbon conversion into fuels. Detailed process economics have to be performed to make knowledgeable recommendations for designing an economically viable gasification-fermentation process.

A major issue in syngas fermentation is the gas liquid mass transfer rate, ${\rm{d}}{N_S}^G$, which can be expressed assuming mass transfer limitation as:

${{{\rm{d}}{N_S}^G} \over {{V_L}{\rm{dt}}}}{\rm{ = }}{{{k_L}{\rm{a}}} \over {\rm{H}}}P_S^G$

(4)

Where, ${\rm{d}}{N_S}^G$ is the number of moles of gas transported from the gas phase

${V_L}$ is the liquid volume of the reactor

$t$ is time

${k_L}{\rm{a}}$ is the mass transfer coefficient

H is the Henry’s law constant

$P_S^G$ is the partial pressure of substrate in gas phase

From the equation, it can be observed that the rate of reaction is proportional to the partial pressure of the gaseous substrates, which depends on the total pressure of the reactor and can be improved by providing gases rich in CO, CO₂ and H₂. Therefore, it is highly desirable to have an undiluted syngas (with little or no nitrogen), because the resulting syngas will naturally have higher partial pressure of syngas components. This will result in improved mass transfer rates for sparingly soluble CO and H₂.

Hurst and Lewis ^[85] showed that increasing the partial pressure of CO in 350 ml Pyrex bioreactors from 0.35 to 2.0 atm increased cell mass and ethanol concentrations and promoted the reduction of acetic acid into ethanol, thereby increasing the product specificity of the microbe towards ethanol. In a different study, increasing partial pressure of gases by using different gas compositions (Syngas I- 20% CO, 15% CO₂, 5% H₂ and 60% N₂ versus syngas II- 40% CO, 30% CO₂ and 30% H₂) using newly isolated moderately alkaliphilic strains of A. bacchi resulted in increased ethanol productivity and yields from CO ^[7]. Increased concentrations of CO, CO₂ and H₂ from gasifiers are only possible through indirect gasification or by providing pure O₂ as a gasification medium.

Gas-liquid mass transfer is one of the major challenges in gas-liquid fermentations. The commonly used CSTRs will have to be operated with additional impellers and at a high power density (power applied to move a unit volume of fermentation broth) to break gas bubbles and enhance gas-liquid mass transfer. Numerous studies have compared the mass transfer characteristics of different reactorconfigurations ^{[86,87,88,89]}. Munasinghe and Khanal ^[87] compared various reactor configurations and observed that an air lift reactor attached with a bulb diffuser would provide a better CO mass transfer coefficient in aqueous phase in comparison to a submerged composite hollow fiber membrane module and column diffuser. Orgill et al. ^[86] observed that a non-porous polydimethylsiloxane (PDMS) hollow fiber reactor provided the highest mass transfer coefficient (K_TOTA/V) of 1,062 h⁻¹, which was 152% and 832% higher than the total mass transfer coefficients observed in a trickle bed reactor with 6mm glass beads (421 h⁻¹) and a stirred tank reactor (114 h⁻¹), respectively. However, Orgill et al. ^[86] used O₂ to calculate their mass transfer coefficients. Another study by Munasinghe and Khanal achieved a total mass transfer coefficient with a polyethylene/polypropylene/polyurethane composite hollow fiber reactor that was similar to that observed in ^[86] using CO (947 h⁻¹) ^[88]. Shen et al. ^[89] achieved a CO mass transfer coefficient of 1096 h⁻¹ with a polypropylene hollow fiber membrane. They also produced a maximum ethanol concentration of 24 g/L with a productivity of 3.44 g/L*day using C. carboxidivorans in continuous operation, demonstrating the operational feasibility of hollow fiber membrane based reactors ^[89]. In addition, ethanol production of 6 g/L was achieved in semi-continuous syngas fermentation in a trickle bed reactor using C. ragsdalei ^[90].

---

3.4. Toxicity of CO to hydrogenase

Another critical issue requiring attention during syngas fermentation is the toxicity of CO to hydrogenase enzymes. CO inhibition in Clostridium hydrogenases has been widely observed in acetone-butanol-ethanol (ABE) fermentations ^[91]. During syngas fermentation, CO and H₂ serve as electron donors required for the various reduction reactions of the metabolic pathway. The production of reducing power from CO originates from the water gas-shift reaction (CO + H₂O → CO₂ + 2H⁺ + 2e⁻) and is catalyzed by the enzyme carbon monoxide dehydrogenase (CODH). While A. woodii, A. kivui, C. ljungdahlii, C. ragsdalei, C. carboxidivorans and A. bacchi have the ability to simultaneously consume CO and H₂, other microorganisms such as P. productus, E. limosum, A. notarae, C. aceticum, C. thermoaceticum, S. sphaeroides, R. gelatinosa and R. rubrum are unable to simultaneously consume CO and H₂ ^{[7,8,9,40,92]}. Ramachandriya et al. ^[9] showed that C. ragsdalei can consume more H₂ than C. carboxidivorans under similar fermentation conditions. In the same study, it was also observed that the amount of CO₂ produced by C. carboxidivorans was almost equal to the amount of CO consumed, indicating that the water-gas shift reaction was the main source of reducing power.

Hu et al. ^[93] indicated that CO (and not H₂) was thermodynamically a preferred source of electrons at any given pH, ionic strength, gas partial pressure and electron pair carrier. The generation of reducing power from CO is undesirable because it not only makes an inefficient use of CO as a source of electrons (that could be potentially be carried out by hydrogenase enzymes using H₂), but it also diverts the carbon flux of CO towards CO₂ and away from ethanol or other products. Consequently, the reaction for the bioconversion of syngas into ethanol is likely occurring by the stoichiometric equation 6 (Table 3), which is an inefficient reaction because the products assimilate only 33% of carbon in CO. In such a scenario, CO₂ will be a byproduct of these fermentations and most of the unconsumed H₂ will come out of the bioreactor.

---

3.5. Preference to CO as a carbon substrate over CO2

CO₂ will always be present as an integral component of syngas irrespective of feedstock, gasifier type, gasifying medium and gasification conditions. The ratio of CO to CO₂ varied between 0.80 and 2.0 for most of the gasifications performed in the presence of air in a fluidized or downdraft reactor (Table 1), except for syngas produced from an industrial fluidized bed reactor that uses O₂ and steam as gasifying agents and coal as the feedstock ^[29]. Formation of both ethanol and acetic acid from CO (equations 6 and 11) is thermodynamically more favorable than from CO₂ and H₂ (equations 4 and 12), which indicates CO as the preferred substrate for carbon and energy (Table 3). Supporting experimental evidence for CO preference during syngas fermentation can be found in fermentations using C. ragsdalei, C. carboxidivorans, A. bacchi and P. productus, which preferentially consumed CO when a mixture of CO, CO₂ and H₂ was provided ^{[7,8,9,79,94]}. Although CO₂ is not harmful to syngas fermenting microbes, unconsumed CO₂ in the exhaust stream reduces the amount of usable carbon converted into products. Utilization of CO₂ is important from an economic standpoint, and will require an additional fermentation step for complete utilization of CO₂.

CO₂ can be fermented into solvents and acids only in the presence of H₂ (equations in Table 3). Ramachandriya et al. ^[95] demonstrated an ethanol yield of 66.5% of theoretical C. carboxidivorans with a feed gas composition of 75% H₂ and 25% CO₂. This study highlighted that CO₂ that is typically generated from syngas fermentations can be converted into solvents and acids by additional fermentation steps utilizing H₂. Such a process will increase carbon conversion from biomass to solvents. Furthermore, CO₂ fermentations using syngas fermenting microbes can also become a bolt-on technology for CO₂ conversion into biofuels and biochemicals if appropriate H₂ sources can be identified.

---

4 Conclusion

In comparison to traditional yeast fermentation, the fermentation of syngas produced from biomass is a relatively new technology and has potential to produce fuels and chemicals. The merits of syngas fermentation will allow feedstock flexibility during the gasification process. Besides lignocellulosic materials, refuse such as waste tires and municipal sludge can prove to be inexpensive and renewable feedstocks for gasification. However, many issues with the integration of gasification and syngas fermentation technology must be addressed for large scale commercial deployment. Some of the challenges of this integrated platform, including conversion efficiency of the gasification and syngas fermentation processes, effect of minor gaseous species, and effect of H₂:CO:CO₂ ratios on syngas composition, were discussed extensively in this review. With further aggressive and concerted fundamental and applied research, gasification-syngas fermentation technology can prove to be a major source of renewable fuel and chemical production.

---

Acknowledgements

The authors acknowledge the support of the Oklahoma Agricultural Experiment Station in developing this review.

---

Conflict of Interest

All authors declareno conflict of interest.

---