1. Introduction
A bias-variance dilemma in categorical data mining and analysis is the fact that a prediction method can aim at either maximizing the overall point-hit accuracy without constraint or with the constraint of minimizing the distribution bias, but can hardly achieve both at the same time. The dilemma was notified, analyzed and illustrated by S. Geman et al. [9] in 1992. The origin of this dilemma is that a machine learning algorithm claiming to be distribution unbiased has to pay the price of high variance. It means that the prediction distribution to be as close as possible to the real target's distribution has to expect a high point-to-point prediction error, and vice versa.
This issue has also been widely discussed from practical technic points of view since then, sometimes under different terminologies. Yaniv and Foster[23] examined an "accuracy-informativeness" trade-off in three judgement estimation studies and proposed a trade-off model and a trade-off parameter to describe the penalty for lack of informativeness. Friedman[8] describes the similar problem in classification about distribution bias versus variance, suggesting that a lower bias tend to increases variance and thus there is always a "bias-variance trade-off". It has been noticed that the Monte Carlo method, which is usually considered distribution unbiased, has a problem in point-hit accuracy compared to optimal estimation. Mark and Baram [21] then suggested an improvement to increase the accuracy with a loss to unbiasedness. Yu et al. [24] extended the tradeoff to a bias-variance-complexity trade-off framework and proposed a complex system modeling approach by optimizing a model selection criterion of bias, variance and complexity. Zhou et al. [25] detailed a solution in a recommender system to solve the dilemma. They linearly combines two methods, one of which favors diversity and one on accuracy, and suggest that the solution is to define a utility function regarding the combinations and to optimize the function by tuning the combination coefficient.
Most of the discussions above study the bias and variance on a numerical response variable. R. Tibshirani discussed their categorical equivalence in [22]. A generalized bias-variance formulation is discussed in [5] and [16].
To illusrate this dilemma, we only consider the purely categorical data situation: both explanatory and response variables are of (nominal) categorical type in this article. We also consider a data set consisting of only two categorical variables X and Y, assume that Y is at a certain degree associated with X and that Y has some unknown values to be estimated.
However it should be noted that a data set in the practice of big data mining is usually high dimensional with mixed data type. It can be viewed as two categorical variables though after a few proper processes. A numerical target variable Y can be categorized by unsupervised discretization methods; same can be accomplished to the numerical source variables by supervised discretization methods; a proper supervised feature selection can reduce the number of source variables to such a small yet powerful number that they can be viewed as one explanatory variable. One can refer to [4, 11, 14, 19] for details regarding feature selection. The discussions to discretization can be found in [15].
To estimate the unknown values of Y for any given known value of X, we may either estimate Y by maximum likelihood, a.k.a conditional mode or the optimal prediction in [10, Section 5], or by expectation or the proportional prediction in [10, Section 9]. The former would yield the highest point-hit accuracy rate without any considerations of distribution bias. The latter would produce the highest point-hit accuracy with a constraint to the least distribution bias of Y. The point-hit accuracy rate achieved by the latter approach is in general lower than that by the former. Indeed, when sample size is large enough and representative, and the unknown part of Y is random, the point-hit accuracy rate difference between the optimal and proportional predictions is, according to [10, Sections 5 and 9],
|
n∑i=1maxj∈{1,2,...,k}p(X=xi,Y=yk)−n∑i=1k∑j=1p(X=xi,Y=yj)p(Y=yj|X=xi)≥0
|
where the equality holds if and only if Y is completely dependent of X.
A very simple example of this dilemma can be described as follows. A table with 90 rows and 2 columns, A and B, has 10 unknown values in B to be estimated (or predicted), shown in Table 1. Please note that NA represents an unknown value in the table. The mission is to estimate the unknowns with low distribution bias and high point-hit accuracy.
Table 1. Contingency table to a simple example.
| A |
B |
Tot. |
| a1 |
b1 |
30 |
| a1 |
b2 |
10 |
| a2 |
b1 |
15 |
| a2 |
b2 |
25 |
| a1 |
NA |
16 |
| a2 |
NA |
16 |
For simplicity, we assume that the unknown part has exactly the same conditional distribution as the known part, i.e., the proportion of b1 and b2 in a1 is 3:1 and that b1:b2 in a2 is 3:5. To minimize the imputation error, the prediction to A=a1 has to be b1 and the prediction to A=a2 be b2, which is an inevitably biased imputation; to reduce the level of bias, the ratio of b1 and b2 when A=a1 needs to be 3:1 and that same should be 3:5 when A=a2. The expected accurate rate of the first case is 0.6875 and that of the second case is only 0.578125.
In general, for a given conditional distribution {p(y1|xi)}, {p(y2|xi)},…,{p(yk|xi)}, the predicted conditional distribution has to be {p(ˆy1|xi)}=0, …,{p(ˆyM|xi)=1}, ,…,{p(ˆyk|xi)=0} where p(yM|xi)=maxj=1,...,k{p(yj|xi)} to get the expected maximum accuracy. The overall accuracy rate is then
|
n∑i=1p(xi)p(yM|xi)=n∑i=1p(xi,yM)
|
(1)
|
It is equivalent to the Goodman-Kruskal λ[10, Section 5], denoted by λY|X,
where
|
ρim=maxj∈{1,2,...,k}{p(X=xi;Y=yj)}
|
and
On the other hand, the least distribution biased prediction, or the prediction with the maximum expectation (or the proportional prediction [10, Section 9] is to predict Y by the exact conditional probability of Y on X, i.e, {p(ˆY=yj|X=xi)}=p(Y=yj|X=xi)}. The expected accuracy rate is
|
ωY|X:=n∑i=1k∑j=1p(Y=yj|X=xi)p(X=xi,Y=yj)
|
(2)
|
The accuracy rate is linked to the Goodman-Kruskal-tau[10, Section 9] (or the GK-tau, denoted by τY|X) as follows
|
ωY|X=(1−∑jp(Y=yj)2)τY|X+∑jp(Y=yj)2,
|
where,
|
τY|X=∑ni=1∑kj=1p(Y=j|X=xi)p(X=xi;Y=yj)−∑ki=1p(Y=yj)21−∑ki=1p(Y=yj)2.
|
It can be proven ([14]) that τY|X is the highest point-hit accuracy rate under the constraint that the estimated part of Y has the same distribution as the known part of Y.
More details and discussions about λ and τ can be found in [10, 14]. Other prediction procedures can be found in [1, 2, 7, 12, 13, 20].
Thus if all variables are categorical and samples are representative and (the sample size is large) enough, either the highest observable (realistic) point-hit accuracy rate with the lowest distribution bias or the highest point-hit accuracy with no care of response distribution bias can be achieved via an appropriate feature selection based on the corresponding association measures as discussed above. But generally the two optimizations cannot be realized at the same time hence one may want to achieve a certain level of balance between these two. This is exactly what we propose in this article: a scheme to balance the optimizations goal to maximizing the prediction accuracy and that to minimizing the prediction bias. Some experiments with real data Famex96 are conducted to demonstrate the characteristics of this scheme. Basic mathematical properties of this scheme are also discussed. Please note that these experiments are designed to estimate the unknown values in a table with a response variable. To focus on this subject, we ignore all other important issues in high dimensional, mix-typed data prediction such as discretization, feature selection, model selection, etc.
The definition of this scheme is described in Section 2 along with the prediction strategy. The experiments are discussed in Section 3. The relationship between the parameter introduced in this scheme and the prediction performance is also studied in that section. The last section is the conclusion remarks and the future work.
2. The balancing scheme
Our discussion is about a framework balancing the expected point-hit accuracy with distribution faithfulness and the likely maximum point-hit-accuracy. The variable with unknown values is considered as the response (or dependent) variable, while others are the explanatory (or independent) variables. The data set is divided into two parts by the values in the response variable. All rows with known values in the response variable goes to the learning part and others go to the prediction part. The response variable in the prediction part will be predicted using the values of its independent variables and the information learned from the learning part. Please note that all the variables in both parts are considered as categorical.
Assume that the response variable Y in the learning part has k distinct values: y1, y2, ..., yk. To simplify the discussion, we assume that there is only one source variable X in both parts and X in the learning part has n distinct values: x1, x2, ..., xn. A threshold θ is then defined as follows.
where α∈[0,1] while
|
ρm=0.5×min1≤i≤nmax1≤j≤kp(Y=yj|X=xi),
|
|
ρM=max1≤i≤nmax1≤j≤kp(Y=yj|X=xi)
|
and p(∗) is the probability of ∗.
Apparently, it is a point between the half of the minimum maximum conditional probability and the maximum maximum conditional probability. The prediction method for a given X=xi can be then described as follows. If its maximum conditional probability is greater the predefined threshold θ, its prediction is in favor of increasing point-hit accuracy; otherwise its prediction is in favor of lowering bias. The underlying idea of this scheme is that how to predict the unknowns depends on the tradeoff level, or a balancing rate α, between lowest bias and highest accuracy. Please note that the coefficient of 0.5 is just a choice of convenience. Any positive number less than 1 can play the same trick, which is to assure all predictions to be conditional mode based when α=1.
Our prediction to increase the point-hit accuracy is to predict the unknowns by the conditional mode. Monte-Carlo simulation is used to lower bias, which is to randomly pick yj according to a simulated distribution of p(Y=yj|X=xi).
3. Empirical experiment and discussion
The data set that we use in this experiment is The Survey of Family Expenditure conducted by Statistic Canada in 1996 (Famex96)[6]. This data set has 10,417 rows and 239 columns. We specifically choose some of its categorical variables to investigate how the prediction accuracy and bias are affected by the balancing rate introduced in the last section and the unknown proportion of the response variable. To focus on this subject, only two categorical variables are included in each experiment, one as the independent variable and another one as the dependent variable. We also randomly generate unknown values only in the response variable for the same reason.
It is needed to mention that there are various types of unknown (or missing) values. Three types were introduced in [3, 18]: missing completely at random (MCAR), missing at random (MAR)and not missing at random (NMAR). [1] classifies missing values as four: missing by definition of the subpopulation, missing completely at random (MCAR), missing at random (MAR), and nonignorable (NI) missing values. Each type usually requires a different processing method. The missing values are generated completely at random for the sake of simplicity.
The first experiment uses type of dwelling (HSG_TYPE) as the independent variable and household type categories (HH_TYPE) as the dependent variable. When the missing rates, denoted as r are 0.05, the learning part has 9, 899 rows and the prediction part has 518 rows. The contingency table for the learning part is listed in Table 2.
Table 2. X=HSG_TYPE;Y=HH_TYPE;r=0.05: learning.
| x |
y |
# |
p(y|x) |
x |
y |
# |
p(y|x) |
x |
y |
# |
p(y|x) |
| 1 |
1 |
755 |
0.13 |
3 |
1 |
98 |
0.20 |
5 |
1 |
1209 |
0.51 |
| 1 |
2 |
1543 |
0.26 |
3 |
2 |
84 |
0.175 |
5 |
2 |
430 |
0.18 |
| 1 |
3 |
2552 |
0.432 |
3 |
3 |
152 |
0.32 |
5 |
3 |
229 |
0.1 |
| 1 |
4 |
401 |
0.07 |
3 |
4 |
20 |
0.04 |
5 |
4 |
36 |
0.02 |
| 1 |
5 |
328 |
0.06 |
3 |
5 |
83 |
0.17 |
5 |
5 |
251 |
0.11 |
| 1 |
6 |
203 |
0.03 |
3 |
6 |
22 |
0.05 |
5 |
6 |
101 |
0.04 |
| 1 |
7 |
130 |
0.02 |
3 |
7 |
22 |
0.05 |
5 |
7 |
125 |
0.05 |
| 2 |
1 |
56 |
0.17 |
4 |
1 |
112 |
0.23 |
6 |
1 |
89 |
0.29 |
| 2 |
2 |
69 |
0.21 |
4 |
2 |
104 |
0.21 |
6 |
2 |
73 |
0.23 |
| 2 |
3 |
118 |
0.37 |
4 |
3 |
143 |
0.29 |
6 |
3 |
77 |
0.25 |
| 2 |
4 |
17 |
0.05 |
4 |
4 |
21 |
0.04 |
6 |
4 |
7 |
0.02 |
| 2 |
5 |
32 |
0.1 |
4 |
5 |
69 |
0.14 |
6 |
5 |
36 |
0.12 |
| 2 |
6 |
16 |
0.05 |
4 |
6 |
18 |
0.04 |
6 |
6 |
16 |
0.05 |
| 2 |
7 |
14 |
0.04 |
4 |
7 |
24 |
0.05 |
6 |
7 |
14 |
0.045 |
Observe that the bold part in this table represent the maximal conditional probabilities, which will be the result of a prediction by (conditional) mode(s). Table 3 and Table 4 are the prediction results for the balancing rate α=0 and α=1 respectively.
Table 3. X=HSG_TYPE;Y=HH_TYPE;r=0.05;α=0: prediction.
| y∖ˆy |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
SUM |
| 1 |
37 |
29 |
29 |
4 |
9 |
7 |
5 |
120 |
| 2 |
33 |
28 |
44 |
6 |
11 |
3 |
6 |
131 |
| 3 |
24 |
40 |
81 |
6 |
12 |
6 |
4 |
173 |
| 4 |
3 |
8 |
11 |
4 |
1 |
0 |
1 |
28 |
| 5 |
10 |
6 |
8 |
3 |
4 |
2 |
3 |
36 |
| 6 |
6 |
3 |
6 |
3 |
0 |
0 |
0 |
18 |
| 7 |
5 |
3 |
3 |
0 |
1 |
0 |
0 |
12 |
| SUM |
118 |
117 |
182 |
26 |
38 |
18 |
19 |
518 |
Table 4. X=HSG_TYPE;Y=HH_TYPE;r=0.05;α=1: prediction.
| y∖ˆy |
1 |
3 |
SUM |
| 1 |
62 |
58 |
120 |
| 2 |
34 |
97 |
131 |
| 3 |
22 |
151 |
173 |
| 4 |
|
28 |
28 |
| 5 |
16 |
20 |
36 |
| 6 |
5 |
13 |
18 |
| 7 |
5 |
7 |
12 |
| SUM |
144 |
374 |
518 |
The simple match rate is used to measure the point-hit accuracy, which gives us an accuracy rate of 0.41 when α=1 and an accuracy of 0.3 when α=0. The distribution bias is evaluated by 4, inspired by Kullback-Leibler divergence[17], as follows.
|
d(ˆY|Y)=m∑j=1p(yj)|p(ˆyj)−p(ˆyj)|
|
(4)
|
As in the K−L divergence, 4 is smaller when the prediction's distribution is closer to the real ones. There are also two advantages of 4 over the K−L divergence: (1) 4 does not over estimate the case of category missing in the prediction; (2) 4 has a fixed range of [0,1]. By this definition of bias, α=1 gives a bias of 0.3 and α=0 gives a bias of 0.14 which supports our claims to the balancing rate's property regarding bias.
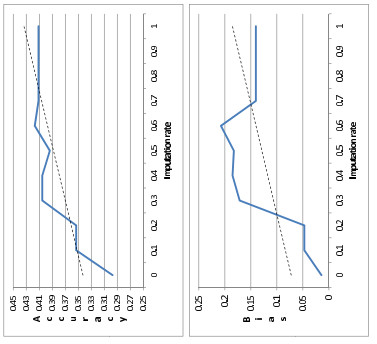
When α varies from 0 to 1, Figure 1 shows the increase of accuracy and bias as expected.
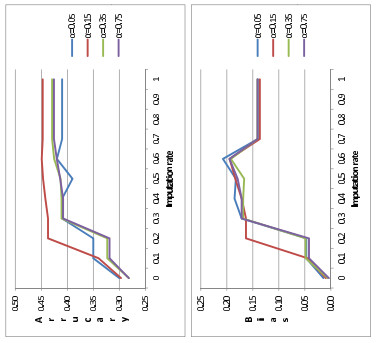
Finally Figure 3 shows that the effect of the missing rate to the prediction performance is negligible.
4. Discussion and future work
In conclusion, sacrifices in maximizing point-hit accuracy has to be made to achieve least bias in prediction and vise versa. To address this tradeoff issue, we define a balancing scheme so the prediction accuracy can be reduced to certain level to tune down the prediction distribution bias. We introduce a balancing rate, a parameter, α, where 0≤α≤1 to measure this tradeoff level. When one categorical independent value's conditional mode is less than a threshold calculated by this rate, it is considered less important in contributing to the accuracy rate, thus needs to be predicted to minimize the bias, i.e., by a Monte Carlo simulation. Otherwise, it is better to predict by conditional mode to achieve the best accuracy. Experiments show how the balancing rate affects the prediction performance and how the tradeoff effect changes along with it. We will be focusing on how this scheme is extended to other predictive methods like neural network, clustering and decision tree in the future.









 DownLoad:
DownLoad: