The effect of inoculum types on microbial growth, β-glucan formation and antioxidant activity during tempe fermentation

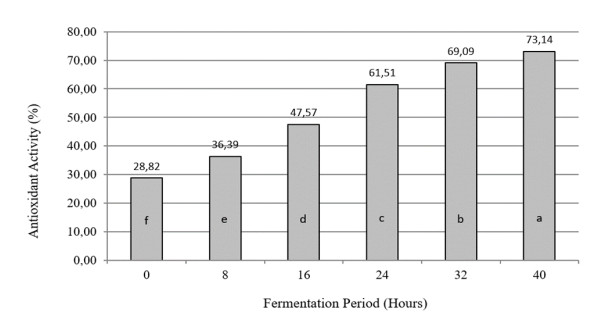
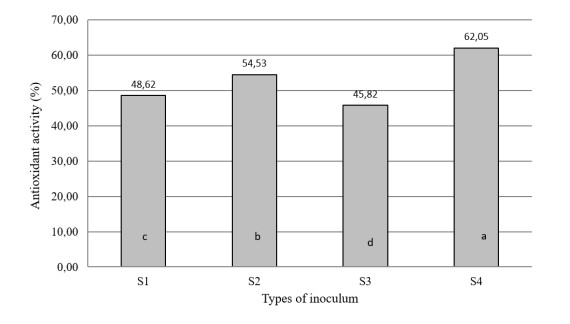
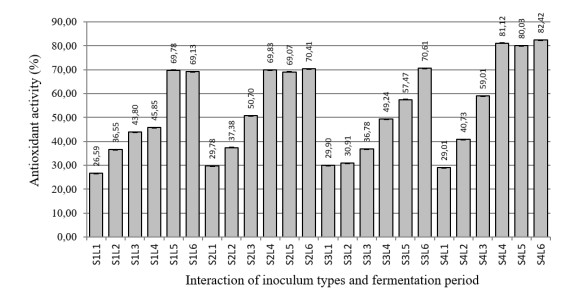
1.   Introduction

Magnetic Resonance Imaging (MRI) is a well-known medical imaging method based on the Nuclear Magnetic Resonance (NMR) phenomena. The reconstructions of 2D or 3D images representing the spatial density of the target area or volume are achieved by using the MRI. During MRI imaging, the sampled signal is reconstructed from the spatial frequency component of the image. Under a fully sampled data acquisition followed by the Nyquist criterion, the conventional Inverse Fast Fourier Transform (IFFT) is commonly used to reconstruct the image. Unfortunately, the time required for acquiring a complete data set is time-consuming; therefore, its broader applications such as real-time diagnosis and emergencies are less concerned. Over the last few decades, many advanced techniques have been used to incredibly improve the quality and acquisition speed of the NMR image. The recent advanced methods have been mainly focused on accelerating hardware operation and imaging algorithms.

The currently emerging of two main research fields enable to reduce the scan time of the MRI without significantly reducing the quality of the images. The first approach is associated with the development of the parallel MRI (pMRI) that allows speeding up the MRI acquisition. In this technique, the MR image's most important information is spontaneously received using an array of radiofrequency (RF) coils ^[1,2]. Many groups have tried to improve the pMRI with different reconstruction algorithms such as simultaneous acquisition of spatial harmonics (SMASH) that increases the speed of image acquisition by an integer factor over traditional fast-imaging methods ^[3], the SENSE (Sensitivity encoding) that uses the sensitivity maps for reducing the scan time of MRI acquisition ^[4], the Generalized autocalibrating partially parallel acquisitions (GRAPPA) ^[5], and the iterative self-consistent parallel imaging reconstruction ^[6]. The second method is the novel sampling technique of compressed sensing (CS) that utilizes the spatial redundancy of medical images ^[7,8,9]. In fact, the MR image can be recovered from a tiny amount of sampled data. Since the first introduction of CS by Lustig et al. ^[10], the CS has been developed using various strategies and optimization algorithms. Some well-developed methods of random under-sampling were described in ^[11,12]. Some recent work tried to optimize both the random ^[13] and non-random ^[14] under-sampling patterns. More recently, it has been found that the 2D Cartesian random under-sampling can be optimized better by using a hybrid under-sampling approach ^[15]. In this hybrid under-sampling, the number of horizontal sample lines taken from the K-space is defined by the under-sampling ratio r, which consists of two sampling parts: (i) a major part is still randomly sampled by following the power-law; (ii) the rest minor one is regularly sampled by the remaining lines surrounding the center of the K-space. The numerical simulation evaluations have confirmed that when applying the hybrid under-sampling approach to the K-space of MRI, the reconstructed image is more accurate than the use of the traditional random under-sampling methods because a more considerable amount of useful information near the origin of the K-space is permanently taken.

Although both CS and pMRI can significantly reduce the image acquisition scan time, they have their limitations. The combination of CS and pMRI has been developed for mitigating the drawbacks when they are used together ^[16,17], such as the CS was used for highly accelerating first-pass cardiac perfusion pMRI ^[18] and the hybrid regularized reconstruction for the combination of pMRI and CS ^[19]. The uniform and random under-sampling methods were also individually applied to parallel imaging for better image reconstruction ^[20]. CS-pMRI has been used for reducing the scan time of brain imaging without significantly reduced image quality ^{[21,22,23,24,25,26,27,28,29,30,31,32]}. The CS-SENSE is denoted for the combination of CS and pMRI, which used the reconstruction algorithm SENSE. The development of CS-SENSE can be divided into some directions as following:

Firstly, calibration and calibrationless image reconstruction approach: conventional SENSE requires the knowledge of coil sensitivity profiles. For calibrationless image reconstruction approaches, the authors introduce a calibrationless image reconstruction approach that no longer requires this knowledge ^{[24,25,26,27]}.

Secondly, conventional and improved reconstruction algorithms approach: based on the original reconstruction algorithm SENSE, the author proposed some enhanced algorithms for better reconstruction ^{[27,28,29,30]}. For example, in ^[28], the authors presented a reconstruction algorithm that promote joint sparsity by using additional spatial information from multiple coils.

Thirdly, design the under-sampling patterns approach: the authors design different kinds of under-sampling patterns and adjustments to improve imaging reconstruction ^{[31,32,33,34,35]}. In ^[33], the authors proposed HF-SENSE, which is an enhanced partially parallel imaging using a high-pass filter. This method explores artificial sparsity to improve the image quality of SENSE reconstruction. Previously, we combined the chaotic under-sampling and the pMRI for improving the CS-MRI reconstruction ^[31,32]. This chaotic CS approach can speed up the image acquisition of the MRI due to reducing the number of samples.

Recently, in 2019, the authors in ^[21] compared the image quality of CS-SENSE accelerated 3D T1-echo-spoiled gradient echo and T2-FLAIR (CS-SENSE FLAIR) sequences with the conventional ones. They found that CS-SENSE accelerated sequences provide the image quality equivalent to that of conventional ones. In ^[22], the authors proposed CS-pMRI supported by a modified fast spin-echo to accelerate data acquisition for the susceptibility-based positive contrast MRI. MR imaging data acquired from several phantoms (i.e., biopsy needles, stents, and brachytherapy seeds) to validate the proposed technique. Also, in 2019, the authors in ^[23] proposed using a preconditioner in the reconstruction procedure. The preconditioner can be constructed quickly, and its inverse can be evaluated fast using only two fast Fourier transformations. They verified the preconditioner's performance for the conjugate gradient method as the linear solver, integrated into the well-established Split Bregman algorithm. The designed circulant preconditioner reduces the number of iterations required in the conjugate gradient method by almost a factor of 5.

Inspired by these works, we propose a combination of the hybrid under-sampling design and pMRI in this paper. In this sense, instead of using the traditional random or chaotic method, the pMRI reconstruction measurements are obtained by hybrid under-sampling the k-space. As reporting from our previous findings ^[15,32], when a certain amount of encoding information is permanently taken around the origin of the K-space, the hybrid under-sampling method will improve the quality of the reconstructed image for the pMRI. Our results based on simulation evaluations of the recovered image error, the universal image $Q$ index and the peak signal to noise ratio ($PSNR$) have confirmed the significant improvement of image reconstruction compared to the all our previous der-sampling methods.

The rest of this paper is organized as follows. In section 2, the pMRI acquisition based on SENSE, the proposed method of hybrid compressed, and the imaging reconstruction using our proposed method are introduced. Evaluation results of the proposed method and compared to conventional methods are described in section 3. These achieved results are discussed in section 4 while conclusions are drawn in section 5.

2.   Materials and methods

2.1.   Parallel MRI acquisition based on SENSE

In MRI, to create an image, the number of phase-encoding steps is repeated for obtaining a necessary amount of measurements or horizontal lines of the K-space trajectory, which will determine the total scan time of the image acquisition. Differently, in the pMRI, the total number of horizontal lines of the K-space trajectory is spontaneously obtained from an array of individual coils ^[4]. However, the drawbacks of this parallel imaging are the reduction of the sensed size of the image (also called the field-of-view (FOV)) and the creation of the aliasing artifacts in image reconstruction. To solve this problem, the previous studies used SENSE based methods to remove the aliasing effects caused by the combination of different images from individual coils. In this method, the inversion value of the aliasing transformation for each pixel is individually estimated. A 2D MRI slice image of an object is considered as m (x; y), and the number of coils is L. Each coil will contribute its values of image intensity. The K-space data acquired by the l-th coil is determined by Eq (1),

where k_x and k_y are encoding information of the K-space according to a specific location of the corresponding image with x and y coordinates. The C_l(x; y) is the sensitivity function of the l-th coil, and k = {${k}_{x}$, ${k}_{y}$} will lie in the K-space. S_l(${k}_{x}$ ; ${k}_{y}$ ) implied in Eq (1) is the Fourier transform of the multiplication of its respective coil's sensitivity function and the weighted image produced from that coil. Moreover, the image acquired from each coil, m_l(x; y), can be calculated by multiplying the ideal image by the corresponding sensitivity function, as described in the following Eq (2),

Subsequently, the intensity value of each pixel in the full FOV image can be calculated by the Eq (3).

where C = [C₁; : : :; C_L] is a vector of the sensitivity function of all coils. The sensitivity of each coil is practically measured and calibrated by using reference images. These reference images are selected to ensure that they do not contain any aliasing artifact and noise. Moreover, smoothing and extrapolation algorithms are utilized for each coil sensitivity data to obtain a good sensitivity map. To apply the compressed sensing into SENSE, the K-space's fully sampling data can be discretized by Eq (4),

where N_x and N_y are the numbers of pixels along $x$ and $y$ axes of the image, while ${n}_{x}$ and ${n}_{y}$ are the pixel values at coordinate ($x$, $y$). It can be seen that S_l(k_x; k_y) is expressed as a vector x within the compressed sensing scheme. Thus, the under-sampled data ${\hat S_l}$ (k_x; k_y) in the l-th coil can be calculated by applying the hybrid under-sampling matrix Φ to ${S_l}$ (k_x; k_y) which can be also expressed as a vector y within the compressed sensing setting.

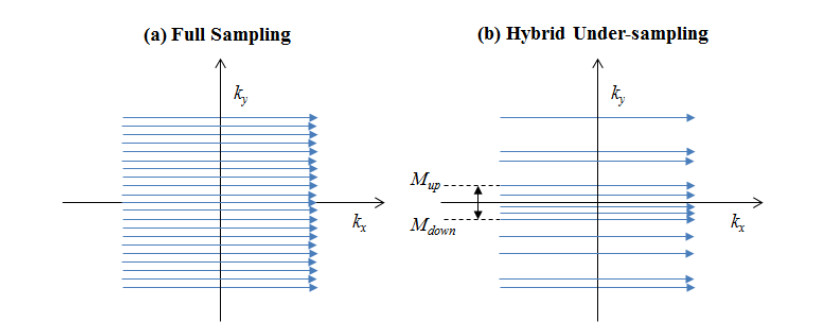
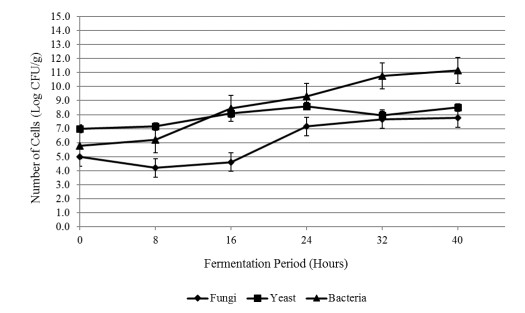
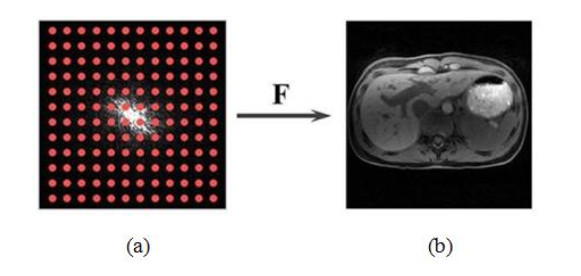
In this paper, the Cartesian K-space data of a 2D MRI image is used for evaluating the efficiency of the combination of the hybrid under-sampling approach and the pMRI. The Fourier relationship between the K-space domain and the 2D image is shown in Figure 1; the K-space's full sampling performance, followed by the Nyquist criterion, which ensures most of the encoded information of the K-space is taken (the red dots), is shown in Figure 1a; the image reconstruction is simply performed by applying the 2D IFFT to the K-space data domain, as depicted in Figure 1b.

2.2.   Hybrid compressed sensing

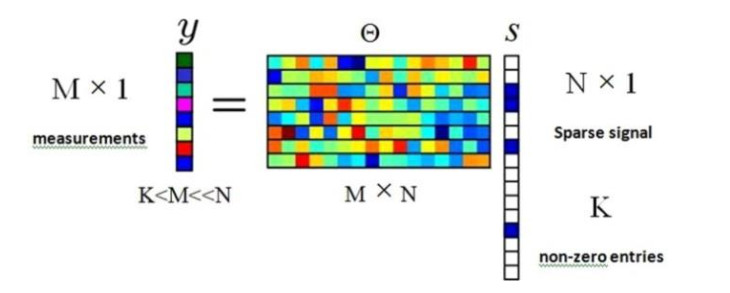
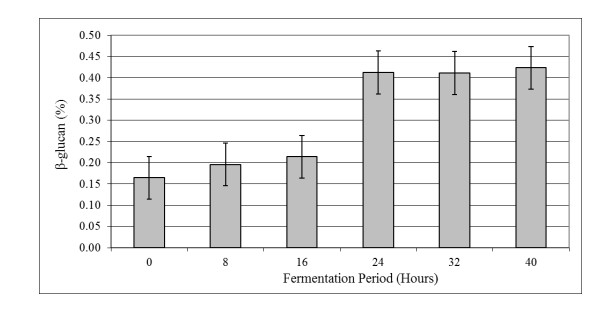
For a signal which can be expressed by a vector $x$ ($x \in {R^N}$), it can be sparsely represented in some domains by algorithms such as Fourier ^[36,37] and Wavelet ^[38,39] transformations. The sparse representation can be expressed by $x = \mathit{\Phi} *s$ ($s \in {R^N}$ and $\mathit{\Phi} \in {R^{N \times N}}$) as a L-sparse vector ($L$ is the number of nonzero values in $s$ and Φ is a sparsifying matrix). If the signal $x$ is supposed to be sensed by using a linear function $\mathit{\Psi} \in {R^{M \times N}}$, the acquired samples, $y \in {R^M}$, will be determined by $y = \mathit{\Psi} *x$. The signal $x$ is expected to recover from its acquired samples y. This work can be performed by recovering $s$ from $y$ as the obtained samples can also be expressed by $y = \mathit{\Theta} s$ (with $\mathit{\Theta} = \mathit{\Phi} \mathit{\Psi}$).

The mathematical model of compressive sampling performance is illustrated in Figure 2. Here, a measurement matrix, Ψ or Θ, is often under-determined. To accurately reconstruct signal $x$, a critical factor of CS, the restricted isometry property (RIP), must be satisfied. It is found that the RIP condition is satisfied if the number of measurements M $\ge$ c * K * log (N/K) (c is a constant) ^[40]. It ensures that Φ is incoherent with Ψ, which is required when performing the CS ^[41]. Consequently, S can be reconstructed from y by using sparse approximation approaches, such as l₁- BP ^[1] or orthogonal matching pursuit (OMP) ^[9]. The CS has been practically applied to the MRI by designing random and chaotic measurement matrixes for accelerating image acquisition ^[11,31].

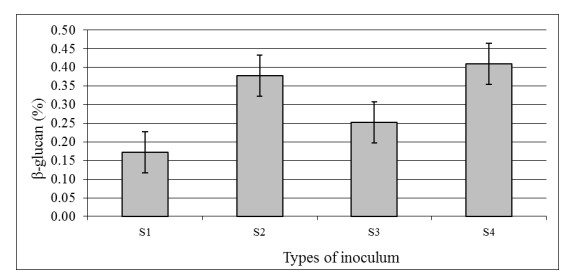
In the 2D Cartesian sampled K-space, the total time required to obtain the K-space data is proportional to the number of phase-encoding steps ^[42]. It has been found that the regular Cartesian under-sampling caused the artifacts to manifest as coherent copies of the image structure. The rational random Cartesian K-space under-sampling followed by the power-law can significantly improve the image reconstruction, but still suffer incoherent artifacts, especially at a low under-sampling ratio. The random or chaotic under-sampling approaches can be used to interrupt the regularity of Cartesian K-space as they ensure the incoherence. However, the signal intensity of the K-space data reduces from the focal point of K-space to the periphery, which consequently causes the problem that only random or chaotic schemes with their sampling distributions are dense at the origin and sparse at the periphery of the K-space domain will guarantee a better image reconstruction. Suppose that a small value of under-sampling ratio $R$ is applied to the CS profile. In that case, the reconstruction's quality is low because the random or chaotic under-sampling schemes will be lost the critical portion of the phase-encoding steps around the center of K-space even that the center of the scheme is at the origin of the K-space domain. Therefore, in this research, the following three under-sampling approaches are evaluated: i) the traditional random under-sampling approach followed by the Gaussian random measurements along the phase-encoding (k_y) in the K-space ^[9,11]; ii) Chaotic under-sampling approach ^[31,32]; iii) The new hybrid under-sampling approach ^[15].

As illustrated in Figure 3, the Cartesian hybrid under-sampling approach is implemented as compared to the fully sampled Cartesian trajectories of the K-space (followed by the Nyquist criteria). Different from the full Cartesian sampling (shown in Figure 3a), the hybrid under-sampling takes much smaller phase encoding rows of the Cartesian Nyquist sampling, which is defined by the under-sampling ratio. The under-sampled rows in this hybrid under-sampling method are dividing into two portions. Specifically, 70% of the rows are for random under-sampling, and 30% of the remaining rows are for the regular under-sampling row (defining by the M_up and M_douwn border rows around the K-space center domain as shown in Figure 3b).

2.3.   Multi-channel compressed sensing with the conjugate gradient SENSE

The hybrid under-sampling matrix is applied to the pMRI acquisition procedure. The values of k_x and ${k}_{y}$ of the under-sampled K-space are obtained using the combined algorithm of regular and random processes, as described above. The image recovery of the pMRI can be implemented using some iterative reconstruction algorithms such as gradient descent and conjugate approaches ^[10,12,40]. These algorithms begin with an aliased MR image and continuously update to remove this artifact. In these algorithms, the regularization parameter λ is used to balance between information consistency (ℓ₂-norm) and the advancement of sparsity (ℓ ₁-norm). In this paper, the well-developed and optimized Nonlinear Conjugate Gradient (NCG) is utilized for recovering the image from under-sampled K-space data ^[10]. Let m be the imaging object. The recovered image of the object, $\hat m$, is obtained by solving the following Eq (5) under the specific condition:

where F_u is the Fourier operator, y is the obtained measurements, and Ψ is the sparsifying transform operator. The scheme can be briefly described in this following algorithm.

The algorithm of hybrid Under-sampling scheme for pMRI Acceleration:

Step 1: Generate the under-sampled data (k_x, k_y) defined by the hybrid under-sampling pattern. The number of sampled data is based on the pre-defined under-sampling ratio $r = M/N$, (select r₁ for random sampling and R₂ for regular sampling, and r=r₁+ r₂).

Step 2: Determine coordinates (k_x, k_y) of the K-space for each coil and store them as a template.

Step 3: Acquire digital data of the K-space based on the template and store them in a vector for each coil.

Step 4: Create sensing maps by using polynomial fitting.

Step 5: Perform the multi-channel CS-SENSE reconstruction using the NCG algorithm.

To evaluate the efficiency of investigated under-sampling methods, the averaged error between the recovered object and the initial object is firstly compared. Taking an image m with a size of $N\times M$ for the initial object and $\hat m$ is the recovered object, the normalized averaged error can be calculated by this Eq (6):

The Peak Signal Noise Ratio (PSNR) index is also estimated for evaluating the image compression quality of the reconstructed images for both under-sampling approaches ^[43]. To compute the PSNR, the mean-squared error (MSE) is firstly calculated by Eq (7):

where $\mathrm{M}$ and $\mathrm{N}$ are the numbers of rows and columns in the original image respectively. Thus, the PSNR is calculated by Eq (8):

Another performance index, the universal image quality ($Q$) index, is used as proposed by Wang and Bovik ^[44]. This index represents the distortion based on three different components: loss of correlation, luminance distortion, and contrast distortion. The $Q$ index is defined as Eq (9):

where $\bar x$ and $\bar y$ are the mean of the original image and the reconstructed one, respectively; ${\sigma }_{x}^{2}$ and ${\sigma }_{y}^{2}$ are the variances of $x$ and $y$; and ${\sigma }_{xy}$ is the covariance between $x$ and $y$. Notice that $Q$ index varies between -1 and 1. The $Q$ index reaches to 1 if two images are identical.

3.   Numerical simulation results

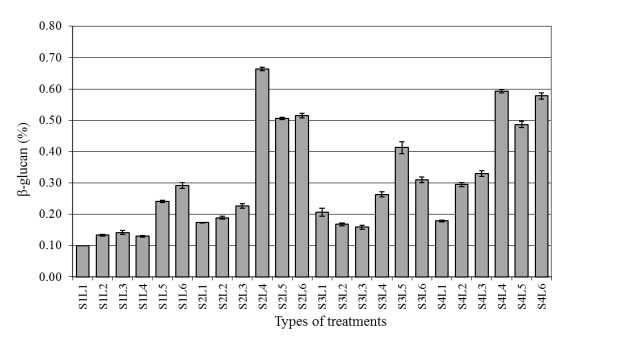
The numerical simulations are performed for a data source obtained from the human MPRAGE data from an 8-channel head array coil. This used data source has an image size of 128 × 128, as shown in Figure 4. To prove the advantage of the proposed method, the under-sampling ratio $\mathrm{r}$ is selected from 0.03 to 0.3 for evaluating the error $E$, the $PSNR$ ratio $P$, and the $Q$ index from reconstructed images of all investigated under-sampling methods.

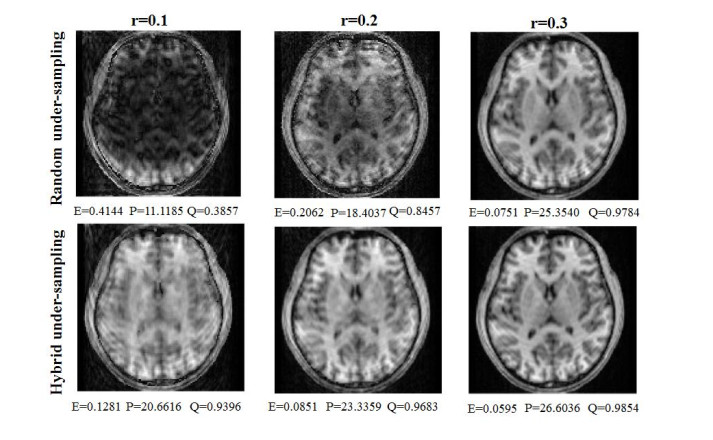
The binary mask that illustrates the under-sensing implemented in the k-space based on the power-law using the traditional random and the hybrid under-sampling approaches for different $r = 0.1$, $0.2$, and $0.3$ is shown in Figure 5. It can be seen that, with the small under-sampling ratio of $0.05$, only a small number of sampled horizontal rows are taken from the K-space. These sampled rows are distributed in the random distribution for the traditional random under-sampling or in a random manner with partially enhanced rows in the origin of the K-space for the hybrid under-sampling. For a higher under-sampling ratio, more sampled rows are permanently taken near the center of the K-space in the hybrid under-sampling method as compared to the traditional random approach. The reconstructed images of the under-sampled K-space for the respective under-sampling ratio are shown in Figure 6. Besides the visual image quality, the normalized parameters of the image quality are also evaluated, such as the error, the $PSNR$, and the $Q$ -index between the original and the reconstructed images. Interestingly, these parameters being assessed have indicated the significant quantitative improvement of our proposed under-sampling method. For example, with the under-sampling ratio of 0.05, the error and $Q$ -index of the reconstructed image by the hybrid under-sampling can be improved more than twice as compared to the traditional random sampling.

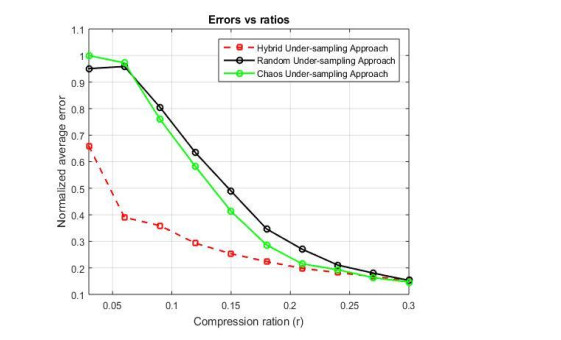
To confirm the improvement of the proposed combination of the hybrid under-sampling and the parallel imaging, the simulation has been repeated form each under-sampling ration for statistical evaluation of the reconstructed image quality. Averaged values of the $E$ calculated by 100 simulations of the traditional random, our previous work (the chaotic under-sampling ^[32]), and the hybrid under-sampling ^[15] methods for different under-sampling ratios ($\mathrm{r}$) from 0.03 to 0.3 are shown in Figure 7. It can be seen that the E calculated by the hybrid method is significantly lower than the value calculated by the traditional random and chaos methods, especially at the under-sampling ratio of 0.06. This difference is gradually reduced when the r is increased to 0.3.

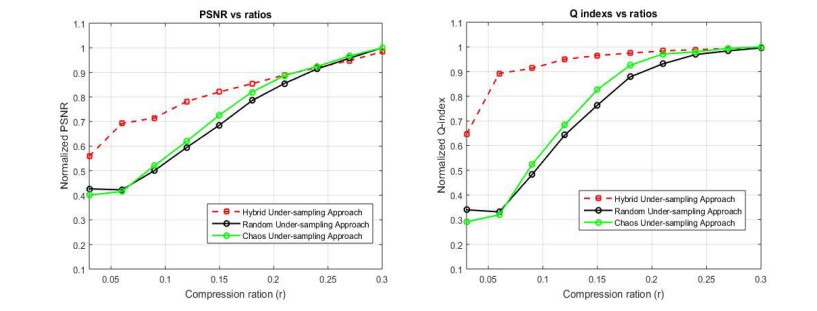
Results of the PSNR and the Q-index comparison between three under-sampling approaches are also shown in Figure 8. It can be seen that for under-sampling ratios that are less than 0.3, the image reconstructed by the proposed approach offers a better value of the normalized PSNR than that reconstructed from other investigated methods (the left graph of Figure 8). A similar observation is also indicated for the normalized Q index comparison between the three under-sampling methods is shown in the right graph of Figure 8. As expected, for under-sampling ratios which are less than 0.3, the image reconstructed by the proposed approach offers a better enhancement of the Q index among studied under-sampling methods.

4.   Discussion

The CS reconstruction implements sparsity of the solution to suppress the incoherent aliasing artifacts and maximizes data consistency between the solution and the available under-sampling data. The combination of the CS and the parallel imaging has been found in its improvement in comparison with applying CS or pMRI individually.

An improved SENSE method termed HCS-SENSE is proposed in this article. In our data acquisition scheme, the under-sampled data of the K-space is performed by taking both regular sampling and traditional random under-sampling approaches. As shown in Figure 7, the normalized averaged error of the proposed combination method decreased to 59% at the under-sampling ratio of 0.06 compared to other methods. Analogously, the statistic evaluations of the normalized $PSNR$ and $Q$ index also confirm the significant enhancement of 63 and 39% for the hybrid under-sampling method over other schemes when applied to the parallel imaging, as indicated respectively in Figure 8. The most significant improvement in using the hybrid under-sampling approach to the pMRI is observed in the low under-sampling ratios of under 0.3 compared to the others. At the same time, there are almost no differences between them at the higher ratios. This finding is consistent with the recent study ^[15].Nevertheless, the reconstructed image quality and the image acquisition time are improved. The time processing of this CS-pMRI algorithm is only a few seconds compared to the performance of hybrid under-sampling alone (commonly more than 30 seconds).

The complexity of the HCS-SENSE method is not larger than conventional CS-SENSE because only a proposed under-sampled data of the K-space is applied before and after SENSE reconstruction individually; both work in K-space. Thus, it would not add any calculation compared to conventional CS-SENSE. The performance of the proposed method can be also compared with recent work ^[29] in terms of: 1) complexity (i.e., none of high-pass filter and its corresponding inverse filter are needed before and after SENSE reconstruction); and 2) reconstruction error. In addition, HCS-SENSE can be combined with the other improved methods in the calibrationless approaches ^[24,25,26] or the improved reconstruction algorithm approaches ^[27,28,29].

5.   Conclusions

A new SENSE method termed HCS-SENSE is proposed in this paper for significant quality improvements of the image reconstruction by applying the simple and efficient under-sampling scheme to the parallel imaging. Focusing on the concentrated information at the origin of the K-space, instead of individually using the random or chaotic under-sampling approaches, we propose to use a significant portion of the phase-encoding (k_y) lines in the K-space with the traditional random under-sampling. Simultaneously, the minor rest part is permanently enhanced by the regular sampling around the center part of the K-space. It ensures that a certain amount of encoding information closed to the origin of the K-space is always taken to obtain the under-sampled K-space. Therefore, the image reconstruction is significantly improved for parallel imaging, especially at the low under-sampling ratios of smaller than 0.3. The numerical simulations and evaluations of all investigated under-sampling approaches have exhibited the efficacy of the combined method.

Conflict of interest

No conflict of interest.

Acknowledgements

This work was supported by National Foundation for Science & Technology Development (NAFOSTED) under Grant 103.05-2020.13.