|
[1]
|
IPCC (2014) Climate Change 2014: Impacts, adaptation, and vulnerability-Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom: Cambridge University Press.
|
|
[2]
|
IPCC (2014) Climate Change 2014: Synthesis Report. Geneva, Switzerland: Intergovernmental Panel on Climate Change. Retrieved July 1, 2019, Available from: https://www.ipcc.ch/site/assets/uploads/2018/05/SYR_AR5_FINAL_full_wcover.pdf.
|
|
[3]
|
Abidoye BO, Kurukulasuriya P, Mendelsohn R (2017) South-East Asian farmer perceptions of climate change. Clim Change Econ 8: 1740006. doi: 10.1142/S2010007817400061

|
|
[4]
|
Konchar KM, Staver B, Salick J, et al. (2015) Adapting in the shadow of Annapurna: a climate tipping point. J Ethnobiol 35: 449-471. doi: 10.2993/0278-0771-35.3.449

|
|
[5]
|
Aldunce P, Handmer J, Beilin R, et al. (2016) Is climate change framed as 'business as usual' or as a challenging issue? The practitioners' dilemma. Environ Plann 34: 999-1019.
|
|
[6]
|
Scheffers BR, Meester L, Bridge TC, et al. (2016) The broad footprint of climate change from genes to biomes to people. Science 354: 6313.
|
|
[7]
|
Voccia A (2012) Climate change: What future for small, vulnerable states? Int J Sust Dev World Ecol 19: 101-115. doi: 10.1080/13504509.2011.634032

|
|
[8]
|
Spires M, Shackleton S, Cundill G (2014) Barriers to implementing planned community-based adaptation in developing countries: A systematic literature review. Clim Dev 6: 277-287. doi: 10.1080/17565529.2014.886995

|
|
[9]
|
Bockel L, Vian L, Torre C (2016) Towards sustainable impact monitoring of green agriculture and forestry investments by NDBs: Adapting MRV methodology. Rome, Italy: Food and Agriculture Organization.
|
|
[10]
|
Glenn A, James WE, Fuller RA (2016) Global mismatch between greenhouse gas emissions and the burden of climate change. Sci Rep 6: 20281. doi: 10.1038/srep20281

|
|
[11]
|
Jackson G, McNamara K, Witt B (2017) A framework for disaster vulnerability in a small island in the Southwest Pacific: A case study of Emae Island, Vanuatu. Int J Disaster Risk Sci 8: 358-373. doi: 10.1007/s13753-017-0145-6

|
|
[12]
|
Easterling WE (1996) Adapting North American agriculture to climate change in review. Agric For Meteorol 80: 1-53. doi: 10.1016/0168-1923(95)02315-1

|
|
[13]
|
FAO (2007) Adaptation to climate change in agriculture, forestry and fisheries: Perspective, framework and priorities. Rome: Food and Agriculture Organization.
|
|
[14]
|
Berrang-Ford L, Pearce T, Ford JD (2015) Systematic review approaches for climate change adaptation research. Reg Environ Chang 15: 755-769. doi: 10.1007/s10113-014-0708-7

|
|
[15]
|
Ifejika-Speranza C (2010) Resilient adaptation to climate change in African Agriculture. Bonn: Deutsches Institut für Entwicklungspolitik (DIE).
|
|
[16]
|
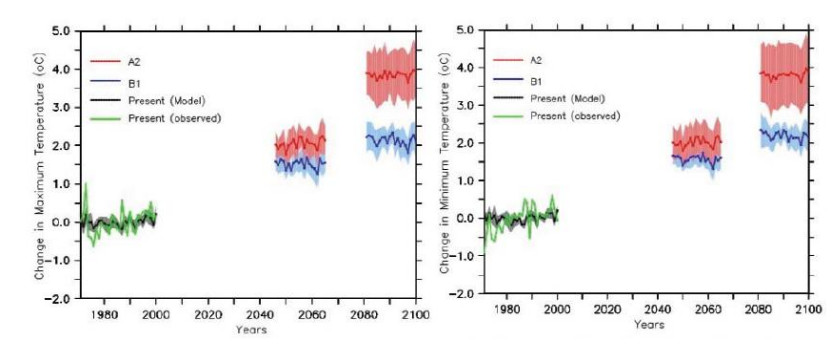
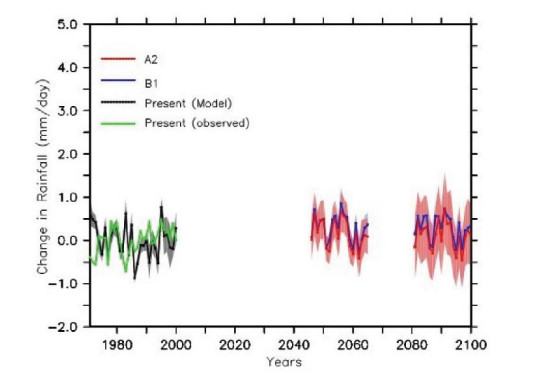
Abiodun BJ, Salami AT, Tadross M (2011) Climate change scenarios for Nigeria: Understanding biophysical impacts. Ibadan, Nigeria: Building Nigeria's Response to Climate Change (BNRCC) Project.
|
|
[17]
|
IPCC (2018) Global warming of 1.5 ℃ Geneva, Switzerland: Intergovernmental Panel on climate change.
|
|
[18]
|
NBS (2017) Nigerian Gross Domestic Product Report, Abuja, Nigeria: National Bureau of Statistics.
|
|
[19]
|
Yakubu MM, Akanegbu BN (2015) The Impact of international trade on economic growth in Nigeria: 1981-2012. Eur J Bus Econ Account 3: 26-36.
|
|
[20]
|
Berg A, de Noblet-Ducoudre N, Benjamin S, et al. (2013) Projections of climate change impacts on potential C4 crop productivity over tropical regions. Agric For Meteorol 170: 89-102. doi: 10.1016/j.agrformet.2011.12.003

|
|
[21]
|
Mereu V, Santini M, Cervigni R, et al (2018) Robust decision making for a climate-resilient development of the agricultural sector in Nigeria. In: Lipper L, McCarthy N, Zilberman D, et al., Eds., Climate Smart Agriculture: Building Resilience to Climate Change, Rome, Italy: Food and Agriculture Organization of the United Nations (FAO), 277-306.
|
|
[22]
|
Adejuwon JO (2005) Food crop production in Nigeria. Present effects of climate variability. Clim Res 30: 53-60.
|
|
[23]
|
Odekunle TO (2004) Rainfall and the length of the growing season in Nigeria. Int J Climatol 24: 467-479. doi: 10.1002/joc.1012

|
|
[24]
|
Remling E, Veitayaki J (2016) Community-based action in Fiji's Gau Island: A model for the Pacific? Int J Clim Chang Str Manage 8: 375-398. doi: 10.1108/IJCCSM-07-2015-0101

|
|
[25]
|
Ogbo A, Lauretta NE, Ukpere W (2013) Risk management and challenges of climate change in Nigeria. J Hum Ecol 41: 221-235.
|
|
[26]
|
Obioha EE (2008) Climate change, population drift and violent conflict over land resources in Northeastern Nigeria. J Hum Ecol 23: 311-324. doi: 10.1080/09709274.2008.11906084

|
|
[27]
|
Mburu BM, Kung'u JB, Muriuku JN (2015) Climate change adaptation strategies by small-scale farmers in Yatta District, Kenya. Afr J Environ Sci Technol 9: 712-722. doi: 10.5897/AJEST2015.1926

|
|
[28]
|
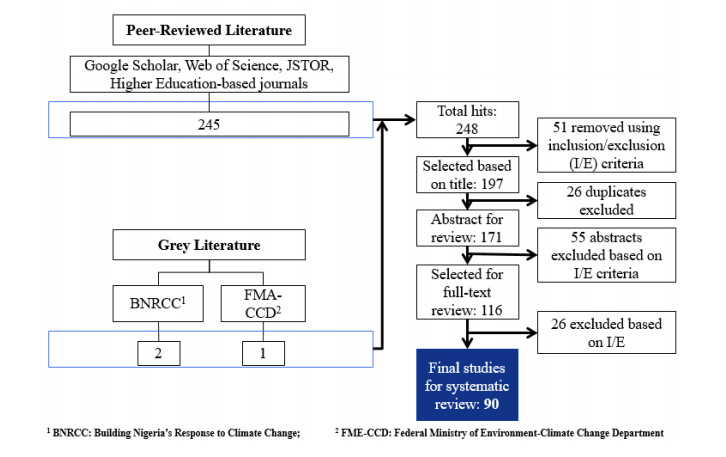
Cooper C, Booth A, Varley-Campbell J, et al. (2018) Defining the process to literature searching in systematic reviews: A literature review of guidance and supporting studies. BMC Med Res Methodol 85: 1-14.
|
|
[29]
|
Babatunde KA, Begum RA, Said FF (2017) Application of computable general equilibrium (CGE) to climate change mitigation policy: A systematic review. Renew Sust Energ Rev 78: 61-71. doi: 10.1016/j.rser.2017.04.064

|
|
[30]
|
Escarcha JF, Lassa JA, Zander KK (2018) Livestock under climate change: A systematic review of impacts and adaptation. Climate 6: 54. doi: 10.3390/cli6030054

|
|
[31]
|
Folke C (2006) Resilience: The emergence of a perspective for social-ecological systems analyses. Global Environ Chang 16: 253-267. doi: 10.1016/j.gloenvcha.2006.04.002

|
|
[32]
|
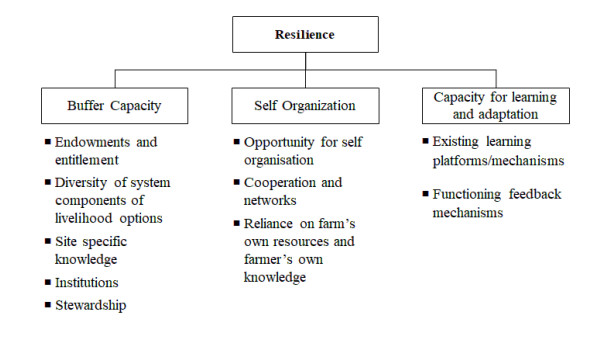
Ifejika-Speranza C (2013) Buffer capacity: Capturing a dimension of resilience to climate change in African smallholder agriculture. Reg Environ Chang 13: 521-535. doi: 10.1007/s10113-012-0391-5

|
|
[33]
|
Pretty J (2008) Agricultural sustainability: Concepts, principles and evidence. Philos Trans R Soc Lond B Biol Sci 363: 447-465. doi: 10.1098/rstb.2007.2163

|
|
[34]
|
Dorward A, Anderson S, Clark S (2001) Asset functions and livelihood strategies: A framework for pro-poor analysis, policy and practice. Imperial College at Wye, Department of Agricultural Sciences: ADU Working Papers 10918.
|
|
[35]
|
Shaffril HA, Krauss SE, Samsuddin SF (2018) A systematic review on Asian's farmers' adaptation practices towards climate change. Sci Total Environ 644: 683-695. doi: 10.1016/j.scitotenv.2018.06.349

|
|
[36]
|
Moher D, Liberati A, Tetzlaff J, et al. (2009) Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med 6: e1000097. doi: 10.1371/journal.pmed.1000097

|
|
[37]
|
Singh C, Deshpande T, Basu R (2017) How do we assess vulnerability to climate change in India? A systematic review of literature. Reg Environ Chang 17: 527-538.
|
|
[38]
|
Rusinamhodzi L, Corbeels M, Nyamangara J, et al. (2012) Maize-grain legume intercropping is an attractive option for ecological intensification that reduces climatic risk for smallholder farmers in central Mozambique. Field Crops Res 136: 12-22. doi: 10.1016/j.fcr.2012.07.014

|
|
[39]
|
Challinor A, Wheeler T, Garfoth C, et al. (2007) The vulnerability of food crop systems in Africa to climate change. Clim Chang 83: 381-399. doi: 10.1007/s10584-007-9249-0

|
|
[40]
|
Morton JF (2007) The impact of climate change on smallholder and subsistence agriculture. Proc Natl Acad Sci USA 104: 19680-19685. doi: 10.1073/pnas.0701855104

|
|
[41]
|
Armbrecht I, Gallego-Ropero MC (2007) Testing ant predation on the coffee berry borer in shaded and sun coffee plantations in Colombia. Entomol Exp Appl 124: 261-267. doi: 10.1111/j.1570-7458.2007.00574.x

|
|
[42]
|
Lin BB (2011) Resilience in agriculture through crop diversification: Adaptive management for environmental change. BioScience 61: 183-193. doi: 10.1525/bio.2011.61.3.4

|
|
[43]
|
Grubben G, Klaver W, Nono-Womdim R, et al. (2014) Vegetables to combat the hidden hunger in Africa. Chronica Hort 54: 24-32.
|
|
[44]
|
Luoh JW, Begg CB, Symonds RC, et al. (2014) Nutritional yield of African indigenous vegetables in water-deficient and water-sufficient conditions. Food Nutri Sci 5: 812-822.
|
|
[45]
|
Lunduka RW, Mateva KL, Magoroshoko C, et al. (2019) Impact of adoption of drought-tolerant maize varieties on total maize production in south Eastern Zimbabwe. Clim Dev 11: 35-46. doi: 10.1080/17565529.2017.1372269

|
|
[46]
|
Akinnagbe OM, Irohibe IJ (2014) Agricultural adaptation strategies to climate change impacts in Africa: A review. Bangladesh J Agric Res 39: 407-418.
|
|
[47]
|
Waha K, Müller C, Bondeau A, et al. (2013) Adaptation to climate change through the choice of cropping system and sowing date in sub-Saharan Africa. Global Environ Chang 23: 130-143. doi: 10.1016/j.gloenvcha.2012.11.001

|
|
[48]
|
Atedhor GO (2015) Strategies for agricultural adaptation to climate change in Kogi state, Nigeria. Ghana J Geogr 7: 20-37.
|
|
[49]
|
Westengen OT, Brysting AK (2014) Crop adaptation to climate change in the semi-arid zone in Tanzania: The role of genetic resources and seed systems. Agri Food Secur 3: 1-12. doi: 10.1186/2048-7010-3-1

|
|
[50]
|
Sanz MJ, de Vente J, Chotte JL, et al. (2017) Sustainable land management contribution to successful land-based climate change adaptation and mitigation: A report of the science-policy interface. Bonn, Germany: United Nations Convention to Combat Desertification (UNCCD).
|
|
[51]
|
FAO (2017) Voluntary guidelines for sustainable soil management. Rome, Italy: Food and Agriculture Organization.
|
|
[52]
|
Stavi I (2013) Biochar use in forestry and tree-based agro-ecosystems for increasing climate change mitigation and adaptation. Int J Sust DevWorld Ecol 20: 166-181. doi: 10.1080/13504509.2013.773466

|
|
[53]
|
Lal R (2015) Sequestering carbon and increasing productivity by conservation agriculture. J Soil Water Conserv 70: 55-62. doi: 10.2489/jswc.70.3.55A

|
|
[54]
|
Stavi I, Bel G, Zaady E (2016) Soil functions and ecosystem services in conventional, conservation, and integrated agricultural systems. A review. Agron Sustain Dev 36: 1-12. doi: 10.1007/s13593-015-0343-9

|
|
[55]
|
Agbonlahor MU, Aromolaran AB, Aiboni VI (2003) Sustainable soil management practices in small farms of southern Nigeria: A poultry-food crop integrated farming approach. J Sustain Agric 22: 51-62. doi: 10.1300/J064v22n04_05

|
|
[56]
|
Thierfelder C, Matemba-Mutasa R, Rusinamhodzi L (2015) Yield response of maize (Zea mays L.) to conservation agriculture cropping system in Southern Africa. Soil Till Res 146: 230-242.
|
|
[57]
|
Oyekale AS, Oladele OI (2012) Determinants of climate change adaptation among cocoa farmers in Southwest Nigeria. ARPN J Sci Technol 2: 154-168.
|
|
[58]
|
Merrey DJ, Sally H (2008) Micro-AWM Technologies for food security in Southern Africa: Part of the solution or a red herring? Water Policy 10: 515-530. doi: 10.2166/wp.2008.025

|
|
[59]
|
CGIAR (2016) Agricultural practices and technologies to enhance food security, resilience and productivity in a sustainable manner: Messages to SBSTA 44 agriculture workshops, CCAFS Working Paper no. 146, Copenhagen, Denmark, 2016.
|
|
[60]
|
Abraham TW, Fonta WM (2018) Climate change and financing adaptation by farmers in northern Nigeria. Financ Innov 4: 11. Available from: https://doi.org/10.1186/s40854-018-0094-0. doi: 10.1186/s40854-018-0094-0

|
|
[61]
|
BNRCC (2011) Reports of pilot projects in community-based adaptation to climate change in Nigeria. Ibadan, Nigeria: Building Nigeria's Response to Climate Change (BNRCC) Project.
|
|
[62]
|
Asfaw A, Simane B, Hassen A, et al. (2017) Determinants of non-farm livelihood diversification: Evidence from rainfed-dependent smallholder farmers in Northcentral Ethiopia (Woleka sub-basin). Dev Stud Res 4: 22-36. doi: 10.1080/21665095.2017.1413411

|
|
[63]
|
Nzegbule EC, Nwajiuba C, Ujor G, et al. (2019) Sustainability and the effectiveness of BNRCC community-based adaptation (CBA) to address climate change impact in Nigeria. In: Leal FW Eds., Handbook of Climate Change Resilience, Cham: Springer, 1-22.
|
|
[64]
|
Akrofi-Atitianti F, Ifejika-Speranza C, Bockel L, et al. (2018) Assessing climate smart agriculture and its determinants of practice in Ghana: A case of the cocoa production system. Land 7: 30. doi: 10.3390/land7010030

|
|
[65]
|
Adepoju AO, Osunbor PP (2018) Small scale poultry farmers' choice of adaption strategies to climate change in Ogun State, Nigeria. Rural Sustain Res 40: 32-40.
|
|
[66]
|
Salem BH, López-Francos A (2012) Feeding and management strategies to improve livestock productivity, welfare and product quality under climate change. 14th International Seminar of the Sub-Network on Nutrition of the FAO-CIHEAM Inter-Regional Cooperative Research and Development Network on Sheep and Goats. Hammamet, Tunisia.
|
|
[67]
|
IAEA (2010) Improving livestock production using indigenous resources and conserving the environment. Vienna, Austria: International Atomic Energy Agency.
|
|
[68]
|
Lamy E, van Harten S, Sales-Baptista E, et al. (2012) Factors influencing livestock productivity. In: Sejian V, Naqvi SM, Ezeji T, et al. Eds., Environmental Stress and Amelioration in Livestock Production, Berlin, Germany: Springer, 19-51.
|
|
[69]
|
Gebremedhin B, Hoekstra D, Jemaneh S (2007) Heading towards commercialization? The case of live animal marketing in Ethiopia. Nairobi, Kenya: Improving Productivity and Market Success (IPMS) of Ethiopian Farmers. Working Paper 5. ILRI (International Livestock Research Institute).
|
|
[70]
|
Batima P (2006) Climate change vulnerability and adaptation in the livestock sector of Mongolia. Washington, DC: Assessments of Impacts and Adaptations to Climate Change (AIACC), Project No. AS 06.
|
|
[71]
|
Okonkwo WI, Akubuo CO (2001) Thermal analysis and evaluation of heat requirement of a passive solar energy poultry chick brooder. Nig J Renew Energ 9: 83-87.
|
|
[72]
|
Nyoni NM, Grab S, Archer ER (2019) Heat stress and chickens: Climate risk effects on rural poultry farming in low-income countries. Clim Dev 11: 83-90. doi: 10.1080/17565529.2018.1442792

|
|
[73]
|
Elijah OA, Adedapo A (2006) The effect of climate on poultry productivity in Ilorin Kwara State, Nigeria. Int J Poult Sci 5: 1061-1068. doi: 10.3923/ijps.2006.1061.1068

|
|
[74]
|
Ampaire A, Rothschild MF (2010) Effects of training and facilitation of farmers in Uganda on livestock development. Livest Res Rural Dev 22: 1-7.
|
|
[75]
|
Shelton C (2014) Climate change adaptation in fisheries and aquaculture: Compilation of initial examples. FAO Fisheries and Agriculture Circular No. 1088. Rome: Food and Agriculture Organization.
|
|
[76]
|
Ficke AD, Myrick CA, Hansen LJ (2007) Potential impacts of global climate change on freshwater fisheries. Rev Fish Biol Fisher 17: 581-613. doi: 10.1007/s11160-007-9059-5

|
|
[77]
|
Nwabeze GO, Erie AP, Erie GO (2012) Fishers' adaptation to climate change in the Jebba Lake Basin, Nigeria. J Agric Ext 16: 68-78.
|
|
[78]
|
Adebayo OO (2012) Climate change perception and adaptation strategies on catfish farming in Oyo State, Nigeria. Glob J Sci Frontier Res Agric Vet Sci 12: 1-7.
|
|
[79]
|
Huq S, Reid H (2007) Community-based adaptation: A vital approach to the threat climate change poses to the poor. London: International Institute for Environment and Development.
|
|
[80]
|
Achoja FO, Oguh VO (2018) Income effect of climate change adaptation technologies among crop farmers in Delta State, Nigeria. Int J Agric Rural Dev 21: 3611-3616.
|
|
[81]
|
Agomuo CI, Asiabaka CC, Nnadi FN, et al. (2015) Rural women farmers' use of adaptation strategies to climate change in Imo State. Nigeria Int J Agric Rural Dev 18: 2305-2310.
|
|
[82]
|
Ajayi JO (2015) Adaptation strategies to climate change by farmers in Ekiti State, Nigeria. Appl Trop Agric 20: 01-07.
|
|
[83]
|
Ajieh PC, Okoh RN (2012) Constraints to the implementation of climate change adaptation measures by farmers in delta state, Nigeria. Glob J Sci Frontier Res Agric Vet Sci 12: 1-7.
|
|
[84]
|
Akinbile LA, Oluwafunmilayo AO, Kolade RI (2018) Perceived effect of climate change on forest dependent livelihoods in Oyo State, Nigeria. J Agric Ext 22: 169-179.
|
|
[85]
|
Akinwalere BO (2017) Determinants of adoption of agroforestry practices among farmers in Southwest Nigeria. Appl Trop Agric 22: 67-72.
|
|
[86]
|
Anyoha NO, Nnadi FN, Chikaire J, et al. (2013) Socio-economic factors influencing climate change adaptation among crop farmers in Umuahia South Area of Abia State, Nigeria. Net J Agric Sci 1: 42-47.
|
|
[87]
|
Apata TG (2011) Factors influencing the perception and choice of adaptation measures to climate change among farmers in Nigeria: Evidence from farm households in Southwest Nigeria. Environ Econ 2: 74-83.
|
|
[88]
|
Arimi K (2014) Determinants of climate change adaptation strategies used by rice farmers in Southwestern, Nigeria. J Agr Rural Dev Trop 115: 91-99.
|
|
[89]
|
Asadu AN, Ozioko RI, Dimelu MU (2018) Climate change information source and indigenous adaptation strategies of cucumber farmers in Enugu State, Nigeria. J Agric Ext 22: 136-146.
|
|
[90]
|
Ayanlade A, Radeny M, Morton JF (2017) Comparing smallholder farmers' perception of climate change with meteorological data: A case study from southwestern Nigeria. Weather Clim Extremes 15: 24-33. doi: 10.1016/j.wace.2016.12.001

|
|
[91]
|
Ayoade AR (2012) Determinants of climate change on cassava production in Oyo State, Nigeria. Glob J Sci Frontier Res Agric Vet Sci 12: 1-7.
|
|
[92]
|
Chukwuone N (2015) Analysis of impact of climate change on growth and yield of yam and cassava and adaptation strategies by farmers in Southern Nigeria. African Growth and Development Policy Modelling Consortium Working Paper 0012. Dakar-Almadies, Senegal: African Growth and Development Policy Modelling Consortium.
|
|
[93]
|
Chukwuone NA, Chukwuone C, Amaechina EC (2018) Sustainable land management practices used by farm households for climate change adaptation in South East Nigeria. J Agric Ext 22: 185-194.
|
|
[94]
|
Emodi AI, Bonjoru FH (2013) Effects of climate change on rice farming in Ardo Kola Local Government Area of Taraba State, Nigeria. Agric J 8: 17-21.
|
|
[95]
|
Enete AA, Madu II, Mojekwu JC, et al. (2011) Indigenous agricultural adaptation to climate change: Study of Imo and Enugu States in Southeast Nigeria. African Technology Policy Studies Network Working Paper No. 53. Nairobi: African Technology Policy Studies Network.
|
|
[96]
|
Enete AA, Otitoju MA, Ihemezie EJ (2015) The choice of climate change adaptation strategies among food crop farmers in Southwest Nigeria. Nig J Agric Econ 5: 72-80.
|
|
[97]
|
Eregha PB, Babatolu JS, Akinnubi RT (2014) Climate change and crop production in Nigeria: An error correction modelling approach. Int J Energ Econ Policy 4: 297-311.
|
|
[98]
|
Esan VI, Lawi MB, Okedigba I (2018) Analysis of cashew farmers adaptation to climate change in South-Western Nigeria. Asian J Agric Ext Econ Sociol 23: 1-12.
|
|
[99]
|
Ezeh AN, Eze AV (2016) Farm-level adaptation measures to climate change and constraints among arable crop farmers in Ebonyi State of Nigeria. Agric Res J 53: 492-500. doi: 10.5958/2395-146X.2016.00098.3

|
|
[100]
|
Ezike KN (2019) Implications for mitigation and adaptation measures: Rice farmers' response and constraints to climate change in Ivo Local Government Area of Ebonyi State. In: Leal FW Eds., Handbook of Climate Change Resilience, Cham: Springer, 1787-1799.
|
|
[101]
|
Falola A, Achem BA (2017) Perceptions on climate change and adaptation strategies among sweet potato farming households in Kwara State, Northcentral Nigeria. Ceylon J Sci 46: 55-63.
|
|
[102]
|
Farauta BK, Egbule CL, Idrisa YL, et al. (2011) Farmers' perceptions of climate change and adaptation strategies in Northern Nigeria: An empirical assessment. African Technology Policy Studies Network Research Paper No 15. Nairobi, Kenya: African Technology Policy Studies Network.
|
|
[103]
|
Henri-Ukoha A, Adesope OM (2019) Sustainability of climate change adaptation measures in Rivers State, South-South, Nigeria. In: Leal FW, Eds., Handbook of Climate Change Resilience, Cham: Springer, 675-683.
|
|
[104]
|
Ifeanyi-Obi CC, Asiabaka CC, Matthews-Njoku E, et al. (2012) Effects of climate change on fluted pumpkin production and adaptation measures used among farmers in Rivers State. J Agric Ext 16: 50-58.
|
|
[105]
|
Ifeanyi-Obi CC, Asiabaka CC, Adesope OM (2014) Determinants of climate change adaptation measures used by crop and livestock farmers in Southeast Nigeria. J Human Soc Sci 19: 61-70.
|
|
[106]
|
Igwe AA (2018) Effect of livelihood factors on climate change adaptation of rural farmers in Ebonyi State. J Biol Agric Healthc 8: 10-15.
|
|
[107]
|
Iheke OR, Agodike WC (2016) Analysis of factors influencing the adoption of climate change mitigating measures by smallholder farmers in Imo State, Nigeria. Sci Papers Ser Manag Econ Eng Agric Rural Dev 16: 213-220.
|
|
[108]
|
Ihenacho RA, Orusha JO, Onogu B (2019) Rural farmers use of indigenous knowledge systems in agriculture for climate change adaptation and mitigation in Southeast Nigeria. Ann Ecol Environ Sci 3: 1-11.
|
|
[109]
|
Ikehi ME, Onu FM, Ifeanyieze FO, et al. (2014) Farming families and climate change issues in Niger Delta Region of Nigeria: Extent of impact and adaptation strategies. Agric Sci 5: 1140-1151.
|
|
[110]
|
Kim I, Elisha I, Lawrence E, et al. (2017) Farmers adaptation strategies to the effect of climate variation on rice production: Insight from Benue State, Nigeria. Environ Ecol Res 5: 289-301.
|
|
[111]
|
Koyenikan MJ. Anozie O (2017) Climate change adaptation needs of male and female oil palm entrepreneurs in Edo State, Nigeria. J Agric Ext 21: 162-175.
|
|
[112]
|
Mbah EN, Ezeano CI, Saror SF (2016) Analysis of climate change effects among rice farmers in Benue State, Nigeria. Curr Res Agric Sci 3: 7-15.
|
|
[113]
|
Mustapha SB, Undiandeye UC, Gwary MM (2012) The role of extension in agricultural adaptation to climate change in the Sahelian Zone of Nigeria. J Environ Earth Sci 2: 48-58.
|
|
[114]
|
Mustapha SB, Alkali A, Zongoma BA, et al. (2017) Effects of climatic factors on preference for climate change adaptation strategies among food crop farmers in Borno State, Nigeria. Int Acad Inst Sci Technol 4: 23-31.
|
|
[115]
|
Nnadi FN, Chikaire J, Nnadi CD, et al. (2012) Sustainable land management practices for climate change adaptation in Imo State, Nigeria. J Emerg Trends Eng Appl Sci 3: 801-805.
|
|
[116]
|
Nwaiwu IU, Ohajianya DO, Orebiyi JS, et al. (2014) Climate change trend and appropriate mitigation and adaptation strategies in Southeast Nigeria. Glob J Biol Agric Health Sci 3: 120-125.
|
|
[117]
|
Nwalieji HU, Onwubuya EA (2012) Adaptation practices to climate change among rice farmers in Anambra State of Nigeria. J Agric Ext 16: 42-49.
|
|
[118]
|
Nwankwo GC, Nwaobiala UC, Ekumankama OO, et al. (2017) Analysis of perceived effect of climate change and adaptation among cocoa farmers in Ikwuano Local Government Area of Abia State, Nigeria. ARPN J Sci Technol 7: 1-7.
|
|
[119]
|
Nzeadibe TC, Egbule CL, Chukwuone NA, et al. (2011) Climate change awareness and adaptation in the Niger Delta Region of Nigeria. Nairobi, Kenya: African Technology Policy Studies Network Working Paper Series No.57. Nairobi, Kenya: African Technology Policy Studies Network.
|
|
[120]
|
Obayelu OA, Adepoju AO, Idowu T (2014) Factors influencing farmers' choices of adaptation to climate change in Ekiti State, Nigeria. J Agric Environ Int Dev 108: 3-16.
|
|
[121]
|
Ofuoku AU (2011) Rural farmers' perception of climate change in central agricultural zone of Delta State, Nigeria. Indones J Agric Sci 12: 63-69. doi: 10.21082/ijas.v12n2.2011.p63-69

|
|
[122]
|
Ogbodo JA, Anarah SE, Abubakar SM (2018) GIS-based assessment of smallholder farmers' perception of climate change impacts and their adaptation strategies for maize production in Anambra State, Nigeria. In: Amanullah, & S. Fahad (Eds.), Corn production and human health in changing climate, 115-138.
|
|
[123]
|
Ogogo AU, Ekong MU, Ifebueme NM (2019) Climate change awareness and adaptation measures among farmers in Cross River and Akwa Ibom States of Nigeria. In: Leal FW (Ed), Handbook of Climate Change Resilience, 1983-2002, Cham: Springer.
|
|
[124]
|
Okpe B, Aye GC (2015) Adaptation to climate change by farmers in Makurdi, Nigeria. J Agric Ecol Res Int 2: 46-57.
|
|
[125]
|
Oluwatusin FM (2014) The perception of and adaptation to climate change among cocoa farm households in Ondo State, Nigeria. Acad J Interdiscipli Stud 3: 147-156.
|
|
[126]
|
Oluwole AJ, Shuaib L, Dasgupta P (2016) Assessment of level of use of climate change adaptation strategies among arable crop farmers in Oyo and Ekiti States, Nigeria. J Earth Sci Clim Chang 7: 369.
|
|
[127]
|
Onyeagocha SU, Nwaiwu IU, Obasi PC, et al. (2018) Encouraging climate smart agriculture as part solution to the negative effects of climate change on agricultural sustainability in Southeast Nigeria. Int J Agric Rural Dev 21: 3600-3610.
|
|
[128]
|
Onyegbula CB, Oladeji JO (2017) Utilization of climate change adaptation strategies among rice farmers in three states of Nigeria. J Agric Ext Rural Dev 9: 223-229. doi: 10.5897/JAERD2017.0895

|
|
[129]
|
Onyekuru NA (2017) Determinants of adaptation strategies to climate change in Nigerian forest communities. Nig Agric Policy Res J 3: 42-59.
|
|
[130]
|
Onyeneke RU (2016) Effects of livelihood strategies on sustainable land management practices among food crop farmers in Imo State, Nigeria. Nig J Agric Food Environ 12: 230-235.
|
|
[131]
|
Onyeneke RU (2018) Challenges of adaptation to climate change by farmers Anambra State, Nigeria. Int J BioSciences Agric Technol 9: 1-7.
|
|
[132]
|
Onyeneke RU, Madukwe DK (2010) Adaptation measures by crop farmers in the Southeast Rainforest Zone of Nigeria to climate change. Sci World J 5: 32-34.
|
|
[133]
|
Onyeneke RU, Iruo FA, Ogoko IM (2012) Micro-level analysis of determinants of farmers' adaptation measures to climate change in the Niger Delta Region of Nigeria: Lessons from Bayelsa State. Nig J Agric Econ 3: 9-18.
|
|
[134]
|
Tarfa PY, Ayuba HK, Onyeneke RU, et al. (2019) Climate change perception and adaptation in Nigeria's Guinea Savanna: Empirical evidence from farmers in Nasarawa State, Nigeria. Appl Ecol Environ Res 17: 7085-7112.
|
|
[135]
|
Onyeneke R, Mmagu CJ, Aligbe JO (2017) Crop farmers' understanding of climate change and adaptation practices in South-east Nigeria. World Rev Sci Technol Sust Dev 13: 299-318. doi: 10.1504/WRSTSD.2017.089544

|
|
[136]
|
Oriakhi LO, Ekunwe PA, Erie GO, et al. (2017) Socio-economic determinants of farmers' adoption of climate change adaptation strategies in Edo State, Nigeria. Nig J Agric Food Environ 13: 115-121.
|
|
[137]
|
Orowole PF, Okeowo TA, Obilaja OA (2015) Analysis of level of awareness and adaptation strategies to climate change among crop farmers in Lagos State, Nigeria. Int J Appl Res Technol 4: 8-15.
|
|
[138]
|
Oruonye ED (2014) An Assessment of the level of awareness of climate change and variability among rural farmers in Taraba State, Nigeria. Int J Sustain Agric Res 1: 70-84.
|
|
[139]
|
Oselebe HO, Nnamani CV, Efisue A, et al. (2016) Perceptions of climate change and variability, impacts and adaptation strategies by rice farmers in south east Nigeria. Our Nature 14: 54-63.
|
|
[140]
|
Oti OG, Enete AA, Nweze NJ (2019) Effectiveness of climate change adaptation practices of farmers in Southeast Nigeria: An empirical approach. Int J Agric Rural Dev 22: 4094-4099.
|
|
[141]
|
Owombo PT, Koledoye GF, Ogunjimi SI, et al. (2014) Farmers' adaptation to climate change in Ondo State, Nigeria: A gender analysis. J Geog Reg Plann 7: 30-35. doi: 10.5897/JGRP12.071

|
|
[142]
|
Ozor N, Madukwe MC, Enete AA, et al. (2012) A framework for agricultural adaptation to climate change in Southern Nigeria. Int J Agric 4: 243-251.
|
|
[143]
|
Sangotegbe NS, Odebode SO, Onikoyi MP (2012) Adaptation strategies to climate change by food crop farmers in Oke-Ogun Area of South Western Nigeria. J Agric Ext 16: 119-131.
|
|
[144]
|
Sanni DO (2018) Local knowledge of climate change among arable farmers in selected locations in Southwestern Nigeria. In: Leal FW, Eds., Handbook of Climate Change Resilience, Cham: Springer, 1-18.
|
|
[145]
|
Solomon E, Edet OG (2018) Determinants of climate change adaptation strategies among farm households in Delta State, Nigeria. Curr Invest Agric Curr Res 5: 615-620.
|
|
[146]
|
Tanko L, Muhsinat BS (2014) Arable crop farmers' adaptation to climate change in Abuja, Federal Capital Territory, Nigeria. J Agric Crop Res 2: 152-159.
|
|
[147]
|
Usman MN, Ibrahim FD, Tanko L (2016) Perception and adaptation of crop farmers to climate change to in Niger State, Nigeria. Nig J Agric Food Environ 12: 186-193.
|
|
[148]
|
Uzokwe UN, Okonkwo JC (2012) Survival strategies of women farmers against climate change in Delta State and implication for extension services. Banat J Biotechnol 3: 97-103.
|
|
[149]
|
Weli VE, Bajie S (2017) Adaptation of Root crop farming system to climate change in Ikwerre Local Government Area of Rivers State, Nigeria. Am J Clim Chang 6: 40-51. doi: 10.4236/ajcc.2017.61003

|
|
[150]
|
Chah JM, Odo E, Asadu AN, et al. (2013) Poultry farmers' adaptation to climate change in Enugu North Agricultural Zone of Enugu State, Nigeria. J Agric Ext 17: 100-114
|
|
[151]
|
Chah JM, Attamah CO, Odoh EM (2018) Differences in climate change effects and adaptation strategies between male and female livestock entrepreneurs in Nsukka Agricultural Zone of Enugu State, Nigeria. J Agric Ext 22: 105-115
|
|
[152]
|
Ibrahim FD, Azemheta T (2016) Climate change effects and perception on smallholder poultry farms in Lokoja Local Government Area of Kogi State: Implications for Policy Intervention. Nig J Agric Food Environ 12: 164-173.
|
|
[153]
|
Tologbonse EB, Iyiola-Tunji AO, Issa FO, et al. (2011) Assessment of climate change adaptive strategies in small ruminant production in rural Nigeria. J Agric Ext 15: 40-57.
|
|
[154]
|
Ume SI, Ezeano CI, Anozie R (2018) Climate change and adaptation coping strategies among sheep and goat farmers in Ivo Local Government Area of Ebonyi State, Nigeria. Sustain Agri Food Environ Res 6: 50-68.
|
|
[155]
|
Adeleke ML, Omoboyeje VO (2016) Effects of climate change on aquaculture production and management in Akure Metropolis, Ondo State, Nigeria. Nig J of Fish Aquacult 4: 50-58.
|
|
[156]
|
Aphunu A, Nwabeze GO (2012) Fish farmers' perception of climate change impact on fish production in Delta State, Nigeria. J Agric Ext 16: 1-13.
|
|
[157]
|
Owolabi ES, Olokor J (2016) Climate change and fish farmers adaptation: A case study of New Bussa fishing population. J Natur Sci Res 6: 123-141.
|
|
[158]
|
Amusa TA, Okoye CU, Enete AA (2015) Determinants of climate change adaptation among farm households in Southwest Nigeria: A heckman's double stage selection approach. Rev Agric Appl Econ 18: 3-11.
|
|
[159]
|
NEST, Woodley E (2012) Learning from experience: Community-based adaptation to climate change in Nigeria. Ibadan, Nigeria: Building Nigeria's response to climate change.
|
|
[160]
|
BNRCC, FederalMinistry of Environment (2011) National Adaptation Strategy and Plan of Action on Climate Change for Nigeria (NASPA-CCN). Abuja, Nigeria: Federal Ministry of Environment (Climate Change Department).
|
|
[161]
|
Oladipo E (2010) Towards enhancing the adaptive capacity of Nigeria: A Review of the Country's state of preparedness for climate change adaptation. Abuja, Nigeria: Report Submitted to Heinrich Böll Foundation Nigeria.
|
|
[162]
|
Tijjani AR, Chikaire JU (2016) Fish farmers perception of the effects of climate change on water resource use in Rivers State, Nigeria. J Sci Eng Res 3: 347-353.
|









 DownLoad:
DownLoad: