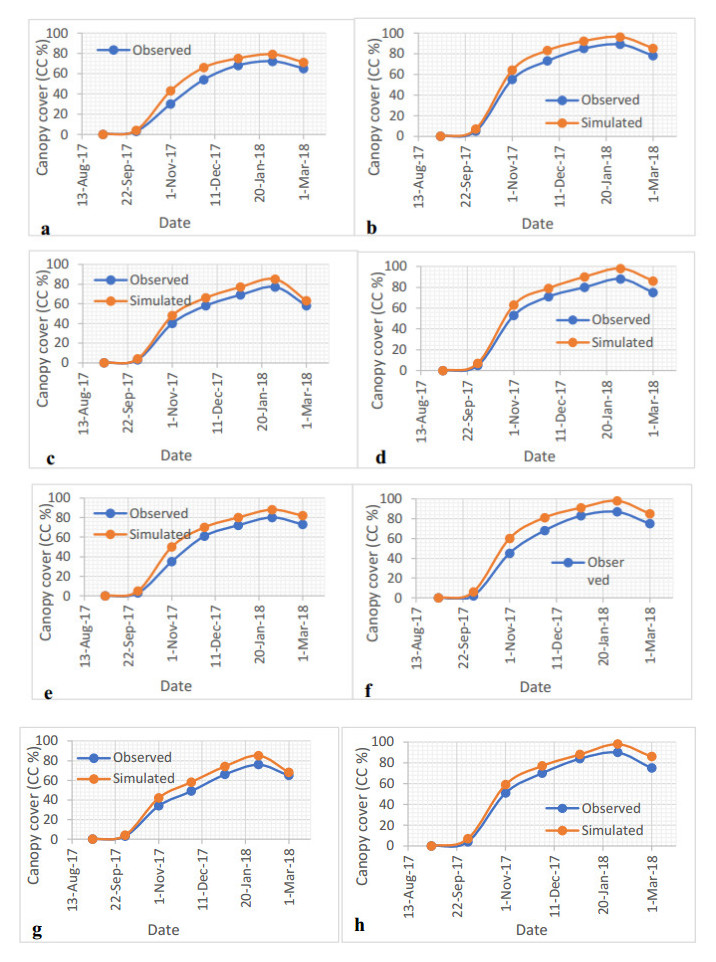
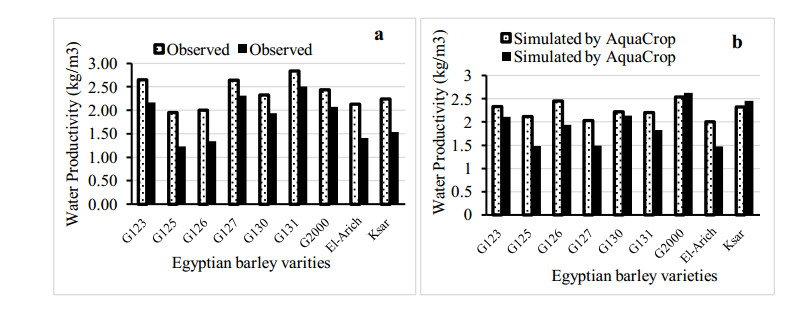
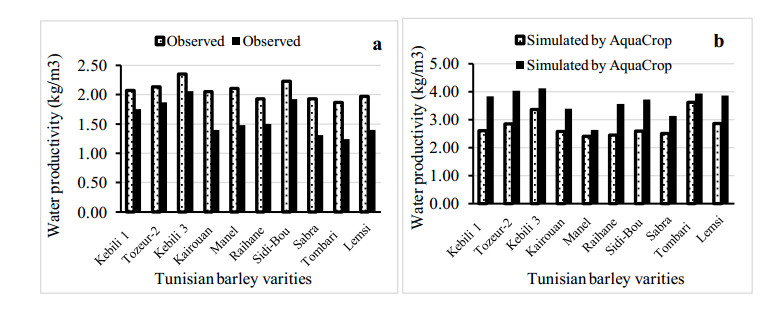
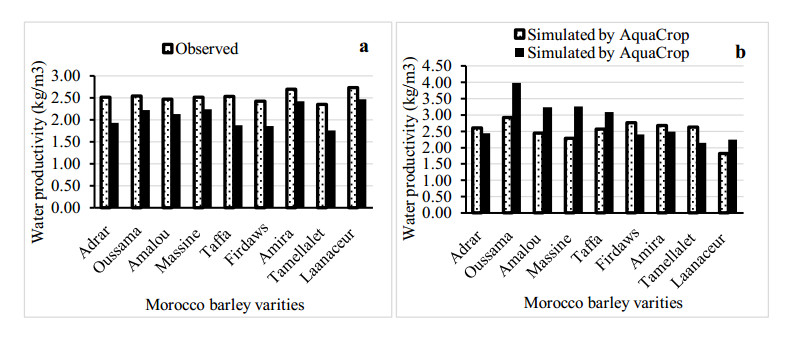
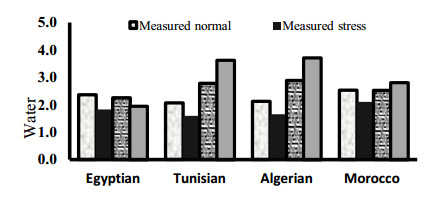
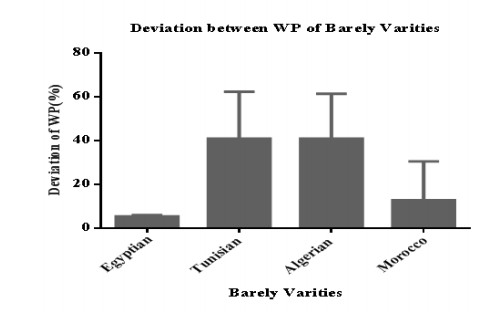
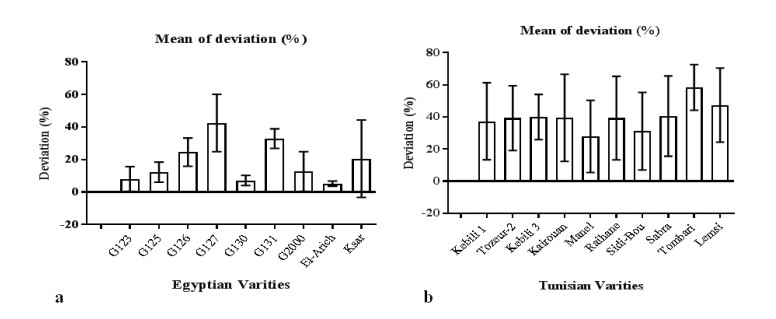
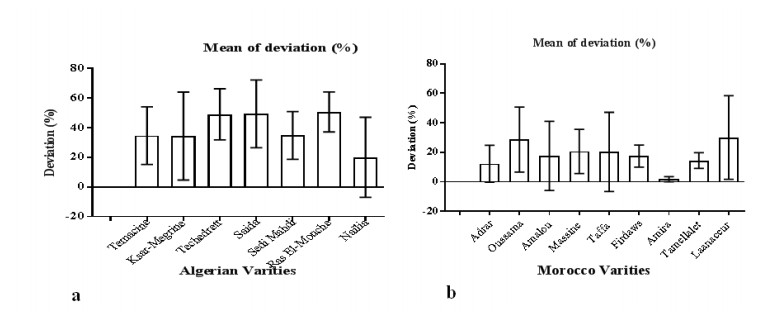
Drought is the major a biotic stress that reduces plant growth and crop productivity worldwide. AquaCrop model is one of the most widely used simulation models, which simulates the growth, yield and water productivity of the crops. Field experiment was carried out in the Experimental Research Station of Nubaria, during two seasons of 2016/2017 and 2017/2018. The study to assess water productivity of Mediterranean barley (Egyptian, Tunisian, Algerian and Morocco) varieties grown under water stress condition (40% of water holding capacity) compared to normal one (75% of water holding capacity) by AquaCrop model. Deviations (%) between observed under normal irrigation water and observed water deficit (stress), AquaCrop model normal and AquaCrop model stress, data obtained were (2.36, 1.84, 2.25 and 1.59%) for Egyptian barley varieties, respectively. For Tunisian barley varieties, deviations (%) were (2.06, 1.59, 2.78 and 3.62%), respectively. For Algerian barley varieties, were (2.12, 1.66, 2.88 and 3.71%), respectively. The percentage of absolute difference between the percentage of variation in the case of water stress and the case without water stress treatment was 5.36% under Egyptian varieties, followed by Morocco varieties (12.78%). Egyptian varieties are the least tolerant of water stress treatment where the percentage difference in the absolute difference between the cases is equal to 25%.
1.
Introduction
There are a number of studies that have investigated the use of quartz nanoparticles as for the detection of biological particles. In addition, other studies have investigated the behavior of nanoparticles in blood flow. The total dissemination tensor of nanoparticles in sheared cellular blood flow has been determined over a wide range of shear rates and hematocrit levels. In the brief timeframe system, nanoparticles (NPs) show strange dispersive practices under high shear and high hematocrit conditions because of the transient lengthening and arrangement of red blood cells (RBCs). In the long timeframe system, the NP dispersion tensor reflects high anisotropy [1]. An examination provides a solution for the tissues, cells, or stopped up conduits of the heart by methods for saturating a thin tube in the body. Small gold particles can float in the free space within catheters that have adaptable dividers with a couple of pressure bloodstream [2]. Nano vaccines are a type of vaccine that utilizes NPs as carriers. Because of the similarity in size between NPs and pathogens, the immune system can be activated effectively, resulting in the activated cell. Advantages of Nano vaccines include their extended persistence in the bloodstream, improved immunogenicity, no requirement for booster doses, a lack of need for refrigeration, and the possibility of performing active targeting [3]. Another study on the behavior of nanoparticles in the blood was a theoretical work investigating gold nanoparticle movement through a tapered vein with overlapping stenosis [4]. Another study investigated how NPs interact with Relevant the blood-brain barrier and found that nanoparticles are suitable and adaptable candidates for use in novel Nano pharmaceuticals and for therapies for neurodegenerative conditions [5].
Another study examined the impacts of nanoparticles on unsteady pulsatile blood flow through a curved stenosed channel. This study analyzed the effects of different degrees of curvature, different types of nanoparticles, and different Grashof numbers on the blood flow pattern. An unequivocally limited contrast method was used to compute the numerical consequences of the given conditions [6]. Furthermore, Prasad et al. investigated the impacts of overlapping stenosis of a micro polar fluid with nanoparticles in a uniform cylinder [7]. The study investigated the impacts of different parameters like coupling number, micro polar parameter, Brownian movement parameter, thermophoresis parameter, neighborhood temperature Grashof number, and nearby nanoparticle Grashof number on flow resistance and wall shear stress [7]. A computational two-way coupled magnetic nanoparticle targeting model was used to investigate the possibility of using NPs for magnetic drug targeting in a diseased left carotid bifurcation artery [8]. Another study showed that NPs can be used for drug delivery into Sinusoidal (or Scavenger) Endothelial Cells (SEC) bringing about the specific deletion of a single vein in the zebrafish developing embryo [9]. An attractive guided medication conveyance framework is used in a virtual situation utilizing a material science-based model of focused medication conveyance including a multi-branch vein and practical blood elements [10]. Transfer in receptor (TfR)-targeted gold nanoparticles (AuNPs) can agammaegate in brain vessels and further travel over the blood-brain barrier (BBB) to enter the cerebrum parenchyma [11]. Ye et al. [12] discussed how various physical forces can result in the imagination of NPs in the bloodstream and tumour microvasculature. A magnetic nanoparticle-based correspondence in a microfluidic channel is viewed as where an outside attractive field is utilized to pull in the data conveying particles to the collector. This work demonstrates that the molecule transport influenced by the Brownian movement, bloodstream, and an outside attractive field can be numerically displayed as a dispersion with drift [13]. Quartz crystal microbalance (QCM) has been utilized for quite a while to research thin magnetic film deposition, scratching, and adsorption of gases. Because of a low-temperature coefficient and high mechanical Q factor, Quartz QCMS is broadly utilized as a sensitive component in gas, chemical and natural sensors [14]. At present, specialists show developing enthusiasm to techniques permitting direct assurance of infections or microscopic organisms. When a body is presented with an infection, the immune system produces new B cells custom-made to battle that infection. The blood tests presented here can test for a single infection at once by taking an example from the blood, and specialists need to know which infection they're searching for, so they can search for a particular arrangement of antibodies. The aim of this study is to use QCM as a biological sensor to detect the presence of more than one virus at the same time in the blood flow. This can make blood tests more efficient in detecting more than one type of virus without wasting time and money.
2.
Proposed methodology: Problem formulation, working principle and modeling
This section presents a formulation of the problem of the research. In addition, the working principle of using Nano-QCM to detect multi viruses in the blood is introduced in details including a suggestion for fabrication and theory of operation. Then the mathematical model of the proposed methodology is presented.
2.1. Problem formulation
Blood tests at present can identify one type of virus. However, it is possible that blood contains more than one virus at the same time. Unfortunately, the usual blood tests to confirm the presence of these viruses at present cannot detect the existence of a number of viruses. Blood tests are carried out for specific viruses and subsequently followed by the allocation of a drug-specific to the virus, regardless of the effect of this drug on other viruses. This is a waste of time, cost of medication and effective treatment. Hence, this study aims to detect a number of viruses present in the blood at the same time by using quartz nanoparticles. However, the effect of these molecules on blood flow, as well as vital functions associated with the process of blood flow such as pressure and speed of flow, need to be studied. Therefore, this study investigates the possibility of using nanoparticles as a biological detector for a number of viruses at the same time, and the effect of their use on the speed of blood flow and pressure in all the types of arteries where viruses can be found. Nano-QCM is used as a very sensitive microbalance.
It was assumed that Nano-QCM particles flow with the flow of blood and that their general structure consists of a number of slides. The function of each chip was to detect a specific type of virus. Each type was determined by comparing the frequency change without loading the virus onto the Nano-QCM particles and then after loading it. The difference between these frequencies led to the identification of the type of virus. This test can detect more than one virus at the same time. The number of viruses detected was related to the number of slides used in the test. The difference in the frequency corresponds to the fundamental harmonic in a quartz crystal between two slides.
2.2. Proposed working principle
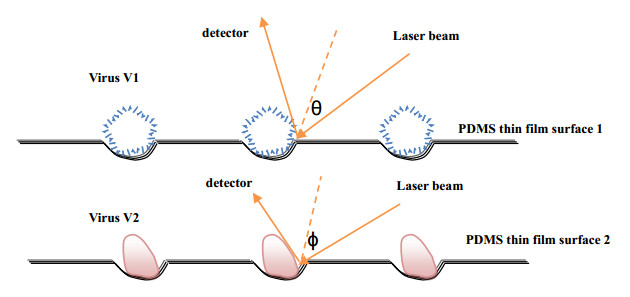
Quartz crystal microbalance (QCM) is defined as a delicate mass balance that measures the microgram level changes from Nano gram to mass per unit area. The heart of the technology may be a quartz disk. Quartz may be a piezoelectric material which will normally oscillate at a frequency defined by the utilization of appropriate voltage through metal electrodes. The piezoelectric material is usually wont to produce field forms within the presence of mechanical stress, and vice versa. Due to this technology depends on the piezoelectric effect, this technology does not need electrical contact. Changing the potential causes the crystal to oscillate; with a properly truncated crystal and an appropriate alternating potential, the resonant frequency of the quartz forms a shear wave standing within the plane. The resonance frequency of the quartz is often determined accurately and, therefore, the bit of fabric (ng/cm2) resonant frequency placed on the crystal surface. The frequency oscillation of oscillation is suffering from adding or removing a little amount of mass on the thin film surface as shown in Figure 1. Measurement of the mass, density and size of particles and nanoparticles can be obtained using suspended microchannel resonators. The mass of individual cells is calculated as transient frequency changes, while the particles transport the microfluidic channel embedded within the resonant cantilever. Since the frequency shift of the particles is proportional to the mass difference with reference to the displaced solute, the particle density is erred from measurements made in several carrier liquids. Such density measurements have significant biological and pathological applications.
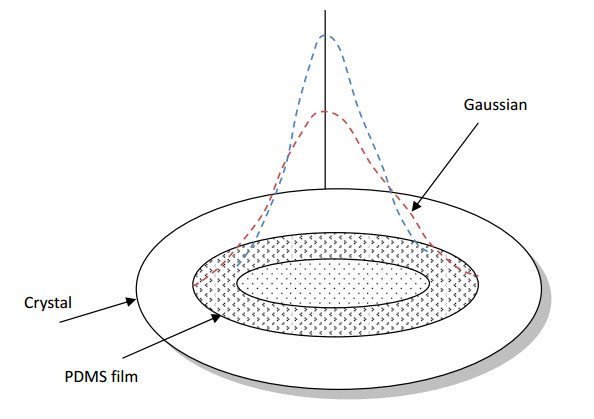
The frequency of oscillation of the quartz crystal depends partly on the thickness of the crystal. During normal operation, all other affecting variables are fixed; therefore, the change in thickness is directly related to the change in frequency. Excitement occurs when the mass of the virus is deposited on the surface of the crystal, increasing in thickness. The proposed method is predicated on testing the presence of several viruses simultaneously by injecting Nano-QCM into the blood. Since Nano-QCM contains many thin films, each film can test the presence of one virus. Therefore, the number of films during a single test tells the number of viruses which will be tested for existence during a test. In the proposed model, it is suggested to use six virus-imprinted Nano patterned polymer film of polydimethylsiloxane (PDMS) films as a maximum number of films. Due to their moderated thickness, the maximum number of viruses that can be found in the blood will be six viruses at once in a single injection. Each film contains cavities have the ability to preferentially capture a target virus from the blood.
The mean size of these cavities is determined according to the size of the targeted virus. For example, if the targeted virus is HIV-1, the mean size of the cavities will be 120 nm. The main idea of the proposed concept is "a thin film can only capture one virus" using PDMS with specific size cavities suitable for the size of the virus. If the viruses flow in the blood of the patient has a noticeable difference in size, then it is easy to differentiate between them using different films with different cavities size. But if there are two types of viruses have similar sizes with different forms. The Surface Plasmon Resonance SPR method could support our proposed methodology to differentiate between these viruses according to their forms. As shown in Figure 2 there are two types of viruses (V1, V2) with the same average size and with different forms. The two viruses can lay in the cavities approximately with the same size. Existing two viruses with nearly the same size in the blood of the patient are rare but it could exist. For example, the difference in size between Adenovirus and Rotavirus is only 10 nm that is too tiny and these two viruses could exist in the same cavity.
By measuring the which is different from virus to another. In Figure 2, V1 and V2 have approximately the same size but with different angles (θ, Φ) between the virus surface and the incident laser beam of SPR in order. So, by measuring these two angles (θ, Φ), we can differentiate accurately between V1 and V2. The device of quartz crystals is identified as a flat mass balance, where the frequency changes of oscillating quartz (f) is linearly linked with its mass change (Δm).
Where OV is the overtone number and k is a constant that depends on the property of the crystal used. Equation (1) referred to as the Sauerbrey equation. For a 5 MHz AT-cut quartz crystal at room temperature, k is approximately equal to 17.7 ng/(cm2·Hz). Equation (1) The noise resistance of quartz with the metallic film is similar to that of quartz. In addition, the change in frequency is attributed to the mass deposited on the surface, and this mass is uniformly distributed over the entire surface of the crystal. The negative inspection of the Sauerbray equation suggests that the – of mass to the resonance leads to a reduction in its resonance frequency, and in vice versa.
2.3. Modeling
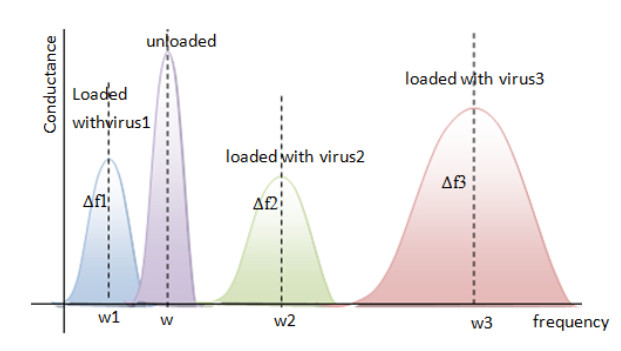
This study assumes that the frequency of the nanotubes of the nanoparticles is f in the absence of any virus on the polymer thin film of polydimethylsiloxane (PDMS) film. If there is a virus of the first type on the tape, the emitted frequency is f1. It is therefore possible to determine whether the magnetic film tape contains a virus or not by measuring the frequency difference between the frequencies f and f1, a value that is equal to ∆f1. Similarly, the presence of type Ⅱ virus can be determined by measuring the frequency difference between the two frequencies f and f2, which is equal to ∆f2. As for the type Ⅲ virus, the difference between the frequencies is ∆f3. This can be extended to n frequencies, which represent the presence of n viruses and corresponds to the existence of n of magnetic film tapes. The value of the wafer is determined based on the structure of the quartz particles and the thickness of the magnetic film tape. Nano-QCM predicts the resonance parameters and the following relation holds as long as the frequency shift is much lower than the frequency itself: ∆fnFf=iπZqZn. Ff is the frequency of the fundamental. Zq is the acoustic impedance of material. For AT-cut quartz, its value is Zq = 8.8 × 106 kg·m−2·s−1.
The existence of the virus is central to the interpretation of Nano-QCM-data. If the average stress-to-speed ratio of the virus at the crystal surface has the load impedance, ZL, then for n viruses, there are ZLn where n = 1, 2, 3, ......n. The limits of the virus approximation are noticeable either when the frequency shift is large or when the overtone-dependence of Δf and Δ(w/2) is analyzed in detail in order to derive the properties of the virus. Figure 3 shows the relationship between unloaded Nano-QCM and loaded one with three different types of viruses. The Nano-QCM motion for each slide refers that the longitudinal oscillations of thin plates represented by the following equation for displacements ux.
and
Where
and
Where Y refers to the Young’s modulus, PC refers to the Poisson coefficient, and Vo is the volume in which blood flows. The blood flows in four types of vessels: large arteries with flow velocity 16.1 ± 5.7 mm/s, large veins with flow velocity 9.33 ± 1.67 mm/s, macular capillaries with flow velocity 0.76 mm/s, and the optic nerve head capillaries with flow velocity 1.39 mm/s. Each one of these types has different volumes: the volume of the large artery is Vola, the volume of large vein is Volv, the volume of macular capillaries is Vomc, and the volume of the optic nerve head capillaries is Vooc. The x-axis is coordinated along the Corridor or vein length. In bloodstream elements, the laminar stream is portrayed by bloodstream particles following smooth ways in layers. The particular computation of the Reynolds number and the qualities where laminar stream happens will rely upon the geometry of the stream framework and stream design. The equation for the mass of each Nano-QCM particle is expressed as follows:
It is assumed that there are a number of Nano-QCM particles and that the total mass (Tm) of these particles is the sum of all the masses that flow in the four types of veins as follows,
The Navier Stokes' conditions that oversee the movement of blood subject to body quickening are written in the round and hollow organized framework as follows:
where Ra and Ai are the radial and the axial velocity components, respectively andρ is density.
The velocity could be represented as follow:
Where P is the pressure amplitude, f is the frequency, vis the longitudinal speed of QCM in the blood, ρ is the blood density and A is the displacement amplitude of QCM from their average equilibrium position.
Then the radial and the axial velocity components could be represented in terms of equation Eq (8). Where radial velocity Ra=Pr(2πf)ρAr and the axial velocity Ai=Pi(2πf)ρAi. Where Pr and Ar are the radial components of the pressure and the displacement. While Pi and Ai are the axial components of the pressure and the displacement respectively.
The radial and the axial velocity components differ from one vein to another. Therefore, Rla and Ala are the radial and the axial velocity components in the large artery, Rlv and Alv are the radial and the axial velocity components in the large vein, Rmc and Amc are the radial and the axial velocity components in the macular capillaries, and Roc and Aoc are the radial and the axial velocity components in the optic nerve, head, and capillaries, respectively. The Navier-Stokes’ equations that govern the motion of blood in the four different veins could be described regarding the volume of each vein as follows:
where
where
where
where
The conditions containing protection of mass, force, and vitality for the progression of Nano-QCM in a vertical stenosed vein are communicated in the dimensional structure, where Nano-QCM is introduced by its mass in the four kinds of vessels as:
Then
where
where
where
where
where g is the gravity, and the heat transfer is represented by giving temperature T0 to the upper mass of the vessel and i = la,lv,mcoroc.
In the above expressions, the physical parameters for base blood flow are defined in the following way: ρ is density, μ is viscosity, γ is the thermal expansion coefficient, and k is thermal conductivity.
3.
Results
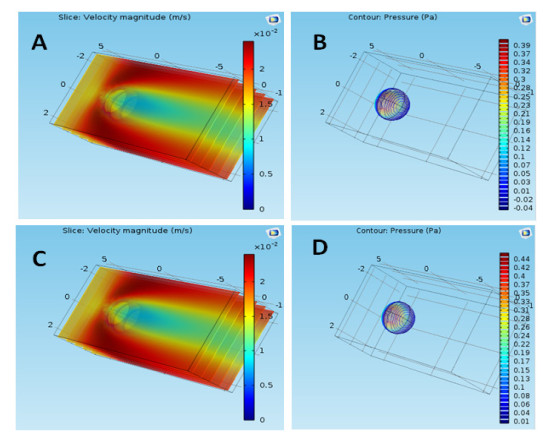
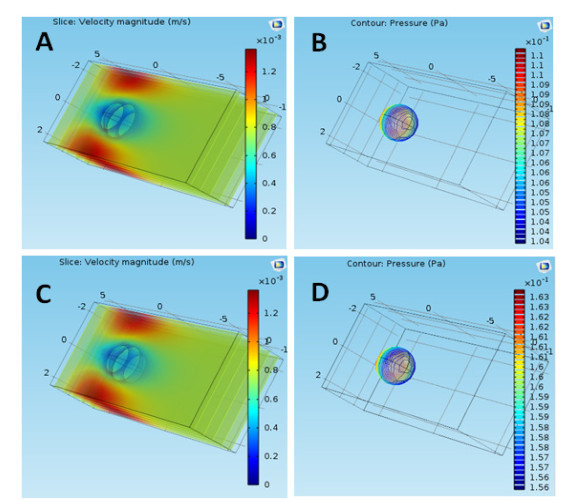
In this section, the flow of Nano-QCM through the blood was simulated by the COMOSL program. The simulation was carried out by imposing the presence of a partial quartz metal onto a section of a blood vessel in different conditions and environments (Figures 4 and 5). The degree of the NPs’ impact on the surrounding pressure and their rate of speed were also studied. The simulation was performed using quartz metal blood flow parameters under the influence of Laminar flow and took into account the four main types of blood vessels. Figure 4A shows the velocity of Nano-QCM particle flow in a large artery under normal diastolic blood pressure. Figure 4B shows the pressure exerted by particle flow in a large artery under normal diastolic blood pressure. Figure 4C shows the velocity of particles flows in a large artery under normal systolic blood pressure. Figure 4D shows the pressure exerted by particle flow in a large artery during normal systolic blood pressure. Figure 5A shows the velocity of particle flow in macular capillaries under normal diastolic blood pressure. Figure 5B shows the particle flow pressure in macular capillaries under normal diastolic blood pressure. Figure 5C shows the velocity particle flow in macular capillaries under normal systolic blood pressure. Figure 5D shows the pressure of particle flow in macular capillaries under normal systolic blood pressure. Viruses that can be present in the blood vary in size. Same results of both figures are obtained in the cases of the optic nerve and a large vein. Table 1 shows the names and size of a sample of these viruses. This table shows the variation of the pressure according to the size of the virus. In this extension of this simulation, we proposed six films and each film contains a specific virus with specific mass (with actual size).
Calculations in Comsol Multi-physics are done in the large artery in the systolic pressure. The results are shown in the table 1. The frequency is calculated according to Eq (1). It is observed that the pressure around the Nano-QCM surface differs according to the size of each virus. The pressure is calculated related to only one virus at one capture. It is observed that the frequency and the pressure are in direct relation. This means by increasing the change of the frequency, the pressure around Nano-QCM increases.
4.
Discussions
Figure 4A shows that the speed of blood flow around the quartz nanoparticles increases on both sides of the nanoparticles and peaks at 3 × 10-2 m/s at the front of the quartz nanoparticle. This speed decreases when the nanoparticle moves from its old position to a new position. Figure 4B shows that the pressure surrounding the quartz molecules is −0.4 Pa, as low as possible, which means that the composition of the proposed quartz metal particles will not be affected by the surrounding pressure. This allows it to perform its work perfectly. Figure 4C shows that the speed of quartz particles does not change under either systolic or diastolic pressure, suggesting means that the stability and performance of the particles will not be affected in both cases. Figure 4D shows that the pressure around these particles increases to reach its maximum value at 0.01 Pa. This means that these molecules may be at risk of being damaged under systolic blood pressure in comparison to diastolic pressure. In Figure 5A, there is a decrease in the blood flow velocity around the quartz nanoparticles where the velocity reached 1.4 × 10-2 m/s; this continuous decrease in velocity is normal due to a decrease in the volumes of the blood vessels. In Figure 5B, the pressure decreases to a minimum of 1.04 × 10-1 Pa. The velocity in Figure 5C is the same as in Figure 5A due to the similarity in blood vessel volumes. In Figure 5D, the pressure increases to a maximum of 1.56 × 10-1 Pa.
5.
Conclusions
Current blood tests cannot detect more than one virus at a time and usually involve collecting a single blood sample from a blood vessel. This leads to a waste of time and it is costly to test for more than one virus in the blood. This test has a wide range of uses and is one of the most common types of medical test. This study aims to shed light on a new a qualitative method that can test the presence of a number of viruses simultaneously, by inserting a number of quartz nanoparticles into the blood vessels containing a number of slides. Each chip emits a frequency indicating a specific type of virus. The main blood vessels in which Nano-QCM can flow in the blood are the large artery, the large vein, the macular capillaries, and the optic nerve head capillaries. The results showed that quartz nanoparticles can function consistently with any type of blood vessel. However, they work very efficiently without obstructions if they flow with blood in the large artery.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Groups Program under grant number (R.G.P.2/35/40).
Conflict of interest
The authors declare no conflict of interest regarding the publication of this paper.









 DownLoad:
DownLoad: