Factors influencing the adoption of improved wheat varieties by rural households in Sindh, Pakistan

To Sandro Salsa, a fine mathematician with a taste for life.

1.   Introduction

In this paper we consider some entire solutions of a degenerate elliptic equation with non linear forcing term, where the behaviour of the solutions is quite different from the uniformly elliptic case.

We begin by recalling the linear uniformly elliptic model problem we have in mind in order to underline the differences with the degenerate elliptic case that we shall treat here. Consider the entire solutions of the Allen-Cahn equation

where $N \geq 2$.

Writing the variable as $x = (x', x_N)$, with $x_N \in \mathbb{R}$, we are interested in solutions that satisfy the following conditions:

Any solution of (1.1) satisfying (1.2) is necessarily a function of $x_N$, i.e. it is independent of $x'$. This was referred to as Gibbons conjecture and it has been proved by several authors ^{[3, 5, 18, 19]} and then it has been generalized to different contexts ^[15,20,23]. It is well known that this conjecture is somehow related to a famous conjecture of De Giorgi on the 1 dimensionality of monotone solutions in low dimension, see for its proof ^[4,21] in the 2 dimensional case, ^[2] for the 3 dimensional case and for higher cases with some mild further assumptions, the work of Savin ^[24]. For a counterexample in dimensions $N\geq 9$, providing a sharpness of the conjecture, was constructed by Del Pino, Kowalczyk and Wei in ^[17]

The function $f(u) = u-u^3$ can be replaced by a much more general class of functions and the result is still valid. On the other hand, if instead of the Laplacian one considers some degenerate elliptic operators, there are few results, let us mention e.g., the works in the Heisenberg group and in Carnot groups ^[14,16].

In this work we shall mainly focus on equations whose leading term is the operator $\mathcal{P}^-_{k}$ which is sometimes referred to as the truncated Laplacian. The operator $\mathcal{P}^-_{k}$ is defined, for any $N\times N$ symmetric matrix $X$, by the partial sum

of the ordered eigenvalues $\lambda_1\leq\ldots\leq\lambda_N$ of $X$. We shall consider solutions of the equation

for a general class of functions $f$ modelled on $f(u) = u-u^3$. Clearly $\mathcal{P}^-_{k}(D^2u)$ corresponds to the Laplacian when $k = N$, hence in the whole paper we shall suppose that $k = 1, \dots, N-1$.

These operators are degenerate elliptic in the sense that

In order to emphasize the strong degeneracy of these operators, let us mention that for any matrix $X$ there exists $M\geq 0$, not identically zero, such that

It is immediate to see that, for example, one can take $M = v_N\otimes v_N$ where $v_N$ is an eigenvector corresponding to the largest eigenvalue of $X$.

In previous works we have, together with Hitoshi Ishii and/or Fabiana Leoni ^[9,10,11,13], encountered a certain number of surprising results, related to these degenerate operators. It would be too long to recall them all here but we shall briefly recall some of those closer to the results in this paper.

The classical Liouville result states that any harmonic function which is bounded from below is a constant. This is not true for bounded from below entire solutions of $\mathcal{P}^-_{k}(D^2u) = 0$.

Similarly, concerning the semi-linear Liouville theorem, the existence of entire non negative solutions of $F(D^2u)+u^p = 0$ is quite different if $F(D^2u) = \Delta u$ or if $F(D^2u) = \mathcal{P}^-_{k}(D^2u)$. Indeed, for the Laplacian there is a threshold for $p$ between existence and non existence. This threshold is different for solutions and supersolutions and it depends on the dimension of the space. Instead, for solutions of the equation

the following hold:

$1).$ For any $p > 0$ there exist nonnegative viscosity solutions $u\not\equiv0$;

$2).$ For any $p\geq1$ there exist positive classical solutions;

$3).$ For $p < 1$ there are no positive viscosity supersolutions of (1.4).

Interestingly, if one considers instead non positive solutions, the non existence results are very similar to those of the Laplacian in $\mathbb{R}^k$. These Liouville theorems were proved in ^[13].

Hence this lead us to wonder what happens to bounded entire solutions of the equation

which satisfy $|u| < 1$ and which, a priori, may change sign. Can one expect solutions to be one dimensional? Precisely, can we extend Gibbons conjecture to this degenerate case?

In order to answer these questions the first step is to study the one dimensional solutions, which is what we do in Section 2. Interestingly the results are completely different from the uniformly elliptic case and this leads to different conjectures. Precisely, we consider only one dimensional solutions $u(x', x_N) = v(x_N)$ of (1.5) that satisfy $|u| < 1$. The results can be summarized in the following way:

1). The only classical solution is $u\equiv 0$;

2). Any viscosity subsolution is non negative and there exists a non trivial viscosity solution that satisfies

3). There are no solutions that are strictly monotone or positive

Observe that, even though $u^3-u$ is the derivative of the double well potential $F(u) = \frac14(1-u^2)^2$, the lack of ellipticity does not allow the solutions to go from $-1$ to $1$. This is the first surprising result.

Hence Gibbons conjecture should be reformulated in the following way:

Question 1. Is it true that if $u$ is a solution of (1.5), $|u| < 1$, satisfying

then $u$ is 1 dimensional?

If the answer was positive, this would imply that there are no solutions of (1.5) that satisfies (1.2), since such one dimensional solutions don't exist in view of point 2 above. Or, equivalently, if such a solution of (1.5) exists then the answer to Question 1 is negative.

Question 2. Is it true that if $u$ is a solution of (1.5), $|u| < 1$, satisfying

then $u$ is 1 dimensional?

This is more similar in nature to the uniformly elliptic case. Nonetheless, classical proofs of these symmetry results rely heavily on the strong maximum principle, or strong comparison principle, and on the sliding method and the moving plane method ^[7], which in general don't hold for the truncated Laplacian (see ^[9,12]). And in particular they are not true here since we construct ordered solutions that touch but don't coincide.

Another remark we wish to make is that, even though the solutions we consider are one dimensional, since they are viscosity solutions, the test functions are not necessarily one dimensional. Hence the proofs are not of ODE type.

Other surprising results concern Liouville type theorems for (1.5) i.e., existence of bounded entire solutions bounded without requiring conditions at infinity. Aronson and Weinberger in ^[1] and more explicitly, Berestycki, Hamel and Nadirashvili in ^[6] have proved the following Liouville type result:

If $v$ is a bounded non negative classical solution of

then either $u\equiv 0$ or $u\equiv 1$.

Once again this result fails if one replaces the Laplacian with the truncated Laplacian.

Indeed we prove that there exists infinitely many bounded non negative smooth solutions of

for a general class of nonlinearities that includes $f(u) = u-u^3$. This is done by constructing infinitely many radial solutions of $\mathcal{P}^-_{k}(D^2u)+f(u) = 0$ which are positive in $\mathbb{R}^N$ but tend to zero at infinity.

Finally in Section 4 we show a different surprising phenomena related to the so called principal eigenvalue of $\mathcal{P}^-_{k}$. This is somehow different in nature but we believe that it sheds some light to these extremal degenerate operators.

2.   One dimensional solutions

We consider one dimensional viscosity solutions $u$, i.e., $u(x) = v(x_N)$ for $x = (x_1, \ldots, x_N)$, of the problem

The main result is the following.

Proposition 1. Concerning problem (2.1), the following hold:

i) If $u\in USC(\mathbb R^N)$ is a viscosity one dimensional subsolution then $u\geq0$.

ii) The only classical one dimensional solution is $u\equiv 0$.

iii) There exist nontrivial viscosity one dimensional solutions, e.g., $u(x) = v(x_N)$, satisfying either

or

iv) There are no positive viscosity one dimensional supersolutions.

v) If $u\geq 0$ is a viscosity one dimensional supersolution e.g., $u(x) = v(x_N)$ and it is nondecreasing in the $x_N$-direction then there exists $t_0\in\mathbb R$ such that

Remark 1. A consequence of i) and v) is that there are no viscosity one dimensional solutions increasing in the $x_N$-direction.

Proof. i) Fix $\hat x = (\hat x_1, \ldots, \hat x_N)\in\mathbb R^N$ and, for $\alpha > 0$, let

Then

and

Moreover, using the one dimensional symmetry, for any $x\in\overline B_1(\hat x)$ we have

Hence $u(x)-\alpha(x_N-\hat x_N)^2$ has a maximum in $(\hat x_1, \ldots, \hat x_{N-1}, x^\alpha_N)\in B_1(\hat x)$ for $\alpha$ large in view of (2.4). Then

We deduce that $u(\hat x_1, \ldots, \hat x_{N-1}, x^\alpha_N)\geq0$ for every $\alpha$ big enough. Using semicontinuity and (2.4) we conclude

ii) By contradiction, let us assume that $u(x) = v(x_N)$ is a classical solution of (2.1) and that $v(t_0)\neq0$ for some $t_0\in\mathbb R$. By i), $v(t_0) > 0$. Let

If $\delta^- = -\infty$ and $\delta^+ = +\infty$, then $v > 0$ in $\mathbb R$ and, since $v^3-v < 0$, we deduce by the Eq (2.1) that $v''(t) < 0$ for any $t\in \mathbb{R}$. In particular $v$ is concave in $\mathbb R$, a contradiction to $v > 0$.

If $\delta^- > -\infty$, then $v(t) > 0$ for any $t\in(\delta^-, t_0]$ and $v(\delta^-) = 0$. Moreover there exists $\xi\in(\delta^-, t_0)$ such that $v'(\xi) > 0$. Using the Eq (2.1) we deduce that $v''\leq0$ in $[\delta^-, t_0]$, hence $v'(\delta)\geq v'(\xi) > 0$. This implies that for $\varepsilon$ small enough $v(\delta^–\varepsilon) < 0$, a contradiction to i).

The case $\delta^+ < +\infty$ is analogous.

iii) Let $u(x) = \tanh\left(\frac{x_N}{\sqrt{2}}\right)$. Then

If $x_N\geq0$ then $u^3-u\leq0$ and $\mathcal{P}^-_{k}(D^2u) = u^3-u$, while if $x_N < 0$ the function $u$ fails to be a solution since $\mathcal{P}^-_{k}(D^2u) = 0 < u^3-u$.

Instead we claim that

is a viscosity solution of (2.1). This is obvious for $x_N\neq0$. Now take $\hat x = (\hat x_1, \ldots, \hat x_{N-1}, 0)$. Since there are no test functions $\varphi$ touching $\tilde u$ by above at $\hat x$, automatically $\tilde u$ is a subsolution. Let us prove the $\tilde u$ is also a supersolution. Let $\varphi\in C^2(\mathbb{R}^N)$ such that $\varphi(\hat x) = \tilde u(\hat x) = 0$ and $\varphi\leq u$ in $B_{\delta}(\hat x)$. Our aim is to show that $\lambda_{N-1}\left(D^2\varphi(\hat x)\right)\leq0$, from which the conclusion follows.

Let $W_0 = \left\{w\in\mathbb R^N\, :\; w_N = 0\right\}$ and for any $w\in W_0$ such that $|w| = 1$ let

Since $\varphi$ touches $\tilde u$ from below at $\hat x$ and $\tilde u = 0$ when $x_N = 0$, we deduce that $g_w(t)$ has a maximum point at $t = 0$. Then

Using the Courant-Fischer formula

as we wanted to show.

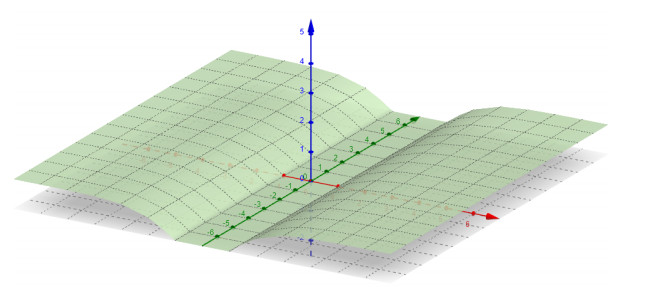
As above one can check that, for any $c\geq0$, the one dimensional function

see figure 1, is non monotone in the $x_N$-direction and it is a solution of (2.1).

iv) By contradiction suppose that $u(x) = v(x_N)$ is a positive viscosity supersolution of (2.1). We claim that $v$ is strictly concave, leading to a contradiction with $v > 0$ in $\mathbb R$.

We first prove that $v$ satisfies the inequality

in the viscosity sense. For this let $\varphi\in C^2(\mathbb{R})$ be test function touching $v$ from below at $t_0$. If we consider $\varphi$ as a function of $N$ variables just by setting $\tilde\varphi(x) = \varphi(x_N)$, then $\tilde\varphi$ is a test function touching $u$ from below at $(x_1, \ldots, x_{N-1}, t_0)$, for any $(x_1, \ldots, x_{N-1})\in\mathbb R^{N-1}$. Hence

and then necessarily $\varphi''(t_0) < 0$.

If $v$ was not strictly concave, then there would exist $t_1 < \bar t < t_2\in \mathbb{R}$ such that

Then using $\varphi(t) = v(t_1)+\frac{v(t_2)-v(t_1)}{t_2-t_1}(t-t_1)$ as a test function in (2.5) we obtain a contradiction.

v) By iv) there exists $t_0\in\mathbb R$ such that $v(t_0) = 0$. By the monotonicity assumption we get $v(t) = 0$ for any $t\leq t_0$.

3.   Radial solutions

This section is concerned with the existence of entire radial solutions of the equation

where $f:\mathbb R\mapsto\mathbb R$ satisfies the following assumptions: there exists $\delta > 0$ such that

Prototypes of such nonlinearities are

with $\alpha > 0$, $\gamma > 1$ and any $\beta\in\mathbb R$.

Proposition 2. Under the assumptions (3.2) there exist infinitely many positive and bounded radial (classical) solutions of the Eq (3.1).

Proof. For any $\alpha\in[0, \delta)$ let $v_\alpha$ be the solution of the initial value problem

defined in its maximal interval $I_\alpha = [0, \rho_\alpha)$. Since $v_0\equiv0$, then $v_\alpha(r) > 0$ for any $r\in I_\alpha$ if $\alpha > 0$. We claim that $I_\alpha = [0, \infty)$. For this first note that $v'_\alpha(r)$ is nonpositive in a neighborhood of the origin since, using (3.2)–(3.3), one has

If there was $\xi_\alpha\in(0, \rho_\alpha)$ such that $v'_\alpha(r) < 0$ in $(0, \xi_\alpha)$ and $v'_\alpha(\xi_\alpha) = 0$, then by monotonicity $0 < v_\alpha(\xi_\alpha) < \alpha$ and by (3.3) we should obtain that $f(v_\alpha(\xi)) = 0$. But this is in contradiction with (3.2). Hence $v_\alpha$ is monotone decreasing and positive, so $I_\alpha = [0, \infty)$. Using again (3.3) we deduce moreover that $\lim_{t\to\infty}v_\alpha(r) = 0$ and for any $r > 0$

In the last inequality we have used the facts that $v_\alpha$ is monotone decreasing, $0 < v_\alpha(r) < \alpha$ for any $r > 0$ and that $f$ is nondecreasing in $[0, \delta)$ by assumption.

By (3.3)

and a straightforward computation gives that the function $v_\alpha$ can be written as

$F^{-1}$ being the inverse function of $F(\tau) = \int_\tau^\alpha\frac{1}{f(s)}\, ds$ in $(0, \alpha]$.

From the above we easily deduce that for any $\alpha\in(0, \delta)$ the radial function

is a positive radial solution of (3.1).

In the model case $f(u) = u-u^3$ the assumptions (3.2) are satisfied with $\delta = \frac{1}{\sqrt{3}}$. Moreover, for $\alpha\in(0, \frac{1}{\sqrt{3}}]$, we have

and

Hence, by (3.5)–(3.6), we infer that the functions

see figure 2, are smooth and positive radial solutions of

Let us explicitly remark that the condition $\alpha\in(0, \frac{1}{\sqrt{3}}]$ ensures the validity of the inequality (3.4).

4.   Another unusual phenomena

Let us recall that in ^[9], given a domain $\Omega$, following Berestycki, Nirenberg and Varadhan ^[8] we define

We proved many results among them that $\mu_1^-$ could be called an eigenvalue since under the right conditions on $\Omega$ we construct $\psi < 0$ solution of

But, differently from the uniformly elliptic case, $\mu_1^-$ does not satisfy the Faber-Krahn inequality, see ^[11].

Another feature of $\mu_k^-$ is that it is the upper bound for the validity of the maximum principle. Precisely if $\mu < \mu_k^-$ and

then $v\geq 0$ in $\Omega$.

It is well known that for uniformly elliptic operators, the principal eigenvalue goes to infinity when the domain decreases to a domain with zero Lebesgue measure.

In this section we shall construct a sequence of domains $Q_n\subset\mathbb R^2$ that collapse to a segment such that $\mu_1^-(Q_n)$ the principal eigenvalue of $\mathcal{P}^-_{1}$ stays bounded above by 1. Hence not only they collapse to a zero measure set, but they are narrower and narrower.

Indeed we consider

And we define

Obviously $w_n < 0$ in $Q_n$ and $w_n = 0$ on $\partial\Omega$. We shall prove that

This will imply that $\mu_1^-(Q_n)\leq 1$. Indeed if $1 < \mu_1^-(Q_n)$ the maximum principle would imply that $w_n\geq 0$ which is a contradiction.

Let us show (4.1). Clearly

We shall divide $Q_n$ in three areas. In $Q_n\cap(0, \frac{\pi}{n})\times (0, \pi)$ both $\sin(nx)$ and $\sin y$ are positive, then

In $Q_n\cap (\{-\frac{\pi}{2n} < x\leq 0\}\cup \{\frac{\pi}{n}\leq x < \frac{3\pi}{2n}\})$ where $\sin(nx)\leq 0$ and $\sin y\geq 0$, then

Finally, in $Q_n\cap (\{\pi\leq y < \frac{3\pi}{2}\}\cup \{-\frac{\pi}{2} < y\leq0\})$ where $\sin(nx)\geq 0$ and $\sin y\leq 0$ we have

This ends the proof.

Remark 2. During the revision of the present paper a new preprint, ^[22], which improves the result of this Section, has been uploaded on ArXiv. In particular, applying [22, Corollary 3.2] to $Q_n$, one would obtain that for any $n\in\mathbb N$, $\mu_1^-(Q_n) = \frac14$.

Acknowledgments

This research is partially supported by INDAM-GNAMPA.

Conflict of interest

The authors declare no conflict of interest.