Light-emitting diode (LED) technology is paving the way to increase crop production efficiency with electric lamps. Users can select specific wavelengths to elicit targeted photomorphogenic, biochemical, or physiological plants responses. In addition, LEDs can help control the seasonality of flowering plants to accurately schedule uniform flowering based on predetermined market dates. Research has shown that the monochromatic nature of LEDs can help prevent physiological disorders that are common in indoor environments, and help reduce incidence of pest and disease pressure in agriculture, which could ultimately increase crop production efficiency by preventing crop losses. Furthermore, a significant attribute of LED technology is the opportunity to reduce energy costs associated with electric lighting. Studies have shown that by increasing canopy photon capture efficiency and/or precisely controlling light output in response to the environment or to certain physiological parameters, energy efficiency and plant productivity can be optimized with LEDs. Future opportunities with LED lighting include the expansion of the vertical farming industry, applications for space-based plant growth systems, and potential solutions to support off-grid agriculture.
1.
Introduction
A large variety of models of interactions between agents have been developed within the framework of thermostatted kinetic theory [1,2] and notably applied to traffic [3], swarming [4] and cell competition [5,6,7,8]. The interactions between immune system and cancer are known to be complex. The competition between immune system cells and cancer cells can be compared to the interactions between immune system cells and viruses. In both cases, pathogenic cells induce immune system responses [9,10,11,12]. Different cell types are involved in the defense mechanism. Three types of cells are commonly recognized as being involved in the immune response, antigen-presenting cells, T cells and B cells. Dentritic cells ingest cancer cells, isolate antigens and present them to T cells, which leads to their activation and proliferation [13]. Activated T cells mutate into killer T cells, which destroy cancer cells. Like innate dendritic cells, B cells are antigen-presenting cells developed by the adaptive immune system. B cells produce antibodies, specific to each pathogen, which bind to the surface of an invading cell and mark it for destruction by T cells. When a cancer cell is killed, additional antigens are released, which stimulates further activation, i.e. learning of new T and B cells. In addition, regulatory T cells are produced to control the response of immune system. They adjust the level of antibody secretion, i.e. the regulation of B and T cell production and activation. While T cells are activated, cancer cells mutate and acquire the ability to avoid detection and destruction by the immune system. Specifically, cancer cells express proteins on their surface that induce the inactivation of immune cells, thus promoting the proliferation of cancer cells [14,15]. Through cellular interactions, cancer cells learn not to be detected, misleading the regulatory T cells, which in turn limits the production of immune system cells and let the cancer cells proliferate [16,17]. In the model, the learning processes and activation of both immune system cells and cancer cells is reproduced by the increase of a real quantity called activity and carried by each cell [2].
Stimulating the immune system of a patient can lead to disappointing results and conversely, chemotherapy may boost immune system response [18]. For some cancers, immunotherapy leads to a long remission followed by a fatal outcome, reflecting the complex relationship between the immune system and the cancer. This phenomenon, known as the three Es characterizes the following three phases commonly observed in a patient, elimination, equilibrium and escape of cancer, introduced in the theory of immunosurveillance as early as the mid-20th century [9,19]. The initial elimination of cancer cells is only apparent and corresponds to the attack by killer T cells, before the cancer cells have learned to mislead the immune system. During the pseudo-equilibrium phase, a small number of cancer cells remain and learn from the immune system cells. Eventually, the cancer cells are able to proliferate and the cancer escapes the control of the immune system. C-Reactive Protein (CRP) levels have been used as markers of inflammation in response to antigen exposure in relation to the progression of many cancers, such as melanoma and lung cancer [20]. Oscillations of CRP concentration in advanced cancer patients have been observed and interpreted in terms of immune regulatory cycles [21,22]. The oscillations of CRP concentration reveal the antagonistic effects of immune system stimulation on a tumor. Many macroscopic models of interactions between cancer and immune system leading to oscillating solutions for concentrations after a Hopf bifurcation can be found in the recent literature [23,24,25,26], in particular after introduction of one or more delays in the equations [27,28], but without direct connection with a description at cell scale.
We recently designed a minimal model of interactions between cancer and immune system cells in a homogeneous system, ignoring the spatial description of a tumor [7,8]. The spatio-temporal description of the immune system [29] or tumors [30] often involves partial differential equations for macroscopic quantities, with nevertheless an emphasis on the importance of multiscale modeling [31]. In this work we introduce a space-velocity description of tumor growth at cell scale in the framework of thermostatted kinetic theory. The homogeneous model includes autocatalytic cell production and increased cell activity during favorable interactions. In chemical kinetics, autocatalysis refers to the formation of a product which is also a reactant. Hence, the production rate of the autocatalytically formed species depends on its own concentration, leading to long induction times, when the species is present in low concentration at the beginning of the reaction, and then to explosive behaviors, when the concentration exceeds a threshold. Autocatalysis is a crucial ingredient in the destabilization of a steady state and the emergence of more complex behaviors such as oscillations [32,33]. In the model, the fluctuations of cell activity are regulated by a so-called thermostat [2]. The introduced interaction processes only consider the death of a cell when its activity is not favorable. However, all cells [34], including memory T cells involved in the long-lasting protection acquired after vaccination [35,36,37,38], have a finite life span, whether or not they are very active. Thus, the spontaneous death of educated cells leads to a loss of information. In order to take this phenomenon into account, the model introduces the regulation of activity fluctuations, by imposing that its second moment remains constant. By analogy with the dissipation of energy in a system maintained at constant temperature [1], the activity regulator is also called a thermostat.
We design a kinetic Monte Carlo algorithm inspired by the direct simulation Monte Carlo (DSMC) method initially devoted to dilute gases [39,40] and simulate the evolution of cell position, velocity, nature, and activity. Contrary to the standard DSMC method in which the velocities of the dilute gas particles are updated due to binary collisions, jump processes are introduced to randomize the direction of cell velocities in the present inhomogeneous model involving dense soft matter. Specifically, the algorithm that we develop harnesses the discretization of space into boxes and the implementation of interactions only between cells randomly chosen inside a same spatial box, as suggested by standard DSMC. In spite of this powerful procedure, which earns the name of Monte Carlo to the algorithm, the simulations remain expensive in computation time, because of the large number of cancer cells often created in the case of cancer escape. Our aim is to check if the inhomogeneous model contains enough biological ingredients to reproduce the complex antagonistic effects observed in cancer evolution, including the "three Es" (elimination, equilibrium, and escape of cancer from immunosurveillance) [19,26] and spontaneous oscillations in the number of immune system cells observed during tumor growth [21,22] but not included in the homogeneous model [7,8]. In addition, the simulations of an inhomogeneous system reported in the present paper give access to the evolution of the geometry of the tumor, its possible deformation, shifting, and splitting that were clearly not affordable in the framework of a homogeneous description.
The paper is organized as follows. In section 2, we present the inhomogeneous model and the kinetic equations governing the evolution of the probability distributions of cancer, immune system and normal cells. The kinetic Monte Carlo algorithm is made precise. Simulation results for an initially localized tumor are presented in section 3. Specifically, we examine if, for a poorly effective thermalization, the number of cancer cells rapidly drops, then slightly increases during a long quasi-steady regime, and eventually explodes, although the autocatalytic production of immune system cells is much more favored than cancer cell formation. The existence of oscillations for the total number of immune system cells is also discussed. A sensitivity analysis is performed and the different behaviors observed as the field that regulates activity and the rate constant related to the production of immune system cells vary are shown. The variations of the pseudo-period of oscillations with the field and the rate constant are determined. Section 4 contains conclusions.
2.
The inhomogeneous thermostatted kinetic theory model
The competition between immune system cells and cancer cells can be compared to the interactions between immune system cells and viruses. In both cases, the foreign cells induce responses from the immune system [10,11,12]. Different types of cells are involved in the defense mechanism [41,42]. Dentritic cells ingest cancer cells, isolate antigens and present them to T cells, leading to their activation and proliferation [13]. Killer T cells are able to destroy cancer cells and regulatory T cells control the number of lymphocytes and prevent their overproduction [18,43]. In parallel with the learning of the immune system cells, the learning of the cancer cells takes place, which may lead to cancer escape. Through cell interactions, the cancer cells learn not to be detected, misleading the regulatory T cells which in turn limit the production of immune system cells and let cancer cells proliferate [16,17].
Recently, we have introduced a homogeneous model of competition between cancer cells and immune system cells which reproduces cell interactions, activation, and learning processes [7,8] and accounts for the three Es of immunotherapy. We propose to develop a space-velocity description of tumor growth, which requires to model the updating of cell position x and velocity v in addition to their nature j and activity u. As in the homogeneous model, we introduce normal cells n, cancer cells c, and immune system cells i as a whole with the aim of introducing as few variables and parameters as possible and providing qualitative interpretations of clinical observations.
Inhomogeneous initial conditions with tumor cells located in the middle of the system are preferably considered. A Gaussian distribution Pu(u) of mean μ and variance σ is used to generate the initial activities of the cells, regardless of their nature. Possible heterogeneity in initial activity distribution may be considered. All the cells are supposed to have the same speed which remains constant. The direction of cell velocity v is defined by an angle θv∈]0,2π] randomly chosen using a uniform distribution Pv(θv).
2.1. The different processes affecting cell evolution
Cell activity u and nature j=c,i,n, where c stands for cancer, i for immune, and n for normal, may change during local interactions that are assumed to leave position x and velocity v of cancer cells and immune system cells unchanged. We consider only three processes which include interaction, activation, proliferation or death, in a similar manner as autocatalytic chemical processes
where the rate constants κcn(v,u,v′,u′), κic(v,u,v′,u′), and κci(v,u,v′,u′) have the following nontrivial dependence on the activities and the velocities of the interacting couple:
where kcn, kic and kci are constant, θinter∈]0,π] is the maximum angle between the velocity directions permitting interaction and θ(v,v′) is defined as follows:
where θv∈]0,2π] is the angle defining the direction of v. The condition on the directions of the velocities of the interacting pair imposed by the Heaviside function H(θinter−θ(v,v′)) ensures that the two cells remain close during a sufficient time for activation and learning to take place.
The learning process is reproduced by the small increase ε of the activity of the cell with the already larger activity before the interaction. The process described in Eq. (2.1) has the form of an autocatalytic production of cancer cells, the presence of a cancer cell being a pre-requisite for the formation of another cancer cell, as in a chemical process catalysed by a product of the reaction.
Equation (2.1) accounts for both the mutation of a normal cell into a cancer cell and the division of a cancer cell. The specific rate constant expression ensures that proliferation of cancer cells is more favorable when they have already learned to blend into their environment, i.e. have increased their activity u. The reservoir R of normal cells maintains their number constant and plays also the role of reservoir of activity. The notion of reservoir is useful in far-from-equilibrium systems able to self-organize. The formation of complex structures requires that the system is maintained far from equilibrium, which occurs through the consumption of energy or matter. A reservoir is an ideal device which is supposed to be able to maintain the concentration of a given species constant by instantaneously absorbing incoming fluxes or injecting the species to compensate for losses [32]. In the present model, the condition on the activities of the interacting cells imposed by the Heaviside function H(u−u′) introduces a selection. The normal cell which disappears has a smaller activity than the interacting cancer cell, which could induce a non physical increase in the mean activity of the remaining normal cells. The model provides for reinjecting a normal cell with a randomly chosen activity u″ using the initial Gaussian distribution Pu(u) of fixed mean value μ, so that the mean activity of normal cells remains constant, consistent with biology. The velocity v″ of the reinjected normal cell is randomly chosen using the initial uniform distribution Pv(θv).
The process given in Eq. (2.2) corresponds to the autocatalytic production of immune system cells and accounts for both the death of a cancer cell attacked by a killer T cell and the proliferation of immune system cells with increased activity, i.e. the knowledge of the presence of cancer cells in their environment. As in Eq. (2.1), the rate constant depends on a Heaviside step function H(u−u′) implying that the increase of the number of immune cells is locally more probable when they have a larger activity than the neighboring cancer cells.
The regulation of the number of immune cells by T-regulatory cells and the learning process of cancer cells are taken into account in the third process given in Eq. (2.3). This process accounts for both the death of an immune system cell and the division of a cancer cell. The rate constant being proportional to H(u−u′), the proliferation of cancer cells locally occurs if their activity is larger than the one of the surrounding immune system cells. Hence, the model accounts for the ability of trained cancer cells to mislead the immune system and trigger the detrimental response of T-regulatory cells.
In order to introduce a regulation of the explosive cell production due to autocatalytic processes, we impose that the rate of each process is proportional to the difference of activities of the interacting pair. Specifically, according to Eq. (2.3), further growth of a cluster of cancer cells with a smaller activity than the surrounding immune system cells is not likely to be observed. Following Eq. (2.2), an analogous phenomenon is expected for immune system cells: A local increase in the number of immune system cells will not be sustained if their activity is smaller that the one of the neighboring cancer cells. According to Eqs. (2.4) and (2.5), the expression of the rate constants, proportional to the relative activity of the interacting cells introduces a remote analogy to the collision term of the Boltzmann equation, which depends on the relative velocity of the encounters [44].
In order to mimic the preferential increase in the number of cancer cells due to the deleterious response of T-regulatory cells rather than by mutation of normal cells, we assign values of kci in Eq. (2.3) larger than the values of kcn in Eq. (2.1).
The processes given in Eqs. (2.1-2.3) associate learning process with systematic increased cell activity. However, cell interactions that are not explicitly taken into account in the scheme make learning less effective. In the model the regulation of the activity fluctuations is ensured by a thermostat mimicking information loss due to dissipation. Thermalization, characterized by a field E and a friction coefficient α, acts on the activity uk of each cell k according to [1,5]
Choosing
where ⟨u⟩ is the mean activity of the entire system, ensures that the second moment ⟨u2⟩ remains constant.
All cells are supposed to move at constant speed in all directions. We introduce a stochastic turning operator that modifies the direction of cell velocities inside a cone of apex angle θjump with 0<θjump≤π/2. Hence, the rate constant associated with the velocity jumps obeys
where kv is constant.
2.2. The kinetic equations
The distribution function fj for cells of type j=c,i,n obeys the following kinetic equation
where v⋅∇x is the standard advection operator, ∂u((E−αu)fj) is the thermalization operator, Ij is the interaction operator and Vj is the velocity randomization operator. Following Eqs. (2.1-2.3), the interaction operator Ic associated with cancer cells reads
with κcj(v,u,v′,u′) and κic(v,u,v′,u′) given in Eqs. (2.4) and (2.5). The two first terms of the right-hand side account for the positive contributions to the distribution function of cancer cells of velocity v and activity u after the interaction of a cancer cell and a normal cell through the process given in Eq. (2.1). Specifically, the first term corresponds to the formation of a cancer cell with the desired properties from a cancer cell of initial activity u−ε after update by the increment ε. All contributions are obtained by integrating over all acceptable velocities v′ and activities u′ of the interacting normal cell. The second term is obtained when assigning the velocity v and activity u of the disappearing normal cell to a newly formed cancer cell and integrating over all acceptable velocities v′ and activities u′ of the interacting cancer cell. The fourth term is related to the process given in Eq. (2.2) and the fifth to seventh terms are associated with Eq. (2.3). The interaction operator Ii for immune system cells is formed following analogous rules as for cancer cells:
For normal cells, the interaction operator In reads
The second term of the right-hand side is related to the action of the reservoir, which injects a normal cell of velocity v and activity u exactly at the same rate as a normal cell of velocity v″ and activity u″ just disappeared through Eq. (2.1). The contribution to the evolution of fn(t,x,v,u) includes integration over all velocities v″ and weighting by Pv(θv), integration over all activities u″ and weighting by Pu(u), as well as integration over all acceptable velocities v′ and activities u′ of the interacting cancer cell.
Finally, the velocity randomization operator Vj which models the velocity-jump process inside a cone reads
where the rate constant κv(v,v′) of clockwise or anticlockwise jump of velocity direction is given in Eq. (2.9).
2.3. The simulation algorithm
Graeme Bird [39,40] introduced an efficient algorithm, the direct simulation Monte Carlo (DSMC) method, to simulate the Boltzmann equations associated with a dilute gas [45] and successfully adapted to concentrated solutions [46]. The performance of DSMC with respect to molecular dynamics is related to considering collisions only for particles belonging to a same spatial box and following an acceptance-rejection technique to treat the collisions. Our aim is to show that these hypotheses can be satisfactorily extended to cellular dynamics in order to directly solve the three kinetic equations given in Eq. (2.10) for the different cell types j=c,i,n. We propose the following algorithm. During a time step Δt, cell natures, activities, positions and velocities are updated according to the model of interactions, thermalization and velocity jumps described in the previous section. Specifically, for given values of the constants kcn, kic, and kci, the maximum number of interactions between pairs is determined in each spatial box and the corresponding interactions between randomly chosen pairs are actually accepted provided that the conditions on activities and velocities expressed in Eqs. (2.4) and (2.5) are met. The nature and the activity of the interacting cells are then updated. After the interactions in all spatial boxes have been considered, the activity of each cell is thermalized according to Eqs. (2.7). Cell positions are modified according to their velocities, which may result in changing of spatial box. Finally, the directions of cell velocities are updated following the stochastic deflection process of rate constant given in Eq. (2.9).
In the next section we present the simulation results obtained for a two-dimensional inhomogeneous system.
3.
Results
Two-dimensional simulations are performed in a square of side lx=ly=30 divided in boxes of side Δx=Δy=1. Periodic boundary conditions are applied. Initially, 20 normal cells and 20 immune system cells per box are homogeneously spread in the entire system. In order to study the growth of an initially localized tumor, we start from 20 cancer cells per box in a central discretized disc of diameter D=5 and no cancer cells elsewhere. The effects of the rate constant values on the system behavior have been studied in detail in a homogeneous system [7,8] and we have checked that they are not sensitively different in the inhomogeneous case. The absolute values of the rate constants are arbitrary. We choose to present the results obtained in a boosted immune system such that kic>kci. This choice results in the more favorable autocatalytic formation of immune system cells than cancer cells for populations with similar activities. We impose kci>kcn in order to comply with the much more probable division of cancer cells under the pressure exerted by regulatory T cells through Eq. (2.3) than the mutation of normal cells into cancer cells reproduced by Eq. (2.1). We impose kci/kcn=103. We refer to the sensitivity analysis performed in a homogeneous system for a detailed discussion of the effect of the parameters introduced in the model [8]. In order to speed up the simulation, we accept the interaction between two cells without condition on the direction of their velocities, which amounts to choosing θinter=π. The rate constant for velocity deflection kv and the maximum angle of velocity jump θjump are chosen sufficiently large for the randomization of velocity direction to be efficient. We have kv=0.1 and θjump=π/6.
Before performing a sensitivity analysis and showing the different behaviors encountered as essential parameters of the model vary, we focus on two nontrivial behaviors reproducing clinical observations, the three Es of immunotherapy [19] and oscillations of the number of immune system cells [21,22]. The same parameter values are chosen to illustrate the two typical behaviors, except the ratio kic/kci, equal to 20 for the 3Es and 10 for the oscillations.
3.1. The three Es of immunotherapy
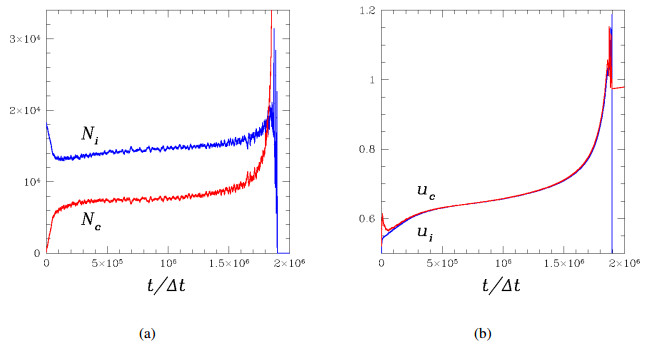
Figure 1 shows the evolution of the total number Nc of cancer cells and the total number Ni of immune system cells in the entire system. Due to the action of the reservoir, the number of normal cells is constant by construction in agreement with biological requirements. In the simulations, the total number of normal cells is set at 18000 in a system of 30×30 spatial boxes. A phenomenon analogous to the three Es (elimination, equilibrium, and escape of cancer) observed in immunotherapy [19] is reproduced by the inhomogeneous model for a critical value of the field E depending on the values of the other parameters. The initial elimination phase observed in a homogeneous system [7,8] is not observed and the number Nc of cancer cells first slightly increases. Then, Nc remains nearly constant during a long pseudo-equilibrium phase. The elimination phase would be recovered for an initial number of cancer cells larger than the value of the plateau reached during the equilibrium phase. Finally, Nc explodes, becomes greater than the number of cells of the immune system, Ni, which in turn fluctuates with a large amplitude. Shortly after a very large fluctuation, Ni cancels out and the cancer escapes from immunosurveillance. In the inhomogeneous system, we rather observe the 2Es, for equilibrium and escape. If one excepts the very beginning of the evolution, the behaviors of the homogeneous and inhomogeneous systems are similar and reproduce a very long induction period before explosion, obtained for sufficiently inefficient thermalization in a small interval of field values.
Cancer cells invade the entire system despite kci<kic: Inefficient control of activity fluctuations severely limits the chances of success of immunotherapy. Following the expression of the rate constant κci given in Eq. (2.4), the local important production of cancer cells is related to the learning of these cells, i.e. to the increase of their activity with respect to the neighboring immune system cells. The learning process implemented in the model consists of a small activity increase through cell interactions and a rate dependence on the relative activity of the interacting pairs. This simple procedure is refined enough to reproduce the complex learning process of cancer cells, which can mislead the immune system and induce a harmful regulatory T cell response that wrongly orders a decrease in the production of immune cells.
The spatial description gives access to the evolution of the clusters of cancer cells and immune system cells. A cluster of cancer cell is defined as a continuous set of spatial boxes with neighboring boxes containing at least 20 cancer cells, having a common side and not only a common corner. The value 20 corresponds to the initial number of cancer cells per box in the small, localized tumor. An analogous definition is used for a cluster of immune system cells. The size of a cluster is given by the number of boxes it contains. We use the Hoshen-Kopelman algorithm to build the clusters [47,48]. Figure 2 gives the evolutions of the averaged number of clusters and the size of the biggest cluster for each cell type for the same conditions as in Figure 1.
During the short transient initial period preceding the pseudo-equilibrium phase, the number of clusters of immune system cells rapidly increases while the size of the biggest cluster decreases from the total system size 30×30 to a small value around 10, revealing the rapid fragmentation of the initial big cluster. During the same period, the number of clusters of cancer cells slightly fluctuates between 1 and 0 and the size of the biggest cluster instantaneously drops from 21 to 0, meaning that the number of cancer cells per box rapidly becomes smaller than 20. During the long pseudo-equilibrium phase, the number of clusters of immune system cells linearly decreases due to two phenomena, the coalescence of growing clusters and the decrease of the number of immune system cells, in agreement with the slight increase of the size of the biggest cluster. During the same phase, the number of clusters and the size of the biggest cluster of cancer cells vanish, as if cancer has been eliminated. Then, the number of clusters of cancer cells exponentially grows implying a global, nonlocal escape of cancer while the number of clusters of immune system cells drops. Eventually, the clusters of cancer cells coalesce and a single cluster invades the entire system while the immune system disappears: Cancer becomes out of control. System size has an impact on the time at which an initially localized tumor invades the entire system but does not affect the qualitative behavior of the system.
3.2. Oscillations of cell numbers and mean activities
The main contribution of the inhomogeneous description is shown in Figure 3. The total numbers Ni of immune system cells and the mean activities, uc, and ui, of both types of cells display pseudo-oscillations of quite well-defined period and increasing amplitude. The total number Nc of cancer cells rapidly becomes much larger than the total number Ni of immune system cells and the chosen scale prevents from showing the end of the evolution of Nc. The extrema of the mean activities uc and ui are associated with typical spatial configurations as shown in the different snapshots of Figures 3-5. A minimum of uc is rapidly followed by a maximum of ui and then a maximum of uc.
As shown in Figure 3, a minimum of uc corresponds to a nearly symmetric disc of cancer cells attacked by a small cluster of immune system cells due to a local favorable fluctuation of ui. Rapidly, the cluster of immune system cells grows and, after a small delay, the mean activity ui reaches a maximum, as displayed in Figure 6. The cluster of immune system cells has an exotic shape which corresponds to a domain of the central tumor in which the number of cancer cells is depleted. According to Figure 5, the symmetry of the entire system is rapidly restored: due to their larger activities in average, the cancer cells deplete the immune system cells in the central part of the tumor, where they are more abundant. As a result, the immune system cells are pushed outwards the disc, forming an external ring. Over a longer period of time, the ring of immune system cells will dissolve, leading to a minimum of Ni, a nearly homogeneous distribution of immune system cells, and a nearly perfect disc of cancer cells. A new local fluctuation of ui will appear and trigger the cycle again.
As exemplified by the Brusselator model [32], a chemical model presenting time oscillations contains the autocatalytic production of one species X to the detriment of another species Y as well as a feedback mechanism which regenerates Y and consumes X. In the model of cancer/immune system interaction, the conditions on the relative activity of an interacting pair of cells given in Eqs. (2.2) and (2.3) introduce such a feedback mechanism. In a small, localized cluster containing a high number of immune system cells with high activity, the autocatalytic production of immune cells by the process given in Eq. (2.2) is first favored. Then, the total number of cancer cells Nc decreases. The effect on the average activity ui is non-trivial, the activity of the already present immune system cell being increased by ε and the newly formed immune system cell inheriting the lower activity of the interacting cancer cell. Simultaneously, the interaction tends to deplete the cancer cell population of its lowest activity elements. As a result, the number of cancer cells decreases but their mean activity ui increases. The autocatalytic production of cancer cells is then promoted by the process given in Eq. (2.3), which in turn tends to decrease the total number of immune cells Ni but increase their average activity ui. The system is again in the situation where the process given in Eq. (2.2) favors the autocatalytic production of immune cells and a new cycle begins. Hence, activity-weighted rate constants for the autocatalytic productions of immune system cells and cancer cells is able to induce an oscillating behavior and reproduce immune regulatory cycles observed in advanced cancer patients and revealed by oscillations of C-Reactive Protein concentration [20,21].
The interaction processes do not only select cells depending on their activity, they also introduce criteria on their velocity direction. Small values of the angle of interaction θinter coupled to inefficient velocity randomization, i.e. small values of both the rate constant kv and the maximum angle of velocity jump θjump, could induce a bias in the results for large values of v/Δt with respect to box size Δx. Specifically, a cluster of autocatalytically formed immune system cells with increased activity would move in a similar direction during a certain time, inducing a persistent anisotropy in cluster shape, which would induce a persistent deformation of tumor shape. Adapted parameter values could be chosen to simulate specific tumor shapes. Conversely, efficient velocity randomization is essential to restore the initial tumor symmetry in the presence of velocity selection during cell interactions. The simulation results shown in Figures 3-5 are given for θinter=π, i.e. in the absence of selection of the angle of the interacting pair, which prevents the formation of clusters with a selected velocity. Cell speed and time step obey v=10−3 and Δt=1, respectively. The choice of kv=0.1 for the rate constant of velocity deflection leads to about 100 velocity jumps before a cell leaves a box, which consists of an efficient velocity randomization. Hence, a randomly occurring cluster of immune system cells surrounded by cancer cells gives rise to the isotropic propagation of a radial front of immune system cells. Then, the cluster depletes from the center. Indeed, the cancer cells in the boxes occupied by the initial cluster of immune system cells which have not been consumed have an increased activity and are thus able to inhibit the immune system cells, leading to the formation of an external ring of immune system cells with radial velocity, similar to the one observed in Figure 4.
The evolution of the averaged number of clusters and size of the biggest cluster are given in Figure 6 for each cell type and for the parameter values of Figures 3-5 leading to oscillations. The number of clusters of cancer cells slightly increases during the entire duration of the simulation, the biggest cluster presenting a first fluctuating growing period followed by a faster increase accompanied by more regular oscillations. The behavior of the size of the biggest cluster is close to the one of the mean number Nc of cancer cells, which shows that the tumor swarms little, remains localized and grows around the initial cluster of cancer cells. The size of the biggest cluster of cancer cells does not exceed 600 boxes and remains smaller than system size equal to 30×30 cells, making explicit that the oscillating behavior shown in Figures 3-5 is not affected by small size effects and boundary conditions. The dependence of the pseudo-period of oscillations on system size is checked in the next subsection.
The first increase of the number of clusters of immune system cells reveals the fragmentation of the big cluster initially occupying the entire system. Then the number of clusters of immune system cells decreases while the size of the biggest cluster remains constant in average, proving that clusters disappear due to immune system cells destruction and not to coalescence. As shown in the snapshot of Figure 4, the maxima of Ni correspond to the periodic appearance of a small cluster containing a large number of immune system cells in the central disc occupied by the large killing population of cancer cells, in which the immune system cells will be soon consumed before a new cycle.
3.3. Sensitivity analysis
Qualitatively different behaviors are observed as some relevant parameters of the model vary. In a homogeneous system, the field E controlling activity fluctuations and one of the rate constants, kic or kci, related to immune system cell or cancer cell production proved to have a significant impact on the phenomena [8]. In the case of an inhomogeneous system, we perform systematic analyses for increasing values of either E or kic with the other parameters set to the values shown in the caption of Figure 1.
Figures 7 and 8 illustrate typical evolutions of the numbers of cells and mean activities, respectively, as the field E varies for kic=0.05, chosen smaller than kci. The same vertical scale is chosen for all subfigures of a given figure. For a sufficiently small value of the field, typically E≲10−5, corresponding to an inefficient control of activity fluctuations, a fast monotonous convergence toward elimination of the immune system and cancer growth is obtained. As E increases, the evolutions of both cell numbers and activities become oscillating, in a chaotic manner for E≃5×10−5 and a more regular way illustrated in Figures 3-5 for E≃10−4. For a critical value of the field, E≃1.4×10−4, associated with a bifurcation, irregular fluctuations appear after a long induction period and the behavior illustrates the 3Es, with the final escape of cancer from immunosurveillance. For a slightly larger value of the field, E≃1.5×10−4, the behavior is completely different and the system monotonically converges toward a steady state in which the activities of the two cell types are equal: Cancer is controlled, exactly as in the case of a sufficiently well thermalized homogeneous system [8]. The choice kic>kci implies that the final steady number of immune system cells is larger than the final steady number of cancer cells.
The results shown in Figures 7 and 8 correspond to simulations stopped at different times such that the immune system cells have disappeared, the number of cells in a spatial box exceeds a threshold set to 3000 as obtained for the critical value E≃1.4×10−4, or when the mean activities of the cancer cells or the immune system cells are equal. The two first cases obtained for E≤1.4×10−4 correspond to cancer escape. The last case observed for E≥1.5×10−4 is associated with cancer control and the simulation time is then supposed to mimic the life expectancy of a patient dying of a disease other than cancer. The characteristic times of the evolution are completely different depending on the field values, in particular because the 3Es are associated with a bifurcation, i.e. a divergence of the induction time before explosion [32]. Sufficiently far from the critical field value, the relaxation toward the stationary state is much faster.
Figure 9 represents the variation of the mean pseudo-period of oscillations of the total number of immune system cells Ni versus E in the field range where they are observed. The uncertainty about their determination is minimum for E≃10−4 associated with the most regular oscillations of both Ni, ui, and uc and increases as the boundaries of the domain of existence get closer. Even for E≃10−4 the time between two maxima of Ni decreases over the evolution, leading to rather large error bars for the pseudo-period. The averaged pseudo-period ⟨T⟩ slightly decreases as E increases. The value of ⟨T⟩ in a system of 30×30 boxes is satisfactorily compared to the result obtained in a system of 20×20 boxes. The difference between the two results is much smaller than the variability of the pseudo-period during time, proving that the simulation results deduced from a 30×30 system or even a 20×20 system are not sensitive to boundary effects and reliable.
The different typical behaviors encountered as the rate constant kic controlling the autocatalytic formation of immune system cells increases are represented in Figures 10 and 11, all other parameters being fixed.
As shown in Figure 11 for sufficiently small values of kic obeying kic≲0.007, the system rapidly and monotonously converges to a steady solution with the same final value uendc=uendi of the mean activities of the two cell types c and i. The final cell numbers obey Nendc>Nendi for kic<kci, they coincide for kic=kci, and obey Nendc<Nendi for kci<kic≲0.007, as shown in Figure 10. The symmetric roles played by the constants kic and kci clearly appear. In all these cases, cancer is controlled. On the contrary, for sufficiently large kic, such that kic≳0.01, cancer escapes from the surveillance of the immune system. The case obtained for kic=0.01, already shown in Figure 1, illustrates the 3Es, with a long induction period and the eventual explosion of cancer cell number and both activities. For kic≃0.05, rather regular oscillations of cell numbers and activities are obtained. Before disappearing for larger values of kic, the oscillations become erratic for kic≃0.25. The value kic=0.01 can be considered as critical, smaller values leading to monotonous cancer control and similar mean activities of both cell types, larger values to oscillating cancer escape and larger mean activity for cancer cells. The results presented in Figures 10 and 11 are nonintuitive since increasing kic, which should reinforce the production of immune system cells, induces the exit from the domain where cancer is controlled. This result is explained by the feedback effect associated with the activity-dependence of the rate constant κic given in Eq. (2.5). At constant field E, increasing kic locally depletes the population of cancer cells from its most active representatives, which induces a local increase of cancer cell activity. This fluctuation of cancer activity is then responsible for cancer cell production through the autocatalytic process given in Eq. (2.3), which explains the eventual explosion of the number of cancer cells and cancer escape from immunosurveillance. In other words, a larger value of kic leads to a larger critical value Ec of the field associated with the 3Es and delimiting the domains between cancer escape and cancer control: As shown in Figures 7 and 8, for kic=0.05 we find Ec≃1.4×10−4 and in Figures 10 and 11, for kic=0.01 the bifurcation arises for a smaller critical field value Ec≃10−4. A stronger stimulation of the immune system requires a more efficient regulation of activity fluctuations for cancer to be controlled.
Figure 12 shows the variation of the mean pseudo-period of oscillations ⟨T⟩ versus the rate constant kic in the range in which they exist. The uncertainty is much smaller than the variation of the averaged pseudo-period and we conclude without ambiguity that ⟨T⟩ increases as kic increases. It was not easy to anticipate such a result, due, once again, to the antagonistic effects included in the model. At first glance, increasing kic should lead to the faster production of immune system cells according to the autocatalytic process given in Eq. (2.2), which should decrease the time between two maxima of Ni or ui. However, as shown in Figures 4 and 5, the formation of a cluster of immune system cells associated with a maximum of mean activity ui is rapidly followed by a maximum for the mean activity uc of the cancer cells, due to the depletion of small activity cancer cells induced by the process given in Eq. (2.2). Then, the very active cancer cells consume the immune system cells according to the autocatalytic process given in Eq. (2.3). As a result, the feedback effect on the activities is stronger than the increase of kic and the time between two maxima of Ni or ui is longer for larger kic.
We end the sensitivity analysis of the system to the field E and the rate constant kic with a few remarks about the effect of the other parameters. As explicitly shown in the case of a homogeneous system [8], the role of kci is symmetrical to the one of kic. The results displayed in Figures 10 and 11 for kic<kci, kic=kci, and kic>kci illustrate this property. A small change of cell speed v modifies the critical values of the field and the constant kic for which the 3Es are observed but does not qualitatively alter the behavior of the system. However, another issue, far beyond the scope of this article, could be addressed in a different domain of parameter space. The model could be extended to the study of the anisotropic growth of a tumor by choosing smaller interaction angles θinter, larger cell speeds v, smaller rate constants kv of velocity randomisation and smaller deflection angles θjump in order to favor the formation of clusters of cancer cells with a high activity moving in the same direction during a sufficiently long time to distort the tumor.
4.
Conclusion
The interactions between cancer and the immune system are complex and nontrivial antagonistic effects have been observed in patients with long-standing tumors and revealed by oscillations of some markers of inflammation [21]. We extend a model of cancer and immune system competition [7,8] to an inhomogeneous system in order to follow the dynamics of tumor growth at cell scale within the framework of thermostatted kinetic theory. The model includes cell-cell interactions mimicking mutation, death, division, regulation, and learning associated with increased activity. Activity fluctuations are thermostatted to account for dissipation of information through nonspecific cell interactions. We implement a kinetic Monte Carlo algorithm to directly simulate the kinetic equations in the spirit of DSMC method [39]. The impact of thermalization on the behavior of the system is important and a bifurcation occurs as the field controlling activity fluctuations increases. For small field values, cancer invades the entire system whereas, for large field values, the system reaches a steady state with non vanishing numbers of cancer cells and immune system cells. Cancer is then controlled and the tumor reaches a stationary size. For a critical value of the field for which large activity fluctuations are eventually generated, the model reproduces the three Es of immunoediting [19], leading to the unexpected escape of cancer from immune system control after the elimination and equilibrium phases. For a field value slightly smaller than the critical value, the model is sufficiently complex to reproduce an observed feature of tumor growth associated with rather regular oscillations of the immune response.
We did not observe time oscillations in simulations of a homogeneous system [7,8]. Their stimulation requires non trivial initial conditions that are spontaneously generated in the simulations of the inhomogeneous system. In particular oscillations may begin when a cluster of immune system cells have a sufficiently higher activity than the neighboring cancer cells. The simulations have been performed for an efficient cell velocity randomization which ensures the rapid recovery of the initial symmetry of the tumor. Following the evolution of the mean number of clusters as well as the size of the biggest cluster reveals that the tumor remains a connected space apart from the loss of very small clusters on its periphery. The model involves two autocatalytic reactions, the one producing cancer cells, the other, immune system cells, with a regulation through activity-dependent rate constants. In the present case, large-activity immune system cells kill low-activity cancer cells, leading to increased activity for the remaining cancer cells. These educated cancer cells are then able to kill low-activity immune system cells. Consequently, the mean activity of the remaining immune system cells increases and a new cycle may begin.
It is worth noting that decreasing the rate constant kic controlling the autocatalytic production of immune system cells has a similar effect on the behavior of the system as increasing the field E. The same succession of bifurcations from cancer proliferation associated with chaotic oscillations, periodic oscillations, long induction related to the 3Es, and cancer control is observed as shown when comparing Figures 7 and 10. Counterintuitively, larger rates of autocatalytic production of immune system cells require more efficient thermalization for cancer to be controlled, due to the feedback effect induced by activity-dependent rate constants.
To our knowledge, the results of the model we developed are the first to account for the 3Es of immunotherapy and oscillations of immune system response within the framework of thermostatted kinetic theory and, in particular, at cell scale. As a perspective, macroscopic equations for concentrations and activities could be derived from the kinetic equations in the limit of appropriate space and time scaling [5,6]. This derivation could give a microscopic interpretation at the scale of cell interactions to mean-field models [23,24,25,26] and to the delays [27,28] introduced in the equations for macroscopic quantities such as the concentrations of different cell types.
The results suggest improved treatment protocols, combining vaccination and chemotherapy at proper times. Reducing the dominance of regulatory T cells over killer T cells may be crucial in immunotherapy: Whereas killer T cells destroy cancer cells, regulatory T cells are susceptible to improperly reduce the number of immune system cells, due to misleading information conveyed by cancer cells. Although the model introduces a single type of immune system cells, it takes into account the role of killer T cells through the process (2.2) and the role of regulatory T cells through the process (2.3). Vaccination can be used to maximize killer T cell response and chemotherapy or radiotherapy, to deplete, inter alia, regulatory T cell population. Hence, the choice of the timing of vaccination, on the one hand, and chemotherapy, on the other hand, with respect to the immune regulatory cycle revealed for example by C-Reactive Protein oscillations, could be crucial in the treatment of some tumors. The model, which reproduces intrinsic oscillations could be used to minimize the averaged number of cancer cells after periodic series of immune system boosting followed by immune system cell depletion at different times of the cycle. The results could give some hints on how a tumor reacts to periodic double disturbances mimicking vaccination and chemotherapy.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:














