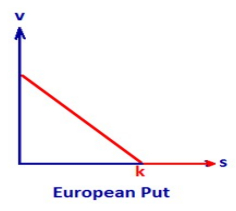
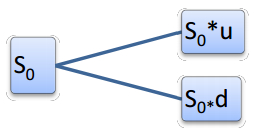
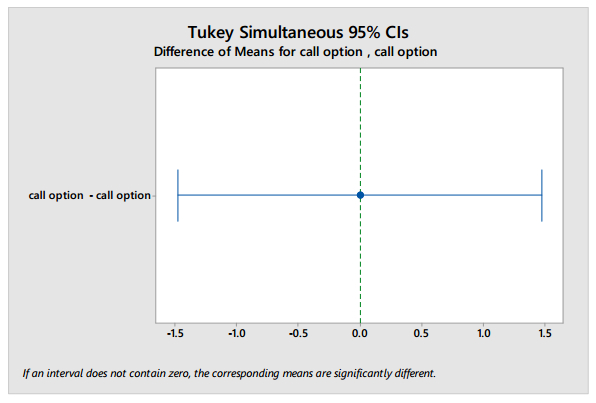
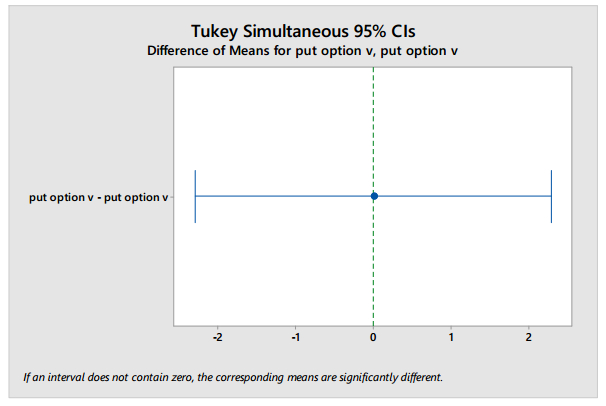
The Binomial Model and the Black Scholes Model are the popular methods that are used to solve the option pricing problems. Binomial Model is a simple statistical method and Black Scholes model requires a solution of a stochastic differential equation. Pricing of European call and a put option is a very difficult method used by actuaries. The main goal of this study is to differentiate the Binominal model and the Black Scholes model by using two statistical model -t-test and Tukey model at one period. Finally, the result showed that there is no significant difference between the means of the European options by using the above two models.
1.
Introduction
The motion dynamics of incompressible isotropic elastodynamics is characterized as a wave system in Lagrangian coordinates, which inherently satisfies the null condition. Based on this structure, a series of studies have been conducted to establish the global well-posedness of classical solutions to this system; see[1,2]. However, these studies reveal a certain time growth for the highest-order generalized energy. In this paper, we investigate the time growth of the Sobolev norm for classical solutions to three-dimensional inhomogeneous incompressible isotropic elastodynamics with small initial perturbation and establish the uniform bound for the highest-order energy.
Before presenting the main result of this paper, we briefly review related known results. For three-dimensional elastic waves, John [3] proved that the genuine nonlinearity condition leads to singularity formation even for arbitrarily small spherically symmetric displacement. We also refer readers to [4] regarding large displacement singularity. The existence of almost global solutions was established in [5,6] for three-dimensional quasilinear wave equations with sufficiently small initial data. Significant contributions toward global existence were independently made by Sideris [7,8] and Agemi [9] under the assumption that nonlinearity satisfies the null condition in three dimensions. In terms of three-dimensional incompressible elastodynamics, the only waves presented in the isotropic systems are shear waves, which are linearly degenerate. The global existence of a solution was demonstrated by Sideris and Thomases in [1,2] through two different methods. It is more challenging to obtain the global existence for the two-dimensional incompressible elastodynamics due to the weaker dispersive decay. In [10], the authors proved almost global existence for a two-dimensional incompressible system in Eulerian coordinates. By introducing the concept of strong null condition and observing that the incompressible elastodynamics automatically satisfies such strong null structure in Lagrangian coordinates, Lei [11] successfully proved the global well-posedness for two-dimensional incompressible elastodynamics by the method of Klainerman and Alinhac's ghost weight method [12]. We also see [13] for a different approach using the spacetime resonance method. All the aforementioned works considered the homogeneous fluids. In [14], the authors established the global well-posedness for the three-dimensional inhomogeneous incompressible elastodynamics in Lagrangian coordinates. It is noteworthy that the upper bound of the highest-order generalized energy in those studies depends on time. Utilizing the Klainerman's generalized energy method, an analysis of the inherent structure of the system and the ghost weight method, [15,16] established the uniform bound for the highest-order generalized energy estimates for two-dimensional and three-dimensional incompressible elastodynamics, respectively. Based on the above foundational works, it is natural to verify the uniform bound for the highest-order generalized energy for three-dimensional inhomogeneous incompressible isotropic elastodynamics. To establish the time growth of the Sobolev norm of classical solution, two novel methods are presented in this paper. First, based on the Sobolev embedding inequality and the structure of the system, the refined decay rates were derived for the solution in the domain away from the light cone. Second, we apply the KSS-type estimate to overcome the difficulties posed by insufficient time decay resulting from density perturbation.
This paper is organized as follows. In Section 2, we introduce the system of three-dimensional inhomogeneous isotropic elastodynamics and define the notations utilized throughout this paper. Besides, the main result along with several useful lemmas are presented in this section. The energy estimates are discussed in Section 3.
2.
Preliminaries
We first formulate the inhomogeneous isotropic elastodynamics and denote some notations that are used frequently in this paper.
2.1. Equations and notations
For any given smooth flow map X(t,x), we call it incompressible if
for any smooth bounded connected domain Ω, which yields that
Denote
Simple calculation shows that the incompressible condition is equivalent to
Without loss of generality, we assume that the density of fluid is a small perturbation around the constant state 1, that is, ρ(x)=1+η(x). For the inhomogeneous isotropic material, the motion of the elastic fluid in the Lagrangian coordinate is determined by
Here W(∇X)∈C∞ is the strain energy function. p(t,x) is a Lagrangian multiplier that is used to force the flow maps to be incompressible. To simplify the presentation, we only study the typical Hookean case for which the strain energy functional is given by
By calculating the variation of (2.2), we obtain the equation
Now, we introduce the following derivative vector fields
The scaling operator is denoted by
Here, the radial derivative is defined by ∂r=xr⋅∇, r=|x|. The angular momentum operators are denoted by
In the application, we usually use the modified rotational operators and scaling operator; that is, for any vector v and scalar p and ρ, we set
where
Let
and for any multi-index α=(α1,α2,⋯,α8)∈N8, we denote
We apply the derivatives Γα to the equations (2.1) and (2.3), and then the three-dimensional inhomogeneous isotropic elastodynamics can be written as
with the incompressible condition
Here the binomial coefficient Cβα is given by
2.2. Main result
We denote the Klainerman's generalized energy by
We also define the weighted energy norm
To describe the space of initial data, we introduce the time-independent analogue of Γ as
and the space of initial data is defined by
As the first step to investigate our problem, we introduce the following lemma, which helps us to solve the additional terms resulting from density perturbation. Let
with μ∈(0,12) and μ′>μ. Without loss of generality, we choose μ=14 and μ′=12 in this paper. In the case of μ′=μ, we see LEκ(T) is the KSS norm, and we denote it by KSSκ(T).
Lemma 1. Let f0=[r/(1+r)]2μ, fk=r/(r+2k) with k≥1, μ∈(0,1/2), and v be the solution to the equation ∂2tv−c2Δv+hab∂a∂bv=N in [0,T]×Rn with hab=hba, ∑0≤a,b≤n|hab|≤min(1,c2)/2 for any integer n≥3. Then there exists a positive constant C0 that depends only on the dimension n such that
where |h|=∑na,b=0|hab| and |∂h|=∑na,b,c=0|∂chab|.
This lemma can be found in [17]. See also [18,19] and references therein.
Based on the previous statement, we are ready to show the main result of this paper.
Theorem 1. Let W(∇X)=12|∇X|2 be an isotropic Hookean strain energy function and (v0,∂tv0)∈HκΛ with κ≥12. Let C0>0 be given constant in Lemma 1. Suppose v0 satisfies the structural constraint condition (2.1) and
If
then there exist two sufficiently small constants, ε0,δ0 and constant C1, that depend only on κ and C0 such that if ε≤ε0 and δ≤δ0, the system (2.3) has a unique global classical solution that satisfies
uniformly for all t∈[0,+∞).
2.3. Calculus inequalities
In this part, we establish several lemmas that are crucial for the energy estimates. Throughout this paper, we denote ⟨⋅⟩=(1+|⋅|2)12. The notation f≲g stands for f≤Cg for some generic constant C>0, which may vary from line to line. In the process of deriving the energy estimates, we usually separate the whole integration domain R3 into two parts:
We first recall the Sobolev-type inequalities, which were justified in [8].
Lemma 2. For any v∈C∞0(R3)3, r=|x| and ˜r=|y|, we have
The following lemma concerns the dispersive decay of solutions in the domain away from the light cone.
Lemma 3. For any v∈H2(R3), there holds
Proof. The proof can be found in Lemma 4.3 in [16]. □
Let s=8r⟨t⟩. We introduce a radial cutoff function ξ(s)∈C∞0 that satisfies
It is easy to observe from Lemmas 2 and 3 that
To control the weighted energy norm by the generalized energy norm, the pressure must be estimated via the system (2.4)-(2.5). A similar proof can be found in [14]. For a self-contained presentation, we include its proof below.
Lemma 4. For any integer κ≥6 and multi-index α satisfying |α|≤κ−2, if E[κ/2]+3(t) and ‖⟨r⟩Λαη‖L2 are small. Then there holds
Proof. It observes from (2.4) that
We apply ∇Δ−1∇⋅ to the above equality and take the L2 norm. By the L2 boundness of the Riesz operator, one has
Special attention is paid to the first term on the right-hand side of (2.8). We apply the derivative operator (∂2t−Δ) to the incompressible condition (2.5). Without loss of generality, we assume at least one order derivative operator of (∂2t−Δ) works on the first component of the velocity field in the second line of (2.5). Then we obtain
Based on the above equality, we handle the first term on the right-hand side of (2.8) as follows
By (2.8), (2.9), the Sobolev embedding inequality, and the smallness of ‖∇η‖L3, we have
By (2.4), the above inequality and the smallness of E[κ/2]+3(t), one obtains
We deduce from Lemma 2 that
It completes the proof. □
As an application of the above result, we establish the estimate of weighted energy.
Lemma 5. Let v∈HκΓ(R3) be the solution to the system (2.3) with the constraint condition (2.1). For any integer κ≥6, if Eκ(t) and ‖⟨r⟩Λαη‖L2 are small, then we have
Proof. For any multi-index α satisfying |α|≤κ−2, we apply Γα to Lemma 3.3 in [11] to get
It follows from the above inequality and Lemma 4 that
By the smallness of δ and Eκ(t), we arrive at the lemma. □
In preparation for the energy estimates, more detailed analysis of pressure is needed. In what follows, we always assume that Eκ(t) and ‖⟨r⟩Λαη‖L2 are small.
Lemma 6. For any integer κ≥8 and multi-index α satisfying |α|≤κ−1, we have
and
Proof. Following the calculations in Lemma 4, we arrive at (2.9). Special attention is paid to the last three terms on the right-hand side of (2.9). From (2.4), one has
We use the above equality and the Sobolev embedding inequality to solve the last three terms on the right-hand side of (2.9) by
Utilizing (2.4), (2.8), the above estimate, and the Sobolev embedding inequality, we arrive at
The smallness of δ and Eκ(t) leads to (2.10).
To verify (2.11), we use (2.12), Lemma 2, and the smallness of Eκ(t) to get
The smallness of δ and Eκ(t) implies (2.11). □
In the subsequent part, we present the improved decay properties for the third-order spatial derivatives of unknown variables in the domain away from the light cone.
Lemma 7. For any integer κ≥10 and multi-index α satisfying |α|≤[κ/2], it holds that
Proof. We apply the derivative operator ∇ to the equation (2.4) to get
By multiplying the above equality by t2ξ(s) and taking the L2 inner product, one has
Since for any f∈H2(R3), the following Sobolev embedding inequality holds true
By Lemma 2, the first term on the right-hand side of (2.13) is estimated by
By a similar argument, we handle the second term on the right-hand side of (2.13) as follows
In view of (2.7), the smallness of δ and Eκ(t), one has
We substitute the above inequality into the third term on the right-hand side of (2.13) to get
We come back to the fourth term on the right-hand side of (2.13). We apply the divergence operator to the equality (2.7) and multiply t2 on both sides of the resulting equality. By taking the L2 inner product, one has
For the first two terms on the right-hand side of (2.17), we deduce from Lemma 3 that
For the third and fourth terms on the right-hand side of (2.17), we have
By the definition of ˜S and the Sobolev embedding inequality, we solve the first term on the right-hand side of (2.18) by
In terms of (2.5) and the definition of ˜S, the last two terms on the right-hand side of (2.18) are estimated by
Along the same line, the last term on the right-hand side of (2.17) is dealt with by
Combining all the estimates, Lemma 4, and the fact
the fourth term on the right-hand side of (2.13) is estimated by
We employ the similar method as (2.15) and (2.16) to estimate the fifth and sixth terms on the right-hand side of (2.13) by
For the last term on the right-hand side of (2.13), we have
Collecting the above estimates and the fact
we complete the proof. □
By Lemma 7, we obtain the following estimate.
Lemma 8. For any integer κ≥12 and multi-index α satisfying |α|≤[κ/2], there holds
Proof. By the definition of ˜S and Lemma 7, we have
The inequalities (2.14), (2.21), and Lemma 7 yield that
To consider (2.20), the definition of ˜S, combined with inequalities (2.14) and (2.21) and Lemmas 3 and 7, implies that
which implies the desired. □
Before concluding this section, we formulate the following two lemmas, which are utilized in the process of deriving energy estimates.
Lemma 9. For any integer κ≥12 and multi-index α satisfying |α|≤[κ/2], we have
Proof. We separate two cases to consider this lemma. For the case x∈R, we use the Sobolev embedding inequality (2.14) to get
For the integer i satisfying 1≤i≤2, one has
We estimate the first term on the right-hand side of (2.22) by
By (2.4), we solve the second term on the right-hand side of (2.22) as follows
For the first term on the right-hand side of (2.23), by Lemmas 3 and 4, we have
Adopting the same method as was used in (2.17), we estimate the second term on the right-hand side of (2.23) by
For the third term on the right-hand side of (2.23), by the definition of ˜S and (2.6), we obtain
The last term on the right-hand side of (2.23) is estimated by
We verify the case x∈Rc. By Lemmas 2 and 6, we have
Collecting all of the estimates together, we justify the lemma. □
Lemma 10. For any integer κ≥12 and multi-index α satisfying |α|≤[κ/2], one has
Proof. We deduce from the definition of ˜S that
By Lemma 2 and (2.6), one has
This completes the proof. □
3.
Energy estimates
This section is devoted to the energy estimates. For any integer κ≥12 and multi-index α∈N8 satisfying |α|≤κ−1, we apply Lemma 1 to the system (2.4)-(2.5) to get
For the second term on the right-hand side of (3.1), by Lemma 2, one has
By utilizing (2.4), we formulate the third term on the right-hand side of (3.1) as follows
We handle term by term on the right-hand side of (3.2). For the first term on the right-hand side of (3.2), since (∇X)−T is composed of elements of the form ∂lvj∂mvk, ∂jvj, ∂ivj and the constant 1, where j,k,l,m=1,2,3, it follows that
For the first term on the right-hand side of (3.3), by (2.6) and Lemma 6, we have
To handle the second and third terms on the right-hand side of (3.3), we apply (2.11) and (2.19) to show
Along the same line, the last term on the right-hand side of (3.3) is estimated by
For the second term on the right-hand side of (3.2), by the definition of ˜S and (2.6), one has
It is left to estimate the last term on the right-hand side of (3.2). Two cases are considered. By Lemmas 2, 4, and (2.6), we solve the case |\gamma| < |\beta| < |\alpha| by
Utilizing Lemmas 9 and 10, we solve the case |\beta|\leq|\gamma| by
By summing up the above estimates, we deduce that
We continue to handle the last term on the right-hand side of (3.1). The identity (2.4) yields that
We use Lemmas 9 and 10 to handle the first two terms on the right-hand side of (3.4) by
We rewrite the last term on the right-hand side of (3.4) as follows
For the first two terms on the right-hand side of (3.5), the Lemma 6 and (2.19) imply that
We use (2.7) to formulate the last term on the right-hand side of (3.5) by
By (2.19) and Lemma 6, we estimate the first term on the right-hand side of (3.6) by
The second and third terms on the right-hand side of (3.6) can be solved using the same method employed by the first two terms of (3.4).
For the last term on the right-hand side of (3.6), we observe that
In view of (2.5), we write the first term on the right-hand side of (3.8) by
The first two terms on the right-hand side of (3.9) are dealt with by the same method as (3.7). By (2.6), the third and fourth terms on the right-hand side of (3.9) are estimated by
To consider the fifth term on the right-hand side of (3.9), we separate two cases to consider it. For the case x\in \mathcal{R} , by (2.20), we have
To consider the case x\in \mathcal{R}^c , we use the integration by parts to get
For the first term on the right-hand side of (3.10), we have
We use (2.5) to estimate the second term on the right-hand side of (3.10) by
For the last term on the right-hand side of (3.9), it follows from the Sobolev embedding inequality, (2.6), and (2.19), that
To solve the second term on the right-hand side of (3.8), we rewrite it as follows
In view of (2.5), we formulate the first term on the right-hand side of (3.11) by
Since the second term has analogous estimates to the first term of (3.12), it suffices to concentrate on the first term. We observe that
Here, we restrict our analysis to the first term on the right-hand side of (3.13), as the remaining two terms have similar estimates.
For the first term on the right-hand side of (3.14), we deduce from (2.4) that
We formulate the first term on the right-hand side of (3.15) as follows
The first three terms on the right-hand side of (3.16) can be estimated by
We utilize (2.19) to solve the last two terms on the right-hand side of (3.16) by
Along the same line, the second term on the right-hand side of (3.15) can be handled by
The same estimates hold for the last two terms on the right-hand side of (3.14).
Applying (2.4), we formulate the second term on the right-hand side of (3.11) as follows
The first term on the right-hand side of (3.17) is solved by
The calculations in (2.12) imply that
Substituting (3.18) into the second term on the right-hand side of (3.17), we have
For the third term on the right-hand side of (3.17), we have
We use (2.4) to formulate the first term on the right-hand side of (3.20) as follows
For the first term on the right-hand side of (3.21), we have
The second term on the right-hand side of (3.21) can be solved as (3.19). We employ the analogous method utilized for the first two terms on the right-hand side of (3.4) to solve the last two terms on the right-hand side of (3.21).
For the second term on the right-hand side of (3.20), we have
For the last term on the right-hand side of (3.17), by Lemmas 2 and 6, we have
Combining all the estimates, we conclude that
where C > 0 is some positive constant. By the smallness of \delta , \mathcal{E}_\kappa(t) , and the standard continuity method, we arrive at the main result.
Author contributions
All authors contributed equally.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work of the first author was partially supported by the National Natural Science Foundation of China under Grants 12401278. The work of the second author was partially supported by the RFS grant and GRF grants from the Research Grants Council (Project Nos. PolyU 11302021, 11310822, and 11302523). The authors would like to thank the research center for nonlinear analysis at PolyU for the opportunity of discussions and encouragement.
Conflict of interest
The authors declare there is no conflict of interest.














 DownLoad:
DownLoad: