Figure 1.
Hedging strategy with cap on growth.
Citation: Manuel Padeira Navarro, Margarida Catalão-Lopes. A structured financial product applied to renewable energies[J]. Green Finance, 2019, 1(1): 82-93. doi: 10.3934/GF.2019.1.82
| [1] | Alexander Ryota Keeley, Shunsuke Managi . The importance of financial cost for renewable energy projects: economic viability assessment of renewable hybrid mini-grid systems in Indonesia. Green Finance, 2019, 1(2): 139-155. doi: 10.3934/GF.2019.2.139 |
| [2] | Laura Grumann, Mara Madaleno, Elisabete Vieira . The green finance dilemma: No impact without risk – a multiple case study on renewable energy investments. Green Finance, 2024, 6(3): 457-483. doi: 10.3934/GF.2024018 |
| [3] | Yoram Krozer . Financing of the global shift to renewable energy and energy efficiency. Green Finance, 2019, 1(3): 264-278. doi: 10.3934/GF.2019.3.264 |
| [4] | Clement Allan Tisdell . Renewable energy use and the renewable energy sector’s development: public finance, environmental externalities and sustainability. Green Finance, 2019, 1(2): 156-173. doi: 10.3934/GF.2019.2.156 |
| [5] | Samuel Asante Gyamerah, Bright Emmanuel Owusu, Ellis Kofi Akwaa-Sekyi . Modelling the mean and volatility spillover between green bond market and renewable energy stock market. Green Finance, 2022, 4(3): 310-328. doi: 10.3934/GF.2022015 |
| [6] | Gireesh Shrimali . Do clean energy (equity) investments add value to a portfolio?. Green Finance, 2019, 1(2): 188-204. doi: 10.3934/GF.2019.2.188 |
| [7] | Reinhard Haas, Amela Ajanovic, Jasmine Ramsebner, Theresia Perger, Jaroslav Knápek, Jan W. Bleyl . Financing the future infrastructure of sustainable energy systems. Green Finance, 2021, 3(1): 90-118. doi: 10.3934/GF.2021006 |
| [8] | Mihaela Onofrei, Bogdan Narcis Fîrțescu, Florin Oprea, Dana Claudia Cojocaru . The effects of environmental patents on renewable energy consumption. Green Finance, 2024, 6(4): 630-648. doi: 10.3934/GF.2024024 |
| [9] | Cristina Ballester, Dolores Furió . Analysing the impact of renewables on Iberian wholesale electricity market prices using machine learning techniques. Green Finance, 2024, 6(2): 363-382. doi: 10.3934/GF.2024014 |
| [10] | Ali Omidkar, Razieh Es'haghian, Hua Song . Developing a machine learning model for fast economic optimization of solar power plants using the hybrid method of firefly and genetic algorithms, case study: optimizing solar thermal collector in Calgary, Alberta. Green Finance, 2024, 6(4): 698-727. doi: 10.3934/GF.2024027 |
One of the core tasks of investment banking is the constant search for opportunities to create new financial instruments. Typically, this task is fulfilled by innovatively combining already existing components to form new financial instruments. In this way it is possible to cater to the special needs of individual groups of customers. This process is called "financial engineering", as investment bankers act similarly to engineers or natural scientists when planning and creating complex financial innovations (Célérier and Vallée, 2015).
The aim of this paper is to provide an innovative framework for the Portuguese context of renewable energy investment. We propose the creation of a structured product adapted to the renewable energy sector, a task that became a possibility only after the restructuring of the Portuguese electricity market, when it moved away from the traditional regulated principles to those of the free market that obey the rules of supply and demand. According to Castro (2012) the beginning of the market liberalization process dates back to 1995. However, it is only in 2007 that the market takes the shape known today. Under this new regime all agents involved trade electricity at a power exchange, with a monetary value defined by the point where supply meets demand.
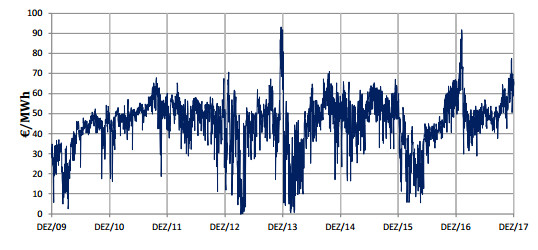
The initial idea was to provide a structured financial product that was able to derive its value (for the variable component) directly from the renewable energy being injected in the grid. However, failing to do so due to the fact that there is still no legal framework that contemplates the ability of separating energy sources as seen in EEX (2017), we have decided to address this component by looking at the electricity spot market as a whole. We assumed this to be a reasonable assumption given that all technologies operate in the same market and renewable sources are dispatched with priority. Consequently, the price is always defined by the marginal cost of production, which makes the spot price (as it is) a reasonable indicator of "how much" is being injected from renewable sources. We use data provided by OMIP (the Portuguese acronym for Operator of the Iberian Energy Market), the organization responsible for gathering both supply and demand data and for setting the spot price for the day ahead market.
Note that these investment products can be seen as the combination of two or more financial instruments being one of them, at the very least, a derivative—as it derives its value from an underlying asset or a combination of assets. Such derivatives written on this commodity are already traded in foreign markets as, for instance, the Nord Pool. Hence, integrating this concept with the knowledge that structured products tend to increase demand when traditional products are offered with low interest rates may prove to be interesting for our purpose.
Ambiguous opinions arose since the creation of structured products, due to their complexity, especially if one bears in mind that financial engineering was on the basis of the recent financial crisis spread worldwide (e.g., Buffett, 2003). Hence the importance of maintaining this research at a socially responsible level, particularly if one considers electricity to be a financial asset that cannot be addressed as traditional instruments are, in the sense that any financial irresponsibility could pose a threat to a whole sector and its consumers. Based on this premise we consider that in the wake of deregulation of power markets "a proper representation of the dynamics of spot prices becomes a necessary tool for trading purposes" (Geman and Roncoroni, 2006).
In this paper we establish a framework that combines both the Black-Scholes-Merton formula, as in Geman (2005), and Monte Carlo simulations for up to 10.000 outcomes. This way we are able to deal with one of the major problems that active trading companies face when attempting to choose a model that reaches for simplicity while capturing the most important moments of the markets in "real life" as posed by Hafner (2003).
Correctly representing the dynamics of spot prices in electricity markets is a key element for trading purposes. As a new contribution applied to the Portuguese market, which had not yet been addressed in this context, we develop a model of our own, based on several authors such as Escribano et al. (2002), Geman and Roncoroni (2006), and Benth et al. (2007). The work by Benth et al. (2012) proved to be extremely useful when carrying out the analysis on the different possible models and deciding for which to apply to our market.
The rest of the paper is organized as follows. First, we address the creation of a structured financial product while pinpointing the main features and providing the framework to create one. Then, in section 3, we detail our derivative component focusing on the underlying asset, since we know from the literature that a proper representation is essential to produce adequate results. Electricity spot prices modeling in the Portuguese context is addressed in the fourth section. Presentation of results and discussion is provided in section 5. Finally, section 6 presents the conclusions and comments on the viability of this research for practical purposes.
Typically, a structured product consists of two main components that can be distinguished: A part that establishes a capital guarantee or minimum profitability, and a part that works with the variable payment. The first component can be seen as "insurance" on the money being invested, depending on the client's risk profile, or as a means to minimize eventual losses with the variable part. It can guarantee the investor's full or partially recover of the initial capital being invested. This can be achieved by applying a part of the initial capital in a fixed rent asset (as treasury bonds) that at maturity will recover the pre- established amount. The second component usually relies on the use of an option portfolio whose return is indexed to the performance of any financial market (see the Portuguese financial market in OMIP, 2017). These structured products combine the lower risk feature of the bond markets with the variable return component that is enhanced in periods of high volatility of the underlying financial asset. The variable component is responsible for the requirement of a proper valuation model in order to adequately valuate the whole structured product. We first argue the main features to include when creating a structured product, presenting a simple version that comes from combining a working contract (from a very well-known Portuguese bank, Banco BPI) with an example provided in Nunes (2015). The reasoning is that for hedging purposes the product is decomposed in:
| GC=C⋅[1−[1(1+r)T]]r+F V(1+r)T | (1) |
where
● CG: Guaranteed Capital
● C: Coupon payment
● r: Interest rate
● T: Time to maturity
● FV: Face value
And
| VRT=max(0%;ST−S0S0)×X%=X%S0max(0;ST−S0) | (2) |
where the variable return VRT to be paid at maturity is given by the percentage X% of the growth of an index, if any, i.e., max(0%;ST−S0S0). Note that max(0 ;ST−S0) is the terminal payoff of a call option with maturity at time T, which means that for an investor to consider this, X% has to be such that the guaranteed capital added to the variable return's present value is equal to at least 100% of the issue price.
It is important to note that the structure being issued depends on the perception regarding the future of any given underlying asset. There are innumerous strategies for the replicating portfolio to be used, namely barrier options. Despite this, we have addressed this issue under the simplest scenario where the financial instrument is a European Call that depends on the performance of a hypothetical index that tracks the percentage of renewable energy being injected on the grid. Since we wish to promote new investment in new installed capacity and consequently an increase in injected power from these sources, we believe that our choice is adequate.
We illustrate this with the following structured product: bonds with guaranteed capital recovery and coupon rate of 1% with variable return annually distributed and indexed to the performance of an hypothetical index that accurately tracks the amount of electricity being injected on the grid from renewable sources, i.e., the variable return to be paid at maturity (T = 3 years) is given by a percentage of the growth rate (if any) of the index. They have a face value of €1,000 and the interest rate is equal to the latest known treasury bonds issued by the government, i.e., 1.939%.
Under this scenario we investigate what would X% be equal to, such that the fair value of the product would be 100% of the issue price, yielding:
GC0 = 97.289%
VR0 = 2.711%
X% = 11.856%
given that max(0 ;S3−S0)=c0(S0;k=S0;T=3) is the present value of an ATM call option with maturity in three years, the replicating portfolio is given by:
(1) A deposit today worth €972.89
(2) 3.95 European ATM Call options, given by:
| #Calls=FV×VR0c0(S0;k=S0;T=3) | (3) |
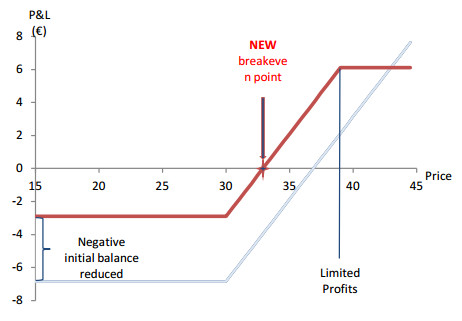
We then proceed with an evaluation of the performance of such product under different scenarios. We realize the need to create a strategy to reduce potential losses in premiums in the option market. This strategy is presented in a structured product by means of introducing a cap on growth, such that the replicating option strategy is as depicted in Figure 1.
Such strategy is known as a Bull Vertical Spread and the losses are reduced (from the negative initial balance) by selling an OTM contract and consequently collecting on that credit. Although the net position is still negative initially, the breakeven point is much smaller at the cost of reducing potential gains.
The example we give, although very simple, is an adequate starting point to provide a framework to design the financial structured product we initially proposed, once policy makers enable us to separate the electricity market by sources. Being currently unable to do so, has forced us to address the task of pricing the derivative component of the contract while addressing the market as a whole. However, if we think in terms of electricity prices and injection of renewable power one can understand that they follow the same path in an inversely proportional manner. Hence, we believe that a correct model for electricity spot price can be a good first step towards modeling the renewable injection market.
To address this issue, we have decided to cross examine two widely used models for pricing derivatives: The Black-Scholes-Merton formula and the Monte Carlo process (for 10.000 simulations). Despite the fact that the first one relies on unrealistic assumptions, it has proved to be the chosen method to price options due to the fact that the users do not need to develop much elaborate mathematical models in order to produce accurate results as it only depends on the adequate choice of the inputs to use. Yet another reason for us to decide to investigate this model resides in the fact that under the framework provided in Geman (2005) the Merton extension could be used to price options on commodity spot prices as long as we consider its behavior as that of a stock paying continuous dividend equal to the convenience yield. However, since this concept is directly related with the ability to maintain a storage level we should question its applicability in electricity markets as (apart from hydroelectricity) no efficient form of electricity is known to be storable. We also question its use due to the fact that the main underlying assumption of the model is that the underlying asset price follows a geometric Brownian motion
| dStSt=(r−g)dt+σWQt | (4) |
where WtQ is a Q-measured standard Brownian motion. However, this measure does not account for the occurrence of jump events which, as we prove with the Monte Carlo model, are very important to address when pricing electricity derivatives. In fact it is argued that this later framework can accommodate more realistic stochastic processes, as is the case of the one we present. However, we have decided to preserve both the models, as our main purpose is to rather present all the tools for a potential investor to understand the market.
It is clear that Monte Carlo provides an estimate for the value of some function by simulating a sufficiently large number of times the path of its underlying independent variable. Given the time step and the number of simulations, by running the objective function it will provide n paths that will have their own value.
As is widely known, correctly representing the dynamics of spot prices in electricity markets is a key element for trading purposes.
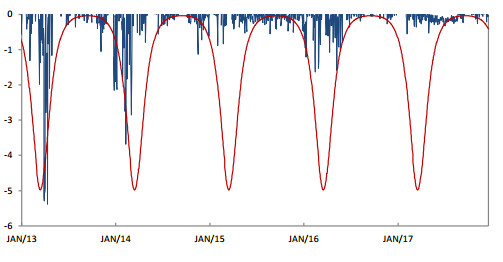
Among innumerous authors that have been working on electricity modeling, some stand out (Benth et al., 2007; Geman and Roncoroni, 2006; Escribano et al., 2002). As they suggest, to correctly model the market implies to properly capture the main features that characterize this utility and path, as depicted in Figure 2.
Regarding these features, we can first point out the mean reverting trend that most markets exhibit. This means that there exists a mean (probably deterministic) level to which prices fall after an extreme event, and this level can be described by the average marginal cost of production as Burger et al. (2006), Geman and Roncoroni (2006) propose.
The second property (and dependent on the first) that needs to be well captured is the occurrence of small random movements of the price process around the trend which come as a consequence of temporary supply/demand imbalances, as Geman and Roncoroni (2006) suggest.
Lastly (but not less important) there is a feature that is intimately related to the (lack of) capacity of generating inventories when referring to electricity production and also to the inelastic nature of demand for this commodity, i.e., the so called price spikes (up and downward directed).
To correctly accomplish the task of spot price modeling, we will use the logarithmic scale of the price in order to guarantee the strict positiveness of those prices, enhancing the robustness of the calibration procedure as originally suggested by Cartea and Figueroa (2005). As already mentioned, we use data provided by OMIP (the Portuguese acronym for Operator of the Iberian Energy Market), the organization responsible for gathering both supply and demand data and for setting the spot price for the day ahead market.
Under that reasoning combined with the initial proposal by Lucia & Schwartz (2000), the model we employ is described as follows:
| ln(St)=μ(t)+X(t) | (5) |
where St represents the spot price and μ(t) the trend it follows and to which the process mean reverts. The last term X(t) is the stochastic process responsible for modeling the random fluctuations. To capture such pattern we adapt the method used in Geman & Roncoroni (2006) without any harm to the model itself. The equation reads as:
| μ(t)=θ1+θ2t+θ3cos(θ4+2πt)+θ5cos(θ6+4πt) | (6) |
The first variable in the function can be seen as the fixed cost associated to power production, while the second term is responsible for the growth rate of the total production cost. The remaining components will attribute the required periodicity to the function translating into two maxima per year that can be interpreted as extreme seasons, i.e. summer and winter. These parameters can be determined by fitting the trend line to empirical observations as in (e.g., ) a least squares method.
For the stochastic process we decided to employ:
| dXt=(α−κXt)dt+σdWt+J(μj,σj)d∏(λ) | (7) |
where (α-κ) is responsible for bringing prices back to normal, with (α) accounting for the risk-neutral assumption as in Lucia & Schwartz (2000). The jump size, as in Cartea & Figueroa (2005) and Villaplana, is modeled through a normal distribution with mean μj and standard deviation σj. Finally, ∏(λ) accounts for the arrival of the extreme events, that is, it is a Poisson process with a time-dependent constant rate of arrival (λ), i.e., jump intensity. However, we felt that we could introduce a minor change here in a similar way as in Geman and Roncoroni (2006) and transform it into an inhomogenous Poisson process. The arrival of these events can be deterministic and modeled as:
| s(t)=[(21+|cos[π(t−τ)k]|)−1]d | (8) |
This model takes into account that peaking levels are spread by k multiple years beginning at time τ. The exponent d is responsible for the events spread in time. We have decided to set the parameters to capture the spike clustering moments with one annual peak (k = 1) in March-April (τ = 0.722) The process can be seen in Figure 3.
Once the model is built, we start by computing the seasonality function which is then removed from the process in order to compute the stochastic component. A discretization process is employed as in Villaplana (2003) in order to facilitate the task of discovering the parameters. This is accomplished by minimizing the negative likelihood function applied to the density function that drives Xt conditional to Xt-1 in order to withdraw the parameter vector that we want to calibrate:
| v={α,∅,μj,σ2,σ2j,θ} | (1) |
from
| f(Xt | Xt−1)=(θstΔt)N1(Xt | Xt−1)+(1−(θstΔt))N2(Xt | Xt−1) | (10) |
| (N1(Xt | Xt−1)=(2π(σ2+σ2j))−12exp[−(Xt−αΔt−∅Xt−1−μj)22(σ2+σ2j)] | (12) |
| N2(Xt | Xt−1)=(2π(σ2))−12exp[−(Xt−αΔt−∅Xt−1)22σ2] | (13) |
Following the implementation of the processes described for the Portuguese electricity market (from 01/01/2013 to 17/12/2017) we argue on the quality of such representation (Table 1).
| R2=0.23 p-value ≪ 0.05 |
||
| Parameter | Interpretation | Estimate |
| θ1 | Average (log) fixed cost/price level | 3.5165 |
| θ2 | Average (log) cost slope | 0.0798 |
| θ3 | Yearly trend | 0.3177 |
| θ4 | Trend displacement | 1.6581 |
| θ5 | 6-month trend | 0.1855 |
| θ6 | Trend displacement | 0.3700 |
DownLoad:
CSV
The low figure obtained for R2 might induce us into thinking that a seasonality with such a low correlation with empirical data cannot be used to explain the process. However, the model obtains a p-value way below the rejection point, which means that there is a high degree of confidence in adding this model to our simulation as from the predictor's perspective its changes are related to changes in actual data. This means that the stochastic component will carry great weight to statistical significance around this trend.
Since this model was created to account for positive jumps only, as Geman & Roncoroni (2006) suggest, it seems only logical that adapting it to capture downward movements is possible but probably at the expense of some misguiding results. Usually mean reverting effects take place during times of price pressure in the electric system, that naturally tries to bring them back to normal. When the same "treatment" is applied to downward jumps it may become an unrealistic assumption, as it does not account for the weather factor that determines the mean reversion force. Despite that, and despite the fact that the reverting forces are very high, the results we obtained are very satisfactory from the statistical perspective (Table 3). Due to the statistical quality of the data obtained, one may think that among the simulations performed there can be some that better fit the path followed by empirical data and, consequently, we are able to suggest that perhaps strong reverting forces can be used to explain how weather variables also tend to mean revert.
| Parameters | Interpretation | Estimate |
| α | Mean reverting speed parameters | 4.3468 |
| κ | 287.3376 | |
| σ | Volatility | 4.8003 |
| θ | Number of spikes per unit time1 | −1 |
| μj | Jump size mean | 0.6689 |
| σj | Jump size deviation | 0.05 |
DownLoad:
CSV
1 We have modeled the number of spikes as a random number (0, 1) wi parameter from the original formula stands as the direction of the event.
| Empirical | Simulated | |
| Average | 0.000331 | 0.000375 |
| Standard Deviation | 0.379371 | 0.254794 |
| Skewness | −0.34398 | −1.98287 |
| Kurtosis | 42.8778 | 42.78973 |
DownLoad:
CSV
For obvious reasons we will not go deeper on how important the first two statistical moments are, especially because the other two are the ones we find more relevant financially speaking, i.e., starting with the skewness one can observe that both empirical and simulated data are negatively skewed which means that they both have their "tails" pointing left (Table 3). The implications of this from the financial perspective are that returns below (to the left of) the average occur less frequently but have higher magnitudes, meaning that there can be major negative price returns movements, which can be rather interesting when considering short positions. On the other hand kurtosis is also an important indicator, and one we were able to perfectly match, in the sense that it reveals the degree to which exceptional values occur. In our case a high kurtosis reveals that these extreme events can be very frequent and this information not only can be useful in finance, but also in decision making for electricity markets' designing.
At this stage, failing to derive the risk premium from the market due to difficulties in accessing data required for such, we were forced to conduct our option pricing analysis under the real world probability measure. Under this analysis what stands out the most is the difference between the prices obtained for both models (Tables 4 and 5). That is mostly due to the fact that the BSM relies on certain assumptions that are inadequate for our market, particularly the inability to account for the occurrence of jumps. On the other hand, the Monte Carlo pricing method is extremely biased by the absence of the risk neutral measure, since the pricing measure is directly obtained from the real probabilities given by the simulations performed.
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 15.59 | 0.00 | 1.56 | 1.42 | 0.00 | 14.32 |
| T=6 | 15.70 | 0.00 | 2.64 | 2.30 | 0.08 | 14.11 |
| T=12 | 15.92 | 0.02 | 3.88 | 3.20 | 0.50 | 14.04 |
DownLoad:
CSV
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 3.55 | 1.19 | 0.10 | 13.20 | 0.00 | 27.55 |
| T=6 | 22.11 | 0.00 | 8.14 | 1.39 | 1.70 | 9.32 |
| T=12 | 26.45 | 0.00 | 12.00 | 0.76 | 3.57 | 6.56 |
DownLoad:
CSV
In Portugal, the liberalization of a regulated energy market came as an opportunity for outside investors to take part in the sector. As the former monopoly status of the electric sector did not prove to contribute to its efficient operation, the deregulation of the market had to take place. Removing control over the prices and leaving it subject to market competition provided benefits for consumers and private entities. However, there is still a lack of financial assets/instruments that allow any investor to take part in this still apparently monopolized (by some) industry. As a consequence, those instruments are still scarce and exclusive to a minor fraction of the population.
This paper presented the framework required to financially engineer a product that allows any investor to become active. We focused on a socially responsible structured product that would protect companies issuing those products, companies willing to abandon traditional feed in tariffs by tax reduction and also, and most importantly, protect the small investors. Policy makers become major players in promoting the creation of new investment vehicles, while bearing in mind that constant monitoring is important to ensure that neither the financial market and electricity market, nor retail investors and consumers can be harmed for introducing such strategy. Our paper has shown that there is in fact a market from which everyone can benefit, but its success is subject to transparency and openness.
Although policy making concerning Renewable Energy has a great influence in Portugal, it cannot be considered the essential driver, or at least not alone. Policy making is required no longer to subsidize but rather to allow and promote new environmentally and socially responsible solutions that target the increase in installed capacity in renewable sources, whilst avoiding harmful economic practices. The liberalization of a regulated energy market came as an opportunity for such. By reducing taxes on financial products, such as the one we propose that help address the issue of gathering new renewable energy investment, could be the first and most immediate solution towards sustainability, in the sense that it could encourage retail investors to invest a part of their income on renewable energy and consequently increase production. The market could benefit from it, especially if we consider major European players that are struggling to find solutions to replace nuclear power stations (such as Germany, that aims to shut down 17 nuclear power stations by 2022) and other conventional technologies.
Financial institutions should also be encouraged to create these products through tax benefits. Profits derived from them (commissions, etc.) should be taxed differently. However, those products should at all times be kept transparent and open to constant monitoring from public entities. To ease this task, banks could use credits granted to producers to directly issue the financial product, hence enabling keeping track of the process and directly connecting retail investors to the renewable sector.
In order to obtain further conclusions regarding the potential attractiveness of the proposed product, we suggest a survey directed to potential clients, in order to understand what the retail market would expect from such a product. We also find it important that the current research on the choice of the model to represent the spot price is extended once it is possible to separate electricity production by source. Note that this analysis should be conducted with full access to market data, and hence we recommend that such information is obtained in advance, in order to correctly calibrate the risk measure, promote market transparency and liquidity.
The authors declare no conflict of interest.
| [1] | Banco BPI (2019) Particulares. Available from: http://www.bancobpi.pt/particulares/poupar-investir/produtos-estruturados. |
| [2] | Benth Fred E, Kallsen Jan, Meyer-Brandis Thilo (2007) A Non-Gaussian Ornstein-Uhlenbeck process for electricity spot price modeling and derivatives pricing. Appl Math Finance 14: 153–169. |
| [3] | Benth Fred E, Rüdiger Kiesel, Anna Nazarova (2012) A critical empirical study of three electricity spot price models. Energy Econ 34: 1589–1616. |
| [4] | Buffett, Warren E (2003) Berkshire Hathaway INC. Annual Report. |
| [5] | Burger Markus, Bernhard Klar, Alfred Müller, et al. (2006) A spot market model for pricing derivatives in electricity markets. J Quant Finance 4: 109–122. |
| [6] | Cartea Álvaro, Marcelo G Figueroa (2005) Pricing in electricity markets: A mean reverting jump diffusion model with seasonality. Appl Math Finance 12: 313–335. |
| [7] | Castro Rui (2012) Uma introdução às Energias Renováveis: Eólica, Fotovoltaica e Mini-hidrica. IST Press. |
| [8] | Célérier Claire, Boris Vallée (2015) Catering to investors through product complexity. ESRB Working Paper Series 14. |
| [9] | EEX (2017) Wind Power Futures. Available from: https://www.eex.com/en/products/energiewende-products/wind-power-futures. |
| [10] | Escribano Alvaro, Juan I Peña, Pablo Villaplana (2002) Modeling electricity prices: International evidence. Econ Series 8: 2–27. |
| [11] | Escribano Alvaro, Juan I Peña, Pablo Villaplana (2002) Modeling electricity prices: International evidence. Econ Series 8: 2–27. |
| [12] | Geman Hélyette (2005) Commodities and Commodity Derivatives-Modeling and Pricing for Agriculturals, Metals and Energy. John Wiley & Sons, Ltd. |
| [13] | Geman Hélyette, Andrea Roncoroni (2006) Understanding the fine structure of electricity prices. J Bus 79 (The University of Chicago Press): 1225–1261. |
| [14] | Hafner CM (2003) Simple approximations for option pricing under mean reversion and stochastic volatility. Comput Stat 18: 339–353. |
| [15] | Lucia Julio J, Schwartz Eduardo S (2000) Electricity prices and power derivatives: Evidence from the Nordic Power Exchange. Rev Deriv Res 5: 5–50 |
| [16] | Nunes João PV (2017) Lecture Notes. Appl Deriv, Nova SBE, April 2015. |
| [17] | OMIP (2017) Derivatives Market-Products. OMIP (The Iberian Energy Derivatives Exchange). Available from: http://www.omip.pt/MarketInfo/Produtos/tabid/76/language/en-GB/Default.aspx. |
| [18] | Pinto, Ana Sofia Nunes Alves (2013) Os produtos Estruturados Colocados no Mercado Português: Evolução das Características e da Complexidade. Faculdade de Economia da Universidade do Porto. |
| [19] | Villaplana Pablo (2003) Pricing power derivatives: A two-factor Jump-Diffusion approach. Bus Econ Series 5: 3–18. |
| 1. | Lei Fan, Yunyun Zhang, Meilin Jin, Qiang Ma, Jing Zhao, Does New Digital Infrastructure Promote the Transformation of the Energy Structure? The Perspective of China’s Energy Industry Chain, 2022, 15, 1996-1073, 8784, 10.3390/en15238784 |
Figures(3) / Tables(5)
Manuel Padeira Navarro, Margarida Catalão-Lopes. A structured financial product applied to renewable energies[J]. Green Finance, 2019, 1(1): 82-93. doi: 10.3934/GF.2019.1.82
| R2=0.23 p-value ≪ 0.05 |
||
| Parameter | Interpretation | Estimate |
| θ1 | Average (log) fixed cost/price level | 3.5165 |
| θ2 | Average (log) cost slope | 0.0798 |
| θ3 | Yearly trend | 0.3177 |
| θ4 | Trend displacement | 1.6581 |
| θ5 | 6-month trend | 0.1855 |
| θ6 | Trend displacement | 0.3700 |
DownLoad:
CSV
| Parameters | Interpretation | Estimate |
| α | Mean reverting speed parameters | 4.3468 |
| κ | 287.3376 | |
| σ | Volatility | 4.8003 |
| θ | Number of spikes per unit time1 | −1 |
| μj | Jump size mean | 0.6689 |
| σj | Jump size deviation | 0.05 |
DownLoad:
CSV
| Empirical | Simulated | |
| Average | 0.000331 | 0.000375 |
| Standard Deviation | 0.379371 | 0.254794 |
| Skewness | −0.34398 | −1.98287 |
| Kurtosis | 42.8778 | 42.78973 |
DownLoad:
CSV
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 15.59 | 0.00 | 1.56 | 1.42 | 0.00 | 14.32 |
| T=6 | 15.70 | 0.00 | 2.64 | 2.30 | 0.08 | 14.11 |
| T=12 | 15.92 | 0.02 | 3.88 | 3.20 | 0.50 | 14.04 |
DownLoad:
CSV
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 3.55 | 1.19 | 0.10 | 13.20 | 0.00 | 27.55 |
| T=6 | 22.11 | 0.00 | 8.14 | 1.39 | 1.70 | 9.32 |
| T=12 | 26.45 | 0.00 | 12.00 | 0.76 | 3.57 | 6.56 |
DownLoad:
CSV
| R2=0.23 p-value ≪ 0.05 |
||
| Parameter | Interpretation | Estimate |
| θ1 | Average (log) fixed cost/price level | 3.5165 |
| θ2 | Average (log) cost slope | 0.0798 |
| θ3 | Yearly trend | 0.3177 |
| θ4 | Trend displacement | 1.6581 |
| θ5 | 6-month trend | 0.1855 |
| θ6 | Trend displacement | 0.3700 |
| Parameters | Interpretation | Estimate |
| α | Mean reverting speed parameters | 4.3468 |
| κ | 287.3376 | |
| σ | Volatility | 4.8003 |
| θ | Number of spikes per unit time1 | −1 |
| μj | Jump size mean | 0.6689 |
| σj | Jump size deviation | 0.05 |
| Empirical | Simulated | |
| Average | 0.000331 | 0.000375 |
| Standard Deviation | 0.379371 | 0.254794 |
| Skewness | −0.34398 | −1.98287 |
| Kurtosis | 42.8778 | 42.78973 |
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 15.59 | 0.00 | 1.56 | 1.42 | 0.00 | 14.32 |
| T=6 | 15.70 | 0.00 | 2.64 | 2.30 | 0.08 | 14.11 |
| T=12 | 15.92 | 0.02 | 3.88 | 3.20 | 0.50 | 14.04 |
| k=20 | k=35.5 | k=50 | ||||
| Months | Call | Put | Call | Put | Call | Put |
| T=3 | 3.55 | 1.19 | 0.10 | 13.20 | 0.00 | 27.55 |
| T=6 | 22.11 | 0.00 | 8.14 | 1.39 | 1.70 | 9.32 |
| T=12 | 26.45 | 0.00 | 12.00 | 0.76 | 3.57 | 6.56 |
