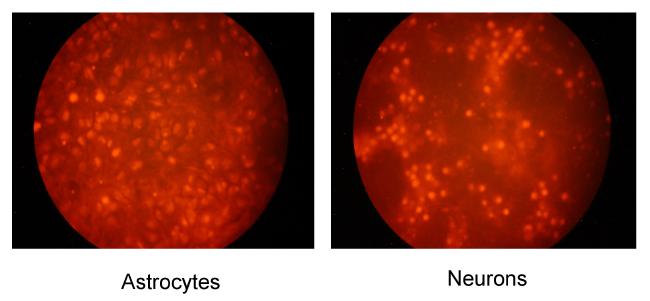
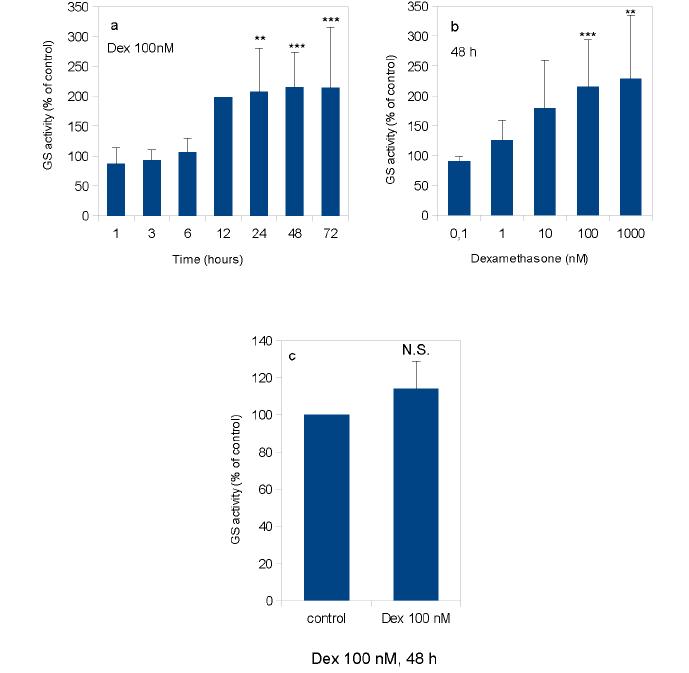
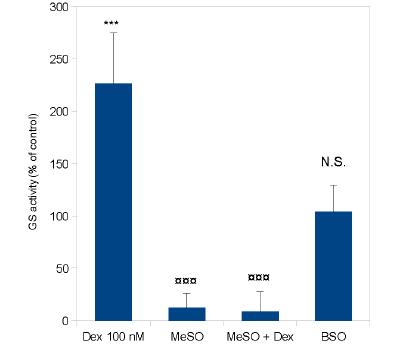
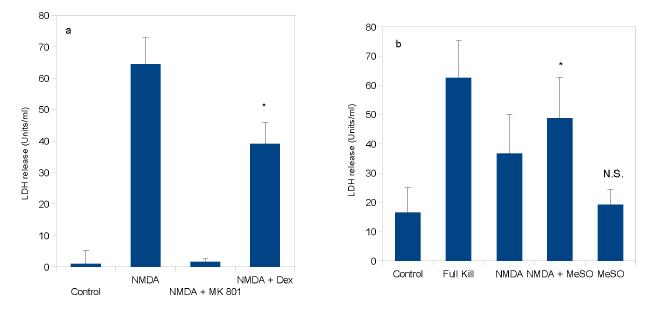
Astrocytes are claimed to protect neurons against excitotoxicity by clearing glutamate from the extracellular space and rapidly converting it into glutamine. Glutamine, is then released into the extracellular medium, taken up by neurons and transformed back into glutamate which is then stored into synaptic vesicles. Glutamine synthetase (GS), the key enzyme that governs this glutamate/glutamine cycle, is known to be upregulated by glucocorticoids. In the present work we have thus studied in parallel the effects of dexamethasone on glutamine synthetase activity and NMDA-induced neuronal death in cultures derived from the brain cortex of murine embryos. We showed that dexamethasone was able to markedly enhance GS activity in cultures of astrocytes but not in near pure neuronal cultures. The pharmacological characteristics of the dexamethasone action strongly suggest that it corresponds to a typical receptor-mediated effect. We also observed that long lasting incubation (72 h) of mixed astrocyte-neuron cultures in the presence of 100 nM dexamethasone significantly reduced the toxicity of NMDA treatment. Furthermore we demonstrated that methionine sulfoximine, a selective inhibitor of GS, abolished the dexamethasone-induced increase in GS activity and also markedly potentiated NMDA toxicity. Altogether these results suggest that dexamethasone may promote neuroprotection through a stimulation of astrocyte glutamine synthetase.
1.
Introduction
Fractional calculus is one of today's most popular mathematical tools to model real-world problems. More specifically, it has been applied to model evolutionary systems involving memory effects on dynamical systems. Partial differential equations (PDEs) with fractional operators are important in describing phenomena in many fields such as physics, biology and chemistry [1,2]. Based on the generalizations of fractional derivatives by famous mathematicians such as Euler, Lagrange, Laplace, Fourier, Abel and Liouville, today's mathematicians have explored and introduced many more types of fractional derivatives such as Riemann-Liouville, Caputo, Liouville, Weyl, Riesz and Hifler [3,4,5,6].
PDEs with conformable derivatives attract interested mathematicians using different approaches because of their wide range of applications, such as electrical circuits[7] and chaotic systems in dynamics[8]. We recognize that the conformable and classical derivatives have a close relationship. There is an interesting observation that: If $ f $ is a real function and $ s > 0 $, then $ f $ has a conformable fractional derivative of order $ \beta $ at $ s $ if and only if it is (classically) differentiable at $ s $, and
where $ 0 < \beta \leq 1 $. Another surprising observation is that Eq (1.1) will not hold if $ f $ is defined in a general Banach space. We can better understand why the ODEs with the conformable derivative on $ \mathbb{R} $ have been studied so much. In addition, the relevant research in infinite-dimensional spaces, such as Banach or Hilbert space, is still limited, which motivates us to investigate some types of PDEs with conformable derivatives in Hilbert or Sobolev spaces.
Besides, in some phenomena, the conformable derivative is better simulated than the classical derivative. In [9], the authors considered the conformable diffusion equation
where $ 0 < \alpha \le 1, \, x > 0, \, t > 0, $ $ u(x, t) $ is the concentration, and $ D_\alpha $ represents the generalized diffusion coefficient, which was applied in the description of a subdiffusion process. In particular, the conformable diffusion equation (1.2) reduces to the normal diffusion equation if $ \alpha = 1 $. A natural and fundamental question is, "Does the conformable diffusion model predict better than the normal diffusion model?". The results in [9] show that the conformable derivative model agrees better with the experimental data than the normal diffusion equation.
Let $ \Omega \subset\mathbb{R}^N $ ($ N \ge 1 $) be a bounded domain with smooth boundary $ \partial \Omega $, and $ T > 0 $ is a given positive number. In this paper, we investigate the Sobolev equation with a conformable derivative as follows
where $ \alpha, \beta \in (0, 1] $, $ m > 0 $, the time fractional derivative $ \frac{{ }^{ C}\partial^\alpha}{\partial t^\alpha} $ is the conformable derivative of order $ \alpha, $ defined in Definition 1. The function $ F $ represents the external forces or the advection term of a diffusion phenomenon, etc., and the function $ u_0 $ is the initial condition specified later. The operator $ (-\Delta)^\beta $ is the fractional Laplacian operator, which is well-defined in [10] (see page 3). In the sense of distribution, the study of weak solutions to Problem (1.3) is still limited compared to the classical problem. Thus, the fundamental knowledge in the distributive sense for Problem (1.3) is still open and challenging, which is the main reason and motivation for us to study the problem from the perspective of the semigroup.
Next, we mention some results related to Problem (1.3). There are two interesting observations regarding Problem (1.3).
$ \bullet $ If we take $ m = 0 $ in Problem (1.3), then we obtain an initial boundary value problem of the parabolic equation with a conformable operator as follows
The latest results on the well-posedness of solutions to Problem (1.4) are shown in more detail in [11], and the authors used the Hilbert scales space technique to prove the local existence of the mild solution to Problem (1.4).
$ \bullet $ If $ \alpha = 1 $, the main equation of Problem (1.3) becomes the classical equation
Equation (1.5) is familiar to mathematicians about PDEs, called the pseudo-parabolic equation, also known as the Sobolev equation. The pseudo-parabolic equation describes a series of important physical processes, such as the permeation of a homogeneous liquid through fractured rock, population aggregation and one-way propagation of the nonlinear dispersion length wave [12,13]. Equation (1.5) has been studied extensively; for details, see [12,13,14] and references given there. Concerning the study of the existence and blowup of solutions to pseudo-parabolic equations, we refer the reader to [15,16,17].
For the convenience of readers, we next list some interesting results related to pseudo-parabolic with fractional derivative. Luc et al. in [18] considered fractional pseudo-parabolic equation with Caputo derivative
where $ 0 < \alpha < 1 $, $ \mathcal A = -\Delta $, $ D^\alpha $ is Caputo fractional derivative operator of order $ \alpha $. They studied the local and global existence of solutions to Problem (1.6) when the nonlinear term $ F $ is the global Lipschitz. Based on the work in [18], there are many related results in the spirit of a semigroup representation of the form of the Fourier series. In [12], the authors studied nonlinear time-fractional pseudo-parabolic equations with Caputo derivative on both bounded and unbounded domains by different methods and techniques from [18]. In [19], the authors studied the nonlocal in time problem for a pseudo-parabolic equation with fractional time and space in the linear case. Tuan et al. [20] derived the nonlinear pseudo-parabolic equation with a nonlocal type of integral condition. In [21], the authors considered the time-space pseudo-parabolic equation with the Riemann-Liouville time-fractional derivative, and they applied the Galerkin method to show the global and local existence of solutions.
As far as we know, there has not been any work that considers the initial boundary value problem (1.3) with a conformable derivative. The main results and methods of the present paper are described in detail as follows
● Firstly, we prove the existence of the global solution to Problem (1.3). The main idea is to use Banach fixed point theorem with the new weighted norm used in [22]. In order to prove the regularity and the derivative of the mild solution, we need to apply some complicated techniques on Hilbert scales for nonlinearity terms.Compared with [11], our method has very different characteristics. It is important to emphasize that proving the existence of the global solution is difficult, which is demonstrated in our current paper, but not in the paper [11].
● Secondly, we investigate the convergence of solution to Problem (1.3) when $ m \to 0^+ $, which does not appear in the works related to fractional pseudo-parabolic equation. This result allows us to get the relationship between the solution of Sobolev equation and parabolic diffusion equation. To overcome the difficulty, we need to control the improper integrals and control the parameters. This pioneering work can open up some new research directions for finding the relationship between the solutions of the pseudo-parabolic equation and the parabolic equation.
● Finally, we prove the convergence of the solution when the order of derivative $ \beta \to 1^- $. This direction of research was motivated by the recent paper [23]. Since the current model has a nonlinear source function, the processing technique for the proof in this paper seems to be more complicated than that of [23].
The greatest difficulty in solving this problem is the study of many integrals containing singular terms, such as $ s^{\alpha-1} $ or $ (t^\alpha- s^\alpha)^{- m} $. To overcome these difficulties, we need to use ingenious calculations and techniques to control the convergence of several generalized integrals.
This paper is organized as follows. Section 2 provides some definitions. In Section 3, we give the definition of the mild solution and some important lemmas for the proof of the main results. Section 4 shows the global existence of the solution to Problem (1.3). In addition, we present the regularity result for the derivative of the mild solution. Section 5 shows the convergence of the solution to Problem (1.3) when $ m \to 0^+ $. In Section 6, we investigate the convergence of mild solutions when $ \beta \to 1^- $.
2.
Preliminary results
Definition 2.1. Conformable derivative model: Let $ B $ be a Banach space, and the function $ f:[0, \infty) \to B $. Let $ \frac{{ }^{C}\partial^\beta}{\partial t^\beta} $ be the conformable derivative operator of order $ \beta \in (0, 1] $, locally defined by
for each $ t > 0 $. (For more details on the above definition, we refer the reader to [24,25,26,27].)
In this section, we introduce the notation and the functional setting used in our paper. Recall the spectral problem
admits the eigenvalues $ 0 < \lambda_1 \leq \lambda_2 \leq \dots \leq \lambda_n \leq \dots $ with $ \lambda_n \to \infty $ as $ n \to \infty $. The corresponding eigenfunctions are $ e_n \in H_0^1(\Omega) $.
Definition 2.2. (Hilbert scale space). We recall the Hilbert scale space, which is given as follows
for any $ s \geq 0 $. It is well-known that $ \mathbb H^s (\Omega) $ is a Hilbert space corresponding to the norm
Definition 2.3. Let $ {\bf X}_{a, q, \alpha} ((0, T]; B) $ denote the weighted space of all the functions $ \psi \in C ((0, T];X) $ such that
where $ a, q > 0 $ and $ 0 < \alpha \le 1 $ (see [22]). If $ q = 0 $, we denote $ {\bf X}_{a, q} ((0, T]; B) $ by $ {\mathbb X}_{a} ((0, T]; B) $.
3.
The mild solution and some lemmas
In order to find a precise formulation for solutions, we consider the mild solution in terms of the Fourier series
Taking the inner product of Problem (1.3) with $ e_n $ gives
where we repeat that
The first equation of (3.1) is a differential equation with a conformable derivative as follows
In view of the result in Theorem 5, [26] and Theorem 3.3, [28] the solution to Problem (1.3) is
To simplify the solution formula, we will express the solution in operator equations. Let us set the following operators
and
for any $ f \in L^2(\Omega) $ in the form $ f = \sum_{n\in \mathbb N} \big\langle f, e_n \big\rangle e_n $. Then the inverse operator of $ {\bf S}_{m, \alpha, \beta}(t) $ is defined by
The mild solution is given by
For a qualitative analysis of the solution to (3.2), we need the bounded result for the operators in Hilbert scales space.
Lemma 3.1. (a) Let $ v \in \mathbb H^{s+k-\beta k} (\Omega) $ for any $ k > 0 $. Then we get
and for $ 0 \le \nu \le t \le T $,
(b) If $ v \in \mathbb H^{s} (\Omega) $, then
and
for $ 0 \le \nu \le t \le T $.
(c) If $ v \in \mathbb H^{s} (\Omega) $, then we have
for any $ s $.
Proof. For (a), in view of Parseval's equality, we get that
Using the inequality $ e^{-y} \le C_k y^{-k} $, we find that
where we use
It follows from (3.7) that
By a similar explanation, we also get that for $ 0 \le \nu \le t \le T $,
where we use the fact that
Hence, (a) is proved.
For (b), in view of Parseval's equality, we get that
which allows us to conclude the proof of (3.5). The proof of (3.6) is similar to (3.5), and we omit it here. For (c), noting that $ \left(1+ m \lambda_n \right)^{-1} < 1 $, we can claim it as follows
The proof of Lemma 3.1 is completed.
4.
Well-posedness of Problem (1.3)
Let $ G: \mathbb H^r (\Omega) \to \mathbb H^s (\Omega) $ such that $ G({\bf 0}) = {\bf 0} $ and
for any $ w_1, w_2\in \mathbb H^r (\Omega) $ and $ L_g $ is a postive constant.
Theorem 4.1. (i) Let $ G: \mathbb H^r (\Omega) \to \mathbb H^s (\Omega) $ such that (4.1) holds. Here $ r, s $ satisfy that $ s \ge r+k-\beta k $ for $ 0 < k < \frac{1}{2}. $ Let the initial datum $ u_0 \in \mathbb H^{r+k-\beta k} (\Omega) $. Then Problem (1.3) has a unique solution $ u_{m, \alpha, \beta } \in L^p(0, T; \mathbb H^r(\Omega)) $, where
In addition, we get
where $ C_k $ depends on $ k $.
(ii) Let us assume that $ b < \frac{ \alpha}{2} $ and $ u_0 \in \mathbb H^{s+k-\beta k+\beta-1} (\Omega) \cap \mathbb H^{r+k-\beta k} (\Omega) $. Then we have
Here the hidden constant depends on $ k, b, \alpha, m, p, \beta, L_g $ ($ L_g $ is defined in (4.1)).
Proof. Let us define $ { B}: {\bf X}_{b, \mu, \alpha }((0, T]; \mathbb H^r(\Omega)) \to {\bf X}_{b, \mu, \alpha}((0, T]; \mathbb H^r(\Omega)) $, $ \mu > 0 $ by
Let the zero function $ w_0(t) = 0 $. From the fact $ G(0) = 0 $, we know that
In view of (3.4) as in Lemma 3.3, we obtain the following estimate
Hence, multiplying both sides of the above expression by $ t^b e^{-\mu t^ \alpha} $, we have that
where we use $ b \ge \alpha k $. This implies that $ { B} w_0 \in {\bf X}_{b, \mu, \alpha }((0, T]; \mathbb H^r(\Omega)) $. Let any two functions $ w_1, w_2 \in {\bf X}_{b, \mu, \alpha }((0, T]; \mathbb H^r(\Omega)) $. From (4.4) and (3.3), we obtain that
Since the constraint $ s \ge r+k-\beta k $, we know that Sobolev embedding
From some above observations and noting (4.1), we get that
From the fact that
we follows from (4.7) that
where $ \overline C = C_k L_g \alpha^k m^{-k}. $ Let us continue to treat the integral term as follows
In order to control the above integral, we need to change the variable $ \nu = t \xi^{\frac{1}{ \alpha}} $. Then we get the following statement
Next, we provide the following lemma which can be found in [22], Lemma 8, page 9.
Lemma 4.1. Let $ a_1 > -1 $, $ a_2 > -1 $ such that $ a_1+a_2 \ge -1 $, $ \rho > 0 $ and $ t\in [0, T] $. For $ h > 0 $, the following limit holds
Since $ 0 < b < \alpha $ and $ 0 < k < \min (\frac{b}{ \alpha}, \; \; 1-\frac{b}{ \alpha}) $, we easily to verify that the following conditions hold
By Lemma 4.1 and (4.9), we have
This statement shows that there exists a $ \mu_0 $ such that
Combining (4.8) and (4.10), we obtain
for any $ w_1, w_2 \in {\bf X}_{b, \mu, \alpha }((0, T]; \mathbb H^r(\Omega)) $. This statement tells us that $ B $ is the mapping from $ {\bf X}_{b, \mu, \alpha }((0, T]; \mathbb H^r(\Omega)) $ to itself. By applying Banach fixed point theorem, we deduce that $ B $ has a fixed point $ u_{m, \alpha, \beta} \in {\bf X}_{b, \mu_0, \alpha}((0, T]; \mathbb H^r(\Omega)) $. Hence, we can see that
Let us show the regularity property of the mild solution $ u_{m, \alpha, \beta} $. Indeed, using the triangle inequality and (4.11) and noting that $ B (v = 0) = {\bf S}_{m, \alpha, \beta}(t) u_0 $, we obtain
which combined with (4.5), we get
which allows us to get that
where $ \widetilde C_1 $ depends on $ k, \mu_0, b, \alpha, m $ and
and we remind that $ C_k $ depends on $ k $. Note that the improper integral $ \int_0^T t^{-pb} {\rm d}t $ is convergent for $ 1 < p < \frac{1}{b} $, we deduce that
and the following regularity holds
where $ \widetilde C $ depends on $ k, \mu_0, b, \alpha, m, p $. Our next aim is to claim the derivative of the mild solution $ u_{m, \alpha, \beta} $. Applying the following formula
we obtain the following equality
where the operator $ {\bf Q}_{m, \alpha, \beta}(t) $ is defined by
for any $ v \in L^2(\Omega) $. In view of Parseval's equality, we get that
Using (3.8) and noting that $ \frac{ \lambda_n^\beta }{1+ m \lambda_n} \le m^{-1} \lambda_n^{\beta-1} $, we get that
which implies that
for any $ v \in \mathbb H^{s+k-\beta k+\beta-1} (\Omega) $. In a similar technique as above, we also get that
for any $ 0 \le \nu \le t $. Let us go back to the right hand side of (4.14). By (4.15), we evaluate the first term on the right hand side of (4.14) as follows
Using global Lipschitz of $ G $ as in (4.1) and the fact that $ G({\bf 0}) = {\bf 0} $, the second term on the right hand side of (4.14) is estimated as follows
where we use (4.13). Let us now to treat the third integral term in (4.14). By (4.16), we obtain that
Since $ \beta \le 1 $ and $ 0 < k < 1 $, we can easily verify that $ s+k-\beta k+\beta-1 \le s $, which implies the Sobolev embedding $ \mathbb H^{s}(\Omega) \hookrightarrow \mathbb H^{s+k-\beta k+\beta-1 }(\Omega) $ is true. From these above observations and using (4.13), we derive that
Let us now treat the integral term on the right hand side of (4.20). Controlling it is really not that simple task. By applying Hölder inequality, we find that
where $ \alpha > 2b $. By changing to a new variable $ z = \nu^ \alpha $, we derive that $ {\rm d}z = \alpha \nu^{ \alpha-1} {\rm d}\nu $. Hence, we infer that
where we note that $ 0 < k < \frac{1}{2} $. Combining (4.21) and (4.22), we obtain that the following inequality
By (4.23) and following from (4.19) and (4.20), we have
Summarizing the above results (4.14), (4.17), (4.18), (4.24) and using the triangle inequality, we obtain the following assertion
which shows (4.3). The proof is completed.
5.
The convergence of the mild solution when $ m \to 0^+ $
The main purpose of this section is to investigate the convergence of mild solutions to Problem (1.3) when $ m \to 0^+ $. Our result gives us an interesting connection between the solution of the Sobolev equation and the parabolic equation.
Theorem 5.1. Let $ G: \mathbb H^r (\Omega) \to \mathbb H^s (\Omega) $ such that $ G({\bf 0}) = {\bf 0} $ and (4.1) holds. Here $ r, s $ satisfy that $ s \ge r+k-\beta k $ for $ 0 < k < \frac{1}{2}. $ Let the initial datum $ u_0 \in \mathbb H^{r+k-\beta k} (\Omega) $. Let $ u_{m, \alpha, \beta} $ and $ u^*_{ \alpha, \beta} $ be the mild solutions to Problem (1.3) with $ m > 0 $ and $ m = 0 $ respectively. Then we get the following estimate
where $ \alpha k \le b < \frac{ \alpha}{2} $, $ \gamma = \frac{k(1-\beta)+l\left(\beta-\frac{\varepsilon}{2} \right) }{\beta+1-\frac{\varepsilon}{2}} $, $ 0 < l < k (1-\beta) $ and $ 1 < \varepsilon < \min \Big(2, \frac{2k(1-\beta)+2l \beta}{l} \Big) $.
Remark 5.1. Note that $ m^{ \frac{2\gamma- \varepsilon \gamma+\varepsilon l }{2} } + m^{k} $ tends to zero when $ m \to 0^+ $. Hence, we can deduce that $ \Big\| u_{m, \alpha, \beta}(t)- u^*_{ \alpha, \beta}(t) \Big\|_{\mathbb H^{r} (\Omega)} \to 0 $ when $ m \to 0^+ $.
Proof. In the case $ m = 0 $, thanks for the results on [11], the mild solution to Problem (1.3) is given by the following operator equation
where we provide two operators that have the following Fourier series representation as follows
and
It's worth emphasizing that the existence of the solution to Equation (5.1) has been demonstrated in [11]. Subtracting (5.1) from (4.12), we get the following equality by some simple calculations
Next, we estimate the four terms on the right hand of (5.2) in $ \mathbb H^r(\Omega) $ space. We divide this process into four steps as below.
Step 1. Estimate of $ M_1 $. In view of the inequality $ \Big| e^{-c}- e^{-d} \Big| \le C_\gamma \max (e^{-c}, e^{-d}) |c-d|^\gamma \ \text{with}\ \gamma > 0, $ let $ c = \frac{ \lambda_n^\beta }{1+ m \lambda_n} \frac{ t^ \alpha}{ \alpha} $ and $ d = \lambda_n^\beta \frac{ t^ \alpha}{ \alpha} $, we get the following inequality
by $ e^{-c} > e^{-d} $ and (3.8).
Here $ \gamma $ and $ l $ are two positive constants that are later chosen. For $ 1 < \varepsilon < 2 $ and any $ z > 0 $, we easily verify that $ (1+z)^{\frac{2}{\varepsilon}} \ge 1+ z > z, $ which implies
for any $ \gamma > l > 0 $.
In (5.4), by choosing $ z = 1+ m \lambda_n $ and after some simple calculation, we have $ \left(1+ m \lambda_n\right)^{\gamma-l} > (m \lambda_n)^{\frac{\varepsilon (\gamma-l)}{2} }, $ which leads to the following inequality
Combining (5.3) and (5.5), we find that
Therefore, we have the following estimate
which implies that
Next, we explain how to choose the parameters $ l, \varepsilon, \gamma $. Since $ \beta < 1 $, we can choose $ l $ such that
which implies that $ 2k(1-\beta)+2l \beta > l $, that is $ \frac{2k(1-\beta)+2l \beta}{l} > 1 $. Then we can choose $ \varepsilon $ such that
Let us choose $ \gamma $ such that
It is easy to verify that $ \gamma > \frac{l+l\left(\beta-\frac{\varepsilon}{2} \right) }{\beta+1-\frac{\varepsilon}{2}} = l $ and the following equality
Then the estimate (5.7) becomes
Step 2. Estimate of $ M_2 $. Let $ \psi \in \mathbb H^r (\Omega) $. For $ 0 \le \nu \le t \le T $, we can also get
where we use that
By (5.9) and Sobolev embedding $ \mathbb H^{s}(\Omega)) \hookrightarrow \mathbb H^{r}(\Omega) $, we find that
By the global Lipschitz property of $ G $ as in (4.1) and noting (5.10), it follows that
Step 3. Estimate of $ M_3 $. Let $ f \in \mathbb H^{r+k-\beta k } (\Omega) $. Then using Parseval' s equality, we have the following identity
By a similar explanation as in (5.6), we find that
By (5.12) and (5.13), we get that
In view of (5.14) and $ s \ge r+k -\beta k $, we derive that
By using global Lipschitz property of $ G $ as in (4.1) and noting (4.2), we infer that
where the hidden constant depends on $ k, \alpha, L_g, \mu_0, b $. Combining (5.15) and (5.16), we get the following estimate
Since $ \gamma > l $ and noting that $ b < \alpha $, we infer that
By (5.17) and (5.18), we obtain
Step 4. Estimate of $ M_4 $. By Parseval's equality, we know that
Using the inequality $ e^{-z} \le C(\varepsilon_0) z^{-\varepsilon_0} $, we get the following inequality
By the inequality $ (1+z)^2 > z^{\varepsilon_1} $ for $ 1 < \varepsilon_1 < 2 $, we find that the following inequality
By (5.20)–(5.22), we derive that
Hence, by using Parseval's equality, we obtain the following estimate
Next, we need to choose the appropriate parameters $ \varepsilon_0, \varepsilon_1 $. Let $ \varepsilon_0 = k \in (0, \frac{1}{2}) $ and $ \varepsilon_1 = 2-2k $, we can verify that $ 1 < \varepsilon_1 < 2 $. Hence, it follows from (5.23) that
By (5.16) and Sobolev embedding $ \mathbb H^{s}(\Omega)) \hookrightarrow \mathbb H^{r-\beta k +k}(\Omega), $ we derive that
which implies that
where we use (4.23). Combining (5.8), (5.11), (5.19) and (5.24), we obtain that
Here we note that $ 1-2k > 0 $ and $ \alpha-2b > 0 $. Since the fact that $ \gamma > l $ and $ b < \min (\alpha, (1-k) \alpha) $, it is obvious to see that
which motivate us to put
It follows from (5.25) that
To continue to go further in the proof, we now need to recall the following Lemma introduced in [29].
Lemma 5.1. Let $ v \in L^1[0, T] $. Consider some postive constant $ A, B, \beta', \gamma' $ such that $ \beta'+\gamma' > 1 $ and
Then for $ 0 < t \le T $, we get
Looking Lemma 5.1 and (5.26), we set
$ B = L_g, \; \; \beta' = 1 $ and $ \gamma' = \alpha. $ Then we deduce that
The proof of Theorem 5.1 is completed.
6.
The convergence of the mild solution when $ \beta \to 1^- $
Theorem 6.1. Let $ G: \mathbb H^r (\Omega) \to \mathbb H^s (\Omega) $ such that (4.1) holds. Here $ r, s $ satisfy that $ s > r+k-\beta k $ for $ 0 < k < \frac{1}{2}. $ Let the initial datum $ u_0 \in \mathbb H^{r+k-\beta k+ \varepsilon} (\Omega) $ for any $ \varepsilon > 0 $. Then we get the following estimate
where the hidden constants depends on $ \alpha, k, T, b $. Here
for any $ \varepsilon > 0 $.
Proof. For $ m > 0 $, let $ u_{m, \alpha, \beta} $ and $ u^{**}_{m, \alpha} $ be the mild solutions to Problem (1.3) with $ 0 < \beta < 1 $ and $ \beta = 1 $ respectively. Let us recall the formula of these two solutions
and
Subtracting (6.1) from (6.2) on each side, we derive that
Step 1. Estimate of $ N_1 $. By Parseval' s equality, we have that the following equality
For the term $ N_{1, 1} $, since $ \lambda_n > 1 $ and $ 0 < \beta < 1 $, we note that $ \frac{ \lambda_n^\beta }{1+ m \lambda_n} < \frac{ \lambda_n }{1+ m \lambda_n} $. Hence, we have the following inequality
In view of the above inequality
with $ c = \exp\left(- \frac{ \lambda_n^\beta }{1+ m \lambda_n} \frac{ t^ \alpha}{ \alpha} \right) $ and $ d = \exp\left(- \frac{ \lambda_n }{1+ m \lambda_n} \frac{ t^ \alpha}{ \alpha} \right) $, we derive that
Since the fact that $ \lambda_n > 1 $, we know that $ \Big| \lambda_n- \lambda_n^\beta \Big|^{\gamma'} = \lambda_n^{ \gamma'} \left(1- \lambda_n^{\beta-1} \right)^{\gamma'}. $ Using the inequality $ 1- e^{-y} \le C(\mu) y^\mu $ for any $ \mu > 0 $, we find that
where we note that $ 0 < \log(y) \le y $ for any $ y > 1 $, which implies that
Combining (6.5) and (6.6), we derive that
If we make the assumption $ \varepsilon' \le \gamma' $, then $ \left(1+ m \lambda_n \right)^{\varepsilon'-\gamma'} \le 1 $, which allows us to obtain that
Let us choose $ \mu = \frac{\varepsilon}{k} $ and $ \gamma' = \varepsilon' = k $ for any $ \varepsilon > 0 $. Then we get the following estimate
Before mention to $ N_{1, 2} $, we provide a set $ \overline N = \Big\{ n \in \mathbb N: \lambda_n \le 1 \Big\}. $ Let us give the observation that if $ \overline N $ is an empty set, then $ N_{1, 2} = 0 $. If $ \overline N $ is a non-empty set, then $ \lambda_1 \le 1 $. For the term $ N_{1, 2} $, we note that $ \frac{ \lambda_n^\beta }{1+ m \lambda_n} > \frac{ \lambda_n }{1+ m \lambda_n} $ since $ \lambda_n \le 1 $ and $ 0 < \beta < 1 $. Hence, we have that
By using the fact that
with $ c = \exp\left(- \frac{ \lambda_n^\beta }{1+ m \lambda_n} \frac{ t^ \alpha}{ \alpha} \right) $ and $ d = \exp\left(- \frac{ \lambda_n }{1+ m \lambda_n} \frac{ t^ \alpha}{ \alpha} \right) $, we derive that
Since $ \lambda_1 \le \lambda_n \le 1 $, it is obvious to see that
Combining (6.8) and (6.9), we find that
Hence, it follows from (6.10) that
Let $ \varepsilon_1 = k $ and $ \gamma_1 = \frac{2k+\varepsilon }{\beta}-k $. Since $ 0 < \beta < 1 $, we know that
Hence, in view of Parseval's equality, we get the following estimate
Combining (6.4), (6.7) and (6.11), we obtain the following estimate
By taking the square root of both sides of the above expression and using the inequality $ \sqrt{a+b} \le \sqrt{a}+ \sqrt{b} $ for any $ a, b \ge 0 $, we get
Here we denote
where we observe that $ {\bf D}_\beta (\varepsilon, k) \to 0, \ \beta \to 1^{-}. $
Step 2. Estimate of $ N_2 $. We confirm the following result for any $ \varepsilon_0 > 0 $ using the method similar to Step 1,
Since $ s > r+k-\beta k $, we know that $ \varepsilon_0 = s- r-k +\beta k > 0 $, and using global Lipschitz property of $ G $, we derive that
where $ \overline C_1 = C (k, r, s, \beta, \alpha) $, and we have the following observation
In view of (4.2), we obtain that the following upper bound
where $ \overline C_2 = C(k, \alpha, m, \mu_0, T, b). $ From two latter estimations as above, we infer that
where $ \overline C_3 = K_g \overline C_1 \overline C_2 $. Using (4.23), we obtain that the following inequality
Combining (6.13) and (6.14), we obtain that
Step 3. Estimate of $ N_3 $. By a similar argument as in (4.6), we find that
Since $ s > r+k-\beta k $ and using global Lipschitz property of $ G $, we obtain that
From the two above observations, we confirm the following statement
where $ \overline C_3 = C_k \alpha^k m^{-k}K_g. $ Combining (6.3), (6.12), (6.15) and (6.16), we deduce the following estimate
where $ \widetilde C = C (k, r, \varepsilon, \alpha) $. By the Hölder inequality and in combination with (4.22), we get the estimate of the third term on the right hand side of (6.17) as follows
Combining (6.17), (6.18) and the inequality $ (a+b+c)^2 \le 3 a^2+ 3 b^2 + 3 c^2 $, we derive that
Multiplying both sides of (6.19) by $ t^{2 \alpha k} $, we get the following estimate
which implies that
Looking Lemma 5.1 and (6.20), we set $ v(t) = t^{2 \alpha k} \Big\| u_{m, \alpha, \beta} (t)- u^{**}_{m, \alpha} (t) \Big\|_{\mathbb H^r(\Omega)}^2, $
and
By applying Lemma 5.1, we obtain that
In view of Lemma 3.1 as in [30], we obtain the following upper bound
where $ \mathbb C_ \alpha $ is a positive constant that depends on $ \alpha. $ By (6.21) and (6.22), we get
From Deinition 2.3, we find
The proof is completed.
Acknowledgement
Huy Tuan Nguyen is supported by the Van Lang University. Chao Yang is supported by the Ph.D. Student Research and Innovation Fund of the Fundamental Research Funds for the Central Universities (3072022GIP2403).
Conflict of interest
The authors declare there is no conflict of interest.













 DownLoad:
DownLoad: