We revisit the control problem for a spacecraft to land on the moon surface at rest with minimal fuel consumption. We show that a detailed analysis in the related 3D phase space uncovers the existence of infinitely many safe landing curves, contrary to several former 2D descriptions that implicitly claim the existence of just one such curve. Our results lead to a deeper understanding of the dynamics and allows for a precise characterization of the optimal control. Such control is known to be bang-bang and our results give a full characterization of the switch position.
1.
Introduction
How should we land safely a spacecraft on the moon surface (a so-called moon lander), so as to use the least possible amount of fuel? See Figure 1.
This problem was originally suggested by Miele [5,Section 4.8] in 1962 and subsequently solved by Meditch [4] in 1964. It is our purpose to give a new simplified solution to this optimal control problem and to clarify a delicate point that may create misunderstandings.
To model this problem, we introduce the variables
The function α(t) is the control and we assume that 0≤α(t)≤1, A=[0,1]. If α(t)=0, then the engine is switched off and the spacecraft is in free fall, while α(t)=1 means that the maximal thrust is used against gravity. As the fuel is burnt, the mass m(t) of the spacecraft diminishes over time and the rate of change is negatively proportional to α(t). According to Newton's second law, the motion of the spacecraft is (the upward direction is the positive direction)
with
where the parameter k>0 represents the velocity of the exhaust gases with respect to the spacecraft. Physical constraints such as h(t)≥0 (spacecraft above the moon surface) and m(t)≥ms (total mass larger than the empty spacecraft mass) will pop up in the course. The target is to minimize the amount of fuel used or, equivalently, to maximize the remaining fuel at the landing instant. Hence, the purpose is to maximize
where τ is the first time when h(τ)=v(τ)=0. In spite of its simple formulation, this is a fairly delicate control problem and a full solution requires a great attention to apparently harmless details. The dynamics in (1.1) may be rewritten as the 3×3 system
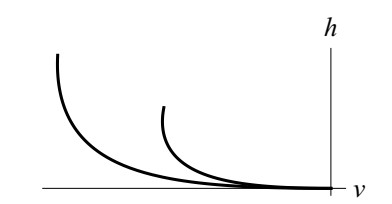
so that the phase space is R3 but, in view of the different roles played by {h,v} on the one hand and by m on the other hand, most studies have been performed by projecting the dynamics on the plane {h,v}. From a physical point of view, one expects a safe landing to occur with a positive acceleration, able to slowdown the free fall of the spacecraft: by looking at (1.1), this translates into the condition α(t)>gm(t), namely that the upward acceleration overcomes the downward weight. This leads to define the so-called safe landing curves able to steer the spacecraft safely at rest on the moon surface. As quite usual in control problems, one is then led to represent geometrically these curves and, since a 3D representation in the space {h,v,m} may be fairly complicated, in former literature the strategy was to depict the safe landing dynamics with a 2D representation in the plane {h,v}. Unfortunately, this strategy has a drawback, the description of the effective dynamics is incomplete. Due to the unknown value of m(τ), there exist infinitely many such curves, and, to our knowledge, a complete analysis in this direction has not been performed, see e.g., the monographs [1,p. 58], [2,Figure 4.10,p. 151], [3,Figure II. 2,p. 36]) and the bibliographies therein. This fact is highlighted in Section 2, where we fully describe the mutual position between these curves in dependence of the residual mass m(τ). Our 3D analysis emphasizes that they remain ordered even if projected onto the {h,v}-plane. In our opinion, this is remarkable because, even if one does expect no intersection in the full space (uniqueness of the related Cauchy problem), in principle it could happen that two of the three components coincide: one could have the same {h,v}-components but a different m. The precise statement is contained in Theorem 1 and a different point of view is highlighted in Corollary 2.
Once the behavior of the safe landing curves is clarified, for the solution of the control problem we partially follow [4], see also [2,3], complementing the arguments therein with more precise information. The full solution is given, step by step, in Section 3 and the resulting statement is given in Theorem 5, complemented with several illustrative pictures.
2.
Characterization of the safe landing curves
The dynamics (1.1) is described by the 3×3 system (1.2) with initial conditions
where m0 is the initial mass of fuel plus the mass of the empty spacecraft ms>0. As already mentioned, the goal is to land on the moon safely, maximizing the remaining fuel m(τ)−ms, where τ=τ(α) is the first time when h(τ)=v(τ)=0. Since α=−˙m/k, this is equivalent to minimize the total applied thrust before landing; hence, the payoff is given by
As we shall see, a safe landing is possible only if the control α satisfies α(t)≡1 in some left neighborhood of the final time τ. Taking this for granted, we analyze here the interval (t∗,τ) when the thrust is switched on (α=1), so that the system (1.2) becomes
Note that we have here no condition on m(τ) which then plays the role of a parameter. The solution of this system is
The last two equations in (2.3) are parametric representations in the phase plane {v,h} of the safe landing curves. This is a delicate point since, while (2.3) is a 3-dimensional problem, the analysis in the plane {v,h} is 2-dimensional and if one restricts to the plane the dependence on m(t) somehow disappears. This is the point that we now clarify with a full analysis in the plane able, however, to take into account the mass through its residual amount m(τ).
Since α(t)∈[0,1], from (1.1) we see that ¨h(t)≤−g+1/m(t) for a.e. t. For a safe landing, since v(τ)=0, v has to be increasing in a left neighborhood of τ (formally, ¨h(τ)=˙v(τ)=−g+1m(τ)>0), which leads to the unavoidable condition
From a physical point of view, condition (2.4) ensures that the spacecraft is able to decelerate its free fall (¨h≥0), at least when there is no fuel left. Clearly, this is a limit situation: if no fuel is left then the thrust cannot be switched on! In order to ensure that the spacecraft is able to decelerate the free fall at any time during its flight (that is, when ms≤m(t)≤m0) one needs the more restrictive assumption that
Physically, condition (2.5) states that the spacecraft is able to decelerate its free fall, since the very beginning, also when the tank is completely full of fuel, namely 0<−g+1/m0≤¨h(t) for a.e. t.
We will show that the (infinitely many) safe landing curves are determined by a unique parameter, the mass of fuel remaining at the safe landing instant τ, namely m(τ)−ms. If m(t∗)=m0, since when α(t)≡1 the fuel is used at rate k, we have that
Moreover, the mass of fuel at time t∗ is m0−ms>0 and, hence,
For the extremal cases in (2.7), we have that
In order to classify the curves for all the intermediate values of m(τ), consider two different final fuel masses m1(τ1)>m2(τ2) in the range (2.7). For simplicity, we put ¯mi=mi(τi); then we prove
Theorem 1. Assume that (2.5) holds. If ms≤¯m2<¯m1<m0, then the safe landing curve (2.3) relative to ¯m1 stays above the safe landing curve (2.3) relative to ¯m2 in the {v,h}-plane as long as both exist. Moreover, the safe landing curves (2.3) can be prolonged backwards (in time) from the origin (vi(τi),hi(τi))=(0,0) until an extremal point (vi,hi)∈R−×R+ (both depending on ¯mi) such that
Proof. Let us label all the related components of the two motions with an index i∈{1,2}. We perform the two changes of variable σ=τi−t and (2.3) becomes (for i=1,2)
Note that, since ¯m1>¯m2, we have m0−¯m1k<m0−¯m2k and, moreover,
In turn, recalling that ˙v1,˙v2<0, this means that the following implication holds
Let us now prove the first statement in a neighborhood of σ=0. Two Taylor expansions give
Hence, we may locally write the curves as functions and obtain
Analyzing the two resulting parabolas, we infer that, if v1=v2=v, then
Since ¯m1>¯m2, this proves the claimed order of the safe landing curves (2.3) in a neighborhood of the origin (v,h)=(0,0).
We still need to show that the same order remains forever (when α(t)≡1). Assume for contradiction that the two curves intersect somewhere else than at the origin, that is,
where we understand that the σi's are the minimal instants where this occurs. Precisely because the σi's are minimal, this means that, prior to these instants, the mutual position of the two curves is the same as in a neighborhood of σ=0. Hence, for the two curves to meet, the tangent vectors must be directed in a given way. More precisely, the tangent vectors are given by
and, for the two curves to intersect, it must be
which contradicts (2.9). This contradiction shows that the two curves never meet and, hence, that the order is the same as in a neighborhood of σ=0. This completes the proof of the first statement.
Concerning the second statement, we notice that the parametric representation (2.8) enables us to determine the extremal points (vi,hi)∈R−×R+ as follows:
By dropping the denominator k2 and the additive constant −m0, we analyze the behavior of hi through the function
where we used (2.5): therefore, ¯mi↦hi(¯mi) is strictly decreasing. Similarly, one can show that ¯mi↦vi(¯mi) is strictly increasing. This completes the proof.
The result in Theorem 1 is illustrated in Figure 2 where, in the plane {v,h} we plot the curves relative to (2.8)2–(2.8)3 for g=1.62, k=1, ¯m1=0.1, ¯m2=0.05, σ∈[0,0.6]. The curve below (on the left) describes (v2,h2), the curve above (on the right) describes (v1,h1). Incidentally, we observe that (2.10) fully characterizes the (horizontal) asymptotic behavior at (0,0) of the safe landing curves in Figure 2.
For later use, we rephrase Theorem 1 in a slightly different form.
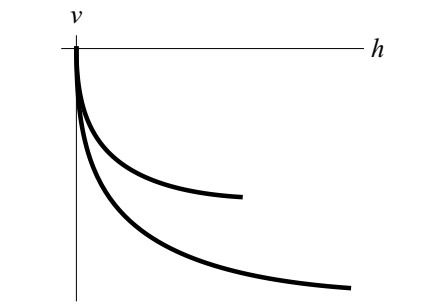
Corollary 2. Assume that (2.5) holds and let
Then ¯h>0 for any ¯m∈[ms,m0) and there exist negative and strictly decreasing functions
such that, on intervals where they are both defined, Φ¯m1(h)>Φ¯m2(h) (h≠0) whenever ¯m1>¯m2. In particular,
The statement of Corollary 2 is qualitatively described in Figure 3.
Back to (2.3), Corollary 2 states that if v(t)=Φ¯m(h(t)) for some ¯m∈[ms,m0) and some t>0, then the dynamics has attained one of the safe landing curves and the spacecraft will land safely at some time τ>t with residual mass m(τ)=¯m. Therefore, of particular interest are the extremal points of the safe landing curves, denoted by (vi,hi) in Theorem 1. This is why we now introduce a more rigorous characterization of these points. Denoting again by ¯m=m(τ)∈[ms,m0) the residual mass, according to (2.12) we may rewrite them as
As we have seen in the proof of Theorem 1, both these maps are strictly monotonic. In particular, since vm0(m0)=0, the map ¯m↦vm0(¯m), defined from [ms,m0) to [vm0(ms),0), is negative and strictly increasing so that it is invertible and we denote by
its inverse map. Subsequently, we define the (strictly decreasing) composite function
From now on, for a given m0>ms we call switching curve the line of the (v,h)-plane defined by h=Γm0(v) (see Figure 6 below) and the final part of Theorem 1 may be reformulated as
Corollary 3. Let m0>ms. Then all the safe landing curves in the (v,h)-plane have one endpoint on the switching curve h=Γm0(v) and the other endpoint at the origin (v,h)=(0,0).
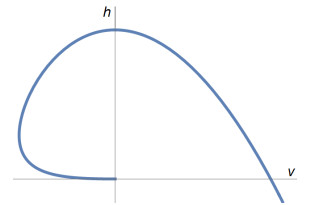
In order to complete the description of the safe landing curves, we merely assume (2.4) and not necessarily (2.5), and we study the parametric representation (2.8) by extending the time interval to σ∈[0,∞). Let us start from the origin (σ=0) and move clockwise, as σ increases. From (2.10) we know that, at the origin, the curve starts with horizontal tangent and behaves like a parabola. We numerically obtained the qualitative plot represented in Figure 4.
The point with vertical tangent corresponds to ˙v(σ)=0 which, recalling (1.1) and that α=1, yields gm(σ)=1. Under the more stringent (physical) assumption that (2.5) holds, this point is not attained and the curve has the plot as in Figures 2 and 3, as already stated in Corollary 2. But if we merely assume (2.4), then the point with vertical tangent exists and, as mentioned above, it represents the instant in which gm(σ)=1. Above this point the thrust is not able to balance the weight gm(σ) and the spacecraft proceeds with negative (downwards) acceleration until the amount of fuel reduces the global mass to m=1/g.
Let us continue moving upwards (clockwise) on the curve in Figure 4. By recalling that ˙h=−v, it is clear that the curve has horizontal tangent at the very same place where it crosses the vertical axis. Finally, less interesting is the part in the half plane v>0, because there is no need to use the thrust therein and, hence, (2.8) does not represent the dynamics of the spacecraft any more.
3.
Solution of the minimal fuel consumption problem
Let us define what is meant by admissible control and data for (1.2).
Definition 4. We say that a trajectory/control quadruple (h,v,m,α) solving (1.2) is admissible if it satisfies the endpoint constraint
We say that, for a given m0≥ms, the initial data (v0,h0)∈R×R+ are admissible if there exists an admissible quadruple (h,v,m,α) satisfying v(0)=v0 and h(0)=h0.
As already mentioned in the introduction, for physical reasons we are interested in solutions satisfying the state constraints m(t)≥ms and h(t)≥0, for any t∈[0,τ). While the former is guaranteed by imposing (3.1), the latter will be deduced a posteriori by our analysis. As outlined in Section 2, too heavy spacecrafts cannot land safely, implying the further constraint (2.5). We prove below that in order to land safely, the control α(t) should be 1, for any t∈(t∗,τ] and some t∗∈[0,τ). Notice that (2.5) is a sufficient condition to have h(t)>0 in (t∗,τ), whenever h(τ)=v(τ)=0. The condition gm(τ)≥1 would imply that gm(t)>1 in (t∗,τ), hence ˙v(t)<0 and, in case of soft landing, v(t)>0, yielding h(t)<0. Since (1.2) and (3.1) ensure that m(τ)≥ms,
Therefore, (2.4) is unavoidable if one aims to analyze the nontrivial dynamics of (1.2).
In order to obtain an optimal control for the problem, we use Pontryagin Minimum Principle. Given an optimal solution (h,v,m,α), there exist
and such that p=(p1,p2,p3) solves the adjoint equation
and satisfies the transversality condition p(τ)∈NC=R×R×(−∞,0] (the normal cone at the endpoint). This means that
We consider the Hamiltonian
which vanishes along the optimal trajectory, that is,
moreover, the optimal control (if any!) fulfills the following minimality condition:
In (3.6) we emphasized the part depending on a which has to be minimized. For the determination of the optimal control, we proceed in several steps.
∙ Step 1: if it exists, the optimal control is bang-bang with at most one switch and α(τ)=1.
This step is quite standard, see the original paper by Meditch [4] or [2,Section 4.7]. Here we suggest a slightly simplified form, by reducing the number of cases to be analyzed and focusing mainly on the control α. Consider the function
so that the minimality condition (3.6) characterizes the optimal control α through the rule
showing that the optimal control is bang-bang with at most one switch, provided that the "ambiguous situation" where ρ(t)=0 occurs at most in one point.
To this end, note that (3.3) implies that p1 is constant, say p1(t)≡λ1 and, using also (1.2), that
The condition (3.8) implies that ρ is monotone, possibly constant. Hence, the ambiguous situation ρ(t)=0 may occur either at most one point or on the whole interval [0,τ]. Assume for contradiction that ρ(t)≡0, then λ1=0 which yields p1(t)≡0. Then (3.5) implies that also p2(t)≡0. Inserted in (3.3), this would imply that also p3 is constant: in view of (3.4), this means that p3(t)≡C≤0 for all t. Putting all these information together, we see that (3.5) implies that (p,μ)=(0,0), which contradicts (3.4). Therefore, it cannot be ρ(t)≡0 and ρ(t) vanishes in at most one point.
In particular, this fact combined with (3.7) shows that α(τ)=1 since α(τ)=0 would mean ˙v(τ)=−g<0, see (1.2), with crash of the spacecraft; to make this fully rigorous we notice that, if we assume v(τ)=0 then v(t)<0 in a left neighborhood of t=τ which implies ˙v(τ)≥0, contradiction.
To conclude, we use again (3.8): since we excluded ρ(t)≡0, we see that ρ has at most one zero at some t∗∈(0,τ). By (3.7), this shows that α has at most one switch and, since α(τ)=1, if this switch exists it is from 0 to 1. This proves the claim of Step 1.
∙ Step 2: explicit form of the solution of (1.2) if the optimal control exists.
From Step 1 we know that, if the optimal control exists, then it has at most one switch on time t∗∈(0,τ). In the interval (0,t∗), when the thrust is switched off (α=0, with spacecraft in free fall), the system (1.2), with initial conditions (2.1), has the solution
This yields the constraint
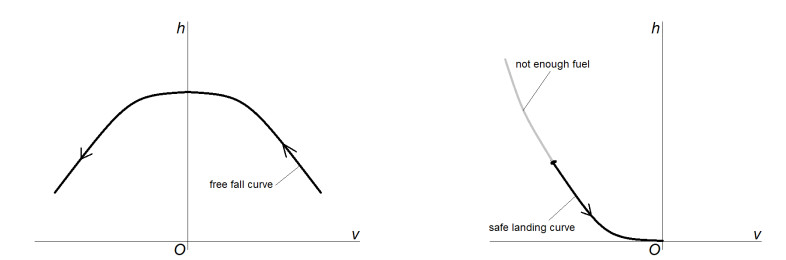
whose representation in the phase plane {v,h} is a concave parabola having the vertex at the point (v,h)=(0,h0+v20/2g), see the left picture in Figure 5. Therefore, if the optimal control α exists, then the solution (h,v,m) of (1.2)-(2.1) is given by (3.9) and (2.3) in which t∗<τ, possibly t∗=0 (no switch, thrust always switched on). These lines are represented (separately) in Figure 5.
∙ Step 3: geometric interpretation of the existence of a switch on time.
If (2.5) is satisfied, the components (v,h) of the optimal trajectories behave as in Figure 5: the engine is switched off until the free fall trajectory reaches a safe landing curve, and this happens at a point of the switching curve. In other words, there exists t∗≥0 and ¯m∈[ms,m0) such that (v(t∗),h(t∗))=(v,Γm0(v)) for some v∈[vm0(ms),0), see (2.13). Then the engine is switched on and the optimal trajectory follows the safe landing curve (2.8) corresponding to a final fuel mass equal to ¯m−ms, that is, m(τ)=¯m.
In the extreme situation where v=vm0(ms), the safe landing occurs with no fuel left. This means that (v(t∗),h(t∗))=(vm0(ms),Γm0(vm0(ms))) and this is the corner point of the black line in the left picture of Figure 6: when the spacecraft reaches this point the thrust must be switched on and safe landing is possible but with no fuel left after landing.
The part of black line connecting the corner point and the origin is called the extremal curve and is the trajectory in the (v,h)-plane followed by the spacecraft when landing with no residual fuel. The switching curve (where h=Γm0(v)) has the same endpoints as the extremal curve: it is depicted with a thinner line, see also the zoomed picture on the right of Figure 6. The gray region outside this line represents the crash region: if (v(t),h(t)) reaches this region (including at the initial instant!), then the thrust is not powerful enough to allow safe landing because the velocity v(t) is too negative compared to the (low) altitude h(t). Indeed, if the spacecraft is (e.g., ) initially at height 1m and the initial velocity is −1000km/h (downwards), there is no way to land safely. This is a very delicate part, where the 2D pictures in Figure 6 may be misleading. The points between the extremal curve and the switching curve are not admissible initial values for (v0,h0)! The reason is that they are only projections of the orbits in the 3D space. Finally, if the initial data are within the white region, then the spacecraft cannot land safely because of the lack of fuel, the corresponding parabola intersects no safe landing curves.
Apart of the extremal case, the intermediate situations are described analytically in Theorem 1 and geometrically in the right picture of Figure 6. The switching curve on the right of the extremal curve (landing with no fuel left), contains all the switch on points for α. Each point on this curve is the intersection between a concave parabola and the corresponding safe landing curve, with some positive amount of fuel left at the landing time τ.
∙ Step 4: analytic formulation of the geometric pattern.
Aiming to make the geometric observations in Step 3 fully rigorous, we recall that the (lower) boundary of the "safe landing region" is the switching curve whose equation is h=Γm0(v) for v∈[vm0(ms),0), see (2.13) and Figure 6. Its extremal point (vm0(ms),Γm0(vm0(ms))) may also be expressed through the parametric representation of the switching curve so that, if t∗ denotes the switching instant, we have
It is clear, and fully apparent from (3.11), that the corner point depends on m0. With this extremal point at hand, we seek the "critical parabola", namely the set of initial data such that, following (3.10), reach the point in (3.11) at some time t∗>0. This gives
that represents the condition for the parabola to intersect the switching curve at the lack of fuel extremal point (3.11). But only the part of the parabola on the right of the switching curve contains the initial data allowing for a safe landing.
∙ Step 5: conclusions.
There are three different situations where the optimal control does not exist and the spacecraft cannot land safely:
(i) the thrust is too weak, unable to stop the free fall;
(ii) there is not enough fuel to stop the spacecraft;
(iii) the spacecraft is too close to the moon surface and/or with too large downwards velocity.
The situation described by (i) occurs if (2.5) is violated, which means that (2.4) is a necessary condition for the existence of initial data allowing a safe landing, see Step 2. Formally, this leads to our first conclusion:
If (2.5) is satisfied, then from (2.13) and (3.12) we derive the second conclusion:
In this case, there exists a unique admissible control which is then optimal; these initial data lie either on the switching curve or on the concave parabola bounding the safe landing region, see the left picture of Figure 6.
Let us then see what happens when (2.5) is satisfied but (3.12) does not hold, namely when the first term in (3.12) differs from the third term. If the inequality > holds in (3.12) (either v0 is "too negative" of h0 is "too large"), then the spacecraft cannot land safely on the moon, due to a lack of fuel. The related parabola intersects none of the safe landing curves and the spacecraft ends again in the gray (crash) part. This gives the third conclusion
which means, in fact, that there are no admissible controls.
If the inequality < holds in (3.12) (meaning that the initial data are placed below the critical parabola), two subcases may occur. If v0≤vm0(ms) or v0>vm0(ms) and h0<Γm0(v0) (gray region in the left picture in Figure 6) then the spacecraft cannot land safely because it is either too close to the moon or moving too quickly downwards. This gives the fourth conclusion
which means that, also in this case, there are no admissible controls. In the second subcase where < holds in (3.12) we are in the safe landing region (yellow part in the left picture in Figure 6): then the spacecraft may land safely after one switch on time, which gives the last conclusion
In this case, there exists infinitely many admissible controls and the optimal one is bang-bang with a unique switch on time. This statement suggests to define
namely the abscissa v>0 of the intersection between the critical parabola and the v-axis.
In summary, the above steps and conclusions prove the following statement
Theorem 5. If gms≥1, then the only admissible initial data are the trivial ones, (h0,v0)=(0,0).
If gms<gm0<1, then there exists an optimal control for the problem of minimizing (2.2) among the solutions of (1.2) if and only if
In such case, the optimal control is bang-bang with no switch if h0=Γm0(v0) and exactly one switch in all the other cases.
Finally, if v0∈[vm0(ms),Vm0] and h0+v202g=ms−m0k2+12gk2log2m0ms+msk2logm0ms, then there exists a unique admissible control and all the fuel has to be used for safe landing.
The statement of Theorem 5 is summarized in Figure 6 that describes the different regions for a given m0>ms. The switch points belong to the switching curve, namely the part of the boundary connecting the (extremal) corner point with the origin, see the right picture in Figure 6. By increasing m0 the switching curve is prolonged on the separation between the insufficient fuel and crash regions (white and gray) and the related extremal parabola is shifted upwards.
Acknowledgments
The first author is supported by PRIN project Equazioni alle derivate parziali di tipo ellittico e parabolico: aspetti geometrici, disuguaglianze collegate, e applicazioni. Both the authors are members of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: