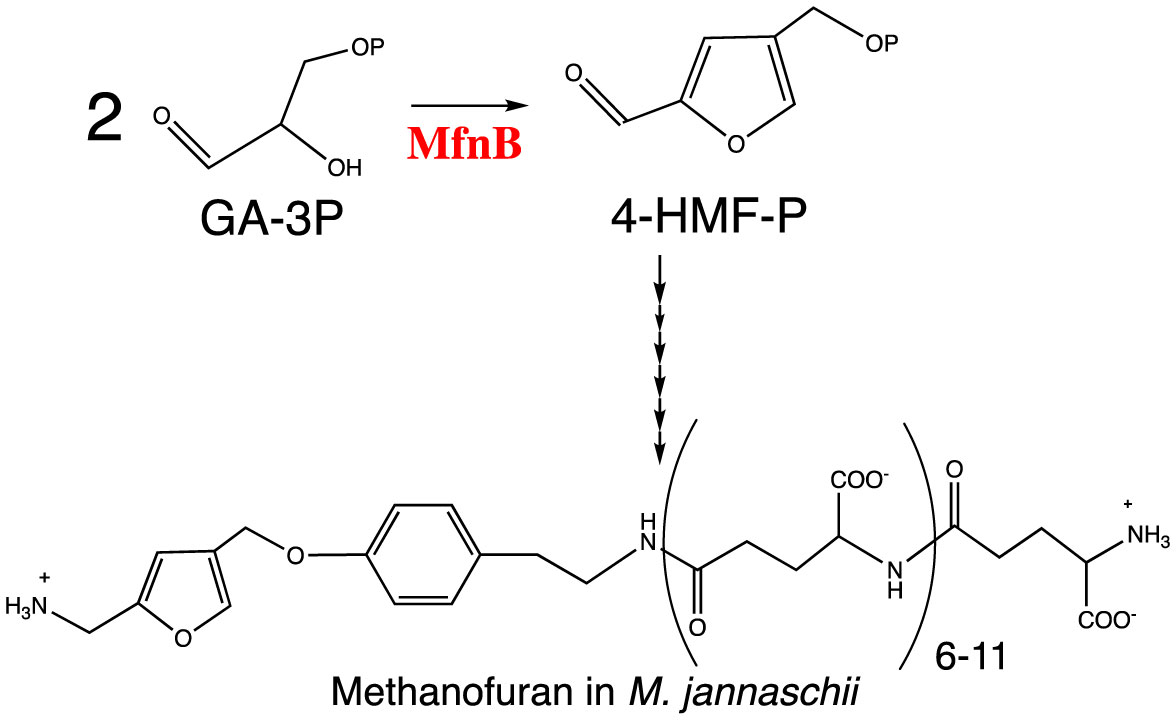
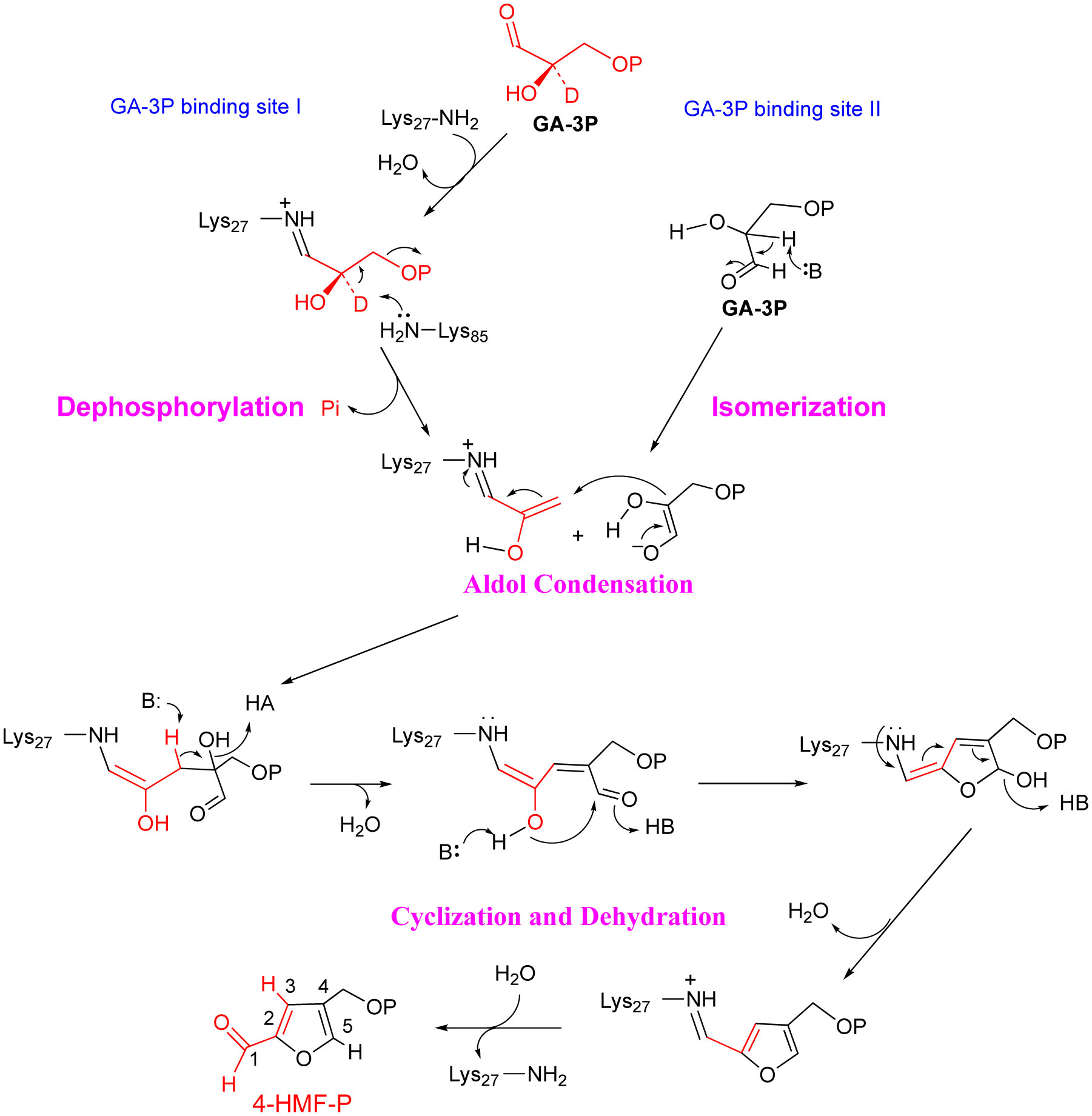
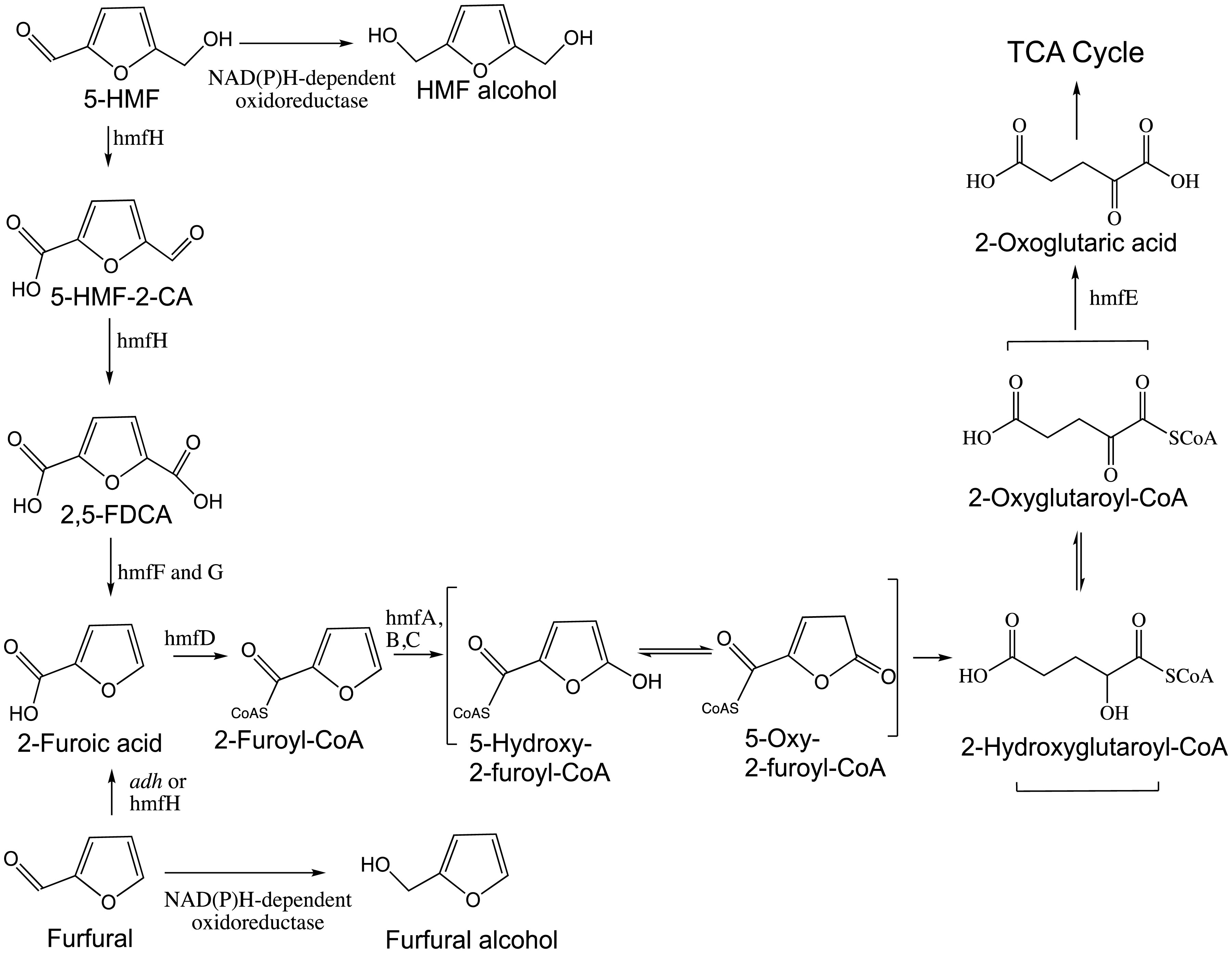
1. Introduction and motivation
Discrete choice models (DCMs) have applications in many areas such as social sciences, health economics, transportation research and health systems (see [18,11,7]). DCMs focus on predicting consumer's choices in products or services. In many cases, they are time dependent but such research has not been implemented in practice. In this manuscript, we apply the models over a time sequence to quantify and measure consumer behavior and derive the utilities using Markov decision processes (MDPs). The change in utilities from the consumer is described. The utility is composed of a systematic component dependent on the key attributes of the product and a random component. [24] presents multiple models based on different assumptions about the distribution of the random component. In some of his suggested models, the error terms are assumed to be homogeneous and uncorrelated [24]. By assuming the covariates are generated under a normal distribution and the error terms under a generalized extreme value distribution, the output data is then modeled as binary and conditional logit. We will focus on the conditional logit assumption, but add a dependence structure through time and transition probabilities under MDPs
DCMs as described by the associated attribute-levels, are modeled at different cases. [12] and [14] provide three cases of the best worst scaling experiments: 1) best-worst object scaling, 2) best-worst attribute-level scaling or profile case and 3) best-worst discrete choice experiments (BWDCEs) or multi-profile case. We are interested in the profile case, also referred to as Case 2 best-worst scaling (BWS).
By scaling the attributes and the attribute-levels, it is possible to determine the utility impact on consumer behavior. We simulate data from [5] experimental design and compute the associated parameter estimates. The results of this simulation are used to project the expected discounted utility over time using MDPs.
The manuscript is organized as follows. In Section 2, we present the model design and properties for attribute-level best-worst experiments. Extensions of MDPs for Case 2 BWS with time dependent factor are provided in Section 3. Simulated data example of Case 2 BWS models over time and results are described in Section 4. A conclusion is provided in Section 5.
2. Attribute-level best-worst design
Assume we have a sample of $ n $ consumers with $ J $ alternate choices. The utility function as described in [17] for the $ i^{th} $ consumer/individual selecting the $ j^{th} $ choice is given as:
where $(V_{ij}) $ is the systematic component and $ \epsilon_{ij} $ is the unobserved component, or error term, where $ i = 1, 2, ..., n $, $ j = 1, 2, ..., J $.
The common distribution for the error terms comes from [17], where he proposed the type Ⅰ extreme value distribution or Gumbel distribution for the error terms, that leads to the conditional logit for modelling the data. [24] presented various models and associated assumptions in modelling the choice made by the consumers. To allow for dependence in choices, the error terms may be distributed as normal and that assumption allow the outcomes to be modeled under the probit or the generalized extreme value distribution.
Let $ Y_{ij} $ denote $ i^{th} $ individual choosing the $ j^{th} $ alternative (alternate choice), where
|
$ Y_{ij} = {1, if ith individual chooses the jth alternative,0, otherwise.
$
|
Using the results from the conditional logit, the utility associated with the various choices may be estimated. The error term of the utility would come from the type Ⅰ extreme value distribution. The systematic component in the utility of the choice is given as
|
$ V_{ij} = \mathbf{x'}_{ij} \beta_{j}, $
|
with $ \mathbf{x'}_{ij} $ describing the $ i^{th} $ individual's covariates on the $ j^{th} $ alternative and $ \beta_{j} $ is defined as the individual specific covariate estimates.
The utility is then given as in Equation (2.1). Hence, the probability of the $ j^{th} $ choice being chosen is:
|
$ P(Y_{ij} = 1) = \frac{\exp{(\mathbf{x'}_{ij} \beta_j)}}{\Sigma_{\mathbf{x}_{ij'} \in C} \exp{(\mathbf{x'}_{ij'} \beta_j)}} = \frac{\exp{(V_{ij})}}{\Sigma_{\mathbf{x}_{ij'} \in C} \exp{(V_{ij'})}}, $
|
for $ C $ the set of all possible choices.
The above can be seen as a special approach at the intersection of information theory (entropy function) and the multinomial logit [1]. Following the setup as described by [23], there are $ K $ attributes that describe the products denoted as $ A_{i} $ with each attribute consisting of $ l_k $ levels for $ k = 1, . . . , K $. In the study done by [9] and [8] for contraceptive data, there were $ K = 7 $ attributes, with attribute levels $ l_1 = 8, l_2 = 3, l_3 = 4, l_5 = 4, l_6 = 8, l_7 = 9 $, and $ l_8 = 6 $. The $ 2^{nd} $ attribute is the contraceptive effect on acne, and the levels associated with this attribute are; no effect, improves, or worsens acne symptoms. Each product is represented by a profile $ \mathbf{x} = (x_1, ..., x_K) $ where $ x_i $ is the attribute level for $ A_i $ that makes up the product where the attribute-levels take values from $ 1 $ to $ l_K $ for $ k = 1, 2, ..., K $.
The choice task considered here is to look at the pairs of attribute-levels. For every profile the choice set (pairs of attribute levels) is then given as:
|
$ C_{x} = \{(x_{1}, x_{2}), . . ., (x_{1}, x_{K}), (x_{2}, x_{3}), . . ., (x_{K-1}, x_{K}), (x_{2}, x_{1}), . . ., (x_{K}, x_{K-1})\}, \notag $
|
where the first attribute-level is considered to be the best and the second is the worst. From the profile $ C_x $, the consumer evaluates the choice set and determines from the $ \tau = k(k-1) $ choices given which is the best-worst pair.
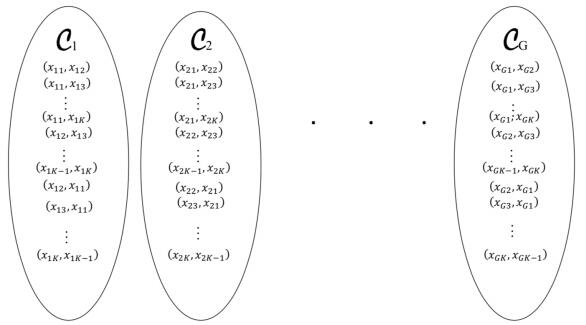
In our setup, we extend the state of choices as follows. Consider $ G $ choice sets and the associated profiles given as,
|
$ x1=(x11,x12,...,x1K)x2=(x21,x22,...,x2K)⋮xG=(xG1,xG2,...,xGK).
$
|
The corresponding choice pairs for the $ G $ choice sets are given in Figure 1. To simplify the notation, let $ C_{x_1}, C_{x_2}, ..., C_{x_G} $ be denoted as $ C_1, C_2, ..., C_G $, respectively.
[15] and [23] gave the best-worst choice probability for profile $ x_{i} $ to be:
|
$ BWxi(xij,xij′)=b(xij)b(xij′)∑∀(xij,xij′)∈Cxi,j≠j′b(xij)b(xij′),
$
|
(2.2)
|
where $ x_{ij} $ is chosen as the best attribute-level and $ x_{ij'} $ is the worst, and $ b $ is some positive scale function or impact of attribute for $ j, j' = 1, 2, ..., K, j\neq j' $ and $ i = 1, 2, ..., G $. Thus, the following assumptions hold:
|
$ BWxi(xij,xij′)≥0,∀i,j,and∑∀(xi,xj)∈Cxi,j≠j′BWxi(xij,xij′)=1.
$
|
With such assumptions, the consumer is expected to select choices with higher $ BW_{x_i} $ values, and authors have taken advantage of selecting a subset from all possible cases.
Under random utility theory, the probability an alternative is based on the utility as defined in Equation (2.1). [12] provided the utility for Case 2 BWS models and the definition of the probability as given in Equation (2.2) under the conditional logit model. [13] and [16] described other measure of utility of parameters as a function of log of odds. Here we consider the choice set $ C_{x_i} $, $ (x_{ij}, x_{ij'}) $ be the chosen pair, and the utility for choosing this pair within set $ C_{x_i} $ is then given by:
|
$ Uijj′=Vijj′+ϵijj′,
$
|
(2.3)
|
where $ V_{ijj'} $ is the systematic component, $ \epsilon_{ijj'} $ is the error term, $ j, j' = 1, 2, ..., K, j\neq j', $ and $ i = 1, 2, ..., G $.
The systematic component can be expressed as,
|
$ Vijj′=Vij−Vij′=(xij−xij′)′β,
$
|
for $ {\bf x}_{ij} $ and $ {\bf x}_{ij'} $ as in Equation (2.1) and $ \boldsymbol{\beta} $ parameter vector of best and worst choice. The data $ x_{ij} $ are indicators of the $ i^{th} $ attribute $ x_{ij} \in A_j $ and its $ j^{th} $ attribute-level $ x_{ij} $. The systematic component $ V_{ij} $ is written as:
Under the conditional logit, the probability that $ (x_{ij}, x_{ij'}) $ is chosen is
|
$ Pijj′=exp(Vijj′)∑∀(xi,xj)∈Cxi,j≠j′exp(Vijj′).
$
|
(2.4)
|
Equation (2.2) with the choice of the scale function $ b(x_{ij}) = \exp{(\beta_{A_i} + \beta_{A_{i}x_{ij}})} = \exp{(V_{ij})} $ becomes Equation (2.4). This is easily seen by:
|
$ b(xij)b(xij′)=exp(Vij−Vij′)=exp(Vijj′).
$
|
We assume the error terms come from a Type Ⅰ extreme value distribution and use the conditional logit to estimate the parameter vector:
|
$ β′=(βA1,βA2,…,βAK,βA10,βA11,…,βA1l1−1,…,βAK0,…,βAKlK−1).
$
|
[10] suggested connecting models, their parameters in estimating analysis and producing measures that are related to policy and practice. We include the time feature in Case 2 BWS model structure.
3. Time dependent modelling under Markov decision processes
Markov decision processes (MDPs) are sequential decisions making processes. MDPs seek to determine the policy or set of decision rules, under which maximum reward over time is obtained. MDPs are defined by the set $ (S, R, D) $, where $ S $ is the finite set of states, $ R $ the set of rewards, and $ D $ the set of decisions. These processes may be of discrete or continuous in time with a finite or infinite horizon, respectively. Our interest is with discrete time finite horizon MDPs, that is $ t = 1, 2, \dots , T $ where $ T $ is fixed number of time periods. The rewards (or expected rewards) are maximized by the best sequential decisions over time, making MDPs a dynamic optimization tool as used in [3] to identify the right choices of substitution behaviors of consumers.
Let $ s_t \in S $ be the states occupied at time $ t $, $ r_t(s_t) $ be the reward associated with $ s_t $, and $ d_t(r_t, s_t) $ be the decision based on the possible rewards and states at time $ t $. The decision process maps the movement from one state to another over time $ t $ based on rewards received and an optimal decision set. As the decision process is Markovian, the transition probability to the next state, $ s_{t+1} $ based solely on the decision made at the current state, $ s_t $ is $ p(s_{t+1}|s_t) $, where $ t = 0, 1, \dots , T $ [19]. There is a decision rule $ \delta $ that governs the action the consumer makes and rewards the results from the action. The decision of choices is made such that maximizes their rewards. [20] and [2] applied MDPs to DCMs. [4] applied them to solve problems in an ecological setting. As they mentioned, to suggest guidance would require running several scenarios. To our knowledge, such technique has not yet been applied to consumer choice experiments with attribute and attribute-level best-worst experiments.
For DCMs, the reward is defined by the utility function, $ r(s_t, d_t) = U(s_t, d_t) $, where $ d_t = \delta(t) $ is the decision rule at time $ t $ that maximizes the utility, and the decision rule $ \delta $ is the one that maximizes the expected discount utility given as the value function.
The value function for DCMs comes from Bellman's equation and is given as:
|
$ Vt(xt,ϵt)=maxdt∈DE(T∑t′=tγt′−tU(xt′,dt′)+ϵ(d′t)|xt,ϵt),
$
|
where the discount utility rate is given by $ \gamma \in (0, 1) $. The steps for determining the value function follow.
The decision rule used by a consumer is the one under which the utility is maximized, but assuming that a person's perceived utility is impacted by time. [6] reviewed the work done on the discount utility including consumers' discount time factor step. The discount utility rate weights the utility a person gains from an option at some ulterior time based on their current state at time $ t $ and guarantees the convergence in the infinite sum of rewards.
MDPs model the sequence of decisions based on expected rewards and transition probabilities. We defined state transition as
|
$ P(s_{t+1}|s_t) = P(s_{t+1} = s'|s_t = s) = P_{ss'} , $
|
and the corresponding transition probability of the decision can be written as $ P(d_{t+1} |d_t, x_t) $ with the decision $ d_t $ made at time $ t $ that satisfies
|
$ \max\limits_{d_t \in D} E(U^{t}(x_t, \epsilon_t)), $
|
for $ t = 1, 2, \dots, T. $
Since no closed form expression for this dynamic optimization problem is available, the value functions are computed recursively via dynamic programming, under backwards recursion algorithm. First we compute,
|
$ V^T(x_T) = \sum\limits_{d_T \in D} U(x_T, d_T) P(d_T), $
|
with $ P(d_T) $ as the probability that $ d_T $ was made. We denote $ P(d_j|d_{j-1}) $ as the transition probability of decision $ d_j $ given previous decision $ d_{j-1} $ for $ j = 1, \dots, T $.
Next we move one time step back and compute,
|
$ V^{T-1}(x_{T-1}, d_{T-1}) = U(x_{T-1}, d_{T-1})+\sum\limits_{d_{T}\in D} \gamma V^{T}(x_{T}) P(d_{T}|d_{T-1}), $
|
and another,
|
$ V^{T-2}(x_{T-2}, d_{T-2}) = U(x_{T-2}, d_{T-2})+\sum\limits_{d_{T}\in D} \gamma V^{T-1}(x_{T-1}, d_{T-1}) P(d_{T-1}|d_{T-2}). $
|
Following this pattern, we get:
|
$ V^{t}(x_{t}, d_{t}) = U(x_{t}, d_{t})+\sum\limits_{d_{T}\in D} \gamma V^{t+1}(x_{t+1}, d_{t+1}) P(d_{t+1}|d_{t}), $
|
for $ t = 1, 2, \ldots, T-1 $. For these experiments, we consider discrete time finite horizon MDPs where:
● $ G $ choice sets are modeled across time of length $ T $.
● $ x_{t} $ are the attributes and attribute-levels corresponding to the choices in $ C_{g}, \mbox{for} g = 1, 2, \ldots, G $.
● The decision set depends on the choice set evaluated $ d_{t}\in D_{i} $ where $ i = 1, 2, \ldots, G $, and $ t = 1, 2, \ldots, T. $
● Transition probabilities depend on a set of parameters $ \boldsymbol{\theta} $ that are assumed known or data estimable. $ \boldsymbol{\theta} $ is a function of attribute and attribute level not necessarily identical to $ \boldsymbol{\beta} $, as described in [2].
● Transition probability matrices are dependent on time and on the choice set being evaluated.
There are $ G $ choice sets with $ \tau = k(k-1) $ choice pairs in each set. To compute the transition probabilities, the parameters are assumed known [2]. Let $ \boldsymbol{\theta}_{d_{t+1}|d_{t}} $ be the parameter vector for the transition probability from choice $ d_{t} $ to $ d_{t+1} $ that captures consumer's behavior or preference.
Let the choice pair $ (x_j , x_{j'}) $ denote the $ q^{th} $ best-worst choice pair. Compute
|
$ πqr=exp((xj−xj′)′θq|r),
$
|
for $ j, j' = 1, 2, ..., J $, where $ J $ is the total possible choices for experiment, and $ \boldsymbol{\theta}_{q|r} $ are the parameters estimating the transition from choice $ r $ to choice $ q $.
In Case 2 BWS models, a set of $ G $ choice sets are considered in the experiment. In MDPs, there exists a set of states $ s_{t}\in S $ and possible decisions in $ d_{t}\in D $ for $ t = 1, 2, \ldots, T $. For Case 2 BWS MDPs, the possible states in each choice set are the alternatives, and the decision made at each time point will also be one of the alternatives. For choice set $ C_{i} $ the state $ s_{ti} $ and decision $ d_{ti} $ are such that $ 1 \leq s_{ti}, d_{ti} \leq \tau $ where $ i = 1, 2, \ldots, G $ and $ t = 1, 2, \ldots, T $.
Let $ s_{it+1} = s_{i}' $ and $ s_{it} = s_{i} $, where $ s_{i}', s_{i} \in S_{i} $ for $ i = 1, 2, \ldots, G $ and $ t = 1, 2, \ldots, T $. The transition probability is denoted as
|
$ P^{t}_{iss'} = P^{t}(s_{i}'|s_{i}, \boldsymbol{\theta}^t_{s_{i}}), $
|
where
|
$ \boldsymbol{\theta}^{t}_{s_{i}} = (\theta^{t}_{s_{i}A_{1}}, \ldots, \theta^{t}_{s_{i}A_{K}}, \theta^{t}_{s_{i}A_{1}1}, \ldots, \theta^{t}_{s_{i}A_{K}l_{k}}) $
|
is the set of parameters guiding the transition from $ s_{i} $ to $ s_{i}' $, for $ i = 1, 2, \ldots, G $. In Case 2 BWS models, the parameters would be the measure of relative impact/preference associated with the attributes and attribute-levels corresponding to the different choice pairs, or states, given the current state is $ s_{i} $, where $ i = 1, 2, \ldots, G $. [21] and [2] state that $ \boldsymbol{\theta}^{t}_{s_{i}} $ is assumed known under some rationale with regards to consumer behavior or preferences.
The parameter estimates determined by fitting the conditional logit model, as described in Section 2, produced $ \hat{\boldsymbol{\beta}} $ a $ p = K+\sum\limits_{k = 1}^{K}l_{k} $ vector. These parameter estimates measure the relative impact of each attribute and attribute-level in the decisions made by consumers. The parameters $ \boldsymbol{\theta}^{t}_{s_{i}} $ are the assumed impacts of the attributes and attribute-levels in consumers decisions given they currently occupy state $ s_{i} $. We define these parameters as functions of the parameter estimates $ \hat{\boldsymbol{\beta}} $, where there is a rate of change in the impacts over time, as follows:
|
$ ˆθtsi=(asiA1(t)ˆβA1,…,asiAK(t)ˆβAK,asiA11(t)ˆβA11,…,asiAKlk(t)ˆβAKlK),
$
|
where $ a_{i}'s $ are the time factor change and $ \hat{\beta}_{A_{k}} $ and $ \hat{\beta}_{A_{k}l_{k}} $ are fixed for $ i = 1, 2, \ldots, G $, $ 1\leq s_{i} \leq \tau $, $ k = 1, 2, \ldots, K $, and $ t = 1, 2, \ldots, T $. The definition of
|
$ asi(t)=(asiA1(t),…,asiAK(t),asiA11(t),…,asiAKlk(t)),
$
|
depends on the state $ s_{i} $ and time $ t = 1, 2, \ldots, T $. We have considered $ a_{s_{i}j}(t) = a_{s_{i}j}^{t} $, where if $ |a_{s_{i}j}|<1 $ the impact of the attribute or attribute-level would be lessening with time, where $ i = 1, 2, \ldots, G $ and $ j = 1, 2, \ldots, K $. Also, if $ a_{s_{i}A}(t)\hat{\beta}_{A} = a_{s_{i}A}^{t}\hat{\beta}_{A} > 0 $, then the attribute or attribute-level has a positive impact evolving at the rate $ a_{s_{i}A}^{t} $ over time for $ A = A_1, A_2, \ldots, A_K $, $ i = 1, 2, \ldots, G $, and $ t = 1, 2, \ldots, T $. A static, or non-time dependent, system is considered if $ a_{s_{i}A}(t) = 1 $, where $ i = 1, 2, \ldots, G $, $ A = A_1, A_2, \ldots, A_K $, and $ t = 1, 2, \ldots, T $.
These $ a_{s_{i}A}(t) $ are rates of change that guide how the dynamic transition of the decision process. We can easily consider them to be non-time dependent, $ a_{s_{i}A}(t) = a_{s_{i}A} $, defining the transition probabilities as stationary over time. As was mentioned earlier, there are infinitely many possibilities in how we define the transitions. [21] states that when using rational observation to define the transitions, many possible choice behaviors on the consumers are possible. [4] recommends running many scenarios to determine the transition probabilities that will maximize the expected reward. Our definition also offers infinitely many possibilities in terms of the definition; however, we defined a rate of change to consider an evolving system. In this way, the researcher can determine what they consider feasible rates and see if the system eventually evolves to the decision they desire and how long it would take to get there.
Given $ \boldsymbol{\theta}^{t}_{s_{i}} $, the transition probabilities may be determined using random utility theory, or inverse random utility theory in the case attribute-level best-worst models as shown in Section 3. Let $ s_{ijj'}' = (x_{ij}, x_{ij'}) $, where $ j\neq j' $, $ j, j' = 1, 2, \ldots, \tau $, and $ i = 1, 2, \ldots, G $. The probability that $ s_{ijj'}' $ is the chosen state means that given $ \boldsymbol{\theta}^{t}_{s_{i}} $, the utility for $ s_{ijj'}' $ is the maximum utility. The transition probability is given as,
|
$ Pt(s′ijj′|si,θtsi)=Pt(Utijj′>Utikk′,∀k≠k′∈Ci|si,θtsi)=Pt(Vtijj′+ϵtijj′>Vtikk′+ϵtikk′,∀k≠k′∈Ci|si,θtsi)=Pt(ϵtikk′<ϵtijj′+Vtijj′−Vtikk′,∀k≠k′∈Ci|si,θtsi),
$
|
where $ j\neq j' $, $ j, j' = 1, 2, \ldots, \tau $, $ i = 1, 2, \ldots, G $, and $ t = 1, 2, \ldots, T $. If we assume the random error terms are independently and identically distributed as type Ⅰ extreme value distribution, the probability would then be found using the conditional logit, and is given as:
|
$ Pt(s′ijj′|si,θtsi)=Pt(Utijj′>Utikk′,∀k≠k′∈Ci|si,θtsi)=exp(Vtijj′)∑k,k′∈Ciexp(Vtikk′),
$
|
where $ j\neq j' $, $ k\neq k' $, $ j, j' = 1, 2, \ldots, \tau $, $ i = 1, 2, \ldots, G $, and $ t = 1, 2, \ldots, T $.
The transition matrix is then a $ \tau \times \tau $ matrix of the form,
|
$ P_{i}^{t} = \left( Pti11Pti12...Pti1τPti21Pti22...Pti2τ..................Ptiτ1Ptiτ2...Ptiττ
\right) = \left( P^{t}_{iss'}\right)_{\tau \times \tau} $
|
where $ i = 1, 2, \ldots, G, \quad s, s' = 1, 2, \ldots, \tau $, and where $ \sum\limits_{s' = 1}^{\tau} P^{t}_{iss'} = 1 $.
The transition matrix may be either stationary or dynamic in nature. In our definition of $ \boldsymbol{\theta}^{t}_{s_{i}} $, this is determined by the rate $ a_{s_{i}j}(t) $, where $ i = 1, 2, \ldots, G $, $ 1\leq j \leq p $, and $ t = 1, 2, \ldots, T $. In Section 4, we provide simulations under stationary and dynamic transition probabilities and make comparisons.
The decision at time $ t $ is denoted by $ d_t $ are the choice pairs, and are the different states within a choice set. In Case 2 BES experiments, the $ d^{i}_{t} = (x_{ij}, x_{ij'}) $, where $ i = 1, 2, ..., G, j, j' = 1, 2, ..., K $, and $ j \ne j' $. Then the parameter vector $ \boldsymbol{\theta}_{d_t} $ is a known vector relating the decision made at time $ t $ given the decision made at time $ t-1 $ for $ t = 1, 2, ..., T $. Different assumptions about the parameters $ \boldsymbol{\theta}_{d_t} $ yield different results and value functions within the experiments. However, this variability in constructing these parameters allows us to view hypothetical future and the values they offer to consumers.
We look at the effect of varying hyper-parameters over time to compute the transition probabilities, that is we use the previous parameter estimates as inputs into determining $ \boldsymbol{\theta}_{d_{t+1}} $.
For simplicity, we will first consider stationary transition matrices. That is, $ \boldsymbol{\theta}_{d_{t+1}} = a_r\boldsymbol{\theta} $ where $ a_r $ as independent of time, and will extend to dynamic version.
In practical applications, decisions on how to act or proceed would be dictated under some expected utility. To that end, a backward recursive method is then used and a dynamic planning system that the process from its starting values/stages to its goal stage is provided.
4. Computations
4.1. Data simulation
We adapt our simulations of experiments to [5]. The latter conducted a Case 2 BWS type of study to examine the quality of life of seniors. They considered a balanced design with five attributes (attachment, security, role, enjoyment, and control) with four attribute levels (none, little, lot, and all) for attachment, security, and enjoyment and (none, few, many, all) for role and control. The attribute-levels are about the hypothetical quality of life states of 30 people of age 65 or more studied at one time. In their paper, they provide a partial look at their data and include the parameter estimates. Using that information, data was generated under such rationale and MDP simulations performed.
As mentioned in [23], a full factorial design, with a total of 1024 profile in this case, is costly and places an overwhelming choice task on the shoulders of the consumers. Therefore, an optimal fractional factorial design was considered. In doing the computations in R, we utilized a package DoE.design. A subset of 32 profiles, with $ \tau = 20 $ choice pairs in each choice set, was selected and used in the simulations based on a sample of $ n = 100 $ consumers. Using the parameter estimates from [5], we generated data from that model since real data was not available. We will first compare the model parameters with those from [5]. Results are shown in Table 1. Our simulated data appears to be similar to their data. Based on the data, we aim to compute the probabilities, $ BW_{x_i}(x_{ij}, x_{ij'}) $, the utilities on the choice set $ C_{i} $ dynamically over $ T = 5 $ time periods using MDPs. Time can be thought of in years if we consider such surveys to be conducted annually.
Table 1. Parameter estimates from [5] paper and our simulation of their data.
|
[5] |
Simulated data |
| Parameters |
Estimates |
SE |
Estimates |
SE |
| Constant |
-0.3067 |
0.0750 |
0.0500 |
* |
| Attachment |
0.8105 |
0.0803 |
0.8142 |
* |
| Security |
* |
* |
* |
* |
| Enjoyment |
0.2632 |
0.1010 |
0.2842 |
0.0394 |
| Role |
0.1908 |
0.0974 |
0.1611 |
0.0400 |
| Control |
0.1076 |
0.0971 |
0.1148 |
0.0402 |
| Attachment None |
-1.9678 |
0.1129 |
-1.8535 |
0.0548 |
| Attachment Little |
0.1694 |
0.1012 |
0.1389 |
0.0532 |
| Attachment Lot |
0.9053 |
0.0905 |
0.9210 |
0.0561 |
| Attachment All |
0.8932 |
* |
0.7936 |
* |
| Security None |
-0.6123 |
0.1180 |
-0.6262 |
0.0541 |
| Security Little |
-0.3761 |
0.1302 |
-0.4077 |
0.0547 |
| Security Lot |
0.0373 |
0.1153 |
0.1027 |
0.0543 |
| Security All |
0.9511 |
* |
0.9312 |
* |
| Enjoyment None |
-0.8888 |
0.1286 |
-0.8166 |
0.0542 |
| Enjoyment Little |
-0.3367 |
0.1632 |
-0.3814 |
0.0544 |
| Enjoyment Lot |
0.6561 |
0.1493 |
0.6844 |
0.0548 |
| Enjoyment All |
0.5695 |
* |
0.5136 |
* |
| Role None |
-0.8956 |
0.1239 |
-0.8903 |
0.0546 |
| Role Few |
-0.0277 |
0.1532 |
-0.0079 |
0.0546 |
| Role Many |
0.4435 |
0.1363 |
0.4007 |
0.0546 |
| Role All |
0.4798 |
* |
0.4975 |
* |
| Control None |
-0.8085 |
0.1122 |
-0.7254 |
0.0546 |
| Control Few |
0.0835 |
0.1596 |
0.0755 |
0.0552 |
| Control Many |
0.2780 |
0.1376 |
0.2592 |
0.0543 |
| Control All |
0.4471 |
* |
0.3907 |
* |
Attribute and attribute-level data in the experiments are series of $ 1's $, and $ 0's $ indicating the attributes and attribute-levels in the choice pair. Looking at Table 3 in [5], the attribute-level data when the $ l_{i}^{th} $ attribute-level is chosen as best is coded as $ 1 $ for the attribute-levels $ 1, 2, \ldots, l_{i}-1 $, and the attribute-level data when the $ l_{i}^{th} $ attribute-level is chosen as worst is coded as $ -1 $ for the attribute-levels $ 1, 2, \ldots, l_{i}-1 $. [22] explained that for attribute-level point estimates, they satisfy the condition:
|
$ lk∑i=1βi=0orβlk=−li−1∑j=1βj,
$
|
for all $ k = 1, 2, \ldots, K $.
The probabilities to simulate choice behavior were computed using Equation (2.4). Using the estimates provided in Table 1, the values of $ V_{ijj'} $ were computed. For the choice pair (Attachment None, Enjoyment Lot), the associated parameter estimates with this pair are given as:
$ \hat{\beta}_{A_{1}} = 0.8142 $ for Attachment, $ \hat{\beta}_{A_{4}} = 0.2842 $ for Enjoyment, $ \hat{\beta}_{A_{1}1} = -1.8535 $ for Attachment None, and $ \hat{\beta}_{A_{4}3} = 0.6884 $ for Enjoyment Lot.
The value of $ V_{ijj'} $ for this pair would be:
|
$ ˆVijj′=exp(ˆVij−ˆVij′)=exp((ˆβAj+ˆβAjxj)−(ˆβAj′+ˆβAj′xj′))=exp((0.8142−1.8535)−(0.2842+0.6884)).
$
|
Obtaining these values for all choice pairs, the probabilities of choice selection were determined per profile and consumer choices were simulated. The value function, or expected utility, under our set up for the best-worst pairs from profile 1 are computed with the discount rate $ \gamma = 0.95 $.
The data was exported from R into the SAS® environment. Using the SAS® multinomial discrete choice procedure (MDC), the multinomial logit model was fitted to the data.
From the parameter estimates, we determine the choice pairs with the highest and lowest utilities for the experiment as in Equation (2.3). The choice pairs with the highest utilities are given in Table 2, and the pairs with the lowest utilities are given in Table 3. Capturing the attribute-level information in the choice pair, we consider the notation $ x_{ij} $ be also written as $ x_{ij_l} $ or $ x_{jl} $ (if the profile is obvious) where $ i $ indicates the profile, $ j $ the attribute and $ l $ the attribute-level ($ i = 1, \ldots, G = 32, j = 1, \ldots, K = 5 $ and $ l = 1, \ldots, l_j $). The pair $ (x_{11_3}, x_{15_1}) $ provides the greatest utility of any pair in the experiment as seen in Table 2. The pair $ (x_{11_3}, x_{15_1}) $ has the attribute "Attachment" and attribute-level "Lot" as the best and attribute "Control" and level "None" as the worst. Looking at the attribute and attribute-level impacts and the parameter estimates given in Table 1, this choice pair having the highest utility makes sense. We see that the attribute "Attachment" has the largest impact in comparison to "Security", which was also noted in [5]. The attribute with the smallest impact in comparison to "Security" was "Control." Looking at the attribute-levels for these attributes, we see that the level "Lot" for "Attachment" has the largest positive impact, and attribute-level "None" for "Control" has the largest negative impact.
Table 2. Choice pairs with the highest utility in the experiment.
| Best Attribute |
Level |
Worst Attribute |
Level |
Utility |
| 1 |
3 |
5 |
1 |
8.9107 |
| 1 |
3 |
4 |
1 |
7.7977 |
| 1 |
4 |
5 |
1 |
7.2599 |
| 1 |
3 |
3 |
1 |
6.9108 |
| 1 |
4 |
4 |
1 |
6.6562 |
| 1 |
3 |
2 |
1 |
6.4402 |
Table 3. Choice pairs with the lowest utility in the experiment.
| Best Attribute |
Level |
Worst Attribute |
Level |
Utility |
| 5 |
1 |
1 |
3 |
-4.3159 |
| 4 |
1 |
1 |
3 |
-4.1167 |
| 5 |
1 |
1 |
4 |
-3.9912 |
| 3 |
1 |
1 |
3 |
-3.9082 |
| 4 |
1 |
1 |
4 |
-3.8493 |
| 2 |
1 |
1 |
3 |
-3.7974 |
We next conduct the Case 2 BWS experiment of choosing the pairs and describing the optimal variation over $ T = 5 $ time periods. Under that experiment, the consumer chooses an alternative that provides maximum utility of attributes and attribute-levels over time. We will use numerical maximization to find the expected utility under Bellman's equation of the MDPs. We will consider two options. Under Option 1, stationary transition probabilities are considered while dynamic transition probabilities are presented under Option 2.
4.1.1. Option 1: Stationary transition probabilities
For the simulated data of [5], we consider MDPs where the consumers are more likely to choose the same alternative at each time point. The transition parameters $ \boldsymbol{\theta}^{t}_{s_{i}} $, where $ s^{t}_{i} = (x_{ij}, x_{ij'}) $ are defined as for the attributes as,
|
$ \theta^{t}_{s_{i}A_{k}} = \left\{ 3|βAk|,if xij∈Ak,−3|βAk|,if xij′∈Ak,βAk, otherwise,
\right. $
|
and for the attribute-levels,
|
$ \theta^{t}_{s_{i}A_{k}x_{ik}} = \left\{ 3|βAkxik|,if xij=xik where xik∈Akxik,−3|βAkxik|,if xij′=xik where xik∈Akxik,βAkxik, otherwise,
\right. $
|
where $ j\neq j' $, $ j, j', k = 1, 2, \ldots, K $, $ 1\leq x_{ik}\leq l_{k} $, and $ i = 1, 2, \ldots, G $. The goal of this option was to design the transition probabilities in a way that the choice made at $ t $ is most likely to be made at $ t+1 $. If we considered $ a_{s_{i}m}(t) = \beta_{m} $ for $ i = 1, 2, \ldots, G $, and $ m = 1, 2, \ldots, p $, then the system would remain static and every row of the transition matrix would be the same. Recall that $ p = K+\sum\limits_{k = 1}^{K}l_{k} = 25 $ is the number of parameters. We consider $ 3|\beta_{m}| $ when a state or choice pair at time $ t+1 $ has the same best attribute and attribute-level as the state occupied at time $ t $, and $ -3|\beta_{m}| $ when a state or choice pair at time $ t+1 $ has the same worst attribute and attribute-level as the state occupied at time $ t $. We consider $ |\beta_{m}| $ to control the direction of the impact making sure it is positive for the best attribute and attribute-level of $ s_{i} $ and use $ -|\beta_{m}| $ to make sure its negative for the worst attribute and attribute-level of $ s_{i} $. We use $ 3 $ to increase the impact of the best and worst attributes and attribute-levels of $ s_{i} $. The definition of $ a_{s_{i}m}(t) $ in this way insures that states with common best and worst attributes and attribute-levels as the present state occupied, $ s^{t}_{i} = (x_{ij}, x_{ij'}) $, have a greater probability of being transitioned to, where $ i = 1, 2, \ldots, G $, $ j\neq j' $, $ j, j' = 1, 2, \ldots, K $, and $ t = 1, 2, \ldots, T $.
4.1.2. Option 2: Dynamic transition probabilities
In this option, consumers acquire time dependent decisions with a different impact, making the transition probabilities dynamic. For the simulated data as in [5], we consider MDPs where in the consumers are more likely to choose the same alternative at each time point. The transition parameters $ \boldsymbol{\theta}^{t}_{s_{i}} $ where $ s^{t}_{i} = (x_{ij}, x_{ij'}) $ are defined as for the attributes as:
|
$ \theta^{t}_{s_{i}A_{k}} = \left\{ 3t|βAk|,if xij∈Ak,−3t|βAk|,if xij′∈Ak,βAk, otherwise,
\right. $
|
and for the attribute-levels,
|
$ \theta^{t}_{s_{i}A_{k}x_{ik}} = \left\{ 3t|βAkxik|,if xij=xik where xik∈Akxik,−3t|βAkxik|,if xij′=xik where xik∈Akxik,βAkxik, otherwise,
\right. $
|
where $ j\neq j' $, $ j, j', k = 1, 2, \ldots, K $, $ 1\leq x_{k}\leq l_{k} $, and $ i = 1, 2, \ldots, G $.
4.2. Results and discussions
The responses for choice sets are discussed here. Table 2 reveals that "Attachment" is one of the most important attributes for the models, matching the results obtained in [5]. Since only one level of "Attachment" is represented in each profile, we do not compare the attribute-levels with those found in [5].
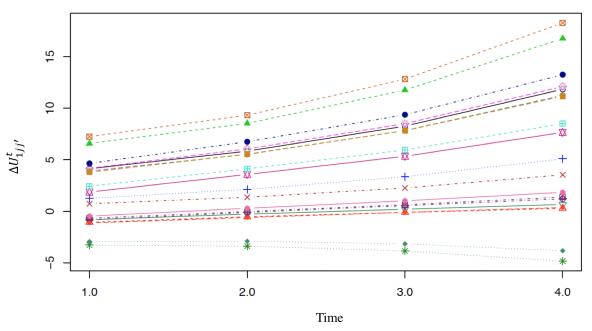
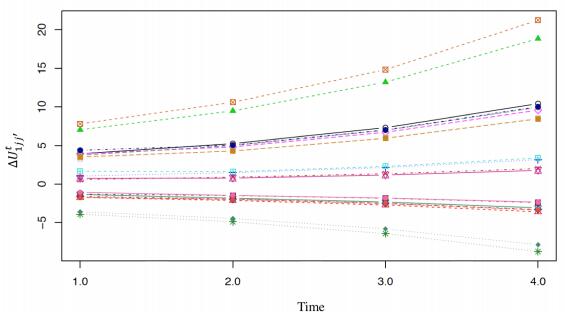
Furthermore, the expected utilities are then obtained for each of the 32 profiles and each of the 20 choices. For summary purpose, the difference of the expected utility values, $ \Delta U^{t}_{1jj'} = U^{t+1}_{1jj'} - U^{t}_{1jj'} $, for Profile 1 at consecutive time periods are given in Figure 2. Choice pair $ (x_{11_2}, x_{15_1}) $, where $ x_{11_2} $ is the attribute-level "Little" of attribute "Attachment" is the best and $ x_{15_1} $ is the attribute-level "None" of attribute "Control" is the worst, corresponds to the highest expected utility.
The transition matrices are built for each of the options of previous subsections. For Option 1 the transition matrix is the same at all the time points since it is stationary, and it is given in Table 4. For Option 2, the transition matrix at time $ t = 1 $ is kept the same as it was in Option 1 in Table 4, and subsequent transition probabilities at time $ t = 2, 3, 4 $ are given in Tables 5, 6, and 7, respectively. The same best-worst pair $ (x_{11_2}, x_{15_1}) $, where $ x_{11_2} $ is the attribute-level "Little" of attribute "Attachment" is the best and $ x_{15_1} $ is the attribute-level "None" of attribute "Control" is the worst, corresponds to the highest expected utility as it was in Option 1 with a slight difference in the expected utilities. This is because the transition matrices are reinforcing those choices over time. This explains why the transition matrix under Table 7 is the identity matrix as expected under the trend in the expected utilities. We also note a clustering in Figure 3 of the expected utilities into $ 5 $ groups. This clustering based on the suggested transition probabilities seems to better capture the estimates from the DCEs as was suggested in [5] when they considered gender in the quality of life study. Such results open up new ideas of supervised temporal learning algorithm in DCMs.
Table 4. Stationary transition matrix in Option 1 for Profile 1 for $ t = 2, 3 $ and $ 4 $.
| $ (x_{12}, x_{23}) $ | 0.518 | 0.000 | 0.038 | 0.001 | 0.081 | 0.000 | 0.192 | 0.000 | 0.000 | 0.069 | 0.001 | 0.032 | 0.002 | 0.014 | 0.011 | 0.002 | 0.026 | 0.001 | 0.012 | 0.002 |
| $ (x_{23}, x_{12}) $ | 0.000 | 0.487 | 0.000 | 0.226 | 0.000 | 0.105 | 0.001 | 0.044 | 0.010 | 0.002 | 0.022 | 0.001 | 0.052 | 0.000 | 0.010 | 0.002 | 0.024 | 0.001 | 0.011 | 0.002 |
| $ (x_{12}, x_{33}) $ | 0.025 | 0.000 | 0.703 | 0.000 | 0.037 | 0.000 | 0.088 | 0.000 | 0.065 | 0.000 | 0.003 | 0.002 | 0.008 | 0.001 | 0.000 | 0.043 | 0.000 | 0.018 | 0.005 | 0.001 |
| $ (x_{33}, x_{12}) $ | 0.000 | 0.076 | 0.000 | 0.703 | 0.000 | 0.051 | 0.000 | 0.021 | 0.000 | 0.021 | 0.003 | 0.002 | 0.008 | 0.001 | 0.032 | 0.000 | 0.075 | 0.000 | 0.005 | 0.001 |
| $ (x_{12}, x_{42}) $ | 0.091 | 0.001 | 0.063 | 0.001 | 0.331 | 0.000 | 0.032 | 0.000 | 0.006 | 0.012 | 0.031 | 0.002 | 0.030 | 0.002 | 0.044 | 0.002 | 0.043 | 0.002 | 0.008 | 0.009 |
| $ (x_{42}, x_{12}) $ | 0.000 | 0.223 | 0.000 | 0.320 | 0.000 | 0.262 | 0.001 | 0.063 | 0.005 | 0.010 | 0.006 | 0.008 | 0.024 | 0.002 | 0.008 | 0.005 | 0.034 | 0.001 | 0.028 | 0.002 |
| $ (x_{12}, x_{51}) $ | 0.025 | 0.000 | 0.018 | 0.000 | 0.038 | 0.000 | 0.701 | 0.000 | 0.002 | 0.003 | 0.004 | 0.002 | 0.065 | 0.000 | 0.005 | 0.001 | 0.093 | 0.000 | 0.043 | 0.000 |
| $ (x_{51}, x_{12}) $ | 0.000 | 0.076 | 0.000 | 0.110 | 0.000 | 0.051 | 0.000 | 0.681 | 0.002 | 0.003 | 0.003 | 0.002 | 0.000 | 0.020 | 0.005 | 0.001 | 0.000 | 0.014 | 0.000 | 0.031 |
| $ (x_{23}, x_{33}) $ | 0.003 | 0.011 | 0.229 | 0.000 | 0.012 | 0.002 | 0.029 | 0.001 | 0.469 | 0.000 | 0.025 | 0.001 | 0.058 | 0.001 | 0.000 | 0.101 | 0.001 | 0.043 | 0.013 | 0.002 |
| $ (x_{33}, x_{23}) $ | 0.082 | 0.000 | 0.001 | 0.034 | 0.013 | 0.003 | 0.031 | 0.001 | 0.000 | 0.501 | 0.001 | 0.036 | 0.002 | 0.015 | 0.078 | 0.000 | 0.185 | 0.000 | 0.013 | 0.002 |
| $ (x_{23}, x_{42}) $ | 0.009 | 0.038 | 0.020 | 0.018 | 0.103 | 0.003 | 0.100 | 0.003 | 0.040 | 0.009 | 0.211 | 0.002 | 0.206 | 0.002 | 0.098 | 0.004 | 0.095 | 0.004 | 0.018 | 0.019 |
| $ (x_{42}, x_{23}) $ | 0.226 | 0.001 | 0.016 | 0.015 | 0.020 | 0.012 | 0.084 | 0.003 | 0.001 | 0.215 | 0.001 | 0.176 | 0.006 | 0.042 | 0.019 | 0.013 | 0.079 | 0.003 | 0.065 | 0.004 |
| $ (x_{23}, x_{51}) $ | 0.002 | 0.010 | 0.005 | 0.005 | 0.011 | 0.002 | 0.206 | 0.000 | 0.011 | 0.002 | 0.023 | 0.001 | 0.422 | 0.000 | 0.011 | 0.002 | 0.196 | 0.000 | 0.091 | 0.000 |
| $ (x_{51}, x_{23}) $ | 0.095 | 0.000 | 0.007 | 0.006 | 0.015 | 0.003 | 0.001 | 0.038 | 0.001 | 0.090 | 0.001 | 0.042 | 0.000 | 0.557 | 0.014 | 0.003 | 0.001 | 0.040 | 0.001 | 0.087 |
| $ (x_{33}, x_{42}) $ | 0.014 | 0.006 | 0.002 | 0.058 | 0.053 | 0.002 | 0.051 | 0.002 | 0.001 | 0.088 | 0.035 | 0.003 | 0.034 | 0.003 | 0.319 | 0.000 | 0.312 | 0.000 | 0.009 | 0.010 |
| $ (x_{42}, x_{33}) $ | 0.011 | 0.005 | 0.324 | 0.000 | 0.010 | 0.006 | 0.040 | 0.001 | 0.214 | 0.000 | 0.006 | 0.009 | 0.027 | 0.002 | 0.000 | 0.251 | 0.001 | 0.060 | 0.031 | 0.002 |
| $ (x_{33}, x_{51}) $ | 0.004 | 0.002 | 0.000 | 0.016 | 0.006 | 0.001 | 0.110 | 0.000 | 0.000 | 0.024 | 0.004 | 0.002 | 0.073 | 0.000 | 0.036 | 0.000 | 0.672 | 0.000 | 0.049 | 0.000 |
| $ (x_{51}, x_{33}) $ | 0.004 | 0.002 | 0.113 | 0.000 | 0.006 | 0.001 | 0.000 | 0.015 | 0.075 | 0.000 | 0.004 | 0.002 | 0.000 | 0.023 | 0.000 | 0.050 | 0.000 | 0.668 | 0.000 | 0.035 |
| $ (x_{42}, x_{51}) $ | 0.010 | 0.004 | 0.007 | 0.006 | 0.008 | 0.005 | 0.272 | 0.000 | 0.00 | 0.009 | 0.00 | 0.008 | 0.179 | 0.000 | 0.008 | 0.005 | 0.258 | 0.000 | 0.211 | 0.000 |
| $ (x_{51}, x_{42}) $ | 0.020 | 0.009 | 0.014 | 0.013 | 0.073 | 0.002 | 0.002 | 0.078 | 0.009 | 0.019 | 0.048 | 0.004 | 0.002 | 0.118 | 0.070 | 0.003 | 0.002 | 0.082 | 0.000 | 0.432 |
Table 5. Dynamic transition matrix in Option 2 for Profile 1 at time $ t = 2 $.
| $ (x_{12}, x_{23}) $ | 0.980 | 0.000 | 0.002 | 0.000 | 0.005 | 0.000 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{12}) $ | 0.000 | 0.974 | 0.000 | 0.015 | 0.000 | 0.007 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{33}) $ | 0.000 | 0.000 | 0.999 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{33}, x_{12}) $ | 0.000 | 0.000 | 0.000 | 0.999 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{42}) $ | 0.048 | 0.000 | 0.033 | 0.000 | 0.748 | 0.000 | 0.170 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{12}) $ | 0.000 | 0.129 | 0.000 | 0.185 | 0.000 | 0.650 | 0.000 | 0.036 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.999 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{51}, x_{12}) $ | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.998 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{33}) $ | 0.000 | 0.000 | 0.016 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.973 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.007 | 0.000 | 0.003 | 0.000 | 0.000 |
| $ (x_{33}, x_{23}) $ | 0.001 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.980 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.000 | 0.012 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{42}) $ | 0.000 | 0.031 | 0.001 | 0.001 | 0.012 | 0.000 | 0.003 | 0.000 | 0.033 | 0.000 | 0.737 | 0.000 | 0.167 | 0.000 | 0.011 | 0.000 | 0.003 | 0.000 | 0.000 | 0.002 |
| $ (x_{42}, x_{23}) $ | 0.180 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.000 | 0.000 | 0.171 | 0.000 | 0.600 | 0.000 | 0.033 | 0.000 | 0.002 | 0.002 | 0.000 | 0.008 | 0.000 |
| $ (x_{23}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.016 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.962 | 0.000 | 0.000 | 0.000 | 0.015 | 0.000 | 0.007 | 0.000 |
| $ (x_{51}, x_{23}) $ | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.989 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.005 |
| $ (x_{33}, x_{42}) $ | 0.000 | 0.000 | 0.000 | 0.032 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.048 | 0.000 | 0.000 | 0.000 | 0.000 | 0.749 | 0.000 | 0.170 | 0.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{33}) $ | 0.000 | 0.000 | 0.193 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.127 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.643 | 0.000 | 0.036 | 0.000 | 0.000 |
| $ (x_{33}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.998 | 0.000 | 0.000 | 0.000 |
| $ (x_{51}, x_{33}) $ | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.998 | 0.000 | 0.000 |
| $ (x_{42}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.168 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.111 | 0.000 | 0.000 | 0.000 | 0.160 | 0.000 | 0.561 | 0.000 |
| $ (x_{51}, x_{42}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.055 | 0.000 | 0.000 | 0.000 | 0.039 | 0.000 | 0.868 |
Table 6. Dynamic transition matrix in Option 2 for Profile 1 at time $ t = 3 $.
| $ (x_{12}, x_{23}) $ | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{12}) $ | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{33}) $ | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{33}, x_{12}) $ | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{42}) $ | 0.001 | 0.000 | 0.000 | 0.000 | 0.996 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{12}) $ | 0.000 | 0.002 | 0.000 | 0.004 | 0.000 | 0.993 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{12}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{51}, x_{12}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{33}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{33}, x_{23}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{42}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.996 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{23}) $ | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.000 | 0.992 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{23}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{51}, x_{23}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{33}, x_{42}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.996 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{33}) $ | 0.000 | 0.000 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.993 | 0.000 | 0.001 | 0.000 | 0.000 |
| $ (x_{33}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| $ (x_{51}, x_{33}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| $ (x_{42}, x_{51}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.004 | 0.000 | 0.990 | 0.000 |
| $ (x_{51}, x_{42}) $ | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.998 |
Table 7. Dynamic transition matrix in Option 2 for Profile 1 at time $t = 4$.
| $(x_{12}, x_{23})$ | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{23}, x_{12})$ | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{12}, x_{33})$ | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{33}, x_{12})$ | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{12}, x_{42})$ | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{42}, x_{12})$ | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{12}, x_{51})$ | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{51}, x_{12})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{23}, x_{33})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{33}, x_{23})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{23}, x_{42})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{42}, x_{23})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{23}, x_{51})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{51}, x_{23})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| $(x_{33}, x_{42})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| $(x_{42}, x_{33})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| $(x_{33}, x_{51})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| $(x_{51}, x_{33})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| $(x_{42}, x_{51})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| $(x_{51}, x_{42})$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
5. Conclusion
DCMs have applications in many areas. However, challenging issues are faced because of the large number of covariates, reliability of model, and the condition that consumer behavior is time dependent. By extending the idea of choices into time dependent and with transition probabilities process, we presented a time dependent Case 2 BWS model with evaluation under random utility analysis. Our study showed that clustering can be captured and the design can predict time stages needful to reach some target. With the simulated examples, dynamic programming algorithms reveal the highest and lowest utility trends.
Acknowledgment
The authors are very thankful to the support provided by the editor. The feedbacks and comments from the anonymous reviewers helped considerably improve the quality of the manuscript.









 DownLoad:
DownLoad: