Differences in how interventions coupled with effective reproduction numbers account for marked variations in COVID-19 epidemic outcomes

1.   Introduction

The COVID-19 outbreak was designated a "pandemic" by the World Health Organization (WHO) on 11 March 2020, having spread rapidly to affect more than 180 countries/territories worldwide. The number of the novel coronavirus disease COVID-19 cases worldwide topped 2, 639, 243 as of at 1000 GMT on 23 April 2020, according to the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University ^[1]. Outside China, the countries that have reported over 100, 000 cases include the United States of America (USA), Spain, Italy, France, Germany and the United Kingdom. So far, the USA has suffered the most deaths from the disease. China's prevention and control policy resulted in marked progress following the lockdown of Wuhan city on 23 January, as the number of new cases each day had reduced from thousands to 15 by 11 March ^[2]. Within the time interval studied in this article, no new or only single digit numbers of domestically transmitted cases of COVID-19 have been reported per day on the Chinese mainland since 18 March 2020.

Although there are differences in the specific measures adopted by different countries in their COVID-19 prevention and control strategies, these measures during early epidemic stages can be separated into two broad categories according to their essential characteristics ^[3]. The first strategy adopted by China, South Korea, Thailand and other countries, can be described as a "SARS-like containment strategy (SARS$\_$LCS)" and the second strategy, adopted by the United States, Japan, Italy, France, Switzerland and other countries, can be considered as a "pandemic influenza-like mitigation strategy (PAIN$\_$LMS)". The essential difference between the two policies is that SARS$\_$LCS aims to control the epidemic, completely block its spread and eliminate adverse impacts, while PAIN$\_$LMS aims to mitigate the spread, delay the epidemic speed and reduce the overall harm ^[3]. The rationale for PAIN$\_$LMS is based on the assumption that COVID-19 cannot be completely blocked, so it focuses mainly on the treatment of severe cases and even limits the detection of COVID-19 in mildly infected patients. With the deterioration of the COVID-19 epidemic in some countries, the prevention and control measures, including increasing social distance rules, extending national emergency periods etc., have been continuously strengthened. Some countries adopt these two strategies simultaneously, but there is a big difference between the strength and intensity of their implementations.

The questions we seek to answer in this paper are (a) why are outbreaks of COVID-19 under effective control in some countries, while in others they are continuing with high intensities at large scales? and (b) What lessons can other countries learn from the Chinese government's strong and strengthened containment and mitigation strategies? Here we link the timings of interventions against COVID-19 epidemics to effective reproduction numbers to illustrate the efficacy of the prevention and control measures in several countries at various epidemic stages.

2.   Methods

2.1.   Sources of data

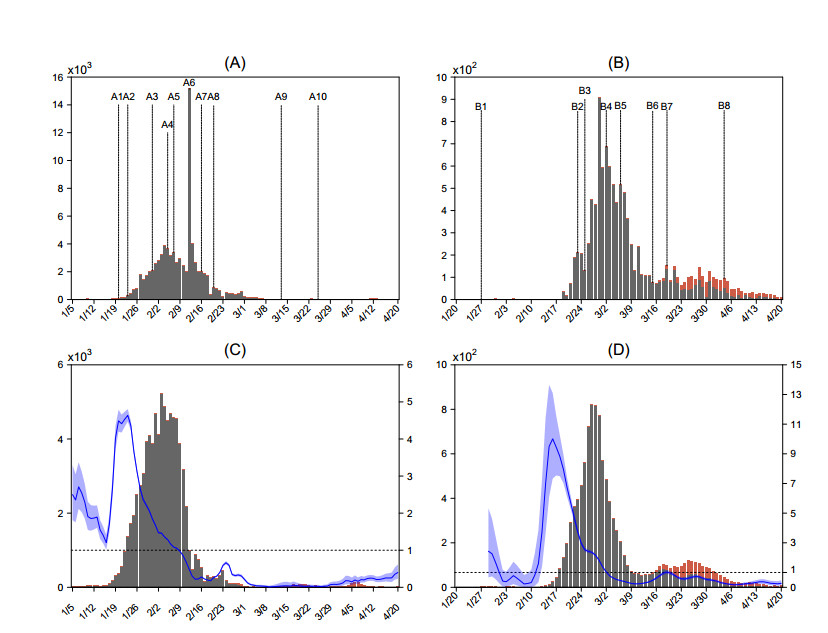
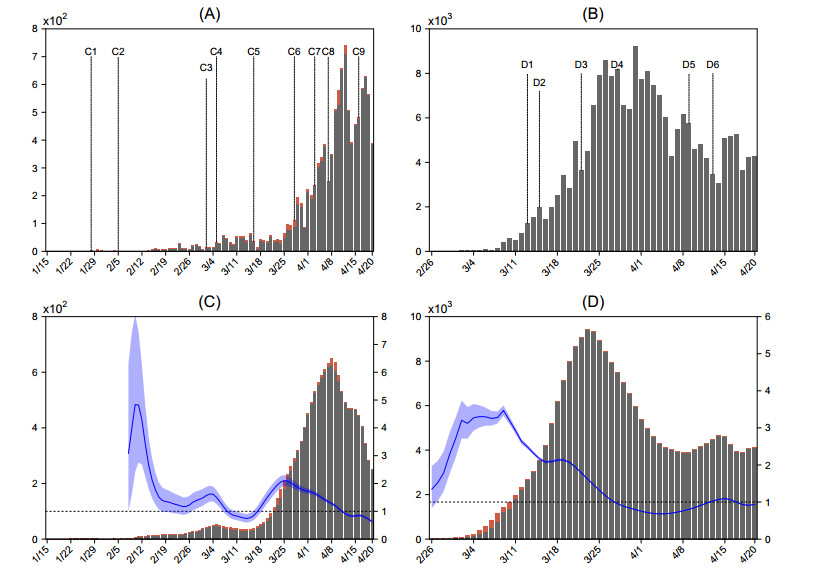
We obtained the numbers of daily confirmed cases of COVID-19 in mainland China from the National Health Commission of the People's Republic of China ^[2], and those in South Korea, Japan, and Spain from the Korea Centers for Disease Control and Prevention ^[4], the Japanese Ministry of Health, Labour and Welfare ^[5], the Spanish Ministry of Health ^[6] and the World Health Organization ^[7], respectively, shown in Figure 2(A-B) and Figure 3(A-B). Detailed information about some cases including dates of illness onset, laboratory confirmation and importation (for imported cases) was obtained from the COVID-2019 Data Working Group ^[8].

Figure 1.  Cumulative number of confirmed imported cases for Japan. Hollow points denote actual data, solid dots denote the estimated missing data under the assumption of exponential growth.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Numbers of confirmed cases for (A) Mainland China and (B) South Korea and estimated numbers of illness onset cases and estimated effective reproduction numbers for (C) Mainland China and (D) South Korea. Histograms and the left vertical axes represent the numbers of daily new imported cases (red) and local cases (gray). Colored lines (shaded regions) and right vertical axes represent the posterior means and 0.95 credible intervals of estimated effective reproduction numbers $R_t$ over sliding 3-day windows. Horizontal dashed lines indicate $R_t = 1$. For explanations of interventions (A1 etc. and B1 etc), see Table 2.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Numbers of confirmed cases for (A) Japan and (B) Spain and estimated numbers of illness onset cases and estimated effective reproduction numbers for (C) Japan and (D) Spain. Histograms and the left vertical axes represent the number of daily new imported cases (red) and local cases (gray). Colored lines (shaded regions) and right vertical axes represent the posterior means and 0.95 credible intervals of estimated effective reproduction numbers $R_t$ over sliding 3-day windows. Horizontal dashed lines indicate $R_t = 1$. For explanations of interventions (C1 etc. and D1 etc), see Table 3.

DownLoad: Full-Size Img PowerPoint

2.2.   The model

Let $S_t$ and $C_t$ be the number of cases with illness onset on day $t$ and the number of newly confirmed cases on day $t$, respectively. $S_t$ is assumed to follow a Poisson distribution with mean $\lambda_t$ (to be estimated) and for any $a\neq b$, $S_a$ and $S_b$ are assumed to be independent. $T$ represents the duration from illness onset to confirmation for confirmed cases. Given the daily number of newly confirmed cases $C_{s_1}, ..., C_{s_m}$ on $m$ consecutive days $s_1, ..., s_m$ and the probability $p_{ij} = P(i-j\leq T < i-j+1)$ that a confirmed case with illness onset on day $j$ was confirmed on day $i$, then we can estimate parameters $\{ \lambda_j \}_{j = t_1, ..., t_k}$ by $C_{s_1}, ..., C_{s_m}$ and $p_{ij}$ for $k (t_1, ..., t_k)$ consecutive days that satisfy $q_j > 0, j = t_1, ..., t_k$ and $q_j = 0, j < t_1 or j > t_k$ with $q_{j} = \sum_{i = max\{j, s_{1}\}}^{s_m}p_{ij}$ using a deconvolution method. We use the Richardson-Lucy iterative algorithm ^[9] to solve this problem. The procedure is iterative according to the following formulae:

where $C_{i}^{(n)}$ and $\lambda_{j}^{(n)}$ are fitted values of $C_i$ and $\lambda_{j}$ in the $n^{th}$ iteration, respectively. We stop the iteration when the error of fitting

becomes small and the values of $\lambda_{t_{1}}^{(n)}, ..., \lambda_{t_{k}}^{(n)}$ are reasonable. Here, the duration from illness onset to confirmation $T$ is assumed to follow a Weibull distribution and the date of illness onset of imported cases is defined as the later one of either importation date or illness onset date.

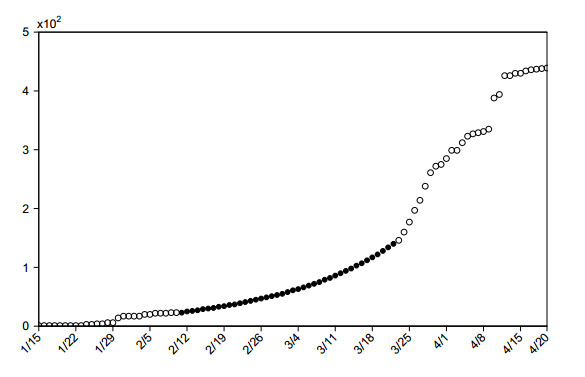
For Japan and South Korea, on the basis of the daily number of confirmed local (imported) cases before 22 April 2020 and onset-to-confirmation distribution for local (imported) cases, we estimated the daily number of local (imported) illness onset cases before 20 April 2020 by the deconvolution method. Since the cumulative number of confirmed imported cases in Japan from 11 February to 22 March is missing, we estimated the missing data by assuming that the cumulative number of confirmed imported cases increased exponentially during this period, as shown in Figure 1.

For mainland China, on the basis of the daily number of confirmed local (imported) cases for the period 20 January to 22 April 2020 and the onset-to-confirmation distribution for local (imported) cases, we estimated the daily number of local (imported) illness onset from 14 January to 20 April 2020 by the deconvolution method. Note that the daily number of confirmed cases before 20 January 2020 was not accurate, so we then estimated the daily number of illness {onsets} before 14 January as follows: Let $S_{t}^{China}$ be the daily number of illness onsets on day $t$ and 8 December 2019 be the day when $t = 0$. We obtained $\{S_{t}^{China} \}_{t = 0, ..., 30}$ from ^[10]. We fitted the following generalized linear model to the data $\{S_{t}^{China} \}_{t = 0, ..., 30}$:

and estimated $S_{t}^{China} = exp(c+rt)$ for $t = 31, ..., 36$. Where $E[\cdot]$ represents the expectation of a random variable.

For Spain, the reported number of confirmed cases does not distinguish between local cases and imported cases, but we obtained the proportion of local cases and imported cases to the total number of cases with illness onset before 13 March 2020 from ^[6]. Then we initially estimated the daily number of illness onsets in Spain before 20 April 2020 by the deconvolution method and then multiplied the number of illness onsets by the proportion of local (imported) cases to get the number of local (imported) illness onsets. The proportion of imported cases to the total number of cases with illness onset after 13 March 2020 was set to be 0 because measures of entry restrictions and lockdown had been in place since mid-March.

To estimate the effective reproduction number $R_{t}$, we used the transmission model in ^[11]:

where $E[\cdot]$ represents the expectation of a random variable. $p_{j}$ denotes the discretized serial interval distribution. $L_{t}$ and $I_{t}$ are the numbers of new local cases and new imported cases on day $t$ respectively and both of them are assumed to follow Poisson {distributions}. Parameter $\alpha$ $(0\leq \alpha \leq1)$ quantifies the relative contribution of imported cases to the secondary disease transmission.

Based on this formula, we can use a Bayesian method to estimate $R_{t}$ ^[12]. We assume that $R_t$ is constant in the time interval $[t-\tau+1, t]$ and the prior distribution of $R_t$ is a Gamma distribution with shape parameter $a$ and scale parameter $b$. Then the posterior probability density function of $R_t$ is

which is proportional to

Therefore the posterior distribution of $R_t$ is a Gamma distribution with shape parameter $a+\sum_{s = t-\tau+1}^{t}L_s$ and scale parameter $[\frac{1}{b}+\sum_{s = t-\tau+1}^{t}\sum_{j = 1}^{s}p_j(L_{s-j}+\alpha I_{s-j})]^{-1}$.

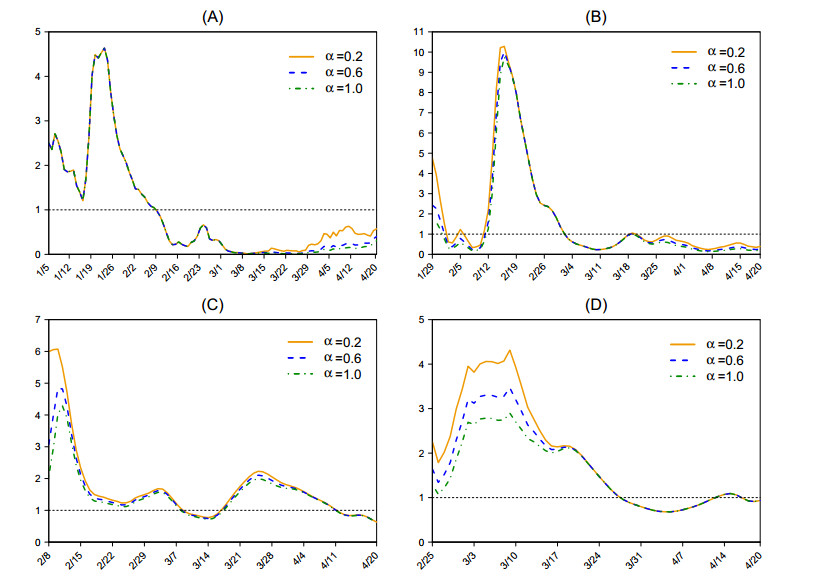
We used the estimated daily number of local (imported) illness onset cases to replace $L_t$ ($I_t$) in formula (2.3) to obtain posterior distribution $\pi(R_t|L, I)$. The estimated value of $R_t$ was set to be the mean of $\pi(R_t|L, I)$, and the 95% credible interval of $R_t$ was constructed using the 0.025 and 0.975 quantiles of $\pi(R_t|L, I)$. Parameter $\alpha$ was chosen to be 0.6. To investigate the variation in estimated $R_{t}$ with $\alpha$, we carried out a sensitivity analysis by varying the value of $\alpha$.

3.   Results

3.1.   Development of the epidemics and estimates of effective reproduction numbers

We initially estimated parameters of the onset-to-confirmation distribution for mainland China, Japan and South Korea by onset-to-confirmation data with the detailed information from some cases, and the parameters of the distribution for Spain according to the information posted by the Spanish Ministry of Health ^[6]. The results are shown in Table 1. Since we do not have data about imported cases in China and Spain, the onset-to-confirmation distributions for imported cases were set to be the same as those for local cases. The estimated numbers of illness onsets for the four countries are shown in Figure 2(C-D) and Figure 3(C-D), from which we can see the variation in detection and reported delays with interventions in the different countries.

Table 1.  Mean (E) and standard deviation (Std) of the durations from illness onset to confirmation in different countries.

Country	Local cases	Imported cases
Mainland China	E = 6.1, Std = 4.1	E = 6.1, Std = 4.1 (assumed)
South Korea	E = 5.2, Std = 4.1	E = 4.7, Std = 3.8
Japan	E = 8.2, Std = 4.8	E = 4.8, Std = 3.8
Spain	E = 6.6, Std = 4.0	E = 6.6, Std = 4.0 (assumed)

---

 | Show Table

DownLoad: CSV

To determine the posterior distribution $\pi(R_t|L, I)$ by formula (2.3), we chose the serial interval to follow a Gamma distribution with mean 5 days and standard deviation 3 days ^{[13,14,15,16]} and set $a = 1$, $b = 5$. In order to detect the variations of $R_t$ well, we chose a relatively small time window $\tau = 3$. We then obtained the estimated effective reproduction number $R_{t}$ for the four countries based on the estimated numbers of local/imported illness onsets, shown in Figure 2(C-D) and Figure 3(C-D). Results of a sensitivity analysis to investigate the variation in the estimated $R_{t}$ with parameter $\alpha$ show that the estimated $R_{t}$ decreases with increasing values of parameter $\alpha$ for relatively large number of imported cases, while it is not sensitive to the variation of parameter $\alpha$ for few imported cases (shown in Figure 4). This can be explained by formula (2.2), from which we can see that $R_t = R_t(\alpha) = \frac{E(L_t)}{\sum_{j = 1}^{t}p_j(L_{t-j}+\alpha I_{t-j})}$ and that $R_t$ decreases with $\alpha$. Since $0\leq \alpha \leq 1$, We have

Figure 4.  Variation of estimated reproduction numbers $R_t$ for (A) Mainland China, (B) South Korea, (C) Japan, and (D) Spain when parameter $\alpha$ varies.

DownLoad: Full-Size Img PowerPoint

When the number of imported cases $I_{t-j}$ is relatively small compared to the number of local cases $L_{t-j}$ (for $j = 1, ..., d$ with $p_j > 0, j\leq d$ and $p_j = 0, j > d$), then $\frac{I_{t-j}}{L_{t-j}}\ll 1$ and $R_t(1)\approx R_t(0)$. So $R_t(\alpha)$ is not sensitive to parameter $\alpha$. Otherwise $R_t(1) < R_t(0)$ and $R_t(\alpha)$ decreases with $\alpha$ significantly.

The influence of changes in serial interval distribution and parameters $a$, $b$ on the estimated value of $R_t$ is mainly reflected in the time points when $R_t$ is much larger than 1. Since these parameters have little influence on the trend of the $R_t$ curve and the times when $R_t$ falls below 1, we did not carry out sensitivity analysis on these parameters.

Note that strictly speaking, $p_j$ in formula (2.3) is generation time (GT). However, it is difficult to observe GT, so the serial interval (SI) was used to replace GT. Some investigators who studied the reproduction number do not distinguish between SI and GT ^[17,18], so we have followed these examples here and refer to $p_j$ as SI. For the purpose of replacing GT, SI should be assumed to take non-negative values. For this reason some studies on the SI of COVID-19 such as ^[13,15] consider SI as a non-negative random variable. In ^{[13,14,15,16]}, the estimated means of SI or GT are in the range between 4 and 5, the estimated standard deviations of SI or GT are about 3. So, we assumed that SI follows a Gamma distribution with mean 5 and standard deviation 3.

3.2.   Comparisons of control efficacies

Here we compare the efficacies of the two main strategies based on the developing trends of the COVID-19 epidemics, the implemented control strategies and calculated values of the effective reproduction number ($R_{t}$), and conclude with suggestions for the most effective strategies according to epidemic/economic situations, the strength of measures implemented and compliance of the public.

China adopted a strict SARS$\_$LCS, focusing on the detection and isolation of patients, investigation of close contacts and strict management. The Chinese government has continued to increase publicity and education, people's awareness of self-isolation has been growing, and the resumption of work in some provinces and schools has continued to be postponed, which effectively reduces the risk of a second outbreak. As shown in Figure 2, from 21 January, the value of $R_{t}$ in China {was} about 4 in the first week. On 23 January when Wuhan was locked down, $R_{t}$ decreased and remained at around 2 after one week. On 4 and 5 February, Huoshenshan and Leishenshan hospitals and other designated fangcang (shelter) hospitals became operational (dates when different interventions were implemented are shown as A1, ..., A7 in Figure 2(A) and Table 2). The overall trend of $R_{t}$ showed a stable decline, and it dropped to below 1 in the middle of February.

Table 2.  Chronology of events in countries implementing SARS-like containment strategies (SARS$\_$LCS).

Mainland China
A1	Detection kit first used on 16 Jan. Human to human transmission confirmed on 20 Jan.
A2	Lockdown of Wuhan on 23 Jan.
A3	Spring Festival holiday extended on 26 Jan. The public health emergency of international concern declared on 31 Jan.
A4	Huoshenshan special hospital began to treat patients on 4 Feb; Fangcang hospital began to treat patients on 5 Feb.
A5	Support from other provinces for Hubei province on 7 Feb.
A6	Inclusion of clinical diagnosis as confirmation criteria on 12 Feb.
A7	Residential area management cleared in Wuhan on 14 Feb. Further strengthening strategies on 16 Feb: quarantine all, collect all, detect all and treat all.
A8	Work resumed from mid-February.
A9	Restrictions removed in some areas of Hubei on 13 Mar.
A10	Restrictions removed in most areas of Hubei on 25 Mar.
South Korea
B1	Alert register for COVID-19 epidemic raised from "caution" to "alert" on 27 Jan.
B2	The government decided to raise the alert to the highest level on 23 Feb.
B3	Lockdown of Daegu and North Gyeongsang province on 25 Feb. Proposed acts on the COVID-19 was passed by congress on 26 Feb.
B4	The opening of all schools nationwide postponed on 2 Mar.
B5	Entry restrictions to Japanese, travel alert to Japan upgraded on 6 Mar.
B6	Seriously affected prefectures were designated as special disaster areas on 15 Mar.
B7	Entry control extended to all countries and regions in the world on 19 Mar.
B8	The period of social distancing extended on 4 Apr.

---

 | Show Table

DownLoad: CSV

Table 3.  Chronology of events in countries implementing pandemic influenza-like mitigation strategies (PAIN$\_$LMS).

Japan
C1	COVID-19 designated as a "specified infection" on 28 Jan.
C2	Everyone aboard the "Diamond Princess" cruiser quarantined for 14 days from 5 Feb.
C3	All elementary, junior high, and high schools closed from 2 Mar.
C4	New quarantine restrictions for visitors from China and South Korea announced on 5 Mar.
C5	Entry restrictions to foreigners expanded on 16 Mar.
C6	Regional self-isolation requests around Japan from 28 Mar.
C7	Entry ban expanded on 3 Apr.
C8	State of emergency for some prefectures proclaimed on 7 Apr.
C9	State of emergency expanded on 16 Apr.
Spain
D1	Nationwide state of {emergency for} 15 days declared on 13 Mar.
D2	Nationwide lockdown on 15 Mar.
D3	State of Alarm extended on 22 Mar.
D4	All non-essential activity banned on 28 Mar.
D5	State of Alarm extended on 9 Apr.
D6	Workers in some sectors return to work on 13 Apr.

---

 | Show Table

DownLoad: CSV

To keep the persistently declining trend, the Chinese government continuously implemented the policy of "early detection, early report, early quarantine and early treatment". On 14 February, Wuhan refined its management protocol for residential quarters after including clinically diagnosed cases in the confirmed cases category on 12 February, to enhance its quarantine/isolation measures. Moreover, China's National Health Commission revised its New Coronavirus Pneumonia Prevention and Control Plan to further clarify and strengthen the public health interventions as much as possible in four key areas (i.e., quarantine high-risk individuals; test suspected individuals; treat patients and receive and cure all patients) on February 16. Hence, these integrated prevention and control strategies significantly blocked the COVID-19 spread and protected susceptible individuals, which kept the epidemic at a low level. This consequently led to the $R_{t}$ stabilizing below 0.2 until the week before 16 March (Figure 2(C)). Hence, the new local infections reduced to almost zero, and so the comprehensive prevention and control policies had achieved great success in mainland China.

South Korea is also implementing SARS$\_$LCS. After the rapid rise of the epidemic, although no massive lockdowns have been implemented, the South Korean government increased the detection of suspected patients and close contact tracing. The epidemic control has been completed with remarkable results. In South Korea, where early outbreaks were sporadic cases, the $R_{t}$ initially stabilized at a low level in early February and began to rise rapidly and peaked on 20 February, due to the presence of super-spreaders (confirmed case 31) ^[19] on 18 February. On 23 February, the South Korean government decided to raise the early warning of the epidemic to the highest level, and in the following week, it took SARS$\_$LCS measures such as delaying the opening of schools nationwide, blocking access to and from some areas with serious epidemics, forcing isolation of suspected patients, and increasing the detection of suspected patients and close contact tracing, and finally making efforts to achieve the goal of "receiving and managing as much as possible" in the case of patient treatment difficulties. Consequently, after the implementation of these measures for 1 to 2 weeks, the number of daily reported cases decreased from more than 1100 at the peak to dozens at the time of writing (21 March 2020), and then $R_{t}$ dropped to below 1 on 6 March and to 0.3 to 0.5 in the week before 16 March (Figure 2(B, D)).

Japan has adopted a typical PAIN$\_$LMS policy since the end of January. In the earlier period, the Japanese government made it clear that it would only encourage in-patient treatment for severe patients and home treatment for mild cases, and would not encourage asymptomatic patients to be tested for coronavirus, but appealed to the public to avoid going out, and suspended primary and secondary schools. From the end of January to the end of the next two weeks, Japan's $R_t$ fluctuated up and down near 1. Until 7 April (see C8 in Figure 3(A)), the Japanese government announced that seven prefectures, including Tokyo, Kanagawa, Saitama, Chiba, Osaka, Hyogo and Fukuoka, had entered a "state of emergency" until 6 May. However, because Japan's prevention and control policy is unlikely to stop the spread of the COVID-19 epidemic, the numbers of cases quickly increased in April. Although the $R_{t}$ exhibited a gradually declining trend (Figure 3(C)), whether it will keep decreasing or rebound to increase and exceed 1 depends on the strength of later prevention and control measures.

PAIN$\_$LMS was being implemented in Spain and most other European countries. Spain began to implement measures such as closing down cities and land borders from 13 March, but the compliance of the public has been a major problem. At the end of March, Spain further announced a moratorium on industrial and commercial activities throughout the country and a halt to all unnecessary travel and public gatherings. After experiencing rapid growth at the end of March, the COVID-19 epidemic showed a gradual declining trend in early April. Since the early morning of 13 April, the Spanish government began to relax the "comprehensive blockade" policy implemented due to the epidemic, allowing some employees to leave home to work (see D6 in Figure 3(B)). The COVID-19 epidemic is still at a plateau at present (late April). The $R_{t}$ has fluctuated around 1 since the end of March, and there is no obvious downward trend for the time being (Figure 3(D)).

4.   Discussion and conclusion

Note that there are many studies that investigate the reproduction number of COVID-19 outbreaks for different countries or regions. Among these studies, the basic reproduction number ($R_0$) in mainland China was estimated {to be} in the range of 2–7 ^{[10,20,21,22]}, the effective reproduction number ($R_t$) in China dropped from late January and fell below 1 in early February ^[15,23,17]. The $R_0$ in South Korea was estimated as about 2, and $R_t$ there fell below 1 in late February ^[24,25,26]. The $R_0$ in most European countries was estimated to be around 4, with $R_t$ beginning to decrease from mid March and remained above 1 before April ^[18]. Compared with these articles, we estimated $R_t$ from earlier time points and over longer time intervals. Since the number of cases is small at the beginning of an outbreak, our estimated $R_t$ fluctuates greatly during early stages of the COVID-19 outbreaks. It is worth noting that there are differences in reproduction numbers estimated in different models of COVID-19, which may be associated with the parameter settings and/or model assumptions. So, realistic characteristics should be fully considered in future modelling and estimations, so that the modelling hypotheses are closer to the actual situations and the accuracy of the estimation of the reproduction numbers is improved.

Based on the analysis of SARS$\_$LCS strategies adopted by two countries and PAIN$\_$LMS strategies adopted by two other countries, we found that SARS$\_$LCS is more effective and can successfully contain the spread of the virus in a short time based on estimates of $R_{t}$ ^[27]. In contrast, PAIN$\_$LMS cannot effectively cut off the source of infection, resulting in a run on medical resources and consequently a rapid epidemic with increased complexity. At the same time, the successful implementation of SARS$\_$LCS depends on a series of factors, such as the strong execution of the strategy, sufficient medical resources and so on, based on the successful experience of China and South Korea.

It is known that with the deterioration of epidemics, medical resources are on the verge of running out, or have done, in several countries such as Italy, Spain and Iran. In response, strong prevention and control measures were adopted, which were transformed from the PAIN$\_$LMS type to SARS$\_$LCS measures. After the implementation of these strong measures for a period, new infections began to decline. However, due to the compliance of the people, the economic or unemployment rate and other factors, the interventions in some countries have been switched from PAIN$\_$LMS to the SARS$\_$LCS, but the epidemics remain temporarily unable to be completely controlled, as shown by the example of Spain (Figure 3(D)).

With increases in the total number of patients, if the patients' demands exceed the threshold level of what a national medical system can afford, with medical staff required to invoke selective treatment of severe cases, then a large outbreak may follow. This is the fundamental reason why the implementation of the same prevention and control strategy has varying efficacy in different countries. Governments need to assess their countries' medical resources, the likely extent of the public's compliance to different intensities of prevention and control measures ^[28], and factors such as the economic situation before adopting the most appropriate policies to fight the COVID-19 epidemic.

There are some limitations in this study. We mainly estimated the effective reproduction numbers based on single time series, that is, the number of illness-onset cases (from the number of confirmed cases) by using a Bayesian method. To further verify our estimation of reproduction numbers, multi-source data and/or a more detailed modelling approach could be applied to calibrate them. Further, the estimations of reproduction numbers are highly dependent on the chosen serial interval, thus it is necessary to accurately estimate the serial interval for different countries, and we leave this for future work.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (grant numbers: 11631012 (YX)). We would like to thank Dr Hao Wang and Zhe Liu in Baidu Inc. for very helpful suggestions and discussions which {greatly improved} this manuscript.

Conflict of interest

All authors declare that they have no competing interests.