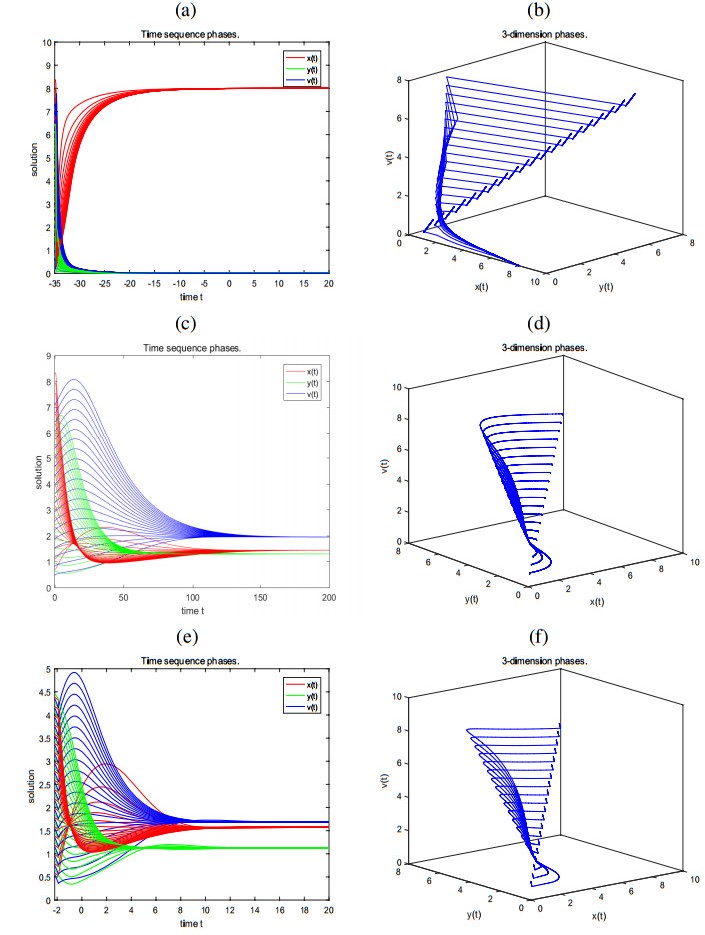
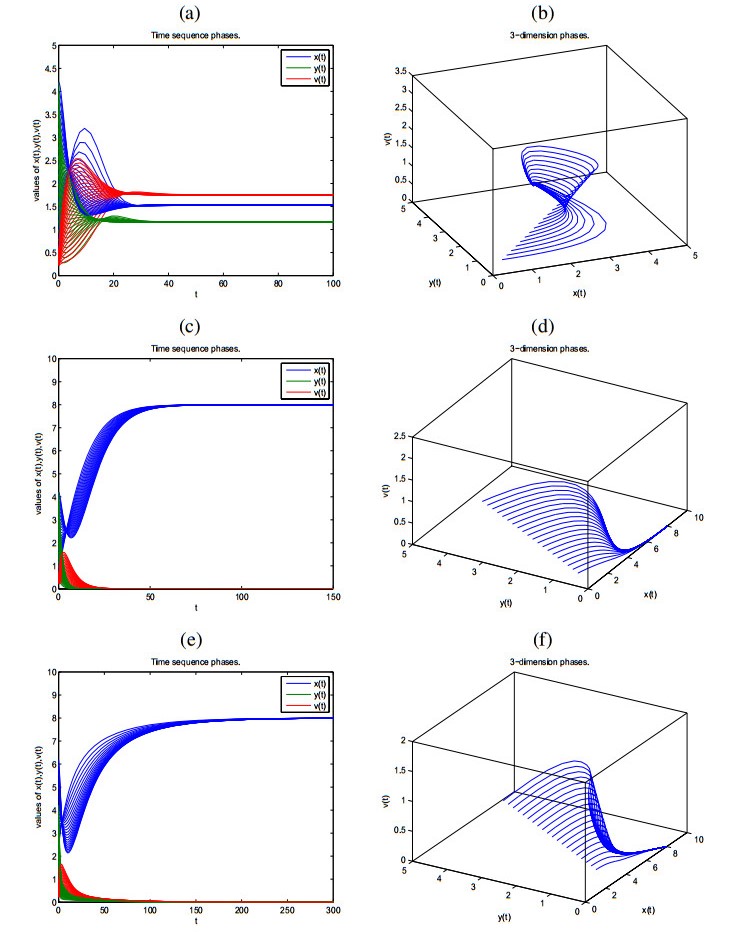
Global stability for a class of HIV virus-to-cell dynamical model with Beddington-DeAngelis functional response and distributed time delay

1.   Introduction

At the end of the Second World War, France needed to repair a large part of its road network as quickly as possible (more than 5,000 bridges and 50,000 km of roads required emergency repairs) and to complete the urban ring road projects planned before the war.

Major motorway projects had to be completed just a few years after the end of the war under growing social needs, including traffic doubling between 1950 and 1955, with a 160% increase in permissible axle load ^[1].

Numerous study missions were carried out in the United States by French engineers to visit transport infrastructure projects, and conferences were organized to pass on the feedback from these observations.

The conclusions drawn from these missions, from the North American experience between 1940 and 1950, and from the rapid changes in traffic, were simple and unequivocal: the entire network was on the verge of wear and tear and French techniques were outdated, as was the French pool of machines.

In order to remedy all these problems, as well as to prevent future difficulties linked to the densification of the network and the need to make the most of local materials and develop design, testing, and construction methods adapted to the difficulties of the terrain, the Ministry of Transport first decided to create the Laboratoire Central des Ponts et Chaussées (LCPC) in 1949 and then to create 11 Laboratoires Régionaux des Ponts et Chaussées (LRPC) in 1952. Six specialized centers were also created at a later date.

The creation of this scientific and technical network within the Ministry has since enabled the development of a French doctrine for the design of roads and civil engineering structures based on a scientific approach based on experimentation and understanding of phenomena, as well as knowing how to take advantage of international feedback.

To better apprehend the behavior of soils and the interaction of the structures with it, as well as to develop testing and coring methods, it was then decided to establish reference tests sites covering a wide range of soils in terms of nature and of state that were well documented and that could be accessible in the long term. Thus, multiple sites were established rapidly. Table 1 summarizes the most notorious of them, as well as their original purpose and their date of establishment. Figure 1 shows their localization in metropolitan France.

Table 1.  Purpose of various reference tests sites.

Test site	Date of establishment	Purpose
Cran	1967	Embankment on compressive clay
Cubzac les Ponts	1971	Piles and Embankment on compressive clay
Plancoët	1973	Piles under lateral loads
Jossigny	1978	Shallow foundations on silt
Labenne	1984	Shallow foundations on sand
Merville	1985	Piles in overconsolidated Flandrian clay

---

 | Show Table

DownLoad: CSV

Figure 1.  Locations of the reference sites in France.

DownLoad: Full-Size Img PowerPoint

Other sites have since been opened, either permanently or only temporarily, as new issues and needs have arisen.

Among these sites, Cran is the oldest and maybe also the most documented and the most active.

2.   Description of the site of Cran

The Cran site is located in the commune of Rieux (Figure 2), at the Vilaine river crossing downstream of Redon. The site has been the subject of numerous studies as part of research programmes organised by the Ponts et Chaussées laboratories. The site was selected on the basis of its relative homogeneity and a minimum depth of 5–10 m of soft sediment.

Figure 2.  Map of the Cran site.

DownLoad: Full-Size Img PowerPoint

The Vilaine alluvial plain downstream of Redon is a sedimentary valley almost 2 km wide. It is underlain by a 10–20-m-thick deposit of clay, resting on a layer of sand and pebbles that covers the bedrock. At Cran, the right bank is made up of a 17 m-thick deposit of soft marine clay resting on bedrock (schist and phtanite). The compressible alluvial layer is of relatively recent origin. It is made up of post-glacial alluvium, whose formation periods range from the boreal period (7,500 years ago) to the sub-Atlantic period (2,500 years ago). Cran clay contains around 40–50% of elements smaller than 2 µm, with the fine fraction consisting mainly of montmorillonite, illite, and kaolinite in smaller proportions.

Generally speaking, Cran clay is grey and contains plant fibers (reeds) that are almost always vertical. A number of glossy surfaces found in the samples are evidence of past landslides that must have occurred when the riverbed evolved.

Three layers can be distinguished:

- the first two meters, overconsolidated by desiccation, correspond to the highest values of undrained cohesion, of the order of 45 kPa;

- between two and four meters below the surface, a layer of relatively soft consistency, with undrained cohesion of around 15 kPa, has a high liquidity limit. According to the LPC classification, it can be identified as a very plastic clay with a low organic content (fO- At);

- between four and 17 meters deep, the clay has a medium consistency, the water content is around 70%, and the undrained cohesion is around 38 kPa. The soil can be identified as a very plastic, low-organic silt (fO-Lt).

Table 2 presents, according to Paute ^[2], the geological context, dividing the clay of medium consistency into two different layers:

Table 2.  Geotechnical model of the Cran site ^[2].

Layer Depth (m)	w (%)	wL (%)	IP	ρd (Mg/m3)	e	MO (%)	cu (kPa)	Cc	σ'p (kPa)	σ'vo (kPa)	c'--ϕ' (kPa-degré)
1
0 à 2 m	48	75	30	1, 10	1, 3	1	45	0, 45	60	7
2
2 à 4 m	108	125	82	0, 66	2, 9	3	15	1, 64	25	16	0,0 - 30
3
4 à 8 m	64	70	31	0, 93	1, 8	2	40	0, 70	96	30
4
8 à 17 m	73	87	47	0, 91	1, 7	4	39	0, 85	105	67	0,0 - 34

---

 | Show Table

DownLoad: CSV

The water table is generally 50 cm deep. The bedrock is locally covered by a 1.50 m thick layer of compact Pliocene gravel.

An indurated overconsolidated crust can be seen near the surface due to the influence of desiccation generated by evapotranspiration from the surface, followed by a much more moderate level of overconsolidation from 2.5 m downwards, following the same phenomenon detailed by Ladd and DeGroot ^[3]. This crust is also observed through the results achieved with the dynamic penetrometer and pressuremeter, as seen in subsequent sections.

3.   Geotechnical reconnaissance campaigns and tests on geostructures at the Cran site

Numerous test campaigns have been carried out on the Cran site over the years, with the first dating back to 1967 and the last to 2024. All these campaigns have been carried out for very different purposes, such as the development of a new type of sampler for example and the study of the behaviour of a pile realized in soft clay. The tests carried out are therefore both varied and may have been repeated several times over the past 50 years. Figure 3 presents a rough estimation of the position of the most important tests carried out on the site.

Figure 3.  Position of tests at Cran site: (1) different sampling equipment, (2) self-boring pressuremeter, (3) embankment monitoring, (4) shallow foundation tests, (5) piles tests, (6) sampling zone.

DownLoad: Full-Size Img PowerPoint

3.1.   Sampling and laboratory tests

3.1.1.   Evaluation of the performance of a sampling equipment

Multiple laboratory campaigns were performed in the sole purpose of assessing the efficiency of a coring material in soft clay. Thus, numerous samplers were tested on this site. Most of them are succinctly presented in Table 3.

Table 3.  Features of samples with different coring material ^[6,7].

Sampler	Laval 200	CPS I100	CPS M100	CS Ⅰ 100	CPS 100	CPS 80	CPS M80	A+
D1 (mm)	208	100	96, 4	98	95, 8	77	76, 9	148, 5
D2 (mm)	218	104	103, 3	102	105	85	82, 4	156, 5
D3 (mm)	208	100	97, 2	98	97	77, 8	77, 6	150
D4 (mm)	218	104	103, 2	102	105	88	82, 4	154
Ca (%)	10	8, 2	14, 8	8	20	22	14, 8	11
Ci (%)	0	0	0, 9	0	1, 3	1	0, 9	1
Co (%)	0	0	0, 09	0	0	0	0	1, 6
α (degree)	5	5	5	5	5	5	5	5
Lt	660	600	769	580	1070	845	769	550
Lt / D1	3	6	8	6	11	11	10	3, 7

---

 | Show Table

DownLoad: CSV

The different parameters Ca, Ci, and Co are indexes related to the disturbance of the sample and are defined in international and French standards focusing on soil sampling ^[4,5], using the usual inner and outer diameters of the sampler as presented in Figure 4.

Figure 4.  Schematic views of a sampler.

DownLoad: Full-Size Img PowerPoint

The results achieved in oedometer and triaxial tests are known to be greatly influenced by the methods of sampling, transport, storage, preparation, and testing ^[8]. This has an impact on both strength and deformability parameters.

The results shown in Figure 5 demonstrate the importance of careful sampling. Indeed, they show that the A+ sampler allows us to achieve more intact samples than the University of Laval 200 mm sampler (Laval 200) and the CPS 80 sampler, through the estimation of pre-consolidation stress σ'_p. In the same manner, the Laval sampler allows us, to a lesser extent, to achieve better samples through the estimation of pre-consolidation stress σ'_p, the E₅₀ modulus, and of the undrained cohesion.

Figure 5.  Results obtained with the A+, Laval 200 and CPS 80 samplers. a) pre-consolidation stress σ'_p, b) E₅₀ modulus, c) undrained cohesion c_u.

DownLoad: Full-Size Img PowerPoint

It should be noted that the E50 modulus was determined in these campaigns following a method similar to the one presented in EurosoilStab ^[9] and that the undrained cohesion measured were achieved through scissometer and unconsolidated and undrained triaxial tests.

The ratio of the achieved values of undrained cohesions c_u and pre-consolidation stresses σ'p can be correlated to the Plastic Index PI. Figure 6 shows this relation for the Laval, CPS 80 and A+ samplers, and compared to the work of Bjerrum ^[10] as well as a few other studies compiled by Reiffsteck ^[11]. It can be seen that the results achieved through the sampler A+ are in good accordance with the past studies, while the results achieved through the Laval and CPS 80 samplers are clearly underestimating the preconsolidation stress, implying a non-negligible disturbance of the soft and medium clay during the sampling phase.

Figure 6.  Relationship between the ratio c_u/σ'_p and PI, for Cran and other studies, compared to the proposition of Bjerrum ^[10].

DownLoad: Full-Size Img PowerPoint

These results underline the importance of the adequacy of the sampling method with the nature and state of soil.

3.1.2.   Evaluation of the influence of the boring method on the mechanical parameters

The consequences of the choice of boring method were also studied on the site of Cran, as it can have a direct impact of the same magnitude as the sampling method on the resistance and deformability parameters.

As the sampler CPS 80 is pushed downward, the soil from the borehole walls is pushed sideways and compressed under the piston. This has the effect of dragging the upper soil downwards, distorting the natural stratification. Unlocking the piston releases this compressed soil, which enters the sampler barrel. If no account is taken of this soil during the pushing phase, the intact soil is compressed inside the corer. The core is then reworked by longitudinal compression, rendering the mechanical properties measured uncertain. Furthermore, the final phase of pushing continues with the sampler already completely filled with soil, acting like a large penetrometer on the underlying soil layers, which are disturbed prior to coring.

Therefore, laboratory tests were carried out on samples either collected via a simple method or a method including realignment by reboring before the sampling phase. The realignment is the process of reboring the borehole in order to avoid the dragging effect that was described previously (Figure 7).

Figure 7.  Phases of the realignment boring process.

DownLoad: Full-Size Img PowerPoint

The results of the UU triaxial and scissometer tests carried out by Bat ^[6] completed by Da Silva ^[12] on the specimens obtained through these samples are presented in Figure 8a, b, and c. It shows that the strain at failure and the modulus E₅₀ are fairly impacted by the boring method, while the undrained cohesion is much less impacted. As well as choosing the right sampling tool, it is therefore also necessary to use a drilling and borehole preparation method that will ensure the best possible sampling.

Figure 8.  Results of UU and scissometer tests with realignment and without. a) Final strain, b) E₅₀ modulus, c) undrained cohesion.

DownLoad: Full-Size Img PowerPoint

3.1.3.   Evaluation of the influence of the testing conditions, procedure, and material on the results of the oedometer test

Of all the studies carried out at the Cran site, one focused on the impact of test conditions, the test procedure, and the choice of equipment on the results obtained in the oedometer test.

It was observed that the consolidation coefficient c_v decreases by roughly 20% between a test carried out at 20 ℃ and one carried out at 10 ℃. Permeability also decreases by a factor of two to three between these two temperature conditions. Thus, it was found that temperature plays a notable role, particularly as the viscosity of the interstitial water changes.

Similarly, soil compressibility changes with temperature. However, this is more pronounced on the swelling index C_s than on the compression index C_c (Figure 9).

Figure 9.  Influence of temperature on soil compressibility.

DownLoad: Full-Size Img PowerPoint

Furthermore, in order to study the influence of the surface treatment of the odometer ring and to see to what extent it contributes to minimizing frictional pressure drop, it was decided to carry out odometer tests using different materials: rings fitted with Teflon rings (AT); teflon-coated rings (BT); teflon-coated and greased rings (BTG); standard stainless steel odometer rings (BS) without surface treatment, which are usually used in the laboratory; and the incremental loading oedometer rings (chromium-plated brass rings).

Detailed examination of the compressibility results seems to show that friction has the effect of over-consolidating the samples. In fact, there is more than a 20% difference between the preconsolidation stress values without surface treatment and with surface treatment.

For some tests, the effect of the loss of load by lateral friction on the walls of the oedometer ring is reflected in the normally consolidated domain by an incorrect evaluation of the compression index C_c. The differences between the values of C_c, achieved with rings without surface treatment (standard rings) and treated rings reach 45%.

Figure 10 shows the normalized compressibility curves for specimens with the same initial voids index and sampled by the Laval 200 corer, in order to eliminate the effect of the natural variability of the soil in place and the effect of the sampling method. It can be concluded that the effect of friction is not clearly visible on the compressibility curves. Overall, an effect of surface treatment cannot be formally distinguished. It should be noted that the standard stainless steel rings normally used in the laboratory were not damaged. The initial aim was to see the influence of variations in the reference oedometer test procedures as performed in the laboratories. Some of the differences can also be attributed to differences in the state parameters of the specimens, which tends to relativize some of the conclusions that could be drawn from such a study.

Figure 10.  Influence of the nature of the oedometer ring on the results of an oedometer test.

DownLoad: Full-Size Img PowerPoint

These tests carried out on many specimens allowed for the refining of the French standard NF XP 94-090-1 dedicated to the oedometer tests ^[13].

3.1.4.   Homogeneity of the site

Of course, all the results presented above, as well as those to come, must be considered in the light of the relative homogeneity of the Cran experimental site.

Indeed, although the site was described in part 2 as relatively homogeneous, heterogeneities are nonetheless apparent in places (Figure 11a). Sliding planes were observed in the cores taken from the site (Figure 11b and c).

Figure 11.  a) Heterogeneity apparent in place, b) and c) heterogeneity observed on cored samples.

DownLoad: Full-Size Img PowerPoint

As part of a new test campaign aimed at developing a new generation of sampler, more than 30 oedometer tests were carried out on samples to evaluate the natural dispersion of the mechanical parameters on the site. Figures 12a and b show the dispersion of the initial void ratio and of the initial water content.

Figure 12.  Results of oedometer tests. a) Initial void ratio, b) initial water content.

DownLoad: Full-Size Img PowerPoint

3.2.   In situ tests

The Cran site has also been used to develop equipment, such as the Ménard pressuremeter and the self-boring pressuremeter, as well as for cross-testing campaigns carried out to assess the influence of the operator and to improve the boring and testing methods.

3.2.1.   Pressuremeter tests

Multiple campaigns of pressuremeter tests were carried out on the site of Cran.

The last one was done in the context of the National Project ARSCOP (new approaches for soil investigation and design of geotechnical works using pressuremeter) ^[14], in the form of a cross-testing campaign.

For this particular campaign, as well as for all others, the reference test is a pressuremeter realized with a simple soft cover, which is particularly well adapted for this kind of soil as it exhibits a very low inertia. The other pressuremeter profiles were achieved by using diverse materials and techniques, such as the driven slotted tube (DST), open hole drilling (OHD), and continuous fight auger with injection (TIN). The numbers after the techniques stand for the rotation speed (in rounds per minute) and the thickness of the pressuremeter cover.

The limit pressure profiles obtained are very comparable, showing both the homogeneity of the site and the low impact of the operator and its practice on a resistance parameter, in this particular context of a soft compressive fine soil (Figure 13a). However, it can be seen that the results are very different when looking at the Menard modulus profiles derived from these same tests : while most of the profiles are very comparable to the reference test, the DST profiles exhibits much higher modulus, as the driven tube densifies the soft clay and increases its stiffness (Figure 13b).

Figure 13.  Pressuremeter profiles in soft compressive fine soil. a) limit pressure and b) Ménard modulus.

DownLoad: Full-Size Img PowerPoint

It is interesting to see that, in the same manner as observed previously, the resistance parameters are not really affected by the execution techniques, while the deformation parameters are much more sensitive to these.

Other campaigns included the realization of self-boring pressuremeter tests to obtain small strains parameters, which in turn were compared to those of a cross-hole tests campaign.

3.2.2.   Penetrometer tests

In the same way as the pressuremeter tests, numerous penetrometric test campaigns have been carried out over the years on the Cran site.

These were sometimes designed to complement related test campaigns (e.g., to study the behavior of surface foundations on soft clayey soil). Partial results of tests carried out with a lightweight dynamic cone penetrometer with variable energy are presented in Figures 14a and b, proving again the relative homogeneity of the site. The results also include the dynamic modulus measured for each blow (Figure 14b). It has been possible with new generation of dynamic penetration test (DPT) including shear wave velocity measurements in rods allowing modulus derivation ^[15].

Figure 14.  Results of a dynamic cone penetrometer test. a) Dynamic cone resistance q_d, b) dynamic modulus E_d.

DownLoad: Full-Size Img PowerPoint

Other campaigns were carried out to develop new testing devices or tests, such as the cone loading test designed to reproduce in a small scale pile load test at different depth and including the dissociation between the base resistance and the shaft resistance.

3.3.   Tests on geostructures

The Cran site was established during the construction of the bridge across the Vilaine river at its western end. This bridge, whose abutment and access embankment on the right side of the river are founded on soft clay. This embankment was fully monitored for over 16 months (Figure 15), in order to study the effectiveness of the drainage system put in place and to compare the behavior of the soil with the calculations ^[2].

Figure 15.  Results after 16 months of the embankment monitoring ^[2].

DownLoad: Full-Size Img PowerPoint

Also, static load tests were conducted in Cran on driven metallic piles as well as on shallow foundations ^[16]. The purpose of these tests, spanning more than 50 years as the first one were conducted in 1967 and the last one in 2020, was to improve the French foundations design methods NF P 94-261 and NF P 94-262 dedicated to shallow and deep foundations, respectively ^[17,18].

The Figures 16a and b represent the load displacement curves and the creep ratio-load relationship respectively, for two static load tests performed on shallow foundations.

Figure 16.  Results of two static load tests S1 and S2 on shallow foundations. a) Load displacement curve, b) creep ratio-load relationship.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

From this brief presentation of the Cran experimental site and the applied research activities that have been and are still being carried out there (a non-exhaustive list that is intended to cover as many issues as possible has been compiled), it is easy to grasp the importance of a site such as this for geotechnics.

Indeed, the geotechnical fields that have benefited from the experience acquired over the last 50 years at Cran are numerous:

- The design and calculation of geotechnical structures (embankments, piles, footings), with the establishment of rules that are still in force today and cited in the French standards for the application of Eurocode 7 ^[17,18] and in all related documents,

- French testing methods, both in the laboratory and in situ, the spirit of which can be found in many international documents. In particular, it was concluded from the different laboratory testing campaigns carried out on the soft clay of Cran that while important, the material and the conditions of realization of oedometer tests do not notably impact the overall results, as the higher incertitude lies with the natural dispersion (due to the heterogeneity of the site) of the soil,

- Test and sampling equipment and associated procedures, which are still in development, as they also have a notable impact on the quality of the laboratory tests performed on the recovered samples, especially when one focus on deformation parameters, which are more sensitive to the choice of sampling material and execution procedure.

The natural dispersion of the parameters measured or derived and achieved either in situ or on cored samples is always difficult to take into account when trying to draw conclusions. Hence, the need for the multiplication of tests carried out on multiple sites to be able to assert its impact on the results achieved. Furthermore, such experimental testing campaigns shall be coupled with parametric studies carried out in the laboratory on model soils and samples exempt of any bias.

The fact that geotechnical engineering has been able to draw on a large number of sites such as Cran, which are well recognized, easy to access, and made up of soil masses of different natures and states, has enabled rapid progresses to be made in technologies, methods, and the design of geotechnical structures.

At a time when new challenges are emerging, such as the needs for climate change adaptation and to save natural resources, it is also evident to keep these sites alive.

Author contributions

Conceptualization: S. Fanelli, F. Szymkiewicz and P. Reiffsteck; Ressources: S. Fanelli, F. Szymkiewicz and P. Reiffsteck; Data curation: S. Fanelli, F. Szymkiewicz and P. Reiffsteck; Formal analysis: S. Fanelli, F. Szymkiewicz and P. Reiffsteck; Supervision : P. Reiffsteck; Validation: F. Szymkiewicz and P. Reiffsteck; Investigation: S. Fanelli, F. Szymkiewicz and P. Reiffsteck; Writing —original draft: S. Fanelli and F. Szymkiewicz; Methodology: F. Szymkiewicz and P. Reiffsteck; Project administration: P. Reiffsteck; Writing—review & editing: F. Szymkiewicz

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflict of interest.