1.
Introduction
The ordinary differential equation
is well known as the logistic equation in both ecology and mathematical biology, where r and K are positive constants that stand for the intrinsic growth rate and the carrying capacity, respectively. It follows from Eq (1.1) that the U′(t)/U(t) is a linear growth function of the density U(t). However, Smith[1] concluded that the Eq (1.1) does not have practical significance for a food-limited population under the influence of environmental toxicants. Based on the above fact, Smith established a new growth function in [1]. Besides, Smith also pointed out that a food-limited population requires food for both preservation and growth in its growth. For another thing, when the specie is mature, food is needed for preservation only. Therefore, the modified system is as follows
where r, K and α are positive constants, and rα is the replacement of mass in the population at K.
In [2], Wan et al. considered a single population food-limited system with time delay:
they studied existence of Hopf bifurcations and global existence of the periodic solutions at the positive equilibrium. Eq (1.3) has been discussed in the literature by numerous scholars, they mainly concluded global attractivity of positive constant equilibrium and oscillatory behaviour of solutions of Eq (1.3) [3,4]. Su et al.[5] considered the conditions of steady state bifurcation and existence of Hopf bifurcation of food-limited population system under the dirichlet boundary condition for Eq (1.1). In addition, Gourley et al.[6] investigated the global stability, boundedness and bifurcations phenomenon of Eq (1.2) with nonlocal delay. About more interesting conclusions for food-limited system, we refer to the literature [7,8,9,10,11].
However, in real world, the interaction of prey and predator is one of the basic relations in biology and ecology. The dynamical analysis of the predator-prey system is a hot issue in biomathematics all the time, an important reason is that compared with single population system, multi-population system can exhibit complex dynamical behavior. The well-known predator-prey system has been widely studied by many ecologists and mathematicians. The authors in [12,13] developed food-limited population system to prey-predator system of functional response. Moreover, the reproduction of predator after preying upon prey is not instantaneous, but is mediated by some reaction time delay τ for gestation. Compared with the predator-prey system without delay, the time-delay predator system is more ecological significance. The delay has an effect on population dynamics and induces very rich dynamical phenomenon, see [14,15,16,17,18,19,20]. Here, we will take ratio-dependent functional response into consideration, i.e., the characteristic of consumption of prey is mUVβU+γV. The predation and reproduction of predator are not simultaneous. Taking into account the delay, the reproduction of predator from consuming the prey is nU(t−τ)VβU(t−τ)+γV. Hence, the prey-predator system with ratio-dependent and food-limited as follows
where the variables U(t) and V(t) denote the densities of the prey and predator at time t, respectively. r, K, m, n and e are all positive constants that stand for the intrinsic growth rate of the prey, the carrying capacity of the prey species, predate rate of prey, converation rate from prey, and mortality rate of predator, positive constants β and γ are half saturation constant, τ(>0) is a time delay which occurs in the predator response term and represents a gestation time of the predators.
In fact, biological resources in the predator-prey system are most likely to be harvested for economic benefit, human need to develop biological resources and capture some biological species, such as in fishery, forestry and wildlife management[21]. Hence, the demand of sustainable development for suitable resources is felt in different region of human activities to maintenance the stability of the ecosystem. We know that harvesting in population has a significant impact on the dynamic behavior of species, because of the reduction of food in the space. There are some basic types of harvesting being considering in the literature, see [21,22,23,24,25,26]. Nevertheless, a great number of mathematicians have a strong interest in nonlinear harvesting, because Michaelis-Menten type harvesting is more realistic in biology and ecology[22]. Inspired by the above discussion, system (1.4) with nonlinear prey harvesting transforms into the following system
where q, E, m1, m2 are also positive constants. q is the catchability coefficient, E is the effort applied to harvest prey species, m1 and m2 are suitable constants. Fang gave some sufficient conditions of the existence of positive periodic solutions for a food-limited predator-prey system with harvesting effect in [24,25].
In nature, the populations all require food, space and spouse and so on for survival and reproduction. When the larger the density of population is, the higher require on the environment. The shortage of food and the change in space always limit its survival and development. Naturally, the populations change position or have a diffusion to search better environment. We assume that the populations are in an isolate patch and ignore the impact of migration, including immigration and emigration. Individuals tend to migrate towards regions with lower population densities for each population. To take spatial effects into consideration, reaction diffusion system become more and more important, see [12,13,23,27,28,29,30,31,32,33,34,35]. In this paper, we study the following reaction diffusion system:
where Ω⊂Rn(n≥1) is a bounded region and it has smooth boundary ∂Ω. D1 and D2, respectively, denote the diffusion coefficients of the prey and predator, and they are positive constants. Δ denotes the Laplacian operator in Rn, ϑ is outer normal vector of a boundary ∂Ω.
To simplify the system (1.6), we use the following nondimensionalization:
Then rewrite the system (1.6) as follows:
Denote F(u,v)=u(1−u)d+u−suvau+bv−huρ+u, G(u,v)=cu(t−τ)vau(t−τ)+bv−δv, Λ={a,b,c,d,h,s,ρ,δ}. In this paper, the domain of system is confined to Ω=[0,lπ], we define a real-valued Hilbert space
The corresponding complexification is XC:={x1+ix2:x1,x2∈X}, with the complex-valued L2 inner product
for Ui=(ui,vi)∈XC(i=1,2).
The rest of the paper is arranged as follows. In section 2, the existence and priori bound of solution of the system (1.7) are considered. In section 3, the existence of nonnegative constant steady state solutions is investigated. In section 4, the stability of the nonnegative constant steady state solutions of system (1.7) and the conditions of Hopf bifurcation and Turing instability are discussed by stability analysis and bifurcation theory. In section 5, we give the detailed formulas to determine the direction of Hopf bifurcation and the stability of the bifurcating periodic solutions by the normal form theory and center manifold theorem for PFDEs. In section 6, some numerical simulations are carried out to illustrate the correctness of the theoretical results. Finally, some conclusions and discussions are given.
2.
Existence of solution and priori estimate
In this section, we establish the existence of solution of system (1.7) and a priori estimate of the solution. Firstly, we have
where f(u,v)=−u2+(1−ρ−h)u+ρ−dh. Define m_=1−ρ−h−√(1−ρ−h)2−4(dh−ρ)2, ¯m=1−ρ−h+√(1−ρ−h)2−4(dh−ρ)2.
Theorem 2.1. The following statements are true for system (1.7).
(1) Given any initial condition u0(x)≥0, v0(x)≥0, and u0(x)≢0, v0(x)≢0, then system (1.7) has a unique solution (u(t,x),v(t,x)), such that u(t,x)>0 and v(t,x)>0 for t∈(0,∞) and x∈Ω.
(2) If one of three conditions holds
(2a) (1−ρ−h)2<4(dh−ρ) and dh−ρ>0,
(2b) (1−ρ−h)2≥4(dh−ρ), 1−ρ−h<0 and dh>ρ,
(2c) (1−ρ−h)2≥4(dh−ρ), 1−ρ−h>0, dh>ρ and u0(x)<m_,
then (u(t,x),v(t,x)) tend to (0,0) uniformly as t→∞.
(3) For any solution (u(x,t),v(x,t)) of system (1.7), if one of two conditions holds
(3a) dh<ρ,
(3b) (1−ρ−h)2≥4(dh−ρ), 1−ρ−h>0 and dh>ρ,
then
where C_{2} = \frac{c}{4ds\delta}|\Omega|+\frac{c\overline{m}}{s}|\Omega| .
(4) If d_{1} = d_{2} and \tau = 0 , then \limsup_{t\rightarrow\infty}\max_{\overline{\Omega}}v(t, x)\leq \frac{c}{4ds\delta}+ \frac{c\overline{m}} {s} for any x\in\Omega .
Proof. (1) Obviously, F(u, v) and G(u, v) are mixed quasi-monotone in set \overline{\mathbb{R}^{2}_{+}} = \big\{(u, v)\big| u\geq0, v\geq0\big\} . According to the definition of upper and lower solutions in [16], denoted (\underline{u}, \underline{v}) = (0, 0) and (\overline{u}, \overline{v}) = (\widetilde{u}, \widetilde{v}) , where (\widetilde{u}, \widetilde{v}) is the unique solution of the following system,
where \overline{u}_{0} = \sup_{\overline{\Omega}}u_{0}(t, x) , \overline{v}_{0} = \sup_{\overline{\Omega}}v_{0}(t, x) , t\in[-\tau, 0] . Consider that
and 0\leq u_{0}(t, x)\leq\overline{u}_{0} , 0\leq v_{0}(t, x)\leq\overline{v}_{0} . Then (\overline{u}, \overline{v}) and (\underline{u}, \underline{v}) are the upper-solution and lower-solution of system (1.7). So we have that any solution of system (1.7) is nonnegative and exists on [0, \infty) , it exhibits that system (1.7) has a global solution \big(u(t, x), v(t, x)\big) satisfying
Then u(t, x) > 0, v(t, x) > 0 by the strong maximum principle for all t > 0 and x\in\overline{\Omega} .
(2) We are able to get from the first equation of system (1.7) that
If (1-\rho-h)^{2} < 4(dh-\rho) , we can obtain that (1-u)(\rho+u)-dh-hu < 0 for all u > 0 , it leads to \widetilde{u}\rightarrow0 as t\rightarrow\infty . Suppose (1-\rho-h)^{2}\geq4(dh-\rho) and dh > \rho hold, if either 1-\rho-h < 0 or 1-\rho-h > 0 and u_{0}(x) < \underline{m} , then \widetilde{u}\rightarrow0 as t\rightarrow\infty . Therefore u(t, x)\rightarrow0 uniformly on \overline{\Omega} as t\rightarrow\infty . Similarly, we have that v(t, x)\rightarrow0 uniformly on \overline{\Omega} as t\rightarrow\infty from the second equation of system (1.7).
(3) Consider any of conditions (3a)-(3b) , then it follows from the first equation of system (1.7) that
according to Eq (2.3) and comparison principle, we can get that
There exists a t_{1} , such that u(t, x)\leq \overline{m}+\varepsilon for t\geq t_{1} and x\in \overline{\Omega} , where \varepsilon is a arbitrarily small positive constant.
To the estimate v(t, x) . Denote \overline{U}(t) = \int_{\Omega}u(t, x)dx and \overline{V}(t) = \int_{\Omega}v(t, x)dx . By the Neumann boundary condition, we obtain
Then
It follows from u(t, x)\leq \overline{m}+\varepsilon that \overline{U}(t)\leq (\overline{m}+\varepsilon)|\Omega| for any t\geq t_{1} , we have
where C_{1} = \frac{c}{4d}|\Omega|+c\delta (\overline{m}+\varepsilon)|\Omega| .
By the comparison principle and Eq (2.4), we obtain
Hence,
(4) When d_{1} = d_{2} and \tau = 0 , let S(t, x) = cu(t, x)+sv(t, x) . By Eq (1.7), we have
From Eq (2.5), we get
for t > 0 and x\in\Omega .
Consider
The solution Z(t, x) satisfies \lim_{t\rightarrow\infty}Z(t, x) = \frac{c}{4d\delta}+c\overline{m} by using [36,Theorem 2.4.6], then the comparison principle displays that
This completes the proof of Theorem 2.1.
3.
The nonnegative constant steady states of system (1.7)
In reality, we are interested in all the nonnegative steady state solution. Next, we give the conditions of existence of nonnegative constant steady state solutions for system (1.7).
Proposition 3.1. (1) The singularity E_{0} = (0, 0) always exists.
(2) If (h+\rho-1)^{2} = 4(dh-\rho) and h+\rho-1 < 0 hold, then semi-trivial steady state E_{10} = (\frac{1-h-\rho}{2}, 0) (the boundary equilibrium) exists.
(3) If \rho > dh holds, then semi-trivial steady state E_{30} = (\overline{m}, 0) exists.
(4) If (h+\rho-1)^{2} > 4(dh-\rho) , h+\rho-1 < 0 and \rho < dh hold, then semi-trivial steady state E_{20} = (\underline{m}, 0) and E_{30} = (\overline{m}, 0) (the boundary equilibrium) exist.
In ecology, we concentrate on the existence of the positive constant steady state solutions. System (1.7) has a positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) , where v_{\ast} satisfies v_{\ast} = \frac{(c-a\delta)u_{\ast}}{b\delta} under c-a\delta > 0 and u_{\ast} satisfies the following quadratic equation
with A_{0} = \frac{(c-a\delta)s}{bc}+1 , A_{1} = \frac{(c-a\delta)(d+\rho)s}{bc}+\rho+h-1 , A_{2} = \frac{(c-a\delta)d\rho s}{bc}+dh-\rho.
For the distribution of roots of Eq (3.1), we are able to get the following results about the existence of a positive constant steady state solution.
Lemma 3.1. Suppose c-a\delta > 0 holds, then the following statements are true.
(1) If A_{1} < 0, A_{1}^{2}-4A_{0}A_{2} > 0 and A_{2} > 0 , then Eq (3.1) has two positive roots u_{\ast}^{\pm} = \frac{-A_{1}\pm\sqrt{A_{1}^{2}-4A_{0}A_{2}}}{2A_{0}} .
(2) If A_{1} < 0, A_{1}^{2}-4A_{0}A_{2} = 0 , then Eq (3.1) has a unique positive root u_{\ast}^{0} = -\frac{A_{1}}{2A_{0}} .
(3) If A_{2} < 0 , then Eq (3.1) has a unique positive root u_{\ast} = u_{\ast}^{+} .
By Lemma 3.1, the following Proposition is existing.
Proposition 3.2. Suppose c-a\delta > 0 holds, then the following statements are true.
(1) When A_{1} < 0, A_{1}^{2}-4A_{0}A_{2} > 0 and A_{2} > 0 , the system (1.7) has two positive steady states E_{\ast}^{+} = (u_{\ast}^{+}, v_{\ast}^{+}) and E_{\ast}^{-} = (u_{\ast}^{-}, v_{\ast}^{-}) , where v_{\ast}^{\pm} = \frac{(c-a\delta)u_{\ast}^{\pm}}{b\delta} .
(2) When A_{1} < 0, A_{1}^{2}-4A_{0}A_{2} = 0 , E_{\ast}^{+} and E_{\ast}^{-} merge, denoted by E_{\ast}^{0} = (u_{\ast}^{0}, v_{\ast}^{0}) .
(3) When A_{2} < 0 , the system (1.7) has a unique positive steady state E_{\ast} = (u_{\ast}, v_{\ast}) .
4.
Stability and bifurcation
In this section, we consider the stability of nonnegative steady state and the conditions of Hopf bifurcation and Turing bifurcation. In [37], we know that Laplacian operator -\Delta exists the eigenvalue \frac{n^{2}}{l^{2}}\big(n\in\mathbb{N}_{0}: = \mathbb{N}\cup\{0\}\big) under the homogeneous Neumann boundary condition, let \varphi_{n}^{1} = (\beta_{n}\; \; 0)^{T} , \varphi_{n}^{2} = (0\; \; \beta_{n})^{T} be eigenfunctions on X , where \beta_{n}(x) = \cos\big(\frac{n}{l}x\big) . The linearization of system (1.7) at a constant steady state \widehat{E} = (\widehat{u}, \widehat{v}) can be represented by
where D = diag (d_{1}, d_{2}) , J_{1} = \left(\begin{matrix} a_{11}&a_{12}\\ 0&a_{22} \end{matrix}\right) , J_{2} = \left(\begin{matrix} 0 & 0\\ a_{21} & 0 \end{matrix}\right) , and
The characteristic equation of system (1.7) is
where I stands for 2\times2 identity matrix and D_{n} = -\frac{n^{2}}{l^{2}} diag (d_{1}, d_{2}) , n\in\mathbb{N}_{0} . Then we obtain
with M_{n} = (d_{1}+d_{2}) \frac{n^{2}}{l^{2}}-a_{11}-a_{22} , N_{n} = d_{1}d_{2} \frac{n^{4}}{l^{4}}-(a_{11}d_{2}+a_{22}d_{1})\frac{n^{2}}{l^{2}}+a_{11}a_{22} , Q = -a_{12}a_{21} .
Firstly, we discuss the stability of the singularity E_{0} = (0, 0) and the semi-trivial steady state solutions E_{i0} (i = 1, 2, 3) .
Theorem 4.1. (1) The singularity E_{0} = (0, 0) is always locally asymptotically stable if dh > \rho , and unstable if dh < \rho .
(2) Suppose (h+\rho-1)^{2} = 4(dh-\rho) and h+\rho-1 < 0 hold, the semi-trivial steady state E_{10} is always locally asymptotically stable if c-a\delta < 0 and (dh+d\rho-1)(\rho+\sqrt{dh-\rho})^{2}+h(d+\sqrt{dh-\rho})^{2} < 0 , and unstable if c-a\delta > 0 or d(\rho+h) > 1 .
(3) Suppose dh < \rho holds, the semi-trivial steady state E_{30} is locally asymptotically stable if c-a\delta < 0 and \frac{d-2d\overline{m}-1} {(d+\overline{m})^{2}}+\frac{h}{(\rho+\overline{m})^{2}} < 0 , and unstable if c-a\delta > 0 or \overline{m} < \frac{d-1}{2d} , d > 1 .
(4) Suppose (h+\rho-1)^{2} > 4(dh-\rho) , h+\rho-1 < 0 and \rho < dh hold,
(i) the semi-trivial steady state E_{20} is locally asymptotically stable if c-a\delta < 0 and \frac{d-2d\underline{m}-1}{(d+\underline{m})^{2}} +\frac{h}{(\rho+\underline{m})^{2}} < 0 , and unstable if c-a\delta > 0 or \underline{m} < \frac{d-1}{2d} , d > 1 ;
(ii) the semi-trivial steady state E_{30} is locally asymptotically stable if c-a\delta < 0 and \frac{d-2d\overline{m}-1}{(d+\overline{m})^{2}} +\frac{h}{(\rho+\overline{m})^{2}} < 0 , and unstable if c-a\delta > 0 or \overline{m} < \frac{d-1}{2d} , d > 1 .
Proof. (1) By Eq (4.1), the corresponding characteristic equation of system (1.7) at E_{0} = (0, 0) is
clearly, we have
Therefore, if dh > \rho , \lambda_{1} and \lambda_{2} have negative real part for all n\in\mathbb{N}_{0} , so we get that the equilibrium E_{0} = (0, 0) is locally asymptotically stable. On the contrary, if dh < \rho , there exists n = 0 that \lambda_{1} > 0 , then E_{0} = (0, 0) is unstable.
(2) At E_{10} , then J_{1} = \left(\begin{matrix} a_{11} & - \frac{s}{a}\\ 0 & \frac{c-a\delta}{a} \end{matrix}\right) , J_{2} = \left(\begin{matrix} 0 & 0\\ 0 & 0 \end{matrix}\right) , we are able to get J(n, E_{10}) = \left(\begin{matrix} a_{11} & - \frac{s}{a}\\ 0 & \frac{c-a\delta}{a} \end{matrix}\right) , where a_{11} = \frac{1-\rho-h}{2}\Big(\frac{d\rho+dh-1}{(d+\sqrt{dh-\rho})^{2}}+\frac{h}{(\rho+\sqrt{dh-\rho})^{2}}\Big) .
For n\geq0 , the corresponding characteristic equation of system (1.7) at E_{10} is
where M_{n} = (d_{1}+d_{2}) \frac{n^{2}}{l^{2}}-a_{11}-\frac{c-a\delta}{a} , N_{n} = d_{1}d_{2} \frac{n^{4}}{l^{4}}-(a_{11}d_{2}+\frac{c-a\delta} {a}d_{1})\frac{n^{2}}{l^{2}}+a_{11}\frac{c-a\delta}{a} .
By c-a\delta < 0 and (dh+d\rho-1)(\rho+\sqrt{dh-\rho})^{2}+h(d+\sqrt{dh-\rho})^{2} < 0 , we have N_{n} > 0 and M_{n} > 0 for n\geq0 , which implies E_{10} is locally asymptotically stable. In a similar method, by c-a\delta > 0 or d(\rho+h) > 1 , it is obvious that J(n, E_{10}) has at least one eigenvalue with a positive real part for n = 0 , which implies E_{10} is unstable.
(3) Suppose dh < \rho holds, then semi-trivial steady state E_{30} = (\overline{m}, 0) exists by Proposition 3.1. We can have J(n, E_{30}) = \left(\begin{matrix} a_{11} & - \frac{s}{a}\\ 0 & \frac{c-a\delta}{a} \end{matrix}\right) , where a_{11} = \overline{m}\big(\frac{d-2d\overline{m}-1}{(d+\overline{m})^{2}}+\frac{h}{(\rho+\overline{m})^{2}}\big) .By c-a\delta < 0 and \frac{d-2d\overline{m}-1}{(d+\overline{m})^{2}}+\frac{h}{(\rho+\overline{m})^{2}} < 0 , we have N_{n} > 0 and M_{n} > 0 for n\geq0 , which means E_{30} is locally asymptotically stable. Similarity, by c-a\delta > 0 or \overline{m} < \frac{d-1}{2d} and d > 1 , it is obvious that J(n, E_{30}) has at least one eigenvalue with a positive real part for n = 0 , which implies E_{30} is unstable.
(4) The proof of (4) is similar to (3) , so we omit it.
This completes the proof.
Theorem 4.2. If (\rho+h-1)^{2} < 4(dh-\rho) holds, then E_{0} = (0, 0) is globally asymptotically stable in \overline{\mathbb{R}^{2}_{+}} for system (1.7) with \tau = 0 .
Proof. Define the following Lyapunov functional
Then
It follows from (\rho+h-1)^{2} < 4(dh-\rho) that for all u\geq0 ,
Furthermore, \frac{d}{dt}V(u, v)\leq0 , \frac{d}{dt}V(u, v) = 0 if and only if (u, v) = (0, 0) . Then we can have that the trivial steady state E_{0} = (0, 0) is globally asymptotically stable for system (1.7) with \tau = 0 .
This completes the proof.
Next, we investigate the stability of positive constant steady state E_{\ast} . In the following discussion, we always assume
(H_{1}): c-a\delta > 0, \frac{(c-a\delta)d\rho s}{bc}+dh-\rho < 0(i.e., A_{2} < 0).
For the convenience of discussion, we make the following hypothesis:
(H_{2}): a_{11}+a_{22} < 0 ;
(H_{3}): a_{11}a_{22}-a_{12}a_{21} > 0 ;
(H_{4}): a_{11}d_{2}+a_{22}d_{1} < 0 ,
where a_{11} = \frac{d-u_{\ast}^{2}-2du_{\ast}^{2}}{(d+u_{\ast})^{2}}-\frac{bsv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{2}}-\frac{h\rho}{(\rho+u_{\ast})^{2}} , a_{12} = - \frac{asu_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{2}} , a_{21} = \frac{bcv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{2}} , a_{22} = \frac{acu_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{2}}-\delta .
Theorem 4.3. Assume that (H_{1})\sim(H_{4}) hold. Then the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) of system (1.7) with \tau = 0 is locally asymptotically stable, that is, system (1.7) has no stationary pattern under these hypothesis.
Proof. If (H_{1}) holds, the system (1.7) has a unique positive constant steady state E_{\ast} . When \tau = 0 , the corresponding characteristic equation of system (1.7) at E_{\ast} is
Obviously,
It follows easily from (H_{2})\sim(H_{4}) that all roots of Eq (4.2) have negative real parts. Hence, by Routh-Hurwitz stability criterion, the unique positive constant steady state E_{\ast} is locally asymptotically stable for \tau = 0 when hypothesis (H_{2})\sim(H_{4}) hold.
This completes the proof.
According to the work by Turing[38], positive constant steady state E_{\ast} is Turing instability, implying that E_{\ast} is asymptotically stable for non-spatial system (1.7) but is unstable for spatial system (1.7) with \tau = 0 . So we make the following hypothesis:
(H_{5}): a_{11}d_{2}+a_{22}d_{1} > 0 ;
(H_{6}): a_{11}d_{2}+a_{22}d_{1}-2\sqrt{d_{1}d_{2}(a_{11}a_{22}-a_{12}a_{21})} > 0 .
Theorem 4.4. If \tau = 0 , then diffusion-driven instability (i.e., Turing instability) occurs for the system (1.7) if (H_{1})\sim(H_{3}) and (H_{5})\sim(H_{6}) hold, that is, system (1.7) has stationary pattern under these hypothesis.
Proof. We know that the positive equilibrium E_{\ast} = (u_{\ast}, v_{\ast}) is stable for the non-spatial system (1.7), and is unstable with respect to the constant steady state solution of the spatial system (1.7) with \tau = 0 . The stability of non-spatial system (1.7) is guaranteed if hypothesis (H_{2})\sim(H_{3}) hold. When \tau = 0 , the corresponding characteristic equation of system (1.7) at E_{\ast} is Eq (4.2). Obviously, for spatial system (1.7), it follows from (H_{5})\sim(H_{6}) that if there is a n\in\mathbb{N}_{0} such that N_{n}+Q < 0 for 0 < k_{1} < n < k_{2} , which implies that Eq.(4.2) has a eigenvalue with positive real part, it is shown that the positive constant steady state E_{\ast} is unstable for spatial system (1.7), that is, the diffusion-driven instability occurs.
This completes the proof.
Now, by regarding \tau as the bifurcation parameter, we investigate the stability and the Hopf bifurcation near the unique positive constant steady state E_{\ast} . Assume that i\omega(\omega > 0) is a root of Eq (4.1), \omega satisfies the following equation
which implies that
By Eq (4.4), adding the squared terms for both equations yields
where
Let S = \omega^{2} , we have
For the following discussion, we make some assumption:
(H_{7}): a_{11}a_{22}+a_{12}a_{21} > 0,
(H_{8}): a_{11}a_{22}+a_{12}a_{21} < 0.
Theorem 4.5. Assume that (H_{1})\sim(H_{4}) and (H_{7}) hold. Then all roots of Eq (4.1) have negative real parts for all \tau\geq0 . Furthermore, the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) of system (1.7) is locally asymptotically stable for all \tau\geq0 .
Proof. From Eq (4.6), we have P_{n} > 0 . By (H_{1})\sim(H_{4}) and Theorem 4.3, we have N_{n}+Q > 0 . If (H_{7}) holds, then
for all \tau\geq0 , which implies that Eq (4.8) has no positive roots, according to [19,Lemma 2.3], therefore the characteristic Eq (4.1) has no purely imaginary roots. Combined with Theorem 4.3, we are able to obtain that all roots of Eq (4.1) have negative real parts for any \tau\geq0 .
This completes the proof.
Lemma 4.1. ([39])Let f(y) be a positive \mathbf{C}^{1} function for y > 0 , and let d > 0, \beta\geq0 be constants. Further, let T\in[T, \infty) and \omega\in\mathbf{C}^{2, 1}\big(\Omega\times(T, \infty)\big)\cap\mathbf{C}^{1, 0}\big(\Omega\times[T, \infty)\big) be a positive function.
(i) If \omega satisfies
and the constant \alpha > 0 , the
(ii) If \omega satisfies
and the constant \alpha\leq0 , the
Theorem 4.6. Suppose that the conditions of Theorem 4.5 are satisfied. Furthermore, assume that d > \rho , \rho-dh- \frac{d\rho s}{b} > 0 hold. Then the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) of system (1.7) is globally asymptotically stable.
Proof. By the strong maximum principle of parabolic equations, for any nonnegative initial values \big(u_{0}(x), v_{0}(x)\big)\not\equiv\big(0, 0\big) , we have u(t, x) > 0, v(t, x) > 0 for all t > 0 and x\in\overline{\Omega} .
From the first equation of system (1.7), we get
By Lemma 4.1, we obtain
for any given \varepsilon > 0 , there exists t_{1} > 0 such that for any t > t_{1} , u(t, x)\leq\overline{u}_{1}+\varepsilon .
Then from the second equation of system (1.7), we have
By Lemma 4.1 again and the any \varepsilon , we obtain that
for t > t_{1}+\tau , there exists t_{2} > t_{1} such that for any t > t_{2} , v(t, x)\leq\overline{v}_{1}+\varepsilon .
On the other hand, from the first equation of system (1.7), we have
where B(u, \overline{v}_{1}+\varepsilon) = (1-u)(au+b(\overline{v}_{1}+\varepsilon))(\rho+u)-s(\overline{v}_{1}+\varepsilon)(d+u)(\rho+u)-h(d+u)(au+b(\overline {v}_{1}+\varepsilon)) .
Here, let u(y) be solution of B(u, y) = 0 . If d > \rho, \rho-dh-\frac{d\rho s}{b} > 0 hold, we get B(-\rho, \overline{v}_{1}+\varepsilon) < 0 , B(-d, \overline{v}_{1}+\varepsilon) < 0 , B(0, \overline{v}_{1}+\varepsilon) > 0 , B(1, \overline{v}_{1}+\varepsilon) < 0 , then B(u, \overline{v}_{1}+\varepsilon) = 0 exists unique positive root u(\overline{v}_{1}+\varepsilon) .
It follows from Lemma 4.1 that
for t > t_{2} and any \varepsilon > 0 , there exists t_{3} > t_{2} such that for any t > t_{3} , u(t, x)\geq\underline{u}_{1}-\varepsilon .
Then from the second equation of system (1.7), we have
By Lemma 4.1 again and the any \varepsilon , we obtain
for t > t_{3}+\tau and any \varepsilon > 0 , there exists t_{4} > t_{3} such that for any t > t_{4} , v(t, x)\geq\underline{v}_{1}-\varepsilon .
Meanwhile, the first equation of system (1.7) can be written as
Similarly, by d > \rho, \rho-dh- \frac{d\rho s}{b} > 0 , we know that B(u, \underline{v}_{1}-\varepsilon) = 0 has a unique positive root u(\underline{v}_{1}-\varepsilon) and
for t > t_{4} and any \varepsilon > 0 , there exists t_{5} > t_{4} such that for any t > t_{5} , u(t, x)\leq\overline{u}_{2}+\varepsilon .
It is easily known that
and \underline{u}_{1}, \overline{u}_{1}, \underline{v}_{1}, \overline{v}_{1} satisfy the following inequalities
The Eq (4.9) reveals that (\overline{u}_{1}, \overline{v}_{1}) and (\underline{u}_{1}, \underline{v}_{1}) are coupled upper and lower solutions of system (1.7) by Definition 2.1 in [16].
Moreover, we derive the following inequality:
It is easy to display that there exists a positive constant K_{i}(i = 1, 2) such that the following Lipschitz condition holds
So we can define sequences (\overline{u}_{n}, \overline{v}_{n}) and (\underline{u}_{n}, \underline{v}_{n}) as follows
where n = 1, 2, \cdot\cdot\cdot , (\overline{u}_{0}, \overline{v}_{0}) = (\overline{u}_{1}, \overline{v}_{1}) and (\underline{u}_{0}, \underline{v}_{0}) = (\underline{u}_{1}, \underline{v}_{1}) .
It is easy to deduce that the sequences (\overline{u}_{n}, \overline{v}_{n}) and (\underline{u}_{n}, \underline{v}_{n}) satisfy the following a series of inequalities
and that the limits
exist and satisfy the following equations
From the conditions of Theorem 4.6, we get that the system (1.7) has a unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) , therefore it follows from Eq (4.10) that \overline{u} = \underline{u} and \overline{v} = \underline{v} . It is well known [36,Theorem 2.4.6] that the solution \big(u(t, x), v(t, x)\big) of system (1.7) satisfies
uniformly for x\in\overline{\Omega} . By Theorem 4.5, if (H_{1})\sim(H_{4}) and (H_{7}) hold, then the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) is locally asymptotically stable. Hence, the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) is globally asymptotically stable.
Denote
and
Therefore, we have the following Lemma.
Lemma 3. Assume (H_{1})\sim(H_{4}) and (H_{8}) hold, then Eq (4.1) has a pair of purely imaginary roots \pm i\omega_{n}(0\leq n\leq N_{\ast}) at \tau_{n}^{j} , where
Clearly, we know that \tau_{n}^{j+1} > \tau_{n}^{j} , therefore the following Lemma exhibits that we get a complete ordering of the Hopf bifurcation parameters \tau_{n}^{j} .
Lemma 4. Assume (H_{1})\sim(H_{4}) and (H_{8}) hold, then
for j\in\mathbb{N}_{0} .
Proof. From Eq (4.11), we have
Obviously, by Eq (4.6) and Eq (4.7), we know that M_{n}^{2}-2N_{n} is increasing in n and Q^{2}-N_{n}^{2} is decreasing in n . Hence we have that
And notice that N_{n} is strictly increasing in n\in[0, N_{\ast}] , then we deduce that \frac{\omega_{n}^{2}-N_{n}}{Q} is strictly decreasing in n\in[0, N_{\ast}] . Hence, \tau_{n}^{j} = \frac{1}{\omega_{n}}\arccos\frac{\omega_{n}^{2}-N_{n}}{Q}+\frac{2j\pi}{\omega_{n}} is strictly decreasing in n\in[0, N_{\ast}] , that is, Eq (4.12) is correct for any n\in[0, N_{\ast}] .
This completes the proof.
It follows from Eq (4.12) we obtain
Let \lambda(\tau) = p(\tau)\pm iq(\tau) be the pair of root of Eq (4.1) near \tau = \tau_{n}^{j} satisfies p(\tau_{n}^{j}) = 0 and q(\tau_{n}^{j}) = \omega_{n} . Then we have the following transversality condition.
Lemma 4.4. For n\in\{0, 1, 2, \cdot\cdot\cdot, N_{\ast}\} and j\in\mathbb{N}_{0} ,
Proof. Differentiating two sides of Eq (4.1) with respect to \tau , we get
Therefore,
Thus, by Eq (4.3) and Eq (4.4), we have
This completes the proof.
According to above analysis, and the qualitative theory of partial functional differential equations, we obtain the following results on the stability and Hopf bifurcation.
Theorem 4.7. Assume (H_{1})\sim(H_{4}) and (H_{8}) hold, then the following statements valid
(1) The unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) of system (1.7) is locally asymptotically stable for \tau\in[0, \tau_{0}^{0}) and always unstable when \tau > \tau_{0}^{0} .
(2) System (1.7) undergoes Hopf bifurcations near the unique positive constant steady state E_{\ast} = (u_{\ast}, v_{\ast}) at \tau_{n}^{j} for n\in\{0, 1, 2, \cdot\cdot\cdot, N_{\ast}\}, j\in\mathbb{N}_{0} . If n = 0 , the bifurcating periodic solutions are all spatially homogeneous. Otherwise, these bifurcating periodic solutions are spatially inhomogeneous.
5.
Stability and direction of Hopf bifurcation
In this section, we investigate the stability of the bifurcating periodic solution and direction of Hopf bifurcation by applying center manifold theorem and normal form theory of PFDEs[40]. For convenience, for fixed j\in\mathbb{N}_{0} , 0\leq n\leq N_{\ast} , we denote \tau_{\ast} = \tau_{n}^{j} .
Firstly, we let \widetilde{u}(t, x) = u(\tau t, x)-u_{\ast} , \widetilde{v}(t, x) = v(\tau t, x)-v_{\ast} and drop the tilde. Then system (1.7) can be transformed into:
Let \mu = \tau-\tau_{\ast} , \mu\in\mathbb{R} , U = \big(u(t, \cdot)\; \; v(t, \cdot)\big)^{T} . After the system (5.1) can be rewritten in an abstract form in the phase space \mathcal{C} = C\big([-1, 0], X\big) as
where D = diag (d_{1}, d_{2}) , L(\tau_\ast)(\phi) and F(\phi, \mu) are defined by
with f(\phi, \mu) = \big(\tau_{\ast}+\mu\big)\big(F_{1}(\phi, \mu)\; \; F_{2}(\phi, \mu)\big)^{T} and
F_{1}(\phi, \mu) = \frac{\big(\phi_{1}(0)+u_{\ast}\big)\big(1-\phi_{1}(0)-u_{\ast}\big)}{d+\big(\phi_{1}(0)+u_{\ast}\big)}-\frac{s\big(\phi_{1}(0)+u_{\ast}\big) \big(\phi_{2}(0)+v_{\ast}\big)}{a\big(\phi_{1}(0)+u_{\ast}\big)+b\big(\phi_{2}(0)+v_{\ast}\big)}-\frac{h\big(\phi_{1}(0)+u_{\ast}\big)}{\rho+\big(\phi_{1}(0)+u_{\ast}\big)} -a_{11}\phi_{1}(0)-a_{12}\phi_{2}(0),
F_{2}(\phi, \mu) = \frac{c\big(\phi_{1}(-1)+u_{\ast}\big)\big(\phi_{2}(0)+v_{\ast}\big)}{a\big(\phi_{1}(-1)+u_{\ast}\big)+b\big(\phi_{2}(0)+v_{\ast}\big)}- \delta\big(\phi_{2}(0)+v_{\ast}\big)-a_{21}\phi_{1}(-1)-a_{22}\phi_{2}(0),
for (\phi_{1}\; \; \phi_{2})^{T}\in\mathcal{C} .
Linearizing Eq (5.2) at (0, 0) , we can obtain the following equation
About the discussion of characteristic roots in section 4, we get that the characteristic equation of Eq (5.3) has a pair of simple purely imaginary eigenvalues \Lambda_{n} = \{i\omega_{n}\tau_{\ast}, -i\omega_{n}\tau_{\ast}\} and consider the following functional differential equation
According to the Riesz representation theorem, there exists a 2\times2 matrix function \eta(\theta, \tau, n)(-1\leq\theta\leq0) , whose elements are of bounded variation functions such that
for \phi\in\mathcal{C} .
Actually, we choose
Let us define \mathcal{C^{\ast}} = C([0, 1], \mathbb{R}^{2\ast}) , where \mathbb{R}^{2\ast} is the two-dimensional vector space of row vectors, A(\tau_{\ast}) denotes the infinitesimal generator of the strongly continuous semigroup induced by the solution of Eq (5.4) and A^{\ast} with domain dense in \mathcal{C^{\ast}} and is the formal adjoint of A^{\ast} under the bilinear form
for \phi\in\mathcal{C} , \psi\in\mathcal{C}^{\ast} .
Let P and P^{\ast} be the center subspace, that is, the generalized eigenspace of A(\tau_{\ast}) and A^{\ast} associated with \Lambda_{n} . A(\tau_{\ast}) has a pair of simple purely imaginary eigenvalues \pm i\omega_{n}\tau_{\ast} , and A^{\ast} has also a pair of simple purely imaginary eigenvalues \pm i\omega_{n}\tau_{\ast} .
Let q(\theta) = (1\; \; M)^{T}e^{i\omega_{n}\tau_{\ast}\theta}(-1\leq\theta\leq0) , q^{\ast}(s) = (1\; \; N)e^{-i\omega_{n}\tau_{\ast}s}(0\leq s\leq1) be the eigenfunctions of A(\tau_{\ast}) and A^{\ast} corresponds to i\omega_{n}\tau_{\ast} and -i\omega_{n}\tau_{\ast} , respectively. By simple calculation, we have
Denote \Phi = (\Phi_{1}\; \; \Phi_{2}) and \Psi^{\ast} = (\Psi^{\ast}_{1}\; \; \Psi^{\ast}_{2})^{T} by
for \theta\in(-1, 0) , and
for s\in(0, 1) .
We define
and construct a new basis \Psi for P^{\ast} by \Psi = (\Psi_{1}\; \; \Psi_{2})^{T} = (\Psi^{\ast}, \Phi)^{-1}\Psi^{\ast} , then (\Psi, \Phi) = I_{2} .
We denote f_{n} = (\varphi_{n}^{1}\; \; \varphi_{n}^{2}) . Let \alpha\cdot f_{n} be defined by
According to [40], the center subspace of linear Eq (5.4) is given by P_{CN}\mathcal{C} , where P_{CN}\mathcal{C} = \Phi(\Psi, \langle\phi, f_{n}\rangle)\cdot f_{n}, \phi\in\mathcal{C} , and \mathcal{C} = P_{CN}\mathcal{C}\bigoplus P_{s}\mathcal{C} , P_{s}\mathcal{C} denotes the complement subspace of P_{CN}\mathcal{C} in \mathcal{C} .
Eq (5.2) can be rewritten the following an abstract ordinary differential equation
where
By the decomposition of \mathcal{C} , the solutions of system (5.2) are
where
and
Following the theory in [40] and [41], the center subspace of the linear system of system (5.3) with \mu = 0 is given by P_{CN}\mathcal{C} where
Then the solutions of system (5.2) are
where W(z, \overline{z}) = h\big(\frac{z+\overline{z}}{2}, \frac{i(z-\overline{z})}{2}, 0\big), z = x_{1}-ix_{2} . According to [40], z satisfies the following equation
where
Let
and \Psi_{1}(0)-i\Psi_{2}(0) = (\chi_{1}\; \; \chi_{2}). By Eq (5.6) and Eq (5.9), then we get
and
where
b_{20} = -\frac{2d(2du_{\ast}+u_{\ast}+1)}{(d+u_{\ast})^{3}}+\frac{2absv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{3}}+\frac{2h\rho}{(\rho+u_{\ast})^{2}} , b_{11} = -\frac{2absu_{\ast}v_{\ast}}{(au_{\ast}+bv_{\ast})^{3}} , b_{02} = \frac{2absu_{\ast}}{(au_{\ast}+bv_{\ast})^{3}} ,
b_{30} = \frac{8d^{2}u_{\ast}+4du_{\ast}-4d^{3}-2d^{2}+6d}{(d+u_{}\ast)^{4}}-\frac{6a^{2}bsv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{4}}-\frac{6h\rho} {(\rho+u_{\ast})^{4}} , b_{21} = \frac{4a^{2}bsu_{\ast}v_{\ast}-2ab^{2}sv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{4}} ,
b_{12} = \frac{4ab^{2}su_{\ast}v_{\ast}-2a^{2}bsu_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{4}} , b_{03} = -\frac{6ab^{2}su_{\ast}}{(au_{\ast}+bv_{\ast})^{4}} , c_{20} = -\frac{2abcv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{3}} , c_{11} = \frac{2abcu_{\ast}v_{\ast}}{(au_{\ast}+bv_{\ast})^{3}} ,
c_{02} = -\frac{2abcu_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{3}} , c_{30} = \frac{6a^{2}bcv_{\ast}^{2}}{(au_{\ast}+bv_{\ast})^{4}} , c_{21} = \frac{2ab^{2}cv_{\ast}^{2}-4a^{2}bcu_{\ast}v_{\ast}}{(au_{\ast}+bv_{\ast})^{4}} , c_{12} = \frac{2a^{2}bcu_{\ast}^{2}-4ab^{2}cu_{\ast}v_{\ast}}{(au_{\ast}+bv_{\ast})^{4}} ,
c_{03} = \frac{6ab^{2}cu_{\ast}^{3}}{(au_{\ast}+bv_{\ast})^{4}}.
Therefore
with \Gamma = \frac{1}{l\pi}\int_{0}^{l\pi}\beta_{n}^{3}(x)dx , \gamma_{1} = \frac{1}{l\pi}\int_{0}^{l\pi}\big(\zeta_{1}\beta_{n}^{2}(x)+\zeta_{2}\beta_{n}^{4}(x)\big)dx, \; \; \; \gamma_{2} = \frac{1}{l\pi}\int_{0}^{l\pi}\big(\nu_{1}\beta_{n}^{2}(x)+\nu_{2}\beta_{n}^{4}(x)\big)dx, and
\zeta_{20} = \frac{1}{4}\big(b_{20}+M(2b_{11}+Mb_{02})\big) , \zeta_{11} = \frac{1}{4}\big(b_{20}+(M+\overline{M})b_{11}+M\overline{M}b_{02}\big) ,
\zeta_{1} = W_{20}^{(1)}(0)\big(\frac{b_{20}+\overline{M}b_{11}}{2}\big)+W_{11}^{(1)}(0)\big(b_{20}+Mb_{11}\big)+W_{20}^{(2)}(0)\big(\frac{b_{11}+\overline{M} b_{02}}{2}\big)
\; \; \; \; \; \; \; \; \; +W_{11}^{(2)}(0)\big(b_{11}+Mb_{02}\big) ,
\zeta_{2} = \frac{b_{30}}{8}+\frac{(2M+\overline{M})b_{21}}{8}+\frac{(M^{2}+2M\overline{M})b_{12}}{8}+\frac{M^{2}\overline{M}b_{03}}{8} ,
\nu_{20} = \frac{1}{4}\big(c_{20}e^{-2i\omega_{n}\tau_{\ast}}+M(2c_{11}e^{-i\omega_{n}\tau_{\ast}}+Mc_{02})\big) ,
\nu_{11} = \frac{1}{4}\big(c_{20}+(Me^{i\omega_{n}\tau_{\ast}}+\overline{M}e^{-i\omega_{n}\tau_{\ast}})c_{11}+M\overline{M}c_{02}\big) ,
\nu_{1} = W_{20}^{(1)}(-1)\big(\frac{c_{20}e^{i\omega_{n}\tau_{\ast}}+\overline{M}c_{11}}{2}\big)+W_{11}^{(1)}(-1)\big(c_{20}e^{-i\omega_{n}\tau_{\ast}} +Mc_{11}\big)
\; \; \; \; \; \; \; \; \; +W_{20}^{(2)}(0)\big(\frac{c_{11}e^{i\omega_{n}\tau_{\ast}}+\overline{M}c_{02}}{2}\big)+W_{11}^{(2)}(0)\big(c_{11}e^{-i\omega_{n}\tau_{\ast}} +Mc_{02}\big) ,
\nu_{2} = \frac{c_{30}e^{-i\omega_{n}\tau_{\ast}}}{8}+\frac{(2M+\overline{M}e^{-2i\omega_{n}\tau_{\ast}})c_{21}}{8}+ \frac{(M^{2}e^{i\omega_{n}\tau_{\ast}}+2M\overline{M}e^{-i\omega_{n}\tau_{\ast}})c_{12}}{8}+\frac{M^{2}\overline{M}c_{03}}{8} .
Consider that
then we deduce
Combine with Eq (5.8), Eq (5.10) and Eq (5.11), we have g_{20} = g_{11} = g_{02} = 0, n = 1, 2, 3, \cdot\cdot\cdot . If n = 0 , g_{20} = (\zeta_{20}\chi_{1}+\nu_{20}\chi_{2})\tau_{\ast}, g_{11} = (\zeta_{11}\chi_{1}+\nu_{11}\chi_{2})\tau_{\ast}, g_{02} = (\overline{\zeta}_{20}\chi_{1}+ \overline{\nu}_{20}\chi_{2})\tau_{\ast} , and for n\in\mathbb{N}_{0} , g_{21} = (\gamma_{1}\chi_{1}+\gamma_{2}\chi_{2})\tau_{\ast} .
By Eq (5.5), we obtain
Moreover, W(z, \overline{z}) satisfies
where
Hence, it follows from Eq (5.8), (5.10) and Eq (5.12–5.14) that
Since A(\tau_{\ast}) has only two eigenvalues \pm i\omega_{n}\tau_{\ast} , Eq (5.15) has only a unique solution W_{ij} .
Next, we need to calculate H_{ij}(\theta), \theta\in[-1, 0] . We get that for -1\leq\theta < 0 ,
Hence, by comparing the coefficients, and notice that
we have
By the definition of A(\tau_{\ast}) and Eq (5.15), we have
That is
Utilizing the definition of A(\tau_{\ast}) and combining Eq (5.15) and the above discussions, it follows that
Thus, we can compute the following formulas which determine the direction and stability of bifurcating periodic orbits:
In fact, \mu_{2} determines the directions of the Hopf bifurcation, \beta_{2} determines the stability of the bifurcating periodic solutions, T_{2} determines the period of bifurcating periodic solutions. Moreover, by [41], we have the following results.
Theorem 5.1. For any critical value \tau_{n}^{j} , the following statements valid
(1) If \mu_{2} > 0 (resp. < 0 ), then the Hopf bifurcation is forward (resp. backward), that is, the bifurcating periodic solutions exist for \tau > \tau_{n}^{j} (resp. \tau < \tau_{n}^{j} ).
(2) If \beta_{2} < 0 (resp. > 0 ), then the bifurcating periodic solutions are orbitally asymptotically stable (resp. unstable).
(3) If T_{2} > 0 (resp. < 0 ), then the period increases (resp. decreases).
6.
Numerical simulations
In this section, we perform some results of the numerical simulations to illustrate our mathematical findings in the previous sections. All of our numerical simulations employ the Neumann boundary conditions.
6.1. Global stability
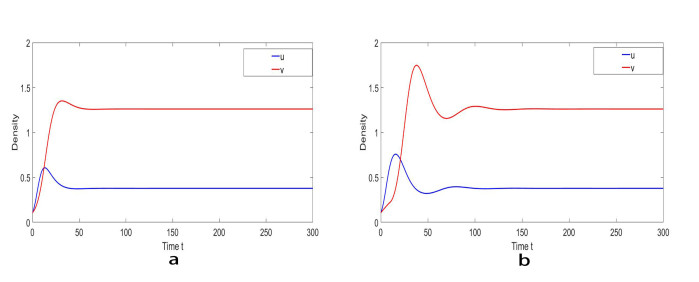
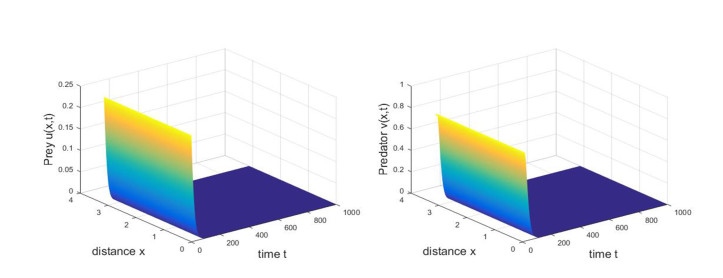
To portray the global stability of trivial steady state E_{0} and the positive constant steady state E_{\ast} , let a = 1.35, b = 0.01, c = 1.353, d = 0.5676, \delta = 1, h = 0.28, \rho = 0.045, s = 0.001 , by simple calculation, we are able to obtain (\rho+h-1)^{2} < 4(dh-\rho) . It follows from Theorem 4.2 that E_{0} is globally asymptotically stable. It can be seen Figure 1a. Moreover, denote a = 0.2, b = 1.5, c = 1.35, d = 0.5676, \delta = 1, h = 0.06, \rho = 0.045, s = 0.01 , then the unique positive constant steady state E_{\ast} = (0.8984, 0.6894) is globally asymptotically stable by Theorem 4.6. As shown in Figure 1b.
6.2. Turing instability
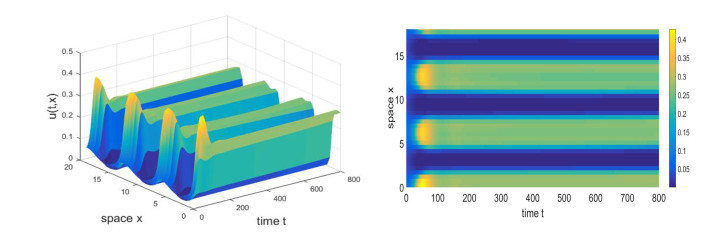
We consider the Turing instability with respect to the unique positive constant steady state E_{\ast} of system (1.7) with \tau = 0 . Let a = 1.2, b = 0.5, c = 0.4, d = 1.8, \delta = 0.15, h = 0.161, \rho = 0.5, s = 0.2, d_{1} = 0.005, d_{2} = 0.5 and l = 4 . By simple calculation, we obtain that system (1.7) has a unique positive steady state E_{\ast} = (0.0527, 0.1547) . It follows from Theorem 4.4 that assumption (H_{1})\sim(H_{3}) and (H_{5})\sim(H_{6}) are satisfied, that is, the positive steady state E_{\ast} for the ODE system is stable. However, for the PDE system, the positive steady state E_{\ast} becomes unstable, and system (1.7) has a stable nonconstant steady state solution, which means that a Turing instability occurs. This is shown in Figure 2. It portrays that the population is irregularly distributed in space. We also observe that the system (1.7) has a stationary spatial pattern, that is shown in Figure 3. Moreover, choose d_{1} = 0.01 , we are able to observe that under the effect of diffusion coefficients of d_{2} , system (1.7) portrays different spatial patterns that can be periodic, stationary, as shown in Figure 4.
6.3. Delay induced Hopf bifurcation in system (1.7)
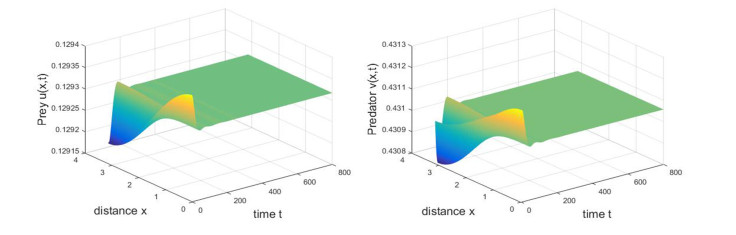
Firstly, we consider that the unique positive constant steady state E_{\ast} of system (1.7) is locally asymptotically stable for all \tau\geq0 . Let a = 1, b = 0.5, c = 0.4, d = 2, \delta = 0.15, h = 0.01, \rho = 0.5, s = 0.2, d_{1} = 0.01, d_{2} = 0.02 . By calculation, the positive constant steady state E_{\ast} = (0.3783, 1.2611) , the conditions (H_{1})\sim(H_{4}) and (H_{7}) are satisfied. It follows from Theorem 4.5 that the unique positive constant steady state E_{\ast} of system (1.7) is locally asymptotically stable for all \tau\geq0 in Figure 5.
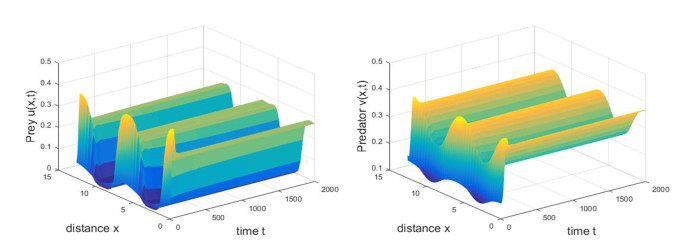
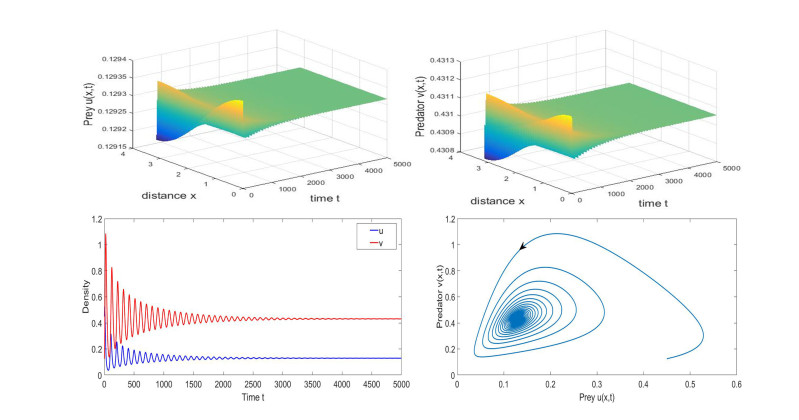
Consider system (1.7) with the parameters a = 1, b = 0.5, c = 0.4, d = 2, \delta = 0.15, h = 0.1, \rho = 0.5, s = 0.2, d_{1} = 0.01, d_{2} = 0.02 and l = 1 . Calculation shows that system (1.7) has a unique positive constant steady state E_{\ast} = (0.1293, 0.4311) . Hypothesis (H_{1})\sim(H_{4}) and (H_{8}) satisfy for n = 0 , by calculation we have \omega_{0} = 0.0652 . It follows from Theorem 4.7 that homogeneous Hopf bifurcations occur at \tau_{0}^{j}\approx6.1868+96.3679j for j\in\mathbb{N}_{0} . We use the forward Euler method to find numerical solutions to system (1.7) with \tau = 0, 5.85, 6.20 , respectively. From Theorem 4.3, the unique positive constant steady state E_{\ast} = (0.1293, 0.4311) of system (1.7) with \tau = 0 is locally asymptotically stable, it can be seen from Figure 6.
As shown in Figure 7 and 8, we observe sustained oscillations when delay \tau crosses the critical value \tau_{0}^{0}\approx6.1868 . We have \lambda'(\tau_{0}^{0})\approx0.0035-0.0014i by Lemma 4.4. From Theorem 4.7, we know that if \tau\in[0, \tau_{0}^{0}) , then the equilibrium E_{\ast} = (0.1293, 0.4311) is locally asymptotically stable. This is shown in Figure 7. And we conclude that the equilibrium E_{\ast} = (0.1293, 0.4311) loses its stability and Hopf bifurcation occurs when \tau crosses the critical value \tau_{0}^{0} . By calculation and Eq (5.16), we get C_{1}(0) = -0.5076-1.4071i, \; \; \mu_{2}\approx145.0286 > 0, \; \; \beta_{2}\approx-1.0152 < 0, \; \; T_{2}\approx3.9916 > 0.
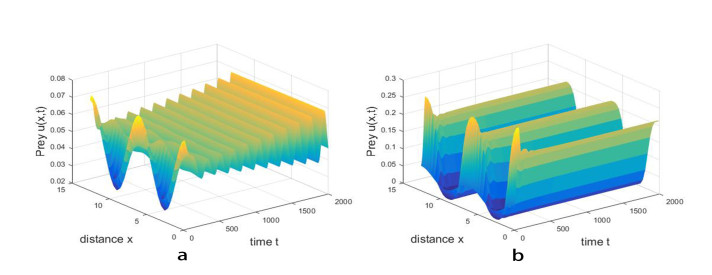
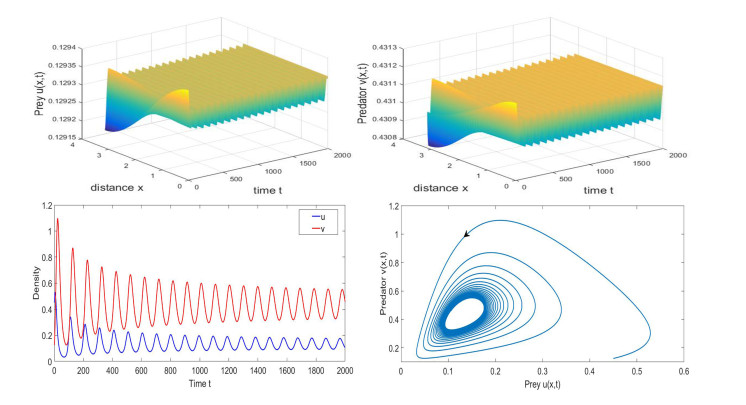
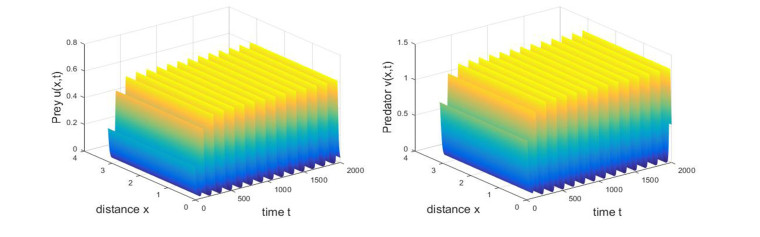
Hence, it follows from Theorem 5.1 that the direction of the bifurcation is forward, and the bifurcating period solutions are locally asymptotically stable. Moreover, the period of bifurcating periodic solutions increases. This is shown in Figure 8. If \tau is increasing crosses the critical value \tau_{1}^{0}\approx10.0462 , a spatially inhomogeneous periodic solution occurs near the positive equilibrium E_{\ast} = (0.1293, 0.4311) . However, the bifurcating periodic solution bifurcating from the critical value \tau_{1}^{0} must be unstable on the whole phase space since the characteristic equation always has roots with positive real parts for \tau > \tau_{0}^{0}\approx6.1868 . This is shown in Figure 9. Besides, as \tau increases further, with the same initial values, the solution of system (1.7) converges to (0, 0) , which implies that the increasing delay may cause the prey and predator to go extinct. As shown in Figure 10.
6.4. The effect of nonlinear harvesting
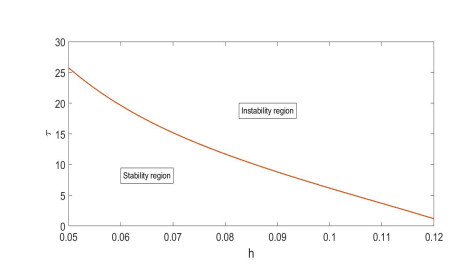
Considering the effect of nonlinear harvesting, we denote the parameters be the same as section 6.3 and h vary in [0.05, 0.12] . The stability and instability regions of the unique positive constant steady state E_{\ast} for system (1.7) is depicted by mapping the nonlinear harvesting to the critical value of the delay \tau in Figure 11. We observe that the nonlinear harvesting effect parameter h increases from 0.05 and 0.12 , the Hopf bifurcation is occurred for lower critical values of \tau . Meanwhile, we observe that the harvesting effect parameter h has a significant effect on the stability of ecosystem.
7.
Conclusions and discussions
In this paper, we focused on a delayed diffusive predator-prey system with food-limited and nonlinear harvesting effect. Firstly, in order to prove the global stability of the solution, we gave the existence of solution and priori bound. Meanwhile, we also derived the conditions of stability of the nonnegative constant steady state solution. Moreover, the global stability of the trivial and positive constant steady state is investigated. The conditions of Turing instability and Hopf bifurcation are obtained for system (1.7), respecitvely. For the positive constant steady state solution, it is demonstrated that Hopf bifurcation can be occurred when bifurcation parameter \tau increases beyond a critical value. We derived the detailed formulas to determine the properties of Hopf bifurcation.
For the system (1.7), it follows from Theorem 4.2 and Theorem 4.6 that the trivial steady state E_{0} and the positive constant steady state E_{\ast} are globally asymptotically stable under the certain conditions (Figure 1), respectively. From an ecological point of view, due to the food-limited in the natural environment, intraspecific competition in prey population increases, so nonlinear prey harvesting is taken into consideration. Increasing the harvesting effect parameter h properly can decrease the density of prey population so that relieve the pressure of intraspecific competition and the system becomes stable under the certain conditions. However, if h crosses a certain value, the density of prey population begins decreasing and may even become extinct (Figures 10 and 11). The diffusion induces the occurrence of Turing instability for the positive steady state E_{\ast} , which means that system (1.7) has a stable nonconstant steady state solution (Figures 2 and 3). Our results also reveal the fact that delay can induce very complex dynamics phenomenon, and a positive constant steady state E_{\ast} is depicted to be locally asymptotically stable when the parameter \tau is less than the critical value \tau_{\ast} (Figure 7), and a stable periodic solutions will bifurcate from the constant steady state E_{\ast} (Figure 8), when the delay \tau increase and it crosses through the critical value \tau_{\ast} , which means that a stable and spatially homogeneous periodic solutions will occur at the critical value of delay \tau_{\ast} , when the delay \tau continues to increase to a certain value, spatially inhomogeneous periodic solution bifurcates from the positive constant steady state E_{\ast} for system (1.7) (Figure 9). When the delay \tau is larger, the solution of system (1.7) tends to (0, 0) , that is, the population becomes extinct eventually (Figure 10).
From the biological point of view, it is clear that delay, nonlinear harvesting and diffusion effect have a significant impact on the stability for ecosystem.
However, there exists many problems will need to be investigated for system (1.7). Firstly, the selection results of Turing patterns are obtained by weakly nonlinear analysis[29,30]. Secondly, the diffusion of the population is random and homogeneous in this paper, actually, individuals often perform a nonlocal diffusion or heterogeneous diffusion in the real world. Finally, spatial memory and cognition of animals has drawn much attention in the mathematical modeling of animal movement (i.e., memory-based diffusion)[42]. These problems will be investigated in the future.
Acknowledgments
We would like to express our gratitude to the referees for their valuable comments and suggestions that led to a truly significant improvement of the manuscript. The work is supported by the National Natural Science Foundation of China (11871475) and the Fundamental Research Funds for the Central University of Central South University (2019zzts212).
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: