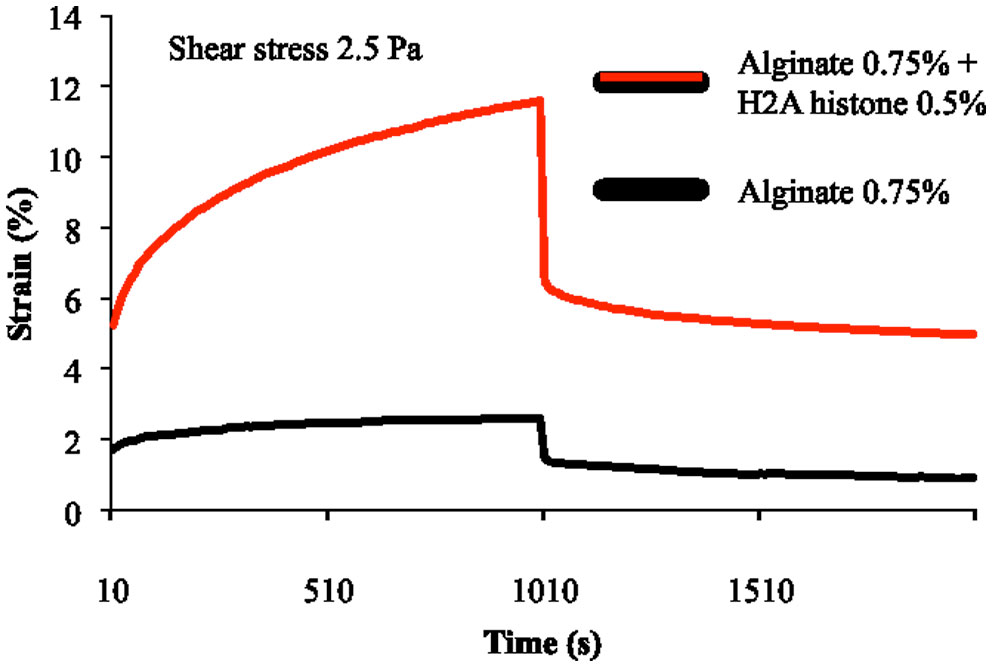
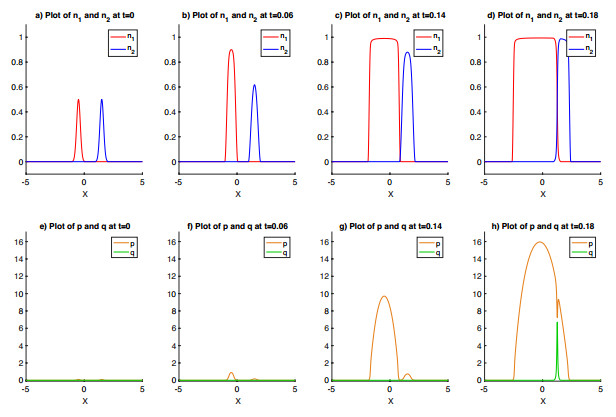
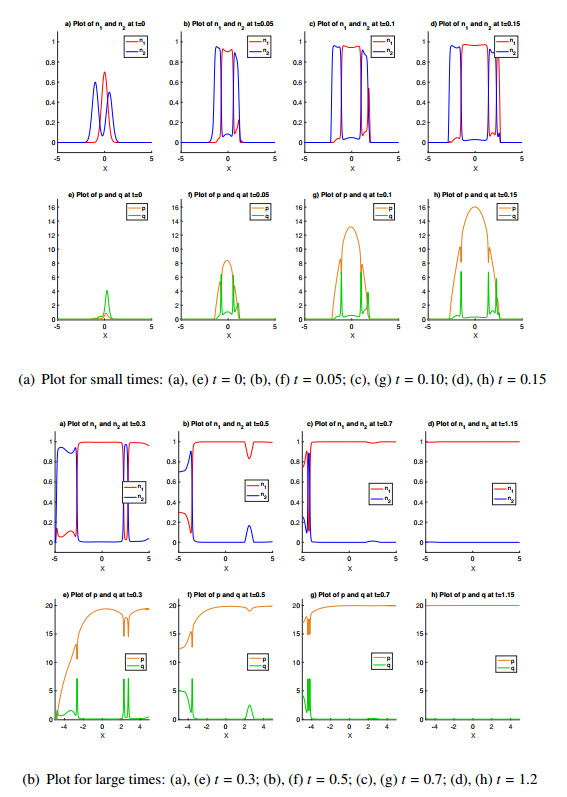
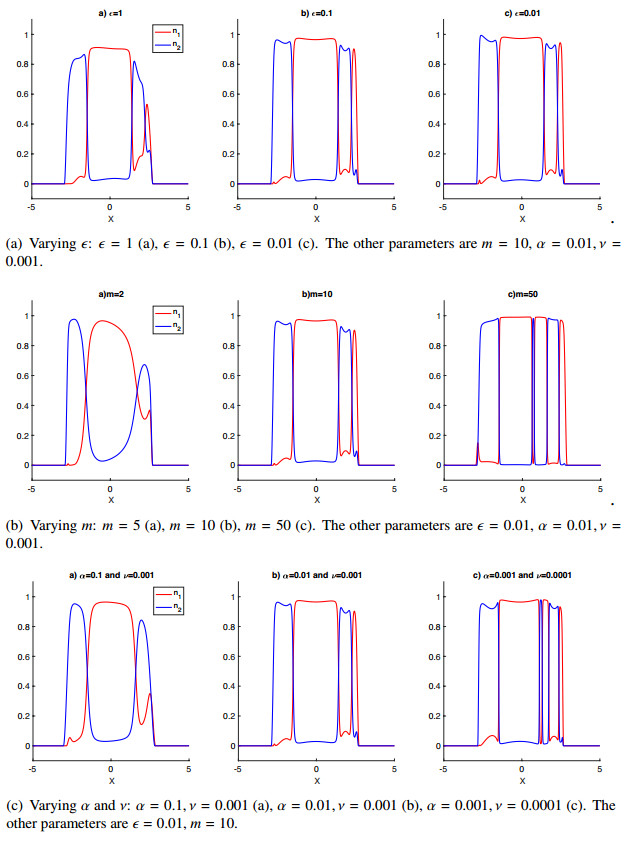
| 1.
|
Lihua Chen, Yaru Zou, Asmaa Abbas Kronfl, Yong Wu,
Type VI secretion system of
Pseudomonas aeruginosa
is associated with biofilm formation but not environmental adaptation
,
2020,
9,
2045-8827,
10.1002/mbo3.991
|
|
| 2.
|
Dylan Chirman, Nancy Pleshko,
Characterization of bacterial biofilm infections with Fourier transform infrared spectroscopy: a review,
2021,
0570-4928,
1,
10.1080/05704928.2020.1864392
|
|
| 3.
|
John A. Glaser,
2020,
Chapter 18,
978-1-78985-899-0,
10.5772/intechopen.92816
|
|
| 4.
|
Chisato Takahashi, Tomomi Yamada, Shinya Yagi, Takaaki Murai, Shunsuke Muto,
Preparation of silver-decorated Soluplus® nanoparticles and antibacterial activity towards S. epidermidis biofilms as characterized by STEM-CL spectroscopy,
2021,
121,
09284931,
111718,
10.1016/j.msec.2020.111718
|
|
| 5.
|
Kaitlyn R. Rouillard, Matthew R. Markovetz, Lawrence G. Bacudio, David B. Hill, Mark H. Schoenfisch,
Pseudomonas aeruginosa Biofilm Eradication via Nitric Oxide-Releasing Cyclodextrins,
2020,
6,
2373-8227,
1940,
10.1021/acsinfecdis.0c00246
|
|
| 6.
|
Poulomi Chakraborty, Payel Paul, Monika Kumari, Surajit Bhattacharjee, Mukesh Singh, Debasish Maiti, Debabrata Ghosh Dastidar, Yusuf Akhter, Taraknath Kundu, Amlan Das, Prosun Tribedi,
Attenuation of Pseudomonas aeruginosa biofilm by thymoquinone: an individual and combinatorial study with tetrazine-capped silver nanoparticles and tryptophan,
2021,
0015-5632,
10.1007/s12223-020-00841-1
|
|
| 7.
|
Nandhini Ashok, Kuang He, Carl E. Bauer, Caroline S. Harwood,
No Light, No Germination: Excitation of the Rhodospirillum centenum Photosynthetic Apparatus Is Necessary and Sufficient for Cyst Germination,
2021,
12,
2150-7511,
10.1128/mBio.03619-20
|
|
| 8.
|
J A Blee, I S Roberts, T A Waigh,
Membrane potentials, oxidative stress and the dispersal response of bacterial biofilms to 405 nm light,
2020,
17,
1478-3975,
036001,
10.1088/1478-3975/ab759a
|
|
| 9.
|
Nirmani N. Wickramasinghe, Mya M. Hlaing, Joshua T. Ravensdale, Ranil Coorey, P. Scott Chandry, Gary A. Dykes,
Characterization of the biofilm matrix composition of psychrotrophic, meat spoilage pseudomonads,
2020,
10,
2045-2322,
10.1038/s41598-020-73612-0
|
|
| 10.
|
Bharti Patel, Subrata Mishra, Indira K. Priyadarsini, Sirisha L. Vavilala,
Elucidating the anti-biofilm and anti-quorum sensing potential of selenocystine against respiratory tract infections causing bacteria: in vitro and in silico studies,
2021,
0,
1437-4315,
10.1515/hsz-2020-0375
|
|
| 11.
|
Namita Shrestha, Abhilash Kumar Tripathi, Tanvi Govil, Rajesh Kumar Sani, Meltem Urgun-Demirtas, Venkateswaran Kasthuri, Venkataramana Gadhamshetty,
Electricity from lignocellulosic substrates by thermophilic Geobacillus species,
2020,
10,
2045-2322,
10.1038/s41598-020-72866-y
|
|
| 12.
|
Ikuyo MAKINO, Yuji YAHAGI, Takahiro NAKAYAMA, Atsushi KOBAYASHI,
METABOLOMIC ANALYSES OF INTRACELLULAR DYNAMICS IN BLOOM - FORMING CYANOBACTERIUM MICROCYSTIS,
2019,
75,
2185-467X,
I_673,
10.2208/jscejhe.75.2_I_673
|
|
| 13.
|
Ahmed Houari, Patrick Di Martino,
Polysaccharide-hydrolysing enzymes enhance the in vitro cleaning efficiency of Nanofiltration membranes,
2019,
5,
2471-1888,
368,
10.3934/microbiol.2019.4.368
|
|
| 14.
|
Cristina Cattò, Francesca Cappitelli,
Testing Anti-Biofilm Polymeric Surfaces: Where to Start?,
2019,
20,
1422-0067,
3794,
10.3390/ijms20153794
|
|
| 15.
|
Michela Relucenti, Giuseppe Familiari, Orlando Donfrancesco, Maurizio Taurino, Xiaobo Li, Rui Chen, Marco Artini, Rosanna Papa, Laura Selan,
Microscopy Methods for Biofilm Imaging: Focus on SEM and VP-SEM Pros and Cons,
2021,
10,
2079-7737,
51,
10.3390/biology10010051
|
|
| 16.
|
Dishon Wayne Hiebner, Caio Barros, Laura Quinn, Stefania Vitale, Eoin Casey,
Surface functionalization-dependent localization and affinity of SiO2 nanoparticles within the biofilm EPS matrix,
2020,
2,
25902075,
100029,
10.1016/j.bioflm.2020.100029
|
|
| 17.
|
Sara I. Faria, Rita Teixeira-Santos, Luciana C. Gomes, Elisabete R. Silva, João Morais, Vítor Vasconcelos, Filipe J. M. Mergulhão,
Experimental Assessment of the Performance of Two Marine Coatings to Curb Biofilm Formation of Microfoulers,
2020,
10,
2079-6412,
893,
10.3390/coatings10090893
|
|
| 18.
|
Xiaofei Yin, Florian Weitzel, Erika Griesshaber, Lurdes Fernández-Díaz, Concepcion Jimenez-Lopez, Andreas Ziegler, Alejandro B. Rodriguez-Navarro, Wolfgang W. Schmahl,
Bacterial EPS in Agarose Hydrogels Directs Mineral Organization in Calcite Precipitates: Species-Specific Biosignatures ofBacillus subtilis,Mycobacterium phley,Mycobacterium smagmatis, andPseudomonas putidaEPS,
2020,
20,
1528-7483,
4402,
10.1021/acs.cgd.0c00231
|
|
| 19.
|
Asim Ali Yaqoob, Mohamad Nasir Mohamad Ibrahim, Khalid Umar, Showkat Ahmad Bhawani, Anish Khan, Abdullah M Asiri, Mohammad Rizwan Khan, Mohammad Azam, Ahmad Moid AlAmmari,
Cellulose Derived Graphene/Polyaniline Nanocomposite Anode for Energy Generation and Bioremediation of Toxic Metals via Benthic Microbial Fuel Cells,
2020,
13,
2073-4360,
135,
10.3390/polym13010135
|
|
| 20.
|
Tianyang Wang, Steve Flint, Jon Palmer,
Magnesium and calcium ions: roles in bacterial cell attachment and biofilm structure maturation,
2019,
35,
0892-7014,
959,
10.1080/08927014.2019.1674811
|
|
| 21.
|
Ogueri Nwaiwu, Lawrence Wong, Mita Lad, Timothy Foster, William MacNaughtan, Catherine Rees,
Properties of the Extracellular Polymeric Substance Layer from Minimally Grown Planktonic Cells of Listeria monocytogenes,
2021,
11,
2218-273X,
331,
10.3390/biom11020331
|
|
| 22.
|
Daniel L. Forwood, Elizabeth K. Bryce, Eleonora Caro, Devin B. Holman, Sarah J. Meale, Alex V. Chaves,
Influence of probiotics on biofilm formation and diversity of bacteria colonising crop sorghum ensiled with unsalable vegetables,
2020,
104,
0175-7598,
8825,
10.1007/s00253-020-10877-5
|
|
| 23.
|
Patrick Di Martino,
Bacterial adherence: much more than a bond,
2018,
4,
2471-1888,
563,
10.3934/microbiol.2018.3.563
|
|
| 24.
|
Yuan-Chieh Yeh, Tse-Hung Huang, Shih-Chun Yang, Chin-Chang Chen, Jia-You Fang,
Nano-Based Drug Delivery or Targeting to Eradicate Bacteria for Infection Mitigation: A Review of Recent Advances,
2020,
8,
2296-2646,
10.3389/fchem.2020.00286
|
|
| 25.
|
Kumar Selvarajoo,
2020,
1374,
9780841298606,
9,
10.1021/bk-2020-1374.ch002
|
|
| 26.
|
Fahad A. Almughem, Ahmad M. Aldossary, Essam A. Tawfik, Mohammad N. Alomary, Waleed S. Alharbi, Mohammad Y. Alshahrani, Abdullah A. Alshehri,
Cystic Fibrosis: Overview of the Current Development Trends and Innovative Therapeutic Strategies,
2020,
12,
1999-4923,
616,
10.3390/pharmaceutics12070616
|
|
| 27.
|
Jung-Whan Chon, Un Jung Lee, Ryan Bensen, Stephanie West, Angel Paredes, Jinhee Lim, Saeed Khan, Mark E. Hart, K. Scott Phillips, Kidon Sung,
Virulence Characteristics of mecA-Positive Multidrug-Resistant Clinical Coagulase-Negative Staphylococci,
2020,
8,
2076-2607,
659,
10.3390/microorganisms8050659
|
|
| 28.
|
Mohammed Abdulsalam, Hasfalina Che Man, Aida Isma Idris, Khairul Faezah Yunos, Zurina Zainal Abidin,
Treatment of Palm Oil Mill Effluent Using Membrane Bioreactor: Novel Processes and Their Major Drawbacks,
2018,
10,
2073-4441,
1165,
10.3390/w10091165
|
|
| 29.
|
Camilo Zamora-Ledezma, Alanis Chicaiza-Zambrano, Nelson Santiago Vispo, Alexis Debut, Karla Vizuete, Víctor H. Guerrero, Cristina E. Almeida, Frank Alexis,
Frequency Based Control of Antifouling Properties Using Graphene Nanoplatelet/Poly(Lactic-co-Glycolic Acid) Composite Films,
2021,
0927-6440,
1,
10.1080/09276440.2020.1865088
|
|
| 30.
|
Chiara Ceresa, Letizia Fracchia, Emanuele Fedeli, Chiara Porta, Ibrahim M. Banat,
Recent Advances in Biomedical, Therapeutic and Pharmaceutical Applications of Microbial Surfactants,
2021,
13,
1999-4923,
466,
10.3390/pharmaceutics13040466
|
|
| 31.
|
Asim Ali Yaqoob, Albert Serrà, Mohamad Nasir Mohamad Ibrahim, Amira Suriaty Yaakop,
Self-assembled oil palm biomass-derived modified graphene oxide anode: An efficient medium for energy transportation and bioremediating Cd (II) via microbial fuel cells,
2021,
14,
18785352,
103121,
10.1016/j.arabjc.2021.103121
|
|
| 32.
|
Bhisma Narayan Ratha, Dibyajit Lahiri, Rina Rani Ray,
2021,
Chapter 9,
978-981-16-0744-8,
209,
10.1007/978-981-16-0745-5_9
|
|
| 33.
|
M. Moradi, G. Ghiara, R. Spotorno, D. Xu, P. Cristiani,
Understanding biofilm impact on electrochemical impedance spectroscopy analyses in microbial corrosion and microbial corrosion inhibition phenomena,
2022,
426,
00134686,
140803,
10.1016/j.electacta.2022.140803
|
|
| 34.
|
Asim Ali Yaqoob, Muhammad Arshiq Bin Abu Bakar, Hyun-Chul Kim, Akil Ahmad, Mohammed B. Alshammari, Amira Suriaty Yaakop,
Oxidation of food waste as an organic substrate in a single chamber microbial fuel cell to remove the pollutant with energy generation,
2022,
52,
22131388,
102282,
10.1016/j.seta.2022.102282
|
|
| 35.
|
Yolande Ikala Openda, Bokolombe Pitchou Ngoy, Jules Tshishimbi Muya, Tebello Nyokong,
Synthesis, theoretical calculations and laser flash photolysis studies of selected amphiphilic porphyrin derivatives used as biofilm photodegradative materials,
2021,
45,
1144-0546,
17320,
10.1039/D1NJ02651H
|
|
| 36.
|
Alessandra Fusco, Vittoria Savio, Debora Stelitano, Adone Baroni, Giovanna Donnarumma,
The Intestinal Biofilm of Pseudomonas aeruginosa and Staphylococcus aureus Is Inhibited by Antimicrobial Peptides HBD-2 and HBD-3,
2021,
11,
2076-3417,
6595,
10.3390/app11146595
|
|
| 37.
|
Krishna R. Salin, Nguyen Tien Vinh,
2023,
9780323912402,
69,
10.1016/B978-0-323-91240-2.00017-8
|
|
| 38.
|
M. Atasoy, W.T. Scott Jr., K. van Gijn, J.J. Koehorst, H. Smidt, A.A.M. Langenhoff,
Microbial dynamics and bioreactor performance are interlinked with organic matter removal from wastewater treatment plant effluent,
2023,
372,
09608524,
128659,
10.1016/j.biortech.2023.128659
|
|
| 39.
|
Michela Relucenti, Orlando Donfrancesco, Loredana Cristiano, Stefania Nottola, Marco Artini, Rosanna Papa, Laura Selan,
2023,
9780323999779,
81,
10.1016/B978-0-323-99977-9.00019-3
|
|
| 40.
|
Muzamil Ahmad Rather, Kuldeep Gupta, Manabendra Mandal,
2021,
9780128244487,
451,
10.1016/B978-0-12-824448-7.00023-1
|
|
| 41.
|
Asim Ali Yaqoob, Albert Serrà, Showkat Ahmad Bhawani, Mohamad Nasir Mohamad Ibrahim, Anish Khan, Hajer S. Alorfi, Abdullah M. Asiri, Mahmoud Ali Hussein, Imran Khan, Khalid Umar,
Utilizing Biomass-Based Graphene Oxide–Polyaniline–Ag Electrodes in Microbial Fuel Cells to Boost Energy Generation and Heavy Metal Removal,
2022,
14,
2073-4360,
845,
10.3390/polym14040845
|
|
| 42.
|
Zhuoran Wu, Brian Chan, Jessalyn Low, Justin Jang Hann Chu, Hwee Weng Dennis Hey, Andy Tay,
Microbial resistance to nanotechnologies: An important but understudied consideration using antimicrobial nanotechnologies in orthopaedic implants,
2022,
16,
2452199X,
249,
10.1016/j.bioactmat.2022.02.014
|
|
| 43.
|
Fatin Syahirah Fadzli, Mohd Rashid, Asim Ali Yaqoob, Mohamad Nasir Mohamad Ibrahim,
Electricity generation and heavy metal remediation by utilizing yam (Dioscorea alata) waste in benthic microbial fuel cells (BMFCs),
2021,
172,
1369703X,
108067,
10.1016/j.bej.2021.108067
|
|
| 44.
|
Xingzhu Huang, Shaofeng Zhou, Jianjun Li, Xiaojun Wang, Shaobin Huang, Guoping Sun, Shan Yang, Jia Xing, Meiying Xu,
Complexing agents-free bioelectrochemical trickling systems for highly-efficient mesothermal NO removal: The role of extracellular polymer substances,
2023,
368,
09608524,
128286,
10.1016/j.biortech.2022.128286
|
|
| 45.
|
Moupriya Nag, Dibyajit Lahiri, Indranil Mukherjee, Shreyasi Ghosh, Bandita Dutta, Ankita Dey, Rina Rani Ray,
2022,
9780323912518,
103,
10.1016/B978-0-323-91251-8.00016-7
|
|
| 46.
|
Giada Caniglia, Andrea Teuber, Holger Barth, Boris Mizaikoff, Christine Kranz,
Atomic force and infrared spectroscopic studies on the role of surface charge for the anti-biofouling properties of polydopamine films,
2022,
1618-2642,
10.1007/s00216-022-04431-7
|
|
| 47.
|
Anh Q. Nguyen, Luong N. Nguyen, Zhicheng Xu, Wenhai Luo, Long D. Nghiem,
New insights to the difference in microbial composition and interspecies interactions between fouling layer and mixed liquor in a membrane bioreactor,
2022,
643,
03767388,
120034,
10.1016/j.memsci.2021.120034
|
|
| 48.
|
Ahmet KÖREMEZLİ, Ergin KARİPTAŞ, Belgin ERDEM,
BAKTERİYEL MİKROORGANİZMALARDA BİR SAVUNMA SİSTEMİ: “BİYOFİLM”,
2021,
2619-9041,
10.19127/bshealthscience.983603
|
|
| 49.
|
Muxue Wang, Xiangjun Zhan, Xiao Ma, Ruixia Wang, Du Guo, Yingying Zhang, Jiangtao Yu, Yunhe Chang, Xin Lü, Chao Shi,
Antibacterial Activity of Thymoquinone Against Shigella flexneri and Its Effect on Biofilm Formation,
2022,
19,
1535-3141,
767,
10.1089/fpd.2022.0056
|
|
| 50.
|
Asim Ali Yaqoob, Mohamad Nasir Mohamad Ibrahim, Amira Suriaty Yaakop, Akil Ahmad,
Application of microbial fuel cells energized by oil palm trunk sap (OPTS) to remove the toxic metal from synthetic wastewater with generation of electricity,
2021,
11,
2190-5509,
1949,
10.1007/s13204-021-01885-6
|
|
| 51.
|
Xiao-Meng Hu, Junbo Zhang, Wen-Yang Ding, Xiao Liang, Rong Wan, Sergey Dobretsov, Jin-Long Yang,
Reduction of mussel metamorphosis by inactivation of the bacterial thioesterase gene via alteration of the fatty acid composition,
2021,
37,
0892-7014,
911,
10.1080/08927014.2021.1981882
|
|
| 52.
|
Ali Zein Alabiden Tlais, Andrea Polo, Pasquale Filannino, Vincenzo Cantatore, Marco Gobbetti, Raffaella Di Cagno,
Biofilm formation as an extra gear for
Apilactobacillus kunkeei
to counter the threat of agrochemicals in honeybee crop
,
2022,
15,
1751-7915,
2160,
10.1111/1751-7915.14051
|
|
| 53.
|
Sathish Sankar, Pitchaipillai Sankar Ganesh, Suganya Subramaniam, Esaki M Shankar, Monal Yuwanati, Rajakumar Govindasamy, Muthu Thiruvengadam,
Host cell responses against the pseudomonal biofilm: A continued tale of host-pathogen interactions,
2023,
174,
08824010,
105940,
10.1016/j.micpath.2022.105940
|
|
| 54.
|
Ram Nageena Singh, Etienne Z. Gnimpieba, Rajesh Kumar Sani,
2022,
Title: Challenges in single cells sequencing Microbial community and biofilm: A case of Oleidesulfovibrio alaskensis G20 NGS protocol,
978-1-6654-6819-0,
3613,
10.1109/BIBM55620.2022.9995610
|
|
| 55.
|
Sofía Díaz-Cornejo, María Carolina Otero, Aparna Banerjee, Felipe Gordillo-Fuenzalida,
Biological properties of exopolysaccharides produced by Bacillus spp.,
2023,
268,
09445013,
127276,
10.1016/j.micres.2022.127276
|
|
| 56.
|
Junhui Guo, Guiqin Yang, Zheng Zhuang, Qijun Mai, Li Zhuang,
Redox potential-induced regulation of extracellular polymeric substances in an electroactive mixed community biofilm,
2021,
797,
00489697,
149207,
10.1016/j.scitotenv.2021.149207
|
|
| 57.
|
Galina Satchanska,
2022,
Chapter 19,
978-1-80355-795-3,
10.5772/intechopen.104813
|
|
| 58.
|
Akiko Ogawa, Shoya Hosaka, Hideyuki Kanematsu, Michiko Yoshitake,
Marine Biofilm Model Comprising a Loop-Type Biofilm Reactor and a Halomonas Strain HIG FST4 1, an Active Biofilm-Forming Bacterium,
2022,
12,
2079-6412,
1605,
10.3390/coatings12101605
|
|
| 59.
|
Qi Peng, Xiaohua Tang, Wanyang Dong, Ning Sun, Wenchang Yuan,
A Review of Biofilm Formation of Staphylococcus aureus and Its Regulation Mechanism,
2022,
12,
2079-6382,
12,
10.3390/antibiotics12010012
|
|
| 60.
|
Thi Minh Nguyen, Phuong Thu Ha, Thi Thu Huong Le, Ke Son Phan, Thi Nhi Cong Le, Thi Thu Trang Mai, Phuong Ha Hoang,
Modification of expanded clay carrier for enhancing the immobilization and nitrogen removal capacity of nitrifying and denitrifying bacteria in the aquaculture system,
2022,
134,
13891723,
41,
10.1016/j.jbiosc.2022.04.006
|
|
| 61.
|
Johnathan R Lex, Robert Koucheki, Nikolaos A Stavropoulos, Joseph Di Michele, Jay S Toor, Kim Tsoi, Peter C Ferguson, Robert E Turcotte, Panayiotis J Papagelopoulos,
Megaprosthesis anti-bacterial coatings: A comprehensive translational review,
2022,
140,
17427061,
136,
10.1016/j.actbio.2021.11.045
|
|
| 62.
|
Sharmistha Das, Payel Paul, Debabrata Ghosh Dastidar, Poulomi Chakraborty, Sudipta Chatterjee, Sarita Sarkar, Debasish Maiti, Prosun Tribedi,
Piperine Exhibits Potential Antibiofilm Activity Against Pseudomonas aeruginosa by Accumulating Reactive Oxygen Species, Affecting Cell Surface Hydrophobicity and Quorum Sensing,
2022,
0273-2289,
10.1007/s12010-022-04280-1
|
|
| 63.
|
Hillol Chakdar, Shobit Thapa, Amit Srivastava, Pratyoosh Shukla,
Genomic and proteomic insights into the heavy metal bioremediation by cyanobacteria,
2022,
424,
03043894,
127609,
10.1016/j.jhazmat.2021.127609
|
|
| 64.
|
Ashley N. White, Brian S. Learman, Aimee L. Brauer, Chelsie E. Armbruster, Craig R. Roy,
Catalase Activity is Critical for Proteus mirabilis Biofilm Development, Extracellular Polymeric Substance Composition, and Dissemination during Catheter-Associated Urinary Tract Infection,
2021,
89,
0019-9567,
10.1128/IAI.00177-21
|
|
| 65.
|
Stephanie P. Gill, Louise Kregting, Ibrahim M. Banat, Joerg Arnscheidt, William R. Hunter,
Rhamnolipids Mediate the Effects of a Gastropod Grazer in Regards to Carbon–Nitrogen Stoichiometry of Intertidal Microbial Biofilms,
2022,
12,
2076-3417,
12729,
10.3390/app122412729
|
|
| 66.
|
Aleksandra Ivanova, Kristina Ivanova, Ilana Perelshtein, Aharon Gedanken, Katerina Todorova, Rositsa Milcheva, Petar Dimitrov, Teodora Popova, Tzanko Tzanov,
Sonochemically engineered nano-enabled zinc oxide/amylase coatings prevent the occurrence of catheter-associated urinary tract infections,
2021,
131,
09284931,
112518,
10.1016/j.msec.2021.112518
|
|
| 67.
|
Phu-Tho Nguyen, Thi-Tho Nguyen, Thi-To-Uyen Nguyen, Quoc-Khanh Hoang, Huu-Thanh Nguyen,
Improve the viability and extracellular polymeric substances bioactivity of Lactiplantibacillus plantarum VAL6 using the environmental adaptation,
2022,
131,
09603085,
149,
10.1016/j.fbp.2021.11.006
|
|
| 68.
|
Adeola Julian Sorinolu, Mariya Munir,
Degradation and horizontal gene transfer analysis of plasmid-encoded antibiotic resistance genes during UV254, hydroxyl radical and sulphate radical treatments,
2022,
450,
13858947,
138380,
10.1016/j.cej.2022.138380
|
|
| 69.
|
Alia Telli, Mohamed Amine Gacem,
2023,
9780128242834,
261,
10.1016/B978-0-12-824283-4.00003-4
|
|
| 70.
|
Ula Rozman, Sabine Filker, Gabriela Kalčíková,
Monitoring of biofilm development and physico-chemical changes of floating microplastics at the air-water interface,
2023,
322,
02697491,
121157,
10.1016/j.envpol.2023.121157
|
|
| 71.
|
Alireza Fathollahi, Stephen J. Coupe,
Effect of environmental and nutritional conditions on the formation of single and mixed-species biofilms and their efficiency in cadmium removal,
2021,
283,
00456535,
131152,
10.1016/j.chemosphere.2021.131152
|
|
| 72.
|
Richa Priyadarshini, Karthik Krishnan, Rashmi Niranjan,
2021,
Chapter 3,
978-1-83962-686-9,
10.5772/intechopen.96449
|
|
| 73.
|
Murali Kumar, Joseph Tierney, Martin Wilkinson,
Enzymatic Disruption of Biofilms During Cheese Manufacturing: A Mini Review,
2021,
12,
1664-302X,
10.3389/fmicb.2021.791061
|
|
| 74.
|
Zeuko’O Menkem Elisabeth,
2022,
Chapter 9,
978-1-80355-795-3,
10.5772/intechopen.104772
|
|
| 75.
|
Qisen Xiang, Liyuan Niu, Yanhong Bai,
2022,
Chapter 4,
978-981-16-1826-0,
75,
10.1007/978-981-16-1827-7_4
|
|
| 76.
|
Rajalekshmi Resmi, Jayasree Parvathy, Ramakrishna Perumal Saravana, Gijo Raj, Roy Joseph,
Biosynthesized Nanosilver from Alginate Dialdehyde: An In Vitro Evaluation,
2021,
6,
2365-6549,
12007,
10.1002/slct.202103220
|
|
| 77.
|
Monika Oleksy-Wawrzyniak, Adam Junka, Malwina Brożyna, Migdał Paweł, Bartłomiej Kwiek, Maciej Nowak, Beata Mączyńska, Marzenna Bartoszewicz,
The In Vitro Ability of Klebsiella pneumoniae to Form Biofilm and the Potential of Various Compounds to Eradicate It from Urinary Catheters,
2021,
11,
2076-0817,
42,
10.3390/pathogens11010042
|
|
| 78.
|
Siarhei A. Dabravolski, Stanislav V. Isayenkov,
Metabolites Facilitating Adaptation of Desert Cyanobacteria to Extremely Arid Environments,
2022,
11,
2223-7747,
3225,
10.3390/plants11233225
|
|
| 79.
|
Jike Yang, Yu Zhang, Weiwei Chang, Yuntian Lou, Hongchang Qian,
Microbiologically influenced corrosion of FeCoNiCrMn high-entropy alloys by Pseudomonas aeruginosa biofilm,
2022,
13,
1664-302X,
10.3389/fmicb.2022.1009310
|
|
| 80.
|
Hasyrul Hamzah, Khalish Arsy Al Khairy Siregar, Ari Nurwijayanto, Retno Wahyuningrum, Seftika Sari,
Effectiveness of Oxalis corniculata L. Ethanol Extract against Mono-Species of Biofilm Staphylococcus aureus,
2021,
4,
26214814,
184,
10.33084/bjop.v4i3.2418
|
|
| 81.
|
Meng-Shiue Lee, Hussein Reda Hussein, Sheng-Wen Chang, Chia-Yu Chang, Yi-Ying Lin, Yueh Chien, Yi-Ping Yang, Lik-Voon Kiew, Ching-Yun Chen, Shih-Hwa Chiou, Chia-Ching Chang,
Nature-Inspired Surface Structures Design for Antimicrobial Applications,
2023,
24,
1422-0067,
1348,
10.3390/ijms24021348
|
|
| 82.
|
Mariana Sousa, Inês B. Gomes, Lúcia C. Simões, Manuel Simões, Marta Ribeiro,
2022,
Chapter 15,
978-3-031-10991-1,
371,
10.1007/978-3-031-10992-8_15
|
|
| 83.
|
Akansha Sharma, Manivannan Ramachandran, Noyel Victoria Selvam,
Investigating the efficacy of Curcuma longa against Desulfovibrio desulfuricans influenced corrosion in low-carbon steel,
2022,
40,
2191-0316,
87,
10.1515/corrrev-2021-0019
|
|
| 84.
|
Thomas J. Tewes, Isabella Centeleghe, Jean-Yves Maillard, Frank Platte, Dirk P. Bockmühl,
Raman Microscopic Analysis of Dry-Surface Biofilms on Clinically Relevant Materials,
2022,
10,
2076-2607,
1369,
10.3390/microorganisms10071369
|
|
| 85.
|
Jan-Philipp Kunze, Klaus Boening, Heike Meissner, Katarzyna Kresse-Walczak, Yulin Deng,
Novel Artificial Biofilm Equivalent for Denture Surfaces: A Pilot Study,
2022,
2022,
1687-9430,
1,
10.1155/2022/6485469
|
|
| 86.
|
Collin Kessler, Eisha Mhatre, Vaughn Cooper, Wook Kim, Irina S. Druzhinina,
Evolutionary Divergence of the Wsp Signal Transduction Systems in Beta- and Gammaproteobacteria,
2021,
87,
0099-2240,
10.1128/AEM.01306-21
|
|
| 87.
|
Marge Puhm, Hanna Ainelo, Maia Kivisaar, Riho Teras,
Tryptone in Growth Media Enhances Pseudomonas putida Biofilm,
2022,
10,
2076-2607,
618,
10.3390/microorganisms10030618
|
|
| 88.
|
Ghada Mohamed Aleid, Anoud Saud Alshammari, Asma D. Alomari, Shehu Sa’ad Abdullahi, Rania Edrees Adam Mohammad, Rokhsana Mohammed Ismail Abdulrahman, Adrián Bonilla-Petriciolet,
Degradation of Metal Ions with Electricity Generation by Using Fruit Waste as an Organic Substrate in the Microbial Fuel Cell,
2023,
2023,
1687-8078,
1,
10.1155/2023/1334279
|
|
| 89.
|
Alexandra Snowdon, Shi-Qi An, Alistair Finnie, Marie Dale, Simon Dennington, Jennifer Longyear, Julian Wharton, Paul Stoodley,
Elastomeric sandpaper replicas as model systems for investigating elasticity, roughness and associated drag in a marine biofilm flow cell,
2022,
266,
00298018,
112739,
10.1016/j.oceaneng.2022.112739
|
|
| 90.
|
Sigrid Hakvåg, Odd Gunnar Brakstad, Stephan Kubowicz, Andy M. Booth,
2023,
9780323898584,
17,
10.1016/B978-0-323-89858-4.00014-2
|
|
| 91.
|
Rajani Sharma, Shubha Rani Sharma,
2022,
Chapter 4,
978-3-030-83810-2,
71,
10.1007/978-3-030-83811-9_4
|
|
| 92.
|
Duaa M. Hijazi, Lina A. Dahabiyeh, Salah Abdelrazig, Dana A. Alqudah, Amal G. Al-Bakri,
Micafungin effect on Pseudomonas aeruginosa metabolome, virulence and biofilm: potential quorum sensing inhibitor,
2023,
13,
2191-0855,
10.1186/s13568-023-01523-0
|
|
| 93.
|
Harmanpreet Kaur, Arashdeep Kaur, Sanjeev Kumar Soni, Praveen Rishi,
Microbially-derived cocktail of carbohydrases as an anti-biofouling agents: a ‘green approach’,
2022,
38,
0892-7014,
455,
10.1080/08927014.2022.2085566
|
|
| 94.
|
Dev Kumar Yadav, M Q Baig,
INFECTION AS A RISK FACTOR FOR GALLBLADDER CANCERLITERATURE REVIEW.,
2021,
48,
10.36106/ijar/0501615
|
|
| 95.
|
Surajit Das,
Genetic regulation, biosynthesis and applications of extracellular polysaccharides of the biofilm matrix of bacteria,
2022,
291,
01448617,
119536,
10.1016/j.carbpol.2022.119536
|
|
| 96.
|
Hui Deng, Qianqian Fu, Dazhen Li, Yuqing Zhang, Jianxiong He, Dan Feng, Yuanyuan Zhao, Gan Du, Huamei Yu, Chengjun Ge,
Microplastic-associated biofilm in an intensive mariculture pond: Temporal dynamics of microbial communities, extracellular polymeric substances and impacts on microplastics properties,
2021,
319,
09596526,
128774,
10.1016/j.jclepro.2021.128774
|
|
| 97.
|
Lilong Yan, Yaoqi Zheng, Mingyue Yin, Shuang Liu, Mengya Yang, Jishuang Jiang,
The coexistence of copper ions and TC affected the binding ability and the reaction order between extracellular polymeric substances of aerobic granular sludge and exogenous substances,
2022,
0944-1344,
10.1007/s11356-022-24423-5
|
|
| 98.
|
Atul Kumar, Sunita Devi, Satish Khasa, Surender Duhan,
2022,
9780323851466,
515,
10.1016/B978-0-323-85146-6.00025-5
|
|
| 99.
|
Andrea Schmeckebier, Ahmed Zayed, Roland Ulber,
Productive biofilms: from prokaryotic to eukaryotic systems,
2022,
97,
0268-2575,
3049,
10.1002/jctb.7208
|
|
| 100.
|
Sergei I. Belikov, Ivan S. Petrushin, Lubov I. Chernogor,
Genome Analysis of the Janthinobacterium sp. Strain SLB01 from the Diseased Sponge of the Lubomirskia baicalensis,
2021,
43,
1467-3045,
2220,
10.3390/cimb43030156
|
|
| 101.
|
Li Shen, Jinju Cheng, Junjun Wang, Linlin Cui, Yejuan Zhang, Wanqing Liao, Zhiru Liu, Hao Zhou, Xueling Wu, Jiaokun Li, Weiming Zeng,
Comparison of extraction methods for extracellular polymeric substances (EPS) and dynamic characterization of EPS from sessile microorganisms during pyrite bioleaching,
2022,
10,
22133437,
107922,
10.1016/j.jece.2022.107922
|
|
| 102.
|
Ahmed J. Al-Fahad, Ahmad M. Aldossary, Abdullah A. Alshehri, Mohammad N. Alomary, Fahad A. Almughem, Sami Alyahya, Essam A. Tawfik,
2021,
Chapter 10,
978-981-16-1922-9,
191,
10.1007/978-981-16-1923-6_10
|
|
| 103.
|
Xiaofang Yan, Jing Sun, Yizhen Wang, Zisha Zhang, Chuning Zhang, Wei Li, Juan Xu, Xiaohu Dai, Bing-Jie Ni,
Low-rate ferrate dosing damages the microbial biofilm structure through humic substances destruction and facilitates the sewer biofilm control,
2023,
235,
00431354,
119834,
10.1016/j.watres.2023.119834
|
|
| 104.
|
Matthew Regulski, Matthew F. Myntti, Garth A. James,
Anti-Biofilm Efficacy of Commonly Used Wound Care Products in In Vitro Settings,
2023,
12,
2079-6382,
536,
10.3390/antibiotics12030536
|
|
| 105.
|
Gabriela Kalčíková,
Beyond ingestion: Adhesion of microplastics to aquatic organisms,
2023,
258,
0166445X,
106480,
10.1016/j.aquatox.2023.106480
|
|
| 106.
|
Raphaëlle Youf, Rosy Ghanem, Adeel Nasir, Gilles Lemercier, Tristan Montier, Tony Le Gall,
Impact of mucus and biofilm on antimicrobial photodynamic therapy: Evaluation using Ruthenium(II) complexes,
2023,
25902075,
100113,
10.1016/j.bioflm.2023.100113
|
|
| 107.
|
Xing Liu, Yin Ye, Zhishuai Zhang, Christopher Rensing, Shungui Zhou, Kenneth H. Nealson,
Prophage Induction Causes Geobacter Electroactive Biofilm Decay,
2023,
0013-936X,
10.1021/acs.est.2c08443
|
|
| 108.
|
Ghada Mohamed Aleid, Anoud Saud Alshammari, Asma D. Alomari, Hanadi A. Almukhlifi, Akil Ahmad, Asim Ali Yaqoob,
Dual Role of Sugarcane Waste in Benthic Microbial Fuel to Produce Energy with Degradation of Metals and Chemical Oxygen Demand,
2023,
11,
2227-9717,
1060,
10.3390/pr11041060
|
|
| 109.
|
Annabel Braem, Nur Hidayatul Nazirah Kamarudin, Nitu Bhaskar, Zoya Hadzhieva, Andrea Mele, Jérémy Soulié, Denver P. Linklater, Linda Bonilla-Gameros, Aldo R. Boccaccini, Ipsita Roy, Christophe Drouet, Elena P. Ivanova, Diego Mantovani, Bikramjit Basu,
Biomaterial strategies to combat implant infections: new perspectives to old challenges,
2023,
0950-6608,
1,
10.1080/09506608.2023.2193784
|
|
| 110.
|
Payel Paul, Ritwik Roy, Sharmistha Das, Sarita Sarkar, Sudipta Chatterjee, Moumita Mallik, Aditya Shukla, Poulomi Chakraborty, Prosun Tribedi,
The combinatorial applications of 1,4-naphthoquinone and tryptophan inhibit the biofilm formation of Staphylococcus aureus,
2023,
0015-5632,
10.1007/s12223-023-01054-y
|
|
| 111.
|
Monika Priyadarshanee, Surajit Das,
Bacterial extracellular polymeric substances: Biosynthesis and interaction with environmental pollutants,
2023,
332,
00456535,
138876,
10.1016/j.chemosphere.2023.138876
|
|
| 112.
|
Joshua Moyal, Preeti H. Dave, Mengjie Wu, Shooka Karimpour, Satinder K. Brar, Huan Zhong, Raymond W. M. Kwong,
Impacts of Biofilm Formation on the Physicochemical Properties and Toxicity of Microplastics: A Concise Review,
2023,
261,
0179-5953,
10.1007/s44169-023-00035-z
|
|
| 113.
|
Fei Tong, Pei Wang, Ziqiang Chen, Yifan Liu, Lianguo Wang, Jun Guo, Zhihua Li, Hu Cai, Junchao Wei,
Combined Ferromagnetic Nanoparticles for Effective Periodontal Biofilm Eradication in Rat Model,
2023,
Volume 18,
1178-2013,
2371,
10.2147/IJN.S402410
|
|
| 114.
|
Alshammari Maryam, Aldossary Ahmad, Manal AlKhulaifi, Al Farraj Dunia, Samar Alsudir, Moahmed Alarawi, Gojobori Takashi, Essam Alyamani,
Reduction of biofilm formation of Escherichia coli by targeting quorum sensing and adhesion genes using the CRISPR/Cas9-HDR approach, and its clinical application on urinary catheter,
2023,
18760341,
10.1016/j.jiph.2023.05.026
|
|
| 115.
|
Miao Wang, Zhe Xu, Zhenlian Qi, Yiwei Cai, Guiying Li, Wonyong Choi, Taicheng An,
Repeated photocatalytic inactivation of E. coli by UV + Ni foam@TiO2: performance and photocatalyst deactivation,
2023,
13858947,
143680,
10.1016/j.cej.2023.143680
|
|
| 116.
|
Ana Barbosa, Sónia Miranda, Nuno F. Azevedo, Laura Cerqueira, Andreia S. Azevedo,
Imaging biofilms using fluorescence in situ hybridization: seeing is believing,
2023,
13,
2235-2988,
10.3389/fcimb.2023.1195803
|
|
| 117.
|
Jia-Wei Liang, Chia-Hung Liu, Kevin C.-W. Wu, Pei-Ru Jheng, Er-Yuan Chuang,
Plasma-treated nano-enabled multimodal coatings made of phototherapeutic molybdenum disulfide and fucoidan prevent catheter-associated urinary tract issues,
2023,
13858947,
143749,
10.1016/j.cej.2023.143749
|
|
| 118.
|
Setyo Budi Kurniawan, Muhammad Fauzul Imron, Siti Rozaimah Sheikh Abdullah, Ahmad Razi Othman, Hassimi Abu Hasan,
Coagulation–flocculation of aquaculture effluent using biobased flocculant: From artificial to real wastewater optimization by response surface methodology,
2023,
53,
22147144,
103869,
10.1016/j.jwpe.2023.103869
|
|
| 119.
|
Yi Zhu, Chen Tao, Cynthia Goh, Annie Shrestha,
Innovative biomaterials for the treatment of periodontal disease,
2023,
4,
2673-4915,
10.3389/fdmed.2023.1163562
|
|
| 120.
|
Robert J. Tournay, Andrea Firrincieli, Shruti S. Parikh, Dominic M. Sivitilli, Sharon L. Doty,
Effect of Arsenic on EPS Synthesis, Biofilm Formation, and Plant Growth-Promoting Abilities of the Endophytes Pseudomonas PD9R and Rahnella laticis PD12R,
2023,
0013-936X,
10.1021/acs.est.2c08586
|
|
| 121.
|
Azza A H Rajab, Wael A H Hegazy,
What’s old is new again: Insights into diabetic foot microbiome,
2023,
14,
1948-9358,
680,
10.4239/wjd.v14.i6.680
|
|
| 122.
|
Allison P. Koehle, Stephanie L. Brumwell, Emily P. Seto, Anne M. Lynch, Camilla Urbaniak,
Microbial applications for sustainable space exploration beyond low Earth orbit,
2023,
9,
2373-8065,
10.1038/s41526-023-00285-0
|
|
| 123.
|
Ghazal Shineh, Mohammadmahdi Mobaraki, Mohammad Jabed Perves Bappy, David K. Mills,
Biofilm Formation, and Related Impacts on Healthcare, Food Processing and Packaging, Industrial Manufacturing, Marine Industries, and Sanitation–A Review,
2023,
3,
2673-8007,
629,
10.3390/applmicrobiol3030044
|
|
| 124.
|
Ridvan Kucukosman, Zelal Isik, Kasim Ocakoglu, Nadir Dizge, Sadin Özdemir, M. Serkan Yalçın, Prabhakar Sharma, Deepanraj Balakrishnan,
Boron-based magnesium diboride nanosheets preparation and tested for antimicrobial properties for PES membrane,
2023,
00456535,
139340,
10.1016/j.chemosphere.2023.139340
|
|
| 125.
|
Sylvia Denis, Suhana Sultana, Ankita Banerjee, Arup Kumar Mitra,
2023,
9780323957151,
49,
10.1016/B978-0-323-95715-1.00014-5
|
|
| 126.
|
Yao Xie, Chi Zhang, Jun Mei, Jing Xie,
Antimicrobial Effect of Ocimum gratissimum L. Essential Oil on Shewanella putrefaciens: Insights Based on the Cell Membrane and External Structure,
2023,
24,
1422-0067,
11066,
10.3390/ijms241311066
|
|
| 127.
|
Samik Biswas, Abdul Wasai, Mrinmoy Ghosh, Corrado Rizzoli, Adhiraj Roy, Sandip Saha, Supratim Mandal,
A mononuclear N,N,N,O donor schiff base Cu (II) complex inhibits bacterial biofilm formation and promotes apoptosis and cell cycle arrest in prostate cancer cells,
2023,
01620134,
112314,
10.1016/j.jinorgbio.2023.112314
|
|
| 128.
|
Michael S. Carter, Matthew J. Tuttle, Joshua A. Mancini, Rhett Martineau, Chia-Suei Hung, Maneesh K. Gupta, Arpita Bose,
Microbially Induced Calcium Carbonate Precipitation by
Sporosarcina pasteurii
: a Case Study in Optimizing Biological CaCO
3
Precipitation
,
2023,
0099-2240,
10.1128/aem.01794-22
|
|
| 129.
|
Anuja Dahal, Kamal Shrestha, Rashmi Karki, Saraswati Bhattarai, Shiva Aryal, Satish Kumar Deo, Balmukunda Regmi, Mark Willcox, Shyam Kumar Mishra, Keiko Hosohata,
Antimicrobial Resistance and Biofilm Production in Uropathogens from Renal Disease Patients Admitted to Tribhuvan University Teaching Hospital, Nepal,
2023,
2023,
1365-2710,
1,
10.1155/2023/4867817
|
|
| 130.
|
Karan J. Pant, Paul D. Cotter, Martin G. Wilkinson, Jeremiah J. Sheehan,
Towards sustainable Cleaning‐in‐Place (CIP) in dairy processing: Exploring enzyme‐based approaches to cleaning in the Cheese industry,
2023,
1541-4337,
10.1111/1541-4337.13206
|
|
| 131.
|
Asim Ali Yaqoob, Mohamad Nasir Mohamad Ibrahim, Nabil Al-Zaqri,
A Pilot Trial in the Remediation of Pollutants Simultaneously with Bioenergy Generation through Microbial Fuel Cell,
2023,
22133437,
110643,
10.1016/j.jece.2023.110643
|
|
| 132.
|
Angela Maria Catania, Pierluigi Di Ciccio, Ilario Ferrocino, Tiziana Civera, Francesca Tiziana Cannizzo, Alessandra Dalmasso,
Evaluation of the biofilm-forming ability and molecular characterization of dairy Bacillus spp. isolates,
2023,
13,
2235-2988,
10.3389/fcimb.2023.1229460
|
|
| 133.
|
Viktor Radzinskiy, Alevtina Savicheva, Sergey Vorob'ev, Elena Spasibova, Kira Shalepo, Ol'ga Budilovskaya, Tat'yana Husnutdinova, Anna Krysanova, Aleksandr Guschin, Ol'ga Raevskaya, Sergey D'yakonov, Nadezhda Katkova, Dar'ya Yacyshina,
2023,
978-5-907218-72-7,
10.29039/978-5-907218-72-7
|
|
| 134.
|
Ghada Mohamed Aleid, Anoud Saud Alshammari, Alamri Rahmah Dhahawi Ahmad, Fida Hussain, Sang-Eun Oh, Akil Ahmad, Mohamad Nasir Mohamad Ibrahim, Khalid Umar,
Advancement in Microbial Fuel Cells Technology by Using Waste Extract as an Organic Substrate to Produce Energy with Metal Removal,
2023,
11,
2227-9717,
2434,
10.3390/pr11082434
|
|
| 135.
|
Sweta Anantharaman, Danielle Guercio, Alicia G. Mendoza, Jason M. Withorn, Elizabeth M. Boon,
Negative regulation of biofilm formation by nitric oxide sensing proteins,
2023,
51,
0300-5127,
1447,
10.1042/BST20220845
|
|
| 136.
|
Ghada Mohamed Aleid, Anoud Saud Alshammari, Asma D. Alomari, Akil Ahmad, Omaymah Alaysuy, Mohamad Nasir Mohamad Ibrahim,
Biomass and domestic waste: a potential resource combination for bioenergy generation and water treatment via benthic microbial fuel cell,
2023,
1614-7499,
10.1007/s11356-023-29430-8
|
|
| 137.
|
Yousra El Fannassi, Adem Gharsallaoui, Simon Khelissa, Mohamed Amin El Amrani, Isabelle Suisse, Mathieu Sauthier, Charafeddine Jama, Saïd Boudra, Nour-Eddine Chihib,
Complexation of Terpenes for the Production of New Antimicrobial and Antibiofilm Molecules and Their Encapsulation in Order to Improve Their Activities,
2023,
13,
2076-3417,
9854,
10.3390/app13179854
|
|
| 138.
|
Christopher J Kovacs, Erika M Rapp, Sophia M McKenzie, Michael Z Mazur, Riley P Mchale, Briana Brasko, Michael Y Min, F John Burpo, Jason C Barnhill,
Disruption of Biofilm by Bacteriophages in Clinically Relevant Settings,
2023,
0026-4075,
10.1093/milmed/usad385
|
|
| 139.
|
Changjoon Keum, Cristina-Maria Hirschbiegel, Soham Chakraborty, Soyeong Jin, Youngdo Jeong, Vincent M. Rotello,
Biomimetic and bioorthogonal nanozymes for biomedical applications,
2023,
10,
2196-5404,
10.1186/s40580-023-00390-6
|
|
| 140.
|
Konstantin S. Kozlov, Daniil A. Boiko, Elena V. Detusheva, Konstantin V. Detushev, Evgeniy O. Pentsak, Anatoly N. Vereshchagin, Valentine P. Ananikov,
Digital biology approach for macroscale studies of biofilm growth and biocide effects with electron microscopy,
2023,
2,
2635-098X,
1522,
10.1039/D3DD00048F
|
|
| 141.
|
Zsolt Datki, Zsuzsanna Darula, Viktor Vedelek, Eva Hunyadi-Gulyas, Brian J. Dingmann, Balazs Vedelek, Janos Kalman, Peter Urban, Attila Gyenesei, Zita Galik-Olah, Bence Galik, Rita Sinka,
Biofilm formation initiating rotifer-specific biopolymer and its predicted components,
2023,
253,
01418130,
127157,
10.1016/j.ijbiomac.2023.127157
|
|
| 142.
|
Ula Rozman, Anej Blažič, Gabriela Kalčíková,
Phytoremediation: A promising approach to remove microplastics from the aquatic environment,
2023,
338,
02697491,
122690,
10.1016/j.envpol.2023.122690
|
|
| 143.
|
Gamze Kalın, Emine Alp, Arthur Chouaikhi, Claire Roger,
Antimicrobial Multidrug Resistance: Clinical Implications for Infection Management in Critically Ill Patients,
2023,
11,
2076-2607,
2575,
10.3390/microorganisms11102575
|
|
| 144.
|
Andrea Teuber, Giada Caniglia, Holger Barth, Christine Kranz, Boris Mizaikoff,
Thin-Film Waveguide Laser Spectroscopy: A Novel Platform for Bacterial Analysis,
2023,
0003-2700,
10.1021/acs.analchem.3c02782
|
|
| 145.
|
Sérgio G. Mendes, Sofia I. Combo, Thibault Allain, Sara Domingues, Andre G. Buret, Gabriela J. Da Silva,
Co-regulation of biofilm formation and antimicrobial resistance in Acinetobacter baumannii: from mechanisms to therapeutic strategies,
2023,
0934-9723,
10.1007/s10096-023-04677-8
|
|
| 146.
|
Meron Getahun, Yonatan Nesru, Muktar Ahmed, Sunita Satapathy, Kebede Shenkute, Neeraj Gupta, Mohammed Naimuddin,
Phytochemical Composition, Antioxidant, Antimicrobial, Antibiofilm, and Antiquorum Sensing Potential of Methanol Extract and Essential Oil from Acanthus polystachyus Delile (Acanthaceae),
2023,
2470-1343,
10.1021/acsomega.3c06246
|
|
| 147.
|
Kayeen Vadakkan, Ajit Kumar Ngangbam, Kuppusamy Sathishkumar, Nelson Pynadathu Rumjit, Meena Kochappan Cheruvathur,
A review of chemical signaling pathways in the quorum sensing circuit of Pseudomonas aeruginosa,
2024,
254,
01418130,
127861,
10.1016/j.ijbiomac.2023.127861
|
|
| 148.
|
Ajuan Liu, Runlan Yu, Guanzhou Qiu, Weimin Zeng,
Insights into the EPS production and distribution of planktonic and attached Sulfobacillus thermosulfidooxidans cells during bioleaching,
2024,
205,
08926875,
108494,
10.1016/j.mineng.2023.108494
|
|
| 149.
|
Sonia Tiquia-Arashiro, Xiaohua Li, Keshav Pokhrel, Amin Kassem, Lana Abbas, Oliver Coutinho, Diana Kasperek, Hawraa Najaf, Somie Opara,
Applications of Fourier Transform-Infrared spectroscopy in microbial cell biology and environmental microbiology: advances, challenges, and future perspectives,
2023,
14,
1664-302X,
10.3389/fmicb.2023.1304081
|
|
| 150.
|
Souad Belkaid, Dalila Mansour, Farida Laadjal Salah, Abdeltif Amrane,
Cuprous ions influence on the biocorrosion of a carbon steel in the presence of Sulphate Reducing Bacteria marine biofilm,
2023,
23524855,
103307,
10.1016/j.rsma.2023.103307
|
|
| 151.
|
Eva Zanditenas, Serge Ankri,
Unraveling the interplay between unicellular parasites and bacterial biofilms: Implications for disease persistence and antibiotic resistance,
2024,
15,
2150-5594,
10.1080/21505594.2023.2289775
|
|
| 152.
|
Shweta Dixit, Swati Varshney, Deepti Gupta, Shilpi Sharma,
Factors affecting biofilm formation by bacteria on fabrics,
2023,
1618-1905,
10.1007/s10123-023-00460-z
|
|
| 153.
|
Jaber Hemmati, Zahra Chegini, Mohammad Reza Arabestani, Zhengwei Huang,
Niosomal-Based Drug Delivery Platforms: A Promising Therapeutic Approach to Fight Staphylococcus aureus Drug Resistance,
2023,
2023,
1687-4129,
1,
10.1155/2023/5298565
|
|
| 154.
|
Magdalena Moryl, Antoni Różalski, Jose Antonio Poli de Figueiredo, Aleksandra Palatyńska-Ulatowska,
How Do Phages Disrupt the Structure of Enterococcus faecalis Biofilm?,
2023,
24,
1422-0067,
17260,
10.3390/ijms242417260
|
|
| 155.
|
Audrey R. N. Ndukwe, Jilong Qin, Sandra Wiedbrauk, Nathan R. B. Boase, Kathryn E. Fairfull-Smith, Makrina Totsika,
In Vitro Activities of Oxazolidinone Antibiotics Alone and in Combination with C-TEMPO against Methicillin-Resistant Staphylococcus aureus Biofilms,
2023,
12,
2079-6382,
1706,
10.3390/antibiotics12121706
|
|
| 156.
|
Ula Rozman, Barbara Klun, Aleksandra Kuljanin, Tina Skalar, Gabriela Kalčíková,
Insights into the shape-dependent effects of polyethylene microplastics on interactions with organisms, environmental aging, and adsorption properties,
2023,
13,
2045-2322,
10.1038/s41598-023-49175-1
|
|
| 157.
|
Assefa Abebe, Alemayehu Birhanu,
Methicillin Resistant Staphylococcus aureus: Molecular Mechanisms Underlying Drug Resistance Development and Novel Strategies to Combat,
2023,
Volume 16,
1178-6973,
7641,
10.2147/IDR.S428103
|
|
| 158.
|
Leanne Cleaver, James A. Garnett,
How to study biofilms: technological advancements in clinical biofilm research,
2023,
13,
2235-2988,
10.3389/fcimb.2023.1335389
|
|
| 159.
|
Louisa Z.Y. Huang, Michelle M. Leong, Soroosh Gharehgozlo, Aaron Elbourne, Rachel A. Caruso,
2023,
05809517,
10.1016/bs.mim.2023.10.004
|
|
| 160.
|
Shubhankar Debnath, Muthusivaramapandian Muthuraj, Tarun Kanti Bandyopadhyay, Md. Nazneen Bobby, Kondi Vanitha, Onkar Nath Tiwari, Biswanath Bhunia,
Engineering strategies and applications of cyanobacterial exopolysaccharides: A review on past achievements and recent perspectives,
2024,
328,
01448617,
121686,
10.1016/j.carbpol.2023.121686
|
|
| 161.
|
Yongsun Jang, Sang-Hoon Lee, Hwa-Soo Ryoo, Hee-Deung Park,
Effects of hydrogen pressure on stabilization with improved denitrification in a hydrogen-based membrane biofilm reactor,
2024,
693,
03767388,
122390,
10.1016/j.memsci.2023.122390
|
|
| 162.
|
Claudia Vuotto, Gianfranco Donelli, Anthony Buckley, Caroline Chilton,
2024,
Chapter 12,
978-3-031-42107-5,
249,
10.1007/978-3-031-42108-2_12
|
|
| 163.
|
Nishitha R. Kumar, Tejashree A. Balraj, Swetha N. Kempegowda, Akila Prashant,
Multidrug-Resistant Sepsis: A Critical Healthcare Challenge,
2024,
13,
2079-6382,
46,
10.3390/antibiotics13010046
|
|
| 164.
|
Dashnyam Punsaldulam, Orgil Amumandal,
Microbial exopolymers for soil restoration and remediation: current progress and future perspectives,
2023,
39,
2788-9823,
30,
10.5564/pib.v39i1.3144
|
|
| 165.
|
Li-Chao Huo, Nai-Yu Liu, Chao-Jie Wang, Yi Luo, Jing-Xia Liu,
Lonicera japonica protects Pelodiscus sinensis by inhibiting the biofilm formation of Aeromonas hydrophila,
2024,
108,
0175-7598,
1,
10.1007/s00253-023-12910-9
|
|
| 166.
|
Jaspreet Kaur, Jasvinder Kaur,
Comparative genomics of seven genomes of genus Idiomarina reveals important halo adaptations and genes for stress response,
2024,
14,
2190-572X,
10.1007/s13205-023-03887-3
|
|
| 167.
|
Ashlesha Kaushik, Helen Kest, Mangla Sood, Bryan Steussy, Corey Thieman, Sandeep Gupta,
Biofilm Producing Methicillin-Resistant Staphylococcus aureus (MRSA) Infections in Humans: Clinical Implications and Management,
2024,
13,
2076-0817,
76,
10.3390/pathogens13010076
|
|
| 168.
|
Anoud Saud Alshammari, Ghada Mohamed Aleid, Alamri Rahmah Dhahawi Ahmad, Asma D. Alomari, Shehu Sa’ad Abdullahi, Rania Edrees Adam Mohammad, Darren Sun,
Oil Palm Biomass Sap-Rotten Rice as a Source to Remove Metal Ions and Generate Electricity as By-Products through Microbial Fuel Cell Technology,
2024,
2024,
2090-9071,
1,
10.1155/2024/5570011
|
|
| 169.
|
Giuseppe Mancuso, Marilena Trinchera, Angelina Midiri, Sebastiana Zummo, Giulia Vitale, Carmelo Biondo,
Novel Antimicrobial Approaches to Combat Bacterial Biofilms Associated with Urinary Tract Infections,
2024,
13,
2079-6382,
154,
10.3390/antibiotics13020154
|
|
| 170.
|
David O. Oluwole, Josue Diaz-Delgado, Will Buchanan, Roberto M. La Ragione, Tao Chen, Lian X. Liu,
Wound recovery efficacy of retinol based-micellar formulations in an organotypic skin wound model,
2024,
653,
03785173,
123875,
10.1016/j.ijpharm.2024.123875
|
|
| 171.
|
Henk Bolhuis, Michele Grego,
Cryopreservation and recovery of a complex hypersaline microbial mat community,
2024,
00112240,
104859,
10.1016/j.cryobiol.2024.104859
|
|
| 172.
|
Urszula Wnorowska, Dawid Łysik, Ewelina Piktel, Magdalena Zakrzewska, Sławomir Okła, Agata Lesiak, Jakub Spałek, Joanna Mystkowska, Paul B. Savage, Paul Janmey, Krzysztof Fiedoruk, Robert Bucki, Geelsu Hwang,
Ceragenin-mediated disruption of Pseudomonas aeruginosa biofilms,
2024,
19,
1932-6203,
e0298112,
10.1371/journal.pone.0298112
|
|
| 173.
|
Shuangshuang Lin, Jiandi Li, Liping Jia, Xuguang Huang, Lei Wang,
Different biological responses of Skeletonema costatum and Prorocentrum donghaiense to polymetallic nodules from seawaters,
2024,
269,
0166445X,
106871,
10.1016/j.aquatox.2024.106871
|
|
| 174.
|
Kerry Candlen, Gregory Reimonn, Md. Akiful Haque, Olivia Hosterman, Wan-Ting Chen,
Biofilm-influenced weathering of polypropylene films submerged in field samples from freshwater and marine ecosystems,
2024,
22133437,
112284,
10.1016/j.jece.2024.112284
|
|
| 175.
|
Feng-Qing Wang, Daniel Bartosik, Chandni Sidhu, Robin Siebers, De-Chen Lu, Anke Trautwein-Schult, Dörte Becher, Bruno Huettel, Johannes Rick, Inga V. Kirstein, Karen H. Wiltshire, Thomas Schweder, Bernhard M. Fuchs, Mia M. Bengtsson, Hanno Teeling, Rudolf I. Amann,
Particle-attached bacteria act as gatekeepers in the decomposition of complex phytoplankton polysaccharides,
2024,
12,
2049-2618,
10.1186/s40168-024-01757-5
|
|
| 176.
|
M.M. Lebeloane, I.M. Famuyide, J.P. Dzoyem, R.O. Adeyemo, F.N. Makhubu, E.E. Elgorashi, K.G. Kgosana, L.J. McGaw,
Influence of selected plant extracts on bacterial motility, aggregation, hydrophobicity, exopolysaccharide production and quorum sensing during biofilm formation of enterohaemorrhagic Escherichia coli O157:H7,
2024,
167,
02546299,
197,
10.1016/j.sajb.2024.02.022
|
|
| 177.
|
Nazia Tabassum, Fazlurrahman Khan, Geum-Jae Jeong, Du-Min Jo, Young-Mog Kim,
Silver nanoparticles synthesized from Pseudomonas aeruginosa pyoverdine: Antibiofilm and antivirulence agents,
2024,
25902075,
100192,
10.1016/j.bioflm.2024.100192
|
|
| 178.
|
Zaixiang Lou, Jiale Dong, Hongwei Tao, Yeexuan Tan, Hongxin Wang,
Regulation and mechanism of organic selenium on quorum sensing, biofilm, and antioxidant effects of Lactobacillus paracasei,
2024,
42,
0263-6484,
10.1002/cbf.3975
|
|
| 179.
|
Syahirah Faraheen Kabir Ahmad, Gobi Kanadasan, Keat Teong Lee, Vel Murugan Vadivelu,
Insight into recent advances in microalgae biogranulation in wastewater treatment,
2024,
0738-8551,
1,
10.1080/07388551.2024.2317785
|
|
| 180.
|
Essam Hebishy, Oktay Yerlikaya, F. Jerry Reen, Jennifer Mahony, Asli Akpinar, Derya Saygili, Nivedita Datta,
Microbiological aspects and challenges of dairy powders – II: Biofilm/biofouling,
2024,
1364-727X,
10.1111/1471-0307.13076
|
|
| 181.
|
Manu Sharma, Reetika Rawat, Easha Pandey, Sheelu Sharma, Veera Sadhu, Raghava Reddy Kakarla,
2024,
978-1-83767-082-6,
53,
10.1039/BK9781837672813-00053
|
|
| 182.
|
Tao Zhang, Haiyan Xing, Miao Xiong, Mengqin Gu, Zhigang Xu, Lei Zhang, Yuejun Kang, Peng Xue,
Carbon dots-based nanoclusters for sonodynamic therapy of bacterial infection enhanced by deep biofilm penetration and hypoxia alleviation,
2024,
13858947,
150819,
10.1016/j.cej.2024.150819
|
|
| 183.
|
Mohammed B. Alshammari, Akil Ahmad,
Electrochemical oxidation (biomass) and degradation of organic pollutant through a microbial fuel cell to produce electricity,
2024,
2190-6815,
10.1007/s13399-024-05597-z
|
|
| 184.
|
Anjitha Theres Benny, Masthan Thamim, Prakhar Srivastava, Sindoora Suresh, Krishnan Thirumoorthy, Loganathan Rangasamy, Karthikeyan S., Nalini Easwaran, Ethiraj Kannatt Radhakrishnan,
Synthesis and study of antibiofilm and antivirulence properties of flavonol analogues generated by palladium catalyzed ligand free Suzuki–Miyaura coupling against Pseudomonas aeruginosa PAO1,
2024,
14,
2046-2069,
12278,
10.1039/D3RA08617H
|
|
| 185.
|
Kaitlin R. Rempfert, Sheryl L. Bell, Christopher P. Kasanke, Qian Zhao, Xiaodong Zhao, Andrew S. Lipton, Kirsten S. Hofmockel,
Biomolecular budget of persistent, microbial-derived soil organic carbon: The importance of underexplored pools,
2024,
932,
00489697,
172916,
10.1016/j.scitotenv.2024.172916
|
|
| 186.
|
Md Monzurul Islam Anoy, Won-Jun Kim, Suzanne Gelston, Derek Fleming, Robin Patel, Haluk Beyenal, Helen Boucher,
Evaluation of treatment of methicillin-resistant
Staphylococcus aureus
biofilms with intermittent electrochemically generated H
2
O
2
or HOCl
,
2024,
0066-4804,
10.1128/aac.01722-23
|
|
| 187.
|
Flávio Rodrigues, Helena F. Pereira, João Pinto, Jorge Padrão, Andrea Zille, Filipe S. Silva, Óscar Carvalho, Sara Madeira,
Zirconia Dental Implants Surface Electric Stimulation Impact on Staphylococcus aureus,
2024,
25,
1422-0067,
5719,
10.3390/ijms25115719
|
|
| 188.
|
Cynthia J. Castro, W. Camilla Kuo-Dahab, Tao Jiang, Sam Downes, Guoping Zhang, Ahmed S. Abouhend, Caitlyn S. Butler,
Water quality indicators influencing the formation and morphology of hydrostatically-formed photogranules,
2024,
2754-7000,
10.1039/D4VA00054D
|
|
| 189.
|
Anna Doménech‐Pascual, Lorena Carrasco‐Barea, Frederic Gich, Judit Boadella, Zeus Freixinos Campillo, Rosa Gómez Cerezo, Andrea Butturini, Anna M. Romaní,
Differential response of bacteria and fungi to drought on the decomposition of Sarcocornia fruticosa woody stems in a saline stream,
2024,
26,
1462-2912,
10.1111/1462-2920.16661
|
|
| 190.
|
Austin B. Featherstone, Arnold J. T. M. Mathijssen, Amanda Brown, Sapna Chitlapilly Dass, Ricardo Santos,
SARS-CoV-2 Delta variant remains viable in environmental biofilms found in meat packaging plants,
2024,
19,
1932-6203,
e0304504,
10.1371/journal.pone.0304504
|
|
| 191.
|
Guobao Huang, Qiang Wang, Huimin Wen, Jinling Li, Shan He, Xiao Wang, Lijian Ding,
Antibiofilm Efficacy and Mechanism of the Marine Chlorinated Indole Sesquiterpene Against Methicillin-Resistant Staphylococcus aureus,
2024,
1535-3141,
10.1089/fpd.2024.0003
|
|
| 192.
|
Xiaohui Niu, Yongqi Liu, Rui Zhao, Luhua Wang, Mei Yuan, Hongfang Zhao, Hongxia Li, Xing Yang, Kunjie Wang,
Chiral carbon nanostructures: a gateway to promising chiral materials,
2024,
2050-7488,
10.1039/D4TA02396J
|
|
| 193.
|
Dongwook Lee, Jintaek Im, A Reum Kim, Woohyung Jun, Cheol-Heui Yun, Seung Hyun Han,
Enterococcus Phage vB_EfaS_HEf13 as an Anti-Biofilm Agent Against Enterococcus faecalis,
2024,
1225-8873,
10.1007/s12275-024-00150-z
|
|
| 194.
|
Paras Ahmad, Dina G. Moussa, Walter L. Siqueira,
Metabolomics for dental caries diagnosis: Past, present, and future,
2024,
0277-7037,
10.1002/mas.21896
|
|
| 195.
|
Ghadir A. Jamal, Ehsan Jahangirian, Michael R. Hamblin, Hamed Mirzaei, Hossein Tarrahimofrad, Neda Alikowsarzadeh,
Proteases, a powerful biochemical tool in the service of medicine, clinical and pharmaceutical,
2024,
1082-6068,
1,
10.1080/10826068.2024.2364234
|
|
| 196.
|
Jason Bosch, Pedro H. Lebre, Eugene Marais, Gillian Maggs‐Kölling, Don A. Cowan,
Kinetics and pathways of sub‐lithic microbial community (hypolithon) development,
2024,
16,
1758-2229,
10.1111/1758-2229.13290
|
|
| 197.
|
Chee Xiang Chen, Veera Koskue, Haoran Duan, Li Gao, Ho Kyong Shon, Gregory J.O. Martin, George Q. Chen, Stefano Freguia,
Impact of nutrient deficiency on biological sewage treatment – Perspectives towards urine source segregation,
2024,
946,
00489697,
174174,
10.1016/j.scitotenv.2024.174174
|
|
| 198.
|
Alessio Cavallaro, Marco Gabrielli, Frederik Hammes, William J. Rhoads, Sébastien P. Faucher, Maria Luisa Ricci, Francesca Pennino,
The impact of DNA extraction on the quantification of
Legionella
, with implications for ecological studies
,
2024,
2165-0497,
10.1128/spectrum.00713-24
|
|
| 199.
|
Wafaa Kendil, Fayçal Dergal, Ikram Tefiani, Yassine Moustafa Mahdad, Zakaria Benladghem, Chewki Ziani-Cherif, Sidi Mohammed Lahbib Seddiki,
Improvement of a low-cost protocol for a simultaneous comparative evaluation of hydrolytic activity between sessile and planktonic cells:
Candida albicans
as a study model
,
2024,
0892-7014,
1,
10.1080/08927014.2024.2376637
|
|
| 200.
|
Jaber Hemmati, Mohsen Chiani, Babak Asghari, Ghodratollah Roshanaei, Sara Soleimani Asl, Morvarid Shafiei, Mohammad Reza Arabestani,
Antibacterial and antibiofilm potentials of vancomycin-loaded niosomal drug delivery system against methicillin-resistant Staphylococcus aureus (MRSA) infections,
2024,
24,
1472-6750,
10.1186/s12896-024-00874-1
|
|
| 201.
|
Chamia C. Chatman, Elena G. Olson, Allison J. Freedman, Dana K. Dittoe, Steven C. Ricke, Erica L-W. Majumder, Gemma Reguera,
Co-exposure to polyethylene fiber and
Salmonella enterica
serovar Typhimurium alters microbiome and metabolome of
in vitro
chicken cecal mesocosms
,
2024,
0099-2240,
10.1128/aem.00915-24
|
|
| 202.
|
Anusha Atmakuri, Bhoomika Yadav, Bhagyashree Tiwari, Patrick Drogui, R. D. Tyagi, Jonathan W. C. Wong,
Nature’s architects: a comprehensive review of extracellular polymeric substances and their diverse applications,
2024,
2524-7980,
10.1007/s42768-024-00205-2
|
|
| 203.
|
Biswa R. Acharya, Satwinder Pal Gill, Amita Kaundal, Devinder Sandhu,
Strategies for combating plant salinity stress: the potential of plant growth-promoting microorganisms,
2024,
15,
1664-462X,
10.3389/fpls.2024.1406913
|
|
| 204.
|
Junyuan Xue, Shutong Li, Liyuan Wang, Yican Zhao, Lu Zhang, Yantong Zheng, Wenxin Zhang, Zhenghong Chen, Ting Jiang, Yundong Sun, Anne-Catrin Uhlemann,
Enhanced fatty acid biosynthesis by Sigma28 in stringent responses contributes to multidrug resistance and biofilm formation in
Helicobacter pylori
,
2024,
0066-4804,
10.1128/aac.00850-24
|
|
| 205.
|
Fabiana Giarritiello, Carlo Luca Romanò, Guenter Lob, Joseph Benevenia, Hiroyuki Tsuchiya, Emanuele Zappia, Lorenzo Drago,
Enhancing Pathogen Detection in Implant-Related Infections through Chemical Antibiofilm Strategies: A Comprehensive Review,
2024,
13,
2079-6382,
678,
10.3390/antibiotics13070678
|
|
| 206.
|
Büşra Sirek, Ayşenur Pamukcu, Nermin Topaloglu, Didem Sen Karaman,
2024,
9780443137884,
157,
10.1016/B978-0-443-13788-4.00013-3
|
|
| 207.
|
Ellen W. van Wijngaarden, Alexandra G. Goetsch, Ilana L. Brito, David M. Hershey, Meredith N. Silberstein,
Engineering bacterial biomanufacturing: characterization and manipulation of Sphingomonas sp. LM7 extracellular polymers,
2024,
1744-683X,
10.1039/D4SM00712C
|
|
| 208.
|
Hafez Al-Momani, Iman Aolymat, Lujain Ibrahim, Hadeel Albalawi, Dua’a Al Balawi, Borhan Aldeen Albiss, Muna Almasri, Sahar Alghweiri,
Low-dose zinc oxide nanoparticles trigger the growth and biofilm formation of Pseudomonas aeruginosa: a hormetic response,
2024,
24,
1471-2180,
10.1186/s12866-024-03441-y
|
|
| 209.
|
Aayushi Laliwala, Ritika Gupta, Denis Svechkarev, Kenneth W. Bayles, Marat R. Sadykov, Aaron M. Mohs,
Machine learning assisted identification of antibiotic-resistant Staphylococcus aureus strains using a paper-based ratiometric sensor array,
2024,
0026265X,
111395,
10.1016/j.microc.2024.111395
|
|
| 210.
|
Samitha Senevirathne, Gayan Ekanayake, Dishan Samarathunge, Oshan Basnayke,
The Use of Polyhexanide and Betaine Combined Preparation in Adult Burn Care in Sri Lanka,
2024,
2168-8184,
10.7759/cureus.67274
|
|
| 211.
|
Tannishtha Biswas, Mehnaz Ahmed, Susmita Mondal,
Mixed species biofilm: Structure, challenge and its intricate involvement in hospital associated infections,
2024,
195,
08824010,
106866,
10.1016/j.micpath.2024.106866
|
|
| 212.
|
Abdolah Razi, Azita Ghiaei, Fahimeh Kamali Dolatabadi, Ramin Haghighi,
Unraveling the association of bacteria and urinary stones in patients with urolithiasis: an update review article,
2024,
11,
2296-858X,
10.3389/fmed.2024.1401808
|
|
| 213.
|
Muhammad Musthafa Poyil, Mohammed Sarosh Khan, Meiyazhagan Gowri,
Repurposing the Anti-Depression Drug Sertraline against Catheter-Associated Urinary Tract Infections,
2023,
13,
2321-8568,
271,
10.4103/aihb.aihb_9_23
|
|
| 214.
|
Sultan Shaikh, Mirna N.A. Abdelnabi, Annette Shoba Vincent, Gordon McKay, Hamish Robert Mackey,
Evaluating bioproducts production in a purple phototrophic biofilm photobioreactor: Fuel-synthesis wastewater vs. simple substrates,
2024,
2589014X,
101945,
10.1016/j.biteb.2024.101945
|
|
| 215.
|
Matthew E. Rogers, Luis Miguel de Pablos, Jack D. Sunter,
Gels and cells: the Leishmania biofilm as a space and place for parasite transmission,
2024,
14714922,
10.1016/j.pt.2024.08.001
|
|
| 216.
|
Zifei Zhao, Ruifang Han, Xiaohan Yan, Xiaodong Zhao, Weijie Fan, Rongfeng Xiao, Yanqian Liu, Jie Yang,
Corrosion resistance and antibacterial activity of 2-mercaptobenzothiazole for 7B04 aluminium alloy in 3.5%NaCl solution,
2025,
1321,
00222860,
139902,
10.1016/j.molstruc.2024.139902
|
|
| 217.
|
Qianqian Dong, Yinghang Chang, Paul H. Goodwin, Qingxiang Liu, Wen Xu, Mingcong Xia, Jie Zhang, Runhong Sun, Shuxia Xu, Chao Wu, Kun Wu, Lirong Yang,
Double-Wing Motif Protein is a Novel Biofilm Regulatory Factor of the Plant Disease Biocontrol Agent, Bacillus subtilis,
2024,
0021-8561,
10.1021/acs.jafc.4c02192
|
|
| 218.
|
Akil Ahmad,
Exploitation of moringa biomass to fabricate graphene electrode for electricity generation with wastewater treatment through microbial fuel cells,
2024,
2190-6815,
10.1007/s13399-024-06134-8
|
|
| 219.
|
Shayesteh Bazsefidpar, Clara Saweres-Argüelles, Gemma Gutiérrez, Maria Matos, Victor Calero, Esther Serrano-Pertierra, Pilar García, María Del Carmen Blanco-López,
Biomolecules for early detection of biofilms through point-of-use devices,
2024,
0026265X,
111702,
10.1016/j.microc.2024.111702
|
|
| 220.
|
Aruna Senthil Kumar Sudaarsan, Asit Ranjan Ghosh,
Appraisal of postbiotics in cancer therapy,
2024,
15,
1663-9812,
10.3389/fphar.2024.1436021
|
|
| 221.
|
Pradip Sarkar, Tarun Kanti Bandyopadhyay, Konga Gopikrishna, Onkar Nath Tiwari, Biswanath Bhunia, Muthusivaramapandian Muthuraj,
Algal carbohydrates: Sources, biosynthetic pathway, production, and applications,
2024,
413,
09608524,
131489,
10.1016/j.biortech.2024.131489
|
|
| 222.
|
Ana C. Afonso, Inês B. Gomes, Francisca Massano, Maria J. Saavedra, Manuel Simões, Lúcia C. Simões,
Coaggregation dynamics in drinking water biofilms and implications for chlorine disinfection,
2024,
480,
03043894,
135948,
10.1016/j.jhazmat.2024.135948
|
|
| 223.
|
Hassimi Abu Hasan, Nurul Farhana Mohd Rahim, Jahira Alias, Jamilah Ahmad, Nor Sakinah Mohd Said, Nur Nadhirah Ramli, Junaidah Buhari, Siti Rozaimah Sheikh Abdullah, Ahmad Razi Othman, Hajjar Hartini Wan Jusoh, Hafizan Juahir, Setyo Budi Kurniawan,
A Review on the Roles of Extracellular Polymeric Substances (EPSs) in Wastewater Treatment: Source, Mechanism Study, Bioproducts, Limitations, and Future Challenges,
2024,
16,
2073-4441,
2812,
10.3390/w16192812
|
|
| 224.
|
Olivia Vasilev, Andrew Hayles, David Campbell, Ruurd Jaarsma, Luke Johnson, Krasimir Vasilev,
Nanoscale antibacterial coatings incorporating silver nanoparticles derived by plasma techniques – A state-of-the-art perspective,
2024,
41,
24685194,
102341,
10.1016/j.mtchem.2024.102341
|
|
| 225.
|
Xu Ji, Xiaonong Zhang, Ting Ju, Li Zhou, Da Jin, Peng Wu,
Mechanisms of inhibition and recovery under multi-antibiotic stress in anammox: A critical review,
2024,
370,
03014797,
122754,
10.1016/j.jenvman.2024.122754
|
|
| 226.
|
Surajit Das, Trisnehi Pradhan, Sourav Kumar Panda, Abhaya Dayini Behera, Swetambari Kumari, Souradip Mallick,
Bacterial biofilm-mediated environmental remediation: Navigating strategies to attain Sustainable Development Goals,
2024,
370,
03014797,
122745,
10.1016/j.jenvman.2024.122745
|
|
| 227.
|
Vanessa Everly, Diana Elizabeth Waturangi, Nurmaya Papuangan, Pande Gde Sasmita Julyantoro,
Metabolite from supernatant of soil and plant-associated bacteria control biofilm of fish pathogens,
2024,
17,
1756-0500,
10.1186/s13104-024-06974-7
|
|
| 228.
|
Manoj Kumar Verma, Shiwangi Kesarwani, Veer Singh, Emanuel Vamanu, Vishal Mishra,
Isolation and characterization of arsenic resistant bacterial strian Kurthia gibsonii MKVVM3 IITBHU from Ganga river,
2024,
6,
2515-7620,
105030,
10.1088/2515-7620/ad85c6
|
|
| 229.
|
Jung-Ah Cho, Sangsoo Jeon, Youngmin Kwon, Yoo Jin Roh, Sukjin Shin, Chang-Hun Lee, Sung Jae Kim,
Identification and comparison of protein composition of biofilms in response to EGCG from Enterococcus faecalis and Staphylococcus lugdunensis, which showed opposite patterns in biofilm-forming abilities.,
2024,
25902075,
100232,
10.1016/j.bioflm.2024.100232
|
|
| 230.
|
Oluwaseyi O. Alabi, Oluwatoyin Joseph Gbadeyan, Olumide A. Towoju, Opeyemi O. Alabi,
2024,
Chapter 7,
978-3-031-71858-8,
115,
10.1007/978-3-031-71859-5_7
|
|
| 231.
|
Baljeet Singh Saharan, Nisha Beniwal, Joginder Singh Duhan,
From formulation to function: A detailed review of microbial biofilms and their polymer-based extracellular substances,
2024,
29501946,
100194,
10.1016/j.microb.2024.100194
|
|
| 232.
|
Clarita Clements, Inbakandan Dhinakarasamy, Manikandan Sivakumar, Subham Chakraborty, Naren Kumar, Anu Chandrasekar, Lakshminarayanan Sivakumar, Ramesh Kumar, Dharani Gopal,
Fabrication of microspore-structured replica-mediated silicone polymers for inhibition of cellular adhesion and biofilm formation,
2024,
1547-0091,
10.1007/s11998-024-01002-6
|
|
| 233.
|
Ferdiye Taner, Buket Baddal, Liana Theodoridis, Steve Petrovski,
Biofilm Production in Intensive Care Units: Challenges and Implications,
2024,
13,
2076-0817,
954,
10.3390/pathogens13110954
|
|
| 234.
|
Rikke Louise Meyer, Gabriel Antonio Minero, Thomas William Seviour, Obinna Markraphael Ajunwa, Dominique Catherine Sammons Evans,
2024,
Chapter 2,
978-3-031-70475-8,
43,
10.1007/978-3-031-70476-5_2
|
|
| 235.
|
Marilyn J. Wells, Xuening Zhou, Vernita D. Gordon,
2024,
Chapter 8,
978-3-031-70475-8,
259,
10.1007/978-3-031-70476-5_8
|
|
| 236.
|
Vijaya Lakshmi Nag, Yashik Bansal, Mahesh Jansari,
2024,
Chapter 18,
978-981-97-5271-3,
387,
10.1007/978-981-97-5272-0_18
|
|
| 237.
|
Shweta Sinha, Shifu Aggarwal, Durg Vijai Singh,
Efflux pumps: gatekeepers of antibiotic resistance in Staphylococcus aureus biofilms,
2024,
11,
2311-2638,
368,
10.15698/mic2024.11.839
|
|
| 238.
|
Ashlesha Kaushik, Helen Kest, Mangla Sood, Corey Thieman, Bryan W. Steussy, Michael Padomek, Sandeep Gupta,
Infective Endocarditis by Biofilm-Producing Methicillin-Resistant Staphylococcus aureus—Pathogenesis, Diagnosis, and Management,
2024,
13,
2079-6382,
1132,
10.3390/antibiotics13121132
|
|
| 239.
|
Neusa Silva, Joana Marques, João Caramês, Filipe Silva, António Mata, Mariana Brito da Cruz,
The Impact of Using Laser and Milling Techniques to Create Zirconia Patterns on Streptococcus oralis Biofilm Formation,
2024,
7,
2571-6131,
1855,
10.3390/ceramics7040116
|
|
| 240.
|
A. Mohankumar, Raghuram Ganesh, Priyadarshini Shanmugam,
Exploring the Connection Between Bacterial Biofilms and Renal Calculi: A Comprehensive Review,
2024,
18,
09737510,
2262,
10.22207/JPAM.18.4.44
|
|
| 241.
|
Mohammed H. Karrar Alsharif, Muhammad Musthafa Poyil, Salman Bin Dayel, Mohammed Saad Alqahtani, Ahmed Abdullah Albadrani, Zainab Mohammed M. Omar, Abdullah MR. Arafah, Tarig Gasim Mohamed Alarabi, Reda M. Fayyad, Abd El-Lateef Saeed Abd El-Lateef,
Eradication of Biofilms on Catheters: Potentials of Tamarix ericoides Rottl. Bark Coating in Preventing Catheter-Associated Urinary Tract Infections (CAUTIs),
2024,
14,
2075-1729,
1593,
10.3390/life14121593
|
|
| 242.
|
Krishnamurthy Mathivanan, Ruiyong Zhang, Jayaraman Uthaya Chandirika, Thangavel Mathimani, Can Wang, Jizhou Duan,
Bacterial biofilm-based bioleaching: Sustainable mitigation and potential management of e-waste pollution,
2025,
193,
0956053X,
221,
10.1016/j.wasman.2024.12.010
|
|
| 243.
|
Agnieszka Cydzik-Kwiatkowska, Sławomir Ciesielski, Maciej Florczyk, Sylwia Pasieczna-Patkowska, Małgorzata Komorowska-Kaufman, Weronika Pomian, Kinga Jóźwiak, Piotr Oleskowicz-Popiel,
Biopolymer Production in a Full-Scale Activated Sludge Wastewater Treatment Plant: Seasonal Changes and Promising Bacterial Producers,
2024,
17,
1996-1073,
6231,
10.3390/en17246231
|
|
| 244.
|
Shagun Sharma, Vandana Jhalora, Shubhita Mathur, Renu Bist,
A Comparison of Antibiotics’ Resistance Patterns of E. coli and B. subtilis in their Biofilms and Planktonic Forms,
2025,
25,
18715265,
10.2174/0118715265278809240101073539
|
|
| 245.
|
Ravi Chauhan, Hardi Patel, Bhavna Bhardwaj, Vijay Suryawanshi, Seema Rawat,
Copper induced augmentation of antibiotic resistance in Acinetobacter baumannii MCC 3114,
2024,
0966-0844,
10.1007/s10534-024-00657-3
|
|
| 246.
|
Yao Yang, Kai Liu, Jiahao Zhang, Mengzhen Xu, Fang Guo, Xinyi Zhou, Congcong Wang, Xiongdong Zhou, Xudong Fu,
Key Environmental Factors Influencing eDNA Quantitative Detection of Golden Mussel (Limnoperna fortunei) in a Long-Distance Water Diversion Project,
2024,
23521864,
103998,
10.1016/j.eti.2024.103998
|
|
| 247.
|
Ali Abdulridha Mussa, Harith Jabbar Fahad Al-Mathkhury,
BACTERIAL HUNGER GAMES: SMALL ALARMONE SYNTHETASES IN MRSA VS. MSSA,
2024,
12,
26644231,
864,
10.21272/eumj.2024;12(4):864-876
|
|
| 248.
|
Nur Bayatli, Ahmad Saleh Malkawi, Azhar Malkawi, Khaled Khaled, Nasr Alrabadi, Airemwen Collins Ovenseri, Lara Alhajj, Lina Al Sarayrih, Sherouk Essam Elnefaily,
Impact of biofilms on healthcare settings and management strategies,
2024,
2770-3150,
10.1097/MRM.0000000000000425
|
|
| 249.
|
Slavica Porobic Katnic, Ram K. Gupta,
From biofilms to biocatalysts: Innovations in plastic biodegradation for environmental sustainability,
2025,
374,
03014797,
124192,
10.1016/j.jenvman.2025.124192
|
|
| 250.
|
Nur 'Izzati Ismail, Nurull Muna Daud, Siti Rozaimah Sheikh Abdullah, Ahmad Razi Othman, Nur Nadhirah Ramli, Israa Abdulwahab Al-Baldawi, Islam J K Elhabil, Hassimi Abu Hasan,
Resistant rhizobacteria of native plant for simultaneous iron and aluminum removal from synthetic mining wastewater and its future potential for phytoremediation development,
2025,
09575820,
106829,
10.1016/j.psep.2025.106829
|
|
| 251.
|
Manchela F. Ratsoma, Quentin C. Santana, Brenda D. Wingfield, Emma T. Steenkamp, Thabiso E. Motaung,
Understanding cargo sorting and interactive effects of membrane vesicles in fungal phytopathogens: Current knowledge and research gaps,
2025,
51,
17494613,
100411,
10.1016/j.fbr.2025.100411
|
|
| 252.
|
Débora Francine Gomes Silva Pereira, Silvia Nietsche, Adelica Aparecida Xavier, Maria Olívia Mercadante-Simões, Marlon Cristian Toledo Pereira,
Biofilm formation by the plant growth promoting bacterium Bacillus cereus (EB-40),
2025,
1517-8382,
10.1007/s42770-025-01617-w
|
|
| 253.
|
Jihen Elleuch, Marwa Drira, Imtinen Ghribi, Farah Hadjkacem, Guillaume Pierre, Christel Causserand, Hamadi Khemakhem, Philippe Michaud, Imen Fendri, Slim Abdelkafi,
Amphora coffeiformis extracellular polymeric substances and their potential applications in lead removal,
2025,
118,
0003-6072,
10.1007/s10482-024-02057-6
|
|
| 254.
|
Ghanim Hassan, Qater Al-Nada Ali Kanaem ALIbady, Ayat Khairi Hashim,
2025,
3224,
0094-243X,
040037,
10.1063/5.0254172
|
|
| 255.
|
Tessa Tuytschaever, Katleen Raes, Imca Sampers,
Biofilm detection in the food industry: Challenges in identifying biofilm eps markers and analytical techniques with insights for Listeria monocytogenes,
2025,
432,
01681605,
111091,
10.1016/j.ijfoodmicro.2025.111091
|
|
| 256.
|
Sarah Gonzalez-Henao, Matthew O. Schrenk, Betül Kaçar,
An astrobiological perspective on microbial biofilms: their importance for habitability and production of detectable and lasting biosignatures,
2025,
0099-2240,
10.1128/aem.01778-24
|
|
| 257.
|
Tanaya Bhowmick, Arnab Sarkar, Kazi Hamidul Islam, Sanmoy Karmakar, Joydeep Mukherjee, Reshmi Das,
Molecular insights into cobalt homeostasis in estuarine microphytobenthos: A meta-transcriptomics and biogeochemical approach,
2025,
490,
03043894,
137716,
10.1016/j.jhazmat.2025.137716
|
|
| 258.
|
Prakash Monika, R. Hari Krishna, Zayaan Hussain, Krithika Nandhini, Samhitha J. Pandurangi, Tausif Malek, S. Girish Kumar,
Antimicrobial hybrid coatings: A review on applications of nano ZnO based materials for biomedical applications,
2025,
27729508,
214246,
10.1016/j.bioadv.2025.214246
|
|
| 259.
|
Aiswarya Sudheer, Debabrata Ghosh Dastidar, Gourav Ghosh, Zarin Taj, Illathu Kandy Nidhin, Indranil Chattopadhyay,
Comprehensive genomics, probiotic, and antibiofilm potential analysis of Streptococcus thermophilus strains isolated from homemade and commercial dahi,
2025,
15,
2045-2322,
10.1038/s41598-025-90999-w
|
|
| 260.
|
Konstantina Tsotsouli, Spyros Didos, Konstantinos Koukaras, Anagnostis Argiriou,
Mixotrophic Cultivation of Dunaliella tertiolecta in Cheese Whey Effluents to Enhance Biomass and Exopolysaccharides (EPS) Production: Biochemical and Functional Insights,
2025,
23,
1660-3397,
120,
10.3390/md23030120
|
|
| 261.
|
Anjali Bhardwaj, Mamta Kumawat, Ekta Menghani,
2025,
9780443220555,
43,
10.1016/B978-0-443-22055-5.00004-4
|
|
| 262.
|
Keyron Hickman-Lewis, Javier Cuadros, Keewook Yi, Tae Eun Hong, Mirang Byeon, Jae Hyuck Jang, Min-Yeong Choi, YoonKyung Seo, Jens Najorka, Wren Montgomery, Krzysztof Matlak, Barbara Wolanin, Caroline L. Smith, Barbara Cavalazzi,
Aluminous phyllosilicates promote exceptional nanoscale preservation of biogeochemical heterogeneities in Archaean siliciclastic microbial mats,
2025,
16,
2041-1723,
10.1038/s41467-025-57727-4
|
|
| 263.
|
Sangeeta Yadav, Diane Purchase,
Biodeterioration of cultural heritage monuments: A review of their deterioration mechanisms and conservation,
2025,
201,
09648305,
106066,
10.1016/j.ibiod.2025.106066
|
|
| 264.
|
Shaivan H. Shivaprakash, Susan E. Burns,
Microbial interactions during carbonate biomineralization via urea hydrolysis metabolic pathway,
2025,
1861-1125,
10.1007/s11440-025-02609-8
|
|
| 265.
|
Yiyang Lou, Ziqi Liu, Qiyi Zhang, Lujie Zhang, Xinyu Liao, Tian Yang, Donghong Liu, Xiaonan Lu, Juhee Ahn, Tian Ding, Jinsong Feng,
Interspecies and intraspecies ‘Talk’ shape the bacterial biofilms,
2025,
9,
2399-1399,
10.1093/fqsafe/fyaf008
|
|
| 266.
|
Mahmudul Hasan, Katherine Alfredo, Sudhir Murthy, Rumana Riffat,
Role of half-saturation coefficient and biofilm thickness on micropollutant biodegradation,
2025,
72,
22147144,
107659,
10.1016/j.jwpe.2025.107659
|
|
| 267.
|
Simran Khera, Sharon Poovathanathil, Mustansir Bhori, Vinothkannan Ravichandran, Kanchanlata Tungare, Renitta Jobby,
2025,
Chapter 20,
978-981-96-1884-2,
473,
10.1007/978-981-96-1885-9_20
|
|
| 268.
|
Stefana Vuletic, Tea Ganic, Branka Loncarevic, Stefana Cvetkovic, Biljana Nikolic, Marija Ljesevic, Dragana Mitic-Culafic,
New insights into the underlying mechanism involved in the Frangula alnus antivirulence potential directed toward Staphylococcus aureus,
2025,
49,
3042-3201,
1,
10.2298/CPB2501001V
|
|
| 269.
|
N. S. Karim, N. R. Sarker, D. Asker, B. Hatton, A. M. Bilton,
Can UVC-LEDs mitigate biofouling in community-scale photovoltaic-powered reverse osmosis systems?,
2025,
1606-9749,
10.2166/ws.2025.044
|
|
| 270.
|
Chloe Calhoun, Ifigenia Geornaras, Peipei Zhang,
Pseudomonas in Meat Processing Environments,
2025,
14,
2304-8158,
1615,
10.3390/foods14091615
|
|
| 271.
|
Veronica LaMastro, Dominique Walker, Joanne Liu, Tobias Meng‐Saccoccio, Anita Shukla,
Peptide‐Decorated Liposomes Enhance Fungal Targeting and Antifungal Drug Delivery,
2025,
1616-301X,
10.1002/adfm.202508570
|
|
| 272.
|
Tomáš Podzimek, Terezie Cisarová, Michal Dvořák, Barbora Vokatá, Christina Karmann, Jaroslav Hanuš, Martin Balouch, Matěj Malý, Jana Hajšlová, Vojtěch Kouba, Jan Bartáček, František Štěpánek, Petra Lipovová,
Isolation of Anammoxosomes From the Aggregate Culture of Ca. Brocadia Sapporoensis and Assembly of Ladderane Liposomes,
2025,
0006-3592,
10.1002/bit.29011
|
|
| 273.
|
Navid Dad, Mohamed A Elsawy, Gavin Humphreys, Alain Pluen, Jian R Lu, Andrew J McBain,
A critical view of antimicrobial peptides: exploring their potential and the barriers to realization,
2025,
136,
1365-2672,
10.1093/jambio/lxaf087
|
|
| 274.
|
Atiye Karadoğan, Fatma Azgin, Esra Sündüz Yiğittekin, Sadik Dinçer,
2025,
10.5772/intechopen.1010579
|
|
| 275.
|
Jens Kreth, Justin Merritt,
2025,
Chapter 13,
978-3-031-82201-8,
361,
10.1007/978-3-031-82202-5_13
|
|
| 276.
|
Yu Gao, Di Su, Jiawei Zhao, Zhongli Luo, Xuemei Lin,
Study on the Feasibility of Self-Assembling Peptides as a Three-Dimensional Culture Tool for Drug Screening of Colorectal Adenocarcinoma Cells,
2025,
11,
2310-2861,
394,
10.3390/gels11060394
|
|
| 277.
|
Peiyun Li, Xiaochen Chen, Tariq Aziz, Ashwag Shami, Fahad Al-Asmari, Fakhria A. Al-Joufi, Haiying Cui,
The anti-biofilm and anti-virulence mechanisms of carvacrol against Listeria monocytogenes and the application in food systems,
2025,
69,
22124292,
106950,
10.1016/j.fbio.2025.106950
|
|
| 278.
|
Lu Tian, Qi Qi, Sichen Liao, Guoli Gong, Zhenbin Liu, Jiayi Zhang, Hongbo Li, Qing Sun, Haizhen Mo, Liangbin Hu,
Uncovering the potential of rosmarinic acid as a natural antimicrobial agent: effective inhibition of growth and biofilm formation in Bacillus cereus,
2025,
178,
09567135,
111462,
10.1016/j.foodcont.2025.111462
|
|
| 279.
|
Nisha K. Rai, Pushkal Sinduvadi Ramesh, Veena A. Shetty,
Utilizing Bacteriophages to Manage Biofilm Infections on Medical Devices: A Systematic Review,
2025,
19,
09737510,
869,
10.22207/JPAM.19.2.31
|
|
| 280.
|
Prabhavati Shinde, Shraddha Jaiswal, Vidya Tale,
Temporal Profiling of Extracellular Polymeric Substances Associated with Biofilm Formation in Bacteria Isolated from Wound Infection,
2025,
19,
09737510,
1174,
10.22207/JPAM.19.2.21
|
|
| 281.
|
Krishna Jadhav, Swati Gautam, Amit Kumar Singh, Rahul Kumar Verma, Awadh Bihari Yadav,
Conquering the tuberculosis Superbug: Innovative approaches for biofilm disruption and antibiotic resistance mitigation,
2025,
111,
17732247,
107173,
10.1016/j.jddst.2025.107173
|
|
| 282.
|
Rajesh Kushwaha, Sangeeta Kumari, Arya Mishra, Anjali Upadhyay, Archana Rai, Malay Nayak, Sudip Mukherjee, Samya Banerjee,
Zn(ii)-metallo-photoantibiotics: experimental and computational approach identifying a therapeutic role for antibacterial and antibiofilm applications,
2025,
1359-7345,
10.1039/D5CC02340H
|
|
| 283.
|
Imran Ullah Khan, Mukhlis A. Rahman, Mohd Hafiz Dzarfan Othman, Musawira Iftikhar, Asim Jilani, Sadia Mehmood, Muhammad Bilal Shakoor, Muhammad Rizwan, Jean Wan Hong Yong,
Innovative Solutions for Palm Oil Mill Effluent Treatment: A Membrane Technology Perspective,
2025,
2690-0637,
10.1021/acsestwater.4c00432
|
|
| 284.
|
Allison J. Renno, Robert C. Shields, Lisa K. McLellan, Elizabeth Anne Shank,
Bacterial evolution in the oral microbiome: the role of conjugative elements and horizontal gene transfer,
2025,
0021-9193,
10.1128/jb.00066-25
|
|
| 285.
|
Sheng Xiong, Yuzhe Xu, Ji Zhou,
Deterioration of Masonry Cultural Relics by Microbes: Current Remediation Strategies and Prospects,
2025,
27,
1462-2912,
10.1111/1462-2920.70142
|
|
| 286.
|
Jinsuo Lu, Jiarui Zhang, Lei An, Ming Xu, Yunfeng Liu, Heliang Pang,
Promoting organic/inorganic separation from sewer sediments by alkaline-thermal hydrolysis: Organic carbon recovery and inorganic cement production,
2025,
76,
22147144,
108180,
10.1016/j.jwpe.2025.108180
|
|
| 287.
|
Wenyue Wang, Yunlong Liu, Zirun Zhao, Rou Liu, Fang Wang, Zhuo Zhang, Qilin Yu,
Moss Biochar Facilitates Root Colonization of Halotolerant Halomonas salifodinae for Promoting Plant Growth Under Saline–Alkali Stress,
2025,
9,
2571-8789,
73,
10.3390/soilsystems9030073
|
|
| 288.
|
Anisa Veledar-Hamalukić, Monia Avdić, Amra Demirović,
In vitro evaluation of antimicrobial and biofilm-modulating effects of commercial cranberry (Vaccinium macrocarpon) extracts against Escherichia coli and Staphylococcus aureus,
2025,
56,
2490-3329,
395,
10.5937/scriptamed56-57135
|
|
| 289.
|
R Jinisha, J Jerlin Regin,
Bioremediation of coal washery effluent using dual-chambered microbial fuel cell for effective pollutant removal and sustainable power generation,
2025,
19443986,
101347,
10.1016/j.dwt.2025.101347
|
|
| 290.
|
Nobumitsu Hirai, Yuhei Miwa, Shunta Hattori, Hideyuki Kanematsu, Akiko Ogawa, Futoshi Iwata,
Three-Dimensional Structure of Biofilm Formed on Glass Surfaces Revealed Using Scanning Ion Conductance Microscopy Combined with Confocal Laser Scanning Microscopy,
2025,
13,
2076-2607,
1779,
10.3390/microorganisms13081779
|
|
| 291.
|
Mythili Ravichandran, Mohammed Al-zharani, Fahd A. Nasr, Lina M. Alneghery, J. M. Mohamed, T. T. Ajith Kumar, B. T. Sureshkumar, R. Dineshkumar,
Biological evaluation and molecular docking of sulfated polysaccharide-derived glucuronic acid from S. platensis as a potential inhibitor of SARS-CoV-2 ORF3a and Envelope (E) proteins,
2025,
0366-6352,
10.1007/s11696-025-04213-2
|
|
| 292.
|
Litzy Yazmin Alvarado-Mata, Jesús Manuel Sánchez-Lozano, Jorge Ignacio Cervantes-de la Torre, Angélica Rubi Álvarez-Valdez, Jenny Priscila Salinas-Mireles, Alán Yazid Chávez Hita-Wong, María José Castro-Alonso, Miriam Paulina Luévanos-Escareño, Rajeswari Narayanasamy, Nagamani Balagurusamy,
Advances in microbially induced carbonate precipitation metabolic pathways and regulatory mechanisms for bioconcrete development,
2025,
2165-0373,
1,
10.1080/21650373.2025.2525559
|
|
| 293.
|
Tracey M Gloster, Ebru Toksoy Öner,
Microbial exopolysaccharide production by polyextremophiles in the adaptation to multiple extremes,
2025,
0014-5793,
10.1002/1873-3468.70138
|
|
| 294.
|
Alessandro Calogero Scalia, Ziba Najmi,
Targeting Bacterial Biofilms on Medical Implants: Current and Emerging Approaches,
2025,
14,
2079-6382,
802,
10.3390/antibiotics14080802
|
|
| 295.
|
Mohammed Zelloufi, Violeta Ramos, Badreddine El Haddaji, Amel Bourguiba, Sam Broom-Fendley, Gavyn K. Rollinson, Alexandra Guedes, Jens Andersen, Nassim Sebaibi, Mohamed Boutouil,
Assessment of bio-colonisation, durability and microstructure of concrete exposed to intertidal and subtidal marine environments,
2025,
23,
22145095,
e05119,
10.1016/j.cscm.2025.e05119
|
|









 DownLoad:
DownLoad: