Time-varying individual host susceptibility to a disease due to waning and boosting of immunity is known to induce rich long-term behavior of the disease transmission dynamics. Simultaneously, the impact of the time-varying heterogeneity of host susceptibility on the short-term behavior of epidemics is not well-studied despite the availability of a large amount of epidemiological data on short-term epidemics. This paper proposes a parsimonious mathematical model describing the short-term transmission dynamics by taking into account waning and enhancing susceptibility following the infection. In addition to the common classification in the standard SIR model, i.e., "no epidemic" as R0≤1 or normal epidemic as R0>1, the proposed model also shows the "delayed epidemic" class when an epidemic takes off after the negative slope of the epidemic curve at the initial phase of the epidemic. The condition for each of the three classes is derived based on the obtained explicit solution for the proposed model.
1.
Introduction
Modelling is often used to understand the transmission dynamics of infectious diseases. The susceptible-infective-removed (SIR) model is known to be the simplest model to describe these transmission dynamics[1,10]. The SIR model describes the transmission of pathogens from infected to susceptible individuals and the removal of infected individuals from the targeted host population due to the establishment of immunity or the host's death or immigration. Due to the wide variation in the natural history of pathogens, many extensions of the basic SIR model have been proposed so far.
An important extension is the inclusion of the evolution of susceptibility to an infection along with a pathogen. The basic SIR model assumes that the host immunity perfectly protects the host from reinfection over time and reinfection can never occur. However, reinfection events are frequently observed for many infectious diseases such as tuberculosis[31] and those caused by coronavirus[20], respiratory syncytial virus[15] and hepatitis C virus[30]. One of the important mechanisms of reinfection is waning immunity. Decreased herd immunity by waning immunity of individuals induces re-emergence of an epidemic, and boosting immunity by re-vaccination is required to control the epidemic[4]. Another mechanism is imperfection of immunity by an infection event. A booster dose of a vaccine is required to establish a high enough immunity level to protect hosts from reinfection[29], which implies that multiple exposures to the pathogen is required to establish the high enough immunity level. Moreover, the enhancement of susceptibility to reinfection is also observed for several infectious diseases[32,24].
An epidemic model incorporating variable susceptibility of recovered individuals was formulated by Kermack and McKendrick[22,23]. However, the authors did not obtain a clear biological conclusion[8,18]. In[17,18] the author performed stability analysis for the Kermack and McKendrick's reinfection model formulated as a system of partial differential equations. The existence and bifurcation of the endemic equilibrium was analyzed in detail. Destabilization of the endemic equilibrium was shown to be possible for epidemic models with waning immunity[9,16,28]. Previous modeling studies showed that waning and natural-boosting immunity by exposing to pathogens can trigger a counter-intuitive effect of vaccination[27]. It is suggested that waning immunity in vaccinated hosts can trigger backward bifurcation of the endemic equilibrium[2,6,26]. Estimating vaccine effectiveness is essential to control epidemics. However, vaccine effectiveness reflects the complicated epidemiological dynamics which is scaled by waning and natural-boosting immunity, e.g., waning and boosting of immunity can induce periodic epidemic outbreaks as part of the long-term behavior of the epidemic[3].
Unlike the long-term behavior of an epidemic, its short-term behavior with waning and boosting of immunity is not well understood despite many field data of short-term epidemics have been analyzed using models that do not consider waning and boosting of immunity. For the short-term behavior of epidemics, the dynamics with the constant immune protection rate against reinfection has been studied so far. However, waning and boosting of immunity change the immune protection rate. In[21] the author analyzed transient dynamics of a reinfection epidemic model, while ignoring the demographic process in the model. In the model, reinfection of recovered individuals occurs assuming that these individuals have suitable susceptibility to the disease. It was shown that the disease transmission dynamics changes qualitatively when the basic reproduction number crosses the reinfection threshold. See also[13] for the model with demographic process.
This paper presents a mathematical model taking into account waning and enhancing susceptibility following an infection. We suppose that reinfection can reduce the immune protection level, e.g., as it is the case in antibody-dependent enhancement[5].
The timescale of natural-waning immunity, which is not due to reinfection, is relatively longer than that of the transmission dynamics e.g., the minimum annual waning rate of immunity is −2.9% for rubella and −1.6% for measles[25], compared to the infectious periods of 11 days for rubella[11] and 14 days for measles[1]. Hence the proposed model focuses only on waning and enhancing susceptibility triggered following an infection.
Since the waning and boosting of immunity can induce periodic infection outbreak on the long-term disease transmission dynamics ([3]), a complicated epidemic curve can be observed in the model for the short-term disease transmission dynamics as well. In this paper, an explicit solution for a number of infective individuals in terms of a number of susceptible individuals is obtained. Consequently, the impact of waning and enhancing susceptibility following an infection on the short-term behavior of the transmission dynamics is explored. The shape of the short-term epidemic curve is analyzed in detail.
The paper is organized as follows. In Section 2 an epidemic model taking into account waning and enhancing susceptibility following an infection is formulated as a nonlinear system of differential equations. The model includes the standard SIR epidemic model and the reinfection epidemic model studied in[21] as special cases. Section 3 studies the disease transmission dynamics when the basic reproduction number R0 exceeds one. The epidemic peak is shown to be one, as is the case for the standard SIR epidemic model. Section 4 considers the disease transmission dynamics when R0≤1. It demonstrates that the epidemic occurs even if R0≤1 due to the enhancement of susceptibility of recovered individuals. The shape of the epidemic curve is analyzed in detail. In Section 5, the relatiton of final epidemic size with the model parameters is derived from the obtained explicit solutions. Plans for future work are discussed in Section 6.
2.
An epidemic model with waning and enhancing susceptibility following infection
First of all let us introduce the epidemic model studied in[21]. In the model it is assumed that the infectious disease induces partial immunity. Denote by S(t), I(t) and R(t) the proportions of susceptible population, infective population and recovered population at time t, respectively. The partial immunity model is formulated as
The positive parameters β and γ are the transmission coefficient and the recovery rate, respectively. The parameter σ is the relative susceptibility of recovered individuals, who have been infected at least once and have recovered from the infection. We obtain the standard SIR epidemic model, if σ=0, i.e., recovered individuals are completely protected from the infection.
In this paper the partial immunity model (2.1) is modified as follows. When a recovered individual is exposed to the force of infection, immunity is boosted with probability 1−α so that one obtains permanent immunity to the disease, while one contracts the disease again with probability α. The partial immunity model (2.1) is modified as
with the following initial conditions
Here B(t) denotes the proportion of population with permanent immunity at time t. We obtain the model (2.1) by α=1 and the SIR model by α=0. Throughout the paper, we assume the following two conditions
We first prove a basic result for asymptotic behavior of the solution.
Lemma 1. There exist limt→∞S(t),limt→∞I(t),limt→∞R(t) and limt→∞B(t). It holds that
Proof. One easily sees that S, R and B are respectively monotone bounded functions. Specifically S is a monotone decreasing function, while B is a monotone increasing function. Therefore, S, R and B tend to some constants. Since S(t)+I(t)+R(t)+B(t)=1 holds for t≥0, limt→∞I(t) also exists. We now claim that (2.5) holds. From (2.2a), (2.2b) and (2.2c) one has
Suppose that limt→∞I(t)>0. Integrating the above equation, we derive a contradiction. Hence (2.5) holds.
3.
One epidemic peak for R0>1
We define the basic reproduction number by
where b=βγ. The basic reproduction number is the expected number of secondary cases produced by one infective individual in the expected one infectious period, 1γ in the initial phase of epidemic. Noting that both susceptible and recovered populations, which compose the initial host population, have susceptibility to the disease, we may call R0 the basic reproduction number, although R0 is conventionally called the effective reproduction number[19].
From (2.2a) and (2.2b) one obtains the following
and
where
Noting that R(S0,R0)=R0, it is easy to see that
i.e., if R0>1 then the epidemic curve initially grows, while if R0<1 then the epidemic curve initially decays.
First we show that R(t) can be expressed in terms of S(t).
Proposition 1. It holds that
Proof. Assume that 1−σbR0≠0 holds. From the equations (2.2a) and (2.2c) we have
Using the separation of variables, we obtain
thus (3.3) follows. It is easy to see that the equality in (3.3) also holds, if 1−σbR0=0. From Lemma 1 we have
where
Then we can show that I(t) and B(t) are explicitly expressed in terms of S(t) and R(t).
Proposition 2. It holds that
for t≥0.
Proof. From (2.2a) and (2.2b) we have
One can compute, using (3.6) and (3.7),
From (3.5) and (3.4) in the proof of Lemma 1 we get
Therefore, we get
Thus we obtain (3.8).
From (2.2a) and (2.2b) we have
Similarly, one obtains (3.9).
To analyze the epidemic curve, we study the function R(S,R) with R=r(S). Let
We then compute the first and second derivatives of ˆR:
From the equation (3.4) in Lemma 1, it is easy to obtain the following result.
Lemma 2. One has
Note that, for σ=1 or 1−σbR0=0, r is a constant function. For σ≠1 and 1−σbR0≠0, , ris either monotone increasing or decreasing function, thus ˆR has at most one extremum.
We now show the standard epidemic case if R0>1 holds.
Proposition 3. Let us assume that R0>1 holds. Then
holds and there exists a unique root of
Proof. It is easy to see that (3.16) holds. First assume that r′(S)≥0 for 0≤S≤S0. Then, from (3.12), one can see that ˆR is an increasing function. Thus we obtain the conclusion. Next assume that r′(S)<0 for 0≤S≤S0. By (3.13) and Lemma 2, one sees that ˆR has at most one minimum for 0≤S≤S0. Therefore, from (3.16), we obtain the conclusion.
Then, from Proposition 3, Lemma 1 and (3.2), we obtain the following result.
Theorem 1. Let us assume that R0>1 holds. Then there is a tp>0 such that I is monotonically increasing for t∈(0,tp) and monotonically decreasing for t>tp. It holds limt→∞I(t)=0.
4.
Delayed epidemic for R0≤1
In the standard SIR model, when R0≤1 holds, then the epidemic curve monotonically decreases and infective population tends to 0 eventually as time goes to infinity. The situation changes in the model with waning and enhancing susceptibility following infection(2.2), due to the susceptibility of the recovered individuals. In particular, if σ>1 then there is a possible delayed outbreak as the recovered population increases which will induce the epidemic later even if R0≤1. The basic reproduction number, which characterizes the initial dynamics, is not a sufficient criterion to determine the outbreak due to the recovered population.
First let us consider a simple case that σ≤1 holds. We have the standard scenario: if R0≤1 then the epidemic does not occur. Subsequently we study the disease transmission dynamics when σ>1. We show that enhancement of susceptibility after the infection can induce an epidemic later.
4.1. σ≤1
We show that the infective population is monotonically decreasing for t≥0, similar to the SIR model, when R0≤1.
Proposition 4. Let us assume that R0≤1 and σ≤1 holds. Then
Proof. Note that
holds. First let us consider the case that σ=1 or 1−σbR0=0. In these cases R(S) is a linear function of S, thus we obtain the conclusion from (4.1). Let us assume that σ<1 and 1−σbR0≠0 hold. If 1−σbR0<0, then one has r′(S)≥0 for 0<S<S0, thus ˆR is an increasing function. We then obtain the conclusion from (4.1). Next assume that 1−σbR0>0. One sees that
Then r′(S)<0 holds for 0<S<S0. By Lemma 2, one sees that ˆR has at most one minimum for 0≤S≤S0. Therefore we obtain the conclusion.
Then, from Propositions 4, Lemma 1 and (3.2), we obtain the following result.
Theorem 2. Let us assume that R0≤1 and σ≤1 hold. Then I is monotonically decreasing for t≥0. It holds limt→∞I(t)=0.
4.2. σ>1
In this subsection we consider the case that
hold. We show the following results for the graph of ˆR.
Proposition 5. Let us assume that R0≤1 and σ>1 hold.
1. If
then ˆR(S)≤1 for 0≤S≤S(0).
2. If
then there is a unique maximum for 0<S<S0 at S=˜S, where
Then
(a) If ˆR(˜S)>1 then there are two roots for ˆR(S)=1 for 0<S<S0. Denote the roots by ˆS1 and ˆS2 such that
then
(b) If ˆR(˜S)≤1 then ˆR(S)≤1 for 0≤S≤S0.
Proof. For σ>1 one sees that
From the monotonicity of ˆR′, if limS↑S0ˆR′(S)>0 then ˆR(S)≤1 for 0≤S≤S0 follows. Computing
one can see that (4.3) is equivalent to that limS↑S0ˆR′(S)>0 holds.
Next assume that (4.4) holds. Then
From the monotonicity of ˆR′, there is a unique maximum for 0<S<S0. Solving ˆR′(S)=0, we obtain ˜S given as in (4.5). It is now straightforward to obtain the statements (a) and (b).
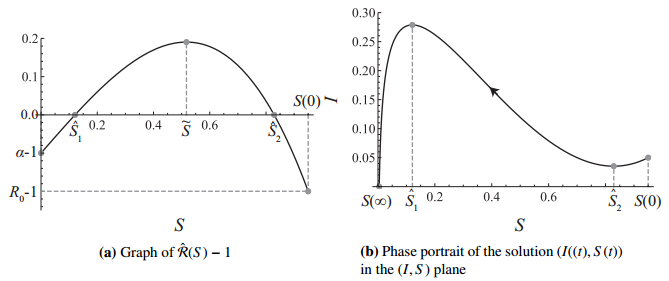
In Figure 1, we plot the graph of the function ˆR(S)−1 for 0≤S≤S0, where R0≤1 and σ>1. Parameters are fixed so that (4.4) and ˆR(˜S)>1 hold.
From Proposition 5, Lemma 1 and 3.2, we first obtain the result for the extinction of the disease.
Theorem 3. Let us assume that R0≤1 and σ>1 holds. If either
1. (4.3) holds, or
2. (4.4) and ˆR(˜S)≤1 hold,
then I is monotonically decreasing for t≥0. It follows that limt→∞I(t)=0.
Now it is assumed that (4.2) holds. If
holds, where ˜S is given by (4.5), then I(t) may attain a minimum and a maximum (see Figure 1). This implies that even if R0≤1, the epidemic curve may grow for a certain time interval, which we call delayed epidemic.
To determine if the delayed epidemic indeed occurs, we evaluate the minimum of I(t) using (3.8) in Proposition 2. If S(t)=ˆS2 for some t, I(t) is given by I_, where
See also Figure 1(B) for the phase portrait in the (I,S)-plane.
Theorem 4. Let us assume that R0≤1 and σ>1 holds. Furthermore, assume that (4.4) and
hold.
1. If I_≤0, then I is monotonically decreasing for t≥0.
2. If I_>0, then there is an interval [t1,t2] such that I increases for t1≤t≤t2 and decreases for 0≤t≤t1 and t2≤t.
It follows that limt→∞I(t)=0.
Proof. One sees that I has a local maximum and minimum with respect to t and S, where ˆR(S)=1 holds (see (3.1) and (3.2)). I has a local minimum at S=ˆS2∈(˜S,S0) and I is increasing for ˆS2≤S≤S0 (see Figure 1(B)). Noting that I(t)>0 for t≥0 and that S is a decreasing function with respect to t, I_≤0 implies that I is monotonically decreasing for t≥0. On the other hand, if I_>0 then I is monotonically increasing for S<ˆS1, decreasing for ˆS1<S<ˆS2 and then increasing for ˆS2<S. There exist t1 and t2 such that S(t1)=ˆS2 and S(t2)=ˆS1. Thus we obtain the conclusion. From Lemma 1, it follows that limt→∞I(t)=0.
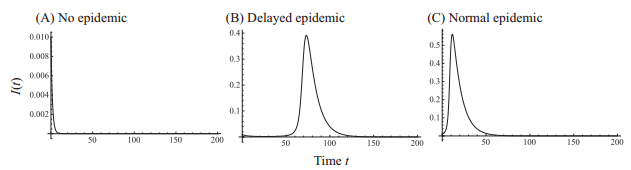
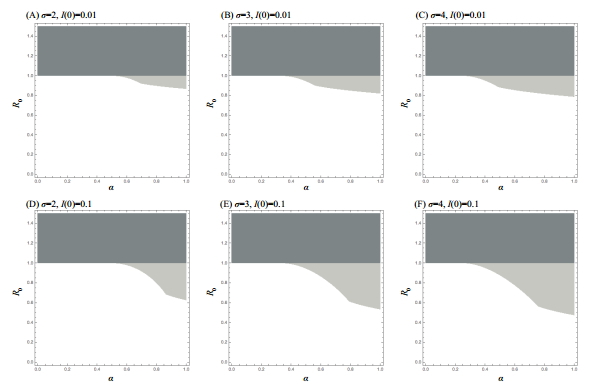
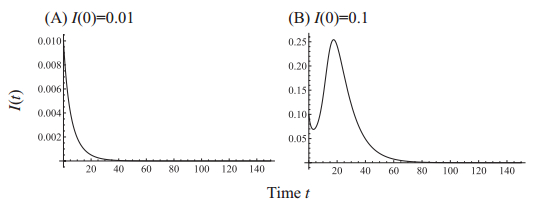
Thus the model has three different transmission dynamics: no epidemic, normal epidemic and delayed epidemic as illustrated in Figure 2. Figure 3 shows parameter regions for the three different disease transmission dynamics. The region for the delayed epidemic become larger with respect to the initial condition of I and the susceptibility σ. Since the initial condition of I is involved in the condition of Theorem 4.3, the initial condition qualitatively changes the epidemic curve, see Figure 4: delayed epidemic is induced by a large initial condition.
Due to the nonlinearity, it may not be possible to explicitly express the condition under which a delayed epidemic occurs in terms of the the initial conditions. We here consider a special case σ=2 in order to illustrate that a certain amount of the initial infectives is required for a delayed epidemic. We assume that R0=B0=0 to keep the presentation simple, although one may follow the approach for R0>0 or B0>0. We let
Then, from (3.5) in the proof of Lemma 1, we get y(t)=x(t)σ. Assume that σ=2 and R0=B0=0 hold. One easily sees that the condition R0≤1 is equivalent to
It can be seen that ˆR(S)=1 has two roots if and only the following equation has two roots
where
Note f(0)=−(1−α)<0 and f(1)=bS0−1≤0. If (bS0)2>4α(1−α) then the equation (4.8) has two roots. Together with the condition (4.7) we now assume that
holds. If (4.8) holds, we have
where we regard x as a free parameter. Under the condition (4.9), equation (4.10) has two roots in [0,1] for 12<α<1 and the larger root exists in the interval (√(1−α)/α,1], thus we vary x in (√(1−α)/α,1].
From (3.8) one can express I(t) in terms of x(t):
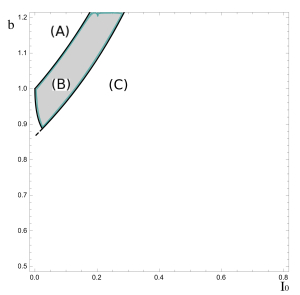
Assume I_=0, which is the threshold condition for a delayed epidemic. Using (4.11) and (4.10), b and S0 can be expressed in terms of x as
for x∈(√(1−α)/α,1]. Then we can plot a parametrized curve in (I0,b) plane, using I0=1−S0, which shows the threshold condition for a delayed epidemic, see Figure 5. In the Figure 5, we also plot two curves bS0=b(1−I0)=1 (corresponding to the condition R0=1) and bS0=b(1−I0)=2√α(1−α). A delayed epidemic occurs in the region enclosed by the three curves, showing that delayed epidemic requires sufficiently large initial infectives. Figure 5 also shows that if I0 decreases, then either the condition R0>1 holds (i.e., normal epidemic) or I_≤0 holds (i.e., no epidemic), depending on the value of b.
Consider a special case that R0→0. The basic reproduction number is given as R0=bS0. The conditions (4.4) becomes
and ˜S=(R0σα)1σ−1S0. If ˆR(˜S)>1 holds, then the delayed epidemic may occur.
5.
Final epidemic size
Let
It follows that I(∞)=0. From the relations (3.8), (3.3) and (3.9), one sees that (S(∞),R(∞),B(∞)) satisfy the following equations
The final epidemic size is given by R(∞)+B(∞), the number of individuals who are infected at least once. From (5.1) and (5.2) we get the following equation
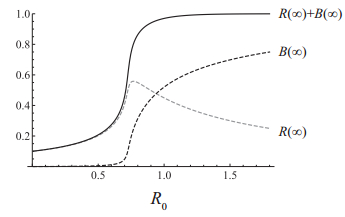
In Figure 6, we plot R(∞)+B(∞)=1−S(∞), R(∞) and B(∞) with respect to R0.
Numerically we observe that R(∞) is not monotone with respect to R0. Small R0 allows the increase of R(∞), on the other hand, does not contribute to the increase of B(t), the outbreak ends before the transition from R(t) to B(t) via I(t) occurs among most R(t). Increase of R0 contributes the transition from R(t) to B(t), consequently, R(∞) decreases. Despite of non-monotnic relation of R(∞) with respect to R0, R(∞)+B(∞) is likely to increase monotonically with the increase of R0 as shown in Figure 6.
When α=0 we obtain the standard SIR setting. Letting I(0)→0 and S(0)→1, the basic reproduction number is given as R0=b. In this case, from (5.1), we obtain the well known final size relation
see e.g.[10,19].
6.
Discussion and conclusion
In this paper, we study a disease transmission dynamics model after incorporating changes in immune protection level following an infection. The proposed modelling approach describing waning and enhancement of susceptibility following an infection captures the delayed epidemics in addition to the standard transmission dynamics. A delayed epidemic shows a negative slope in the initial phase of the epidemic. Therefore, the estimation of R0 using the initial slope of the epidemic makes it difficult to capture the actual epidemic coming later. The condition for a delayed epidemic is derived using the analytic transient solution of I(t).
A delayed epidemic, illustrated in Figures 2 and 4, occurs due to the enhancement of susceptibility of the recovered population (i.e., σ>1). For example, antibody dependent enhancement can boost the viral replication within the host body. Consequently, the host susceptibility can be enhanced at the time of reinfection[33]. Theorem 4.3 formulates a condition for the delayed epidemic. One of the necessary condition for a delayed epidemic is (4.4) in Proposition 5. The condition (4.4) is necessary for the epidemic curve increase; it relates the effective susceptible population increase, which is defined as
Since it holds that
one can see that
Therefore, the effective susceptible population increase at the initial time is necessary for a delayed epidemic and may induce the delayed epidemic even if R0≤1.
We remark that R0 cannot measure the outbreak potential of a delayed epidemic. In principle, R0 is derived based on the linearized system of the the initial disease transmission dynamics. The linearized system at the initial phase does not provide enough information to predict a delayed epidemic. Similar phenomena can be observed in epidemic models that show backward bifurcation of the endemic equilibrium[2,6,14,19,26]. These studies show that there is a stable endemic equilibrium even if the basic reproduction number is less than unity. Unlike these models, the short-term disease transmission dynamics model has many equilibria, which are associated with the zero eigenvalue. Our study illustrates that the outbreak potential should be carefully examined in the short-term disease transmission dynamics using the transient solution.
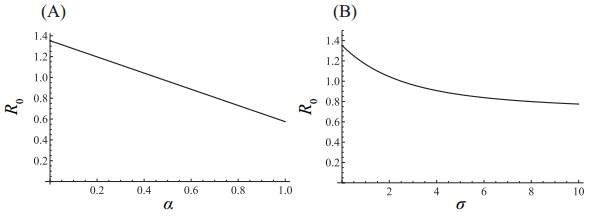
R0 can be estimated from the final epidemic size. It should be noted that R0 can be overestimated if the model neglects the enhancement of susceptibility following an infection. Figure 7 shows the estimated R0 using a fixed final epidemic size of 0.5 with varied α and σ. In this case, our model is equivalent to the standard SIR model when α=0 or σ=0. If waning and boosting of immunity are introduced, i.e., α>0 or σ>0, the estimated R0 is always lower than the estimate obtained using the standard epidemic model with α=0 or σ=0. To estimate the precise R0 from the final epidemic size, an appropriate modelling with respect to waning and boosting of immunity is required.
R0 can also be estimated from the time-series of I(t). Since I(t) in the proposed model can be expressed as the closed-form function of S(t), if I(t)+S(t) is given, e.g., B(t)+R(t) is estimated from a serological survey, I(t) can be obtained as a function of time, which can be used to estimate R0.
The proposed mathematical model describing waning and enhancing susceptibility following an infection has a limitation. In particular, it describes a step-wise level of boosting immunity i.e., R has susceptibility σ to an infectious disease while B has a complete protection against reinfection. This setting is suitable for infectious diseases where multiple infections can establish drastic increase of the immunity level. On the other hand, several classes of R with varied immune protection level are required to describe gradual change of the immunity level resulted from waning and boosting of immunity.
Acknowledgments
The authors thank the reviewer for the careful reading of the manuscript. The original manuscript has been improved by the reviewer's helpful comments. The first author was supported by JSPS Grant-in-Aid for Young Scientists (B) 16K20976 of Japan Society for the Promotion of Science. The second author was supported by CREST, Japan Science and Technology Agency.
Conflict of interest
The author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: