1. Introduction
Mathematical modeling is a very important tool in analyzing the propagation and controlling of infectious diseases. Age structure is an important characteristic in the modeling of some infectious diseases. The first formulation of a partial differential equation(PDE) for the age distribution of a population was due to McKendrick [21]. Since the seminar papers by Kermack and McKendrick [13]-[15], age structure models have been used extensively to study the transmission dynamics of infectious diseases, we refer to the monographs by Hoppensteadt [11], Iannalli [12] and Webb [30] on this topic.
As an ancient disease, TB peaked and declined by 1940's before it became curable, while the downtrend stopped in the middle 1980's and 1990's. As one of the top 3 deadly infectious diseases, TB would cause a higher death rate if not treated, while the disease would be latent in an individual body for months, years or even decades before it outbreaks. McCluskey [20] pointed out that the risk of activation can be modeled as a function of duration age, and this form can be used to describe more general latent period via introducing the duration age in the latent class as a variable.
On the other hand, for the infectious tuberculosis, the removed individuals often have a higher relapse rate. Actually, the recurrence as an important feature of some animal and human diseases has been studied extensively, see [4], [23]. For instance, van den Driessche and coauthors in [4], [5] established two models with a constant relapse period and a general relapse distribution respectively, which showed the threshold property of the basic reproduction number. It is interest to investigate the model with age-dependent relapse rate and to determine whether the threshold property can be preserved or not.
Recently, Wang et al. [24]-[27] considered the global stability of nonlinear age-structured models, Liu et al. [17] introduced age-dependent latency and relapse into an SEIR epidemic model and the local stability and global stability of equilibria are obtained by analyzing the corresponding characteristic equations and constructing the proper Volterra-type Lyapunov functionals, respectively. Wang et al. [28] proposed an SVEIR epidemic model with media impact, age-dependent vaccination and latency, and discussed the global dynamics of the age-structure model.
However, most of the models assumed that TB would show neither its clinical symptoms nor its infectivity during its latent period, while in fact, TB has many early clinical symptoms such as fever, fatigability, night sweat, chest pain, hemoptysis and so on. Here we formulate and analyze an SEIR epidemic model with continuous age dependent latency and relapse. We assumed, as the development of the disease, TB is infectious during its latent period with less infectivity and incomplete treatment comparing with outbreak period. Although epidemic models with age-dependent have been studied extensively, there have been still inadequate results on the full global stability. In this paper, we employ the method developed by Webb [30] for age-dependent models, namely integrating solutions along the characteristics to obtain an equivalent integral equation. We obtain the basic reproduction number in virtue of the method in [7]. Moreover, we study the asymptotic smoothness of the semi-flow generated by the system and the existence of a global attractor [3], [19]. Finally, we show the global stability of equilibria via constructing the proper Volterra-type Lyapunov functionals. For more details concerning the current Lyapunov functionals approach, we refer the reader to recent work [2].
This paper will be organized as follows: In Section 2, we formulate our general SEIR tuberculosis model with latent age and relapse age which is described by a coupled system of ODEs and PDEs. In Section 3, we investigate the existence of equilibria and obtain the expression of the basic reproduction number R0. In Section 4, the local asymptotic stability of the equilibria will be derived. In Section 5, we present the results about uniform persistence. In section 6, we deal with the global stability of equilibria. Finally, some numerical simulations and useful discussions are made in the last section.
2. Model formulation
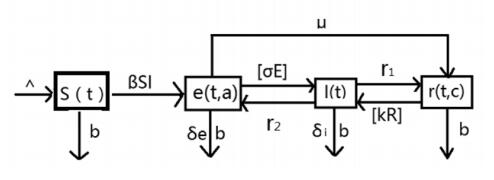
The total population is decomposed into four disjoint subclasses, susceptible class S, latent class E, infectious class I, and removed class R. More precisely, let S(t) denote the number of susceptible individuals at time t. Susceptible individuals would become new infected ones after they contact with infectious individuals at a rate β, while they enter a stage when they are infected with the disease but have little infectivity. This stage is often called latent stage, which maybe enter into the stage of removed class R by receiving treatment at a rate μ. The density of individuals in the latent class is denoted by e(t,a) where t is the duration time spenting in this class and a is called the latent-stage progression age, denoting E(t)=∫+∞0e(t,a)da the total density of latent individuals. The number of individuals in the class I at time t is I(t). The removal rate from latent class E to infectious class I is given by the function σ(a). Thus, the total rate at which individuals progress into the infectious class alive is ∫+∞0σ(a)e(t,a)da. Infectious individuals come into the removed class after recovery due to complete treatment. Let r1 be the recovery rate from the infectious class. The density of individuals in removed class is denoted by r(t,c), where c represents the relapse age, denoting R(t)=∫∞0r(t,c)dc the total density of removed individuals. In fact, infectious individuals might come into the latent class E due to incomplete treatment at the rate r2. Due to the relapse of the disease, the age-dependent relapse rate in the removed class is given by the function k(c). The total rate at which individuals relapse into the infectious class alive is given by the quantity ∫+∞0k(c)r(t,c)dc. We also denote Λ, δe,δi as the density of the recruitment into the susceptible class, the additional death rates induced by the latent disease and infectious disease. The parameter b is the natural death rate of all individuals. All recruitment of the population enters the susceptible class and occurs with constant flux Λ. Further, all parameters are assumed to be positive. FIGURE 1 shows the schematic flow diagram of our model which can be described by a system of ordinary and partial differential equations
|
{dS(t)dt=Λ−bS(t)−βS(t)I(t),(∂∂t+∂∂a)e(t,a)=−(b+δe+μ(a)+σ(a))e(t,a),dI(t)dt=−(r1+r2+b+δi)I(t)+∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc,(∂∂t+∂∂c)r(t,c)=−(k(c)+b)r(t,c),
|
(1)
|
with boundary conditions
|
{e(t,0)=βS(t)I(t)+r2I(t),r(t,0)=r1I(t)+∫∞0μ(a)e(t,a)da,
|
(2)
|
and initial conditions
|
S(0)=S0,e(0,a)=e0(a),I(0)=I0,r(0,c)=r0(c),
|
(3)
|
where S0,I0∈R+, and e0(a),r0(c)∈L1+(0,∞) which is the nonnegative and Lebesgue integrable space of functions on [0,+∞).
In order to simplify the later derivation, we make the following hypotheses about the parameters of the system (1)
(H1) σ(a),k(c),μ(a)∈L1+(0,+∞),
with respective essential upper bounds ˉσ,ˉk,ˉμ;
(H2) σ(a),k(c),μ(a)∈L1+(0,+∞)
are Lipschitz continuous on R+, with
Lipschitzcoefficients Mσ,Mk
and Mμ
respectively;
(H3) There exists b0∈[0,b), such that σ(a),k(c),μ(a)≥b0,foralla,c>0.
For a,c>0, we denote
|
ε(a)=σ(a)+μ(a)+b+δe,η(c)=k(c)+b,ρ1(a)=e−∫a0ε(s)ds,ρ2(c)=e−∫c0η(s)ds,θ1=∫+∞0σ(a)ρ1(a)da,θ2=∫+∞0k(c)ρ2(c)dc,θ3=∫+∞0μ(a)ρ1(a)da.
|
According to Webb [30], by solving the PDE parts of (1) along the characteristic lines t−a=const and t−c=const respectively, we obtain
|
e(t,a)={e(t−a,0)e−∫a0ε(s)ds,t>a≥0,e0(a−t)e−∫aa−tε(s)ds,a≥t≥0,
|
(4)
|
|
r(t,c)={r(t−c,0)e−∫c0η(s)ds,t>c≥0,r0(c−t)e−∫cc−tη(s)ds,c≥t≥0.
|
(5)
|
Define the space of functions X as
|
X:=R+×L1+(0,+∞)×R+×L1+(0,+∞)
|
equipped with the norm
|
∥(x1,x2,x3,x4)∥X=|x1|+∫+∞0|x2(a)|da+|x3|+∫+∞0|x4(c)|dc.
|
The norm has the biological interpretation of giving the total population size. The initial conditions (3) for system (1) can be rewritten as x0=(S0,e(0,⋅),I0,r(0,⋅))∈X. Using standard methods we can verify the existence and uniqueness of solutions to model (1) with the boundary conditions (2) and initial conditions (3) (see Iannelli [12] and Webb [30]). Meanwhile, we can claim that any solution of system (1) with nonnegative initial conditions remains nonnegative. The nonnegativity of e(t,a) and r(t,c) follows from (4) and (5). Next, we shall show that S(t)>0 for t≥0 and I(t)>0 for t≥0. Otherwise, assume that S(t) would lose its positivity for the first time at t1>0, i.e., S(t1)=0. However, from the first equation of (1) we obtain
|
S(t1)=e−bt1−∫t10βI(τ)dτ{S(0)+∫t10ebs+∫s0βI(τ)dτΛds}>0.
|
Similarly, assume that I(t) would lose its positivity for the first time at t2>0, i.e., I(t2)=0. However, from the third equation of (1) we obtain
|
I(t2)=e−(r1+r2+b+δi)t2∫t20(∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc)e(r1+r2+b+δi)s)ds+e−(r1+r2+b+δi)t2I(0)>0.
|
Thus S(t)>0 and I(t)>0 are true for ∀t≥0. This verifies our claim.
Let us consider a function N(t)=S(t)+∫+∞0e(t,a)da+I(t)+∫+∞0r(t,c)dc, which is the total population at time t. We can easily see that the time derivative of N along solutions of model (1) is
|
ddtN(t)=ddtS(t)+ddt∫+∞0e(t,a)da+ddtI(t)+ddt∫+∞0r(t,c)dc.
|
due to ρ1(0)=1,dρ1(a)da=−ε(a)ρ1(a), we have
|
ddt∫+∞0e(t,a)da=ddt(∫t0e(t−a,0)ρ1(a)da+∫+∞te0(a−t)ρ1(a)ρ1(a−t)da)=ddt∫t0(βS(t−a)I(t−a)+r2I(t−a))ρ1(a)da+ddt∫+∞te0(a−t)ρ1(a)ρ1(a−t)da=ddt∫t0(βS(τ)I(τ)+r2I(τ))ρ1(t−τ)dτ+ddt∫+∞0e0(τ)ρ1(t+τ)ρ1(τ)dτ=βS(t)I(t)+r2I(t)−∫+∞0ε(a)e(t,a)da.
|
Similarly, by using ρ2(0)=1,dρ2(c)dc=−η(c)ρ2(c), we can get
|
ddt∫+∞0r(t,c)dc=ddt∫t0(r1I(t−c)+∫+∞0μ(a)e(t−c,a)da)ρ2(c)dc+ddt∫+∞tr0(c−t)ρ2(c)ρ2(c−t)dc=r1I(t)+∫+∞0μ(a)e(t,a)da−∫+∞0η(c)r(t,c)dc.
|
Hence, we have
|
ddt(S(t)+∫+∞0e(t,a)da+I(t)+∫+∞0r(t,c)dc)=Λ−bS(t)−βS(t)I(t)+βS(t)I(t)+r2I(t)−∫+∞0ε(a)e(t,a)da−(r1+r2+b+δi)I(t)+∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc+r1I(t)+∫+∞0μ(a)e(t,a)da−∫+∞0η(c)r(t,c)dc=Λ−bS(t)−∫+∞0br(t,c)dc−bI(t)−∫+∞0(b+δe)e(t,a)da−δiI(t)≤Λ−bN(t).
|
It follows from the variation of constants formula that N(t)≤Λb, for any t≥0, which implies that
|
Ω={(S(t),e(t,⋅),I(t),r(t,⋅))∈R+×L1+(0,+∞)×R+×L1+(0,+∞):N(t)≤Λb}
|
is positively invariant absorbing set for system (1).
Proposition 1. If x0∈X and ‖x0‖X≤M for some constant M≥Λb, then the following statements hold for t≥0,
|
(ⅰ)0≤S(t),∫+∞0e(t,a)da,I(t),∫+∞0r(t,c)dc≤M,(ⅱ)e(t,0)≤βM2+r2M,r(t,0)≤r1M+ˉμM.
|
For convenience, we rewrite (1) as follows
|
{(∂∂t+∂∂a)e(t,a)=−(b+δe+μ(a)+σ(a))e(t,a),(∂∂t+∂∂c)r(t,c)=−(k(c)+b)r(t,c),dV(t)dt=G(e(t,a),r(t,c),V(t))−CV(t),e(t,0)=βS(t)I(t)+r2I(t),e(0,a)=e0(a),r(t,0)=r1I(t)+∫∞0μ(a)e(t,a)da,r(0,c)=r0(c),V(0)=V0,
|
(6)
|
where
|
G(e(t,a),r(t,c),V(t))=(Λ−βS(t)I(t)∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc,).
|
Set Z=Y×R2, where Y=R×L1(R+,R), for any (αϕ)∈Y, we have ‖(αϕ)‖=|α|+‖ϕ‖L1(R+,R). Furthermore, we define
|
Z+=Y+×R2+,Z0=Y0×R2,Z0+=Z0⋂Z+,
|
where
|
Y+=R+×L′+(R+,R),Y0={0}×L′(R+,R).
|
We define A1:Dom(A1)⊂Y→Y, by
|
A1(0ϕ1)=(−ϕ1(0)−ϕ′1−(b+δe+μ(a)+σ(a))ϕ1)
|
with Dom(A1)={0}×W1,1(R+,R). If λ is a complex number with Reλ>−(b+δe), then λ∈ρ(A1) which is the resolvent set of A1. Moreover, if λ∈ρ(A1) and
then we can get
|
ϕ1(a)=e−(λ+b+δe)aθ1+∫a0e−∫as(μ(l)+σ(l))dle−(λ+b+δe)(a−s)ψ1(s)ds.
|
Similarly, we define A2:Dom(A2)⊂Y→Y, by
|
A2(0ϕ2)=(−ϕ2(0)−ϕ′2−(b+k(c))ϕ2)
|
with Dom(A2)={0}×W1,1(R+,R), we can obtain
|
ϕ1(a)=e−(λ+b)cθ2+∫c0e−∫cs(k(l))dle−(λ+b)(c−s)ψ2(s)ds.
|
Thus (6) can be rewritten as
|
{ddt(0e(t,⋅))=A1(0e(t,⋅))+F1((0e(t,⋅)),(0r(t,⋅)),V(t)),ddt(0r(t,⋅))=A2(0r(t,⋅))+F2((0e(t,⋅)),(0r(t,⋅)),V(t)),dV(t)dt=−CV(t)+F3((0e(t,⋅)),(0r(t,⋅)),V(t)),e(0,a)=e0(a),r(0,c)=r0(c),V(0)=V0,
|
(7)
|
where
|
F1((0e(t,⋅)),(0r(t,⋅)),V(t))=(βS(t)I(t)+r2I(t)0),F2((0e(t,⋅)),(0r(t,⋅)),V(t))=(r1I(t)+∫∞0μ(a)e(t,a)da0),F3((0e(t,⋅)),(0r(t,⋅)),V(t))=(Λ−βS(t)I(t)∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc).
|
Let L:D(L)⊂X→X be the linear operator defined by
|
L(u(t))=(A1(0e(t,⋅)),A2(0r(t,⋅)),−CV(t)),
|
where D(L)=P×R2 with P={0}×W1,1(R+,R)×{0}×W1,1(R+,R). It follows that X0=¯D(L) and X0+=¯D(L)⋂X+. So ¯D(L)=X0 is not dense in X. We consider the nonlinear map F:¯D(L)→X defined by
|
F(u(t))=(F1(u(t))F2(u(t))F3(u(t))).
|
Therefore (7) can be rewritten as an abstract Cauchy problem
|
{du(t)dt=L(u(t))+F(u(t)),u(0)=((0e0(⋅)),(0r0(⋅)),V0).
|
(8)
|
By using the results in Magal [19] and Chen et al. [3], there exists a uniquely determined semiflow {U(t)}t≥0 on X0+ such that, for each
u=((0e(t,⋅)),(0r(t,⋅)),V(0)), there exists a unique continuous map U∈C(R+,X0+), which is an integrated solution of the Cauchy problem (8), that is, for all t≥0, ∫t0U(s)uds∈D(L) and U(t)u=u+L∫t0U(s)uds+∫t0F(U(s)u)ds. And Ω is the positively invariant absorbing set under the semi-flow U can be verified, that is, U(t)Ω⊆Ω and for each x∈X0+, d(U(t),Ω):=infy∈Ω∥U(t)x−y∥→0, as t→∞ which means that the semi-flow {U(t)}t≥0 is bound dissipative on X0+. A semi-flow U(t,x0):R+×X⟶X is called asymptotically smooth if each forward invariant bounded closed set is attracted by a nonempty compact set [8], [22]. In order to obtain global properties of the dynamics of the semi-flow U(t), it is important to prove the asymptotically smooth of semi-flow U(t). First we give the following useful lemma.
Lemma 2.1. ([1]) Let D⊆R. For j=1,2, suppose fj:D→R is a bounded Lipschitz continuous function with bound Kj and Lipschitz coefficient Mj. Then the product function f1f2 is Lipschitz with coefficient K1M2+K2M1.
Lemma 2.2. ([1]) If the following two conditions hold, then the semi-flow U(t,x0)=ϕ(t,x0)+φ(t,x0):R+×X⟶X is asymptotically smooth in X:
(ⅰ) There exists a continuous function v:R+×R+⟶R+ such that limt→+∞v(t,h)=0 and ‖ϕ(t,x0)‖X≤v(t,h) if ‖x0‖X≤h;
(ⅱ) For t≥0,φ(t,x0) is completely continuous.
In order to prove Lemma 2.2, we first decompose U:R+×X⟶X into the following two operators ϕ(t,x0),φ(t,x0):R+×X⟶X, ϕ(t,x0)=(0,y2(t,⋅),0,y4(t,⋅)), φ(t,x0)=(S(t),˜y2(t,⋅),I(t),˜y4(t,⋅)), where
|
y2(t,a)={0,t>a≥0,e0(a−t)ρ1(a)ρ1(a−t),a≥t≥0,y4(t,c)={0,t>c≥0,r0(c−t)ρ2(c)ρ2(c−t),c≥t≥0.
|
(9)
|
|
˜y2(t,a)={e(t−a,0)ρ1(a),t>a≥0,0,a≥t≥0,˜y4(t,c)={r(t−c,0)ρ2(c),t>c≥0,0,c≥t≥0.
|
(10)
|
In order to verify condition (ⅰ) of Lemma 2.2, we need to prove the following proposition.
Proposition 2. For h>0, let v(t,h)=he−(b+2b0+δe)t. Then v(t,h)⟶0 as t⟶+∞ and ‖ϕ(t,x0)‖X≤v(t,h) if ‖x0‖X≤h.
Proof. It is obvious that v(t,h)⟶0 as t⟶+∞, with the help of (9) and (H3), we have
|
‖ϕ(t,x0)‖X=|0|+∫+∞0|y2(t,a)|da+|0|+∫+∞0|y4(t,c)|dc=∫+∞t|e0(a−t)ρ1(a)ρ1(a−t)|da+∫+∞t|r0(c−t)ρ2(c)ρ2(c−t)|dc=∫+∞0|e0(τ)e−∫τ+tτε(s)ds|dτ+∫+∞0|r0(τ)e−∫τ+tτη(s)ds)|dτ≤e−(b+2b0+δe)t(|0|+∫+∞0|e0(τ)|dτ+|0|+∫+∞0|r0(τ)|dτ)=e−(b+2b0+δe)t‖x0‖X,
|
by the known condition ‖x0‖X≤h,∀x0∈Ω, we have ‖ϕ(t,x0)‖X≤he−(b+2b0+δe)t≡v(t,h).
Lemma 2.3. ([1]) Let K⊂Lp(0,+∞) be closed and bounded where p≥1. Then K is compact if the following conditions hold
(ⅰ) limh→0∫+∞0|f(z+h)−f(z)|pdz=0uniformlyforf∈K,
(ⅱ) limh→+∞∫+∞h|f(z)|pdz=0uniformlyforf∈K.
Proposition 3. For t≥0,ϕ(t,x0) is completely continuous.
Proof. According to Proposition 1(ⅰ), S(t) and I(t) remain in the compact set [0,Λ/b]⊂[0,M], where M≥Λ/b. Thus, it needs only to show that ˜y2(t,a) and ˜y4(t,c) remain in a precompact subset of L1+(0,+∞), which is independent of x0∈Ω. It suffices to verify that (ⅰ) and (ⅱ) in Lemma 2.3 hold. Now, from Proposition 1(ⅱ) and (10) we have
|
˜y2(t,a)≤(βM2+r2M)e−(b+2b0+δe)a.
|
(11)
|
|
∫+∞0|˜y2(t,a+h)−˜y2(t,a)|da=∫t−h0|e(t−a−h,0)ρ1(a+h)−e(t−a,0)ρ1(a)|da+∫tt−h|0−e(t−a,0)ρ1(a)|da≤∫t−h0e(t−a−h,0)|ρ1(a+h)−ρ1(a)|da+∫t−h0ρ1(a)|e(t−a−h,0)−e(t−a,0)|da+∫tt−h|e(t−a,0)ρ1(a)|da.
|
(12)
|
Recall that ρ1(a)=e−∫a0(σ(s)+μ(s)+b+δe)ds≤e−(2b0+b+δe)a≤1, then ρ1(a) is a non-increasing function with respect to a, we have
|
∫t−h0|ρ1(a+h)−ρ1(a)|da=∫t−h0ρ1(a)da−∫thρ1(a)da=∫t−h0ρ1(a)da−∫t−hhρ1(a)da−∫tt−hρ1(a)da=∫h0ρ1(a)da−∫tt−hρ1(a)da≤h.
|
(13)
|
From Proposition 1 and (H1), we find that |dS(t)/dt| is bounded by MS=Λ+bM+βM2 and |dI(t)/dt| is bounded by MI=ˉσM+ˉkM+(b+δi+r1+r2)M. Therefore, S(⋅) and I(⋅) are Lipschitz on [0,+∞) with coefficients MS and MI. By Lemma 2.1, S(⋅)I(⋅) is Lipschitz on [0,+∞) with coefficient MSI=M(MS+MI). Thus
|
∫t−h0ρ1(a)|e(t−a−h,0)−e(t−a,0)|da
|
|
≤∫t−h0ρ1(a)(|βS(t−a−h)I(t−a−h)−βS(t−a)I(t−a)|+|r2I(t−a−h)−r2I(t−a)|)da≤∫t−h0(βMSI+r2MI)(−h)e−(b+2b0+δe)ada=(βMSI+r2MI)hb+2b0+δe(1−e−(b+2b0+δe)(t−h))≤(βMSI+r2MI)hb+2b0+δe.
|
(14)
|
From (12)-(14), we have
|
∫+∞0|˜y2(t,a+h)−˜y2(t,a)|da≤(βMSI+r2MIb+2b0+δe+2(βM2+r2M))h
|
which converges uniformly to 0 as h→0. The condition (i) in Lemma 2.3 is proved for ˜y2(t,a).
From (11) we have
|
limh→+∞∫+∞h|˜y2(t,a)|da≤limh→+∞∫+∞h(βM2+r2M))e−(b+2b0+δe)ada=limh→+∞βM2+r2Mb+2b0+δee−(b+2b0+δe)h=0
|
which meet the condition (ii) in Lemma 2.3. Similarly, y4(t,c) also satisfies the conditions of Lemma 2.3.
Theorem 2.4. The semi-flow {U(t)}t≥0 generated by system (1) is asymptotically smooth, and has a global attractor A contained in X, which attracts the bounded sets of X.
3. Existence of the equilibria
Now we consider the existence of equilibria of system (1). The steady state (S∗,e∗(⋅),I∗,r∗(⋅)) of system (1) satisfies the equalities
|
{0=Λ−bS∗−βS∗I∗,ddae∗(a)=−ε(a)e∗(a),0=−(r1+r2+b+δi)I∗+∫∞0σ(a)e∗(a)da+∫∞0k(c)r∗(c)dc,ddcr∗(c)=−η(c)r∗(c),
|
(15)
|
with boundary conditions
|
{e∗(0)=βS∗I∗+r2I∗,r∗(0)=r1I∗+∫∞0μ(a)e∗(a)da.
|
(16)
|
From the second equation of (15) and the first equation of (16), we obtain
|
e∗(a)=(βS∗I∗+r2I∗)e−∫a0ε(s)ds.
|
(17)
|
Similarly, by using the fourth equation of (15) and the second equation of (16), we get
|
r∗(c)=(r1I∗+∫+∞0μ(a)e∗(a)da)e−∫c0η(s)ds.
|
(18)
|
If I∗=0, then we have e∗(a)=0 and r∗(c)=0 respectively from (17) and (18). Furthermore, it is easy to know that S0=Λb from the first equation of (15). Thus, system (15) has a disease-free equilibrium E0, and
|
E0=(S0,0,0,0),whereS0=Λb.
|
In order to find any endemic equilibrium, we introduce the basic reproduction number R0, which is the average number of new infections generated by a single newly infectious individual during the full infectious period [7]. It is given by the following expression
|
R0=βS0(θ1+θ2θ3)r1+r2+b+δi−r1θ2−r2(θ1+θ2θ3).
|
Now, if I∗≠0, substituting (17) and (18) into the third equation of (15), we have
|
0=−(r1+r2+b+δi)I∗+∫+∞0σ(a)(βS∗I∗+r2I∗)e−∫a0ε(s)dsda+∫+∞0k(c)(r1I∗+∫+∞0μ(a)(βS∗I∗+r2I∗)e−∫a0ε(s)dsda)e−∫c0η(s)ds=−(r1+r2+b+δi)I∗+(βS∗I∗+r2I∗)(θ1+θ2θ3)+r1I∗θ2.
|
(19)
|
Thus, combining the first equation of (15) and the equation (19), we get
|
S∗=ΛbR0,I∗=bβ(R0−1).
|
(20)
|
If R0>1, we get e∗(a)>0 and r∗(c)>0 from (17) and (18). Therefore, system (15) has a unique positive endemic equilibrium E∗, and
where
|
S∗=ΛbR0,e∗(a)=(βS∗I∗+r2I∗)ρ1(a),I∗=bβ(R0−1),r∗(c)=((βS∗I∗+r2I∗)θ3+r1I∗)ρ2(c).
|
4. Local asymptotic stability of the equilibria
In this section, sufficient conditions for the local asymptotic stability of the equilibria will be derived.
Theorem 4.1. The disease-free equilibrium E0 is locally asymptotically stable in the positive variant set Ω if R0≤1 and unstable if R0>1.
Proof. First, we introduce the change of variables as follows
|
x1(t)=S(t)−S0,x2(t,a)=e(t,a),x3(t)=I(t),x4(t,c)=r(t,c).
|
Linearizing the system (1) about disease-free equilibrium E0, we obtain the following system
|
{dx1(t)dt=−bx1(t)−βΛbx3(t),(∂∂t+∂∂a)x2(t,a)=−(b+δe+μ(a)+σ(a))x2(t,a),dx3(t)dt=−(r1+r2+b+δi)x3(t)+∫+∞0σ(a)x2(t,a)da+∫+∞0k(c)x4(t,c)dc,(∂∂t+∂∂c)x4(t,c)=−(k(c)+b)x4(t,c),x2(t,0)=(βΛb+r2)x3(t),x4(t,0)=r1x3(t)+∫+∞0μ(a)x2(t,a)da.
|
(21)
|
Set
|
x1(t)=x01eλt,x2(t,a)=x02(a)eλt,x3(t)=x03eλt,x4(t,c)=x04(c)eλt,
|
(22)
|
where x01,x02(a),x03,x04(c) will be determined. Substituting (22) into (21), we get
|
{λx02(a)+dx02(a)da=−(b+δe+μ(a)+σ(a))x02(a),x02(0)=(βΛb+r2)x03,
|
(24)
|
|
λx03=−(r1+r2+b+δi)x03+∫+∞0σ(a)x02(a)da+∫+∞0k(c)x04(c)dc,
|
(25)
|
|
{λx04(c)+dx04(c)dc=−(k(c)+b)x04(c),x04(0)=r1x03+∫+∞0μ(a)x02(a)da.
|
(26)
|
Integrating the first equation of (24) from 0 to a yields
|
x02(a)=(βΛb+r2)x03e−(λ+b+δe)a−∫a0(σ(s)+μ(s))ds.
|
(27)
|
Similarly, we have from (26) that
|
x04(c)=(r1x03+∫+∞0μ(a)x02(a)da)e−(λ+b)c−∫c0k(s)ds.
|
(28)
|
Substituting (27) and (28) into (25) and solving (25) gives
|
λ=−(r1+r2+b+δi)+∫+∞0k(c)r1e−(λ+b)c−∫c0k(s)dsdc+∫+∞0σ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s)dsda+∫+∞0k(c)∫+∞0μ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda⋅e−(λ+b)c−∫c0k(s)dsdc
|
(29)
|
which is the characteristic equation. Let
|
F(λ)=∫+∞0k(c)∫+∞0μ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda⋅e−(λ+b)c−∫c0k(s)dsdc−λ−(r1+r2+b+δi)+∫+∞0σ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s)dsda+∫+∞0k(c)r1e−(λ+b)c−∫c0k(s)dsdc.
|
Obviously, F(λ) is a continuously differential function and satisfies
|
F′(λ)=−(βΛb+r2)∫+∞0aσ(a)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda−a∫+∞0k(c)e−(λ+b)c−∫c0k(s)dsdc⋅∫+∞0μ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda−c∫+∞0k(c)e−(λ+b)c−∫c0k(s)dsdc⋅∫+∞0μ(a)(βΛb+r2)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda−r1∫+∞0ck(c)e−(λ+b)c−∫c0k(s)dsdc−1<0,
|
and
|
limλ→+∞F(λ)=−∞,limλ→−∞F(λ)=+∞.
|
Thus, we know (29) has a unique real root λ∗. Obviously,
|
F(0)=[(r1+r2+b+δi)−r1θ2−r2(θ1+θ2θ3)](R0−1),
|
we have λ∗<0,ifR0<1, and λ∗>0,ifR0>1. Let λ=x+yi be an arbitrary complex root to (29), then
which means that λ∗>x. Thus, all the roots of (29) have negative real part if and only if R0≤1 and have at least one eigenvalue with positive real part if R0>1. Therefore we have that the disease-free equilibrium E0 is locally asymptotically stable if R0≤1 and unstable if R0>1.
Theorem 4.2. The unique endemic equilibrium E∗ is locally asymptotically stable if R0>1.
Proof. First, we introduce the perturbation variables as follows
|
y1(t)=S(t)−S∗,y2(t,a)=e(t,a)−e∗(a),y3(t)=I(t)−I∗,y4(t,c)=r(t,c)−r∗(c).
|
Linearizing system (1) at the endemic equilibrium E∗ yields the following system
|
{dy1(t)dt=−by1(t)−βI∗y1(t)−βS∗y3(t),(∂∂t+∂∂a)y2(t,a)=−(b+δe+μ(a)+σ(a))y2(t,a),dy3(t)dt=−(r1+r2+b+δi)y3(t)+∫+∞0σ(a)y2(t,a)da+∫+∞0k(c)y4(t,c)dc,(∂∂t+∂∂c)y4(t,c)=−(k(c)+b)y4(t,c),y2(t,0)=βy1(t)I∗+βS∗y3(t)+r2y3(t),y4(t,0)=r1y3(t)+∫+∞0μ(a)y2(t,a)da.
|
(30)
|
Set
|
y1(t)=y01eλt,y2(t,a)=y02(a)eλt,y3(t)=y03eλt,y4(t,c)=y04(c)eλt,
|
(31)
|
Substituting (31) into (30) gives
|
λy01=−by01−βI∗y01−βS∗y03,
|
(32)
|
|
{dy02(a)da=−(λ+b+δe+μ(a)+σ(a))y02(a),y02(0)=βI∗y01+βS∗y03+r2y03,
|
(33)
|
|
λy03=−(r1+r2+b+δi)y03+∫+∞0σ(a)y02(a)da+∫+∞0k(c)y04(c)dc,
|
(34)
|
|
{dy04(c)dc=−(λ+k(c)+b)y04(c),y04(0)=r1y03+∫+∞0μ(a)y02(a)da.
|
(35)
|
Integrating the first equation of (33) and (35) from 0 to a and from 0 to c respectively, together with the boundary conditions, yields
|
y02(a)=(βI∗y01+βS∗y03+r2y03)e−(λ+b+δe)a−∫a0(σ(s)+μ(a))ds,y04(c)=(r1y03+∫+∞0μ(a)y02(a)da)e−(λ+b)c−∫c0k(s)ds.
|
(36)
|
substituting the above two equations into (34) and solving (34) we get
|
λy03=(βI∗y01+βS∗y03+r2y03)(K1(λ)+K2(λ)K3(λ))+r1y03K2(λ)−(r1+r2+b+δi)y03,
|
(37)
|
where
|
K1(λ)=∫+∞0σ(a)e−(λ+b+δe)a−∫a0(σ(s)+μ(s))dsda,K2(λ)=∫+∞0k(c)e−(λ+b)c−∫c0k(s)dsdc,K3(λ)=∫+∞0μ(a)e−(λ+b+δe)a−∫a0(σ(s)+μ(a))dsda,
|
By combining (37) and (32) we obtain the characteristic equation
|
det(λ+b+βI∗βS∗βI∗(K1(λ)+K2(λ)K3(λ))M)=0.
|
where M=(βS∗+r2)(K1(λ)+K2(λ)K3(λ))+r1K2(λ)−(λ+r1+r2+b+δi), that is
|
M=β2S∗I∗λ+b+βI∗(K1(λ)+K2(λ)K3(λ)).
|
(38)
|
It follows from (20) that (38) can also be rewritten as
|
(βS0R0+r2)(K1(λ)+K2(λ)K3(λ))+r1K2(λ)=βbS0(R0−1)(λ+bR0)R0(K1(λ)+K2(λ)K3(λ))+λ+r1+r2+b+δi.
|
(39)
|
Note that K′i(λ)<0,i=1,2,3. Thus, Ki(λ),i=1,2,3 is decreasing. Further, Ki(0)=θi,i=1,2,3. Assume that Reλ≥0, then K1(λ)≤θ1, K2(λ)≤θ2 and K3(λ)≤θ3 hold. Hence, the modulus of the left-hand side of (39) satisfies
|
(βS0R0+r2)∣(K1(λ)+K2(λ)K3(λ))∣+r1∣K2(λ)∣≤(βS0R0+r2)(θ1+θ2θ3)+r1θ2=r1+r2+b+δi
|
which, together with (39), leads to
|
∣βbS0(R0−1)(λ+bR0)R0(K1(λ)+K2(λ)K3(λ))+λ+r1+r2+b+δi∣≤r1+r2+b+δi.
|
(40)
|
Since R0>1, hence
|
βbS0(R0−1)(λ+bR0)R0(K1(λ)+K2(λ)K3(λ))+λ≤0.
|
(41)
|
that is Reλ≤0. There is a contradiction. This means that all roots of (39) have negative real parts. Consequently, the endemic equilibrium E∗ of (1) is locally asymptotically stable if R0>1.
5. Uniform persistence
In this section, we study the uniform persistence of system (1). Define M0={(S,I,0,0,e,r)T∈X0+:I+∫∞0e(a)da+∫∞0r(c)dc>0}, and ∂M0=X0+∖M0.
Theorem 5.1. M0 and ∂M0 are both positively invariant under the semiform {U(t)}t≥0 generated by system (1) on X0+. Moreover, the infection-free equilibrium E0=(S0,0,0,0,0L1,0L1) is globally asymptotically stable for the semiflow {U(t)}t≥0 restricted to ∂M0.
Proof. Let (S0,I0,0,0,e0,r0)∈M0,T(t)=I(t)+∫∞0e(t,a)da+∫∞0r(t,c)dc. It follows that
|
T′(t)≥−max{(r1+r2+b+δi),(b+δe+μmax)}T(t),
|
where μmax=esssupa∈(0,∞)μ(a). Then,
|
T(t)≥e−max{(r1+r2+b+δi),(b+δe+μmax)}tT(0).
|
This completes the fact that U(t)M0⊂M0. Now let (S0,I0,0,0,e0,r0)∈∂M0, using (4) and (5), we easily find that I(t)=0, for t≥0, and
|
∫∞0e(t,a)da=∫t0e(t−a,0)e−∫a0ε(s)dsda+∫∞te0(a−t)e−∫aa−tε(s)dsda=∫t0[βS(t−a)I(t−a)+r2I(t−a)]e−∫a0ε(s)dsda+∫∞te0(a−t)e−∫aa−tε(s)dsda≤e−εmint‖e0‖L1→0,t→∞.
|
Similarly,
|
∫∞0r(t,c)dc=∫t0r(t−c,0)e−∫c0η(s)dsdc+∫∞tr0(c−t)e−∫cc−tη(s)dsdc≤e−ηmint‖r0‖L1→0,t→∞.
|
Thus U(t)∂M0⊂∂M0. Let (S0,I0,0,0,e0,r0)∈∂M0, we obtain
|
{dIdt=−(r1+r2+b+δi)I(t)+∫∞0σ(a)e(t,a)da+∫∞0k(c)r(t,c)dc,(∂∂t+∂∂a)e(t,a)=−(b+δe+μ(a)+σ(a))e(t,a),e(t,0)=βSI+r2I,(∂∂t+∂∂c)r(t,c)=−(k(c)+b)r(t,c),r(t,0)=r1I(t)+∫∞0μe(t,a)da,I(0)=0,e(0,a)=e0(a),r(0,c)=r0(c).
|
Since S(t)≤S0 as t is large enough, we get I(t)≤˜I(t),e(t,a)≤˜e(t,a) and r(t,c)≤˜r(t,c), where
|
{d˜Idt=−(r1+r2+b+δi)˜I+∫∞0σ(a)˜e(t,a)da+∫∞0k(c)˜r(t,c)dc,(∂∂t+∂∂a)˜e(t,a)=−(b+δe+μ(a)+σ(a))˜e(t,a),˜e(t,0)=βS0˜I+r2˜I,(∂∂t+∂∂c)˜r(t,c)=−(k(c)+b)˜r(t,c),˜r(t,0)=r1˜I+∫∞0μ(a)˜e(t,a)da,˜I(0)=0,˜e(0,a)=e0(a),˜r(0,c)=r0(c).
|
(42)
|
By the formulations (4), (5), we have
|
˜e(t,a)={˜e(t−a,0)e−∫a0ε(s)ds,t>a≥0,e0(a−t)e−∫aa−tε(s)ds,a≥t≥0.
|
(43)
|
|
˜r(t,c)={˜r(t−c,0)e−∫c0η(s)ds,t>c≥0,r0(c−t)e−∫cc−tη(s)ds,c≥t≥0.
|
(44)
|
Substituting (43) and (44) into the first equation of (42), with the help of the third and the fifth equations of (42), we obtain
|
{d˜I(t)dt=(H1+H2+H3+H4)˜I(t)+Fe(t)+Fr(t)+Fer(t),˜I(0)=0,
|
(45)
|
where
|
H1=−(r1+r2+b+δi),H2=∫t0σ(a)(βS0+r2)e−∫a0ε(s)dsda,H3=∫t0k(c)r1e−∫c0η(s)dsdc,H4=∫t0k(c)∫t0μ(a)(βS0+r2)e−∫a0ε(s)dsdae−∫c0η(s)dsdc,Fe(t)=∫∞tσ(a)e0(a−t)e−∫aa−tε(s)dsda,Fr(t)=∫∞tk(c)r0(c−t)e−∫cc−tη(s)dsdc,Fer(t)=∫t0k(c)∫∞tμ(a)e0(a−t)e−∫aa−tε(s)dsdae−∫c0η(s)dsdc.
|
It's simple to know that, for each t→∞,
|
Fe(t)≤e−εmint∫∞tσ(a)e0(a−t)da=0,Fr(t)≤e−ηmint∫∞tk(c)r0(c−t)dc=0,Fer(t)≤∫t0k(c)e−εmint∫∞tμ(a)e0(a−t)dae−∫c0η(s)dsdc=0.
|
Then, we know that equation (45) has a unique solution ˜I(t)=0 and we obtain ˜e(t,0)=0, ˜r(t,0)=0 from the third and fifth equations of (42). If 0≤a<t, according to (43), we have ˜e(t,a)=0. Similarly, If 0≤c<t, according to (44), we have ˜r(t,c)=0. If a≥t,∥˜e(t,a)∥L1≤e−εmint∥e0∥L1, if c≥t,∥˜r(t,c)∥L1≤e−ηmint∥r0∥L1, which yields that ˜e(t,a)→0 as t→∞, and ˜r(t,c)→0 as t→∞. By using I(t)≤˜I(t),e(t,a)≤˜e(t,a) and r(t,c)≤˜r(t,c), we have I(t)→0,e(t,a)→0 and r(t,c)→0.
Theorem 5.2. Assume R0>1, the semiflow {U(t)}t≥0 generated by system (1) is uniformly persistent with respect to the pair (∂M0,M0), that is there exists ε>0, such that for each y∈M0,
|
limt→+∞infd(U(t)y,∂M0)≥ε.
|
Furthermore, there exists a compact subset A0⊂M0 which is a global attractor for {U(t)}t≥0 in M0.
Proof. Since the infection-free equilibrium E0=(S0,0,0,0,0L1,0L1) is globally asymptotically stable in ∂M0, applying Theorem 4.2 in Hale and Waltman [10], we only need to investigate the behavior of the solutions starting in M0 in some neighborhood of E0. Then, we will show that Ws({E0})⋂M0=∅, where Ws({E0})={y∈X0+:limt→+∞U(t)y=E0}. Assume there exists y∈Ws({E0})⋂M0, it follows that there exists t0>0 such that I(t0)+∫∞0e(t0,a)da+∫∞0r(t0,c)dc>0. Using the same argument in the proof of Lemma 3.6(i) in Demasse and Ducrot [6], we have that I(t)>0 for t≥0, and e(t,a)>0 for (t,a)∈[0,∞)×[0,∞), r(t,c)>0 for(t,c)∈[0,∞)×[0,∞). By means of the method of Brauer et al. [2], we define the following functions
|
A(a)=∫∞a(σ(θ)+B(0)μ(θ))e−∫θaε(s)dsdθ,B(c)=∫∞ck(θ)e−∫θcη(s)dsdθ.
|
(46)
|
For, ∀a,c>0,A(a),B(c)≥0, and A(0)=θ1+θ2θ3,B(0)=θ2. Furthermore, for ∀a≥0,c≥0,
|
A′(a)=−σ(a)+ε(a)A(a)−θ2μ(a),B′(c)=−k(c)+η(c)B(c).
|
(47)
|
Consider the function
|
Φ(t)=I(t)+∫∞0A(a)e(t,a)da+∫∞0B(c)r(t,c)dc,
|
which satisfies
|
dΦ(t)dt=βI(θ1+θ2θ3)(S−S0R0).
|
Since y∈Ws({E0}), we have S(t)→S0,I(t)→0, as t→∞. When R0>1, we know that the function Φ(t) is not decreasing for t large enough. Thus there exists t0>0 such that Φ(t)≥Φ(t0) for all t≥t0. Since Φ(t0)>0, this prevents that the function (I(t),e(t,a),r(t,c)) converges to (0,0L1,0L1) as t→∞. A contradiction with S(t)→S0.
6. Global asymptotic stability of the endemic equilibrium
Let
denote g′(x)=1−1x. Thus, g:R+→R+ is concave up. Also, the function g has only one extremum which is a global minimum at 1, satisfying g(1)=0 and ∀x,y∈R,g(xy)≥g(x)+g(y).
Theorem 6.1. The unique endemic equilibrium E∗ is globally asymptotically stable if R0>1.
Proof. Constructing the Lyapunov functional as follows
where
|
Ws=(θ1+θ2θ3)S∗g(SS∗),Wi=I∗g(II∗),We=∫+∞0A(a)e∗(a)g(e(t,a)e∗(a))da,Wr=∫+∞0B(c)r∗(c)g(r(t,c)r∗(c))dc.
|
Since Λ=bS∗+βS∗I∗, then the derivative of Ws along with the solutions of (1) is
|
dWsdt=(θ1+θ2θ3)bS∗(2−SS∗−S∗S)+(θ1+θ2θ3)βS∗I∗(1−SIS∗I∗−S∗S+II∗).
|
Calculating the derivative of We along with the solutions of system (1) yields
|
dWedt=∫+∞0A(a)e∗(a)∂∂tg(e(t,a)e∗(a))da=∫+∞0A(a)e∗(a)∂∂t(e(t,a)e∗(a)−1−lne(t,a)e∗(a))da=∫+∞0A(a)e∗(a)(1e∗(a)−1e(t,a))∂∂te(t,a)da=∫+∞0A(a)e∗(a)(1e∗(a)−1e(t,a))(−∂∂ae(t,a)−ε(a)e(t,a))da=−∫+∞0A(a)e∗(a)(e(t,a)e∗(a)−1)(ea(t,a)e(t,a)+ε(a))da.
|
Note that
|
∂∂ag(e(t,a)e∗(a))=ea(t,a)+e(t,a)ε(a)e∗(a)−ea(t,a)e(t,a)+e∗(a)(−ε(a))e∗(a)=(e(t,a)e∗(a)−1)(ea(t,a)e(t,a)+ε(a)).
|
And
|
dA(a)da=A(a)ε(a)−σ(a)−μ(a)B(0),de∗(a)da=−ε(a)e∗(a).
|
Hence, using integration by parts, we have
|
dWedt=−∫+∞0A(a)e∗(a)∂∂ag(e(t,a)e∗(a))da=−A(a)e∗(a)g(e(t,a)e∗(a))∣+∞0+∫+∞0(ddaA(a))e∗(a)g(e(t,a)e∗(a))da
|
|
+∫+∞0A(a)(ddae∗(a))g(e(t,a)e∗(a))da=−A(a)e∗(a)g(e(t,a)e∗(a))∣+∞+A(0)e∗(0)g(e(t,0)e∗(0))−∫+∞0e∗(a)(σ(a)+μ(a)B(0))g(e(t,a)e∗(a))da.
|
Note A(0)=θ1+θ2θ3,B(0)=θ2,e∗(0)=βS∗I∗+r2I∗,e(t,0)=βS(t)I(t)+r2I(t), thus
|
dWedt=−A(a)e∗(a)g(e(t,a)e∗(a))∣+∞+(θ1+θ2θ3)(βS∗I∗+r2I∗)g(e(t,0)e∗(0))−∫+∞0e∗(a)(σ(a)+μ(a)θ2)g(e(t,a)e∗(a))da.
|
Further, it follows from (r1+r2+b+δi)I∗=∫+∞0σ(a)e∗(a)da+∫+∞0k(c)r∗(c)dc, that the derivative of Wi along with the solutions of system (1) gives
|
dWidt=I∗(ItI∗−ItI)=I∗(1I∗−1I)[−(r1+r2+b+δi)I+∫+∞0σ(a)e(t,a)da+∫+∞0k(c)r(t,c)dc]=∫+∞0σ(a)e∗(a)(1−II∗−I∗e(t,a)Ie∗(a)+e(t,a)e∗(a))da+∫+∞0k(c)r∗(c)(1−II∗−I∗r(t,c)Ir∗(c)+r(t,c)r∗(c))dc.
|
Similar to We, by using B(0)=θ2,r∗(0)=r1I∗+∫+∞0μ(a)e∗(a)da, and r(t,0)=r1I(t)+∫+∞0μ(a)e(t,a)da, the derivative of Wr along with the solutions of system (1) reads
|
dWrdt=∫+∞0B(c)r∗(c)∂∂tg(r(t,c)r∗(c))dc=∫+∞0B(c)r∗(c)∂∂t[r(t,c)r∗(c)−1−lnr(t,c)r∗(c)]dc=∫+∞0B(c)r∗(c)[(1r∗(c)−1r(t,c))∂∂tr(t,c)]dc=∫+∞0B(c)r∗(c)[(1r∗(c)−1r(t,c))(−∂∂cr(t,c)−η(c)r(t.c))]dc=−∫+∞0B(c)r∗(c)(r(t,c)r∗(c)−1)(rc(t,c)r(t,c)+η(c))dc.
|
Note
|
∂∂cg(r(t,c)r∗(c))=(r(t,c)r∗(c)−1)(rc(t,c)r(t,c)+η(c)),
|
and
|
dB(c)dc=B(c)η(c)−k(c),dr∗(c)dc=−η(c)r∗(c).
|
Hence, using integration by parts, we have
|
dWrdt=−∫+∞0B(c)r∗(c)∂∂cg(r(t,c)r∗(c))dc=−B(c)r∗(c)g(r(t,c)r∗(c))∣+∞+B(0)r∗(0)g(r(t,0)r∗(0))−∫+∞0r∗(c)k(c)g(r(t,c)r∗(c))dc=−B(c)r∗(c)g(r(t,c)r∗(c))∣+∞−∫+∞0r∗(c)k(c)g(r(t,c)r∗(c))dc+θ2(r1I∗+∫+∞0μ(a)e∗(a)da)g(r(t,0)r∗(0)).
|
Note
|
∫+∞0(σ(a)+μ(a)θ2)e∗(a)da=(θ1+θ2θ3)(βS∗I∗+r2I∗),∫+∞0k(c)r∗(c)dc=θ2r1I∗+θ2θ3(βS∗I∗+r2I∗).
|
We derive
|
dV∗dt=(θ1+θ2θ3)bS∗(2−SS∗−S∗S)−A(a)e∗(a)g(e(t,a)e∗(a))∣+∞−B(c)r∗(c)g(r(t,c)r∗(c))∣+∞+∫+∞0σ(a)e∗(a)dag(e(t,0)e∗(0))−∫+∞0μ(a)θ2e∗(a)(g(e(t,a)e∗(a))−g(e(t,0)e∗(0)))da+∫+∞0k(c)r∗(c)dcg(r(t,0)r∗(0))+H1+H2+H3
|
where
|
H1=(θ1+θ2θ3)βS∗I∗[−g(SIS∗I∗)−g(S∗S)+g(II∗)]≤(θ1+θ2θ3)(βS∗I∗+r2I∗)[−g(SIS∗I∗)−g(S∗S)+g(II∗)]=∫+∞0(σ(a)+μ(a)θ2)e∗(a)[−g(SIS∗I∗)−g(S∗S)+g(II∗)]da,H2=∫+∞0σ(a)e∗(a)(1−II∗−I∗e(t,a)Ie∗(a)+e(t,a)e∗(a)−e(t,a)e∗(a)+1+lne(t,a)e∗(a))da=−∫+∞0σ(a)e∗(a)(g(II∗)+g(I∗e(t,a)Ie∗(a))da≤−∫+∞0σ(a)e∗(a)(g(II∗)+g(e(t,a)e∗(a))da,
|
|
H3=∫+∞0k(c)r∗(c)(1−II∗−I∗r(t,c)Ir∗(c)+r(t,c)r∗(c)−r(t,c)r∗(c)+1+lnr(t,c)r∗(c))dc=−∫+∞0k(c)r∗(c)(g(II∗)+g(I∗r(t,c)Ir∗(c)))dc
|
|
≤−∫+∞0k(c)r∗(c)(g(II∗)+g(r(t,c)r∗(c)))dc.
|
Hence, dV∗/dt≤0 holds true. Furthermore, the strict equality holds only if S=S∗,I=I∗,e(t,a)=e∗(a),r(t,c)=r∗(c). Consequently, the endemic equilibrium E∗ of (1) is globally asymptotically stable if R0>1.
7. Numerical simulations
In the following, we provide some numerical simulations to illustrate the global stability of the disease-free equilibrium and the endemic equilibrium for system (1). We choose parameters Λ=3;b=0.065;n=0.02;α1=0.01;α2=0.03;r1=0.1;r2=0.2; and
|
σ(a)={0.3a≥τ0τ≥a≥0,k(c)={0.1c≥τ0τ≥c≥0,μ(a)={0.25a≥τ0τ≥a≥0.
|
Under the initial values
|
S(0)=30,e(0,a)=6e−0.3a,I(0)=10,r(0,c)=6e−0.3c.
|
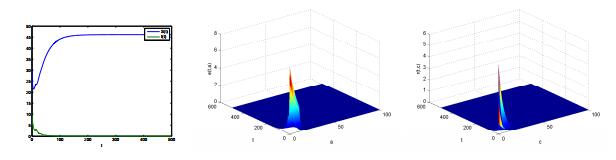
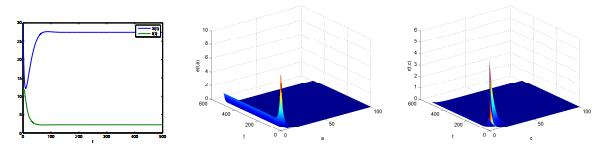
In Figure 2, we choose τ=12, then R0<1, while in Figure 3, we choose τ=1, then R0>1. The figures show the series of S(t) and I(t) which converge to their equilibrium values, and the age distribution and time series of e(t,a) and r(t,c), respectively.
8. Discussion
In this section, we briefly summarize our results. First, a PDE tuberculosis model (1) is proposed here to incorporate the latent-stage progression age of latent individuals and the relapse age of removed individuals. In addition, we assumed that infectious individuals might come into the latent class E due to incomplete treatment, and the relapse in the removed class. Under our assumptions, the expression of the basic reproduction number R0 is given, and we proved that if R0<1 the disease-free equilibrium E0 is globally asymptotically stable, while if R0>1 the unique endemic equilibrium E∗ is globally asymptotically stable. Figure 2 and Figure 3 further verify our results.
Acknowledgments
The author is very grateful to Professors Shigui Ruan and Xingan Zhang for their supervision and assistance. The author also thanks the editor and the anonymous reviewers for their constructive comments that help to improve an early version of this paper.









 DownLoad:
DownLoad: