1. Introduction
Tuberculosis, or TB, is an infectious bacterial disease caused by Mycobacterium tuberculosis, which most commonly affects the lungs. It is transmitted from person to person via droplets from the throat and lungs of people with the active respiratory disease. It is an ancient disease, and the battle against TB never stops. A lower proportion of recent transmissions is observed in the county with long-term DOTS implementation [32]. According to WHO, TB mortality has fallen to 47% since 1990, and that effective diagnosis and treatment of TB have saved about 43 million lives between 2000 and 2014 [29]. The DOTS coverage has achieved 100% since 2005 in China. The total of newly reported TB cases has been falling in China since then, but very slowly. It seems that we have made great progress, but we still face many difficult problems.
Drug-resistant TB has become a major public health problem worldwide. Globally, an estimated 3.3% of new TB cases and 20% of previously treated cases have MDR-TB, a level that has changed little in recent years. Only in 2014, an estimated 190 000 people have died of MDR-TB [29]. It has become a huge burden for many countries. Troubles never come singly, TB now ranks alongside HIV as a leading cause of death worldwide. According to the 2015 World Health Organization Global Report, it has killed 1.5 million people (1.1 million HIV-negative and 0.4 million HIV-positive). The challenges renew interest in the ancient disease. To make better control of the disease, the World Health Assembly has adopted WHO's End TB Strategy, aiming at reducing 90% of TB cases (compared to the 2015 baseline) and eliminating the TB epidemic by 2035 [30]. Therefore, it is urgently necessary to understand the present situation of the epidemic and provide suggestions that how to make a better control of TB infection.
TB is described as a slow disease because of its long and variable latency period [26]. Simple standard compartmental models with some modifications turn out to be quite useful in the study of the long-term dynamics of TB. The models have been used to analyze the spread and control of TB infection [1]. A lot of studies focus on the impact of various factors on the model fitting and the estimation of parameters. Some researchers have analyzed the dynamical models for transmission of TB with a general contact rate [5], drug-resistant strains [3], coinfection with HIV [23] and migration [34], developed TB model with fast and slow dynamics [26] and considered TB model with seasonality [15]. Juan Pablo Aparicio and Carlos Castillo-Chavez have compared the transmission dynamics of TB with three types of models using demographic and epidemiological data, and the effects of population growth, stochasticity, clustering of contacts, and age structure on disease dynamics [1]. On the other hand, there have been several studies about modeling TB transmission with different prevention and control strategies, such as isolation [4,9], treatment [7], vaccination [8] and a combination of control strategy [33].
Above all the studies, because of the 'slow' of TB, the basic reproduction number of TB is much smaller than the 'fast' diseases like measles, then the constant vaccination strategy does not need a very high inoculation rate and it seems that the disease is easy to control by rights. We have been taking a planned constant vaccination for newborns in China since 1982 and the DOTS coverage of 100% has been achieved since 2005. However through this study, we can clearly see that the basic reproduction number of TB in China is still greater than 1. Notice that the protection period of BCG is really short and that it only works for newborns, the adult pulmonary TB accounts for most of the TB disease burden (and transmission) worldwide. In the end, the lack of effective vaccines is the most important reason why the disease has not been vanquished yet. Sixteen different TB vaccine candidates are currently in clinical trials [30], which may give new hope to the control of TB.
Even if the new vaccines are available, our current constant vaccination strategy cannot achieve the goal formulated by WHO within the stipulated time and we show it in Section 3. Then, in order to solve the problem, we introduce pulse vaccination for the control of TB. For the disease, the mixed vaccination strategy will give a rapid control, under the condition that the infection-free periodic solution is asymptotically stable.
This paper consists of five sections. We build a TB model with BCG vaccination compartment in Section 2 to investigate the dynamical behaviors under the current constant vaccination strategy, parameterize the model with reported data in China and derive the basic reproduction number. In Section 3, we integrate the pulse vaccination into the TB model to vaccinate the susceptible individuals periodically to overcome the shortage of the constant vaccination strategy, then analyze the stability of the infection-free periodic solution under the mixed vaccination strategy and provide the simulation results. A brief discussion is given in Section 4. Finally, in Section 5 we conclude the paper with a summary of the main results.
2. Current vaccination strategy
In order to explain the current situation of TB, we propose a concise but practical model to describe the dynamics of TB propagation with respect to time in population.
In this model the population is divided into five classes: BCG vaccination, susceptible, exposed (latent), infectious and recovered with the number in each class denoted by B,S,E,I and R respectively. Let N denote the total population size, i.e., N=B+S+E+I+R. The B class is considered to be the newborns who were vaccinated successfully, and during the vaccination protection period of BCG they will not get infected even if they contact with infectious individuals. The parameter pb(0<pb<1) indicates the fraction of the newborns vaccinated successfully and Λ is the recruitment rate. But the positive effect of BCG is very limited, the vaccinated successfully individuals still develop into susceptible at the rate k. The total population N in China is quite large, then the number of contacts made by an infective per unit time should be limited [5]. To make a better simulation results, the standard incidence βSI/N is applied in this paper. That is, susceptible individuals become infected through contact with infectious individuals and enter the exposed class at a rate of βSI/N. Once infected, the individuals develop into the exposed class E and the progress to the infectious class at a rate of ε. γ is the rate at which the infectious individuals leave the infectious class to become recovered. d is the natural death rate and σ represents the disease-induced death rate. Because the protection period of BCG is really short and the natural death of children under five years old in China is very low (less than 1.17%), we ignore the natural death rate of class B. Since 2005, the coverage of DOTS has reached 100% in China, the diagnosis and treatment have been improved a lot, and the overall recurrence rate of TB is less than 1% [27]. Synthesizing each kind of situation, we make appropriate changes and reasonable neglects to typical SEIR model, the dynamic system of differential equations is given as:
|
{dBdt=Λpb−kB,dSdt=kB+(1−pb)Λ−βSIN−dS,dEdt=βSIN−εE−dE,dIdt=εE−(d+σ)I−γI,dRdt=γI−dR.
|
(1)
|
The infection-free equilibrium of system (1), which is:
The basic reproduction number, denoted as R0, is 'the expected number of secondary cases produced, in a completely susceptible population, by a typical infective individual' [11]. We can obtain the basic reproduction number R0 by using the next generation matrix in [12]
|
R0=ρ(FV−1)=βkε(dpb+k)(ε+d)(d+σ+γ),
|
(3)
|
where ρ denotes the spectral radius and the matrices F and V are given by
|
F=[0βkdpb+k00],V=[ε+d0−εd+σ+γ].
|
Note that each term of the aforementioned expression for R0 has clear epidemiological interpretation. k/(dpb+k) is the fraction of susceptible population among the total population. ε/(ε+d) is the fraction of exposed population becoming infected among those exiting the E class. 1/(d+σ+γ) is the mean duration of exiting the I class.
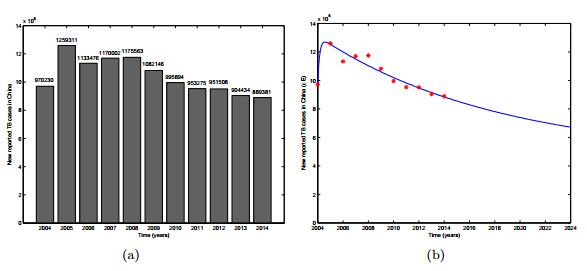
In order to estimate the basic reproduction number R0, we use the data of annual reported TB case numbers which have been released by the National Data [18] of China to do data fitting. The parameters are estimated with the reported data from 2004 to 2014 by LSM (least square method). This consists of minimizing the residual sum of squares (LS):
where Yi,(i=1,2,...,n) is the reported data and Θ are the parameters to be estimated. For given Θ, f(ti,Θ) is the solution that corresponds to εE(t). The birth rate b is 0.0123 in [19] and the total population N of China is about 1.30×109, so the recruitment rate is Λ=1.6×107 per year [24]. By fitting system (1) to the annual reported TB case numbers (shown in Figure 1(a)), we obtain estimates for the transmission rate β and the recovery rate γ, which are listed in Table 1.
Table 1. Parameters and initial data.
| Parm & Init D. |
Description |
Value |
Source |
| Λ | Recruitment rate | 1.6×107 year−1 | see text |
| d | Natural death rate | 0.0139 year−1 | [19] |
| b | Natural birth rate | 0.0123 year−1 | [19] |
| β | Transmission rate of infected population | 0.5905 | LS |
| σ | Disease-induced death rate | 0.06 year−1 | [15,35] |
| ε | Rate of progression to infectious stage from the exposed | 6 year−1 | [14] |
| k | Rate of waning immunity | 0.25 year−1 | [10,14,31] |
| γ | Recovery rate | 0.4055 year−1 | LS |
| pb | The fraction of BCG vaccinated successfully | 0.6 | [10,14,31] |
| B(0) | Initial number of BCG vaccinated successfully population | 3.84×107 | Calculated |
| S(0) | Initial number of susceptible population | 9.44×108 | LS |
| E(0) | Initial number of exposed population | 1.62×105 | [18] |
| I(0) | Initial number of infected population | 3.10×106 | [18,20] |
| R(0) | Initial number of recovered population | 3.14×108 | LS |
| Parm, Parameter; Init D., Initial Data; LS, least square. |
By using the estimated parameters we calculate the basic reproduction number R0=1.1892. This value R0 is consistent with previous studies [6,16,28]. It is strongly related to the promote of diagnosis and treatment.
Although the newly reported TB cases in China have decreased in recent years, the basic reproduction number is still greater than 1. In order to achieve our goal of controlling the disease by 2035, there is still a long way to go.
3. Mixed vaccination strategy
Sixteen different TB vaccine candidates are currently in clinical trials. The new, safe and effective vaccines that in all age groups and more efficacious for a longer period of time are on the way. The WHO says that the major stumbling blocks in TB vaccine development to date have been the lack of the reality that protection in preclinical challenge models does not reflect field efficacy data. According to the description of the new vaccines, we design a mixed vaccination strategy for new vaccines to reach the new End TB goal by 2035.
If the protection period of the new vaccine is long enough, let us see the constant vaccination strategy first. p is the fraction of the newborns vaccinated with new vaccine. The system of constant vaccination strategy will be written as [13]:
|
{dSdt=bN(1−p)−βSIN−dS,dEdt=βSIN−εE−dE,dIdt=εE−(d+σ)I−γI,dRdt=bNp+γI−dR.
|
(4)
|
We use the unitary transform method to simplify the form, let:
and s+e+i+w=1.
After that, the system is given as:
|
{dsdt=b(1−p)−bs−βsi+σsi,dedt=βsi−(ε+b)e+σei,didt=εe−(b+σ+γ)i+σi2,dwdt=bp+γi−bw+σwi.
|
(6)
|
The correctional reproduction number of system (6) is:
|
θ=(1−p)βε(ε+b)(b+σ+γ)=(1−p)θ0.
|
(7)
|
Theorem 3.1. For system (6), the infection-free equilibrium E0=(1−p,0,0,p) is globally asymptotically stable if θ≤1, and unstable if θ>1.
Where θ0 is the correctional reproduction number of system (6) in the absence of vaccine (i.e. p=0). Here θ0≈1.2333 in the parameters we have estimated. It can be concluded that: the BCG can indeed make contribution to the control of TB to some extent. Compared with other acute infections, the basic reproduction number of TB is relatively small. It seems that the condition θ≤1 is very easy to achieve. But do not forget that, our goal must be achieved in limited time.
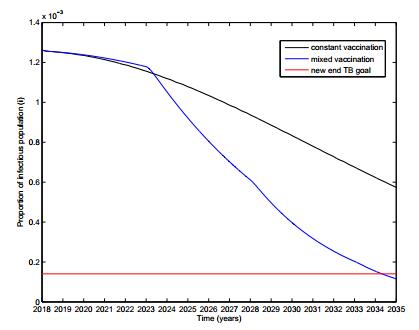
In Figure 2, the black solid line shows that even the fraction of vaccination p is as high as 95%, we still cannot decrease the infectious individuals as the goal in limited time. Because disease in latently infected adults and adolescents accounts for most of the disease burden and transmission, worldwide. The constant vaccination strategy is only for newborns. It is reasonable to eliminate the disease in theory, but it will need more time than we want. The longer time it needs, the problem like multi-drug TB and others will make the situation more complex. In other words, the constant vaccination is not enough to control the disease in limited time.
As the description of the new vaccine, it will come with all age groups. Considering the health system in China, most companies and government agencies take routine health examination periodically. So we take advantage of this policy to bring pulse vaccination strategy into our control [2,25] and design a mixed vaccination strategy to control the disease. In this way, we can achieve the goal in less time and make the best of current constant vaccination at the same time.
And the system for mixed vaccination strategy is as follows:
|
{dsdt=b(1−p)−bs−βsi+σsi,dedt=βsi−(ε+b)e+σei,didt=εe−(b+σ+γ)i+σi2,w=1−s−e−i.}t≠nT,s(t+)=(1−pc)s(t).t+=nT,n∈Z+.
|
(8)
|
The initial value is (s(0),e(0),i(0))∈Ω={(s,e,i)∈[0,1]3|0≤s+e+i≤1}. There exists an infection-free periodic solution (˜s(t),0,0) in Ω.
Under the conditions above, we have
|
dsdt=b(1−p)−bs,t0=(n−1)T≤t<nT.
|
(9)
|
The solution of (9) is:
|
s(t)=[s(t0)−(1−p)]e−b(t−t0)+(1−p),t0=(n−1)T≤t<nT.
|
(10)
|
For a clearer expression, we define M(t)=[s(t0)−(1−p)]e−b(t−t0)+(1−p),t0=(n−1)T≤t<nT. When t=nT,s(t)=(1−pc)M(t).
That is,
|
s(t)={M(t),(n−1)T≤t<nT,(1−pc)M(t),t=nT.
|
(11)
|
Now we can deduce the stroboscopic map F as:
|
s((n+1)T)=(1−pc){[s(nT)−(1−p)]e−bT+(1−p)}=F(s(nT)).
|
(12)
|
The fixed point of the map F is:
|
s∗=F(s∗)=(1−p)(1−pc)(ebT−1)ebT−1+pc.
|
(13)
|
The fixed point s∗ of the map F shows that there is a corresponding cycle of period T in s(t).
And
|
|dF(s(nT))ds|s(nT)=s∗=(1−pc)e−bT<1.
|
(14)
|
The fixed point s∗ is locally stable and it determines s(t) after each pulse, and hence the sequence s(nT) must converge to the fixed point s∗.
Therefore, by setting s(t0)=s∗ in (10), we obtain:
|
{˜s(t)=1−p−ebT(1−p)pcebT−1+pce−b(t−t0),˜e(t)=0,˜i(t)=0.
|
(15)
|
That is the complete expression for the infection-free periodic solution over the n−th time-interval. And also we know that:
|
˜s(t+T)=˜s(t),˜e(t+T)=˜e(t),˜i(t+T)=˜i(t).
|
Define the basic reproductive rate of system (8) as follows (see [17]):
|
R0(T)=βε(ε+b)(b+σ+γ)T∫T0˜s(τ)dτ.
|
(16)
|
3.1. Stability of the infection-free periodic solution
Add small perturbations s1,e1,i1 into the periodic solution, the relevant equations can be expanded in a Taylor series. After neglecting the higher order terms, the linearized equations are:
|
{ds1dt=−bs1−β˜si1+σ˜si1,de1dt=β˜si1−(ε+b)e1,di1dt=εe1−(b+σ+γ)i1,}t≠nT,s1(t+)=(1−pc)s1(t).t+=nT,n∈Z+.
|
(17)
|
Notice that, the second and third equations of (17) are linear ordinary differential with T periodic.
|
{de1dt=β˜si1−(ε+b)e1,di1dt=εe1−(b+σ+γ)i1.
|
(18)
|
According to Floquet theory, λ1 and λ2 are defined as 'Floquet multipliers' [21,22], if
the periodic solution of the system (8) will be locally stable.
The solution of (19) is:
|
1T∫T0˜s(τ)dτ<(ε+b)(b+σ+γ)εβ.
|
(20)
|
That is,
|
R0(T)=θ01T∫T0˜s(τ)dτ<1.
|
(21)
|
Based on the derivation above, Theorem 3.2 characterizes the disease dynamics on the mixed vaccination strategy:
Theorem 3.2. If R0(T)<1, then the infection-free periodic solution of system (8) is asymptotically stable.
In other words, the mean value of ˜s(t) averaged over a single pulse period must be less than 1/θ0 to keep the infection-free periodic solution stay stable. With substituting the exact expression of ˜s(t) into (21), the local stability of the cycle is ensured if
|
(1−p)(ebT−1)(bT−pc)+bT(1−p)pcbT(ebT−1+pc)<1θ0.
|
(22)
|
The maximum allowable period of the pulse, Tmax, can also be given. The critical period of the pulse occurs when there is equality in (22). To simplify the form and calculate Tmax, we expand the left-hand equation of (22) in a Taylor series and neglect the higher order terms and finally obtain:
|
Tmax≈pcθ0(1−p)b−12bθ0(1−p)pc−b.
|
(23)
|
When the pulse vaccination is applied periodically with T<Tmax, the infection-free periodic solution of system (8) is asymptotically stable. The mixed vaccination strategy leads to an infection-free population.
Under this mixed vaccination strategy di/dt<0 for all time, so that i(t) is a decreasing function of time. Although constant vaccination cannot help us achieve our goal in limited time, we do not have to totally repudiate it, because the problem can be solved after adding pulse vaccination.
3.2. Numerical simulations
To show the effect of mixed vaccination more intuitively and illustrate the theoretical results contained in previous section, we give some numerical simulations of system (8).
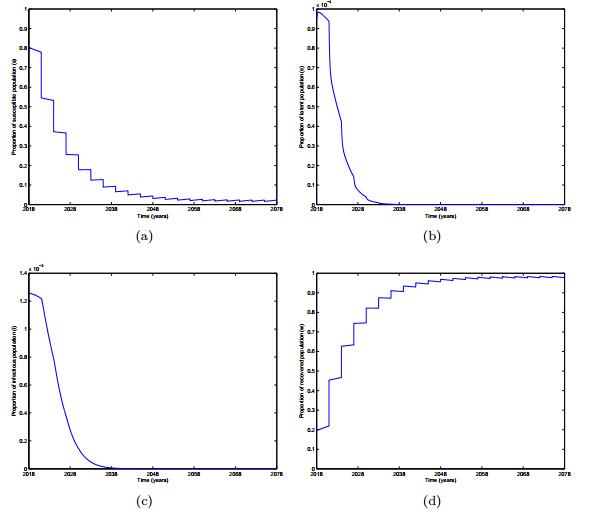
We show the dynamical behaviors of system (8) for a longer time in Figure 3. From Figure 3, we can clearly see the infection-free periodic solution asymptotically tends to zero and that under the mixed vaccination
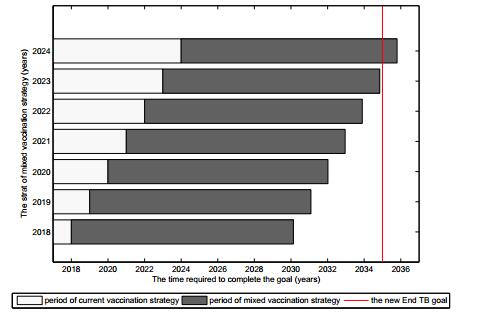
Because the new vaccines are still in clinical trials, the specific time when to start the mixed vaccination strategy is unknown. In Figure 4, we show the time that it takes to achieve the new End TB goal from different starting time. We vary the starting time of mixed vaccination strategy from 2018 to 2024, the duration is 12.13 years, 12.09 years, 12.02 years, 11.96 years, 11.90 years, 11.85 years, and 11.80 years respectively. Due to the effect of the universal coverage of DOTS in China, the newly reported TB cases in China have decreased in recent years. So the duration is in inverse proportion to the starting time, but there is little difference between each other. Notice that numerical simulations are theoretical and idealistic, it may take a few weeks for a robust immune response to develop after vaccination and even longer if, as some anticipation, a second dose is needed, therefore it is not proper that the later making the control strategy, the better it is.
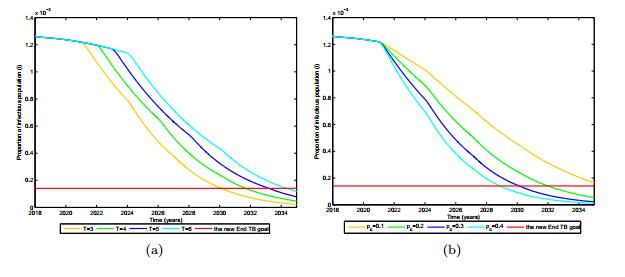
Furthermore, to explore the effect of the inter-pulse interval T and inoculation rate of pulse vaccination pc on the control of the disease, we vary the parameter T from 3 years to 6 years and pc from 10% to 40% respectively. Figure 5(a) shows how the control strategies depend on the various weights of T: as T increases, the duration of the mixed vaccination strategy increases. Figure 5(b) illustrates how the control strategies depend on the various weights of pc: as pc increases, the duration of the mixed vaccination strategy decreases.
The numerical simulations offer intuitive theoretical basis for establishing the final mixed vaccination strategy.
3.3. The comparison between constant vaccination strategy and mixed vaccination strategy
Assuming that the new vaccine will come into use in 2018 (it would be the earliest time for the new vaccine to come into service). In Figure 2, the black solid line shows the constant vaccination strategy with p=0.95, and we can clearly see that the new End TB goal is only about half-finished by the end of 2035. The blue solid line shows that we can achieve the goal in early 2034 under the mixed vaccination strategy, though the pulse vaccination is applied by T=5,pc=0.25 and the fraction of constant vaccination is p=0.7. The vaccination rate of constant vaccination strategy can be looser in the mixed vaccination strategy than the only constant vaccination strategy. So it is conducive to avoid the disadvantageous factors of vaccination for the high-risk infants.
On the other hand, if we just only take the constant vaccination strategy, it will need to maintain high population immunity and take nearly 30 years to achieve the goal set in 2015, and in the meantime, about 4.56×108 individuals will be vaccinated. Using the mixed vaccination strategy, we can reach the new End TB goal (the red line) by 2034 with some easy conditions, and the total number of vaccinated population is about 7.63×108. With the mixed vaccination strategy, the time of achieving the goal reduces by half in spite of increased vaccination level. Furthermore, the vaccinated level does not double.
4. Discussion
In this study, we have used epidemiological models to investigate the transmission dynamics of TB and control strategy. To make a better understand of the TB transmission nowadays, we first formulate the model with partial immunity and it is examined by the reported data in China [18]. With the universal coverage of DOTS, the basic reproduction number R0 is 1.1892 in our estimate, which is similar to other estimates in the literature [6,16,28]. Although enhancing the diagnosis and treatment level has already improved the control of TB, the disease still exists. Our ultimate goal is to make the disease die out. And always remember that 'prevention is better than cure'. Nowadays, we take the constant vaccination strategy, the main audiences are newborns and the protection of the BCG is very limited. The current constant vaccination strategy slows down the disease spreading to some extent, but cannot make the disease die out.
Considering the new vaccines with longer period of protection are on the way, we show numerical simulations of the traditional constant vaccination strategy for the new vaccines, but it cannot achieve the new End TB goal in limited time. In order to achieve the new End TB goal, we put forward a new vaccination strategy: combine constant vaccination with pulse vaccination. We have analyzed the stability of the infection-free periodic solution under mixed vaccination strategy. Although the proportion of constant vaccination p=0.7, we only make the proportion of pulse vaccination pc=0.25, and the periodic of pulse vaccination T is set at 5 years, the infection-free periodic solution will stay stable and we can achieve the goal by 2034. In the numerical simulations, we show pulse vaccination with T=3,p=0.8 and pc=0.3 for a longer time, the effect of mixed vaccination is obvious. The proportion of infectious individuals quickly falls down to a really low level.
Because the new vaccines are still in clinical trials, the specific time when to start the mixed vaccination strategy is unknown, the control strategies for several scenarios have been identified. The effect of T and pc are also shown in the paper. The mixed vaccination strategy follows the current constant vaccination strategy and the pulse vaccination can be implemented with the routine health examination according to the realities of China. Under the mixed vaccination strategy, we can control the disease in a quicker and easier way. Once the new vaccine comes into service, our study can provide theoretical support for making the optimal mixed vaccination strategy.
5. Conclusion
Taking constant vaccination strategy among newborns and improving diagnosis and treatment level will ultimately have a positive impact on the control of TB, but it is difficult to reach the national TB elimination target. More effective vaccines are on the way, and this study provides theoretical basis for making strategy of new vaccines. Using a mathematical model validated by Chinese TB data, this study suggests that a mixed vaccination strategy can make up for the shortage of constant vaccination strategy and give a quicker way to achieve the goal. Numerical simulations provide valuable results, and it will help to design the final mixed vaccination strategy once the new vaccine comes out.
Acknowledgments
The authors thank Professor Juxiu Liu from Jilin Tuberculosis Hospital for all her valuable comments on this study. We are also indebted to the help from Doctor Mingwang Shen. We thank the reviewers for their useful comments and suggestions. This research was supported by the National Natural Science Foundation of China (11171131).









 DownLoad:
DownLoad: