1. Introduction

In the early days of modern research on biological membranes, lipids were chiefly considered as a uniform group of amphipathic components essentially constituting a homogenous solvent phase for proteins ^[1,2]. Following the fluid mosaic model proposal by Singer and Nicolson in 1972 ^[1], a number of biochemical and physico-chemical studies suggested that the so-called solvent phase concept suffered from major caveats. Firstly, it was shown that key regulatory lipids such as sphingolipids are concentrated in discrete areas referred to as membrane microdomains ^[3]. Secondly, it was demonstrated that membrane proteins by themselves could either interact with or be excluded from such microdomains ^[4,5]. In 1997, Kai Simons and Elina Ikonen proposed a new concept, referred to as the lipid "raft" model, that took into account the lateral segregation of selected lipids in the outer leaflet of plasma membranes, suggesting that those lipids could be considered sorting platforms for membrane proteins ^[2]. Just over twenty years after the publication of this seminal article, the lipid raft concept is now well established and generally accepted by biologists, although certain controversies remain. Experimental data obtained with both model and natural membranes has led to several amendments of the concept ^[3,6]. In the original model, lipid rafts were envisioned as small ordered cholesterol-rich domains (liquid-ordered Lo phase) dispersed in a less ordered matrix (liquid-disordered Ld phase) with little cholesterol content ^[2,7]. However, more recent data has challenged this idea, suggesting that lipid raft domains might predominate and possibly cover as much as 75% of the plasma membrane ^[8]. According to the Pubmed bibliography database, the scientific literature on lipid rafts currently includes thousands of citations, including research articles and many state-of-the-art reviews ^[3,6,9,10]. The definition of lipid rafts that consensually emerged from a scientific meeting on the subject was summarily conveyed in a review by Pike "small (10–200 nm), heterogeneous, highly dynamic, sterol-and sphingolipid-enriched domains that compartmentalize cellular processes" ^[6,11]. Nevertheless, the distribution of cholesterol in the plasma membrane and especially its co-localization with sphingolipid-enriched domains is still a matter of debate ^[12,13].

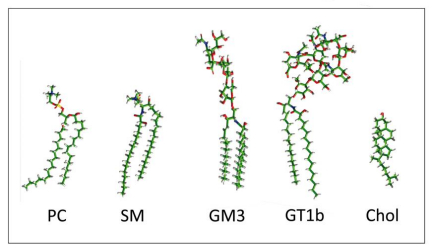
Experimental studies of the molecular organization of the plasma membrane are inherently difficult because the plasmalemma contains numerous lipids displaying distinct specific biochemical and physicochemical properties ^[14]. These lipids coexist in a coherent bilayer structure that serves as a functional matrix for membrane proteins. A sample of representative mammalian plasma membrane lipids is shown in Figure 1. Despite a high level of chemical diversity, one can classify the lipids of animal membranes into three main categories: (ⅰ) Glycerophospholipids [e.g. phosphatidylcholine (PC), phosphatidylethanolamine (PE) or phosphatidylserine (PS)]; (ⅱ) sphingolipids [sphingomyelin (SM), glycosphingolipids (GSL), including gangliosides); (ⅲ) cholesterol. The latter category is a singularity, since it is the only membrane lipid in eukaryotic membranes which does not display any biochemical diversity ^[15]. Other glycerol-derived lipid species occur in plants and algae.

Understanding the structural features accounting for the diverse functions fulfilled by membrane lipids is primordial to fathoming how the plasma membrane works. Here are some clues. On the one hand, the combination of saturated/unsaturated hydrocarbon chains in the apolar moiety of glycerophospholipids (e.g. phosphatidylcholine) allows fine adjustments of membrane fluidity by acting on only two parameters, i.e. chain length and number of double bonds ^[14]. The setting of an adequate level of fluidity in the lipid bilayer is often mandatory for optimal functioning of membrane-embedded receptor proteins ^[16]. Diversity in the polar moiety is achieved by the chemical group in the head region, as is the case with the three main types of glycerophospholipids mentioned above, but this modest variability is overshadowed by the much wider diversity provided by modulation of the sugar moiety in glycosphingolipids such as gangliosides, resulting in hundreds of distinct species performing key regulatory functions in cell-cell communication ^[17].

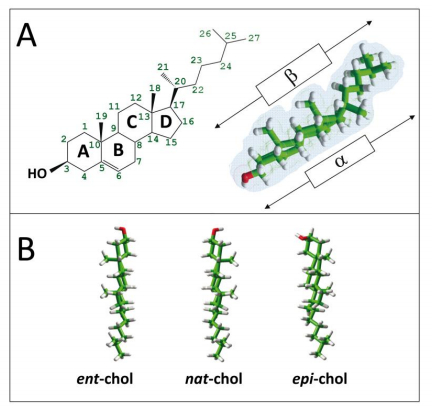
In face of this wide biochemical diversity, cholesterol, through its unique and unvarying structure, helps all other lipids to coexist within the same membrane ^[15]. The key features of cholesterol are summarized in Figure 2A. In marked contrast with the typical pair of hydrocarbon chains that penetrate deeply into the apolar phase of the membrane, cholesterol is built on a tetracycle core called sterane. The second cycle of sterane displays a constrained double bond between carbon atoms C5 and C6. Otherwise there are only four chemical groups bound to the sterane backbone: OH on C3, methyl on C10 and C13, iso-octyl on C17. There are eight chiral centers, which may theoretically give rise to 2⁸ (256) diastereoisomers. However, natural cholesterol corresponds to only one of these numerous stereoisomers, i.e. nat-cholesterol (Figure 2B). Its non-natural enantiomer (ent-cholesterol), which has identical physical properties but opposite three-dimensional configuration to cholesterol (Figure 2B), has been used as a synthetic tool for studying cholesterol function ^[18].

As shown in Figure 2A, the natural stereoisomer of cholesterol has an asymmetric structure with two distinct sides: One smooth (the α face), the other rough (the β face) ^[9]. This unique feature has led us to consider cholesterol as a bifacial lipid able to interact simultaneously with two distinct partners in the plasma membrane, most often a sphingolipid through the α face and a protein through the β face ^[9]. In addition, two cholesterol molecules may interact within the same membrane leaflet (lateral α-α dimer) or in tail-to-tail topology (one cholesterol in each leaflet) ^[15]. Now, if we combine the different possibilities of interaction of each single cholesterol molecule in the plasma membrane, it turns out that cholesterol may have a major impact on receptor 3D structure and function. A representative example of this regulation is given by G-protein coupled receptors (GPCRs).

---

2. How cholesterol controls the 3D structure and function of GPCRs

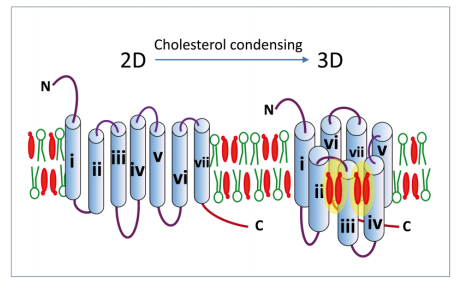
GPCRs share a common topology ^[19] that can be summarized as follows. Consistent with their signaling functions, the "sensor" N-terminal domain is extracellular, and the "transduction" C-terminal domain intracellular ^[20]. The polypeptide chain crosses back and forth between the two membrane halves seven times, delineating seven transmembrane (TM) domains (ⅰ–ⅶ) ^[21]. In classical 2D representations of a GPCR in its membrane environment ^[22], the receptor has a snake-like shape whose undulations form a succession of seven TM domains (Figure 3, left panel). Such 2D representations convey a misleading impression of the real structure of this type of receptor. In the actual 3D membrane-associated structure, all TM domains are clustered together ^[23,24], forming a large cylinder consisting of seven smaller cylindrical units, each corresponding to the seven TM domains (Figure 3, right panel). At first glance, the close proximity of these TM domains is not easy to explain for several reasons. Firstly, each TM domain is an α-helical segment, i.e. a local fold that is stabilized by a network of hydrogen bonds involving the carbonyl and NH groups of two peptide bonds separated by four amino acid residues (i + 4 increment). As a self-stabilized structure, the α-helix does not need additional stabilizing partners. In other words, there is no reason for a TM to interact with another TM unless the lateral chains of some of the amino acid residues in each TM have a strong chemical affinity, as is the case for instance with the glycine zipper motif ^[25]. Since most residues belong to the aliphatic group of amino acids, these interactions, if they exist, would likely be very weak and fundamentally controlled by London dispersion forces ^[26]. In this case, it would be difficult to understand why such aliphatic-aliphatic interactions are energetically more favorable than protein-lipid interactions ^[27], which in the apolar region of the membrane are also mediated by London forces. Alternatively, one could consider more energetic interactions driven by either hydrogen bonds or electrostatic forces between complementary polar residues. Although potentially interesting, this hypothesis is contradicted by the apolar nature of the TM domain which, except for very specific cases, ought to exclude such polar residues. Alternatively, it is possible to envisage cholesterol as a "glue" able to exert a condensing effect on the whole protein, as shown in Figure 3, right panel. In this case, cholesterol could be considered as a lipid chaperone helping the receptor acquire its functional 3D structure in the membrane environment. Such a mechanism has been revealed for instance by the structural characterization of a functional cholesterol-binding site between helices Ⅰ, Ⅱ, Ⅲ and Ⅳ of the human β2-adrenergic receptor ^[28]. Another example is given by the 5-HT1 A receptor, whose functional characteristics, including the delineation of the ligand-binding pocket, are controlled by cholesterol binding ^[29,30,31]. An intriguing aspect of GPCR activation is the formation of a receptor dimer which triggers the signal transduction cascade following ligand binding ^[32,33]. Here again, one could consider a direct TM-TM interaction aimed at controlling this process. However, cholesterol interacting with only one TM domain at the periphery of a receptor protein could perfectly well recruit two vicinal ligand-activated receptors and trigger their dimerization ^[15,28,34], a key step in the activation of a signal transduction cascade ^[32,35].

---

3. Cholesterol binding domains

During the last few years, a wealth of structural, physico-chemical and in silico approaches has greatly improved our knowledge of the molecular mechanisms controlling the binding of cholesterol to TM domains ^[36,37]. Two of them, linear motifs referred to as CRAC and CARC have been identified by simple algorithms applied to sequence data. 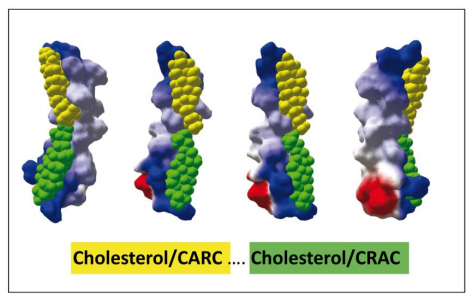CRAC ("Cholesterol Recognition/interaction Amino acid Consensus sequence") fulfills the simple consensus motif (L/V)-X1-5-(Y)-X1-5-(K, R) ^{[38,39,40,41,42]}. CARC is a reverse version of the CRAC algorithm, i.e. (K/R)-X1-5-(Y/F)-X1-5-(L, V) ^[15,36,43]. Both CRAC and CARC motifs have been found and characterized in TM domains of a broad range of receptor proteins ^{[28,29,43,44,45]}. A mirror code based on the presence of a couple of CARC and CRAC motifs within the same TM domain has also been described recently ^[45]. In this case, the TM domain interacts with two cholesterol molecules, one in each leaflet of the plasma membrane, in a typical tail-to-tail topology (Figure 4).

Besides these linear domains, three-dimensional pockets defined by two or three vicinal TM domains have been described ^[28,46,47]. Although such 3D domains are difficult to predict from sequence data, the biochemical basis underlying their mode of interaction with cholesterol is strikingly similar to that involved in the linear-type CRAC and CARC recognition. Three types of aromatic residues have been shown to play a critical role in cholesterol recognition and binding, precisely those defining the CRAC and CARC algorithms ^[36,42,45]. The first one is an aromatic residue, most often Phe or Tyr and more rarely Trp. The aromatic residue may occupy various positions in the motif, according to the variable number of residues separating the aromatic rings from the end of the motif. The totally apolar phenyl ring of Phe can be deeply buried in the apolar phase of the membrane, explaining the high prevalence of this residue in both CRAC and CARC motifs. In the case of Tyr, the OH group linked to the phenyl ring requires a polar partner which can be found near the polar-apolar interface of the membrane. Finally, Trp has two disadvantages that minimize its prevalence in cholesterol-binding motifs. Firstly, its side chain with two aromatic cycles occupies a large volume which may render it difficult to undergo the slight conformational adjustments required for an optimal interaction with cholesterol. Secondly, Trp displays a nitrogen atom in the first cycle, thereby conferring a slightly higher polarity which would affect its rotational mobility in the membrane and restrict its location near the polar-apolar interface. The main mechanism of cholesterol binding to an aromatic structure is the CH-Pi stacking interaction ^[48]. In most cases, the basic residue at the terminus of the motif faces the OH group of cholesterol. Given the particular stereochemistry of this chemical group, this interaction often has a marked impact on the orientation of cholesterol with respect to the TM domain. As a consequence, the TM domain may adjust its orientation in the bilayer through a typical induced-fit mechanism ^[49]. Finally, the terminal branched amino acid residue that completes the motif (Leu or Val) fits well with the methyl groups and/or the iso-octyl chain that constitute the spikes of the rough β-face of cholesterol ^[9]. Overall, these structural features explain why this triad of amino acid residues (basic/aromatic/branched) is found in 3D cholesterol-binding domain. Thus, even though it does not simply follow the linear disposition of the CRAC or CARC sequences, the key triad is nevertheless present in the 3D cholesterol-recognition motifs ^[28,50].

---

4. Stereoselectivity and functional impact of cholesterol-receptor interactions

The high specificity of cholesterol-TM domain interactions is inherent to the unique stereochemistry of natural cholesterol (nat-cholesterol). However, this lipid also participates in more general effects such as fluidity or curvature that affect local membrane properties. Correspondingly, it is not always easy to discriminate between specific cholesterol-protein interactions and regulation of receptors on the basis of the physical properties of the bilayer. Recently, the group led by Irena Levitan published an elegant series of experiments comparing the effects of cholesterol and its isomers on the function of the inwardly rectifying K⁺ channels (Kir) ion channel ^[46,51]. In these experiments, they used nat-cholesterol, its enantiomer ent-cholesterol and epi-cholesterol, which has a distinct orientation of the OH group. Two of them are mirror images (nat-and ent-cholesterol) so they would be expected to exert similar effects on membrane bilayer packing. From a structural point of view, both nat-and ent-cholesterol display a smooth and a rough face. In the case of epi-cholesterol (Figure 2B), the smooth face is interrupted by the orientation of the OH group ^[52]. Molecular models of cholesterol and its isomers are shown in Figure 2. From these studies, Levitan et al. concluded that the "structural requirements of ion channel cholesterol-binding sites are lax, allowing chiral isomers of cholesterol to bind to the same site in a non-stereospecific way" ^[50]. Nevertheless, nat-cholesterol induced a specific effect on the channel, whereas its isomers did not. Therefore, it is not the lack of binding of a cholesterol isomer that explains its lack of functional effect, but the way the sterol interacts with the channel. The 3D structure of these particular cholesterol-binding domains, basically a hydrophobic pocket for the Kir channel ^[46], is consistent with a non-stereoselective binding of sterols. It would be interesting to assess the binding of cholesterol isomers on linear cholesterol binding sites such as CARC. Indeed, docking studies suggest that the binding of cholesterol to a CARC domain is stereospecific, in particular with respect of the orientation of OH group ^[43]. Further studies will help to clarify the molecular mechanisms by which cholesterol affects ion channel functions. It is likely that sterol binding to specific sites could induce significant conformational rearrangements of the channel, resulting in an increase in channel opening probability, as shown for voltage-gated atrial Kir3 channels ^[53], or changes in other channel properties in the case of ligand-gated ion channels.

---

5. Reliability of CARC/CRAC algorithms

Though linear CARC and/or CRAC motifs are very frequently found in the amino acid sequence of membrane proteins ^[45], crystal structures of proteins in complex with cholesterol have revealed a more complex situation ^[54]. For instance, the typical "aromatic/basic/aliphatic" amino acid triad defining both CARC and CRAC motifs may be found in several vicinal TM domains instead of just one ^[28]. Although this complex topology might hinder the prediction of a functional cholesterol binding site from protein sequence databases, it confirms that cholesterol binding is determined by solid biochemical rules ^[15]. As detailed in section 3, these rules can be summarized as follows: (ⅰ) The polar head group of cholesterol is aligned with the cationic group of either Lys or Arg ^[43]; (ⅱ) the aromatic residue stacks onto one of the four cycles of the sterane backbone ^[55]; (ⅲ) the "pikes" of the β-face of the sterol (methyl/iso-octyl groups) favorably interact with branched aliphatic chains (Leu/Val) ^[15]. At the atomic scale, each of these three amino acid side chains has to be located in front of the specific zone of cholesterol with which it interacts ^[44]. In his respect, it is not surprising that the triad may belong to one, two or even three vicinal TM domains. Apart from CRAC, CARC and selective 3D motifs involving several TM domains, the GXXXG (glycine zipper) motif has been shown to bind cholesterol at physiological concentrations ^{[56,57,58,59]}. A particularly representative case is given by the transmembrane C-terminal domain of a bitopic protein, the amyloid protein precursor (APP) that has been included in mixed phospholipid micelles containing either a cholesterol analogue ^[56] or cholesterol ^[59]. By measuring the chemical shift changes between cholesterol-free and cholesterol-containing micelles (nuclear magnetic resonance studies) it has been possible to identify the amino acid residues involved in cholesterol binding. In all cases the glycine residues were involved in cholesterol binding, but the linear motif also included typical CARC/CRAC residues ^[60].

Another recurrent criticism of the predictive value of linear cholesterol binding motifs comes from the bioinformatic analysis of Palmer ^[61] who observed the CRAC motif over 5000 times in the 2100-member proteome of a cholesterol-free bacterium. We have recently shown that the pentameric ligand-gated ion channels (pLGIC) expressed by several bacteria species exhibit the same sterol motifs as mammalian pLGIC ^[49]. Moreover, we have shown that these bacterial motifs could functionally interact with hopanoids ^[49], a class of lipids considered as molecular ancestors of cholesterol ^[62,63]. We proposed that the association of sterols and hopanoid surrogate molecules arose from the early need in prokaryotes to stabilize pLGIC TM regions by means of relatively rigid lipid molecules ^[49]. This hypothesis is supported by recent biophysical studies which demonstrate that hopanoids interact with bacterial glycolipids to form a highly ordered bilayer in a manner analogous to the interaction of sterols with sphingolipids in eukaryotic plasma membranes ^[63]. Further studies will clarify the functional roles of CARC/CRAC motifs in bacterial membrane proteins and their relationship with prokaryotic lipids.

---

6. Lipid regulation of membrane proteins: Physiological and pathological aspects

In addition to cholesterol, several other membrane lipids have been shown to control the function of membrane proteins ^[64]. The molecular mechanisms underlying these functional effects include receptor clustering, dimerization and specific conformational adjustments controlling ligand binding, phosphorylation, signal transduction, internalization and/or recycling ^[64]. In some cases, several distinct lipids may affect the same protein. This occurs with the EGF receptor (a bitopic protein) whose activity is regulated by cholesterol ^[65], gangliosides ^[66], ceramide ^[67], arachidonic acid ^[68], phosphoinositides ^[69]. Specific regulation of ligand binding by selected lipids, most likely through conformational adjustments, has been demonstrated for various neurotransmitter receptors including the serotonin 5HT-1A receptor ^[70], the nicotinic acetylcholine receptor ^[71] and the opioid receptor ^[72]. Interestingly, the interaction of glycosphingolipids with membrane proteins is often mediated by a common structural motif referred to as the sphingolipid binding domain (SBD) ^[73]. This universal domain has been found in viral ^[74], bacterial ^[75], prion proteins ^[5], amyloid proteins ^[76,77,78], as well as in a broad range of host membrane proteins such as the tumor cell marker CD133 ^[79], the TNF receptor ^[80], the GPI-anchored protein Thy-1 ^[9]. Lipid-assisted conformational changes are especially important in the case of amyloid proteins which oligomerize into neurotoxic Ca²⁺-permeable pore channels following a sequential interaction with gangliosides and cholesterol ^[81,82,83]. In this case the lipids act as co-factors that trigger or accelerate pathological processes. Nevertheless, it has been show that in some cases selected raft lipids of neural cells (GalCer, sphingomyelin ^[5]) may stabilize the non-pathological conformation of the cellular prion protein ^[84]. Overall, as extensively discussed in a recent publication ^[26], raft lipids may both concentrate (reduction in dimensionality from a 3D volume to a 2D surface) and induce (or stabilize) α-helical stretches in proteins.

---

7. Conclusions

Taken together all these data emphasize the major impact of membrane lipids on protein structure and function. Historically, lipids were first considered as solvent molecules for membrane proteins; nowadays, such lipids are referred to as annular lipids, i.e. lipids that are more loosely attached to the receptor surface and which exchange with bulk ^[26] at comparably faster rates than non-annular lipids. Non-annular lipids bind more tightly to the receptors, affecting both their 3D structure and function ^[26]. Cholesterol is the prototype of such membrane lipids that finely control the 3D structure and function of receptors. The condensing effect of cholesterol on the TM domains of GPCRs, which may be required to create a functional ligand binding site ^[29], illustrates this important property. Studies with cholesterol isomers have demonstrated that the specificity of cholesterol binding is determinant for the regulation of ion channel function ^[50]. Various linear and 3D cholesterol binding domains have been characterized in a wide range of membrane receptors and channels, which may account for distinct levels of specificity for cholesterol. Apart from cholesterol, several other membrane lipids have been shown to affect/regulate the function of membrane proteins through conformational effects. Microbial and amyloid proteins also interact with membrane lipids which may act as important pathological co-factors. Further studies will be required to determine how the different modes of lipid binding affect the 3D structure and function of proteins in both physiological and pathological processes.

---

Conflict of interest

The author declares no conflict of interest in this paper.

---