1. Introduction
A nanocrystal (NC) can be defined as either a single- or poly-crystalline particle having at least one dimension smaller than 100 nanometres. When the dimensions of a NC are smaller than the Bohr radius of the element(s) in question, then quantum confinement occurs [1], and the particle is termed a quantum dot (QD) [2]. However, in practice quantum effects are observed for particles with diameter up to 2x Bohr radius. Thus, given silicon’s Bohr radius is 5 nm, then a Si-NC with a diameter <10 nm would be considered a Si-QD [3,4,5]. QD particles exhibit different electronic behavior from their bulk homologs. For example, the band gap of bulk silicon is 1.12 eV, but the band gap of Si QDs is much larger and depends on the size of the particle.
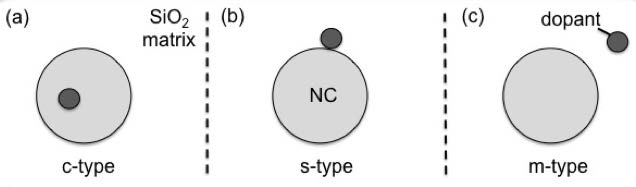
As has been discussed elsewhere [6], doping of a particle at the nanoscale may be achieved via addition of a dopant within the crystal lattice of the QD (or NC), see Figure 1a. As such this is defined as a c-dopant (c = crystal lattice), and the dopant will act in a similar manner to that of a bulk semiconductor. Unlike for bulk semiconductor, doping at the nano-scale can also be accomplished through surface functionalization, i.e., s-dopant (s = surface), see Figure 1b. Researchers have also found that doping of a dielectric matrix (i.e., SiO2) surrounding the QDs has the consequence of providing a doping-like effect on the electronic performance to the QD, most likely through the change in the conduction of the matrix between the individual QDs. Even though this process may not be doping in the traditional sense we have termed it as m-dopant (m = matrix), see Figure 1c. For c-type doping the formation of n- or p-type material would be related to that in bulk semiconductor. In the latter two cases the dopant element can act as an electron donor (which injects electrons into the QD and therefore acts as a n-type material) or electron withdrawing group (resulting in the equivalent effect as injects holes and therefore acting like p-type doped material) [3,4,5,6]. We also note that there is a differentiation between chemical doping (the presence of the element in question) and electronic doping (an effect on the band gap, band energy levels, or Fermi level) of the QD.
While there is significant literature associated with the doping of silicon QDs and NCs [6,8], there is a paucity of examples of doping their germanium analogs. Germanium NCs (3.3-4.1 nm) have been doped (Al, P, Ga, As, In, Sn, and Sb) at a level of about 1 mol%, through the nBuLi reduction of a mixture of GeI2 and GeI4 [9]. Baldwin et al. have reported that either the LiAlH4 or Mg reduction of GeCl4 during synthesis results in nanoparticles (NPs) with a Cl:Ge ratio of 0.27 (as measured by XPS) [10]. Based upon a QD diameter of 5-7 nm this correlates to about 1000 chlorine atoms per QD suggesting s-type doping; however, no determination of the electronic doping effects of the Cl were made. Analog Si NCs have been produced with a plasma reactor with chlorine terminating the surface. These Cl-terminated Si NCs act as Lewis acids ready to receive electrons from Lewis bases like ketones and nitriles. [11] In our routes to creating silica coated Ge QDs (Ge@SiO2) [12,13], it is necessary to convert the as-prepared hydrophobic surface to a hydrophilic one through surface functionalization with allylamine (Figure 2). The addition of ligands to the surface of the preformed NC has been reported to have a possible doping effect [14,15]. Also it has been shown in other NP systems that secondary functionalization of halide functionalized NPs results in the loss of the halogen [16,17,18]. We have investigated the chlorine content pre- and post-surface functionalization as well as the electronic effects on the QD. In addition, we have investigated the potential incorporation of phosphorus, boron and gallium dopants.
2. Materials and Methods
2.1. General
All chemicals were obtained commercially and used without further purification unless noted. Tetraoctylammonium bromide (TOAB), silicon tetrachloride (99.998%), lithium aluminum hydride (1.0 M in tetrahydrofuran), methanol (≥99.8%), hexachloroplatinic acid hydrate (≥99.9%), isopropanol (≥99.5%), tetraethoxysilane (TEOS) (99.999+%), L-lysine (97%), hexanes (≥98.5%), gallium (III) chloride (≥99.99%), boron trifluoride diethyl etherate (for synthesis), and allylamine (99+%) were obtained from Sigma Aldrich. Phosphorus trichloride (99.997%) was obtained from Alfa Aesar. Toluene was obtained from EMD and germanium tetrachloride (99.99%) was obtained from Acros Organics. Methanol, toluene, and isopropanol were further purified of dissolved oxygen using a freeze-pump-thaw method. Ethanol (200 proof) was obtained from Decon Laboratories. All syntheses were performed in a glove box under a N2 atmosphere.
2.2. Characterization
Transmission electron microscopy (TEM) was performed with a JEOL 2010 TEM at 100 kV with a CCD camera. High resolution transmission electron microscopy was performed on a JEOL 2100 field emission gun TEM at 200 kV with a CCD camera. UV-visible spectroscopy was performed on an Agilent 8453 UV-visible spectroscopy system with 1 cm quartz cuvettes. X-ray photoelectron spectroscopy (XPS) was performed on a PHI Quantera X-ray photoelectron spectrometer equipped with a differential argon ion gun with gold coated silicon wafers as a substrate for the samples.
2.3. Inherently doped Ge QDs
Synthesis was undertaken using a variation of a literature procedure [12,13]. GeCl4 (92 μL, 0.8 mmol) and tetraoctylammonium bromide (TOAB) (1.5 g, 2.7 mmol) were dissolved in anhydrous toluene (100 mL). The solution was stirred for 24 hours to ensure that the reverse micelles formed completely and uniformly. To this was added LiAlH4 in THF (0.63 mL, 1.0 M), and the solution was allowed to react for 3 hours while continuously stirred. After which the excess LiAlH4 was quenched using anhydrous MeOH (15 mL). The quantum dots are hydrophobic at this point (sample 1a). To make the particles hydrophilic, H2PtCl6 in anhydrous isopropanol (40 μL, 0.05 M) was added to the quantum dots along with allylamine (2.00 mL, 26.7 mmol); this mixture was allowed to react until the solution stopped producing hydrogen gas. This solution is air stable and was taken out of the glove box to evaporate off the solvent. It should be noted that heat is not applied because the quantum dots easily oxidize upon heating. After drying, the particles were re-suspended in deionized water (35 mL) and filtered through a 0.2 μm pore filter to remove any excess surfactant leaving a solution of the QD (sample 1b). Variations in reagent ratio (samples 2-5) were employed in order to determine the effect on particle size (Table 1). The as synthesized Ge QDs were coated with silica using previously described processes [19].
Table 1. Variation in reagent and reaction conditions for inherently doped Ge QDs.
| Sample | GeCl4 (μL) | TOAB (g) | Reaction time (h) | LiAlH4 (mL) |
| 1 | 92 | 1.5 | 3 | 0.63 |
| 2 | 92 | 0.75 | 3 | 0.63 |
| 3 | 184 | 1.5 | 3 | 1.2 |
| 4 | 92 | 1.5 | 1.5 | 0.63 |
| 5 | 92 | 1.5 | 6 | 0.63 |
2.4. Doped Ge QDs
Quantum dots were synthesized using the procedure described above, however, a suitable dopant precursor was added as needed prior to the addition of the LiAlH4: PCl3 (8 μL, 0.08 mmol, sample 6; 16 μL, 0.16 mmol, sample 7) for phosphorus; BF3(OEt2) (80 μL, 1M) for boron (sample 8), and GaCl3 (0.0142 g, 0.08 mmol) for gallium (sample 9). The remainder of the synthesis was identical to that used for sample 1b.
2.5. Si/Ge@SiO2 layers for I/V measurements
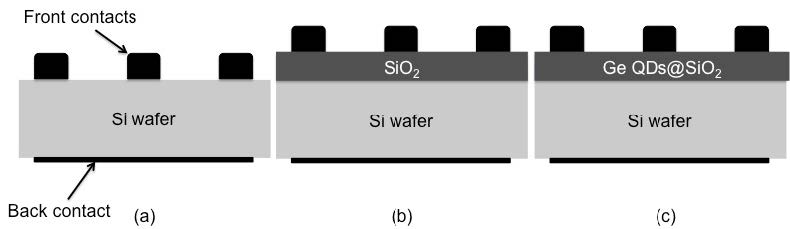
N-type and p-type silicon wafers were provided by Natcore Technology, Inc., doped with phosphorus and boron, respectively. These wafers came with a thick silica passivation layer on top to keep the dopants from migrating out of the silicon. The wafers were cut into 2 × 2 cm2 coupons and were buffer (NH4F/HF) etched to remove the passivation layer. The clean wafers were then plasma (5% O2 in argon) etched to add back a very small (<10 nm) uniform layer of oxide back on the surface. The wafers are placed vertically into a solution of the silica coated quantum dot particles to evaporate the solvent and deposit the particles [20]. Once the wafers are coated with the particles, a back contact of gold is added by sputtering. The front contact (gold or silver) is sputtered using a mask to create fingers across the surface without completely covering it with metal [21]. Both contacts are 100 nm thick, and the metal used depends on the identity of the dopant of the wafer and the presence of a QD layer. The device is then tested in a solar simulator that is monitored by a multimeter connected to computer software. The efficiency of the QD/Si cells were calculated from the I-V curves detected via Keithley 2420 and 2425 High Current SourceMeter with an Oriel Model 81190 Solar simulator equipped with a Xenon lamp, including light intensity feedback control. The intensity of incident light was 100 mW/cm2. The solar cells were kept at a fixed distance of 6 inches from the light source for optimal conditions. The cells were attached to two leads, one connected to the back contact and the other connected to the busbar of the front contact. This setup allowed for the measurement of the current produced by the cell with change in voltage.
3. Results
3.1. Inherently doped Ge QDs
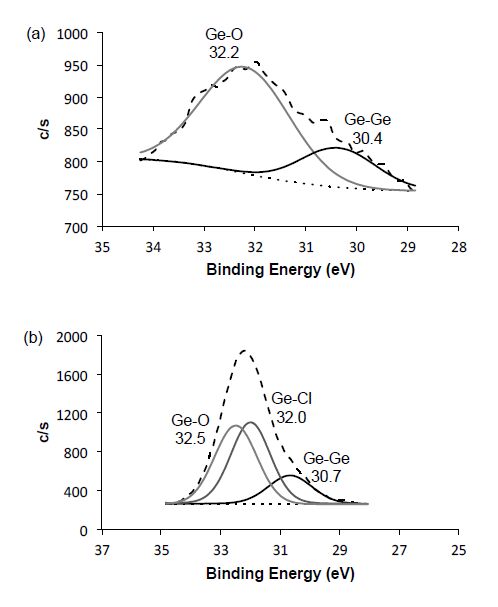
The XPS of as prepared Ge QDs prior to allylamine functionalization (sample 1a) shows the presence of chlorine and oxygen (see Table 2). The presence of oxygen in all the QD samples is a consequence of atmospheric exposure during sample preparation, while the presence of carbon is associated with the allylamine. It should be noted that while XPS is a surface technique with an analysis depth of 3-10 nm for Al-Kα radiation, the analysis of 5 nm QDs (see below) XPS should provides an acceptable estimation of composition. The Cl:Ge ratio (as determined by XPS) of 0.07 for sample 1a is much smaller than the value of 0.27 reported by Baldwin et al. for octyl functionalized Ge QDs prepared by the similar routes [10]. In both cases this value is lower than monolayer coverage: 0.71 (see below). Upon allylamine functionalization (sample 1b, see Figure 2) the chlorine content is significantly increased (Table 2). This is undoubtedly due to the use of the chloroplatinic acid (H2PtCl6) as a catalyst to cap the Ge QDs with amines (see Figure 2). According to the XPS, the Cl:Ge ratio is increased to 0.39 once the QDs are amine functionalized.
Table 2. XPS analysis (at%) of as synthesized and doped Ge QDs.
| Sample | Ge | Cl | O | N | C | Ea |
| 1a | 1.12 | 0.08 | 3.06 | 1.50 | 94.25b | - |
| 1b | 16.17 | 6.31 | 2.10 | 9.81 | 65.61 | - |
| 2 | 4.77 | 7.88 | 9.34 | 14.27 | 63.74 | - |
| 3 | 6.44 | 3.04 | 1.53 | 12.20 | 76.79 | - |
| 4 | 9.53 | 4.50 | 11.52 | 8.71 | 65.74 | - |
| 5 | 7.66 | 3.77 | 7.48 | 10.47 | 72.62 | - |
| 6 | 4.14 | 5.88 | 15.52 | 12.11 | 60.34 | 2.01 (P) |
| 7 | 2.87 | 6.31 | 7.21 | 15.65 | 66.76 | 1.20 (P) |
| 8 | 1.60 | 7.10 | 4.01 | 17.58 | 69.70 | 0.01 (B) |
| 9 | 5.48 | 5.84 | 16.95 | 12.65 | 58.99 | 0.09 (Ga) |
| a Dopant element given in parenthesis. b High C content due to residual surfactant from reaction. |
The high resolution Ge 3d and Cl 2p spectra for samples 1a and 1b are shown in Figures 3 and 4, respectively. The Ge 3d peak shows both Ge-O and Ge-Ge species regardless of amine functionalization. However, we note that the Ge-O peak appears to increase in intensity upon amine functionalization even though the O:Ge ratio decreases. This suggests that the peak at 32.2 eV in Figure 3b is a composite of both Ge-O and Ge-Cl.
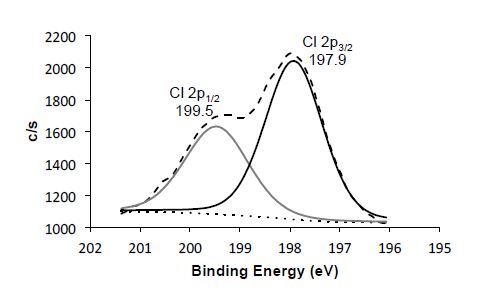
The positions of the Cl 2p peaks (Figure 4) are consistent with Ge-Cl species [22,23]. The XPS peak shift does not differentiate between residual chlorine on the surface of the QD (s-type) or interstitial (c-type); however, as noted the Cl:Ge ratio (0.39), and the surface selectivity of XPS suggest that the chlorine is on the surface of the QDs. It is previously reported that if a low concentration of HCl is added to a Ge QD solution, it caps the QDs with chlorine [24]. These results are in agreement with a theoretical study of Si NCs that reports that chlorine atoms prefer the surface (s-doped) rather than the inside the NC (c-doped) [25].
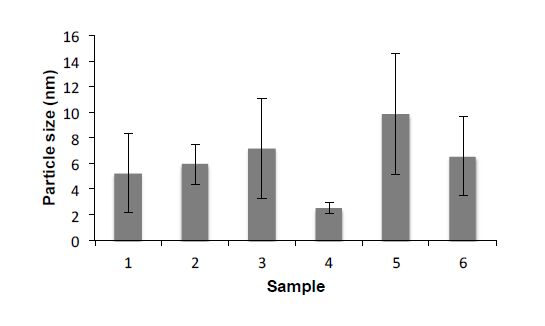
The average diameter of the as synthesized Ge QDs determined to be 5 nm from HRTEM images, with a dispersion shown in Figure 5. As is seen from Figure 6, some of the particles having multiple crystal domains with a particle having a defined grain boundary. In Figure 6b, a single particle is expanded on revealing that there are two different atomic lattice directions in the same particle. Thus, the grain boundary cannot be ruled out as the location of the chlorine atoms detected by XPS. However, the crystal lattice measurements of the Ge QDs (5.65 Å) match that of diamond cubic germanium (5.648 Å) [26] suggests that the chlorine is not interstitial. Given an average diameter of 5 nm (Figure 5) an estimate may be made of the maximum chlorine content per QD. Assuming an ideal crystal lattice and the presence of chlorine on each “dangling bond” site associated with the (100) crystal face then the Cl:Ge ratio would be expected to be ca. 0.71. This is higher than the value determined by XPS (0.39) indicating less than monolayer coverage, which is consistent with the alkylamine functionality (Figure 2). Based upon the chlorine content, it would it is consistent that the chlorine doping may be described as c-type.
Prior to determining whether the Cl atoms act as an active dopant and in what manner (n- or p-type) a series of control studies were first performed to determine if the Si wafers would produce a photocurrent on their own with different metals used for top and bottom contacts (Figure 7a). The I/V curves were measured (see Methods and Materials) from which the efficiency of the cell is determined. The results of the control studies are shown in Table 3.
Table 3. Efficiency data for control devices M|Si|M and M|SiO2|M.
| Si wafer type | SiO2 layer | Front and back contact | Efficiency (%)a |
| p-type | No | Silver | 0.0000 |
| p-type | No | Gold | 0.0000 |
| p-type | Yes | Gold | 0.0000 |
| n-type | No | Silver | 1.3 × 10-3 |
| n-type | No | Gold | 1.4 × 10-3 |
| n-type | Yes | Gold | 0.0000 |
| a Efficiency is defined as power conversion upon exposure to incident light. |
The p-type wafer showed no photoresponse under any conditions, but the n-type wafer did consistently show a very small photoresponse with both metals with gold being slightly more conductive. The small photoresponse that can be observed for the n-type silicon wafer is due to an ohmic contact between the wafer and the metal. This happens because the metal has a work function close to the electron affinity of the n-type silicon and electrons can be easily transferred with very little energy [27]; because of this result gold back contact were used all further measurements. Another set of control wafers was prepared with a SiO2 layer (Figure 7b) without any QDs in the sample. Both the p-type and n-type wafers with SiO2 only did not produce a photoresponse.
Test cells were prepared by depositing the Ge QDs (sample 1b) into a silica matrix as a thin film on the Si wafer (Figure 7c). The QDs were coated with silica to separate them from each other a small distance (<10 nm) using previously described method [13,19], and were then made into a thin film via vertical evaporation on silicon wafer pieces [20]. SEM analysis of the samples showed the films to be highly textured (Figure 8), but uniform in thickness (4.5 μm), see Figure 9. It was found that thin oxide layer is necessary for producing thin films because the completely clean wafers are severely hydrophobic, and adding the silica coated quantum dots does not work with a hydrophobic surface. The thin oxide layer allows the surface to be hydrophilic and the silica coated quantum dots will stick to the surface.
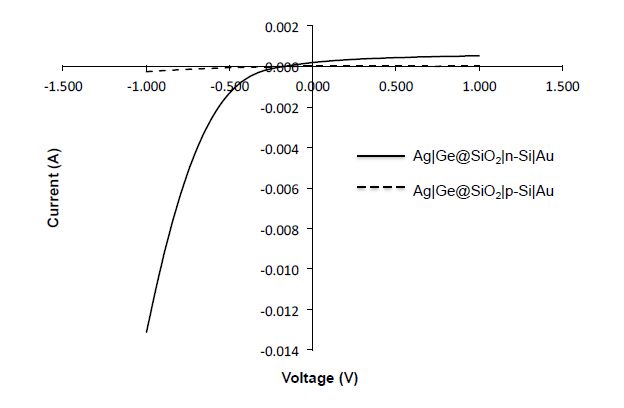
The Ge@SiO2 layer was deposited on both n-type and p-type wafers with varying metals to determine if the material acts as if it is doped and, if so, what metal conducts best with this material. The I/V curves were measured for these cells (Figure 10). As may be seen from Table 4, no photoresponse is observed for p-type wafers, while a larger response is observed for M|Ge@SiO2|n-Si|Au than the simple n-type Si wafer, i.e., M|n-Si|Au where M = Au or Ag (Table 3). This result suggests that the chlorine present in the as synthesized Ge QDs act as p-type dopant. The efficiency that is produced from the n-type wafers with the Ge@SiO2 layer on top is small, but it is significant and reproducible.
Table 4. Efficiency data for M|Ge@SiO2|Si|Au (M = Au, Ag).
| Si wafer type | Front contact metal | Efficiency (%) |
| p-type | Silver | 0.0000 |
| p-type | Gold | 0.0000 |
| n-type | Silver | 2.2 × 10-3 |
| n-type | Gold | 0.1 × 10-3 |
If as suggested from the data the Cl atoms act as ligands on the surface of the QD (s-type) where they are anticipated to act as an electron-withdrawing ligand, which is expected considering the higher electronegativity of the chlorine atom (3.0) as compared to Ge (1.8). A prior theoretical report on chlorine terminated Si NCs [11] suggests that the chlorine polarizes the surface of the NC, which creates a Lewis acid site and surface doping effect. Interestingly, EPR has been used to study the injection of holes or electrons with molecules adsorbed on the surface of Si NCs [15]. Surface adsorption of NO2 injects holes and acts like p-type doped material. In contrast, NH3 injects electrons and acts like n-type doped material. These effects follow the classic activating and deactivating trends observed for these substituents in organic aromatic derivatives [28]. Taking this approach, chlorine is a known electron withdrawing substituent and would inject holes and acts like p-type doped material, which is indeed observed. Given that a highest photoresponse is observed using silver as a front contact, for the rest of the hybrid solar cells, all wafers will be n-type and all of the contacts will be gold on the back and silver on the front, i.e., Ag|Ge@SiO2|Si|Au.
3.2. Effect of synthesis stoichiometry
Although doping is the method of choice to create a bias to induce electron flow in a solar cell, it is not the only method that can be employed. As long as the work functions of the two materials are different enough from each other that would be enough to induce electron flow in a solar cell. Work function is defined as “the minimum energy barrier (hνc) for conductive electrons to leave a metal” [29]. Achieving different work functions in the same material can be accomplished by creating different sizes of QDs, which would absorb different areas of the electromagnetic spectrum. In a semiconductor material, this could also be considered as tuning the band gap. There are many examples reported of the band-gap tune ability of QDs as a function of particle size [24,30,31]. Generally, there are two different approaches for the synthesis of different sized particles: the amounts of starting materials (surfactant or precursor) or varying the reaction time [32].
Varying the amounts of the reagents was investigated first (Table 1). Controlling the concentration of the surfactant may have direct relation to controlling particle size. Generally, the surfactant is used at such a concentration that the molecules organize together to produce micelles, inside of which is where the synthesis actually occurs. A decrease in the concentration of the surfactant results in an increase in the particle size of a NP [32]. TEM analysis (Figure 11a) shows crystalline QDs, from which the size and distribution is determined (Figure 5). As seen from a comparison of Figures 6a and 10b, the average particle size did not change significantly upon alteration of the surfactant concentration. This observation is supported by the proposal made by Baldwin et al. that the micelles that the surfactant creates are not actually the reaction vessels for the synthesis of these particles and, as such, have no bearing on the size or shape of the particles [33]. When the concentration of the germanium starting material was doubled without altering the surfactant concentration (sample 3), there were significantly more particles, which suggests that the starting material controls the number of nucleation sites, but does not control the growth rate. As growth and nucleation are considered separate events, there should be a parameter that controls the growth of the QDs [32]. Once the duration of the reaction was investigated, it became clear that time is the parameter that controls particle growth. When the reaction time was halved (sample 4), the growth was stopped before the particles had time to mature, but when the reaction time was doubled (sample 5), the particles were allowed to grow much larger than normal and with a much broader size distribution (Figure 5).
The XPS analysis (Table 2) of the Ge QDs prepared with low surfactant concentration (sample 2) shows that the Cl:Ge ratio (1.64) is more than that of a full monolayer coverage based upon the particle size (0.71), see above. In fact based on the particle size, there is more chlorine associated with the particles than is practical for having the chlorine occupying the dangling bonds alone (even considering a non-uniform particle shape). This could indicate that there are chlorine atoms in the particles or that there is partially reacted “GeClx” species entrained with the QDs, see below.
Germanium QDs were prepared with a concentration of GeCl4 double the standard concentration (Sample 3, Table 1). Ordinarily, an increase in the metal precursor concentration would result in larger NPs [32]. However, as may be seen from Figures 6a and 10b there is only a slight increase in the average particle size upon increasing the GeCl4 precursor’s concentration (see, Figure 5). A more significant result of doubling the GeCl4 reagent concentration is an increase of the yield of Ge QDs, which is beneficial for scaling up the synthesis. As determined by XPS the Cl:Ge ratio for sample 3 (Table 2) is 0.47 consistent with sub-monolayer coverage.
Decreasing the reaction time to the half of the normal time (sample 4, Table 1) resulted in a sample in which the QDs are very small (Figure 11c) and with a narrow size distribution (Figure 5). It should be noted that there remains a significant amount of excess surfactant in solution. Extending the reaction time to 6 h. (sample 5, Table 1) produces the expected increase in the particle size. As is seen from Figure 11d, increased reaction time not only produces Ge QDs with an average particle size of 10 nm. However, the particle size dispersion is wider than for the standard conditions (see Figure 5). The Cl:Ge ratio as determined from XPS for samples 4 and 5 (0.47 and 0.49, respectively) appear similar. However, based upon their average size (Figure 5) monolayer coverage of Cl:Ge would be expected to be 1.24 and 0.32, respectively. Also interesting to note is the large size variation of sample 5, which makes the chlorine coverage difficult to determine if there truly is an excess of chlorine larger than a monolayer coverage or not.
Regardless of the size dispersion, as seen in Figure 5 all Ge QD sizes are well below the reported Bohr radius of germanium (18 nm); therefore, all of the particles should still be affected by quantum confinement [5]. Efficiency measurements for Ag|Ge@SiO2|n-Si|Au devices using the Ge QDs prepared under different synthetic conditions (Table 1) are shown in Table 5. As expected the sample prepared with double the GeCl4, which are similar in size to those prepared under standard conditions, shows essentially identical performance. However, it is interesting that the sample prepared with lower surfactant concentration did not result in an active device, even though the particles are similar in size (Figure 5). As noted above the Cl:Ge ratio in sample 2 is more than the maximum coverage for a monolayer. Either way this amount of chlorine clearly negatively affects the ability of these particles to create a photoresponse. Conversely, the QDs that were synthesized with double the GeCl4 (sample 3, Table 2) has a Cl:Ge ratio of 0.47 and this provides layers with active photoresponse.
Table 5. Efficiency data for Ag|Ge@SiO2|n-Si|Au.
| Sample | Average QD particle size (nm) | Efficiency (%) | Comment |
| 1b | 5 | 2.2 × 10-3 | Reference sample |
| 2 | 5 | 0.0000 | Decrease surfactant conc. |
| 3 | 5 | 2.5 × 10-3 | Increase GeCl4 conc. |
| 4 | 2 | 0.0000 | Decrease reaction time |
| 5 | 10 | 0.4 × 10-3 | Increase reaction time |
There appears no photoresponse for devices made using small Ge QDs prepared with low reaction time (sample 4), and devices prepared using larger QDs (sample 5) shows a lower efficiency than the standard sample. It has been previously reported for Si NCs that electronic doping can vary with dopant concentration [34]. For Ge NCs, there also appears to be variation with chlorine concentration, but it is less clear. The Ge QDs from sample 1b have a small photoresponse with a Cl:Ge ratio of 0.39, when the ratio is raised to 1.64 as in sample 2 there is no photoresponse due to too much chlorine. However, when the Cl:Ge ratio is raised to 0.47 as in sample 3, there is a slightly higher photoresponse. Based upon a comparison of a similar effect occurs with the chlorine functionality of Ge QDs it appears that a range of 50-80% monolayer coverage provides electronically active doping; however, more detailed studies are needed to define the optimum dopant coverage level.
3.3. Doped Ge QDs
It has been previously reported [35] that Si QDs may be doped by the use of PCl3 during their synthesis (sample 6). Because their process for synthesizing the doped Si QDs was similar to the method used herein for Ge QDs [13], it is reasonable to assume that this reaction may work to dope the Ge QDs with phosphorus. Thus, Ge QDs were prepared using 10% PCl3 as a co-reactant, see Materials and Methods.
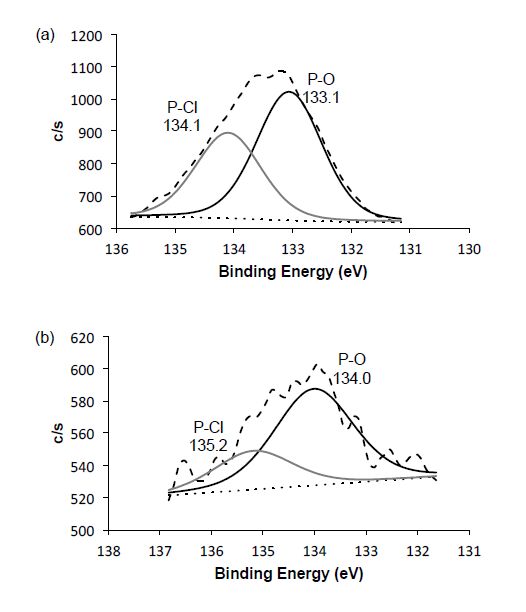
XPS analysis (Table 2) does confirm the presence of phosphorus in the QDs. The composition gives a P:Ge ratio of 0.42. There is also a presence of chlorine (as confirmed by the high resolution 2p spectra, see below). The Cl:Ge ratio (1.42) is much higher than the monolayer coverage of chlorine on the particle. The combined dopant X:Ge (1.90) is much much higher than monolayer coverage. However, the XPS may be able to help explain the excess chlorine in the system. As noted above, despite the surface sensitive nature of XPS the results cannot distinguish between the P being on the surface of the QD or inside the QD itself. Either way, the P atoms could be available as a dopant. If the phosphorus is in the germanium crystal lattice, it will act as n-type, but if the atoms are on the outside of the particles it could be either electron donating or electron withdrawing. The high resolution P 2p spectrum for sample 6 is shown in Figure 12a. The chemical composition is consistent with both P-O (134.1 eV) and P-Cl (133.1 eV) moieties [36,37]. With Ar ion sputtering there is an alteration in the peak position, which makes chemical assignment more difficult [38]. However, there is no significant change in the relative composition of the two peaks observed, suggesting that these are shifted due to charging effects rather than chemical composition changes. Irrespective of the chemical speciation issue, the phosphorus content is significantly decreased (see Figure 12b). This would suggest that like the chlorine (see above), the phosphorous is predominantly on the surface of the QD. Furthermore, it is interesting that the presence of P-Cl moieties suggest incomplete reaction of the PCl3 starting material or colocation of the Cl and P on the surface of the QD, which explains why there is so much excess chlorine in the system. We have previously shown [13] that the as synthesized Ge QDs are coated with a thin native GeO2 layer, thus the presence of P-O species is expected within the surface. König et al. have reported that when trying to dope Si@SiO2 materials, the phosphorus is found mostly at the interface of the Si and SiO2 or in the silica with little phosphorus within the Si NC suggesting that the phosphorus prefers binding to oxygen [38]. Our data supports a similar distribution for the germanium analogs since the high resolution Ge 3d spectra is shown in Figure 13 and is consistent with elemental germanium and GeO2 species [39].
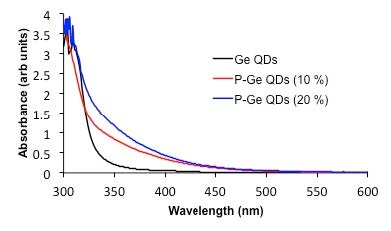
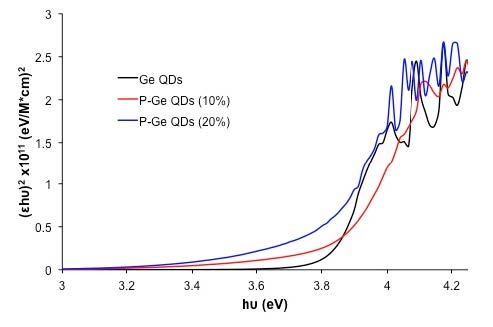
Figure 14 shows the UV-visible spectrum of the Ge QDs prepared without PCl3 (sample 1b) and those with 10% PCl3 (sample 6). As may be seen there is a 9 nm red shift in the band edge from 329 nm to 338 nm [40,41], and an increased adsorption tail. The band edge shifts to 344 nm with the addition of more PCl3 to the reaction mixture (20% PCl3, sample 7). Figure 15 shows the derived Tauc plot from the UV-visible spectra. The calculated band gaps are as follows: 3.84 eV (sample 1), 3.83 eV (sample 6) and 3.79 eV (sample 7).
The shift of band edge could be associated with a change in QD size; however, as may be seen from the TEM image in Figure 16 there is no significant change in the QD size (Figure 5). In addition, there is no change in the crystal lattice of the Ge QDs further suggesting the phosphorus is at the surface of the QDs.
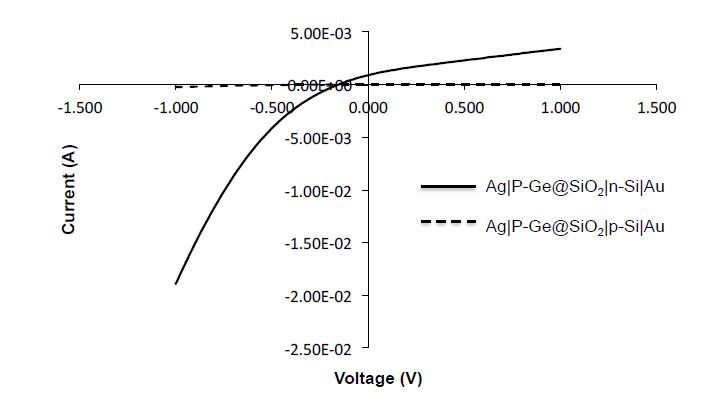
As with the as-prepared QDs, test cells were prepared by depositing the P-doped Ge QDs into a silica matrix as a thin film on the Si wafer (i.e., Figure 7c) [13,19]. Test cells were prepared on both n- and p-type Si substrates and the I/V curves measured (Figure 17). As may be seen from Table 6 the cell results indicate that, like the native Ge QDs, the P-Ge@SiO2 material also behaves as a p-type layer. These results indicate that the phosphorus also acts as an electron-withdrawing ligand. However, it is important to note, that within the limitations of the cell structure, the efficiency is significantly greater than the inherently doped Ge@SiO2 material. It should be noted that as such the enhanced cell performance might be a consequence of “deep defect centers, which appear to provide the most efficient and fastest path for non-radiative carrier recombination” by the inclusion of P in the silica matrix. Such an effect has been proposed to be responsible for photoluminescent quenching with increased phosphorus concentration [38].
Table 6. Efficiency data for Ag|P-Ge@SiO2|n-Si|Au.
| Si wafer type | Efficiency (%) |
| n-type | 0.0000 |
| p-type | 9.3 × 10-3 |
Since phosphorus was found to produce n-type particles, or at least create the effect of making the QD n-type within the test cell structure, boron and gallium doping were attempted. As a suitable boron and gallium precursor BF3OEt2 and GaCl3 were chosen, respectively. Even with the addition of 10% BF3, no doping of the QDs occurred, based upon XPS (Table 2). The XPS survey scan for the samples prepared with the addition of 10% GaCl3 during the synthesis appears to show the presence of gallium; however, the high-resolution Ga 3d spectrum shows that any gallium is at or below the detection limit of the spectrometer (ca. 0.3%).
4. Conclusion
As-synthesized Ge QDs contain significant chlorine, despite subsequent functionalization with organic amines to enhance water solubility. This surface chlorine acts as a p-type dopant, but the chlorine concentration appears to be critical in providing an electronically active dopant. In a similar manner, the addition of PCl3 during the synthesis results in surface inclusion of phosphorus within the native GeO2 coating of the QD. However, the formation (or retention) of P-Cl species is unusual. Despite the inclusion of possible dopant elements during the chemical reduction of the GeCl4 precursor, those that can be detected are all present on the surface of the QD (s-type). This suggests that the self-purification process observed for Si NCs is operative in their germanium analogs [42].
Acknowledgments
This work was supported by in-part by Natcore Technology, Inc., the Robert A. Welch Foundation (C-0002), and the Welsh Government Ser Cymru Programme.
Conflict of Interest
One of the authors (A.R.B.) is the scientific founder of Natcore Technology, Inc., a public company (NXT.V).









 DownLoad:
DownLoad: