A fractional Landweber iterative regularization method for stable analytic continuation

1.   Introduction

The problem for analytic continuation of an analytic function is encountered in many practical applications (see, e.g., ^[1,2,3,4] and the references therein), and the numerical analytic continuation is a more interesting and hard problem. It is well known, in general, to be ill-posed in the sense that the solution does not depend continuously on the data. To obtain stable numerical algorithms for ill-posed problems, some effective regularization methods must be adopted, and several nonclassical methods have been developed rapidly in recent years. In ^[5], the authors used the fourier truncation regularization method to solve this problem. In ^[6], the authors used the modified kernel method to solve this problem. In ^[7], the authors used the generalized Tikhonov regularization method to solve this problem. In ^[8], the authors used the optimal filtering method to solve this problem and obtained the optimal error estimate. However in ^[5,6,7,8], the regularization parameter is chosen by the a priori choice which depends on the a priori bound $E$. But in practice, the a priori bound doesn't know for sure, and working with a wrong constant $E$ may lead to the bad regularization solution. In ^[9], the authors study a continuous fractional regularization method called FAR. In this work, it is strictly proved that FAR is an accelerated algorithm relative to the comparable order optimal regularization method if the fractional order is in the range of $(1, 2)$. In ^[10], the authors study the convergence of Landweber iteration for linear and nonlinear inverse problems in Hilbert scale. Different from the usual application of Hilbert scale in the framework of regularization method, the case of $s < 0$ (for Tikhonov regularization) corresponds to the weaker regularization standard in the regularization method. In ^[11], the authors propose a new iterative regularization method for solving ill-posed linear operator equations. The prototype of these iterative regularization methods is a second-order evolution equation with linear vanishing damping term. It can not only be regarded as an extension of asymptotic regularization, but also as a continuous simulation of Nesterov accelerated scheme. They also discussed the application of the newly developed accelerated iterative regularization method with a posteriori stopping rule in diffusion-based bioluminescence tomography, which is modeled as an inverse source problem of elliptic partial differential equations with both Dirichlet and Neumann boundary data. In ^[12,13], the authors used the modified Tikhonov regularization method to solve this problem, and gave the error estimates between the regularization solution and the exact solution under the a priori and a posteriori regularization parameter choice rules, respectively. However, under the a posteriori regularization selection rule, the form of error estimation is logarithmic. In ^{[14,15,16,17]}, the authors used the iterative regularization method, wavelet regularization method, a modified Tikhonov regularization method and a modified Lavrentiev iterative regularization method to solve this problem. Under two regularization parameter choice rules, the H$\ddot{o}$lder type error estimates were all obtained. In this paper, we use fraction Landweber iterative regularization method and Landweber iterative regularization method to solve this problem. Landweber regularization method which is very useful to solve the inverse problem overcomes the saturation phenomenon of Tikhonov regularization method. The Landweber regularization method first comes from ^[18]. Now, the Landweber regularization method has been used to solve a lot of inverse problem, one can see ^{[19,20,21,22,23,24]}. In ^[25], Xiong firstly proposed Fractional Landweber regularization in 2017. Compared with the standard Landweber method, it reduces the step of the iteration greatly.

We can sum up the problem as follows. Suppose the domain $\Omega$ is

in complex plane $\mathbb{C}$, $i$ is the imaginary unit and $y_{0}$ is a positive constant. The function $g(z) = g(x+iy)$ is an analytic function in $\Omega$. $g(\cdot+iy)\in L^2(R^2)$ for all $y \in [0, y_0]$. The data at $y = 0$ is the given measurement data, i.e., $g(z)|_{y = 0} = g(x) \in L^{2}(\mathbb{R})$. Let the noise data be $g^{\delta}(x)$, which belongs to $L^{2}(\mathbb{R})$. And $g(x)$, $g^{\delta}(x)$ satisfy

where $\delta$ is the noise level, $\|\cdot\|$ is $L^{2}(\mathbb{R})$ norm. Moreover, assume there holds the following a priori bound

where $E$ is a fixed positive constant.

$\hat{g}$ is the Fourier transform of the function $g(x)$, which is expressed as follows

and the inverse Fourier transform of the function $\hat{g}(\xi)$ is

The $L^{2}(\mathbb{R})$ norm for $g(x)$ is defined by

and by utilizing the Parseval formula,

The problem that needs to be solved is wielding the measurement data $g(x+iy)|_{y = 0}$ to recover the data $g(x+iy)$ for $0 < y < y_{0}$. By using the inverse Fourier transform with the respect to the variable $x$,

Therefore, we get the following equation

i.e.,

Problem (1.10) also can be denoted by the linear operator equation

where $\hat{K}(\xi): = e^{y\xi}$ is a multiplication operator. By ^[27], we know that problem (1.10) is a linear ill-posed operator equation.

The clue of this paper is as follows. In section 2, fractional Landweber iterative regularization method and the a priori error estimation are proposed. In section 3, the a posteriori error estimations between the exact solution and the approximate solution are given. In section 4, several examples are selected to show the effectiveness of this method for solving this problem.

2.   The convergence error estimate with an a priori parameter choice rule

Now, we take on a regularization method which is called Landweber regularization method. And the Eq (1.11) could be described as the following operator equation

to replace $\hat{K}\widehat{g(\cdot+iy)}(\xi, y) = \hat{g}(\xi)$, where $0 < a < \frac{1}{\|K\|^{2}}.$ Therefore, the form of iterative scheme is as follows:

$m = 1, 2, 3, \cdots$ is the iterative steps. Combined with noise disturbance term $\hat{g}^{\delta}(\xi)$, the approximate solution obtained by Landweber iterative regularization method can be expressed as

where

The fractional Landweber regularization solution is

where

where $0 < \gamma < 1$ is a constant.

Now, we first give some useful Lemmas.

Lemma 2.1. Take $p > 0, q > 0$, then

where $m, a$ are both positive constants and $a$ satisfies $0 < a < \frac{1}{\|K\|^{2}}$.

Proof. Let $F(s): = (1-ae^{ps})^{m}e^{qs}$. Based on $\lim_{s\rightarrow 0}F(s) = \lim_{s\rightarrow -\infty} = 0$, thus we can presume

where $s_{0} < 0$, satisfies $F'(s_{0}) = 0$. We can easily calculate $s_{0} = \frac{1}{p} \ln\frac{q}{aq+amp}$, so we have

Lemma 2.2 ^[5]. If $\|g(\cdot+iy_{0})\|\leq E$, we obtain

Lemma 2.3. For $\frac{1}{2} < \gamma < 1$, $0 < a < \frac{1}{\|K\|^2}$ and $m\geq1$, we can get

Proof. Because $0 < a < \frac{1}{\|K\|^2}$, so we obtain $0 < ae^{2y\xi} < 1$. We define two functions with $\beta^2 = ae^{2y\xi}$:

and

Consequently, $\varphi(\beta) = a\psi(\beta).$ These two functions are continuous when $\beta\in(0, 1)$.

For $\frac{1}{2} < \gamma < 1$ and $\beta\in(0, 1)$, by Lemma 3.3 in ^[26], we obtain

Therefore,

Theorem 2.3. Assume (1.2) and (1.3) hold, if we select

then we obtain,

where $[m]$ denotes the largest integer less than or equal to $m$, $C_{1} = (\frac{y_{0}-y}{ay})^{\frac{y_{0}-y}{2y}}+\sqrt{a}$.

Proof. By the triangle inequality and Parseval equality, we have

Using (2.6), we obtain

where $B_1(\xi): = \frac{[1-(1-ae^{2y\xi})^{m}]^{\gamma}}{e^{y\xi}}$. According to Lemma 2.3, we obtain

then,

Because $0 < 1-(1-ae^{2y\xi})^{m} < 1$ and $\frac{1}{2} < \gamma < 1$, so $[1-(1-ae^{2y\xi})^{m}]^{\gamma} > [1-(1-ae^{2y\xi})^{m}].$ Futher, we can get $1-[1-(1-ae^{2y\xi})^{m}]^{\gamma} < 1-[1-(1-ae^{2y\xi})^{m}] = (1-ae^{2y\xi})^{m}$. By (1.10), lemma 2.1, and (1.3), (2.6), we get

Then

Due to $m = \big[\frac{E}{\delta}\big]^{\frac{2y}{y_{0}}}$, we obtain

Combining (2.11), (2.12) and (2.13), we obtain

3.   The convergence error estimate with an a posteriori parameter choice rule

In the following text, the Morozov's discrepancy principle is used to select regularization parameter $m$. We choose $m$ to satisfy the first occurrence of

where $\|\hat{g}^{\delta}(\xi)\| > r\delta$, and $r > 1$ is a constant.

Lemma 3.1. Suppose $\rho(m) = \|\hat{K}\widehat{g^{m, \delta}(\cdot+iy)}(\xi, y)-\hat{g}^{\delta}(\xi)\|$, we can deduce the following properties

($\boldsymbol{a}$) $\rho(m)$ is a continuous function;

($\boldsymbol{b}$) $\lim\limits_{m\rightarrow 0}\rho(m) = \|g^{\delta}\|;$

($\boldsymbol{c }$) $\lim\limits_{m\rightarrow\infty}\rho(m) = 0;$

($\boldsymbol{d}$) $\rho(m)$ is a strictly decreasing function.

Lemma 3.2. If $m$ is chosen by (3.1), then we can obtain

here $C_{2} = \frac{y_{0}}{ay}$.

Proof. Because $(1-ae^{2y\xi})\leq 1$ and $\frac{1}{2} < \gamma < 1$, so we have $[(1-ae^{2y\xi})^{m-1}]^{\gamma}\leq1$. According to (3.1), (2.6), (1.10) and lemma 2.1, we obtain

So

Lemma 3.3. Using (1.2) and (3.1), we can obtain

Proof. Because $(1-ae^{2y\xi})\leq 1$ and $\frac{1}{2} < \gamma < 1$, so we have $[(1-ae^{2y\xi})^{m}]^{\gamma}\leq1$. Therefore, we obtain

Theorem 3.4. Assuming that the a priori condition $(1.3)$ and the noise assumption $(1.2)$ hold. If the regularization parameter $m = m(\delta)$ satisfies the iteration stopping criterion (3.1), we can obtain the following convergence error estimates:

where $C_{3} = [(r+1)^{1-\frac{y}{y_{0}}}+\sqrt{\frac{y_{0}}{2y}}(r-1)^{\frac{-y}{y_{0}}}].$

Proof. By Parseval's theorem and triangle equation

Using (2.11) and lemma 3.2, we can approximate $I_{1}$

Because $0 < 1-(1-ae^{2y\xi})^{m} < 1$ and $\frac{1}{2} < \gamma < 1$, so $[1-(1-ae^{2y\xi})^{m}]^{\gamma} > [1-(1-ae^{2y\xi})^{m}].$ Futher, we can get $1-[1-(1-ae^{2y\xi})^{m}]^{\gamma} < 1-[1-(1-ae^{2y\xi})^{m}] = (1-ae^{2y\xi})^{m}$. Using H$\ddot{o}$lder inequality and (1.3), (2.6), lemma 3.3, we can estimate $I_{2}$

Finally, based on the above two estimates, the a posteriori estimate is obtained as follows

4.   Numerical implementation and numerical examples

In this section, we illustrate the effectiveness of the fractional Landweber iterative regularization method for solving this problem through different examples. Examples are the same as those in ^[5]. For the sake of calculation, we fix $y_{0} = 1$ and the domain is

The data $g(x)$ has error, which is expressed as follows

where "randn($\cdot$)" generates a random number that obeys the standard normal distribution. Use the following equation to express the noise level

Under numerical calculation, we select $M = 100$, $p = 2$ and the a priori bound is $E = \|g\|_{L^{2}}$. The way to calculate the approximate solution is fast Fourier transform. We present the error between $g(x+iy)$ and $g^{m, \delta}(x+iy)$ under the means of $L_2$ norm,

Example 1. Take function

with $g(x) = e^{-x^{2}}$, Re$g(z) = e^{y^{2}-x^{2}}\cos(2xy)$, Im$g(z) = e^{y^{2}-x^{2}}\sin(2xy)$.

Example 2. Take function

with $g(x) = \cos(x)$, Re$g(z) = \cosh(y)\cos(x)$, Im$g(z) = -\sinh(y)\sin(x)$.

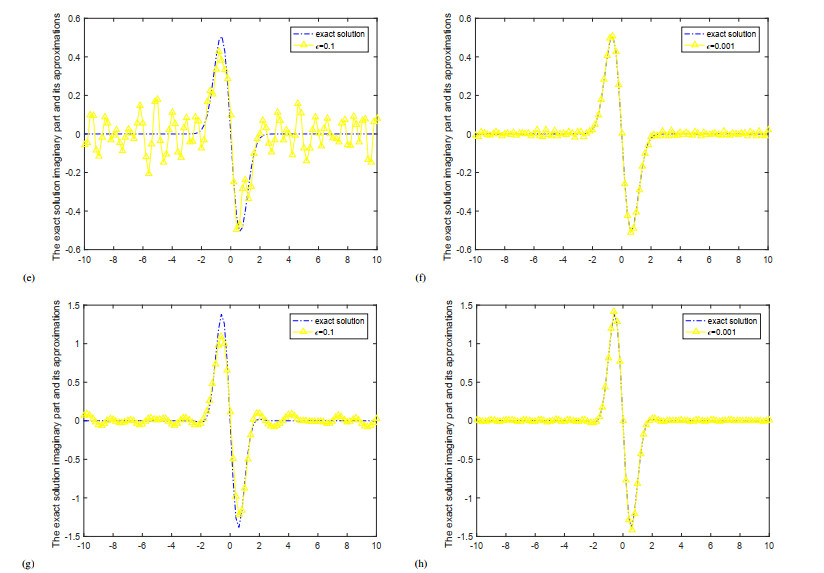
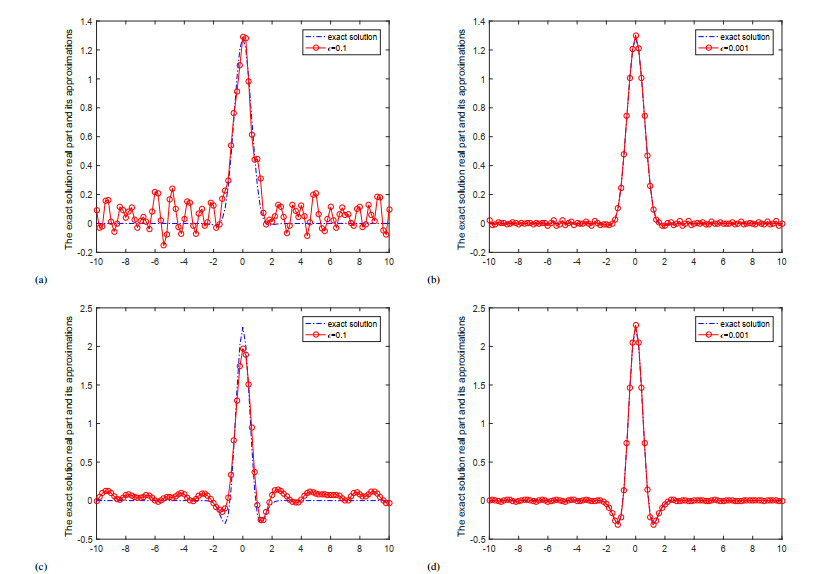
Figure 1 shows the comparison of the real parts of the exact solution and the approximate solution at $y = 0.5$ and $y = 0.9$ for different noise levels $\varepsilon = 0.1, 0.001$ for example 1. Figure 2 shows the comparison of the imaginary parts of the exact solution and the approximate solution at $y = 0.5$ and $y = 0.9$ for different noise levels $\varepsilon = 0.1, 0.001$ for example 1.

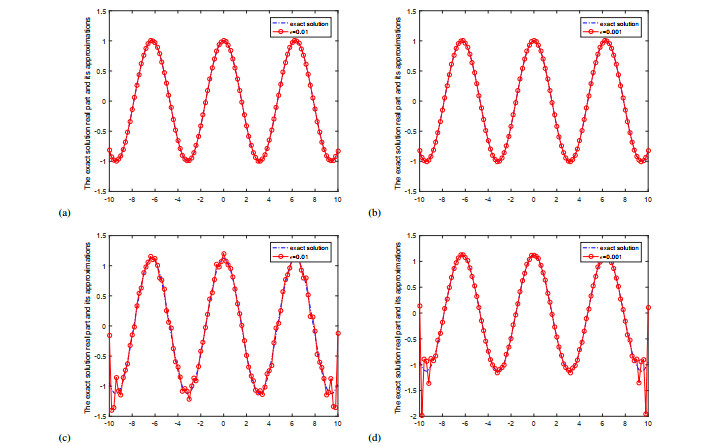
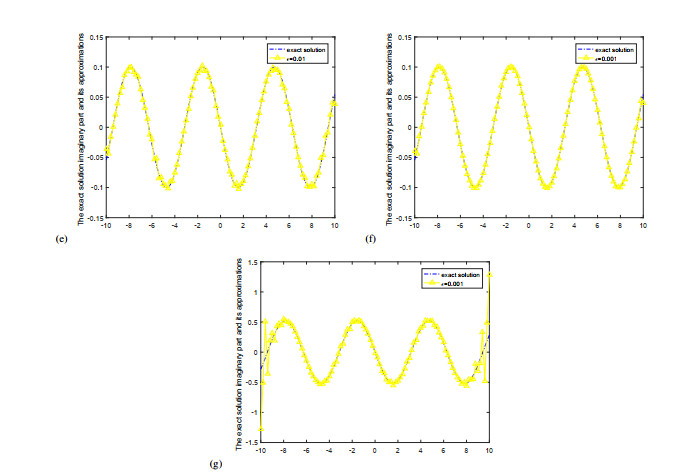
Figure 3 shows the comparison of the real parts of the exact solution and the approximate solution at $y = 0.1$ and $y = 0.5$ for different noise levels $\varepsilon = 0.01, 0.001$ for example 2. Figure 4 shows the comparison of the imaginary parts of the exact solution and the approximate solution at $y = 0.1$ for different noise levels $\varepsilon = 0.01, 0.001$ and $y = 0.5$ for different noise levels $\varepsilon = 0.001$ for example 2.

From Figures 1–4, we can find that the smaller the $\varepsilon$ is, the better the computed approximation is. And the bigger the $y$ is, the worse the computed approximation is. The fitting effect of example 2 is better than that of example 1.

Table 1 shows the error results for different $y$ and $\varepsilon$ in example 1. We take $\gamma = 0.55$ and $\gamma = 1$ for comparison. According to the data in Table 1, we can see that the smaller the $\gamma$, the smaller the error result. The larger $y$ is, the smaller the error result is, which is consistent with the error estimation result obtained in Section 3.

Table 2 shows the results of example 1 for different iteration steps $m$ for $y$ and $\varepsilon$. We take $\gamma = 0.55$ and $\gamma = 1$ for comparison. From the data in Table 2, we can see that the smaller the $\gamma$, the smaller the iteration steps $m$. When $y$ is larger, the number of iteration steps $m$ is larger, which means that the better the image fitting effect, the greater the value of iteration steps $m$.

In addition, when $\gamma = 0.55$, the regularization method involved is fractional Landweber iterative regularization method. When $\gamma = 1$, it is the standard Landweber iterative regularization method. It can be seen from Tables 1–3 that the results of fractional Landweber iterative regularization method are significantly less than those of Landweber iterative regularization method in terms of error and iteration steps $m$. Therefore, the fractional Landweber iterative regularization method is more effective than the Landweber iterative regularization method.

5.   Conclusion

In this paper, we use the fractional Landweber regularization method to solve the problem of analytic continuation on strip domain. We not only give the a priori regularization parameter choice rule, but also we give the a posteriori regularization parameter choice rule. Under these two parameter selection rules, the corresponding convergence error estimates are obtained respectively. For the ill-posed problem discussed in this paper, besides the fractional Landweber iterative regularization method used in this paper, there are also other regularization methods, such as Tikhonov regularization method, quasi-boundary regularization method and so on. In these methods, the process of obtaining a priori and a posteriori error convergence estimates is similar, but in the results obtained, Tikhonov regularization method will produce saturation effect, while the fractional Landweber iterative regularization method will not produce saturation effect. Numerical examples also show this regularization method is effective.

Acknowledgements

The project is supported by the National Natural Science Foundation of China (No.11961044), the Doctor Fund of Lan Zhou University of Technology.

Conflict of interest

The authors declare that they have no competing interests.