Photoinduced transformations of optical properties of CdSe and Ag-In-S nanocrystals embedded in the films of polyvinyl alcohol

Lyudmyla V. Borkovska; Olexander Gudymenko; Olexander Stroyuk; Alexandra Raevskaya; Olena Fesenko; Tetyana Kryshtab; Lyudmyla V. Borkovska; Olexander Gudymenko; Olexander Stroyuk; Alexandra Raevskaya; Olena Fesenko; Tetyana Kryshtab

doi:10.3934/matersci.2016.2.658

AIMS Materials Science

2016, Volume 3, Issue 2: 658-668. doi: 10.3934/matersci.2016.2.658

Previous Article Next Article

Research article Special Issues

Photoinduced transformations of optical properties of CdSe and Ag-In-S nanocrystals embedded in the films of polyvinyl alcohol

1.
V. Lashkaryov Institute of Semiconductor Physics of National Academy of Sciences (NAS) of Ukraine, 41 Pr. Nauky, 03028 Kyiv, Ukraine
2.
L. Pysarzhevsky Institute of Physical Chemistry of NAS of Ukraine, 31 Pr. Nauky, 03028 Kyiv, Ukraine
3.
Institute of Physics of NAS of Ukraine, 46 Pr. Nauky, 03028 Kyiv, Ukraine
4.
Instituto Politécnico Nacional – ESFM, Av. IPN, Ed.9 U.P.A.L.M., 07738 Mexico D.F., Mexico

Received: 31 March 2016 Accepted: 27 May 2016 Published: 01 June 2016

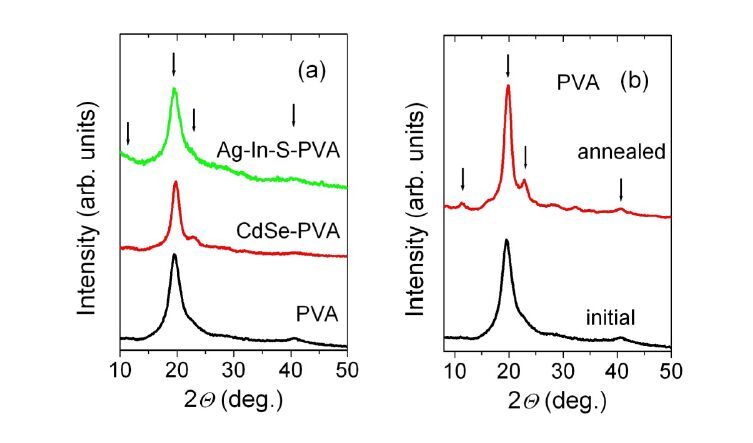
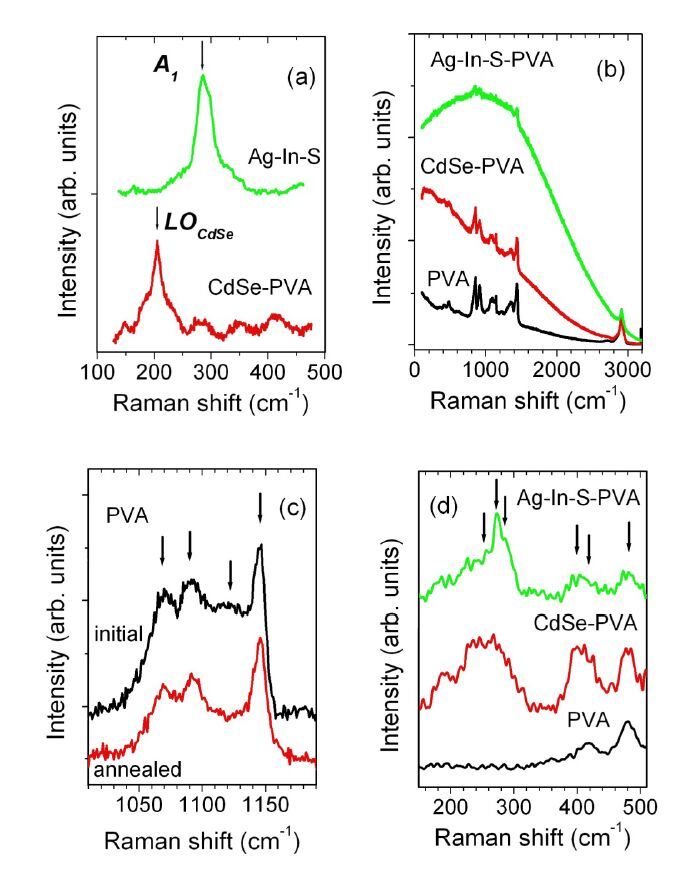
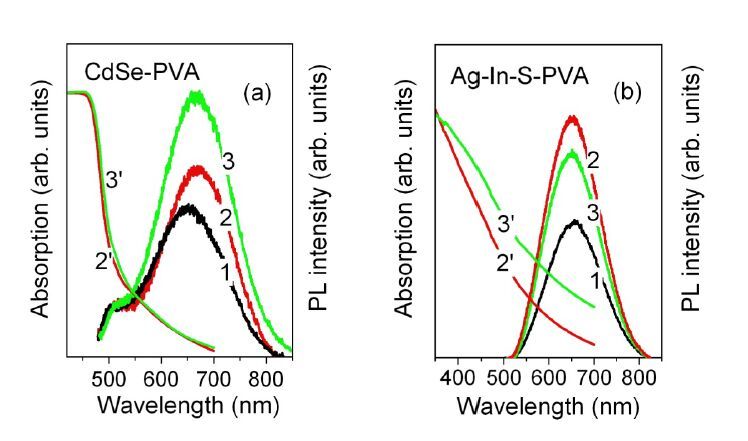
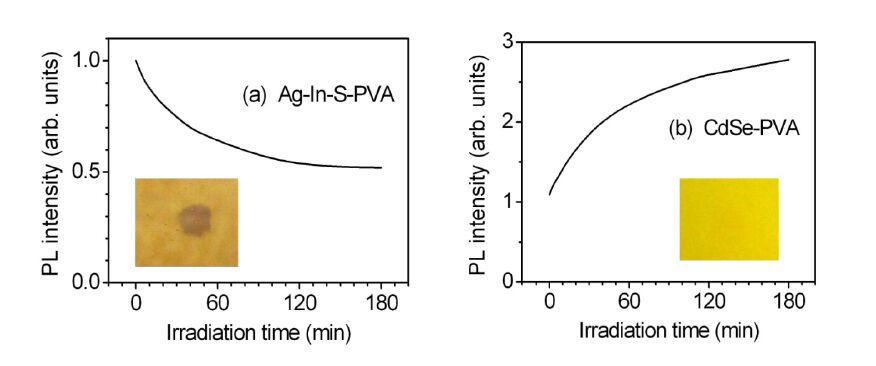
The results of investigation of photostability of the composites of CdSe and Ag-In-S nanocrystals (NCs) embedded in the films of polyvinyl alcohol (PVA) are presented. The films were studied by photoluminescence (PL), optical absorption, micro-Raman and X-ray diffraction methods. It is found that heating of the films to 100 °C promotes PVA crystallization and stimulates an increase of the PL intensity for the NCs of both types. The latter effect is ascribed mainly to the improvement of NC surface passivation by functional groups of PVA. The illumination with the 409-nm LED’s light enhances PL intensity for CdSe NCs and decreases it for Ag-In-S NCs as well as results in the darkening of the films. The color of the Ag-In-S-PVA film restores with time, while the change of the optical properties of the CdSe-PVA composite is irreversible. The possible mechanisms of the revealed effects, such as structural transformations at NC/PVA interface as well as the formation of new light-absorbing species are discussed.

Keywords:

Citation: Lyudmyla V. Borkovska, Olexander Gudymenko, Olexander Stroyuk, Alexandra Raevskaya, Olena Fesenko, Tetyana Kryshtab. Photoinduced transformations of optical properties of CdSe and Ag-In-S nanocrystals embedded in the films of polyvinyl alcohol[J]. AIMS Materials Science, 2016, 3(2): 658-668. doi: 10.3934/matersci.2016.2.658

Related Papers:

[1]	Wangming Lu, Zhiyong Yu, Zhanheng Chen, Haijun Jiang . Prescribed-time cluster practical consensus for nonlinear multi-agent systems based on event-triggered mechanism. Mathematical Biosciences and Engineering, 2024, 21(3): 4440-4462. doi: 10.3934/mbe.2024196
[2]	Yuhan Su, Shaoping Shen . Adaptive predefined-time prescribed performance control for spacecraft systems. Mathematical Biosciences and Engineering, 2023, 20(3): 5921-5948. doi: 10.3934/mbe.2023256
[3]	Jiabao Gu, Hui Wang, Wuquan Li . Output-Feedback stabilization for stochastic nonlinear systems with Markovian switching and time-varying powers. Mathematical Biosciences and Engineering, 2022, 19(11): 11071-11085. doi: 10.3934/mbe.2022516
[4]	Leonid Shaikhet . Stability of a positive equilibrium state for a stochastically perturbed mathematical model ofglassy-winged sharpshooter population. Mathematical Biosciences and Engineering, 2014, 11(5): 1167-1174. doi: 10.3934/mbe.2014.11.1167
[5]	Linni Li, Jin-E Zhang . Input-to-state stability of stochastic nonlinear system with delayed impulses. Mathematical Biosciences and Engineering, 2024, 21(2): 2233-2253. doi: 10.3934/mbe.2024098
[6]	Dongxiang Gao, Yujun Zhang, Libing Wu, Sihan Liu . Fixed-time command filtered output feedback control for twin-roll inclined casting system with prescribed performance. Mathematical Biosciences and Engineering, 2024, 21(2): 2282-2301. doi: 10.3934/mbe.2024100
[7]	Stephan Gerster, Michael Herty, Elisa Iacomini . Stability analysis of a hyperbolic stochastic Galerkin formulation for the Aw-Rascle-Zhang model with relaxation. Mathematical Biosciences and Engineering, 2021, 18(4): 4372-4389. doi: 10.3934/mbe.2021220
[8]	Lin Zhang, Yongbin Ge, Zhi Wang . Positivity-preserving high-order compact difference method for the Keller-Segel chemotaxis model. Mathematical Biosciences and Engineering, 2022, 19(7): 6764-6794. doi: 10.3934/mbe.2022319
[9]	Rinaldo M. Colombo, Mauro Garavello . Optimizing vaccination strategies in an age structured SIR model. Mathematical Biosciences and Engineering, 2020, 17(2): 1074-1089. doi: 10.3934/mbe.2020057
[10]	Yue Song, Yi Zhang, Song Yang, Na Li . Investigation on stability and controller design for singular bio-economic systems with stochastic fluctuations. Mathematical Biosciences and Engineering, 2021, 18(3): 2991-3005. doi: 10.3934/mbe.2021150

Abstract

1. Introduction

Stochastic nonlinear control is a hot topic because of its wide application in economic and engineering fields. The pioneer work is ^{[1,2,3,4,5,6,7,8]}. Specifically, ^[1,2,3] propose designs with quadratic Lyapunov functions coupled with weighting functions and ^[4,5,6,7,8] develop designs with quartic Lyapunov function, which are further developed by ^[9,10,11,12]. Recently, a class of stochastic systems (SSs) whose Jacobian linearizations may have unstable modes, has received much attention. Such systems are also called stochastic high-order nonlinear systems (SHONSs), which include a class of stochastic benchmark mechanical systems ^[13] as a special case. In this direction, ^[14] studies the state-feedback control with stochastic inverse dynamics; ^[15] develops a stochastic homogeneous domination method, which completely relaxes the order restriction required in ^[13], and investigates the output-feedback stabilization for SHONSs with unmeasurable states; ^[16] investigates the output-feedback tracking problem; ^[17] studies the adaptive state-feedback design for state-constrained systems. It should be emphasized that ^{[13,14,15,16,17]}, only achieve stabilization in asymptotic sense (as time goes to infinity). However, many real applications appeals for prescribed-time stabilization, which permits the worker to prescribe the convergence times in advance.

For the prescribed-time control, ^[18,19] design time-varying feedback to solve the regulation problems of normal-form nonlinear systems; ^[20] considers networked multi-agent systems; ^[21,22] investigates the prescribed-time design for linear systems in controllable canonical form; ^[23] designs the output-feedback controller for uncertain nonlinear strict-feedback-like systems. It should be noted that the results in ^{[18,19,20,21,22,23]} don't consider stochastic noise. For SSs, ^[24] is the first paper to address the stochastic nonlinear inverse optimality and prescribed-time stabilization problems; The control effort is further reduced in ^[25]; Recently, ^[26] studies the prescribed-time output-feedback for SSs without/with sensor uncertainty. It should be noted that ^[24,25,26] don't consider SHONSs. From practical applications, it is important to solves the prescribed-time control problem of SHONSs since it permits the worker to set the convergence times in advance.

Motivated by the above discussions, this paper studies the prescribed-time design for SSs with high-order structure. The contributions include:

1) This paper proposes new prescribed-time design for SHONSs. Since Jacobian linearizations of such a system possibly have unstable modes, all the prescribed-time designs in ^[24,25,26] are invalid. New design and analysis tools should be developed.

2) This paper develops a more practical design than those in ^{[13,14,15,16,17]}. Different from the designs in ^{[13,14,15,16,17]} where only asymptotic stabilization can be achieved, the design in this paper can guarantee that the closed-loop system is prescribed-time mean-square stable, which is superior to those in ^{[13,14,15,16,17]} since it permits the worker to prescribe the convergence times in advance without considering the initial conditions.

The remainder of this paper is organized as follows. In Section 2, the problem is formulated. In Section 3, the controller is designed and the stability analysis is given. Section 4 uses an example to explain the validity of the prescribed-time design. The conclusions are collected in Section 6.

2. Problem formulation

Consider the following class of SHONSs

$\begin{eqnarray} dx_{1}& = &x_{2}^{p}dt+\varphi_{1}^{T}(x)d\omega, \end{eqnarray}$ $

(2.1)

$\begin{eqnarray} dx_{2}& = &udt+\varphi_{2}^{T}(x)d\omega, \end{eqnarray}$ $

(2.2)

where $ x = (x_{1}, x_{2})^{T} \in R^{2} $ and $ u \in R $ are the system state and control input. $ p\geq1 $ is an odd integral number. The functions $ \varphi_{i}: R^{2}\rightarrow R^{m} $ are smooth in $ x $ with $ \varphi_{i}(0) = 0 $, $ i = 1, 2 $. $ \omega $ is an $ m $-dimensional independent standard Wiener process.

The assumptions we need are as follows.

Assumption 1. There is a constant $ c > 0 $ such that

$\begin{eqnarray} |\varphi_{1}(x)|&\leq&c|x_{1}|^{\frac{p+1}{2}}, \end{eqnarray}$ $

(2.3)

$\begin{eqnarray} |\varphi_{2}(x)|&\leq&c(|x_{1}|^{\frac{p+1}{2}}+|x_{2}|^{\frac{p+1}{2}}). \end{eqnarray}$ $

(2.4)

We introduce the function:

$\begin{eqnarray} \mu(t)& = &\left(\frac{T}{t_{0}+T-t}\right)^{m}, \quad t\in[t_{0}, t_{0}+T), \end{eqnarray}$ $

(2.5)

where $ m\geq 2 $ is an integral number. Obviously, the function $ \mu(t) $ is monotonically increasing on $ [t_{0}, t_{0}+T) $ with $ \mu(t_{0}) = 1 $ and $ \lim\limits_{t\rightarrow t_{0}+T}\mu(t) = +\infty $.

Our control goal is to design a prescribed-time state-feedback controller, which guarantees that the closed-loop system has an almost surely unique strong solution and is prescribed-time mean-square stable.

3. Controller design and stability analysis

In the following, we design a time-varying controller for system (2.1)–(2.2) step by step.

Step 1. In this step, our goal is to design the virtual controller $ x_{2}^{*} $.

Define $ V_{1} = \frac{1}{4}\xi_{1}^{4} $, $ \xi_{1} = x_{1} $, from (2.1), (2.3) and (2.5) we have

$\begin{eqnarray} \mathcal{L}V_{1}(\xi_{1}) & = &\xi_{1}^{3}x_{2}^{p}+\frac{3}{2}\xi_{1}^{2}|\varphi_{1}|^{2}\\ &\leq&\xi_{1}^{3}x_{2}^{p}+\frac{3}{2}c^{2}\xi_{1}^{p+3}\\ &\leq&\xi_{1}^{3}(x_{2}^{p}-x_{2}^{*p})+\xi_{1}^{3}x_{2}^{*p}+\frac{3}{2}c^{2}\mu^{p}\xi_{1}^{p+3}. \end{eqnarray}$ $

(3.1)

Choosing

$\begin{eqnarray} x_{2}^{*}& = &-\mu\left(2+\frac{3}{2}c^{2}\right)^{1/p}\xi_{1}\\ &\triangleq&-\mu\alpha_{1}\xi_{1}, \end{eqnarray}$ $

(3.2)

which substitutes into (3.1) yields

$\begin{eqnarray} \mathcal{L}V_{1}(\xi_{1})&\leq&-2\mu^{p}\xi_{1}^{p+3}+\xi_{1}^{3}(x_{2}^{p}-x_{2}^{*p}), \end{eqnarray}$ $

(3.3)

where $ \alpha_{1} = (2+\frac{3}{2}c^{2})^{1/p} $.

Step 2. In this step, our goal is to design the actual controller $ u $.

Define $ \xi_{2} = x_{k}-x_{2}^{*} $, from (3.2) we get

$\begin{eqnarray} \xi_{2} = x_{2}+\mu\alpha_{1}\xi_{1}. \end{eqnarray}$ $

(3.4)

By using (2.1)–(2.2) and (3.4) we get

$\begin{eqnarray} d\xi_{2}& = &\left(u+\frac{m}{T}\mu^{1+1/m}\alpha_{1}\xi_{1}+\mu\alpha_{1}x_{2}^{p}\right)dt +\left(\varphi_{2}^{T}+\mu\alpha_{1}\varphi_{1}^{T}\right)d\omega. \end{eqnarray}$ $

(3.5)

We choose the following Lyapunov function

$\begin{eqnarray} V_2(\xi_{1}, \xi_{2})& = &V_{1}(\xi_{1})+\frac{1}{4}\xi_{2}^{4}. \end{eqnarray}$ $

(3.6)

It follows from (3.3), (3.5)–(3.6) that

$\begin{eqnarray} \mathcal{L}V_2 &\leq&-2\mu^{p}\xi_{1}^{p+3}+\xi_{1}^{3}(x_{2}^{p}-x_{2}^{*p}) +\xi_{2}^{3}\left(u+\frac{m}{T}\mu^{1+1/m}\alpha_{1}\xi_{1}+\mu\alpha_{1}x_{2}^{p}\right)\\&& +\frac{3}{2}\xi_{2}^{2}|\varphi_{2}+\mu\alpha_{1}\varphi_{1}|^{2}. \end{eqnarray}$ $

(3.7)

By using (3.4) we have

$\begin{eqnarray} \xi_{1}^{3}(x_{2}^{p}-x_{2}^{*p})&\leq&|\xi_{1}|^{3}|\xi_{2}|(x_{2}^{p-1}+x_{2}^{*p-1})\\ &\leq&|\xi_{1}|^{3}|\xi_{2}|((\beta_{1}+1)\mu^{p-1}\alpha_{1}^{p-1}\xi_{1}^{p-1}+\beta_{1}\xi_{2}^{p-1})\\ & = &(\beta_{1}+1)\mu^{p-1}\alpha_{1}^{p-1}|\xi_{1}|^{p+2}|\xi_{2}|+\beta_{1}|\xi_{1}|^{3}|\xi_{2}|^{p}, \end{eqnarray}$ $

(3.8)

where

$\begin{eqnarray} \beta_{1}& = &\max\{1, 2^{p-2}\}. \end{eqnarray}$ $

(3.9)

By using Young's inequality we get

$\begin{eqnarray} (\beta_{1}+1)\mu^{p-1}\alpha_{1}^{p-1}|\xi_{1}|^{p+2}|\xi_{2}|\leq\frac{1}{3}\mu^{p}\xi_{1}^{p+3}+\frac{1}{3+p}\left(\frac{3+p}{3(2+p)}\right)^{-(2+p)} ((\beta_{1}+1)\alpha_{1}^{p-1})^{p+3}\mu^{-3}\xi_{2}^{p+3} \end{eqnarray}$ $

(3.10)

and

$\begin{eqnarray} \beta_{1}|\xi_{1}|^{3}|\xi_{2}|^{p}&\leq&\frac{1}{3}\mu^{p}\xi_{1}^{3+p}+\frac{p}{p+3}\left(\frac{3+p}{9}\right)^{-3/p} \beta_{1}^{(3+p)/p}\mu^{-3}\xi_{2}^{p+3}. \end{eqnarray}$ $

(3.11)

Substituting (3.10)–(3.11) into (3.8) yields

$\begin{eqnarray} \xi_{1}^{3}(x_{2}^{p}-x_{2}^{*p})&\leq&\frac{2}{3}\mu^{p}\xi_{1}^{p+3}+\Big(\frac{p}{p+3}\left(\frac{p+3}{9}\right)^{-3/p} \beta_{1}^{(p+3)/p}\\&&+\frac{1}{p+3}\left(\frac{p+3}{3(p+2)}\right)^{-(p+2)} ((\beta_{1}+1)\alpha_{1}^{p-1})^{p+3}\Big)\mu^{-3}\xi_{2}^{p+3}. \end{eqnarray}$ $

(3.12)

From (2.3), (2.4), (3.2) and (3.4) we have

$\begin{eqnarray} |\varphi_{2}+\mu\alpha_{1}\varphi_{1}|^{2}&\leq& 2|\varphi_{2}|^{2}+2\mu^{2}\alpha_{1}^{2}|\varphi_{1}|^{2}\\ &\leq& 4c^{2}(|x_{1}|^{1+p}+|x_{2}|^{1+p})+2c^{2}\alpha_{1}^{2}\mu^{2}|x_{1}|^{1+p}\\ &\leq& \beta_{2}\mu^{1+p}|\xi_{1}|^{p+1}+4c^{2}2^{p}|\xi_{2}|^{1+p}, \end{eqnarray}$ $

(3.13)

where

$\begin{eqnarray} \beta_{2}& = &4c^{2}(1+2^{p}\alpha_{1}^{p+1})+2c^{2}\alpha_{1}^{2}. \end{eqnarray}$ $

(3.14)

By using (3.13) we get

$\begin{array}{l} \frac{3}{2}\xi_{2}^{2}|\varphi_{2}+\mu\alpha_{1}\varphi_{1}|^{2}\leq\frac{1}{3}\mu^{p}\xi_{1}^{3+p} +\Big(\frac{2}{3+p}\left(\frac{p+3}{3(1+p)}\right)^{-(1+p)/2} \\(\frac{3}{2}\beta_{2})^{(3+p)/2}+6c^{2}2^{p}\Big)\mu^{3(1+p)/2}\xi_{2}^{p+3}. \end{array}$ $

(3.15)

It can be inferred from (3.7), (3.12) and (3.15) that

$\begin{eqnarray} \mathcal{L}V_2 &\leq&-\mu^{p}\xi_{1}^{p+3} +\xi_{2}^{3}\left(u+\frac{m}{T}\mu^{1+1/m}\alpha_{1}\xi_{1}+\mu\alpha_{1}x_{2}^{p}\right) +\beta_{3}\mu^{3(p+1)/2}\xi_{2}^{p+3}, \end{eqnarray}$ $

(3.16)

where

$\begin{eqnarray} \beta_{3}& = & \frac{p}{3+p}\left(\frac{3+p}{9}\right)^{-3/p} \beta_{1}^{(3+p)/p}+\frac{1}{3+p}\left(\frac{p+3}{3(p+2)}\right)^{-(p+2)} ((\beta_{1}+1)\alpha_{1}^{p-1})^{3+p}\\&&+\frac{2}{3+p}\left(\frac{p+3}{3(1+p)}\right)^{-(1+p)/2} (\frac{3}{2}\beta_{2})^{(3+p)/2}+6c^{2}2^{p}. \end{eqnarray}$ $

(3.17)

We choose the controller

$\begin{eqnarray} u& = &-\frac{m}{T}\mu^{1+1/m}\alpha_{1}\xi_{1}-\mu\alpha_{1}x_{2}^{p}-(1+\beta_{3})\mu^{3(p+1)/2}\xi_{2}^{p}, \end{eqnarray}$ $

(3.18)

then we get

$\begin{eqnarray} \mathcal{L}V_2 &\leq&-\mu^{p}\xi_{1}^{p+3} -\mu^{3(p+1)/2}\xi_{2}^{p+3}. \end{eqnarray}$ $

(3.19)

Now, we describe the main stability analysis results for system (2.1)–(2.2).

Theorem 1. For the plant (2.1)–(2.2), if Assumption 1 holds, with the controller (3.18), the following conclusions are held.

1) The plant has an almost surely unique strong solution on $ [t_{0}, t_{0}+T) $;

2) The equilibrium at the origin of the plant is prescribed-time mean-square stable with $ \lim\limits_{t\rightarrow t_{0}+T} E|x|^{2} = 0 $.

Proof. By using Young's inequality we get

$\begin{eqnarray} \frac{1}{4}\mu \xi_{1}^{4} &\leq&\mu^{p}\xi_{1}^{p+3}+\beta_{4}\mu^{-3}, \end{eqnarray}$ $

(3.20)

$\begin{eqnarray} \frac{1}{4}\mu \xi_{2}^{4} &\leq&\mu^{3(p+1)/2}\xi_{2}^{p+3}+\beta_{4}\mu^{-3}, \end{eqnarray}$ $

(3.21)

where

$\begin{eqnarray} \beta_{4}& = &\frac{p-1}{p+3}(\frac{3+p}{4})^{-4/(p-1)}(\frac{1}{4})^{(3+p)/(p-1)}. \end{eqnarray}$ $

(3.22)

It can be inferred from (3.19)–(3.21) that

$\begin{eqnarray} \mathcal{L}V_2 &\leq&-\frac{1}{4}\mu \xi_{1}^{4}-\frac{1}{4}\mu \xi_{2}^{4}+2\beta_{4}\mu^{-3}\\ & = &-\mu V_{2}+2\beta_{4}\mu^{-3}. \end{eqnarray}$ $

(3.23)

From (2.1), (2.2) and (3.18), the local Lipschitz condition is satisfied by the plant. By (3.23) and using Lemma 1 in ^[24], the plant has an almost surely unique strong solution on $ [t_{0}, t_{0}+T) $, which shows that conclusion 1) is true.

Next, we verify conclusion 2).

For each positive integer $ k $, the first exit time is defined as

$\begin{eqnarray} \rho_k = \inf\{t: t\geq t_0, \; |x(t)|\geq k\}. \end{eqnarray}$ $

(3.24)

Choosing

$\begin{eqnarray} V = e^{\int^{t}_{t _{0}}\mu(s)ds}V_{2}. \end{eqnarray}$ $

(3.25)

From (3.23) and (3.25) we have

$\begin{eqnarray} \mathcal{L}V& = &e^{\int^{t}_{t _{0}}\mu(s)ds}(\mathcal{L}V_{2}+\mu V_{2})\leq 2\beta_{4}\mu^{-3}e^{\int^{t}_{t _{0}}\mu(s)ds}. \end{eqnarray}$ $

(3.26)

By (3.26) and using Dynkin's formula we get

$\begin{eqnarray} EV(\rho_k\wedge t, x(\rho_k\wedge t))& = &V_{n}(t_{0}, x_{0})+E\left\{\int^{\rho_k\wedge t}_{t_{0}}\mathcal{L}V(x(\tau), \tau)d\tau\right\} \\ &\leq&V_{n}(t_{0}, x_{0})+2\beta_{4}\int^{ t}_{t_{0}}\mu^{-3}e^{\int^{\tau}_{t _{0}}\mu(s)ds}d\tau. \end{eqnarray}$ $

(3.27)

Using Fatou Lemma, from (3.27) we have

$\begin{eqnarray} EV(t, x)&\leq&V_{n}(t_{0}, x_{0})+2\beta_{4}\int^{ t}_{t_{0}}\mu^{-3}e^{\int^{\tau}_{t _{0}}\mu(s)ds}d\tau, \quad t\in[t_{0}, t_{0}+T). \end{eqnarray}$ $

(3.28)

By using (3.25) and (3.28) we get

$\begin{eqnarray} EV_{2}&\leq&e^{-\int^{t}_{t _{0}}\mu(s)ds}\left(V_{n}(t_{0}, x_{0})+2\beta_{4}\int^{ t}_{t_{0}}\mu^{-3}e^{\int^{\tau}_{t _{0}}\mu(s)ds}d\tau\right), \quad t\in[t_{0}, t_{0}+T). \end{eqnarray}$ $

(3.29)

By using (3.6) and (3.29) we obtain

$\begin{eqnarray} \lim\limits_{t\rightarrow t_{0}+T} E|x|^{2}& = &0. \end{eqnarray}$ $

(3.30)

4. A simulation example

Consider the prescribed-time stabilization for the following system

$\begin{eqnarray} &&dx_1 = x_2^{3}dt+0.1x_1^{2}d\omega, \end{eqnarray}$ $

(4.1)

$\begin{eqnarray} &&dx_2 = udt+ 0.2x_1x_2d\omega, \end{eqnarray}$ $

(4.2)

where $ p_{1} = 3 $, $ p_{2} = 1 $. Noting $ 0.2x_1x_2\leq 0.1(x_{1}^{2}+x_{2}^{2}) $, Assumption 1 is satisfied.

Choosing

$\begin{eqnarray} \mu(t)& = &\left(\frac{1}{1-t}\right)^{2}, \quad t\in[0, 1), \end{eqnarray}$ $

(4.3)

According to the design method in Section 3, we have

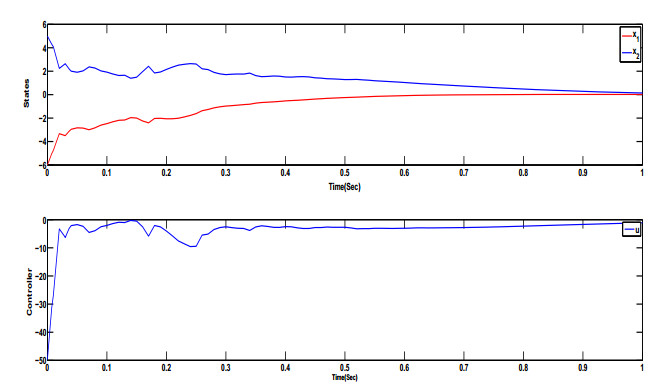
$\begin{eqnarray} u& = & -3\mu^{1.5}x_{1}-1.5\mu x_{2}^{3}-57\mu^{6}(x_{2}+1.5\mu x_{1})^{3} \end{eqnarray}$ $

(4.4)

In the practical simulation, we select the initial conditions as $ x_{1}(0) = -6 $, $ x_{2}(0) = 5 $. Figure 1 shows the responses of (4.1)–(4.4), from which we can obtain that $ \lim\limits_{t\rightarrow t_{0}+T} E|x_{1}|^{2} = \lim\limits_{t\rightarrow t_{0}+T} E|x_{2}|^{2} = 0 $, which means that the controller we designed is effective.

Figure 1. The responses of closed-loop system (4.1)–(4.4).

DownLoad: Full-Size Img PowerPoint

5. Concluding remarks

This paper proposes a new design method of prescribed-time state-feedback for SHONSs. the controller we designed can guarantee that the closed-loop system has an almost surely unique strong solution and the equilibrium at the origin of the closed-loop system is prescribed-time mean-square stable. The results in this paper are more practical than those in ^{[13,14,15,16,17]} since the design in this paper permits the worker to prescribe the convergence times in advance without considering the initial conditions.

There are some related problems to investigate, e.g., how to extend the results to multi-agent systems ^[27], impulsive systems ^[28,29,30] or more general high-order systems ^{[31,32,33,34]}.

Acknowledgments

This work is funded by Shandong Provincial Natural Science Foundation for Distinguished Young Scholars, China (No. ZR2019JQ22), and Shandong Province Higher Educational Excellent Youth Innovation team, China (No. 2019KJN017).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	Talapin DV, Lee J-S, Kovalenko MV, et al. (2010) Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications. Chem Rev 110: 389–458. doi: 10.1021/cr900137k
[2]	Mattoussi H, Palui G, Na HB (2012) Luminescent quantum dots as platforms for probing in vitro and in vivo biological process. Adv Drug Deliv Rev 64: 138–166.
[3]	Murray CB, Norris DJ, Bawendi MG (1993) Synthesis and characterization of nearly monodisperse CdE (E = S, Se, Te) semiconductor nanocrystallites. J Am Chem Soc 115: 8706–8715. doi: 10.1021/ja00072a025
[4]	Wang W, Geng Y, Yan P, et al. (1999) A novel mild route to nanocrystalline selenides at room temperature. J Am Chem Soc 121: 4062–4063.
[5]	Nguyen CQ, Afzaal M, Malik MA, et al. (2007) Novel inorganic rings and materials deposition. J Organometal Chem 692: 2669–2677. doi: 10.1016/j.jorganchem.2006.11.043
[6]	Afzaal M, Crouch D, Malik MA, et al. (2003) Deposition of CdSe thin films using a novel single-source precursor; [MeCd{(SePⁱPr₂)₂N}]₂. J Mater Chem 13: 639–640. doi: 10.1039/b300608p
[7]	Peng Q, Dong Y, Deng Z, et al. (2001) Low-temperature elemental direct- reaction route to II–VI semiconductor nanocrystalline ZnSe and CdSe. Inorg Chem 40: 3840–3841. doi: 10.1021/ic0100424
[8]	Zhu J, Koltypin Y, Gedanken A (2000) General sonochemical method for the preparation of nanophasic selenides: synthesis of ZnSe nanoparticles. Chem Mater 12: 73–78.
[9]	Nafees M, Ali S, Idrees S, et al. (2013) A simple microwave assisted aqueous route to synthesis CuS nanoparticles and further aggregation to spherical shape. Appl Nanosci 3: 119–124. doi: 10.1007/s13204-012-0113-9
[10]	Isac L, Duta A, Kariza A, et al. (2007) Copper sulphide obtained by spray pyrolysis-possible absorbers in solid state solar cells. Thin Sol Films 515: 5755–5758. doi: 10.1016/j.tsf.2006.12.073
[11]	Chang W, Wu C, Jeng M, et al. (2010) Ternary Ag-In-S polycrystalline films deposited using chemical bath deposition for photoelectrochemical applications. Mater Chem Phys 120: 307–312. doi: 10.1016/j.matchemphys.2009.11.003
[12]	Raevskaya AE, Ivanchenko MV, Stroyuk OL, et al. (2015) Luminescent Ag-doped In₂S₃ nanoparticles stabilized by mercaptoacetate in water and glycerol. J Nanopart Res 17: 135. doi: 10.1007/s11051-015-2953-1
[13]	Tomczak N, Janczewski D, Han M, et al. (2009) Designer polymer-quantum dot architectures. Progr Polym Sci 34: 393–430. doi: 10.1016/j.progpolymsci.2008.11.004
[14]	Pritchad JG (1970) Polyvinyl Alcohol. Basic Properties and Uses, London: Gordon and Breach.
[15]	DeMerlis C C, Schoneker D R (2003) Review of the oral toxicity of polyvinyl alcohol (PVA). Food Chem Toxicol 41: 319–326. doi: 10.1016/S0278-6915(02)00258-2
[16]	Borkovska L, Korsunska N, Stara T, et al. (2013) Enhancement of the photoluminescence in CdSe quantum dot–polyvinyl alcohol composite by light irradiation. Appl Surf Sci 281: 118–122. doi: 10.1016/j.apsusc.2012.12.146
[17]	Raevskaya AE, Stroyuk AL, Kuchmiy SY (2006) Preparation of colloidal CdSe and CdS/CdSe nanoparticles from sodium selenosulfate in aqueous polymers solutions. J Colloid Interface Sci 302: 133–141. doi: 10.1016/j.jcis.2006.06.018
[18]	Meulenberg RW, Jennings T, Strouse G (2004) Compressive and tensile stress in colloidal CdSe semiconductor quantum dots. Phys Rev B 70: 235311. doi: 10.1103/PhysRevB.70.235311
[19]	Ohrendorf FW, Hauseler H (1999) Lattice Dynamics of Chalcopyrite Type Compounds. Part I. Vibrational Frequencies. Cryst Res Technol 34: 339–349.
[20]	Badr YA, Abd El-Kader KM, Khafagy RM (2004) Raman spectroscopic study of CdS, PVA composite films. J Appl Polym Sci 92: 1984–1992. doi: 10.1002/app.20017
[21]	Iwamoto R, Miya M, Mima S (1979) Determination of crystallinity of swollen poly(vinyl alcohol) by laser Raman spectroscopy. J Polymer Sci Polym Phys Ed 17: 1507–1515.
[22]	Baskoutas S, Terzis AF (2006) Size-dependent band gap of colloidal quantum dots. J Appl Phys 99: 013708. doi: 10.1063/1.2158502
[23]	Hong SP, Park HK, Oh JH, et al. (2012) Comparisons of the structural and optical properties of o-AgInS₂, t-AgInS₂, and c-AgIn₅S₈ nanocrystals and their solid-solution nanocrystals with ZnS. J Mater Chem 22: 18939–18949. doi: 10.1039/c2jm33879c
[24]	Borkovska L, Romanyuk А, Strelchuk V, et al. (2015) Optical characterization of the AgInS₂ nanocrystals synthesized in aqueous media under stoichiometric conditions. Mat Sci Semicond Proces 37: 135–142. doi: 10.1016/j.mssp.2015.02.041
[25]	Lifshitz E, Dag I, Litvin I, et al. (1998) Optically Detected Magnetic Resonance Study of Electron/Hole Traps on CdSe Quantum Dot Surfaces. J Phys Chem B 102: 9245–9250.
[26]	Carrillo-Carrión C, Cárdenas S, Simonet BM, et al. (2009) Quantum dotsluminescence enhancement due to illumination withUV/Vislight. Chem Commun 5214–5226.
[27]	Shtareva DS, Makarevich KS, Syuya AV (2011) Behavioral features of photostimulated processes in the heterogeneous composition of polymer–semiconductor–salt of a metal. J Photochem Photobiol A Chem 222: 146–158.
[28]	Henglein A (1993) Physicochemical Properties of Small Metal Particles in Solution: “Microelectrode” Reactions, Chemisorption, Composite Metal particles, and The Atom-to-Metal Transition. J Phys Chem 97: 5457–5471. doi: 10.1021/j100123a004
[29]	Stroyuk AL, Shvalagin VV, Kuchmiy SY (2007) Photochemical synthesis of ZnO/Ag nanocomposites. J Nanopart Res 9: 427–440. doi: 10.1007/s11051-006-9086-5
[30]	Kryukov AI, Zinchuk NN, Korzhak AV, et al. (2004) Optical and catalytic properties of Ag₂S nanoparticles. J Mol Catal A Chem 221: 209–221. doi: 10.1016/j.molcata.2004.07.009
[31]	Ershov BG (1999) Short-lived metal clusters in aqueous solutions: synthesis, identification and properties. Izvestia AN Ser Khim No 1: 1–15 (In Russian).

This article has been cited by:

1.	Ran Liu, Hui Wang, Wuquan Li, Prescribed-time stabilization and inverse optimal control of stochastic high-order nonlinear systems, 2024, 67, 1674-733X, 10.1007/s11432-022-3842-2
2.	Liuliu Zhang, Xianglin Liu, Changchun Hua, Prescribed-Time Control for Stochastic High-Order Nonlinear Systems With Parameter Uncertainty, 2023, 70, 1549-7747, 4083, 10.1109/TCSII.2023.3274680
3.	Yang Xu, Xisheng Dai, 2024, Prescribed-Time Stabilizaition of Linear Stochastic Parabolic Systems, 979-8-3503-8778-0, 4059, 10.1109/CCDC62350.2024.10588138
4.	Jianyang Du, Guici Chen, Song Zhu, Junhao Hu, Prescribed-time stabilisation of stochastic high-order nonlinear systems with time-varying powers, 2025, 0020-7179, 1, 10.1080/00207179.2025.2451712

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Materials Science

1.4 3.6

Metrics

Article views(7240) PDF downloads(1256) Cited by(5)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(4) / Tables(1)

AIMS Materials Science

Photoinduced transformations of optical properties of CdSe and Ag-In-S nanocrystals embedded in the films of polyvinyl alcohol

Related Papers:

Abstract

1. Introduction

2. Problem formulation

3. Controller design and stability analysis

4. A simulation example

5. Concluding remarks

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Materials Science

Photoinduced transformations of optical properties of CdSe and Ag-In-S nanocrystals embedded in the films of polyvinyl alcohol

Related Papers:

Abstract

1. Introduction

2. Problem formulation

3. Controller design and stability analysis

4. A simulation example

5. Concluding remarks

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog