1. Introduction
Diamond wire sawing (DWS) is an emerging technology for wafering semiconductor ingots, which promises many advantages over the existing dominant technology of slurry cutting [1,2,3]. These advantages include faster cutting speeds with higher cutting efficiency, production of thinner wafers with improved thickness uniformity, easier way to filter Si debris for slurry recycling (if desired), and use of cutting wire for more than one cut. Diamond wire sawing has particularly strong interest from photovoltaic (PV) community because it is believed that this sawing technique can produce wafers with characteristics that can match the requirements for PV industry, at a significantly lower cost than slurry cutting. Many PV companies are aggressively testing DWS wafers to determine if their solar cell performance and yield match that of the slurry cut wafers. The desired characteristics of PV wafers, which are quite different from those for microelectronics industry, are: (a) Wafer thickness—the thickness of standard 156 mm × 156 mm is typically 180 µm and there is a tendency to go to lower thicknesses; (b) Surface quality—unlike microelectronics wafers, the PV wafers are used without polishing. However, they are textured to improve light confinement properties. Texturing is typically done as one of the first steps in fabricating solar cells using KOH based anisotropic etching, which produces pyramidal surface features of 2 to 4 µm in size. Consequently, the requirements of surface roughness are only moderate and not a critical factor; (c) Surface damage—the damage produced by the wafering process should be small. Because the surface damage must be removed prior to solar cell fabrication, it is important that the depth of damage be only a small fraction of the wafer thickness, which are already quite thin; and (d) Interaction of the wafer surfaces during solar cell fabrication—because each wafer goes through a number of chemical and thermal process steps during cell fabrication, there is possibility that the quality of the wafer surface can influence the process itself. For example, in solar cell fabrication, texturing and damage removal are combined into one process step to reduce the cell fabrication cost. The nonuniformity of the damage is likely to introduce nonuniformity in the texture etching and hence, degrade the cell performance.
The DWS produces distinct surface morphology of as-sawn wafers that is characteristic of the dynamics of cutting process. Thus, a history of the cutting parameters gets “imprinted” on the surfaces of each wafer in the form of pseudo-periodic perturbations of different spatial frequencies. Furthermore, like all other cutting methods, DWS introduces subsurface damage due to very large stresses that occur during the cutting process. These characteristics, the surface roughness and the surface damage, are strongly interwoven and play an important role in how wafers react to various process steps during fabrication of solar cells [4,5]. Hence, it is important to know the surface characteristics of DWS wafers and understand the mechanisms that produce them. Likewise, it is essential to acquire a detailed knowledge of damage produced by cutting. This can help both the sawing companies to improve wafer sawing and solar cell manufacturers.
In this paper, we will first present a brief description of the DWS process, emphasizing various cutting mechanisms that generate surface features, and the subsurface damage. We will then describe nature of damage and methods for measurement of damage. Following that we will present results of our study that show damage characteristics as a function of some key cutting parameters. Finally, we will present results of dependence of damage on cutting parameters and address relationship between surface features and damage.
2. Materials and Methods
In this section we will briefly describe diamond wire sawing method, surface morphology, and damage produced on the wafer surface due to diamond wire sawing.
2.1. A Brief descriptionof diamond wire sawing method
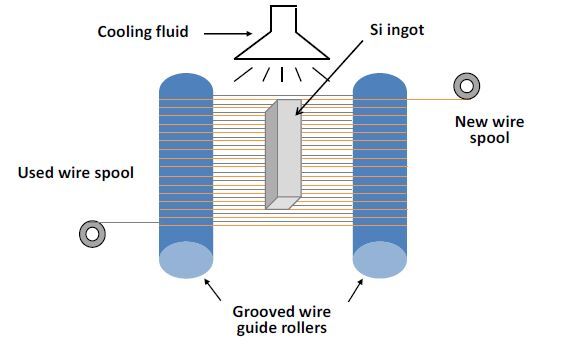
Diamond wire sawing uses a long (typically 50-100 kilometers) wire, impregnated with diamond flakes (grit) as a cutting medium. The cutting wire is made up of a stainless steel core (80-120 µm in diameter) that is coated with diamond flakes (8-25 µm in size) which are then bonded to the wire by a layer of electroplated Ni or a layer of a resin material [6,7]. The diamond chips typically have a tight size distribution and as expected, smaller chip sizes are used with smaller wire sizes. Thus, DWS constitutes a fixed abrasive cutting approach (as compared to free abrasive slurry cutting). The diamond wire saw consists of a wire-web formed by feeding the wire from a feeding-spool into a take-up spool and winding the wire over a set of wire-guide-rollers, as shown in Fig.1. The wire-guides precisely maintain the distance between the wires, which corresponds to the center-to-center distance between the wafers (equal to wafer thickness + kerf). The motion of the wire is controlled to follow certain algorithms. One of them involves feeding a predetermined length of the wire in the forward direction, cutting a given depth of the ingot [7]. The direction of the wire is then reversed but the length traversed is shorter than the forward direction. This length is made up by feeding the additional fresh wire length in the forward direction. The parameters of this reciprocation process control the length of the wire used in cutting a given ingot (also termed as wire use and defined as average length of wire used per wafer). To perform the wafering, the silicon ingot, cut into brick(s), is fed into the wire web (either from the top or bottom) in small steps. The wire tension and the force on the ingot exert a force on diamond particles thereby embedding tips of the particles into Si ingot. In addition, the directional motion of the wire produces sheer stresses on Si ingot causing the diamond grit to “plow-through” Si, dragging chips of Si along the wire direction. The swarf is removed by a water-based cutting fluid, which also stabilizes the wire web by providing adequate surface tension-related forces between the wire and the slot walls [6].
2.2. Experimental design
The main objective of this work was to determine effects of grit size, wire size, and the wire usage on the wafer characteristics. The results described in this paper are for monocrystalline Si. Monocrystalline silicon ingots of pseudo-square cross-section were cut using commercial wire saw platform (Applied Materials) with rocking table, electroplated diamond wire from Asahi Diamond Industrial Co. Ltd., and water-based coolant from Blaser Swisslube. A majority of the ingots were 156 mm × 156 mm in size; however, some 125 mm × 125 mm ingots were also used. Ingots were cut with wires of different sizes, different grit sizes, and wire usage, as described in Table I. The table speed (cutting speed) averaged from 400 to 1500 micron/min. The details of ingots and cutting parameters are presented in Table I. Both P and N type ingots were used.
Table I.Details of ingots/wafers and cutting parameters of diamond wire sawing
| Ingot # (resistivity type)
|
(Saw type)/Wire size(µm)/diamond size (µm)
|
Cutting speed (mm/min)
|
Avg. thickness (µm)
|
TTV (µm)
|
Wire usage a (m/wafer)
|
| Ig-1(P)
|
(b) 120/12-25
|
(b)Hi
|
196-200
|
<20
|
0.8
|
| Ig-2(P)
|
| Ig-3(P)
|
(b)100/8-16
|
(b)Hi
|
178-180
|
<20
|
1
|
| Ig-4(P)
|
| Ig-5(P)
|
(b)100/10-20
|
(b)Hi
|
141-147
|
<20
|
1.2
|
| Ig-6(P)
|
| Ig-7(N)
|
(b) 80/6-12
|
Standard
|
148
|
<30
|
1.68-0.81
|
| Ig-8(N)
|
Note: (a) Wire usage is defined as the average length of wire used per wafer.
(b) “Hi” represents cutting speed between 0.4 and 1.4 mm/min. |
The as-cut wafers were first cleaned in dilute soap water and gently scrubbed with a lint-free cloth and dried. They were then solvent cleaned in acetone and rinsed in isopropyl alcohol. Finally, the wafers were cleaned in piranha H2SO4:H2O2 (2:1) at 80 °C. Their surface morphology/roughness were measured, and then tested for in-depth and lateral damage variations. These data were used to perform fast Fourier transform (FFT). Cleaned wafers were also used for damage depth measurements as described in section 2.4.
2.3. Surface morphology
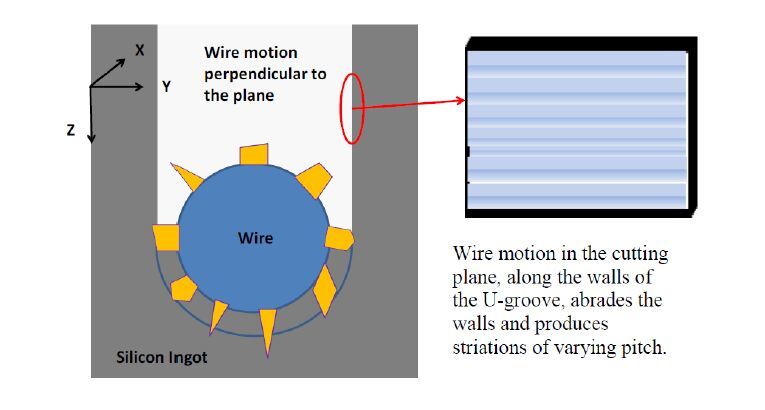
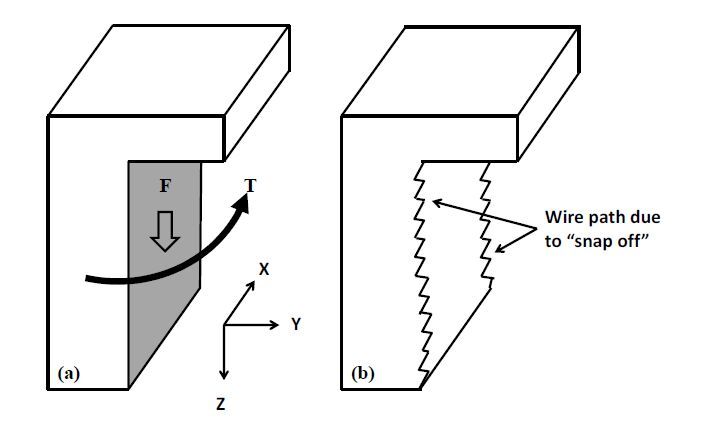
The surface characteristics of as-cut wafers are strongly controlled by the wire movement with respect to the ingot. Hence, to understand the formation of surface features of the as-cut wafers, it is useful to go into some further details of wire movement and its path within the ingot during cutting. Figure 2 shows typical cutting path of each wire segment as it moves into the ingot, along the ingot cutting direction, Z, forming a “U-shaped” channel. The inset in Fig.2 illustrates schematically that the walls of the groove, which constitute the wafer surfaces, have surface features produced by the motion of the cutting wire. These features are formed by the wire motion with respect to the ingot during cutting in response to various forces. As the ingot is pushed with a force F, into the moving wire having a tension force T, it experiences deflections within the cutting plane as well as within the plane perpendicular to it. First consider the wire path in X-Z cutting plane. In this plane, the wire acquires a concave-up (if the ingot is pushed from the top downward) path as illustrated in Fig.3a, indicating that in-plane cutting forces are not uniform. At the bottom of the U-groove, the downward force drives grit particles into Si (in Z direction) creating a drag force against the wire motion, while the velocity of the wire creates a shear force on diamond chips. When the shear stress exceeds the critical shear stress, it causes microcleavage of small chips of Si. As the cutting in Z-direction progresses, material is continuously being removed at the bottom of the U-groove exposing fresh Si. Also, some of the grit above the bottom of the groove (near the center of the wire) is also driven into the walls (Y-Z plane) of the partially-cut wafers, which results in the abrasion of the wafer surfaces along the direction of the wire velocity (X direction). This interaction of the grit (and wire) along the walls of the U-groove leaves features on the wafer surfaces that remain “imprinted” on as-cut wafers.
Thus, even though the primary material removal occurs along Z-direction, there is surface roughness and damage on the vertical walls that form the wafer surfaces. One of the surface features arises due to systematic ingot motion. Because the ingot is fed by a stepping motor, each step of the motor causes grains of grit to be dragged over the wafer surfaces, leaving tracks corresponding to stepping motor. Hence, diamond wire sawn wafers have pseudo-periodic surface morphologies that appear as striations with a range in the spatial wavelengths from microns to many centimeters. This causes a pseudo-periodic surface undulation on the wafer surfaces, creating a grating like pattern with the period of the step size.
In addition to the above described basic processes in cutting, there are two secondary mechanisms that influence the surface features and bring in nonuniformity in DWS wafer surfaces. These are:
1. Distribution of grit on the wire: Because of size and shape variations in the diamond grit, the pressure produced by them over the wafer surfaces is not same. Thus, while some of the grit can cause microcleavage, others may only produce plastic deformation.
2. Wire reciprocation: As mentioned in the earlier section, the direction of the cutting wire is reversed periodically. This wire reciprocation produces a distinct change in the surface roughness and surface damage as the wire goes in forward vs reverse direction. Although, the mechanism for this variation is not fully understood, we believe it is associated with the directional “blunting” of grit as it goes in each directional.
Now, we consider the motion of wire in the YZ plane (perpendicular to the walls of the U-groove): Ideally, one would expect the wire path to be perfectly normal to the ingot with no deflection in the YZ plane. However, at reasonable cutting speeds, the wire path can deviate from being perfectly planar, causing inclination of wire path with respect to the ingot. This causes lateral forces on the wire leading to its movement along Y direction. The dynamics of the wire suggests that as the wire will depart from an ideal condition, it builds up energy to a point and thereafter the wire will snap back to a vertical configuration. An excellent description of this snap-off mechanism that uses energy conservation and its modeling has been done in reference [8]. Figure 3b illustrates path of the wire in Y-Z plane. An important result of this motion is that the surface of each wafer has a long wavelength spatial roughness (few cm) that primarily controls the total thickness variation (TTV) of cut wafers.
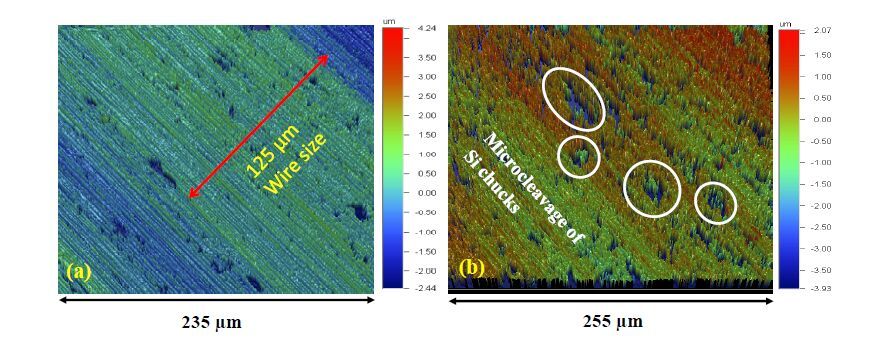
Because of the different pitches of the pseudo-periodic variations, observation of the surface profiling requires a variety of equipment such as an optical interference microscope, SEM, and Dektak. We will start with discussion of surface morphologies having the smallest pitch (highest spatial frequency) and then proceed toward larger pitches. Figure 4 shows interference microscope images of very fine features seen on various DWS wafers. The wafer whose pattern is shown in Fig.4a was sawn by a wire of 100 µm core diameter with grit size in the range of 10-20 µm. As described earlier, this grating-like pattern is caused by “plowing” by the grit along the sides of the wafer and the step motion of feed mechanism. This figure shows a nearly uniform surface structure with almost no microcleavage. Figure 4b is a similar image on a wafer that was cut with 120 µm diameter wire with grit size 12-25 µm distribution (other cutting parameters remaining same). It can be seen that increased grit size causes large chunks of Si to be removed by micro-fracturing (labelled in Fig.4b). It should be noted that the pitch of the grating-like pattern is only 1-2 µm and is not directly related to wire size.
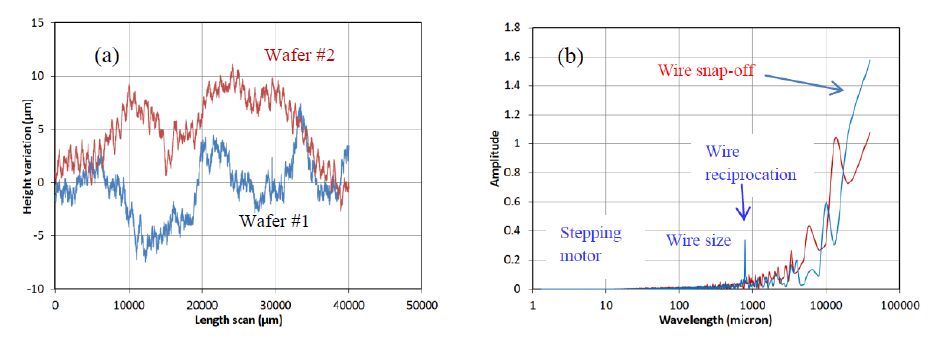
However, in many cases, one can also see the manifestation of the wire size as steps in the pattern, perhaps due to low frequency vibrations causing changes in the lateral force. This indication of the wire size can be seen in the interference image of Fig.4a as change in color due to height variations. In addition to the fine structure described above, the wafer surface has striations that can be visually seen. Figure 5 is a photograph of a 156 mm × 156 mm, monocrystalline DWS wafer showing a variety of striations of different spatial wavelengths that are visible to the naked eye. One can see narrow bands, typically between 700 µm to 1000 µm, which correspond to wire reciprocation. In addition, we have labelled the snap-off periods by white lines (~ 4 cm wavelength) and the wire path along the cutting grove. It should be noted that the visibility of surface features is due to reflectance changes because of changes in the surface height. Hence, these can also be quantified using a profilometer such as Dektak. Surface profiles of two DWS wafers (#1 and #2) measured by Dektak are shown in Fig.6a. These two wafers belong to ingots cut with different wire usage parameter values—1.2 m/wf and 0.8 m/wf for #1 and #2, respectively. An easy way to see the periodicity of different spatial wavelengths is to perform a FFT of the Dektak trace. Figure 6b shows Fast Fourier Transform (FFT) for the Dektak profile of Fig. 6(a). It clearly shows a number of FFT peaks of different amplitudes due to nearly-periodic modulation of surface. We have labelled peaks corresponding to various pseudo-periodic movements. It may be noted that some of the FFT peaks of wafer #2 are not as well defined as that of the wafer #1. In particular, the reciprocation peak is small and there are many small peaks in the spatial wavelength range around 1000 mm. We believe that low wire usage causes diamond grit to become blunt and lose its directional effect. In an earlier publication [9], we have also shown that the damage depth is much deeper for lower wire usage (although the wafer surface can appear rather shinny).
2.4. Surface damage
Surface/subsurface damage is result of very large stresses that are created during cutting. The forces on the wire are transferred to grit, thereby embedding the grit into Si surfaces. The shear forces, exceeding the critical shear stress, cause micro-fracture of Si chips with a concomitant release of stress. Hence, there are local stresses that build up and are released. There are also stresses below the critical shear stress that produce dislocations and other plastic deformations. The nature of damage created by cutting can be understood by considering two mechanisms of cutting - the brittle and ductile modes, as described below.
2.4.1. Cutting mechanisms and damage generation
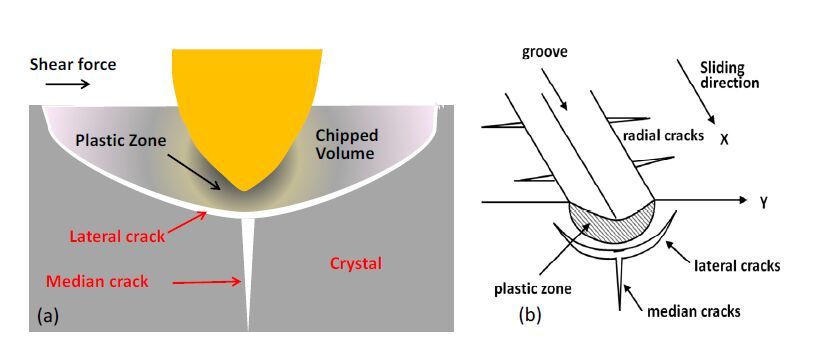
Understanding of cutting mechanisms is important for maximizing cutting speed while minimizing the damage that is introduced below the surface on the wafers. One has to keep in mind that local stresses developed on the ingot and wafer surfaces vary within a wide range because of variation in grit size, nonuniformities in the cutting force, and system vibrations. Because of a broad range of stress, the cutting process invokes both brittle and ductile modes of fracture despite the fact that Si is essentially a brittle material. Furthermore, although the cutting process is dynamic, it is useful to first consider the nature of damage due to static loading, such as during indentation of a Si wafer. This is because the mechanisms occurring at each of the diamond grit are akin to that of an indenter where a force is applied to the indenter tip. First we consider brittle fracture of Si. Figure 7a illustrates a case where the indenter tip is forced into Si. It is known that the pressure under the tip causes formation of a plastic zone directly below the tip and that crack formation takes place in both median and transverse directions, as illustrated in the figure. The average pressure required for this occurrence of brittle fracture for Si is ~ 10-15 GPa. Under the loading (and as a function of time) the crack size increases, the lateral cracks expand and reach the surface causing formation of a chip. It should be noted that lateral cracks are generated not only in the plane of paper as shown in the figure, but also along the other planes (typically in the cleavage planes) [10]. If the indenter tip is dragged over the Si surface (resembling one diamond chip being dragged by the wire), there will be a continuous generation of both lateral and median cracks as shown in Fig.7b. Importantly, it can be seen that lateral cracks propagate into the wafers and can go below the wafer surface. However median cracks are continually removed as the Si material is cut.
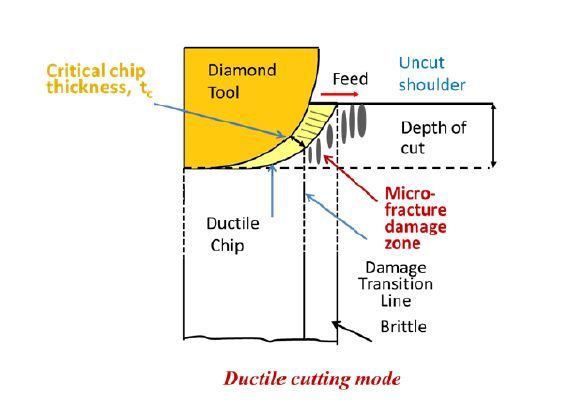
Figure 8 is an illustration of ductile mode cutting in which a diamond tool is being drawn over a workpiece. This figure shows various phases of material ahead of the tool as the tool compresses the material. It is seen that the ductile mode is accompanied by generation of a thin layer of a metallic phase of Si (up to a critical thickness) without any defect formation, and deformation of the material (above the critical thickness) caused by cracking [11,12,13]. Furthermore, micro-fractures are formed preceding the cut. However, as the diamond tool (grit) moves over the damaged layer, it continually removes the damaged layer. The important feature is that the ductile mode cutting can, in principle, occur without generation of microfractures and damage, but because it occurs at lower stresses than the brittle fracture mode, the cutting rate can be very low.
From the brittle and ductile mode cutting, it is clear that each of the cutting modes is accompanied by generation of damage consisting of phase transformed material that predominantly occurs in the plastic region of the deformation, microcracks, and generation of dislocations. The surface morphology along the vertical wall is expected to be “imprinted” on the wafer surfaces.
2.4.2. Damage evaluation
The mechanisms that cause specific surface features described above also produce damage that has a strong similarity to the surface roughness. Thus damage appears as directional “scratches” with localized phase changes, microcracks produced by brittle fracture and micro-cleavage, and dislocations generated by plastic deformation. Typically, the in-depth damage can be observed in XTEM as dislocation loops and conversion of a thin surface layer into amorphous Si [14,15,16]. Phase changes into amorphous Si can also be observed by EBSD and/or Raman imaging. But, determining damage by these techniques over a large area of a wafer is very tedious and time-consuming. One way to observe damage over a larger area is to angle polish a small sample (typically few mm in width) on pads with progressively lower grit size and then dislocation etching the sample. A large improvement in the defect delineation can be done if the final step of the polishing is done by chemical mechanical polishing (CMP).
The damage is manifested as: (a) Pressure-induced phase change into crystalline and amorphous phases. A significant amount of work has been done to establish changes in the crystal structure of Si under hydrostatic pressure as well as by indentation techniques. It has been determined that the standard crystalline phase have been determined to be six crystalline and the amorphous Si phase. A big part of the phase change is the transformation into amorphous Si. We have examined this change using EBSD and Raman imaging to investigate if there is a pattern to regions that show amorphization. Figure 9 shows an EBSD image of a region of a wafer, which has chipping due to microcleavage. Also shown is Raman image of the same region, where red regions represent crystalline and black represent amorphous phases. Although this picture shows chipped regions have an amorphous layer on the surface, our large data base indicates that this probability is only about 60%. Likewise, in the regions that only have deformations and no microfracture, there is no specific trend in regions that show amorphization. We should point out that phase changes are not very significant for solar cells because the thickness of phase changed material (including oxidized material) is typically quite small and get etched away in standard solar cell processing. However, one has to be careful because they can cause nonuniformities in solar cells.
(b) Formation of dislocations as dislocation loops, which remain stagnated near the surface (due to low dislocation propagation velocity at cutting temperature). These dislocations are formed to accommodate plastic flow during cutting. The depth to which dislocations go is important for preparing wafers for device fabrication. Dislocations can be seen in TEM analyses but a simple way to see dislocations and how deep they go into the wafer bulk is to angle polish and defect etch the wafer.
Figure 10a is an optical microscope image of an angle-polished and defect etched sample showing locally deep penetration of dislocations under the original surface. An SEM image of a similar angle-polished and defect etched sample (Fig.4b) shows detailed delineation of dislocations loops that are frozen-in around the regions chipped by the diamond grit. This sample was polished at 10 degrees angle (giving a vertical magnification of ~ 6 times, see Fig.10c).
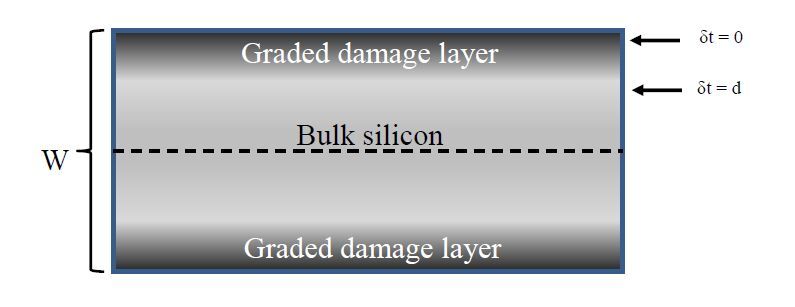
The methods mentioned above for measuring depth of damage such as TEM, SEM, angle polishing and defect etching, and RAMAN imaging, only provide qualitative and local information on depth of damage. We have recently developed a technique for measuring an average damage depth over a large area using minority carrier lifetime measurement [16,17,18,19]. This method is an improvement over previous approach, based on measurement of surface photovoltage as a function of etches depth, which was published quite long back [20]. In the new method, thin layers from the wafer surfaces are sequentially etched using a 1:1:5 (HF:HNO3:CH3COOH) solution and the effective minority carrier lifetime (MCLT) is measured after each etch step. Figure 11 illustrates a wafer having graded damage at each surface due to sawing. Because the electronic effect of damage is manifested as increased minority carrier recombination at the surface, its effect can be lumped into surface recombination (as an approximation). Hence one can express the effective lifetime (${{\tau }_{eff}}$) as:
|
$\frac{1}{{{\tau }_{eff}}}=~\left( \frac{1}{{{\tau }_{B}}} \right)+2~\frac{{{s}_{eff}}\left( \delta t \right)}{W}$
|
(1) |
where ${{\tau }_{B}}$ is the bulk lifetime, w is the wafer thickness, and seff represents recombination effect due to left over damage layer after etching a thickness $\delta t$. Because seff will decrease as thickness from the surface is etched, ${{\tau }_{eff}}$ will increase with $\delta t$ till $\delta t$=d.
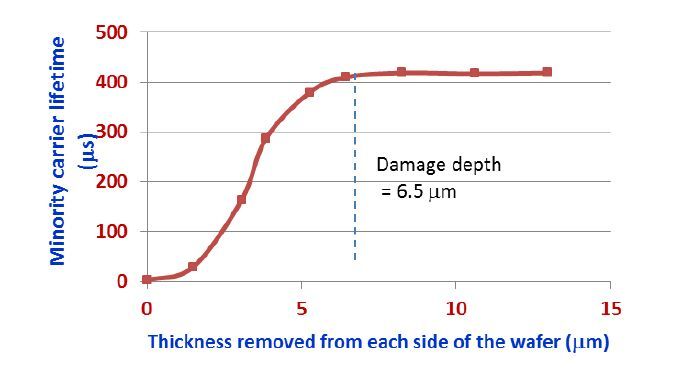
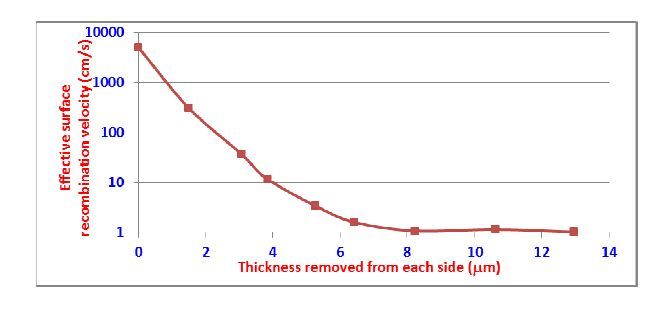
Figure 12a shows a typical plot of lifetime vs thickness removed from each surface. As seen, the lifetime reaches a maximum value when the damage is fully removed and typically stays constant. The damage depth in Fig.12a is 6.5 mm. An important feature of this technique is that one can use equation 1 to calculate effective surface recombination velocity as a function of depth, to get an indication of damage distribution.
Figure 12b is a plot of seff vs thickness etched corresponding to the measured MCLT of Fig.12a. It should be noted that seff represents contribution of the entire damage layer thickness, which must be deconvolved to determine actual damage distribution. But, in most cases, it is sufficient to compare seff vs to get a qualitative profile of damage.
3. Results and Discussion
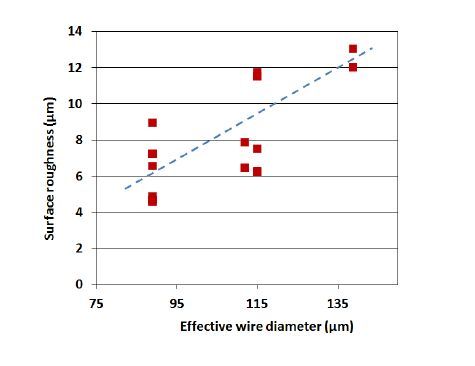
Now we describe some results that relate the surface roughness and damage depth to some important, basic cutting parameters, such as wire diameter and grit size. Figure 13 shows dependence of surface roughness on the effective wire diameter (wire diameter + maximum grit size). These data are generated by cutting different ingots with different wire and grit sizes. However, wire size and grit size are typically not independent - lager grit size goes with the larger wire size. This is shown on the axis as effective wire size. The results in Fig.13 show that surface roughness increases with the increase in effective-wire diameter.
It is important to note that the surface roughness also depends on other parameters such as vibration in the wafer stack, quality of the guides, tension in the wire, and rocking motion the wafer surface. These parameters were kept constant as much as possible.
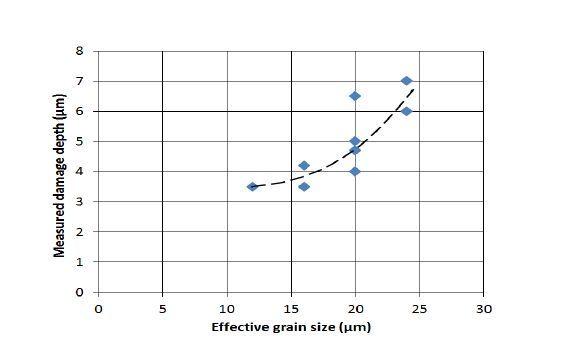
Figure 14 shows the depth of damage created by grit size. Here we have used the maximum value of the grit size because, as expected, the deepest damage is created by the largest grit size and that our new technique based on MCLT measurement identifies damage depth to be the deepest value. It is clear that the depth of damage increases with increase in the grit size. The small scatter of the data points can be understood as the measured damage depth can vary due to the lateral non-uniformities in each wafer.
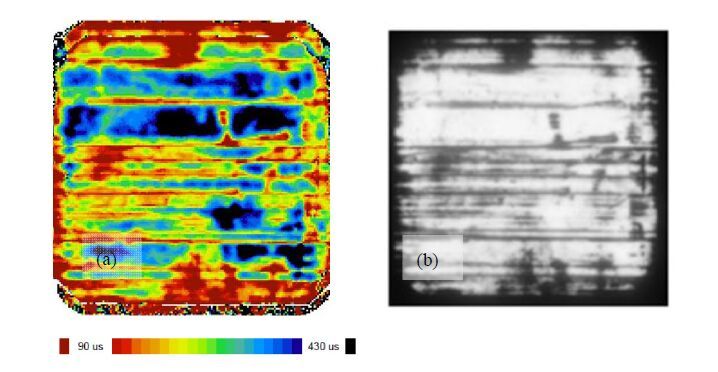
Earlier we saw that the surface modulations of different spatial frequencies are generated by DWS process, as seen in Fig.5. As mentioned earlier in this paper, the mechanisms that cause surface roughness also cause corresponding variations in the damage [9]. Consequently, one expects strong variations in the depth of damage over each wafer - variations that resemble striations seen in Fig.5. To observe the spatial variations in the damage, we isotropically etched 2 µm from each surface of wafers and made minority carrier lifetime maps. Figure 15(a) is a MCLT map of such a wafer, showing damage variations in the MCLT. Because presence of damage reduces the effective MCLT, the damage depth is deeper in the regions of lower MCLT (red regions). This figure indicates striations similar to the surface roughness are also occurring in the damage depth. A similar variation can be observed by photoluminescence map shown in Fig.15(b); but these are only qualitative depictions of the residual damage after uniform etching. Variations in lateral damage can be quite detrimental to solar cell performance and must be prevented. This is particularly important during texture etching step, where care must be taken to etch sufficiently deep to prevent occurrence of any residual damage. This also poses challenge in producing a uniform texture because higher degree of damage causes formation of larger texture peaks [21].
4. Conclusion
We briefly described the diamond wire sawing technique and discussed the mechanisms that cause surface roughness and subsurface damage. Our results show that the surface morphology is strongly controlled by the kinematics of the 3-dimensional wire motion. Fourier transform analysis of the surface profiles show a number of spatial frequency components corresponding to motion of ingot, reciprocation of diamond wire, and other phenomena of motion. Damage by DWS is primarily introduced by the diamond particles as they scratch the wafer walls and chip away chunks of Si. The damage manifests in the form of dislocation loops and phase changes from crystalline to amorphous Si. A number of techniques for measurement of damage were briefly discussed, including use of MCLT as a function of thickness removed from the surfaces. The depth of damage depends on the size distribution of diamond grit - larger grit producing deeper damage. The lateral variations in the damage range from micron to millimeters and relate to distribution of grit size over the wire, the feed mechanism, wire reciprocation, and other motions (intentional or unintentional such as vibrations). These nonuniformities of damage are expected to influence texturing of solar cell cells.
Acknowledgement
This work was supported in part by the NREL/DOE NPO project and by c-Si program at the Photovoltaic Manufacturing Consortium (PVMC), an industry-led consortium for cooperative R&D among industry, university, and government partners, was accomplished under agreement number DE-EE0004947 with the U.S. Department of Energy. Authors would like to thank Applied Materials for providing wafers.
Conflict of Interest
The authors declare no conflicts of interest regarding this paper.









 DownLoad:
DownLoad: