AIMS Materials Science, 2016, 3(1): 190-203. doi: 10.3934/matersci.2016.1.190

Research article Topical Section

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

Particle- and crack-size dependency of lithium-ion battery materials LiFePO4

Michael A. Stamps, Jeffrey W. Eischen, Hsiao-Ying Shadow Huang

1 Mechanical and Aerospace Engineering Department, North Carolina State University, R3311 Engineering Building 3, Campus Box 7910,911 Oval Drive, Raleigh, NC 27695, USA
2 Mechanical and Aerospace Engineering Department, North Carolina State University, R3290 Engineering Building 3, Campus Box 7910,911 Oval Drive, Raleigh, NC 27695, USA
3 Mechanical and Aerospace Engineering Department, North Carolina State University, R3158 Engineering Building 3, Campus Box 7910,911 Oval Drive, Raleigh, NC 27695, USA

Received: , Accepted: , Published:

Topical Section: Elecrtrochemical Analysis of Materials

Abstract    Full Text(HTML)    Figure/Table    Related pages

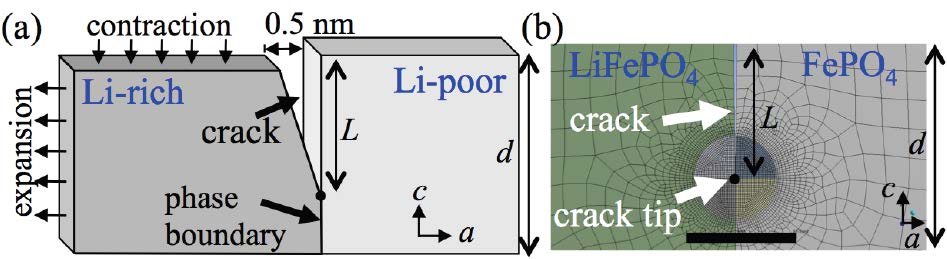
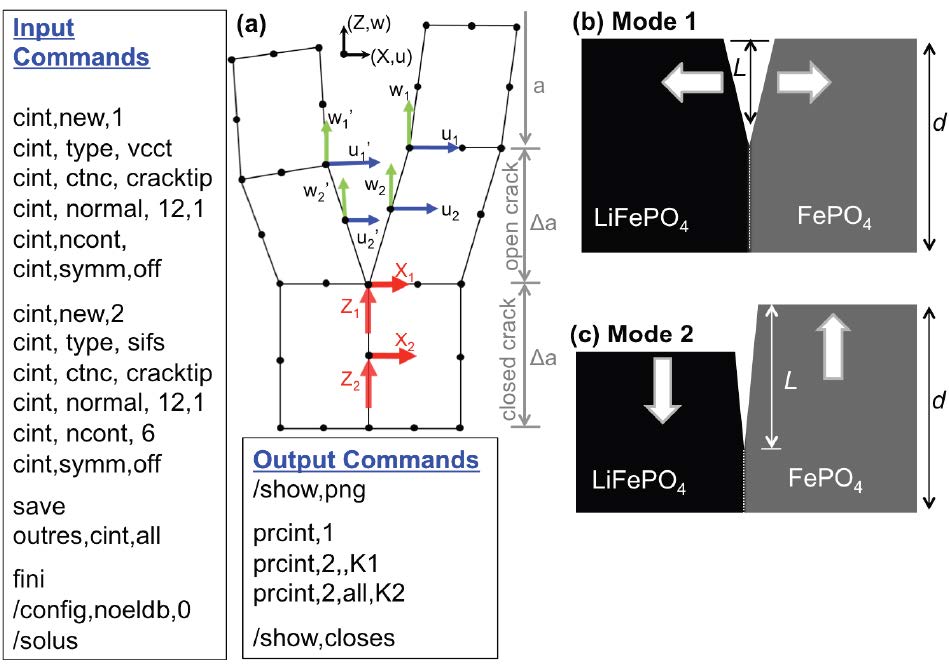
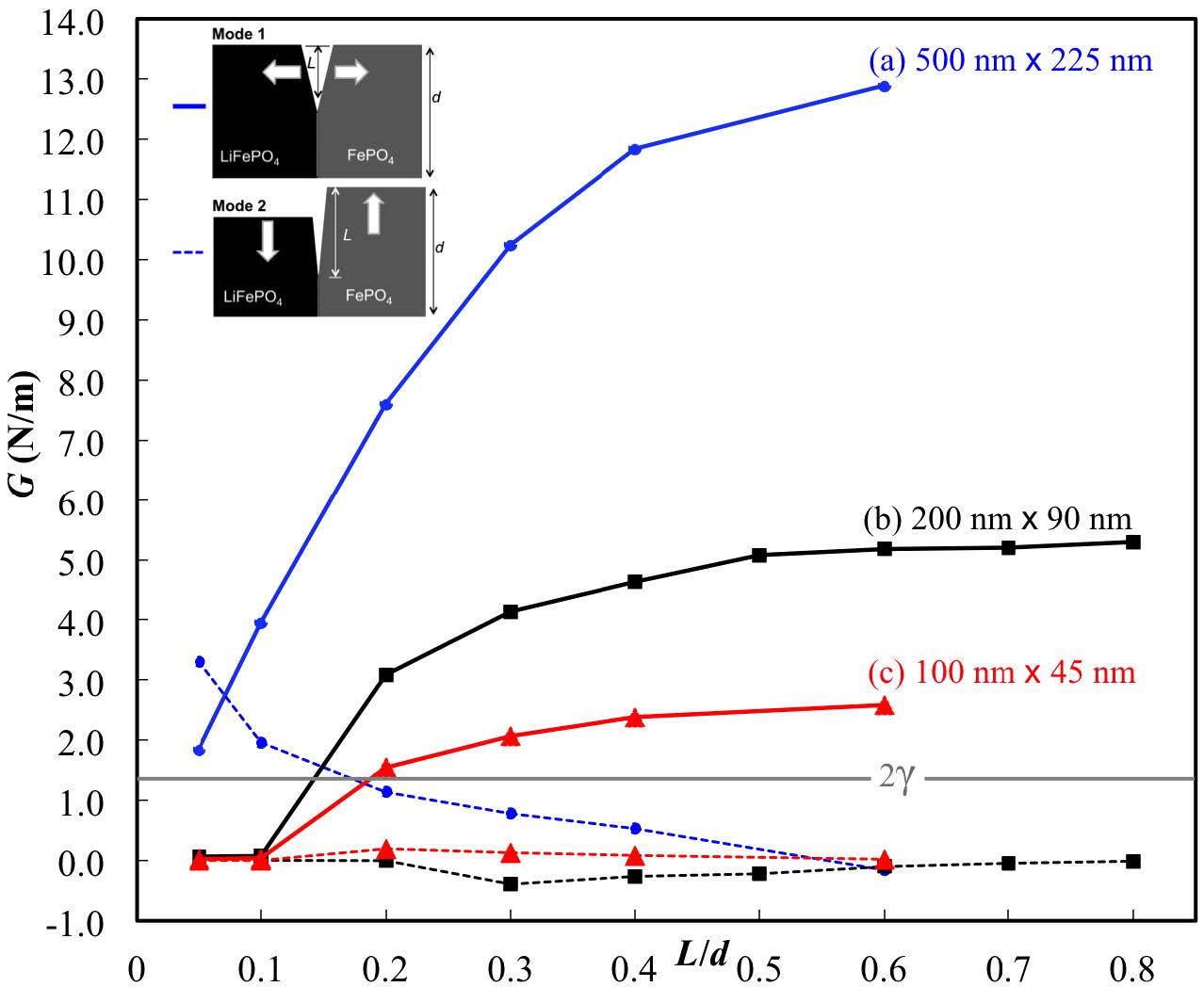
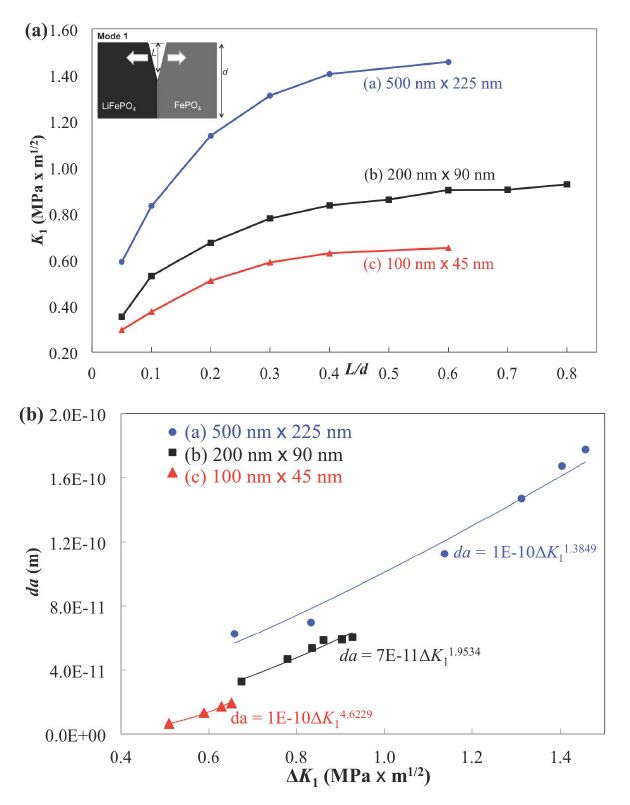
Lithium-ion batteries have become a widely-used commodity for satisfying the world’s mobile power needs. However, the mechanical degradation of lithium-ion batteries initiated by micro cracks is considered to be a bottleneck for advancing the current technology. This study utilizes a finite element method-based virtual crack closure technique to obtain particle- and crack-size-dependent estimates of mixed-mode energy release rates and stress intensity factors. Interfacial cracks in orthotropic bi-materials are considered in the current study, whereas the crack extension along the interface is assumed. The results show that energy release rate, stress intensity factor, and the propensity of crack extension are particle- and crack-size- dependent. In particular, our results show that for smaller plate-like LiFePO4 particles (100 nm × 45 nm), a crack has lesser tendency to extend if crack-to-particle size is less than 0.2, and for 200 nm × 90 nm particles, similar results are obtained for crack-to-particle sizes of less than 0.15. However, for larger particles (500 nm × 225 nm), it requires an almost flawless particle to have no crack extension. Therefore, the current study provides insight into the fracture mechanics of LiFePO4 and the associated crack-to-particle size dependency to prevent crack extensions.
  Figure/Table
  Supplementary
  Article Metrics

References

1. Energy Information Administration (2011) Global Crude Oil and Liquid Fuels Consumption. Official Energy Statistics from the U.S. Government.

2. Environmental Protection Agency (2011) 2017–2025 Model Year Light-Duty Vehicle Greenhouse Gas Emissions and Corporate Average Fuel Economy Standards. Federal Register 76(153).

3. Office of Atmospheric Programs (2010) Environmental Protection Agency Analysis of the American Power Act. U.S. Environmental Protection Agency.

4. US Department of Energy (2008) Emissions of Greenhouse Gases in the United States. Office of Energy Statistics, U.S. Department of Energy, Washington, DC 20585, U.S. Energy Administration. DOE/EIA-0573: 21–26.

5. US Department of Energy (2010) Monthly Energy Review. Office of Energy Statistics. U.S. Department of Energy, Washington, DC 20585, U.S. Energy Administration. DOE/EIA-0035.

6. Padhi AK, Nanjundaswamy KS, Goodenough JB (1997) Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J Electrochem Soc 144: 1188–1194.    

7. Wang Y-X, Huang H-YS (2011) An Overview of Lithium-Ion Battery Cathode Materials. Proc. Materials Research Society 2011 Spring Meeting, pp. 1363-RR1305-1330.

8. Chung S-Y, Bloking JT, Chiang Y-M (2002) Electronically conductive phospho-olivines as lithium storage electrodes. Nat Mater 1: 128–128.

9. Chung SY, Bloking JT, Chiang YM (2003) From our readers - On the electronic conductivity of phosphoolivines as lithium storage electrodes – Reply. Nat Mater 2: 702–703.    

10. Delacourt C, Poizot P, Levasseur S, et al. (2006) Size effects on carbon-free LiFePO4 powders. Electrochem Solid St 9: A352–A355.    

11. Bai YM, Qiu P, Wen ZL, et al. (2010) Improvement of electrochemical performances of LiFePO4 cathode materials by coating of polythiophene. J Alloy Compd 508: 1–4.    

12. Wang Y, Huang H-YS (2012) Lithium-Ion Battery Materials and Mechanical Stress Fields. TSEST T Control Mech Syst1: 192–200.

13. Duong T. Directions for Energy Storage R&D in the Vehicle Technologies Program. Proc. Symposium on Energy Storage Beyond Lithium Ion: Materials Perspectives.

14. Reid MC (2007) Lithium Iron Phosphate Cell Performance Evaluations for Lunar Extravehicular Activities. NASA Glenn Research Center.

15. Chen G, Song X, Richardson TJ (2006) Electron Microscopy Study of the LiFePO4 to FePO4 Phase Transition. Electrochem Solid-St 9: A295–A298.    

16. Yamada A, Koizumi H, Sonoyama N, et al. (2005) Phase change in LixFePO4. Electrochem Solid St 8: A409–A413.

17. Meethong N, Huang H-YS, Speakman SA, et al. (2007) Strain accommodation during phase transformations in olivine-based cathodes as a materials selection criterion for high-power rechargeable batteries. Adv Funct Mater 17: 1115–1123.    

18. Laffont L, Delacourt C, Gibot P, et al. (2006) Study of the LiFePO4/FePO4 two-phase system by high-resolution electron energy loss spectroscopy. Chem Mater 18: 5520–5529.    

19. Gibot P, Casas-Cabanas M, Laffont L, et al. (2008) Room-temperature single-phase Li insertion/extraction in nanoscale Li(x)FePO(4). Nat Mater 7: 741–747.    

20. Zhu M, Park J, Sastry AM (2012) Fracture Analysis of the Cathode in Li-Ion Batteries: A Simulation Study. J Electrochem Soc 159: A492–A498.    

21. Zhang X, Sastry AM, Shyy W (2008) Intercalation-induced stress and heat generation within single lithium-ion battery cathode particles. J Electrochem Soc 155: A542–A552.    

22. Zhao KJ, Pharr M, Vlassak JJ, et al. (2010) Fracture of electrodes in lithium-ion batteries caused by fast charging. J Appl Phys 108.

23. ChiuHuang CK, Huang HYS (2013) Stress Evolution on the Phase Boundary in LiFePO4 Particles. J Electrochem Soc 160: A2184–A2188.    

24. ChiuHuang C-K, Stamps MA, Huang H-YS (2013) Mechanics of Diffusion-Induced Fractures in Lithium-ion Battery Materials. Proc. Materials Research Soaciety 2013 Spring Meeting, pp. 1541-F1504-1504.

25. ChiuHuang C-K, Huang H-YS (2012) A Diffusion Model in a Two-Phase Interfacial Zone for Nanoscale Lithium-ion Battery Materials. Proc. Proceedings of the ASME International Mechanical Engineering Congress and Exposition, pp. 1231–1237.

26. ChiuHuang CK, Huang H-YS (2015) Critical Lithiation for C-rate Dependent Mechanical Stresses in LiFePO4. J Solid State Electrochem19: 2245–2253.

27. Gabrisch H, Wilcox J, Doeff MM (2008) TEM study of fracturing in spherical and plate-like LiFePO4 particles. Electrochem Solid St 11: A25–A29.    

28. Maxisch T, Ceder G (2006) Elastic properties of olivine LixFePO4 from first principles. Phys Rev B 73: 174112–174112.    

29. Hu Y, Zhao X, Suo Z (2010) Averting cracks caused by insertion reaction in lithium-ion batteries. J Mater Res 25:1007–1010.    

30. Renganathan S, White RE (2011) Semianalytical method of solution for solid phase diffusion in lithium ion battery electrodes: Variable diffusion coefficient. J Power Sources 196: 442–448.    

31. Sih GC, Paris PC, Irwin GR (1965) ON CRACKS IN RECTILINEARLY ANISOTROPIC BODIES. IntJ Fract Mec 1: 189–203.

32. Sanford RJ (2003) Principles of fracture mechanics, Prentice Hall, Upper Saddle River, NJ.

33. Hutchinson JW, Suo Z (1992) MIXED-MODE CRACKING IN LAYERED MATERIALS. Adv Appl Mec 29: 63–191.

34. Qian W, Sun CT (1998) Methods for calculating stress intensity factors for interfacial cracks between two orthotropic solids. Int J Solids Struct 35: 3317–3330.    

35. Sun CT, Manoharan MG (1989) STRAIN-ENERGY RELEASE RATES OF AN INTERFACIAL CRACK BETWEEN 2 ORTHOTROPIC SOLIDS. J Compos Mater 23: 460–478.

36. Rybicki EF, Kanninen MF (1977) Finite-Element Calculation of Stress Intensity Factors by a Modified Crack Closure Integral. Eng Fract Mech 9: 931–938.    

37. Dattaguru B, Venkatesha KS, Ramamurthy TS, et al. (1994) Finite-Element Estimates Of Strain-Energy Release Rate Components At The Tip of An Interface Crack Under Mode-I Loading. Eng Fract Mech 49: 451–463.    

38. Xie D, Waas AM, Shahwan KW, et al. (2004) Computation of energy release rates for kinking cracks based on virtual crack closure technique. Cmes-Comp Model Eng Sci6: 515–524.

39. Krueger R (2004) Virtual crack closure technique: History, approach, and applications. Appl Mech Rev 57: 109–143.    

40. Agrawal A, Karlsson AM (2006) Obtaining mode mixity for a bimaterial interface crack using the virtual crack closure technique. Int Fracture 141: 75–98.    

41. Raju IS (1987) CALCULATION OF STRAIN-ENERGY RELEASE RATES WITH HIGHER-ORDER AND SINGULAR FINITE-ELEMENTS. Eng Fract Mech 28: 251–274.    

42. Woodford WH, Carter WC, Chiang YM (2012) Design criteria for electrochemical shock resistant battery electrodes. Energy Environ Sci 5: 8014–8024.    

43. Woodford WH, Chiang YM, Carter WC (2013) Electrochemical Shock in Ion-Intercalation Materials with Limited Solid-Solubility. J Electrochem Soc 160: A1286–A1292.    

44. ChiuHuang C-K, Zhou C, Huang H-YS (2014) In-Situ Imaging of Lithium-ion Batteries Via the Secondary Ion Mass Spectrometry. ASME J Nanotechnol Eng Med.

45. Cogswell DA, Bazant MZ (2013) Theory of Coherent Nucleation in Phase-Separating Nanoparticles. Nano Lett 13: 3036–3041.    

46. Cogswell DA, Bazant MZ (2012) Coherency Strain and the Kinetics of Phase Separation in LiFePO4 Nanoparticles. Acs Nano 6: 2215–2225.    

47. Bai P, Cogswell DA, Bazant MZ (2011) Suppression of Phase Separation in LiFePO4 Nanoparticles During Battery Discharge. Nano Lett 11: 4890–4896.    

48. Tang M, Carter WC, Chiang YM (2010) Electrochemically Driven Phase Transitions in Insertion Electrodes or Lithium-Ion Batteries: Examples in Lithium Metal Phosphate Olivines. Annu Rev Mater Res 40: 501–529.    

49. Streltsov VA, Belokoneva EL, Tsirelson VG, et al. (1993) MULTIPOLE ANALYSIS OF THE ELECTRON-DENSITY IN TRIPHYLITE, LIFEPO4, USING X-RAY-DIFFRACTION DATA. Acta Crystallogr B 49: 147–153.    

50. Zhao K, Pharr M, Cai S, et al. (2011) Large Plastic Deformation in High-Capacity Lithium-Ion Batteries Caused by Charge and Discharge RID F-8640-2010 RID G-3919-2010 RID F-5774-2010 RID B-1067-2008. J Am Ceram Soc 94: S226–S235.    

51. Zhao K, Wang WL, Gregoire J, et al. (2011) Lithium-Assisted Plastic Deformation of Silicon Electrodes in Lithium-Ion Batteries: A First-Principles Theoretical Study RID F-8640-2010 RID G-3919-2010 RID B-1067-2008. Nano Lett 11: 2962–2967.    

52. Rousse G, Rodriguez-Carvajal J, Patoux S, et al. (2003) Magnetic structures of the triphylite LiFePO4 and of its delithiated form FePO4. Chem Mater 15: 4082–4090.

53. Cook RD, Malkus DS, Plesha ME (1989) Concepts and Applications of Finite Element Analysis, John Willey and Sons, Inc.

54. Cook RD (1995) Finite element modeling for stress analysis, John Wiley & Sons, Inc., New York.

55. Ansys I (2013) ANSYS commands reference, release 15.0, ANSYS, Inc, Canonsburg, PA.

56. Hwu CB (1993) FRACTURE PARAMETERS FOR THE ORTHOTROPIC BIMATERIAL INTERFACE CRACKS. Eng Fract Mech 45: 89–97.

57. Hwu CB (1993) EXPLICIT SOLUTIONS FOR COLLINEAR INTERFACE CRACK PROBLEMS. Int J Solids Struct 30: 301–312.

58. Wang L, Zhou F, Meng YS, et al. (2007) First-principles study of surface properties of LiFePO(4): Surface energy, structure, Wulff shape, and surface redox potential. Phys Rev B 76.

59. Fischer-Cripps AC (2007) Introduction to Contact Mechanics (2nd Edition), Springer, Boston, MA, USA.

60. Griffith AA (1921) The Phenomena of Rupture and Flow in Solids. Philos T Roy Soc A 221: 163–198.    

61. Huang H-YS, Wang Y-X (2012) Dislocation Based Stress Developments in Lithium-Ion Batteries. J Electrochem Soc 159: A815–A821.    

62. Krstic VD, Khaund AK (1981) PARTICLE-SIZE DEPENDENCE OF THERMOELASTIC STRESS INTENSITY FACTOR IN 2-PHASE MATERIALS. J Mater Sci 16: 3319–3323.    

63. Balluffi RW, Allen SM, Carter WC (2005) Kinetics of materials, Wiley-Interscience, Hoboken, N.J.

64. Deshpande R, Verbrugge M, Cheng YT, et al. (2012) Battery Cycle Life Prediction with Coupled Chemical Degradation and Fatigue Mechanics. J Electrochem Soc 159: A1730–A1738.    

Copyright Info: © 2016, Hsiao-Ying Shadow Huang, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Export Citation

Article outline

Show full outline
Copyright © AIMS Press All Rights Reserved