1. Introduction

The phenomenon of wave propagation in multiphase poroelasticity theory is appealing extensive attention due to its importance in large number of practical applications in the fields of seismology, geophysics, rock mechanics, soil mechanics and hydrogeology.Biot ^[1,2,3,4] was the first who introduce the equations of motion for the propagation of elastic waves in a porous solid saturated with single fluid. He found that three (two longitudinal and one shear) waves exist in such a porous medium. In comparison to the porous medium saturated with single fluid, the studies of porous media saturated by multi-fluids are rare. For more realisticinterpretations of elastic waves propagation in porous media demand an accurate and developed mathematical theory.An approach, based on mixture concept, Brutsaert ^[5] was the first who extended Biot's theory as Mixture theory to includes the effects of two immiscible pore fluids on the behaviour of elastic waves propagation. Mixture theory, generally, developed for two-fluid system, was further improved and generalised by many authors (Brutsaert and Luthin ^[6]; Bedford and Drumheller ^[7]; Garg and Nayfeh ^[8]; Berryman et al. ^[9]; Santos et al. ^[10,11]; Corapcioglu and Tuncay ^[12]; Tuncay and Corapcioglu ^[13]; Wei and Muraleethara ^[14,15]; Hanyga ^[16]; Lu and Hanyga ^[17]; Lo ^[18]; Lo et al. ^[19,20,21]). In multiphase poroelasticity theory, the solution of coupled differential equations of motion showed that four (three longitudinal and one shear) mode of elastic waves exist. Based on the above mentioned models, a study of reflection of plane harmonic waves at the stress-free surface of porous solid have been carried out by some researchers e.g. Sharma and Kumar ^[22]; Kumar and Kumari ^[23]; Sharma ^[24]; Sharma ^[25]; Tomer and Goyal ^[26].A latest book by Carcione ^[27] is referred for relevant references and detailed procedures.In all the above mentioned hydrologic models of subsurface multiphase flow, the effect of viscous resistance due to relative velocity between two adjacent fluids on elastic waves behavior in unsaturated porous media still remains ignored. A recent mathematical model 'based on continuum mixture theory' presented by Lo et al. ^[28] incorporated the viscous cross-coupling between two immiscible pore fluids. Thus, all the above mentioned models can be derived as the special case of this model. Further, in case of single fluid in medium, this model reduced to Biot ^[1,2] theory. To account the viscous resistance, they first generalised the equations of motion proposed by Lo et al. ^[19]. Next, they derived the dispersion relations, which physically shows the existence of four (three longitudinal and one shear) waves in such a medium. At different frequency and water saturation level, the essence of viscous cross coupling on the phase speed and attenuation coefficient of these four elastic waves is analysed for Columbia fine sandy loam containing an gas-water mixture.Keeping the importance of viscous cross-coupling in mind, in this work, we have extended the work of Lo et al. ^[28]. Present study considers the reflection of inhomogeneous waves at the stress-free plane surface. The methodology is analogous to that presented in Sharma ^[28]. Firstly, the mathematical model developed by Lo et al. ^[28] is solved for the propagation of three compressional waves and lone transverse wave after that definition and suitable boundary conditions for the problem are described. By using the appropriate boundary conditions, the closed-form analytical expressions for the reflection coefficients are derived at the stress-free surface. The analytical expressions for the energy shares of various reflected inhomogeneous waves are derived by using these reflection coefficients. Further, a numerical example is considered to illustrate the influences of viscous cross-coupling, porosity, saturation of gas, pore-characteristics and wave frequency on the energy flux characteristics of seismic waves respectively. Specifically, the Lo-Yeh-Lee theory (LYLT) ^[28] considering viscous cross-coupling between two immiscible fluids in an isotropic porous solid is compared with Tuncay-Corapcioglu theory (TCT) ^[13], and Lo-Sposito-Majer theory (LSMT) ^[19] of porous solid containing two immiscible fluids. In mathematical framework, the conservation of incident energy is confirmed by considering an interaction energy between two dissimilar waves. It validates that the numerical calculations are analytically correct. Finally, some conclusions are addressed which may be drawn from the discussions of the numerical results.

---

2 Basic Equations

The mathematical model proposed by Lo et al. ^[28] has been considered as reference work, wherein equations of motion for deformable porous media containing two immiscible fluids (say, a gas and a water) incorporating the viscous cross-coupling due to relative velocity between two adjacent fluids are derived. The equations of motion, in the absence of body force, are given by

$\begin{align} & {{\langle {{\tau }_{s}}\rangle }_{ij,j}}={{\rho }_{s}}{{\alpha }_{s}}\overset{..}{\mathop{{{u}_{i}}}}\,+{{A}_{11}}(\overset{..}{\mathop{{{v}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)+{{A}_{12}}(\overset{..}{\mathop{{{w}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)+{{A}_{21}}(\overset{..}{\mathop{{{v}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)+{{A}_{22}}(\overset{..}{\mathop{{{w}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,) \\ & +{{R}_{11}}(\overset{.}{\mathop{{{v}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,)+{{R}_{12}}(\overset{.}{\mathop{{{w}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,)+{{R}_{21}}(\overset{.}{\mathop{{{v}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,)+{{R}_{22}}(\overset{.}{\mathop{{{w}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,), \\ & {{\langle {{\tau }_{1}}\rangle }_{ij,j}}={{\rho }_{1}}{{\alpha }_{1}}\overset{..}{\mathop{{{v}_{i}}}}\,-{{A}_{11}}(\overset{..}{\mathop{{{v}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)-{{A}_{12}}(\overset{..}{\mathop{{{w}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)-{{R}_{11}}(\overset{.}{\mathop{{{v}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,)-{{R}_{12}}(\overset{.}{\mathop{{{w}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,), \\ & {{\langle {{\tau }_{2}}\rangle }_{ij,j}}={{\rho }_{2}}{{\alpha }_{2}}\overset{..}{\mathop{{{w}_{i}}}}\,-{{A}_{21}}(\overset{..}{\mathop{{{v}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)-{{A}_{22}}(\overset{..}{\mathop{{{w}_{i}}}}\,-\overset{..}{\mathop{{{u}_{i}}}}\,)-{{R}_{21}}(\overset{.}{\mathop{{{v}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,)-{{R}_{22}}(\overset{.}{\mathop{{{w}_{i}}}}\,-\overset{.}{\mathop{{{u}_{i}}}}\,), \\ \end{align}$

(1)

where $u_i$, $v_i$ and $w_i$ represent the solid, gas and water particles displacement components respectively.The indices s, 1 and 2 represent the three phases of composite medium such as solid, gas and water, respectively. Else, the variable indices in the tensors can take the values 1, 2, 3. The partial time derivative is represented by a dot over variable.The $\tau$'s are used to define stresses, $\rho$'s arematerial densities and $\alpha$'s are volume fractions of thedifferent phases. Coefficients $A_{11}$ and $A_{22}$ represent theinertial coupling of two fluid phases with solid.$A_{12}~(=A_{21})$ identifies inertial coupling between twofluids. Coefficients $R_{11}$ and $R_{22}$ define the viscouscoupling of two fluid phases with solid particles whereas $R_{12}$and $R_{21}$ represents the viscous cross coupling between twofluids.

The stress-strain relations for the composite medium are given by

$\begin{align} & {{\langle {{\tau }_{s}}\rangle }_{ij}}=(({{a}_{11}}-\frac{2}{3}G){{u}_{k,k}}+{{a}_{12}}{{v}_{k,k}}+{{a}_{13}}{{w}_{k,k}}){{\delta }_{ij}}+G({{u}_{i,j}}+{{u}_{j,i}}), \\ & {{\langle {{\tau }_{1}}\rangle }_{ij}}=({{a}_{12}}{{u}_{k,k}}+{{a}_{22}}{{v}_{k,k}}+{{a}_{23}}{{w}_{k,k}}){{\delta }_{ij}}, \\ & {{\langle {{\tau }_{2}}\rangle }_{ij}}=({{a}_{13}}{{u}_{k,k}}+{{a}_{23}}{{v}_{k,k}}+{{a}_{33}}{{w}_{k,k}}){{\delta }_{ij}}, \\ \end{align}$

(2)

where $\delta_{ij}$ is Kronecker symbol. G is the shear modulus of the porous frame and the elastic coefficients $a_{ij}~(=a_{ji})$ of the porous aggregate are given in the Appendix.

Equations of motion, in terms of the displacement components are written as follows.

$\begin{align} & ({{a}_{11}}+\frac{1}{3}G){{u}_{j,ij}}+{{a}_{12}}{{v}_{j,ij}}+{{a}_{13}}{{w}_{j,ij}}+G{{u}_{i,jj}}=({{\rho }_{s}}{{\alpha }_{s}}-{{A}_{11}}-{{A}_{12}}-{{A}_{21}}-{{A}_{22}})\overset{..}{\mathop{{{u}_{i}}}}\, \\ & +({{A}_{11}}+{{A}_{12}})\overset{..}{\mathop{{{v}_{i}}}}\,+({{A}_{12}}+{{A}_{22}})\overset{..}{\mathop{{{w}_{i}}}}\,-({{R}_{11}}+{{R}_{12}}+{{R}_{21}}+{{R}_{22}})\overset{.}{\mathop{{{u}_{i}}}}\,+({{R}_{11}}+{{R}_{21}})\overset{.}{\mathop{{{v}_{i}}}}\,+({{R}_{22}}+{{R}_{12}})\overset{.}{\mathop{{{w}_{i}}}}\, \\ & {{a}_{12}}{{u}_{j,ij}}+{{a}_{22}}{{v}_{j,ij}}+{{a}_{23}}{{w}_{j,ij}}=({{A}_{11}}+{{A}_{12}})\overset{..}{\mathop{{{u}_{i}}}}\,+({{\rho }_{1}}{{\alpha }_{1}}-{{A}_{11}})\overset{..}{\mathop{{{v}_{i}}}}\,-{{A}_{12}}\overset{..}{\mathop{{{w}_{i}}}}\, \\ & +({{R}_{11}}+{{R}_{12}})\overset{.}{\mathop{{{u}_{i}}}}\,-{{R}_{11}}\overset{.}{\mathop{{{v}_{i}}}}\,-{{R}_{12}}\overset{.}{\mathop{{{w}_{i}}}}\,, \\ & {{a}_{13}}{{u}_{j,ij}}+{{a}_{23}}{{v}_{j,ij}}+{{a}_{33}}{{w}_{j,ij}}=({{A}_{21}}+{{A}_{22}})\overset{..}{\mathop{{{u}_{i}}}}\,-{{A}_{21}}\overset{..}{\mathop{{{v}_{i}}}}\,+({{\rho }_{2}}{{\alpha }_{2}}-{{A}_{22}})\overset{..}{\mathop{{{w}_{i}}}}\, \\ & +({{R}_{21}}+{{R}_{22}})\overset{.}{\mathop{{{u}_{i}}}}\,-{{R}_{21}}\overset{.}{\mathop{{{v}_{i}}}}\,-{{R}_{22}}\overset{.}{\mathop{{{w}_{i}}}}\,. \\ \end{align}$

(3)

---

3 Harmonic Plane Waves

The displacement components to study the propagation of plane harmonic wave in the medium are given by

$({{u}_{i}},{{v}_{i}},{{w}_{i}})=({{A}_{i}},{{B}_{i}},{{C}_{i}})\exp \{i\omega ({{s}_{j}}{{x}_{j}}-t)\},~~(i=1,2,3),$

(4)

where the vectors $(A_{1}, A_{2}, A_{3})$, $(B_{1}, B_{2}, B_{3})$ and $(C_{1}, C_{2}, C_{3})$ are defined as the polarizations of the solid, gas and water particles in the composite medium respectively. The slowness vector $(s_1, s_2, s_3)=n/V$ represents the propagation/attenuation of a wave through a unit vector $n=(n_1, n_2, n_3)$ and the velocity $V$. By substituting (3.1) in (2.3), we get nine homogeneous equations, given by

$[({{a}_{11}}+\frac{1}{3}G){{n}_{i}}{{n}_{j}}+(G-{{\rho }_{ss}}{{V}^{2}}){{\delta }_{ij}}]{{A}_{j}}+[{{a}_{12}}{{n}_{i}}{{n}_{j}}-{{\rho }_{s1}}{{V}^{2}}{{\delta }_{ij}}]{{B}_{j}}+[{{a}_{13}}{{n}_{i}}{{n}_{j}}-{{\rho }_{s2}}{{V}^{2}}{{\delta }_{ij}}]{{C}_{j}}=0,~$

(5)

$[{{a}_{12}}{{n}_{i}}{{n}_{j}}-{{\rho }_{1s}}{{V}^{2}}{{\delta }_{ij}}]{{A}_{j}}+[{{a}_{22}}{{n}_{i}}{{n}_{j}}-{{\rho }_{11}}{{V}^{2}}{{\delta }_{ij}}]{{B}_{j}}+[{{a}_{23}}{{n}_{i}}{{n}_{j}}-{{\rho }_{12}}{{V}^{2}}{{\delta }_{ij}}]{{C}_{j}}=0,$

(6)

$[{{a}_{13}}{{n}_{i}}{{n}_{j}}-{{\rho }_{2s}}{{V}^{2}}{{\delta }_{ij}}]{{A}_{j}}+[{{a}_{23}}{{n}_{i}}{{n}_{j}}-{{\rho }_{21}}{{V}^{2}}{{\delta }_{ij}}]{{B}_{j}}+[{{a}_{33}}{{n}_{i}}{{n}_{j}}-{{\rho }_{22}}{{V}^{2}}{{\delta }_{ij}}]{{C}_{j}}=0,$

(7)

where

$\rho_{ss}=\rho_{s}\alpha_{s}-A_{11}-A_{12}-A_{21}-A_{22}-\frac{\iota}{\omega}(R_{11}+R_{12}+ R_{21}+R_{22}),$

$\rho_{s1}=A_{11}+A_{12}+\frac{\iota}{\omega}(R_{11}+ R_{21}),$

$\rho_{s2}=A_{12}+A_{22}+\frac{\iota}{\omega}(R_{12}+ R_{22}),$

$\rho_{1s}=A_{11}+A_{12}+\frac{\iota}{\omega}(R_{11}+ R_{12}),$

$\rho_{11}=\rho_{1}\alpha_{1}-A_{11}-\frac{\iota}{\omega}R_{11},$

$\rho_{12}=-A_{12}-\frac{\iota}{\omega}R_{12},$

$\rho_{2s}=A_{21}+A_{22}+\frac{\iota}{\omega}(R_{21}+ R_{22}),$

$\rho_{21}=-A_{21}-\frac{\iota}{\omega}R_{21},$

$\rho_{22}=\rho_{2}\alpha_{2}-A_{22}-\frac{\iota}{\omega}R_{22}.$

The equations (3.4) and (3.5) are solved into two relations, given by

${{B}_{i}}={{\Gamma }_{ij}}{{A}_{j}},\quad \Gamma =\frac{{{b}_{0}}}{{{a}_{0}}}(\mathbf{I}-{{\mathbf{n}}^{T}}\mathbf{n})+\frac{{{b}_{0}}{{V}_{4}}+{{b}_{1}}{{V}^{2}}+{{b}_{2}}}{{{a}_{0}}{{V}_{4}}+{{a}_{1}}{{V}^{2}}+{{a}_{2}}}{{\mathbf{n}}^{T}}\mathbf{n},$

(8)

${{C}_{i}}={{\Delta }_{ij}}{{A}_{j}},\quad \Delta =\frac{{{c}_{0}}}{{{a}_{0}}}(\mathbf{I}-{{\mathbf{n}}^{T}}\mathbf{n})+\frac{{{c}_{0}}{{V}_{4}}+{{c}_{1}}{{V}^{2}}+{{c}_{2}}}{{{a}_{0}}{{V}_{4}}+{{a}_{1}}{{V}^{2}}+{{a}_{2}}}{{\mathbf{n}}^{T}}\mathbf{n},$

(9)

where, $\textbf{I}$ is the identity matrix and $\textbf{n}^T$ identify the transpose of the row-matrix $\textbf{n}=(n_1, ~n_2, ~n_3)$. The above relations interrelate the polarisations (displacements) of solid particles with gas and water particles in the porous aggregate. The polarisation vector ${\bf A}$ defines the polarisation of solid particles in the aggregate. Polarisations of the gas and water particles are calculated from the relations (3.5) and (3.6), respectively.

where, $a_0=\rho_{11}\rho_{22}-\rho_{12}\rho_{21}$, $a_1=a_{23}\rho_{12}+a_{23}\rho_{21}-a_{22}\rho_{22}-a_{33}\rho_{11}$, $a_2=a_{22}a_{33}-a_{23}^2$,

$b_0=\rho_{12}\rho_{2s}-\rho_{1s}\rho_{22}$, $b_1=a_{12}\rho_{22}+a_{33}\rho_{1s}-a_{13}\rho_{12}-a_{23}\rho_{2s}$, $b_2=a_{13}a_{23}-a_{12}a_{33}$,

$c_0=\rho_{1s}\rho_{21}-\rho_{2s}\rho_{11}$, $c_1=a_{13}\rho_{11}+a_{22}\rho_{2s}-a_{12}\rho_{21}-a_{23}\rho_{1s}$, $c_2=a_{12}a_{23}-a_{13}a_{22}$.

Substituting (3.5) and (3.6) in (3.3), we get the following relations

${{D}_{ij}}{{A}_{j}}=0,\qquad D={{a}_{3}}(\mathbf{I}-{{\mathbf{n}}^{T}}\mathbf{n})+{{b}_{3}}{{\mathbf{n}}^{T}}\mathbf{n},$

(10)

$a_3=G-(\rho_{ss}+\frac{b_0}{a_0}\rho_{s1}+\frac{c_0}{a_0}\rho_{s2})V^2$,

$b_3=a_{11}+\frac{4}{3}G-\rho_{ss}V^2+(a_{12}-\rho_{s1}V^2)\left( \frac{b_0V_4+b_1V^2+b_2}{a_0V_4+a_1V^2+a_2}\right) +(a_{13}-\rho_{s2}V^2)\left(\frac{c_0V_4+c_1V^2+c_2}{a_0V_4+a_1V^2+a_2}\right).$

The system of equation (3.7) represent the Christoffel equations. Non-trivial solution of this system is ensured by a cubic equation (in $V^2$)

${{d}_{3}}{{V}^{6}}+{{d}_{2}}{{V}^{4}}+{{d}_{1}}{{V}^{2}}+{{d}_{0}}=0,$

(11)

where,

$\begin{align} & \left( \begin{matrix} {{d}_{3}} \\ {{d}_{2}} \\ {{d}_{1}} \\ {{d}_{0}} \\ \end{matrix} \right)=\left[ \begin{matrix} {{a}_{0}} & {{b}_{0}} & {{c}_{0}} \\ {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\ 0 & 0 & 0 \\ \end{matrix} \right]\left( \begin{matrix} {{\rho }_{ss}} \\ {{\rho }_{s1}} \\ {{\rho }_{s2}} \\ \end{matrix} \right)-\left[ \begin{matrix} 0 & 0 & 0 \\ {{a}_{0}} & {{b}_{0}} & {{c}_{0}} \\ {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\ \end{matrix} \right]\left( \begin{matrix} {{a}_{11}}+\frac{4}{3}G \\ {{a}_{12}} \\ {{a}_{13}} \\ \end{matrix} \right), \\ & \\ \end{align}$

and a linear equation (in $V^2$), given by

$G-({{\rho }_{ss}}+\frac{{{b}_{0}}}{{{a}_{0}}}{{\rho }_{s1}}+\frac{{{c}_{0}}}{{{a}_{0}}}{{\rho }_{s2}}){{V}^{2}}=0.$

(12)

The three roots of the cubic equation (3.8) explains the existence of three longitudinal waves (i.e., polarization vector is parallel to propagation vector) propagating with velocities ($V_j, ~j=1, 2, 3$). For convenience, the three longitudinal waves identified with velocities $V_1, ~V_2$ and $V_3$ are termed as $P_1, P_2$ and $P_3$ wave, respectively.

In an analogs manner, the single root of equation (3.9), explains the existence of lone transverse wave (i.e., polarization vector is normal to propagation vector) propagating with velocity $V_4$, given by the relation $V_4^{2}=G/(\rho_{ss}+\frac{b_0}{a_0}\rho_{s1}+\frac{c_0}{a_0}\rho_{s2})$. This lone transverse wave is identified as $SV$ wave.

---

4 Reflection at Plane Boundary

In this study our goal is to analyze the effects of viscous cross-coupling, porosity, saturation of gas, pore-characteristics and wave frequency on the energy shares of various reflected inhomogeneous waves at the stress free surface of partially porous solid.

---

4.1 Definition of the Problem

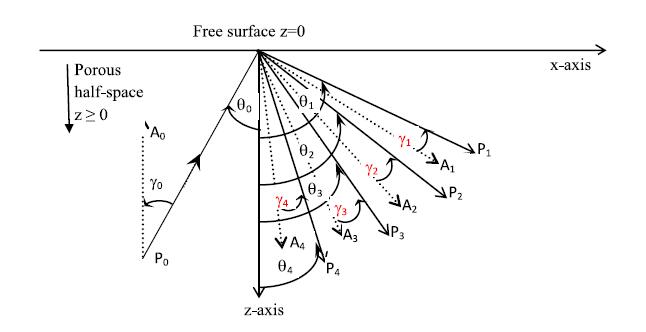
Consider a rectangular coordinate system $(x, y, z)$, in which half-space $z>$ $0$ is occupied by a saturated porous solid with its depth increasing along the $z$-direction as shown in geometrical Fig.1. The plane $z=0$ is considered as stress free surface of this medium. Following Borcherdt ^[29], in terms of angle of propagation ($\theta_0$), angle of attenuation ($\gamma_0$), propagation vector ($\textbf{P}$) and attenuation vector ($\textbf{A}$), the horizontal slowness is defined as

$s=|\mathbf{P}|\sin {{\theta }_{0}}-\iota |\mathbf{A}|\sin ({{\theta }_{0}}-{{\gamma }_{0}}),$

(13)

where, for incident wave of velocity $V_0$, we have

$|\mathbf{P}{{|}^{2}}=\frac{1}{2}[Re(\frac{{{\omega }^{2}}}{V_{0}^{2}})+\sqrt{{{(Re(\frac{{{\omega }^{2}}}{V_{0}^{2}}))}^{2}}+{{(Im(\frac{{{\omega }^{2}}}{V_{0}^{2}}))}^{2}}/{{\cos }^{2}}{{\gamma }_{0}}}],$

(14)

$|\mathbf{A}{{|}^{2}}=\frac{1}{2}[-Re(\frac{{{\omega }^{2}}}{V_{0}^{2}})+\sqrt{{{(Re(\frac{{{\omega }^{2}}}{V_{0}^{2}}))}^{2}}+{{(Im(\frac{{{\omega }^{2}}}{V_{0}^{2}}))}^{2}}/{{\cos }^{2}}{{\gamma }_{0}}}].$

(15)

Due to the dissipative nature of porous medium, the incident wave at the boundary $z=0$ is specified through its propagation direction ($\theta_0$) and attenuation direction ($\gamma_0$). The vector ($s, 0, q_0$) specify the slowness vector of incident wave, where $q_0 (=\pm\sqrt{V_0^2-s^2})$ is the vertical slowness of incident wave. To ensure the propagation of incident wave towards the boundary (i.e., negative $z$-direction), we must have $\Re(q_0)<0$. According to Snell's law the horizontal slowness($s$) of both incident and reflected waves will be remains same. Then, the vector ($s, 0, q_k$) specify the slowness vector for reflected waves, where $q_k=\pm\sqrt{V_k^2-s^2}, (k=1, 2, 3)$. To assure the decay of reflected waves moving away from boundary (i.e., positive $z$-direction), we must have $\Im(q_k)>0$. Then, the total displacement of material particles of medium is the sum of displacements associated with incident wave and three reflected waves. Hence, for two dimensional motion in $xz$-plane, the general displacement of material particles is expressed as

$\begin{align} & {{u}_{j}}=[A_{j}^{(0)}\exp (-\iota \omega {{q}_{0}}z)+\sum\limits_{k=1}^{4}{{{f}_{k}}}A_{j}^{(k)}\exp \left\{ \iota \omega (sx+{{q}_{k}}z-t) \right\}], \\ & {{v}_{j}}=[B_{j}^{(0)}\exp (-\iota \omega {{q}_{0}}z)+\sum\limits_{k=1}^{4}{{{f}_{k}}}B_{j}^{(k)}\exp \left\{ \iota \omega (sx+{{q}_{k}}z-t) \right\}], \\ & {{w}_{j}}=[C_{j}^{(0)}\exp (-\iota \omega {{q}_{0}}z)+\sum\limits_{k=1}^{4}{{{f}_{k}}}C_{j}^{(k)}\exp \left\{ \iota \omega (sx+{{q}_{k}}z-t) \right\}],\quad (j=x,z), \\ \end{align}$

(16)

where, $f_k$ are the excitation factors for reflected waves relative to incident wave. The index $`0$' represent the incident wave. The index $`k$'$(=1, 2, 3)$ represent, respectively, the reflected $(P_1, P_2, P_3, SV)$ waves. To define polarization of a longitudinal and transverse wave, the required unit vector $\textbf{n}$ is obtained as $\textbf{n}=(s, 0, q_k)V_k$.

---

4.2 Boundary Conditions

In the present geometry, boundary conditions for the particle motion are considered at the stress free plane surface $z=0$. In this problem, we consider two kinds of boundary conditions at the plane $z=0$, one is impermeable boundary (sealed pores) and other is permeable boundary (fully-opened pores). In case of impermeable boundary (sealed pores), no discharge of interstitial fluid is allowed at the surface with the passage of waves. While in case of permeable boundary (fully-opened pores), the fluid pressure should be vanish at the plane $z=0$. Hence, the suitable boundary conditions to be satisfied at the plane $z=0$ are given by

$\begin{align} & i)~{{\langle {{\tau }_{s}}\rangle }_{zz}}=0, \\ & ii)~{{\langle {{\tau }_{s}}\rangle }_{zx}}=0, \\ & iii)~\zeta {{T}_{0}}{{v}_{z}}-(1-\zeta ){{\langle {{\tau }_{1}}\rangle }_{zz}}=0, \\ & iv)~\zeta {{T}_{0}}{{w}_{z}}-(1-\zeta ){{\langle {{\tau }_{2}}\rangle }_{zz}}=0, \\ \end{align}$

(17)

where, $T_0$ is a scaling parameter that ensures dimensional homogeneity. The parameter $\zeta=1$ define the impermeable boundary (sealed surface-pores) and $\zeta=0$ define the permeable boundary (fully-opened surface-pores).

---

4.3 Reflection Coefficients

We obtain a system of four simultaneous non-homogeneous linear equations after solving the four boundary conditions (4.5) using displacements defined in equation (4.4). The system of four equations, are given by

$\sum\limits_{k=1}^{4}{{{b}_{lk}}}{{f}_{k}}=-{{b}_{l0}},\qquad (l=1,2,3,4).$

(18)

For $(k=1, 2, 3, 4)$, we have

$b_{1k}=(a_{11}-2G/3)[sA_{x}^{(k)}+q_kA_{z}^{(k)}]+a_{12}[sB_{x}^{(k)}+q_kB_{z}^{(k)}]+a_{13}[sC_{x}^{(k)}+q_kC_{z}^{(k)}]+2Gq_kA_z^{(k)},$

$b_{2k}=G[q_kA_x^{(k)}+sA_z^{(k)}], \quad b_{3k}=\zeta T_0 B_z^{(k)}-(1-\zeta)Y_k, \quad b_{4k}=\zeta T_0 C_z^{(k)}-(1-\zeta)Z_k,$

where, $Y_k=a_{12}[sA_{x}^{(k)}+q_kA_{z}^{(k)}]+a_{22}[sB_{x}^{(k)}+q_kB_{z}^{(k)}]+a_{23}[sC_{x}^{(k)}+q_kC_{z}^{k}]$

and $Z_k=a_{13}[sA_{x}^{(k)}+q_kA_{z}^{(k)}]+a_{23}[sB_{x}^{(k)}+q_kB_{z}^{(k)}]+a_{33}[sC_{x}^{k}+q_kC_{z}^{(k)}].$

System (4.6) is solved for four unknowns $f_k (k=1, 2, 3, 4)$ by using Gauss elimination method. These unknown may be treated as reflection coefficients.

---

4.4 Energy Partition

In this article, our goal is to study the partition of incident wave energy into distinct reflected waves. The energy communicated per unit area at the plane $z=0$ is the scalar product of surface traction and particle velocity (Achenbach ^[30]). Due to dissipative nature of porous medium, the concept of interaction energy (Borcherdt ^[29]; Krebes ^[31]) or the interference energy (Ainslie and Burns ^[32]) between two dissimilar waves is also involved. Therefore, total energy flux is the sum of energy flux carried out by reflected waves and interaction energy between two dissimilar waves. In the present geometry, medium supports the propagation of four (one incident and three reflected) waves. Hence, to described the distribution of incident energy at the surface $z=0$, an energy matrix is defined as

${{E}_{lk}}=\Re ({{P}_{lk}}{{f}_{l}}\overline{{{f}_{k}}})/\Re ({{P}_{55}}),\quad \quad (l,k=1,2,3,4,5);$

(19)

where $f_5=1$. A bar over a complex quantity denotes conjugate. The elements $P_{lk}$ in equation (4.7) are given by

$\begin{align} & {{P}_{lk}}=\left[ ({{a}_{11}}-2G/3)[sA_{x}^{(l)}+{{q}_{l}}A_{z}^{(l)}]+{{a}_{12}}[sB_{x}^{(l)}+{{q}_{l}}B_{z}^{(l)}]+{{a}_{13}}[sC_{x}^{(l)}+{{q}_{l}}C_{z}^{(l)}]+2G{{q}_{l}}A_{z}^{(l)} \right]\bar{A}_{z}^{(k)} \\ & +G\left[ sA_{z}^{(l)}+{{q}_{l}}A_{x}^{(l)} \right]\bar{A}_{x}^{(k)}+{{Y}_{l}}\bar{B}_{z}^{(k)}+{{Z}_{l}}\bar{C}_{z}^{(k)}. \\ \end{align}$

(20)

The energy matrix $E_{ij}, ~(i, j=1, 2, 3, 4),$ calculates the energy shares of three reflected ($P_1, ~P_2, P_3, ~SV$) waves in porous medium. The diagonal entries $E_{11}, ~E_{22}, ~E_{33}$ and $E_{44}$ identify the energy shares of reflected $P_1, ~P_2, ~P_3$ and $SV$ waves, respectively. The interaction energy due to the interference of each reflected wave with incident wave is given by $E_{IR}=\sum_{i=1}^{4}(E_{5i}+E_{i5})$. The interaction energy due to the interference between each pair of reflected waves is given by $E_{RR}=\sum_{i=1}^{4}(\sum_{j=1}^{4}E_{ij}-E_{ii})$. Then, conservation of energy at the stress free surface is assured through the relation $\sum_{l=1}^{5}\sum_{k=1}^{5}E_{lk}=0$.

---

5 Numerical Results and Discussion

---

5.1 Numerical Example

The main purpose of this study is to analyze the effects of viscous cross-coupling, porosity, saturation of gas, pore-characteristics and wave frequency on the energy shares of various reflected inhomogeneous waves at the stress free surface of partially porous solid. Numerical study is carried out by Matlab. Hence, a numerical example is considered. To choose the numerical values of various parameters, we consider a reservoir rock (sandstone) saturated with water and $CO_2$. The values of relevant material and fitting parameters (Garg and Nayfeh ^[8]; Lo et al. ^[19]) are given in Table 1.

---

5.2 Discussion of Numerical Results

The partitions of incident energy among various reflected waves and interaction energy between two distinct waves is defined by the energy matrix $E$ in the section 4.4. The variations of these energy shares with incident direction ($\theta_0\in(0, ~90^0)$) are presented in figures 2 to 7 (for incident $P_1$ wave) and in figures 8 to 13 (for incident $SV$ wave). The detailed discussion on figures is as follows.

---

5.2.1 For the Incidence of $P_1$ Wave

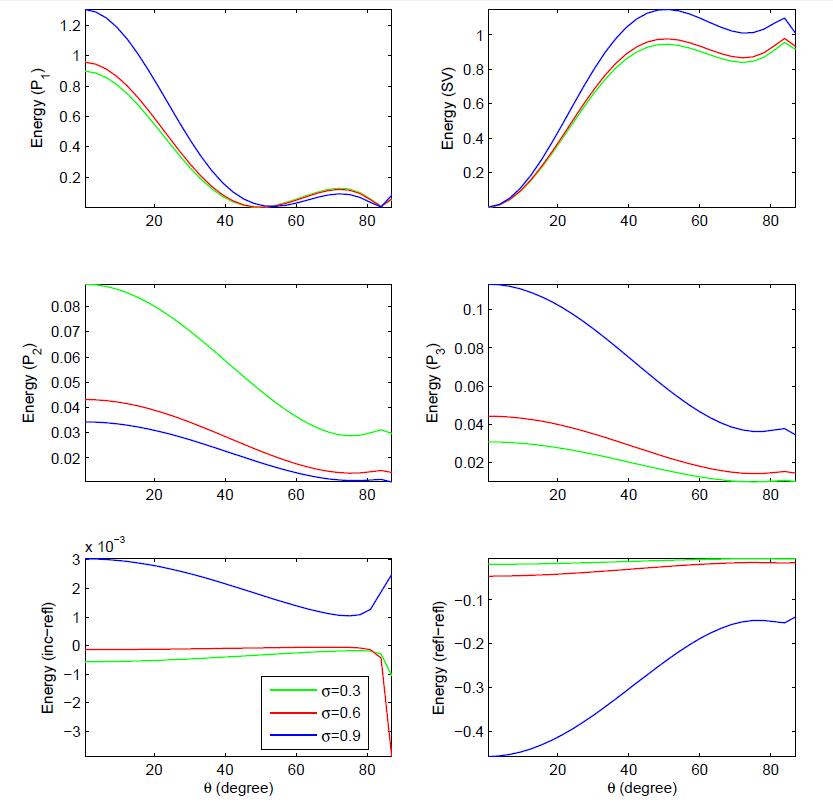
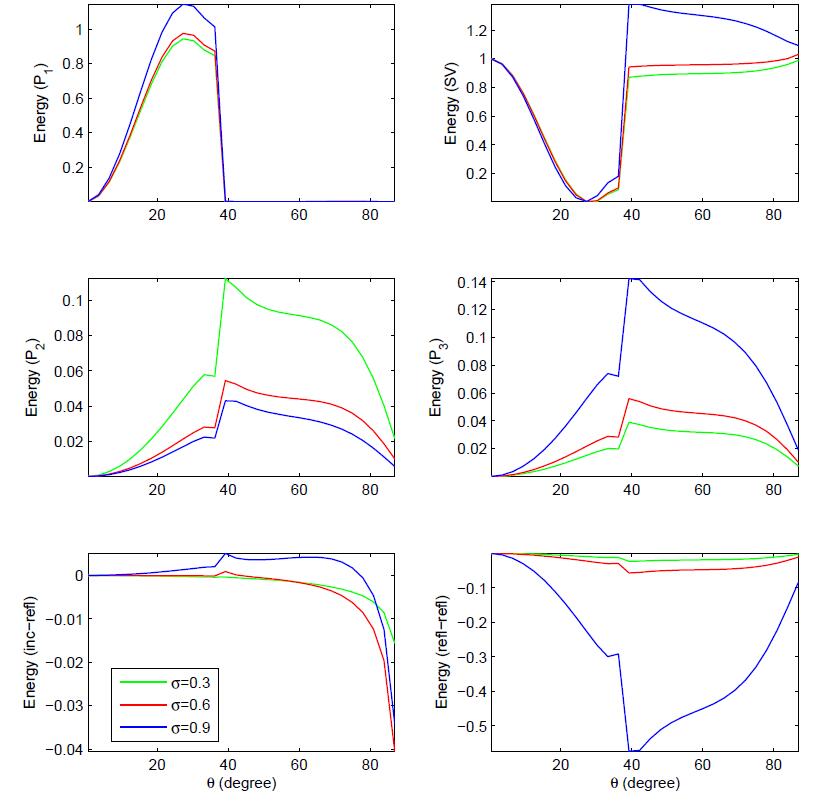
Fig.2 presents the essence of incident direction ($\theta_0$) and gas saturation ($\sigma$) on the various energy shares and interaction energies. A significant effect of gas saturation is clearly seen on all the reflected waves and interaction energy between two dissimilar waves. For the incidence below $55^0$, $P_1$ wave strengthens with the increase of gas shares in pores. However, beyond $55^0$ it weakens slightly with this change. The $SV$ wave strengthens with the increase of gas share in pores, particularly beyond $25^0$. Further, it is clear that $P_2 (P_3)$ wave weakens (strengthens) with the increase of gas share in pores. Near normal (grazing) incidence domination shift in favour of $P_1 (SV)$ wave. In the mathematical framework, energy conservation at the boundary is confirmed by considering the interference energy between two dissimilar waves.

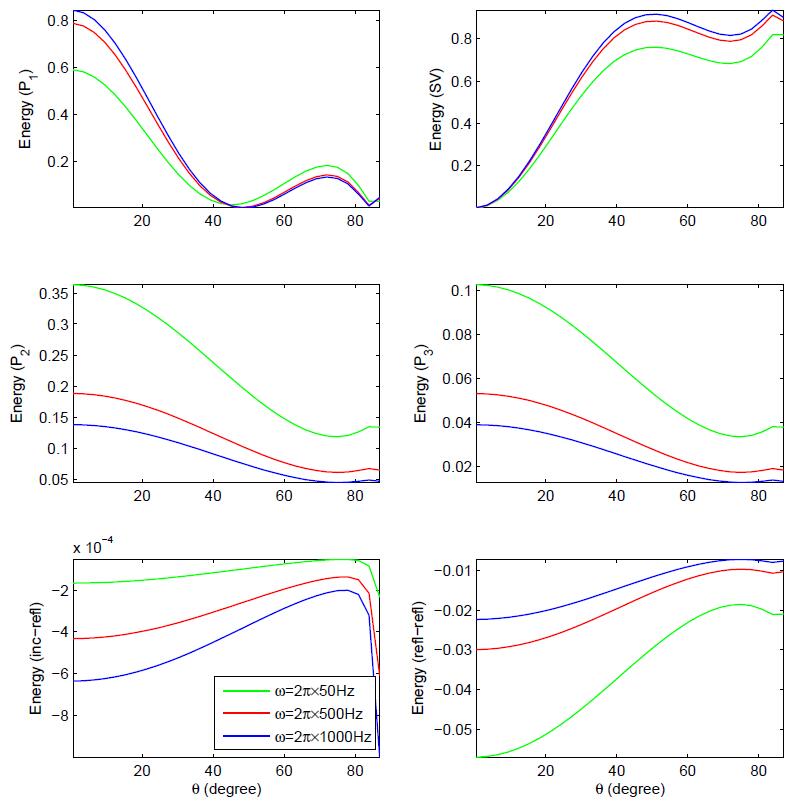
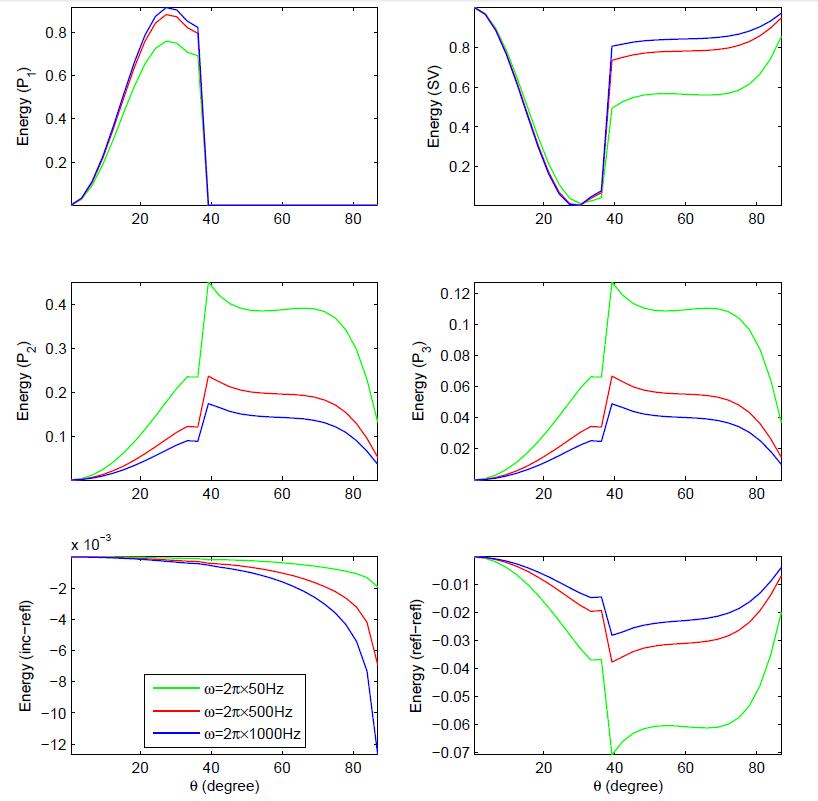
Fig.3 displays the essence of frequency on the various energy shares. The $P_1$ wave strengthens with the increase of frequency and beyond incidence $50^0$, it weakens with the increase of frequency. For incidence beyond $20^0$, $SV$ wave strengthens with the increase of frequency. Further, it is noted that qualitative behaviour of $P_2$ and $P_3$ waves are alike. All the waves are dispersive in nature.

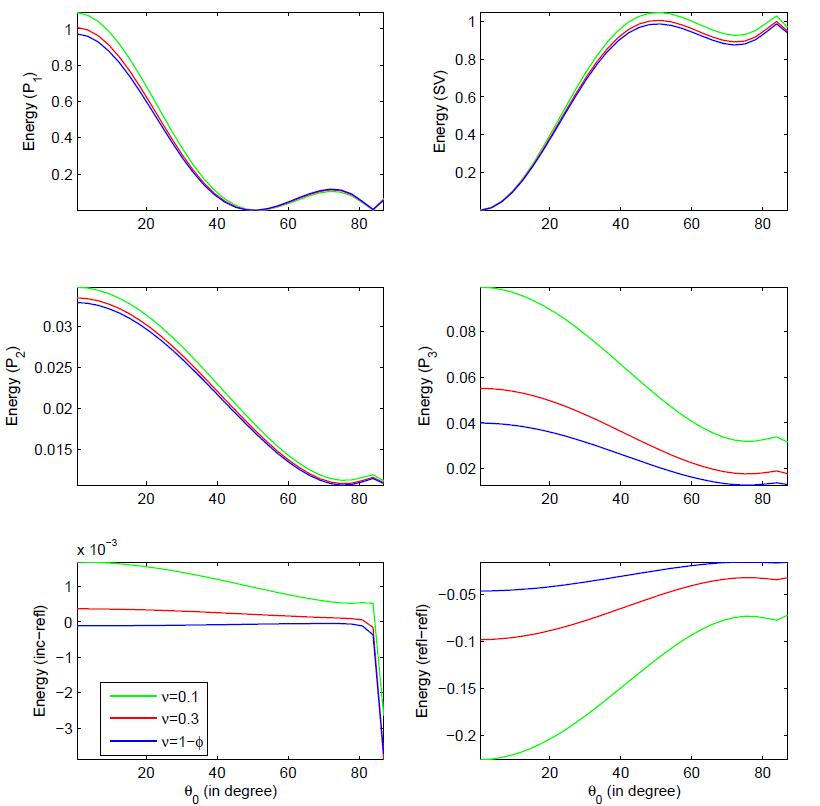
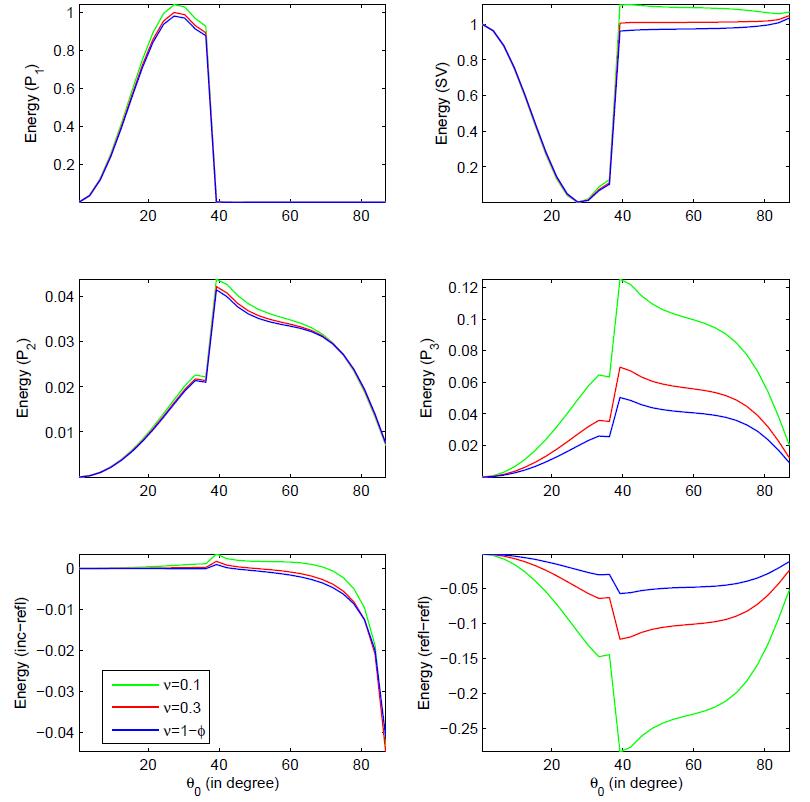
Fig.4 shows the effect of viscous cross-coupling parameter ($\nu$) on the various energy shares with the incident direction $\theta_0$. The negligible influence of viscous cross-coupling is visible on the $P_1, ~P_2$ and $SV$ waves. Whereas, a significant effect of viscous cross-coupling is noticed on the propagation of $P_3$ wave and interaction energies. All the waves are weakens with the increase of viscous cross-coupling.

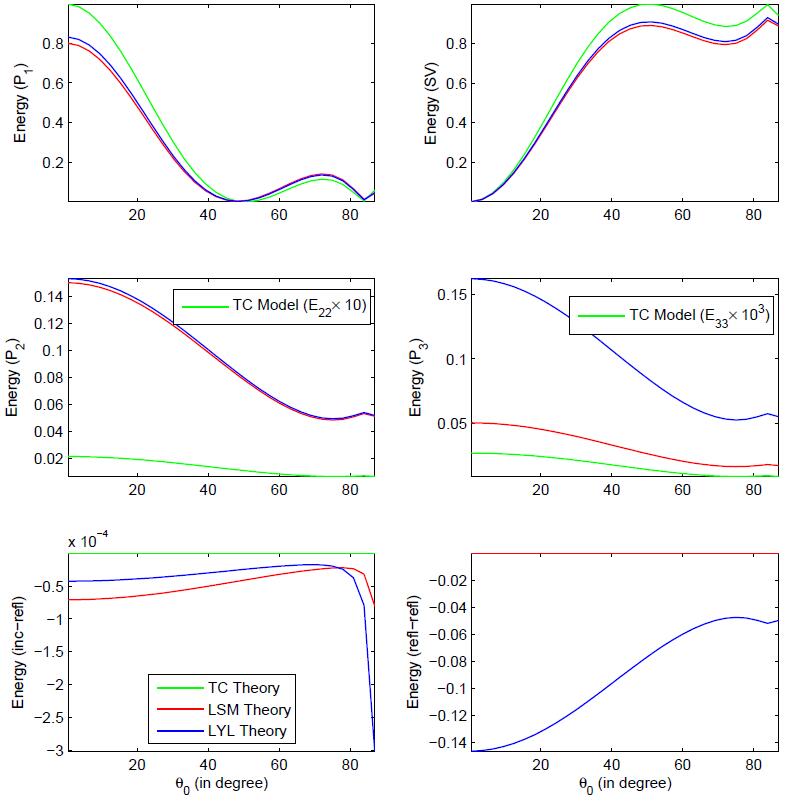
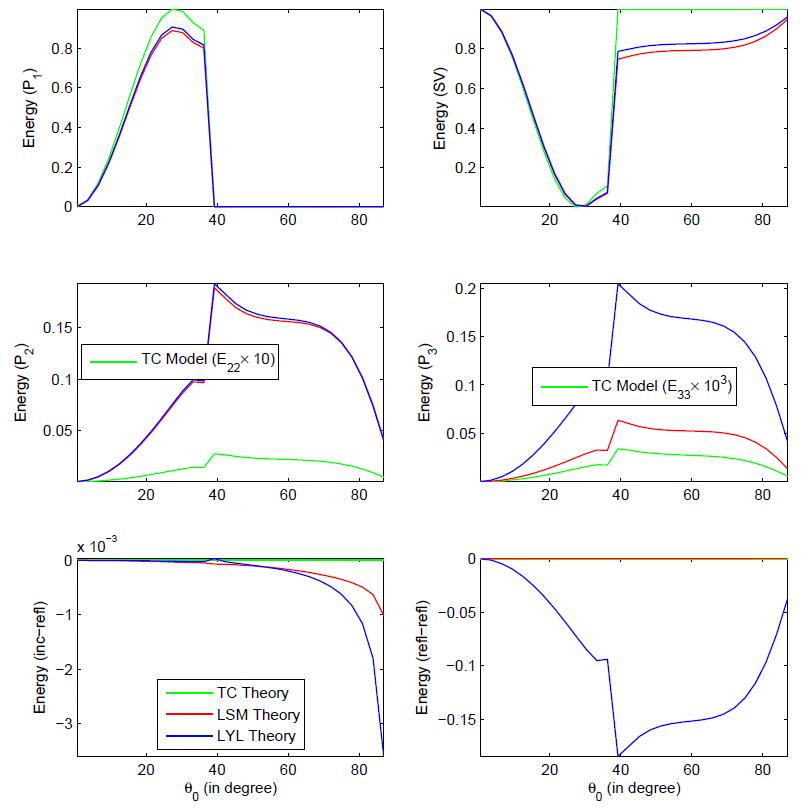
Fig.5 displays the variations of various energy shares with incident direction ($\theta_0$), corresponding to three different theories. Mathematical theory presented by Lo et al. ^[28] (LYLT) incorporated the viscous cross-coupling between two immiscible pore fluids. It is observed that after neglecting the viscous cross-coupling terms from equations of motion, the LYLT reduces to LSMT. Further, in the absence of both inertial coupling and viscous cross-coupling terms, it reduces to TCT. It is clear that the qualitative behaviour of all energy shares are alike in all the three different theories.

In case of $P_3$ wave, a significant quantitative difference between these theories appear. Further, the energy shares of $P_1$ and $SV$ waves are maximum for TCT and minimum for LYLT. While, the energy shares of reflected $P_2$ and $P_3$ waves are maximum for LYLT and minimum for TCT. A weaker quantitative difference in all energy shares is observed corresponding to LYLT and LSMT except the energy share of $P_3$ wave.

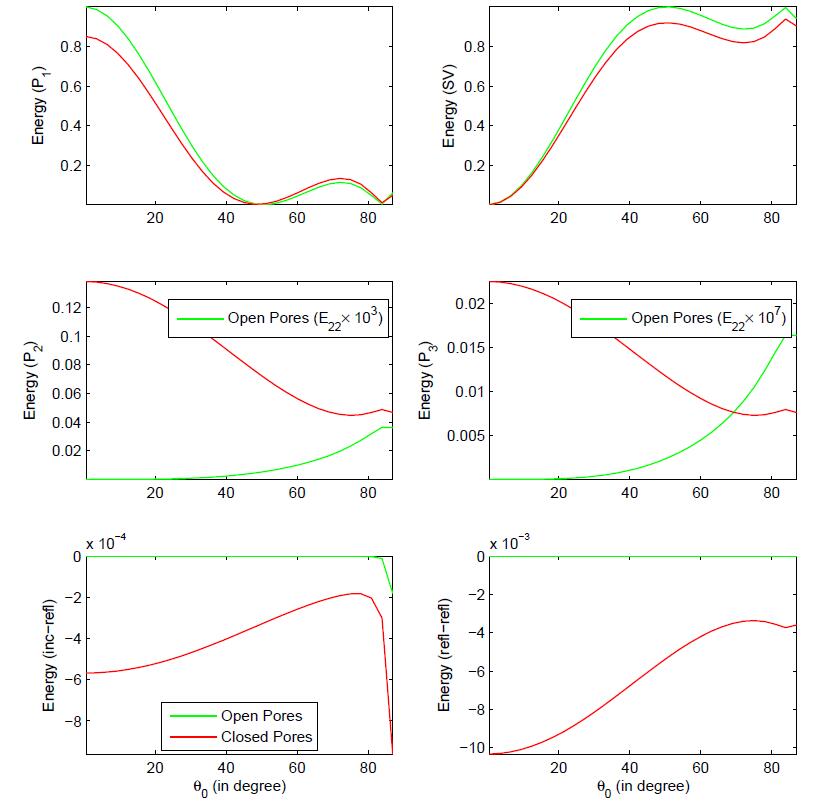
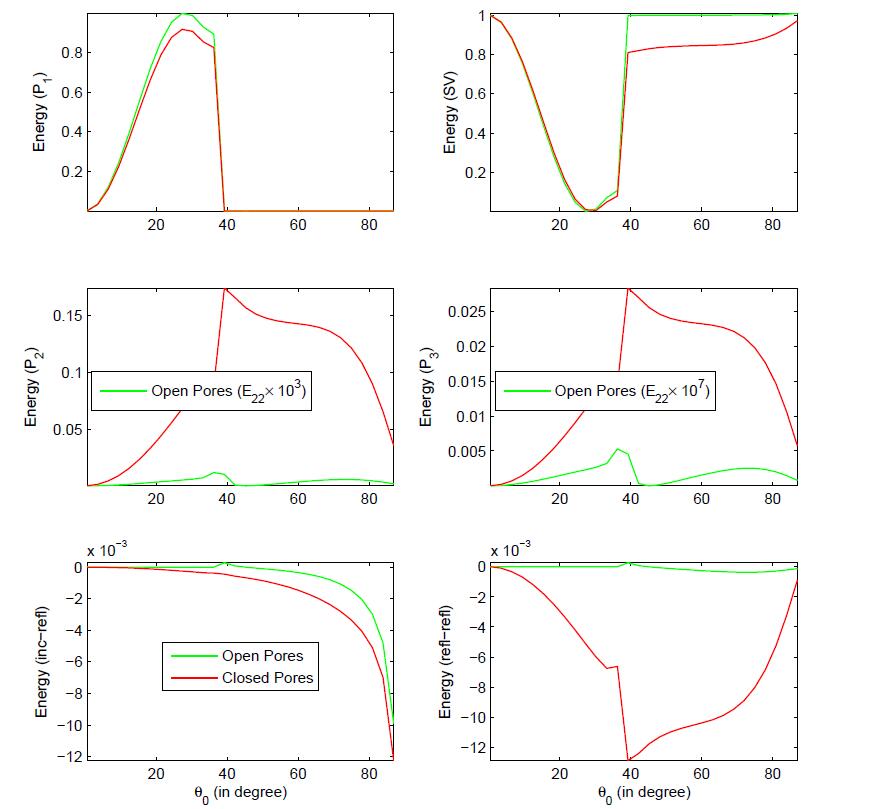
The variations in energy partition with incident direction ($\theta_0$), corresponding to open and sealed surface-pores is depicted in Fig.6. A permeable boundary surface reflect a stronger $P_1$ wave, below the incidence $50^0$. The reflected $SV$ wave at permeable boundary (fully-opened surface-pores) is almost dominated on impermeable boundary (sealed surface-pores), for $\theta_0\in(0, ~90^0)$. Further, a large quantitative difference is noticed in the reflected $P_2$ and $P_3$ waves at permeable and impermeable boundary. At impermeable (permeable) boundary, the $P_2$ and $P_3$ waves are significant (insignificant).

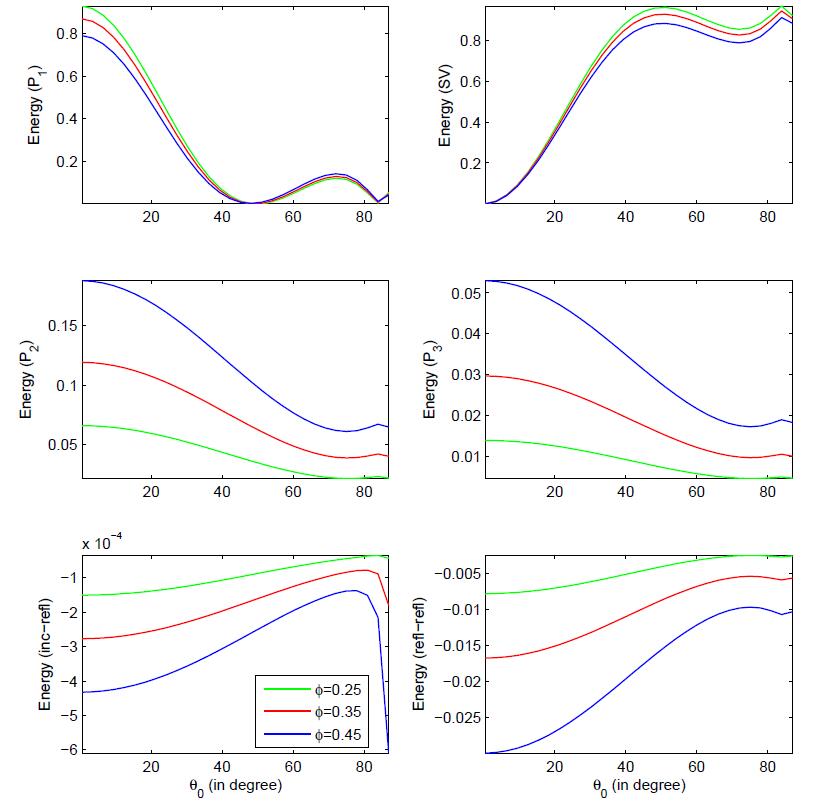
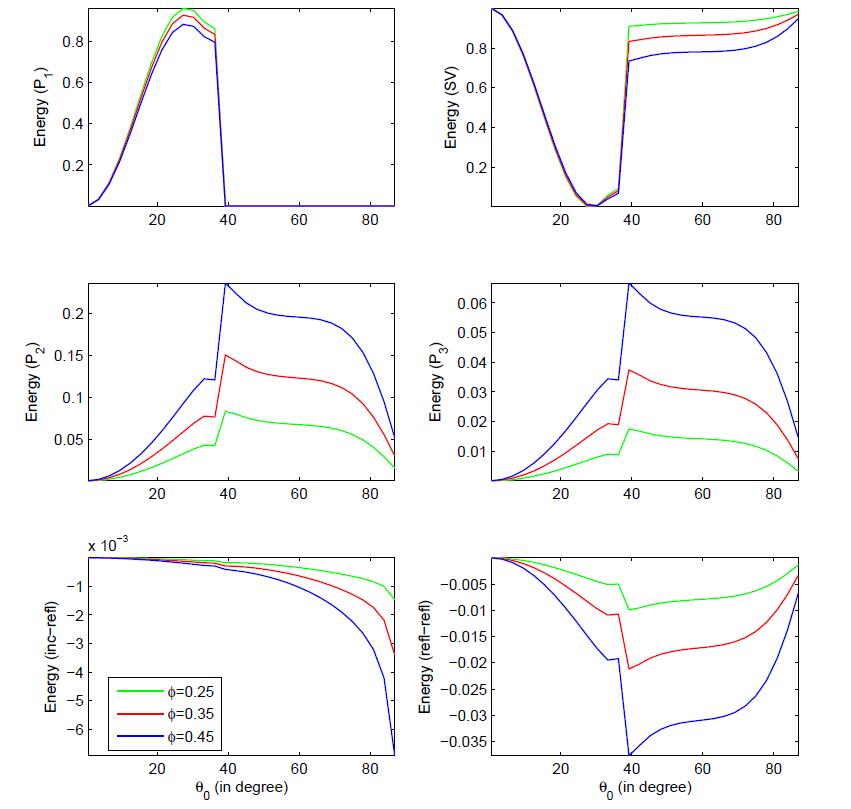
The effect of porosity on the various energy partition is shown in Fig.7. The effect of porosity on $P_1$ wave is quite significant below the incidence $55^0$. Whereas, for the incidence beyond $30^0$, a little bit essence of porosity is observed on the $SV$ wave. Further, reflected $P_2$ and $P_3$ waves becomes stronger with the increase in porosity.

---

5.2.2 For the Incidence of $SV$ Wave

Fig.8 displays the variations of energy shares with incident direction ($\theta_0$) and gas saturation ($\sigma$). Alike the incident $P_1$ wave in Fig.2, a significant essence of gas saturation is clearly visible on all the energy shares. The critical angles are found for $P_1$ and $SV$ waves around $40^0$ and $28^0$, respectively. Variational pattern of $P_1$ wave shows a reverse behaviour to that of the $SV$ wave. For the incidence below $40^0$, $P_1$ wave strengthens with the increase of gas saturation. Whereas, for the incidence beyond $40^0$, $SV$ wave strengthens with the increase of gas shares in pores. Moreover, $P_2 (P_3)$ wave weakens (strengthens) with the increase of gas shares in pores. For near normal incidence, it is observed only $SV$ wave survive quantitatively.

Fig.9 displays the effect of wave frequency ($\omega$) on the various energy shares. With the increase of wave frequency, $P_1$ and $SV$ waves becomes quite stronger but $P_2$ and $P_3$ waves becomes weaker with this change. Further, variational pattern of $P_2$ and $P_3$ waves are almost alike.

Fig.10 shows the essence of viscous cross-coupling parameter ($\nu$) on the various energy shares. Almost all the energy shares decreases with the increase of viscous cross-coupling. The effect of viscous cross-coupling on $P_1, P_2$ and $SV$ waves is little bit significant.

The variations in energy partition with incident direction ($\theta_0$), corresponding to three different theories are shown in Fig.11. In case of $P_3$ wave, a significant difference is observed between these theories. Whereas, in case of $P_1, P_2$ and $SV$ waves, a insignificant difference is observed between LYLT and LSMT.

The variations in energy partition with incident direction ($\theta_0$), corresponding to open and sealed surface-pores is depicted in Fig.12. The observation found corresponding to these surface-pores characteristics are nearly same as the case of incident $P_1$ wave in Fig.6.

The effect of porosity on the various energy shares with incident direction $\theta_0$ is shown in Fig.13. It is clearly visible that for incidence below $40^0$, $P_1$ wave strengthens with the increase of porosity and beyond $40^0$, $SV$ wave strengthens with the increase of porosity. Further, $P_1$ and $P_2$ waves also strengthens with the increase of porosity.

---

6 Conclusions

In this article, reflection of inhomogeneous waves at the stress-free plane surface of partially saturated porous solid is investigated. Porous medium is considered dissipative due to the involvement of viscosity in pores fluid. Four waves (three longitudinal and one shear) are found to be reflected, as a result of incident wave. All the reflected waves are inhomogeneous in nature (i.e., different direction of propagation and attenuation). Appropriate boundary conditions are used for opened surface-pores (permeable boundary) and fully closed surface-pores (impermeable boundary). For both incident $P_1$ and $SV$ waves, energy flux characteristics of seismic waves are studied analytically and numerically for a particular model. The closed-form analytical expressions for the reflection coefficients of various reflected waves are computed analytically at the stress-free plane surface. Further, these reflection coefficients are used to calculate the energy shares of various reflected waves. Conservation of the incident energy at the plane interface is confirmed by considering the interaction energy between two dissimilar waves. Finally, for particular model, effect of hydrological properties (like, viscous cross-coupling, porosity, saturation of gas, pore-characteristics) and wave frequency has been studied on energy flux characteristics of seismic waves. The energy flux characteristics correspond to the TCT, LSMT and LYLT are also presented in this study. Finally, some conclusions are addressed which may be drawn from the discussions of the numerical results.

• At the normal incidence of $SV$ wave, only $SV$ wave is survive quantitatively among all the reflected waves. While at the normal incidence of $P_1$ wave, only $SV$ wave is not survive quantitatively.

• The $P_2$ wave weakens but $P_3$ wave strengthens, with the increase of gas saturation.

• For both incident $P_1$ and $SV$ waves, $P_2$ and $P_3$ waves are found to be strengthens (weakens), with the increase of porosity (frequency).

• The $P_2$ and $P_3$ waves are strengthens (weakens) when the pores at the reflecting boundary are fully-closed (fully-opened). Whereas, $P_1$ and $SV$ waves are weakens (strengthens) when the pores at the reflecting boundary are fully-closed (fully-opened).

• The basic difference between TCT, LSMT and LYLT is mainly observed in the behaviour of $P_2$ and $P_3$ waves. Due to the involvement of viscous cross-coupling between two fluids in the equations of motion, energy shares of $P_2$ and $P_3$ waves are found to be strengthen.

• The energy shares of $P_3$ wave is found to be greatly influenced due to the involvement of viscous cross-coupling terms in the equations of motion. Hence, this fact shows that the present study is in good agreement with the Lo et al. ^[28] study. This is due to the fact that Lo et al. ^[28] study shows that the presence of viscous cross-coupling between two fluids, significantly influenced the phase speed of $P_3$ wave.

• All the waves are dispersive (i.e., frequency dependent) in nature.

• In mathematical framework, the conservation of the incident energy is confirmed by considering the interaction energy between two dissimilar waves due to the dissipative nature of the considered medium. This validates that the numerical calculations are analytically correct.

Finally, for both incident $P_1$ or $SV$ wave, it is found that the energy flux characteristics of seismic waves depend on several factors, such as wave frequency, gas saturation, porosity, pore-characteristics and viscous-cross coupling between two fluids. Therefore, the study of energy flux characteristics can yield to useful information about the rock properties.

---

7 Apendix

Following Lo et al. ^[21], the elasticity coefficient $a_{ij}$ in terms of directly measurable parameters are given as

$a_{11}=K_0[\alpha_0 N_1\{K_1 K_2+K_1 N_2\sigma+K_2 N_2(1-\sigma)\}+K_b K_0(1-\alpha_0)\{K_1(1-\sigma)+K_2\sigma+N_2\}]/N_3$,

$a_{12}=[K_0 K_1(1-\alpha_0)\sigma N_1(K_2+N_2)]/N_3$, $a_{13}=[K_0 K_2(1-\alpha_0)(1-\sigma) N_1(K_1+N_2)]/N_3$,

$a_{22}=[K_1(1-\alpha_0)\sigma\{K^{2}_0 (1-\alpha_0)(\sigma K_2+N_2)+K_2(1-\sigma)N_1 N_2\}]/N_3$,

$a_{23}=-[K_1 K_2(1-\alpha_0)(1-\sigma)\sigma\{N_1 N_2-(1-\alpha_0)K^2_0\}]/N_3$,

$a_{33}=[K_2(1-\alpha_0)(1-\sigma)\{K^{2}_0 (1-\alpha_0)(K_1(1-\sigma)+N_2)+K_1\sigma N_1 N_2\}]/N_3$,

$\frac{dp_c}{d\sigma}=(\rho_2 g/(n-1)m)[\{(1-\sigma)^{-(\frac{n}{n-1})}-1\}^{(\frac{1-n}{n})}(1-\sigma)^{-(\frac{2n-1}{n-1})}]$,

$N_1=K_0\alpha_0-K_b, N_2=\frac{dp_c}{d\sigma}\sigma(1-\sigma)$,

$N_3=[N_1\{K_1 N_2\sigma+K_1 K_2+K_2 N_2(1-\sigma)\}+K^2_0(1-\alpha_0)\{K_1(1-\sigma)+N_2+K_2\sigma\}]$,

where $K_0, ~K_1, ~K_2$ and $K_b$ denote the bulk moduli of three constituent phases and porous skeleton, respectively.

Viscous cross-coupling coefficients are given by

$R_{11}=-\frac{\lambda_{22}\alpha_{1}^{2}}{\Delta}$, $R_{12}=\frac{\lambda_{12}\alpha_{1}\alpha_{2}}{\Delta}$, $R_{21}=\frac{\lambda_{21}\alpha_{1}\alpha_{2}}{\Delta}$, $R_{22}=-\frac{\lambda_{11}\alpha_{2}^{2}}{\Delta}$,

$\lambda_{11}=\left( \frac{1+\nu_1}{2}\right)b_1^{*}$, $\lambda_{12}=\left( \frac{1-\nu_1}{2}\right)b_1^{*}$, $\lambda_{21}=\left( \frac{1-\nu_2}{2}\right)b_2^{*}$, $\lambda_{22}=\left( \frac{1+\nu_2}{2}\right)b_2^{*}$,

$\Delta=\lambda_{11}\lambda_{22}-\lambda_{12}\lambda_{21}$, $\chi_1=\sigma^\chi[1-(1-\sigma)^\frac{n}{n-1}]^{\frac{2(n-1)}{n}}$, $\chi_2=(1-\sigma)^\chi[1-\{1-(1-\sigma)^\frac{n}{n-1}\}^\frac{n-1}{n}]^{2}$,

$b_1^{*}=\chi_1/\eta_1$, $b_2^{*}=\chi_2/\eta_2$, where $\nu_j$ signifies the interfacial coupling parameter of fluid phases $j$ (Ayub and Bentsen ^[33]). For an idealized channel flow, according to Ayub and Bentsen ^[33] $\nu_1=\nu_2=\nu=1-\phi$ ($\phi$ being the porosity). $\eta_1$ and $\eta_2$ denote the viscosities of gas and liquid phases, respectively. The relative permeabilities $\chi_1, ~\chi_2$ for the flow of two pore-fluids are defined in comparison to the intrinsic permeability ($\chi_0$) of the composite medium. The capillary pressure ($p_c$) is due to the interfacial interactions between the two viscous pore-fluids. It varies with the fraction ($\sigma$) of gas or the fraction of liquid ($1-\sigma$) in twin-fluid mixture filling the pore space. The quantities $m$, $n$ and $\chi$ are model parameters. These are obtained by fitting the experimental data on the $p_c$-$\sigma$ and $\chi_j$-$\sigma$ relations, which are used in defining $a_{ij}$.

According to Lo et al. ^[19], inertial-coupling coefficients are given by

$A_{11}=\rho_1\alpha_1(1-\beta_s)$,

$A_{22}=\rho_2\alpha_2(1-\beta_s)$,

$A_{12}=A_{21}=-0.1\sqrt{\alpha_1\alpha_2\rho_1\rho_2\beta^2_s}$,

$\beta_s=\frac{\alpha_0}{2(\alpha_0-1)}$.

---