1. Lateral flow assays
The reliable detection of contaminants in food and of toxins, hormones, proteins, etc. in biological samples is crucial to assess and reduce risks for the human health. The major obstacles in monitoring and controlling these parameters remain the lack of infrastructure, shortages in trained personnel and increase in healthcare associated infections, especially in developing countries [1]. Lateral flow assays (LFAs) belong to the group of point-of-care (POC) devices and can overcome all these challenges by combining features like ease of use, rapid response, robustness and low costs. During the development process, difficulties can arise from the potential for either false negative results due to the hook effect, where a high concentration of target prevents a proper signal generation, or false positive results due to non-specific binding to the LFA [2]. In addition, multiplexed sensing of several analytes on one LFA is still not trivial. Despite these drawbacks, LFAs represent powerful tools that can detect almost any analyte, such as proteins [3,4], toxins [5], hormones [6], ions [7] and even whole cells or viruses [8]. Consequently, intensive research focused on the development of new types of LFAs and some of the more recent examples are reviewed below.
1.1. Lateral flow assay components
A LFA test strip comprises several overlapping membranes fixed on a backing card that provides a certain mechanical stabilization. In a typical assay, the sample solution is applied to the sample pad, which can filter specific components and adjust assay conditions by changing e.g. the pH value. The solution migrates in a lateral direction via capillary forces towards the conjugation pad, where the fluid rehydrates a detection label composed of a recognition element coupled to a reporter molecule like gold nanoparticles (AuNPs), that build a complex with the target [9]. Capturing molecules, such as antibodies or aptamers, form a test- and a control zone after deposition onto a membrane made of e.g. nitrocellulose [10]. As soon as the solution reaches the test line, the capturing molecules bind to the target, thereby immobilizing the complex. The enrichment of reporter molecules produces a signal that is detectable by a read-out device or even by the naked eye. While the test line indicates the presence of the analyte in the sample, the control line validates a proper fluid flow through the assay, as well as activity of the assay reagents [2]. The absorbent pad provides driving force based on the capillary effect and prevents the back flow of the fluid. Overlapping of adjacent membranes is necessary to coordinate a proper fluid flow [10].
Generating a signal by binding of reporter molecules like AuNPs onto the test line is essential for a successful assay. Basically, sandwich or competitive formats are possible to achieve an effective detection. In a sandwich assay, detection labels provided within the conjugation pad react with the target analyte to form a complex, which is subsequently captured in the test zone via interaction between the analyte and the corresponding immobilized capturing molecules. In the competitive format, the conjugation pad provides target molecules coupled to a reporter molecule. Thereby, the fluid reaching the test zone contains both, labeled target molecule and unlabeled target molecules originating from the sample, which consequently compete for binding to the capture molecules immobilized in the test zone. In a similar approach, the reporter-modified recognition element can bind to target molecules deposited in the test zone. In this manner, the analyte of the sample competes with target molecules of the test zone for the binding sites of the recognition elements. Both, sandwich and competitive assays are suitable formats for qualitative and semi-quantitative detection of analytes. Independently of target present in the sample, capture molecules of the control line bind to the excess of detection labels, thus indicating a proper fluid flow. In general, sandwich format assays are performed when the analyte possesses multiple binding sites (for aptamers these sites are called aptatopes [11]), while analytes with a low molecular weight or a single binding site make competitive platforms more convenient [12].
2. Aptamers
Recognition elements are key components of a LFA, determining the sensitivity and selectivity of the assay. Antibodies have been the ligand of choice for decades, owing to high affinities towards their targets and the possible production against a variety of molecules [13,14]. Nevertheless, antibodies exhibit some disadvantages, mostly due to their protein origin, such as irreversible temperature-induced denaturation or the difficult introduction of modifications [15]. These disadvantages led researchers to strive for alternative ligands and in 1990 aptamers were described [16,17].
Aptamers are single-stranded oligonucleotides, composed of RNA or DNA, that fold into well-defined three-dimensional structures, which enable binding of a corresponding target via molecular recognition with high specificity and affinity [18]. The typical length of aptamers varies from 15 to 120 bases [19]; shorter aptamers usually do not show high affinities because not enough bases can participate in folding and binding of the aptamer. Longer sequences exist, but tend to misfold or aggregate [20] and the yield in chemical synthesis decreases, making them more expensive [21].
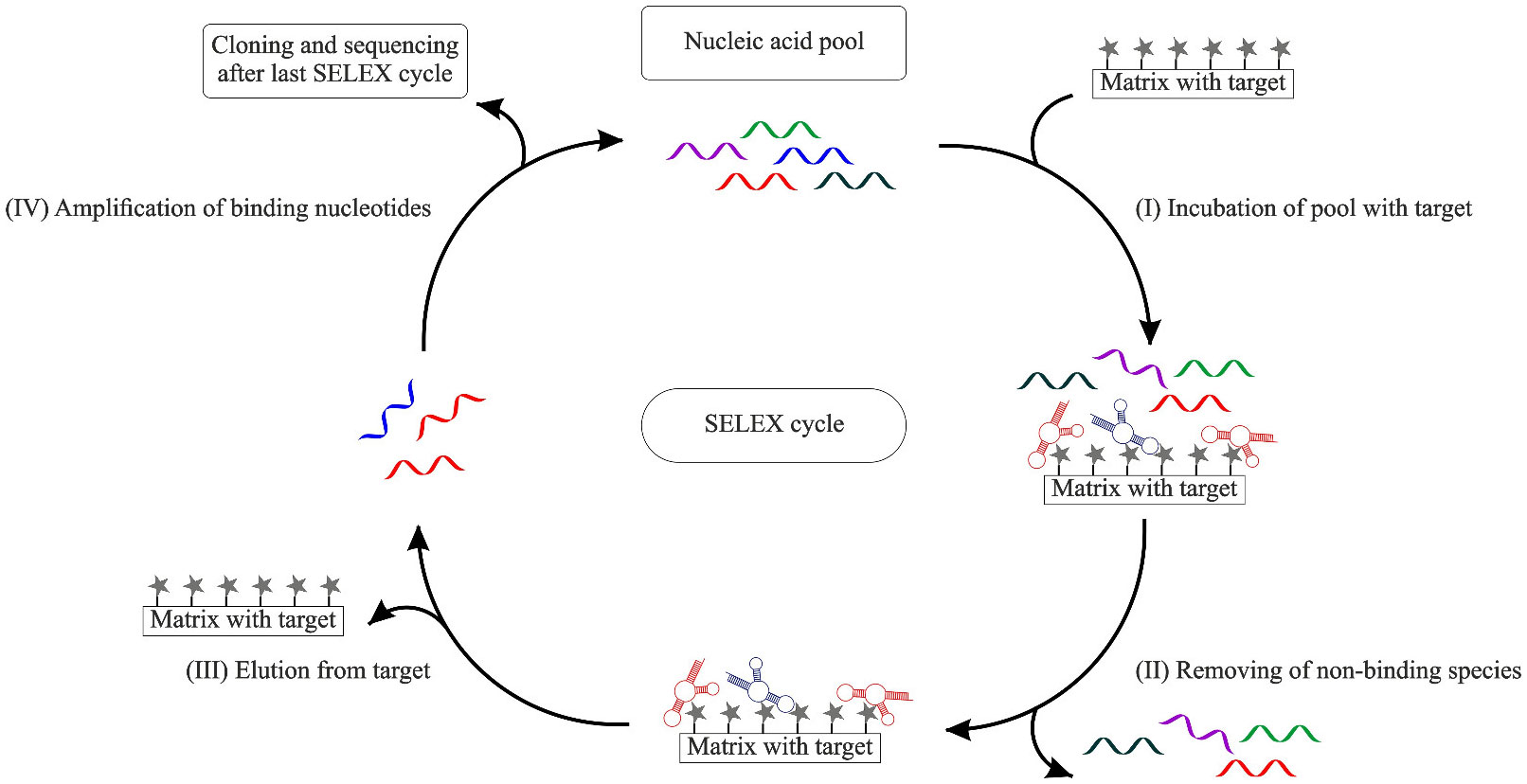
An in vitro selection and amplification technique, known as SELEX (systematic evolution of ligands by exponential enrichment, Figure 1), allows the selection of aptamers directed against virtually all kinds of target molecules [22]. Moreover, the functionality of aptamers is not dependent on physiologic conditions, hence buffer compositions can be adjusted during SELEX concerning intended assay applications. Consequently, the adaption of assay parameters, to ensure a high activity of recognition elements, is unnecessary [23]. The in vitro selection process represents one of the major advantages of the aptamer technology due to possible modifications. The SELEX process can generate highly specific aptamers by employing counter-selection with target analogues to eliminate cross-reactivity [24]. By varying the SELEX process, identification of aptamers against almost every type of target is possible, which is proven by the selection of aptamers against targets like proteins [25], viruses [26], cells [27] as well as small molecules like vitamins [28], organic dyes [17], toxins and antibiotics [29].
Following SELEX procedure, standard phosphoramidite chemistry for synthesis of oligonucleotides is applied for the production of aptamers with high reproducibility and minimal batch-to-batch variations [21]. The introduction of linker, fluorophores and different functional groups fused to either the 3′ or the 5′ end of the aptamer represent possible modifications, which can be introduced during the chemical synthesis to enhance the stability of the aptamers or simplify detection [31]. These advantageous properties of aptamers are substantiated by the versatile applications like the detection of small molecules [32,33,34], purification of proteins [35], and depletion of small molecules [36], as well as in cell targeting and drug delivery [37,38]. The possibilities to combine recognition elements with biosensors are almost endless and are reviewed elsewhere [39]. Here, we focus on the combination of aptamers as recognition elements and LFAs as sensing platforms reducing the design strategies to a small number of underlying principles, of which some can also be realized with other recognition elements, while others are unique for aptamers [40,41]:
a Target-induced dissociation or displacement mode (TID-mode)
b Target-induced reassembling of aptamer fragments (TIR-mode)
c Target-induced structure switching mode (TISS-mode)
d Sandwich mode
e Competitive replacement mode
This part of the review will introduce recent advances on the field of aptamer-based LFAs for the detection of small molecules, proteins and whole cells or viruses, while the design strategies mentioned above will serve as a basis. A more comprehensive summary of LFAs can be found in Table 2, Table 4 and Table 6 respectively.
3. Detection of small molecules with lateral flow assays
3.1. Introduction to the detection of small molecules
Small molecules like toxins or antibiotics pose a threat to the human health and evoke potential risks. The detection and monitoring of contaminants in food and environment is crucial, but the sensitive and specific detection of small molecules remains challenging [42]. As recognition elements, aptamers have emerged as a preferable alternative to antibodies, especially for the detection of small molecules due to several advantages. In contrast to aptamers, antibodies are mainly selected in vivo, which contributes to possible problems in the antibody selection process.
One difficulty is the selection of toxic and non-immunogenic targets including small molecules like haptens [41], which usually do not induce an immune response unless coupled with macromolecules such as proteins [43]. As a result, the selected antibodies show high affinities against a complex and the use of the target without the carrier in LFAs can alter the affinity of the antibody towards the target. While the development of antibodies depends in most cases on the immunization of animals, aptamers are selected by in vitro techniques, thus eliminating the need for an immune response. Aptamers offer the possibility of counter selection of target analogues during the selection process as mentioned before. For the detection of small molecules, the specificity of recognition elements can suffer from the structural similarities between the target and its derivatives. The counter selection introduces closely related molecules of the target to the SELEX process, and only aptamer sequences differentiating between the target and their analogues are chosen for further experiments. Therefore, aptamers can exhibit a greatly reduced cross-reactivity to similar molecules, resulting in a higher selectivity against their targets [44].
3.2. Target-induced dissociation
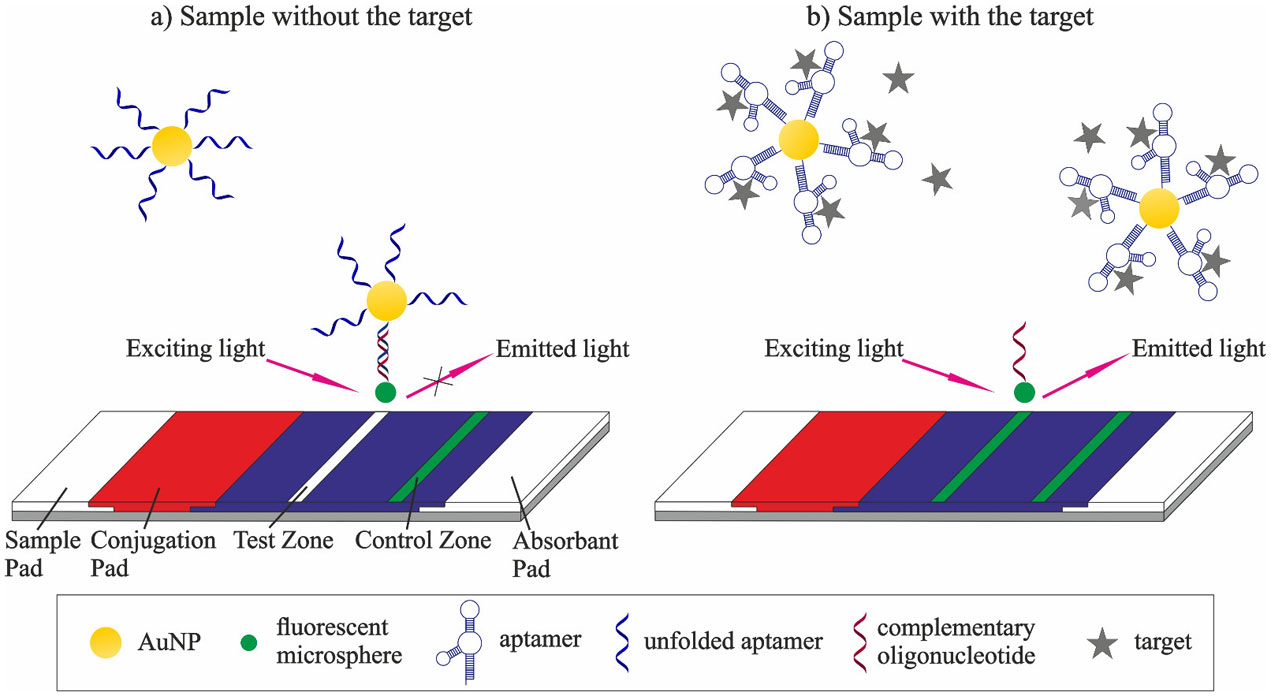
One mechanism for the detection of small molecules is the target-induced dissociation or displacement (TID)-mode. Aptamers are ssDNA and can bind to a DNA probe with a complementary sequence (oligonucleotide) to form a duplex. The aptamers' target can replace the complementary oligonucleotide, and consequently the principle of a LFA based on the TID-mode is competitive binding of the target molecule and a complementary oligonucleotide [45]. This approach is the most common one for the detection of small molecules by aptamer-based LFAs (Table 2). In a typical assay setup, the conjugation pad of the LFA contains dried detection labels, such as aptamer-modified AuNPs, which migrate after resuspension towards the test- and control zone [46,47].
In a sample not containing the analyte of interest, after reaching the test zone the AuNPs-aptamer conjugates bind via hybridization to the complementary oligonucleotides to form a duplex resulting in a detectable signal (Figure 1). In the presence of the analyte, the target competes with the complementary oligonucleotide sequence for the same binding site of the aptamer, which prevents the hybridization of aptamer and complementary oligonucleotide on the test line, thus a weaker or no signal is generated [48].
The design of a complementary oligonucleotide sequence, suitable for TID, is a rather complicated task because the dissociation constant must fit in a certain range. If the sequence is too short, binding to the aptamer can be weak, resulting in unspecific dehybridization. On the other hand, a long oligonucleotide sequence can hybridize strongly, leading to false-negative signals due to incomplete displacement [49].
As an example, Wu et al. [50] used the TID-mode to create a LFA for the detection of mercury (II)-ions in river water. Mercury is one of the most toxic heavy metals and due to industrialization, an increased amount of mercury is released to rivers creating an urgent need for a sensitive detection assay. To meet these challenges, Wu et al. developed a fluorescence-quenching assay, where fluorescent microspheres (FMs) were coupled to an oligonucleotide with a sequence complementary to the mercury (II)-ion aptamer (Table 1) and subsequently immobilized them on the test line of a lateral flow device. The conjugate pad contained aptamer-conjugated AuNPs that hybridized with the oligonucleotide sequence on the test line, in the absence of mercury in the sample. The gold particles quenched the fluorescence of the microspheres, resulting in a decreasing intensity of emitted light. When mercury was present, the ions bound to the aptamer and hampered the hybridization to the complementary oligonucleotide. The aptamer-AuNPs conjugates did not quench the signal of the FMs, resulting in a bright fluorescent test line. In general, competitive assays are switch-off sensors, but this special design lead to the generation of a signal as the target binds to aptamer-modified AuNPs, thus in a switch-on assay mode. Using this LFA, Wu et al. were able to detect mercury (II)-ions in a range of 0.13 ng/ml to 4 ng/ml with a limit of detection (LOD) of 0.13 ng/ml and read out times of less than 15 min.
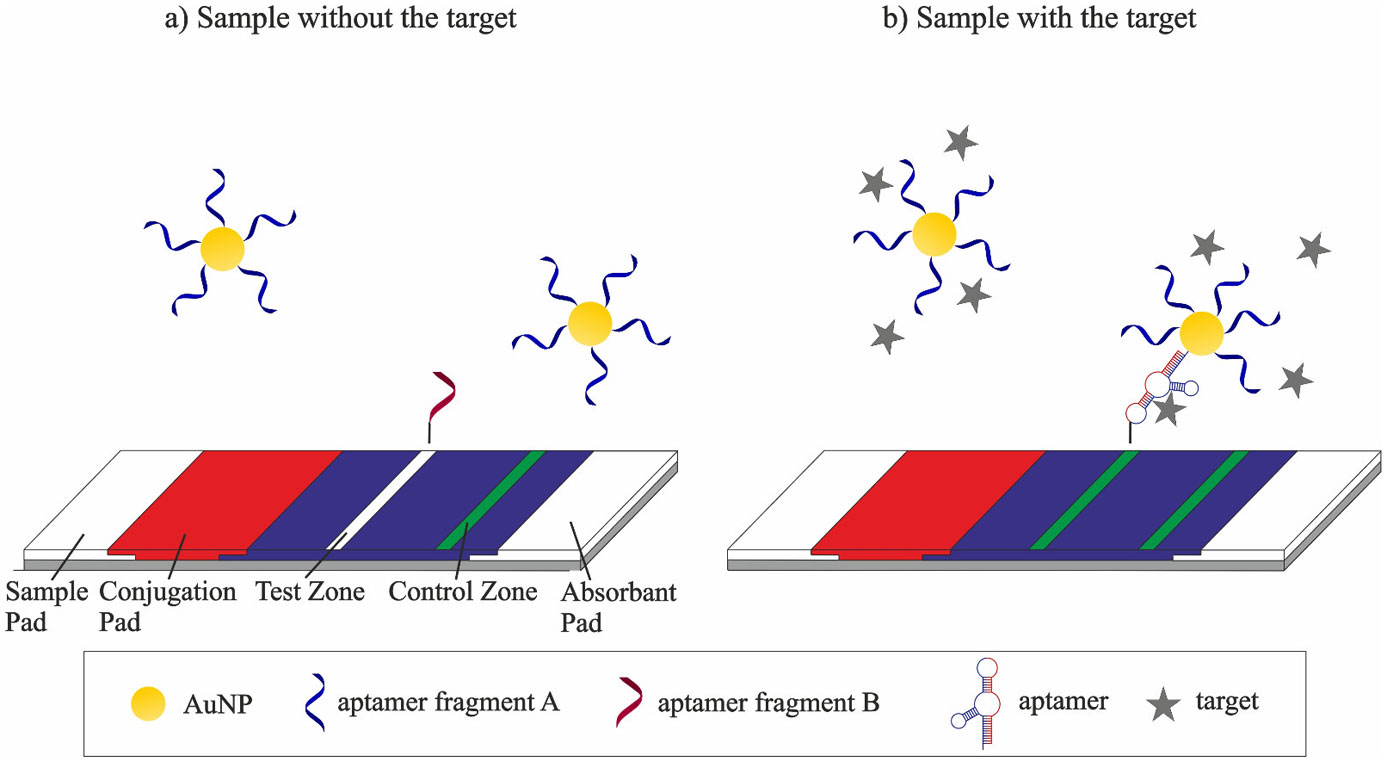
3.3. Target-induced reassembling of aptamer fragments
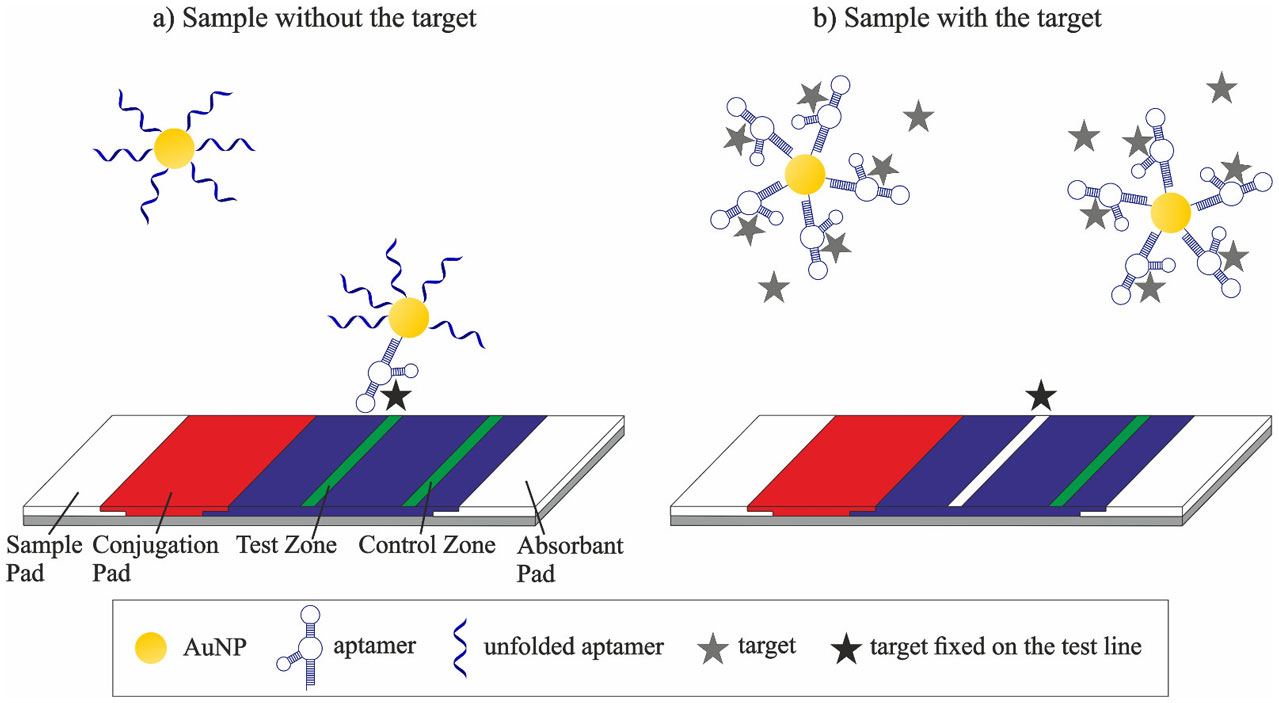
A sandwich assay is always preferred for protein detection because of its high specificity and sensitivity resulting from a dual recognition mechanism [51]. However, small molecules often lack a second binding site, making the competitive assay more convenient. To circumvent this drawback, a split-aptamer strategy was developed by Stojanovic et al. [52], in which a nucleic acid aptamer was split into two fragments that could specifically form a ternary assembly in the presence of a target. When both aptamer fragments come close to each other, they can fold in their three-dimensional structure and bind their target, thereby stabilizing the ternary complex. In 2016, split aptamers against six targets (ATP [53], Cocaine [54], Thrombin [55], 17β-Estradiol [56], D-vasopressin [57]) were reported. In principle, split aptamers can be generated by dividing any aptamer sequence into two separate strands, but structural information about the aptamer is necessary to find candidate split sites [52,58].
Zhu et al. [59] developed a LFA for the detection of ATP based on the split aptamer mechanism (Figure 3). In this method, one part of the aptamer was conjugated to the surface of gold nanoparticles, while the other part was labeled with biotin and immobilized on the surface of the test line via biotin-streptavidin interaction. The detection label migrated with the target towards the test zone, where the immobilized aptamer fragment reassembled with the cognate aptamer fragment building a sandwich-like complex with the target. A characteristic red band appeared, arising from the accumulation of AuNPs in the test zone. Once the solution reached the control line, excess AuNPs, conjugated with aptamer fragments, were captured in the control zone via the reaction between a biotinylated complementary oligonucleotide and the aptamer fragment-AuNPs conjugates, which produced a second red band. In this sandwich-like dipstick assay a linear logarithmic response to the ATP concentration was obtained within the range of 0.5 µM to 5 mM. The LOD of 0.5 µM was reached at a signal-to-noise ratio of three [59].
3.4. Target-induced structure switching
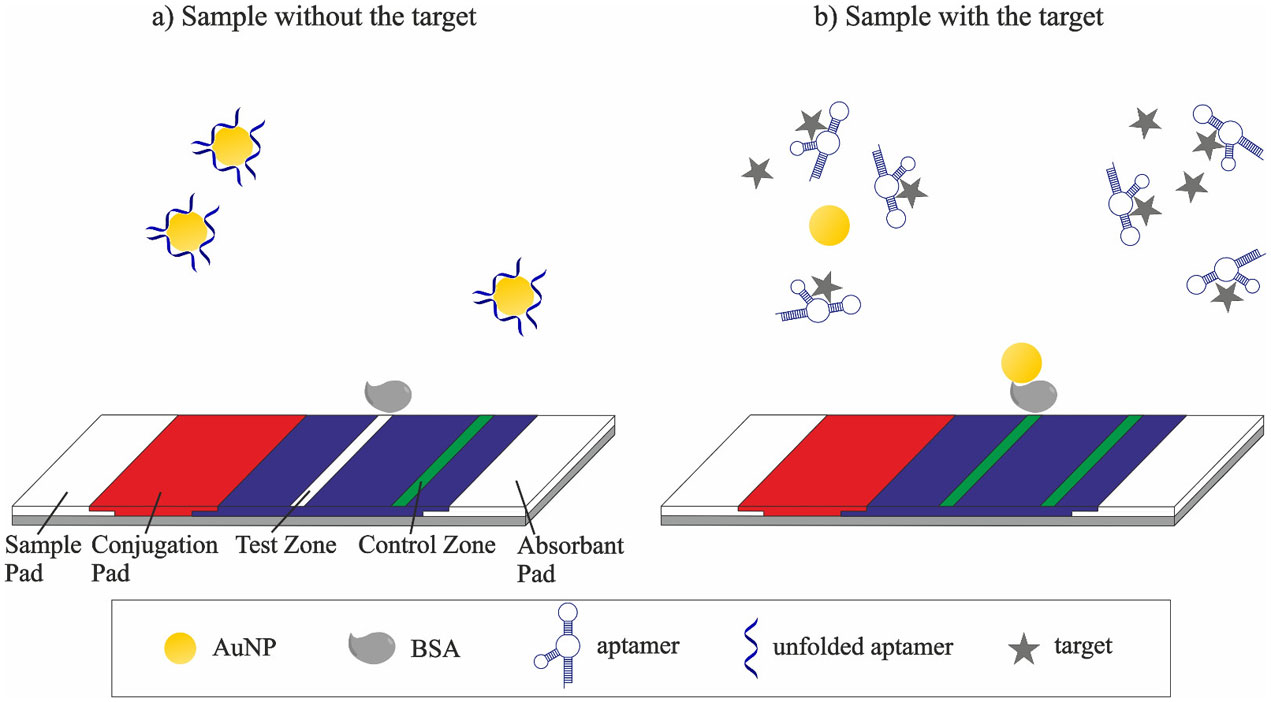
It is well known that aptamers can undergo large conformational changes upon binding to their target, a phenomenon called target-induced structure switching (TISS) [60]. Binding of target molecules subsequently leads to detectable changes in the tertiary structure of the aptamer from a random flexible state to rigid specific patterns, such as G-quadruplexes [40]. The TISS-mode is quite common for electrochemical sensors, where e.g. the switching of the aptamers' structure upon target binding results in changes in the distance between the electrode surface and the aptamer [61,62]. For aptamer-based LFAs, up to now, only one example utilizes the TISS-mode for the detection of small molecules (Table 2), which relies on unmodified aptamers, adsorbed to the surface of AuNPs [63].
Alsager et al. [64] constructed a LFA for the detection of 17β-estradiol that responded to the target with a LOD of 50 nM in a dynamic range from 50-1000 nM and excellent selectivity against potential interfering molecules (Figure 4). The LFA design avoids the need to engineer and label aptamer sequences (Table 1) by relying on the adsorption of free aptamers onto AuNPs and the desorption of the aptamers in the presence of the target.
The detection label consisted of aptamers that were physically adsorbed to the surface of AuNPs, through interaction between the bases of the aptamer and nanoparticles, resulting in a negative charged surface coating. Pre-incubation of aptamer-coated AuNPs with the target was necessary to ensure efficient target binding and subsequently the desorption of aptamers from the surface of AuNPs. Upon target binding, the aptamers' structure switched from a flexible state into a more rigid, ordered, tertiary structure, leading to a reduced number of bases involved in binding to AuNPs. Therefore, desorption of aptamers from the particles' surface occurred. After applying the pre-incubated sample onto the LFA, the solution migrated towards the test line composed of negatively charged bovine serum albumin (BSA) that displayed a strong affinity to AuNPs. In the absence of target, the negatively charged, aptamer-coated AuNPs prevented the particles from being captured on the test line. A solution containing the analyte of interest produced a red test line because the bare AuNPs were captured and immobilized by the BSA. The positively charged protein lysozyme, deposited on the control line interacted with all AuNPs whether or not they are still coated with aptamers.
Table 1. Aptamer sequences and KD-values of the examples for the detection of small molecules by aptamer-based LFAs.
| Target |
Aptamer Sequence (5′-3′) |
KD-value [nM] |
| Hg (II) ion |
A10-TTC TTT CTT CCC CTT GTT TGT T |
- |
| ATP |
aptamer 1: A6-ACC TGG GGG AGT AT |
6000 [65] |
| aptamer 2: A6-TGC GGA GGA AGG T |
| 17β-estradiol |
AAG GGA TGC CGT TTG GGC CCA AGT TCG GCA TAG TG |
11 [66] |
Table 2. Published aptamer-based LFAs for the detection of small molecules. The LFAs are listed after their design strategy as well as their target. The table contains additional information about the reported LOD, dynamic range and sample matrix.
| Design strategy |
Target |
LOD |
Dynamic range |
Sample |
Comments |
Ref. |
| TIR |
ATP |
0.5 µM |
0.5-5 µM |
Urine |
High specificity |
[59] |
| TIR |
ATP |
10 µM |
- |
Buffer |
Strip logic gate |
[67] |
| TID |
ATP |
20 µM |
- |
Buffer |
- |
[68] |
| TID |
ATP |
69 µM |
100 µM-2 mM |
Serum |
Gated nanopores |
[69] |
| TID |
OTA |
1.9 ng/ml |
0-10 ng/ml |
Buffer |
- |
[70] |
| TID |
OTA |
1 ng/ml |
- |
Buffer |
- |
[5] |
| TID |
OTA |
0.18 ng/ml |
0-0.25 ng/ml |
Buffer |
Also in red wine |
[71] |
| TID |
OTA |
0.4ng/ml |
1-1000 ng/ml |
Buffer |
Also in corn sample |
[72] |
| TID |
Cocaine |
10 µM |
- |
Buffer |
- |
[68] |
| TID |
Cocaine |
7.7 µM |
0-300 µM |
Buffer |
Personal glucose meter |
[73] |
| TID |
Hg (II) ion |
0.13 ng/ml |
0.13-4 ng/ml |
River water |
- |
[50] |
| TID |
Aflatoxin B1 |
0.1 ng/ml |
- |
Buffer |
- |
[74] |
| TID |
Aflatoxin B1 |
0.1 ng/ml |
0.1-1000 ng/ml |
Buffer |
Dual competitive LFA |
[75] |
| TID |
P-aminohippuric acid |
200 ppm |
- |
Urine |
- |
[49] |
| TID |
Kanamycin |
0.0778nM |
1-30 nM |
Buffer |
Signal amplification |
[76] |
| TID |
Zearalenone |
20ng/ml |
5-200 ng/ml |
Buffer |
Also in corn sample |
[77] |
| TISS |
17β-estradiol |
50 nM |
50-1000 nM |
River water |
- |
[64] |
| Competitive |
Ampicillin |
10.6 nmole |
- |
Buffer |
Cross-recognition |
[78] |
4. Detection of proteins with lateral flow assays
4.1. Introduction to the detection of proteins
The success of LFAs began with the development of the pregnancy immunoassay in the 1960s, which is still one of the major LFAs on the market [79]. In this assay, the protein human chorionic gonadotropin (hCG) is trapped on the test line between one antibody immobilized on the membrane and one antibody coupled to the reporter molecule [80].
Since then, antibodies represent the gold standard for recognition elements in LFAs for the detection of proteins. Some well-established antibody-based LFAs were adopted for the use of aptamers to compare the two different ligands [47]. As an example, the LFAs for thrombin detection show a comparable performance of antibodies and aptamers and the decision for the preferred ligand must be made individually for each LFA [81].
Often rather small target concentrations and a vast amount of other proteins present in the sample solution contribute to the analysis complexity rendering sensitivity as a key feature for the detection of proteins with LFAs. Amplification strategies enhance the signal intensity resulting in higher sensitivity and lower LODs. The possible amplification strategies for aptamer-based sensors can be divided into two broad categories, the assays using nucleic acid amplification strategies and the assays using signal amplification strategies [82]. Most of the following examples for the detection of proteins, whole cells, bacteria and viruses make use of one of these amplification strategies.
4.2. Sandwich format
As mentioned above, the first commercially successful LFA is based on the sandwich-mode as the sensing strategy. Sandwich assays offer several advantages like high sensitivity and simple readout mechanisms for the untrained user [83,84]. Moreover, due to the utilization of two recognition elements binding to different sites of the target protein, sandwich assays offer higher specificity in comparison to simple binding assays relying on only one recognition element. In addition, the platform allows probe modifications for a specific signal development and amplification. Hence, the sandwich assay is preferred if two aptamers for the desired target are available, which can bind to different aptatopes simultaneously [9]. In general, the sandwich assay utilizes one aptamer, conjugated to a reporter molecule, as the signal generator and a second aptamer for target fixation in the test zone. The target proteins in the sample bind sequentially to the two aptamers, resulting in the analyte being sandwiched between the reporter molecule-linked aptamer and the second aptamer deposited on the test line [85]. In the control zone, immobilized complementary oligonucleotides interact with the labeled aptamers at a rate directly proportional to the signaling intensity. In this way, Raston et al. [9] developed a LFA for the detection of vaspin, based on a sandwich approach with a LOD of 0.137 nM in buffer and 0.105 nM in spiked serum samples, respectively (Table 4).
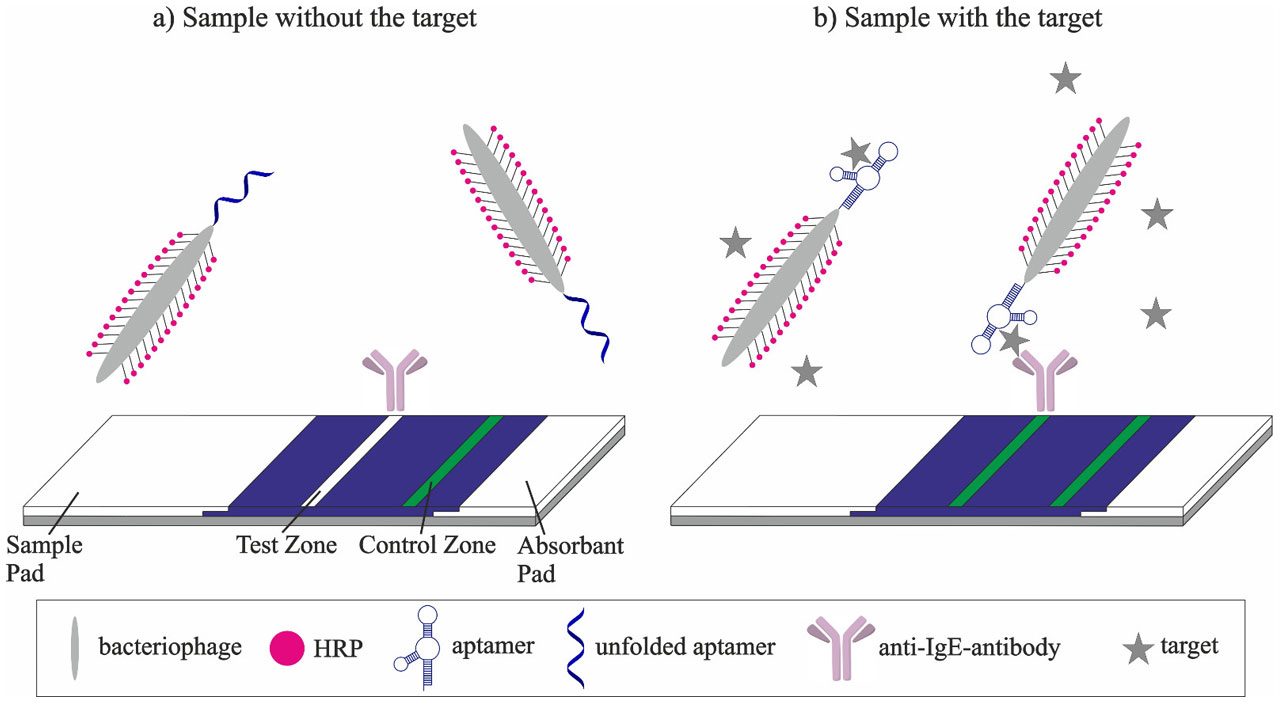
As a signal amplification strategy, enzymes can be used to create LFAs with impressive sensitivities due to the conversion of multiple substrate molecules by one enzyme, generating highly enhanced signals. Adhikari et al. [86] fabricated a sandwich-like LFA for the detection of IgE antibodies, but substituted AuNPs with engineered bacteriophages as reporters (Figure 5). M13 phage particles functionalized with both, target-specific aptamers (Table 3) and enzymes were integrated into the LFA. The enzyme horseradish peroxidase (HRP), which was coupled to copies of the M13 coat protein, generated an enhanced signal per individual aptamer. Each aptamer that was conjugated to a bacteriophage is responsible for fixation of several HRP enzymes on the test line and each enzyme can convert several substrates, leading to a dual amplification mechanism.
A phage-displayed “AviTag” peptide, which could be biotinylated in vivo or in vitro by biotin ligase, displayed an intelligent coupling method that allowed the convenient modification of phage reporter particles with any biotinylated molecular recognition element, including antibodies and aptamers [86].
Adding the bacteriophage particles after the target solution onto the sample pad, rendered the conjugation pad unnecessarily. The IgE in the sample solution bound to immobilized anti-IgE antibodies on the test line and subsequently, aptamer-modified bacteriophages were added, which accumulated in the test zone upon binding to the target-antibody complex. A clear signal at the anti-M13 antibody control line for all samples confirmed that the phage reporters successfully moved through the membrane. This sandwich assay for the detection of IgE antibodies displayed a LOD of 0.13 ng/ml IgE [86].
4.3. Competitive replacement
To obtain a perfect matching pair of recognition elements during selection renders the development for a sandwich LFA rather difficult and in conclusion, some aptamer-based LFAs use a competitive design for the detection of proteins (Table 4). In the competitive replacement assay, the target originating from the sample competes with other target molecules, integrated in the LFA, for the binding sites of aptamers; hence immobilization of the analyte is required.
In this context, Jauset-Rubio et al. [87] developed a competitive replacement LFA for the detection of β-conglutin with an impressive LOD of 55 pM, without using any amplification strategy (Figure 6). Immobilized β-conglutin on the test line and β-conglutin from the test sample competed for binding to AuNP-labeled aptamers. With increasing concentrations of target in solution, less aptamer was free to bind to the immobilized β-conglutin on the membrane and thus, the intensity of the test line decreased. With this LFA, Jauset-Rubio et al. managed to detect concentrations up to 10 µM. A smartphone camera represented the readout device, followed by analysis with ImageJ software to calculate the intensity of the test- and control zone. The control zone contained oligonucleotides, complementary to the full length of the AuNP-labeled aptamer, which led to the displacement of β-conglutin from the aptamer, demonstrating a general method for creating the control line [87]. This direct competition on the LFA strip facilitated an extremely rapid test, which took less than 5 min for completion.
Table 3. Aptamer sequences without modifications and respective KD values of the presented examples for the detection of proteins by aptamer-based LFAs.
| Target |
Aptamer Sequence (5′-3′) |
KD-value [nM] |
| IgE |
GGG GCA CGT TTA TCC GTC CCT CCT AGT GGC GTG CCC C |
10 [88] |
| β-Conglutin |
AGC TCC AGA AGA TAA ATT ACA GGG GCC GGG GTG GCT CAG GCA AGG GGT TGA CCT GTC GTA GGG ATT GTT TTA ACA ACT AGG ATA CTA TGA CCC C |
24 [89] |
Table 4. Published aptamer-based LFAs for the detection of proteins. The LFAs are listed after their design strategy as well as their target. The table contains additional information about the reported LOD, dynamic range and sample matrix.
| Design strategy |
Target |
LOD |
Dynamic range |
Sample |
Comments |
Ref. |
| Sandwich |
Vaspin |
0.137 nM |
0.137-25 nM |
Buffer |
- |
[9] |
| Sandwich |
IgE |
0.13 ng/ml |
- |
Buffer |
- |
[86] |
| Sandwich |
Salivary α-amylase |
0.5 nM |
0.5-20 nM |
Buffer |
- |
[90] |
| Sandwich |
Lysozyme |
20 ppm |
- |
Wine |
- |
[49] |
| Sandwich |
Thrombin |
2.5 nM |
5-100 nM |
Human Plasma |
- |
[81] |
| Sandwich |
Thrombin |
0.25 nM |
0.5-120 nM |
Buffer |
- |
[91] |
| Sandwich |
Carcinoembryonic antigen |
0.7 nM |
0.8-300 nM |
Buffer |
Strip logic gate |
[92] |
| Sandwich |
Mucin 1 |
1.13 nM |
1.6-400 nM |
Buffer |
Strip logic gate |
[92] |
| TISS |
Thrombin |
1.61 nM |
3.2-250 nM |
Buffer |
Strip logic gate |
[92] |
| TID |
Thrombin |
4.9 pM |
0.0064-500 nM |
Buffer |
- |
[93] |
| TIR |
Thrombin |
2 nM |
- |
Buffer |
Strip logic gate |
[67] |
| Competitive |
Renin |
380 ng/ml |
0.38-280 µg/ml |
Buffer |
Peptide aptamer |
[94] |
| Competitive |
β-Conglutin |
55 pM |
- |
Buffer |
- |
[87] |
| Enzymatic |
pfLDH |
5 ng/ml |
5-1000 ng/ml |
Serum |
- |
[95] |
5. Detection of cells or viruses with lateral flow assays
5.1. Introduction to the detection of cells or viruses
Binding of aptamers to cells most commonly occurs via binding to surface proteins, lipids etc.; the diverse types of molecules expressed on the cellular membrane provide various binding sites for the aptamers. Modification of the SELEX process enables the selection of aptamers using whole cells offering multiple advantages like selection of aptamers, even without prior knowledge of cell surface targets [96] or the identification of new cell surface marker, which is of utmost importance in cancer research [97]. Unlike other methods, cell-SELEX carried out under physiologic conditions allows the selection against molecular targets in their natural folding and native state [98]. Introduction of counter-selection steps generates aptamers that differentiate between the target cells and e.g. other cell subtypes or strains [99]. A major concern for developing aptamer-based LFAs for the detection of cells, represents the low sample volume conventionally applied to LFAs. This small volume in combination with typically low concentrations of target cells in the sample, drastically decreases the chance to detect any cells without pre-concentration steps.
5.2. Sandwich format
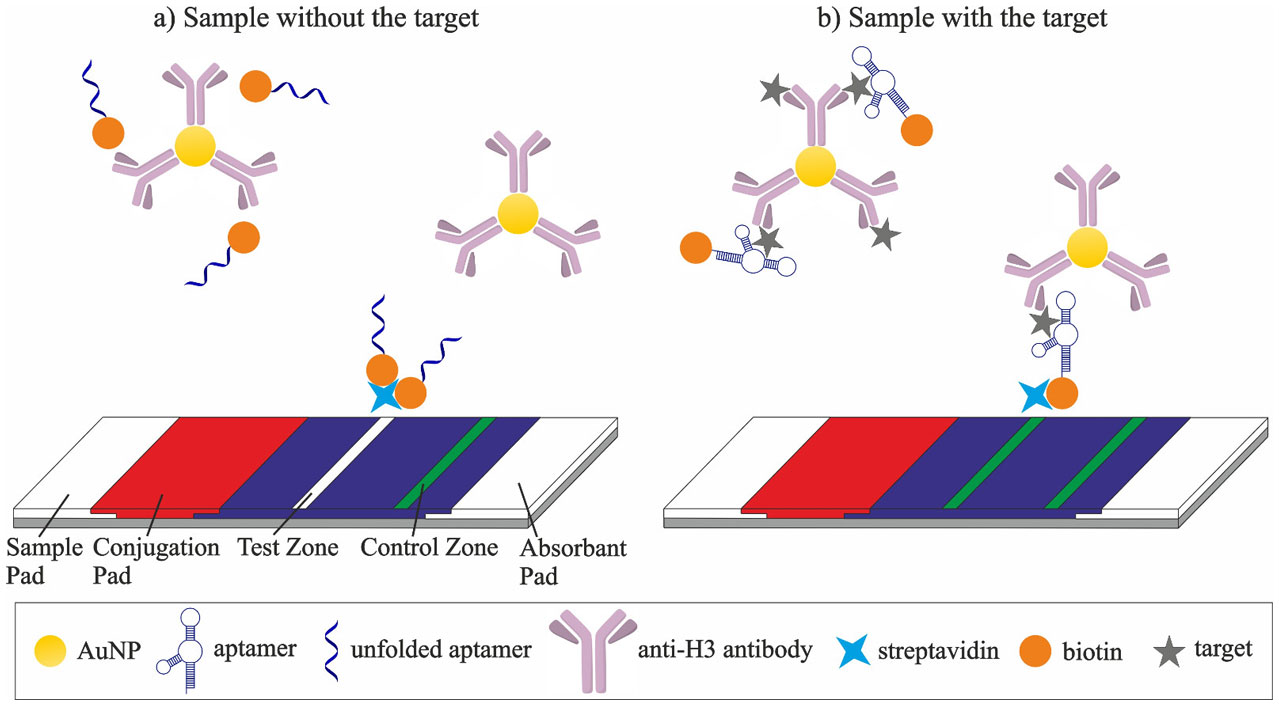
The huge amount of different aptatopes on the surface of cells simplifies the selection of cognate aptamer pairs. Therefore, the format of choice for the detection of cells is the sandwich assay (Table 4). Le et al. [24] recently built a sandwich-like LFA for the detection of the influenza strain A/Panama/2007/1999 of H3N2 virus by pairing a highly strain-specific, biotin-modified aptamer (Table 5) with a less specific antibody conjugated to AuNPs (Figure 7).
As a result, the LFA displayed a high selectivity by discriminating a particular virus strain against others of the same subtype, and a good sensitivity as indicated by the LOD of 2 × 106 virus particles. For the LFA, the biotinylated aptamer and the antibody-conjugated AuNPs were dried on the conjugation pad of the LFA while streptavidin was immobilized onto the test line. In the presence of the target, the virus formed a sandwich complex with both, the biotin-modified aptamer and the monoclonal antibody, which was then captured at the test line via streptavidin-biotin interaction. In the absence of the target, the complex did not form, corresponding to no visible signal of the test line. A second antibody on the control line captured the excess of AuNP-labeled monoclonal antibodies [24].
5.3. Other formats
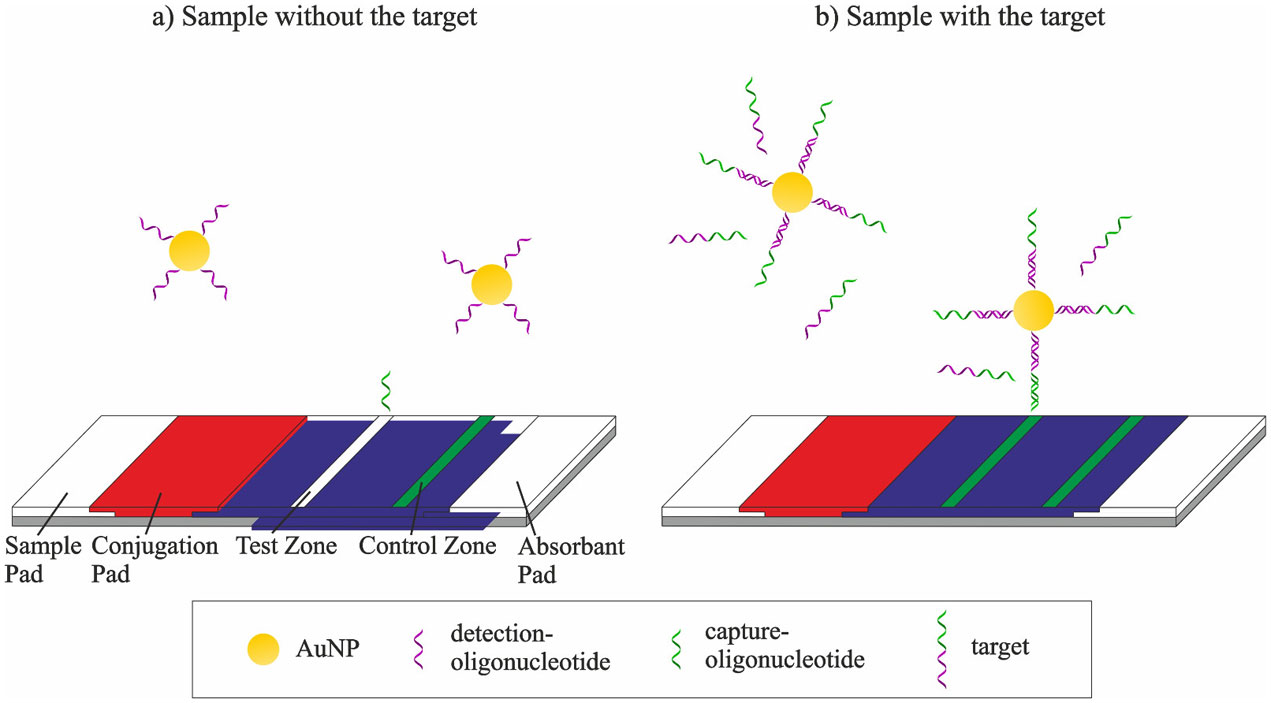
To overcome the concerns of low sensitivity resulting from small sample volumes and low concentrations of target cells elaborated above, other LFA formats which benefit from amplification technologies have been developed. Cells or viruses contain DNA that can be detected on nucleic acid-based lateral flow assays (NALFA) [100]. These assays detect target nucleic acids via hybridization to complementary sequences, serving as detecting and capturing ligands. In general, a immobilized DNA-probe and another DNA probe, coupled to a reporter molecule, build a sandwich-like complex in presence of a target DNA sample [101]. In contrast to aptamer-based sensors, NALFAs use nucleic acid sequences as recognition elements instead of aptamers. However, aptamers are single-stranded DNA molecules and can be detected by NALFAs displaying the target DNA sample (Figure 8).
Fang et al. [102] presented an extraction-free aptamer-based biosensor for rapid detection of Salmonella enteritidis (S. enteritidis), utilizing an aptamer sequence (Table 5) as target DNA in a NALFA. To obtain the target DNA for analysis, tedious cell lysis and DNA extraction steps are usually necessary. Instead of DNA-extraction, the concentration of bacteria in the sample solution was increased by magnetic bead enrichment. After that, an aptamer binding to the outer membrane of S. enteritidis served as a template for nucleic acid amplification and was subsequently detected as the target in a NALFA. Higher numbers of bacteria in solution yielded a higher amount of amplified and detected aptamer. The assay consisted of three separate steps overall.
The first step included incubation of the bacteria sample with two different aptamers. A biotin-modified capture aptamer, specific for the outer membrane of S. enteritidis, was used for enrichment with streptavidin-coated magnetic beads and an aptamer, modified with a primer sequence, displayed a template for nucleic acid amplification. After the separation of bacteria with magnetic beads, the sequence of the aptamer was multiplied by directly adding the components for the amplification reaction to the test tube. In the last step, a sandwich-type LFA, using nucleic acid probes as recognition elements, detected the amplification aptamer as the target (Figure 8). Nucleic acid labeled gold particles captured the amplified aptamer sequences via hybridization and the complex migrated to the test zone of the LFA, where an immobilized DNA probe hybridized with another part of the aptamer sequence. As low as 10 colony forming units (CFUs) of S. enteritidis were detected in this study [102].
Table 5. Aptamer sequences without modifications and respective KD-values of the presented examples for the detection of whole cells, bacteria and viruses by aptamer-based LFAs.
| Target |
Aptamer Sequence (5′-3′) |
KD-value [nM] |
| Influenza viruses |
H3-P07: GGG AGA AUU CCG ACC AGA AGG GUU AGC AGU CGG CAU GCG GUA CAG ACA GAC CUU UCC UCU CUC CUU CCU CUU CU |
12 [24] |
| Salmonella enteritidis |
SE-3: TCG GCA ACA AGG TCA CCC GGA GAA GAT CGG TGG TCA AAC TGC ATA GGT AGT CCA GAA GCC |
7.8 [103] |
Table 6. Published LFAs for the detection of whole cells, bacteria and viruses. The LFAs are listed after their design strategy as well as their target. The table contains additional information about the reported LOD, dynamic range and sample matrix.
| Design strategy |
Target |
LOD |
Dynamic range |
Sample |
Comments |
Ref. |
| Sandwich |
Arboviruses |
- |
- |
Buffer |
- |
[26] |
| Sandwich |
E.Coli |
10 CFU/ml |
10-106 CFU/ml |
Buffer |
- |
[104] |
| Sandwich |
E.Coli |
300 cells |
- |
Buffer |
- |
[8] |
| Sandwich |
Ramos cells |
800 cells |
800-40000 |
Human blood |
- |
[105] |
| Sandwich |
Alicyclobacillus spores |
9 CFU/ml |
- |
Buffered orange juice |
- |
[49] |
| Sandwich |
Influenza viruses |
2 × 106 viruses |
- |
Buffer |
- |
[24] |
| Sandwich |
Salmonella enteritidis |
10 CFU |
- |
Buffer |
NALF |
[102] |
6. Summary and prospects
The examples given in this article demonstrate that different design strategies render aptamer-based LFAs to powerful tools for POC diagnostics and environmental monitoring. Many different formats with varying read-out techniques have already been applied successfully. Aptamers seem to be ideal biological recognition elements for the design of intelligent sensors based on their specific properties. The wide variety of targets and the possibility to obtain results within 10 min have drawn the attention towards aptamer-based LFAs. In addition, due to their oligonucleotide nature, it is possible to rationally design novel sensing strategies including nucleic acid amplification or target-induced dissociation.
Aptamers represent a suitable alternative to antibodies with advantages in the field of shelf life, costs and specificity. Especially for the detection of small molecules and whole cells, bacteria or viruses where specificity is a key property to distinguish between derivatives of small molecules and closely related cell lines respectively, aptamers are superior to antibodies. In the field of protein detection, aptamers show comparable affinities to antibodies, but are not as well established in the laboratory use. Another disadvantage of aptamers should also be mentioned: The selection of high affinity aptamers might be limited for targets exhibiting a negative charge, as indicated by a low isoelectric point (PI) in case of protein targets. In this context, Ahmad et al. [106] compared 75 dissociation constants (KD) of published aptamers against different proteins to their PI. They reported an inverse relationship between the protein PI and the aptamer affinity. Although this might restrict the accessibility of some targets, aptamers against a great number of proteins have already been selected and some of them have already been successfully applied to LFAs (Table 4).
The biggest impact of aptamers can be attributed to the detection of small molecules, seen by the high number of publications concerning analytes like toxins and antibiotics (Table 2). Most of these publications successfully incorporated the TID-mode in LFAs with some impressive LODs. In contrast, other aptamer-based detection modes are less often used in LFAs. Although the TISS-mode is implemented in many electrochemical biosensors, the use in LFAs is more problematic since it is not easy to translate the differences in aptamer structure into optical signals. The TIR-mode suffers from the necessity to identify suitable aptamer fragments. To bind efficiently and avoid a loss of sensitivity, potential splitting sites need to be determined by structural analysis of the aptamer.
Table 7. Advantages and disadvantages of aptamers and antibodies in LFAs regarding their development, production, implementation, stability and the possibility to analyze real samples.
| Characteristics |
Antibodies |
Aptamers |
| Development |
Antibodies against small, toxic and non-immunogenic molecules might be difficult to obtain [107] |
The in vitro SELEX process can generate aptamers against almost every target |
| Production |
Viral or bacterial contaminations possible
Normally produced in vivo, batch-to-batch variations may occur |
Viral and bacterial contamination not problematic
Chemical synthesis is easy, fast and reliable |
| Application |
Limited close to physiologic conditions |
In vitro SELEX-process allows selection for various conditions without limitations to physiologic conditions [22,107] |
| Stability/Storage |
Sensitive to pH and temperature changes
More likely to aggregate
No nuclease degradation |
Tolerant to pH and temperature changes
Little or no aggregation [10]
Degradation by nucleases can occur [108] |
| Immobilization |
Easy, through adsorption |
More complicated, immobilization by biotin/streptavidin or chemical coupling (e.g. EDC/NHS) required [45] |
| Costs |
Expensive, e.g. 100 µg antibody directed against VEGF costs approx. 300 €1 |
Less expensive, e.g. 1 mg of anti-VEGF aptamer cost approx. 80€1 |
|
| 1 Prices are based on the authors' experiences. Please note that for antibodies prices might vary significantly for different targets. In contrast for aptamers the prices mainly depend on their length. |
Although the number of developed aptamer-based LFAs has increased significantly in the past decade, until today, not even one is commercially available. In contrast to aptamers, antibodies are well-established recognition elements in the industry and the integration of new technologies is associated with costly and time-consuming approval processes. This is one reason, why aptamers have not competed out antibodies in LFAs yet. In addition, the patents on the SELEX process, which restricted the implementation of aptamers to new technologies, ran out as recently as in 2010. Until then, the selection of aptamers was quite complicated. Therefore, it can be expected, that aptamers acceptance and use in LFAs will further increase in the near future based on their advantages over antibodies (Table 7).
Through modifications of the SELEX process, it is possible to select aptamers under intended assay conditions while the usage of antibodies is limited to close to physiological conditions. In principle, this advantage of aptamers enables the analysis of samples in complex matrices. However, it should be noted, that changes of parameters like the buffer composition, the pH or even the temperature can have a significant impact on the aptamers' affinity as indicated by Schax et al. [109]. The affinity of an ochratoxin A aptamer in different concentrations of beer as the complex matrix was tested, and an increase of the dissociation constant from 32.49 nM in binding buffer to 1964.4 nM in 50% binding buffer and 50% beer was observed. In conclusion, aptamers offer a wider application range than antibodies, but the transfer to matrices, which differs from selection conditions, can result in a loss of aptamer affinity.
For a long shelf-life of the LFAs, especially advantageous in limited resource settings such as developing countries, the stability of recognition elements is an important issue. Aptamers are tolerant to pH and temperature changes, while antibodies denature at a low pH or at high temperatures (Table 7). Therefore, the shelf-life of LFAs benefits from utilizing aptamers. In general, DNA-aptamers are preferred over RNA-aptamers due to their higher stability and lower costs. One main challenge, that need to be addressed, is the immobilization of aptamers onto gold nanoparticles or the LFA membrane, where an oriented conjugation is necessary to ensure high aptamer activities. The immobilization onto the nitrocellulose membrane poses a problem, because most developed LFAs utilize the biotin/streptavidin interaction, thereby diminishing the stability advantage of aptamers.
The same problem is valid for the sensitive detection of low concentrated analytes, where amplification strategies are crucial, but many published methods are either not suited for incorporation into LFAs or need extra biological compounds like enzymes. As antibodies, enzymes are prone to irreversible temperature-induced denaturation reducing the shelf-life of aptamer-based LFAs [100]. Moreover, extra components always add more complexity and extra steps making the application of LFAs more difficult to the end-user.
The main differences in costs of aptamers and antibodies are envisioned to take place in the production process. The costs for antibodies are quite high due to a difficult production process based on cell culture techniques. Compared to aptamers, antibodies can be more than ten times as expensive (Table 7), resulting in an anticipated cost reduction, when using aptamers as recognition elements. While most of the disadvantages of aptamers today can be expected to be ruled out in the near future, through intense research, especially in the area of the SELEX process as well as immobilization and amplification techniques, many disadvantages of antibodies will remain, because their drawbacks are linked to their protein origin. Further developments in the field of aptamer-based LFAs are envisioned to move the analytical sensing from centralized laboratories to unspecialized end-user.
Acknowledgements
This work was funded by the Federal Ministry of Economic Affairs and Energy (BMWi) within the Central Innovation Program for SMEs (ZIM). The publication of this article was funded by the Open Access fund of Leibniz Universität Hannover.
Conflict of interest
All authors declare no conflicts of interest.









 DownLoad:
DownLoad: