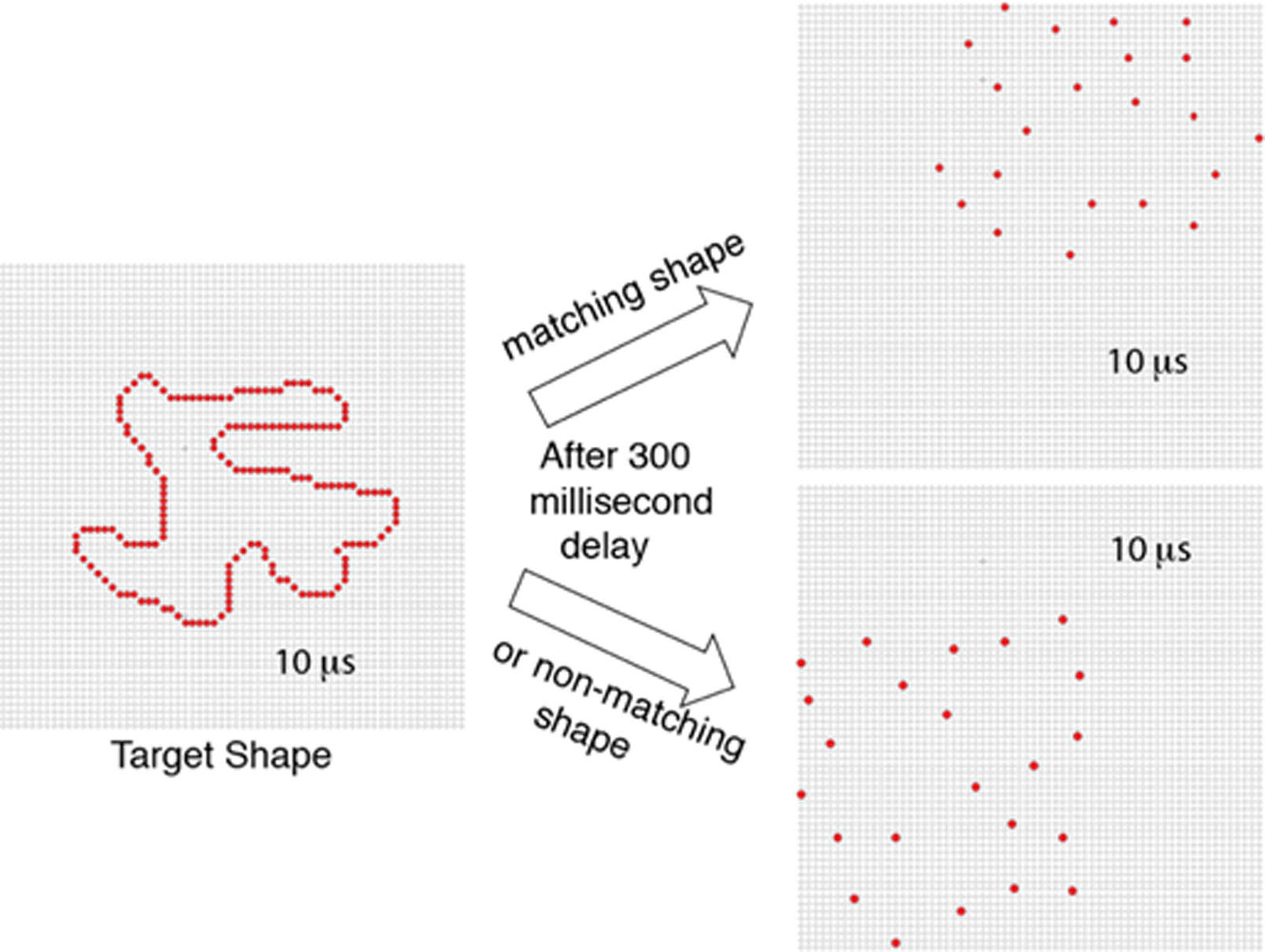
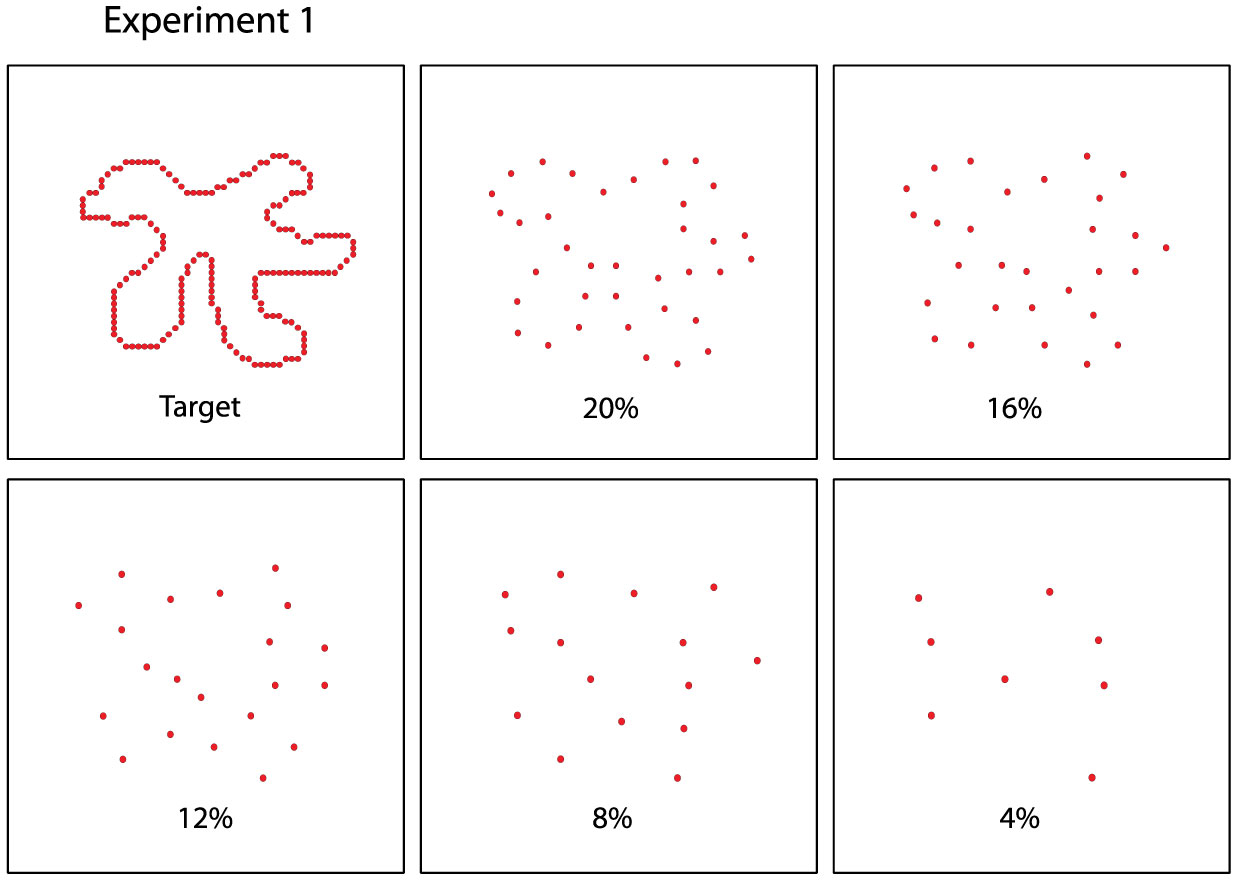
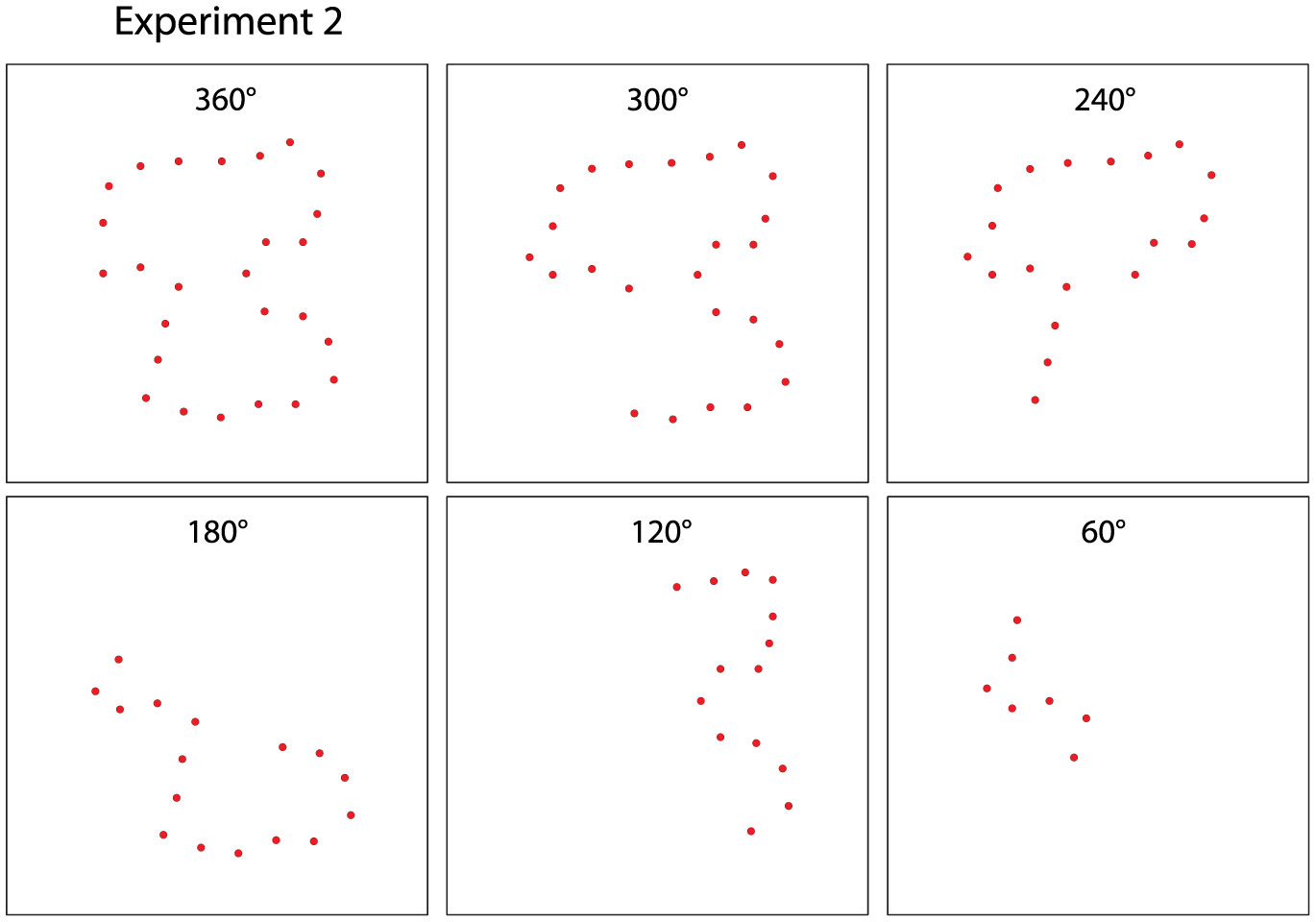
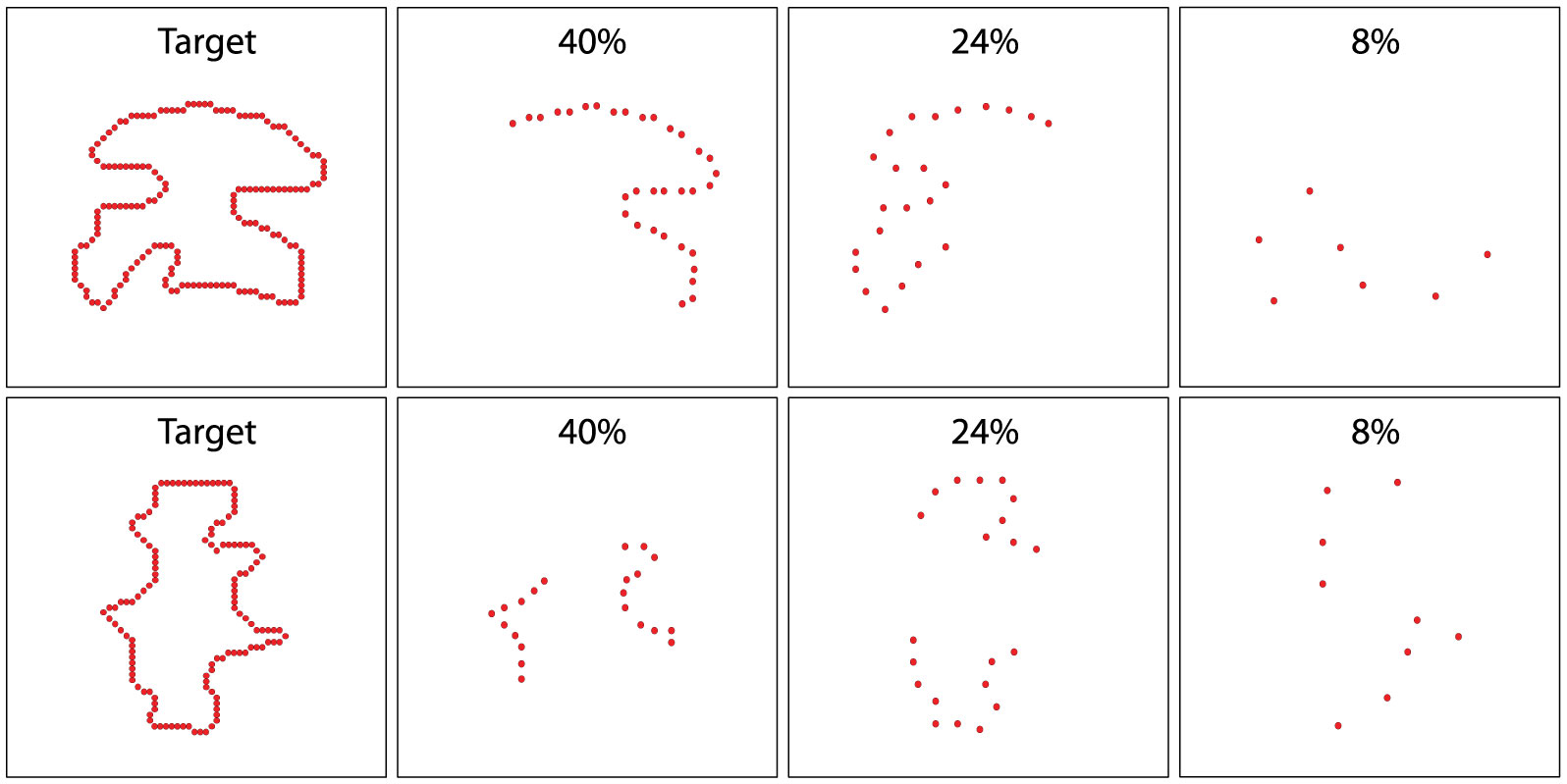
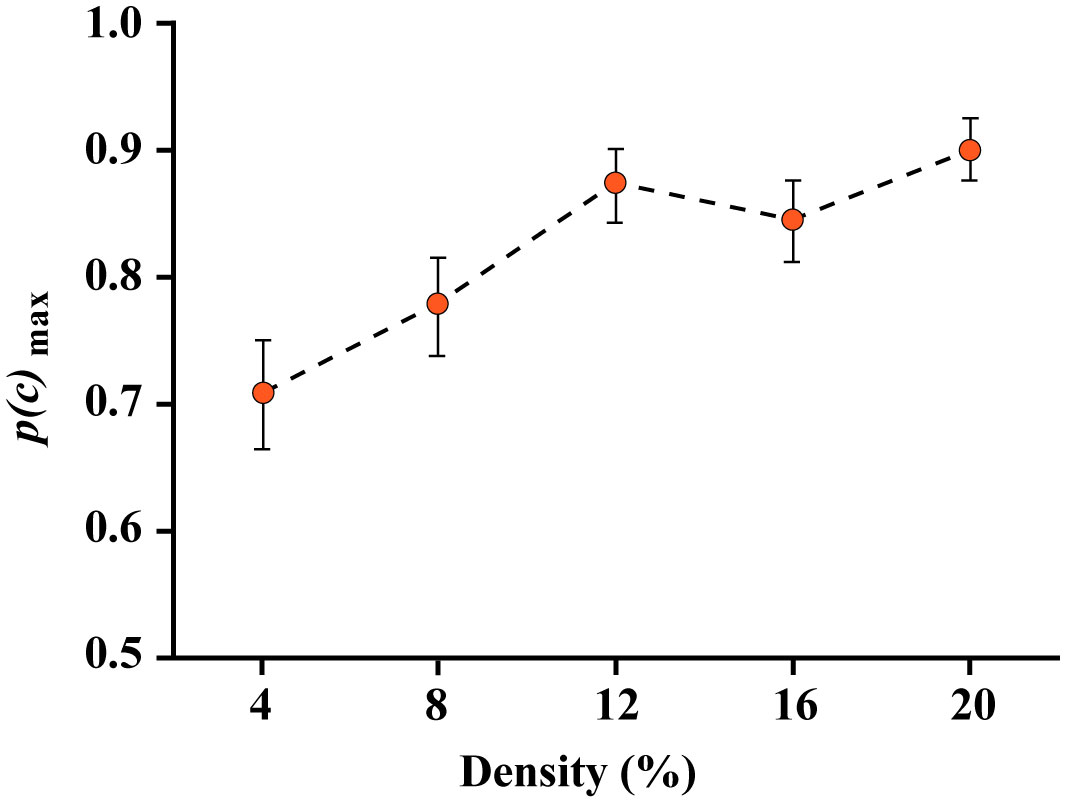
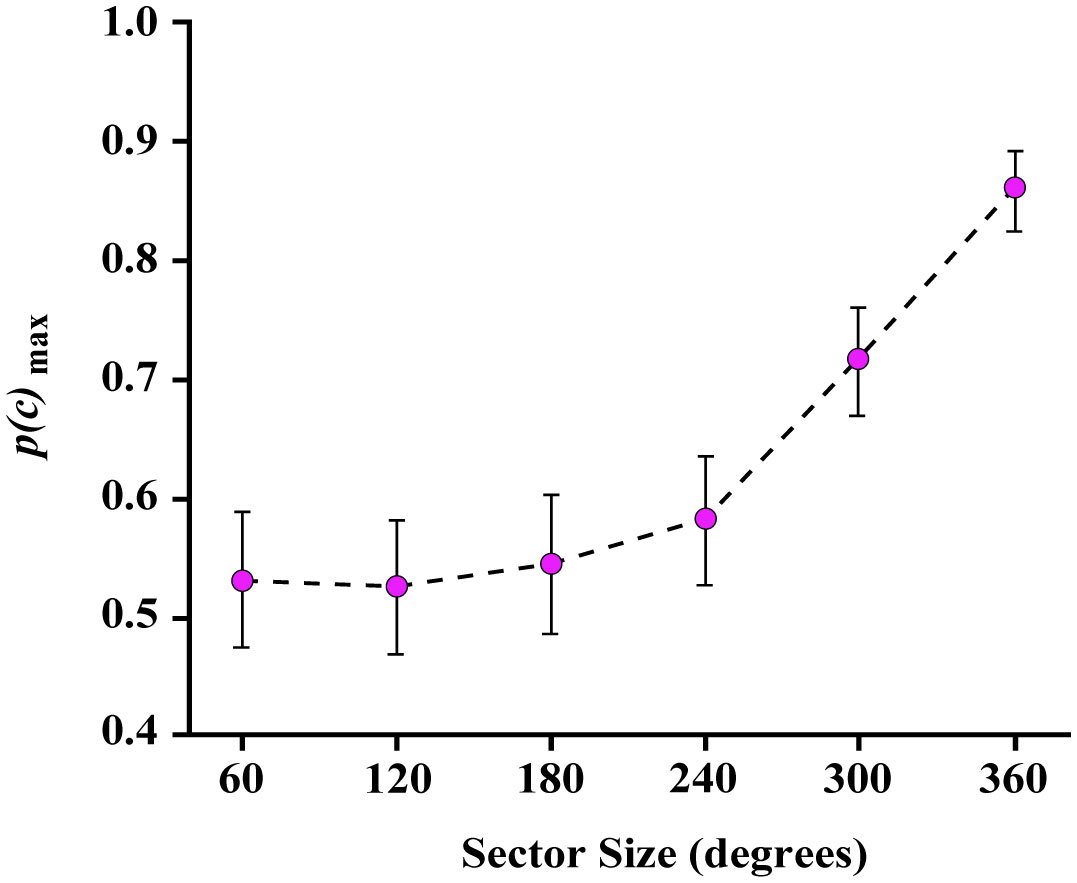
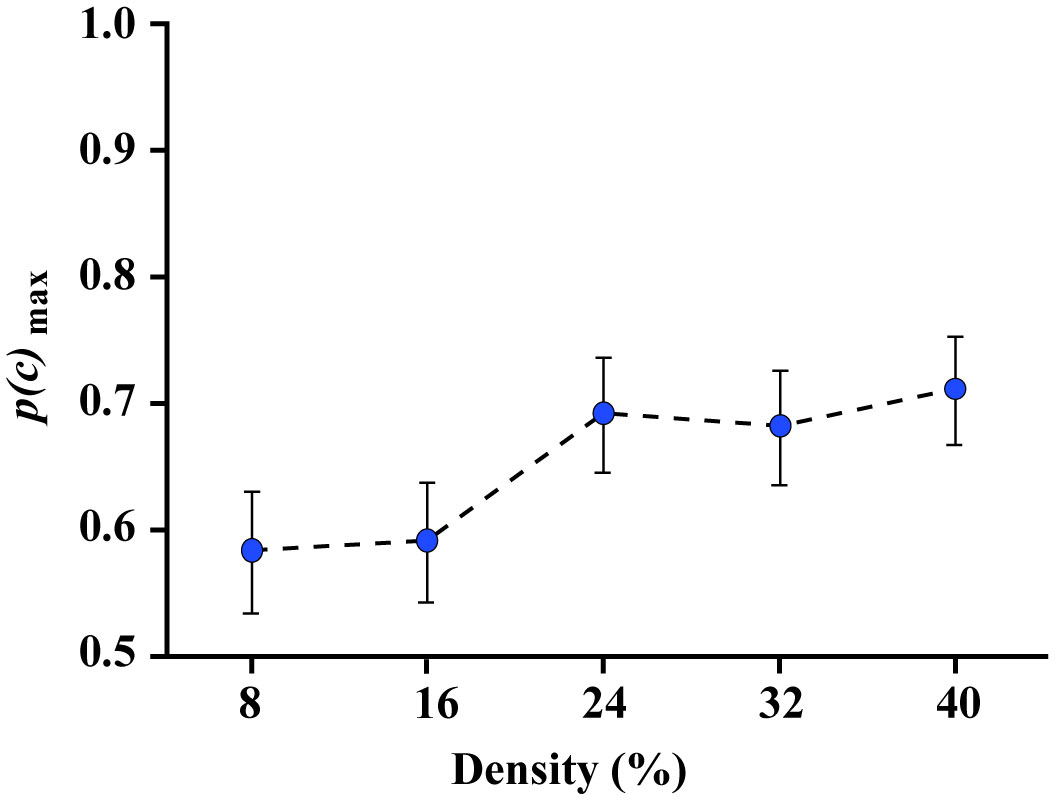
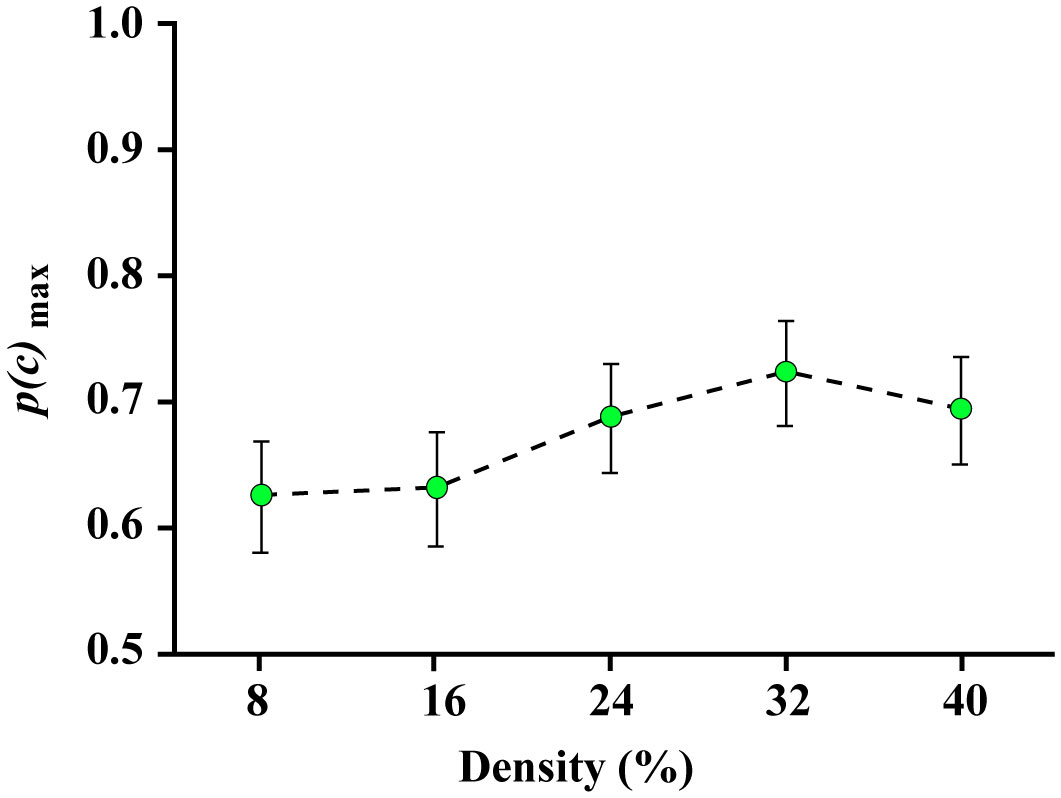
Prior research has found that known shapes and letters can be recognized from a sparse sampling of dots that mark locations on their boundaries. Further, unknown shapes that are displayed only once can be identified by a matching protocol, and here also, above-chance performance requires very few boundary markers. The present work examines whether partial boundaries can be identified under similar low-information conditions. Several experiments were conducted that used a match-recognition task, with initial display of a target shape followed quickly by a comparison shape. The comparison shape was either derived from the target shape or was based on a different shape, and the respondent was asked for a matching judgment, i.e., did it “match” the target shape. Stimulus treatments included establishing how density affected the probability of a correct decision, followed by assessment of how much positioning of boundary dots affected this probability. Results indicate that correct judgments were possible when partial boundaries were displayed with a sparse sampling of dots. We argue for a process that quickly registers the locations of boundary markers and distills that information into a shape summary that can be used to identify the shape even when only a portion of the boundary is represented.
1.
Introduction
Functionally graded materials (FGMs) are a class of composite materials that have been manufactured by a unique process to achieve impossible properties with monolithic materials and perform better than traditional composites [1]. In general, two types of property gradients result from the manufacturing process: stepwise and continuous [2]. FGM concepts are gaining importance in several fields of material science, and the pressing necessity of practical application of materials has generated additional requirements. FGMs can address and resolve issues that result from the development and application of advanced composite materials [3].
In the field of advanced engineered materials, polymer matrix composites are utilized in various industrial applications due to their unique benefits, which include simplicity of manufacturing, light weight, ductility, and relatively low cost [4]. The matrix consists of thermoplastic polymers and thermosetting resins [5]. Polymer composites have been intensively studied for a long time; inorganic fillers predominantly fill these organic polymer composites, and their characteristics include those of the inorganic filler material (toughness and thermal stability) and organic polymer (ductility, flexibility, and processability) [6,7,8]. Shen and Bever studied polymer composite gradients [9]. They began their research on the structures and properties of polymer materials with spatial gradients and expressed interest in potential applications of these materials. Mulugeta et al. [10] mentioned that fillers such as clay, silica, glass, or carbon fiber could improve the toughness and often perform in synergy with elastomeric toughness.
In various studies, silica fillers enhanced the mechanical properties, including the modulus, strength, and stiffness. However, the characteristics of the composites were uniformly distributed throughout the materials and produced homogeneous products [11]. Thus, many applications necessitate the use of FGMs, which mechanically outperform conventional composites with homogeneous compositions [12]. FGM designs focus on certain desired traits of each constituent material. For instance, silica may be utilized on the hotter side of the FGM specimen and polymer on the cooler side to benefit from the higher mechanical and heat transmission qualities of each material [13,14]. Consequently, to mitigate problems caused by an abrupt change in thermomechanical characteristics, e.g., in the case of composite materials, and to obtain the necessary qualities, FGMs are heterogeneous composites where the material properties gradually vary between two surfaces [15]. In other words, FGMs can be described as composites where the material characteristics gradually change along a certain direction as a function of the appropriate attributes [16].
FGMs with polymer and ceramic components are commonly known for improving mechanical and thermal characterization due to the seamless transition between the components' characteristics [17]. In this paper, epoxy-silica FGMs are studied, and certain distinctions between graded and composite materials are discussed. Thermal conductivity and mechanical property tests were performed on an FGM specimen and the five layers of its functional gradation. The outcomes will help readers understand that FGMs can solve practical issues that arise from the production and application of innovative types of polymer-based composites with polymer ceramic combinations to improve their properties via gradation in epoxy-silica composition. We hope that our findings will help researchers who are interested in the science and engineering of gradient materials for epoxy-silica compositions.
2.
Materials and methods
2.1. Preparation of FGM specimens
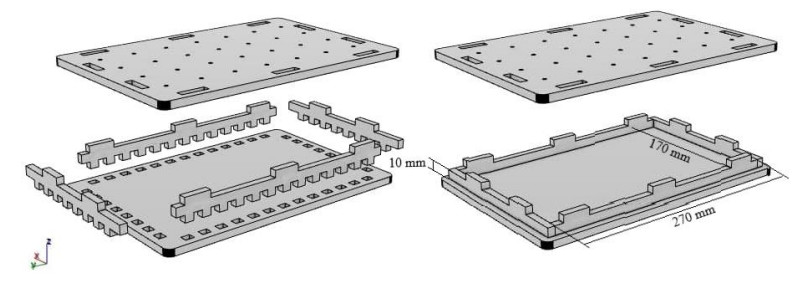
The polymer utilized was an epoxy resin with low viscosity. Silicon dioxide (SiO2) powder with a particle size of 100 μm was used as the filler material in the epoxy matrix to prepare stepwise FGMs. An FGM sample consisting of five layers of graded epoxy-silica was prepared using the hand layup technique and poured into a mold made of poly(methyl methacrylate), which is also known as acrylic, with internal dimensions of 270 mm × 170 mm × 10 mm. This process is shown in Figure 1.
The mold was created using a computer numerical control (CNC)/laser/plasma machine to cut an acrylic transparent sheet (8 mm) into six pieces according to the given dimensions. Then, the mold parts were assembled, and a gradient scale was added to the side parts of the acrylic mold every 2 mm to show the height level for each layer of stepwise FGM during the manufacturing process. A mold release agent (honey wax) was utilized to coat the mold's joints to prevent the composite from leaking out of the mold during the pouring process, avoid sticking, and facilitate the elicitation of the FGM sample [18,19,20]. As shown in Table 1, the FGM was manufactured according to a weight gradient for each layer, where the epoxy resin was mixed with varying amounts of silicon dioxide (0, 20, 40, 60, and 80 wt%). At room temperature, the material was manually mixed with a glass rod until it was homogeneous; then, it was poured into the mold in a gravity-molding process using the hand layup technique [21,22]. The FGM generated using this step-by-step casting approach was formed by pouring resin with varying filler volume contents in succession [23,24]. The mold was partially filled with the first layer of pure epoxy; then, the second layer of epoxy, which was mixed with a specific volume of silicon dioxide, was poured on top of the partially solidified first layer. The layers were arranged from 0–80 wt% silicon dioxide. When the layers were complete, the mold cover was placed on top to obtain a homogenous thickness. Figure 2 depicts a model of the stepwise FGM profile. In addition to the five-layer graduated sample, five additional samples that represented each layer of the graduated sample were prepared to examine and identify the characteristics of each layer in the graded sample.
2.2. Test specimen preparation
The final FGM sheets were extracted by pulling them from the mold. Then, the samples were cut to standard specimen dimensions with three replicates for each test according to the standard specifications in Table 2 to create the final specimen using a CNC/router machine, as depicted in Figure 3.
3.
Experiments
3.1. X-ray diffraction (XRD)
An X-ray diffraction (XRD) diffractometer equipped with Fe-K alpha radiation was used to explore the microstructure, analyze the distribution of silica particles within the epoxy matrix, and evaluate the miscibility of the silicon dioxide in epoxy resin at the fractured surfaces of the FGM specimen across a 2 range of 10–60º at a scanning rate of 2 s per step and a step size of 0.02º.
3.2. Infrared spectroscopy
Infrared spectroscopy (IR) was utilized to verify the surface morphology of the silica fillers within the polymer matrix. In this study, the typical examined spectroscopy transmission spectra of the neat epoxy surface and epoxy-silica surface were analyzed. A small portion of the FGM specimen was ground and molded into a typical pellet for FT-IR study in the transmission mode. The scan range was medium: from 4000 to 400 cm−1.
3.3. Density
The density of the composite was determined using ASTM standard D792-08 via Eq 1. All samples were weighed using an accurate electronic scale to within 0.01 g of accuracy.
where ρ is the density of the composite, kg/m3; m is the mass of the material, kg; v is the volume, m3.
3.4. Mechanical properties
The FGM specimen and layer specimen composites Ep1, Ep/S2, Ep/S3, Ep/S4, and Ep/S5 were subjected to tensile, bending, and impact testing, as explained in the following subsections.
3.4.1. Tensile test
Tensile testing of the material specimens was conducted on an industrial universal testing machine—DX-C4A-G7F Model-Instron—in accordance with the ASTM D638-02a standard. These specimens were loaded to failure at a constant rate of 5 mm/min. On the Instron's x-y recorder, a direct plot of the stress-strain curve for each specimen tested was obtained. A modulus of elasticity plot of the five gradient layers of the FGM specimen was computed using Eq 2:
where E is the modulus of elasticity in tensile, MPa; Δσ is the stress change, MPa; Δϵ is the strain change, mm/mm.
3.4.2. Flexural test
A WDW-5E electronic universal testing machine, which had a 5-kN full-scale load, was used to conduct a bending test on the material specimens. According to ASTM D790, the three-point test was used as the flexural test in this study. At a rate of 0.5 mm/min, the load was applied until a rupture occurred. The x-y recorder of the electronic universal testing machine was used to obtain a direct plot of the stress-strain curve for each tested specimen.
3.4.3. Impact test
An impact test was conducted with a Pendulum Wp 400 impact testing equipment in accordance with ASTM D4812 and ISO 180U on the unnotched beam impact resistance. For each tested specimen, impact work results were obtained; the direction of the impact striker was on the 10-mm-wide face of the test specimen. Equation 3 was used to determine the impact strength:
where Is is the impact strength, J/mm2; Iw is the impact energy, J; A is the cross-sectional area of the specimen, mm2.
3.5. Thermal properties
The measured thermal characteristics in this work were based on Lee's disk technique in accordance with ASTM C518-02. The thermal conductivity of each specimen was computed using Eq 4 [25,26]:
where K is the thermal conductivity, W/m·℃; m is the mass of the brass disk, kg; cp is the specific heat capacity, J/kg·℃; dT/dt is the rate of cooling of the brass disk at a steady-state temperature, ℃/s; d is the thickness of the specimen, mm; A is the cross-sectional area, mm2; (T2 − T1) is the temperature difference across the material's thickness, ℃.
4.
Results and discussion
4.1. Sample characterization
The XRD of the FGM sample in Figure 4 revealed silica particles in the epoxy. The SiO2 peaks appeared in the diffuse analysis as a sharp peak at 25º–30º, which was indicative of the phases of silica included in the material. However, in certain regions of the matrix, little particle clustering was detected. Compared to the standard silica test, this result clearly demonstrates that silica particles were strongly bonded to the epoxy matrix via physical bonding, and there was no chemical reaction with other components, as explained by Daramola et al. [27]. In addition, infrared spectroscopy (IR) examinations of the FGM layers indicated that the compositions of silica particles and epoxy had a strong association with their physical structures. Figure 5 depicts the FTIR spectra of epoxy resin and epoxy containing silica (SiO2). The epoxy spectrum clearly shows the presence of epoxide rings (characteristic peaks) at 862 and 914 cm−1. The peaks at 1033.49 cm−1 and 1110.99 cm−1 were due to the symmetrical aromatic C–O stretching and asymmetrical aliphatic C–O stretching, respectively. In contrast, asymmetrical aromatic C–O stretching appeared at 1242.15 cm−1. At 1296.24 cm−1, the vibration mode of the asymmetrical CH2 deformation occurred. The C-C stretching vibrations in the aromatic ring appeared at 1465.9 cm−1 to 1612.49 cm−1. The symmetrical stretching of C–H from the CH3 group appeared at 2854.64 cm−1, while the asymmetrical stretching of C–H from the CH2 group appeared at 2926.7 cm−1, which is consistent with the work of Sipaut et al. [28]. Nonetheless, in the epoxy-silica spectrum, there was clear evidence of the presence of silica in this composite, where some peaks were broader than their initial areas. For instance, the broad peak from 1060–1220 cm−1 is due to the aromatic and aliphatic C–O stretching from epoxy and the vibration of Si–O from silica. Additionally, the band at 798.8 cm−1 is due to the C–O stretching from epoxy and vibration of O–Si–O from silica, which is consistent with Kim et al. [29].
4.2. Density
Figure 6 depicts the density of every layer of the FGM. The addition of silicon dioxide increased the density of the polymer composite because silica has a higher density than epoxy, and the silica particles reduced the porosity of the composites, which is consistent with the work of Misra et al. [30]. When the ratio of silica particles increased, the porosity decreased [31]. Therefore, the density of the samples in the epoxy matrix groups was directly proportional to the ratio of silicon dioxide. When the porosity of the polymer composite diminished, its structure became denser and reached a maximum at 80 wt%, which was 20.95% higher than that of the pure epoxy. The density of the FGM specimen increased by 10.67% on average compared to the density of neat epoxy.
4.3. Tensile test
Figure 7 depicts the tensile stress-strain curve of the FGM specimen. The ultimate tensile strength obtained (29,625 MPa) is the highest stress that a specimen can bear while being pulled before breaking. Figure 8 illustrates the increase in tensile strength of the five layers of the FGM specimen with the increase in silicon dioxide loading from 0% to 60%. The Ep/S3 specimen with 40% SiO2 had the maximum tensile strength (41.9 MPa). The improved tensile strength with SiO2 wt% loading may have been due to the quantity of silica particles and the strong interfacial interaction between reinforcement and matrix, which reduced rapid fracture propagation and enhanced the stress transfer, as reported by Chen et al. [32]. All specimens examined obeyed Hooke's law, which provided data on the modulus of elasticity of the composite. Figure 9 illustrates that all generated composite specimens had higher moduli than the pure epoxy specimen, which is consistent with the work of Yusra et al. [33], the elastic modulus significantly increased because silica has a greater modulus than epoxy, since hard, dispersed phases have higher stiffness than the matrix material. The substantial decrease in tensile strength values at 80 wt% SiO2 can be attributed to the decrease in cross-link density generated by increasing the silica particles, which resulted in the decreased tensile strength of specimen Ep/S5. However, the decrease in tensile strength improved the elastic modulus, which is consistent with the work of Vikram et al. [34]. The enhanced FGM value played a significant role in enhancing the tensile strength and elastic modulus, since it was determined to be of average magnitude and significance.
4.4. Flexural test
According to the stress-strain curve in Figure 10, the flexural strength of the FGM was 25.71 MPa. As depicted in Figure 11, the flexural strength of the five layers of FGM gradually increased from 19.59 to 35.88 MPa from Ep1 to Ep/S3 in the composite reinforced with 40% silicon dioxide.
The increased flexural strength of the epoxy-silica composites was attributed to the interfacial adhesion between epoxy and dispersed silica particles, which limited the mobility of the matrix under further loading, according Jae Jun's report [35]. The lower flexural strength of the Ep/S5-reinforced composite compared to the Ep/S3 composite was caused by an increase in nonstick interface between resin and filler due to a higher silica particle loading percentage, based on Joo Eon et al. [36].
4.5. Impact test
Equation 4 was used to calculate the impact strength of the FGM composite, which was found to be 4,028 J/m2. Figure 12 illustrates that the impact strengths of the five layers of the FGM composites revealed a slight improvement at the Ep/S2 and Ep/S3 content ratios. The Ep/S4 specimen had the highest impact strength, which decreased in the Ep/S5 specimen due to its larger concentration of silica particles. Reinforcement enhances the impact strength and fracture toughness, which highly depend on the filler volume content. Furthermore, the use of silica particles improves the impact resistance, as shown by Umit et al. [37]. The weak borders of specimen Ep/S5 may be due to the effect of the silica particle concentration on the homogeneity of the epoxy network's crosslinking according to Alameri and Oltulu [38].
4.6. Thermal properties
The effects of the silica filler on the thermal conductivity of composites loaded with silica particles are depicted in Figure 13. The measured thermal conductivity of all investigated composites increased when the filler loading increased. Comparing the FGM specimen to the epoxy-silica composites, the FGM specimen had a thermal conductivity of 0.37 W/m·℃. At each filler loading, the composite loaded with a high filler content had a greater thermal conductivity than that with a low filler content. The increase in thermal conductivity can be attributed to an improved bonding between the particles and the matrix. These increases are comparable to those reported by Poh et al. [39].
5.
Conclusions
This study examined the effect of silicon dioxide on epoxy composites subjected to tests of tensile, flexural, and impact strengths and thermal conductivity. FGMs with silica-reinforced epoxy composites were created with weight percentages of 0, 20, 40, 60, and 80. Based on the findings of this investigation, the following conclusions were drawn:
(1) The XRD and IR of silicon dioxide-reinforced epoxy composites revealed homogeneous silica particle dispersion in the epoxy. Silica particles were attached to the epoxy matrix via a strong physical association, and the silica did not interact with the epoxy. Therefore, the compatibility of the polymer and silica significantly affected the mechanical and thermal properties of gradient materials for epoxy-silica compositions.
(2) The density increased when the ratio of silicon dioxide increased, with the maximal value being achieved at 80 wt%. Adding silica particles to epoxy as a control element increased the density by 4.8–20.95% compared to pure epoxy. The FGM specimen reinforced with silica gradients was 10.66% denser than pure epoxy.
(3) The addition of silicon dioxide to the epoxy composite increased the tensile and flexural strength for all groups when the silica particle loading increased from 0% to 60%. The optimal proportion of silica was 40%. The ultimate tensile strength of the FGM specimen was 29,625 MPa and its flexural strength was 25.71 MPa, which are 17.68% and 31.18% greater than the tensile and flexural strengths of pure epoxy, respectively.
(4) The modulus nearly linearly increased when the level of added silica particles increased. The FGM specimen was 306.67% greater than the pure epoxy specimen, while the composite with 80 wt% silica had the highest elastic modulus, which was significantly greater than that of pure epoxy.
(5) The impact strength of the gradient materials slightly increased when the ratio of silica increased from 20 to 40 weight percent and thereafter. The maximal significant increase was observed with 60% silica, followed by a decrease due to the effect of the silica particle concentration on the homogeneity of the epoxy crosslinking. Meanwhile, the impact strength of the FGM specimen was 7.71% higher than that of the epoxy specimen.
(6) The highest thermal conductivity of the composites was found when 80 wt% silica particles were utilized. Additionally, it was discovered that the thermal conductivity increased when the filler content increased. Compared to the epoxy-silica composites, the unfilled epoxy resin had a lower thermal conductivity. The FGM specimen had a 141.83% higher thermal conductivity than the pure epoxy specimen.
Conflict of Interest
The authors confirm that the content of this article has no conflicts of interest.









 DownLoad:
DownLoad: