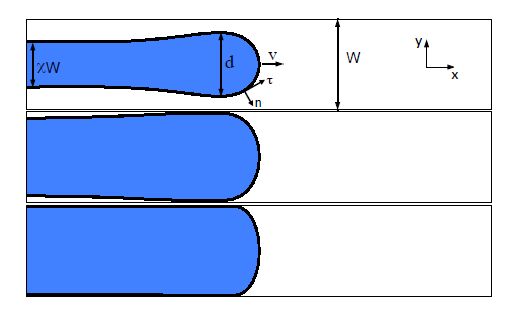
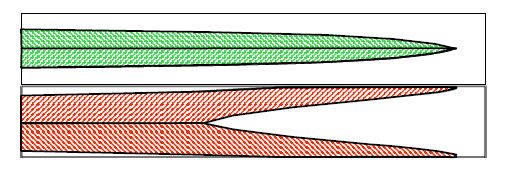
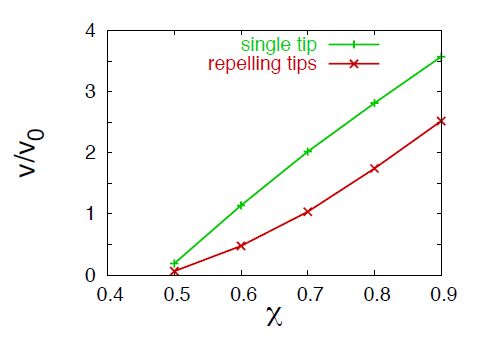
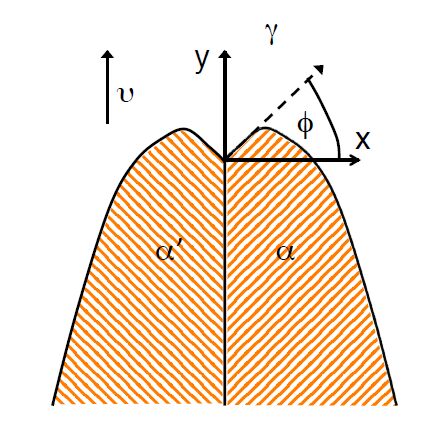
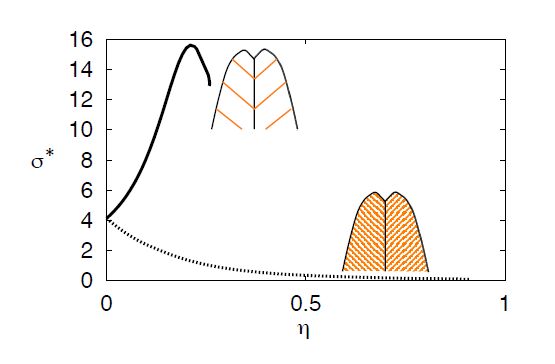
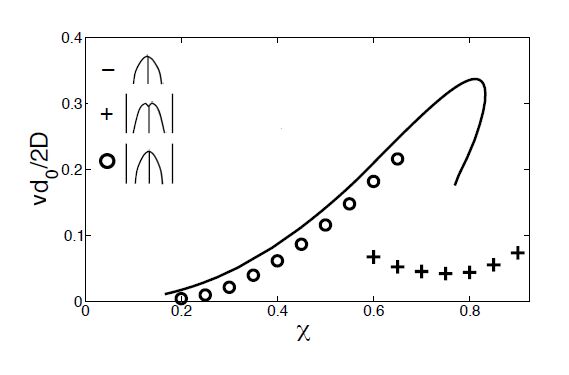
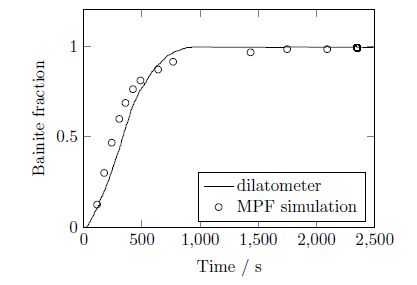
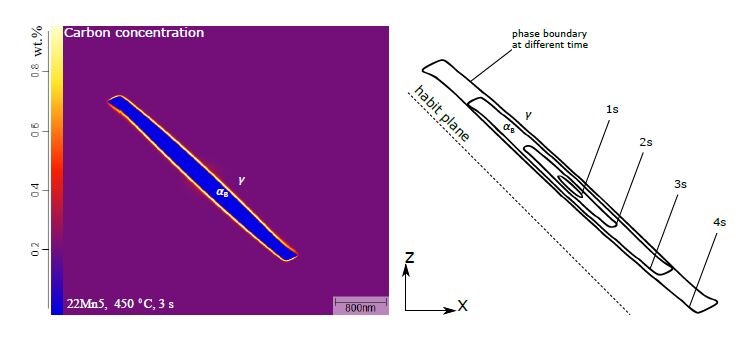
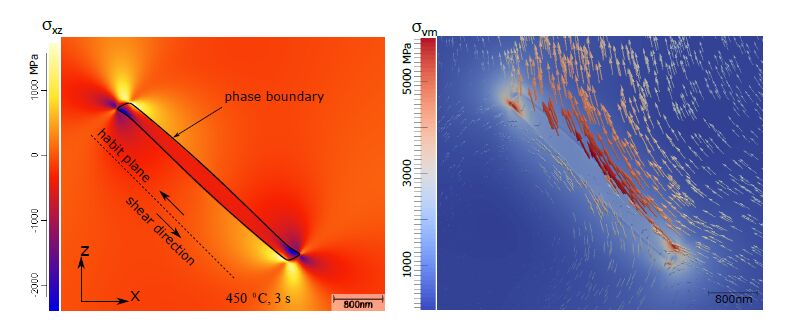
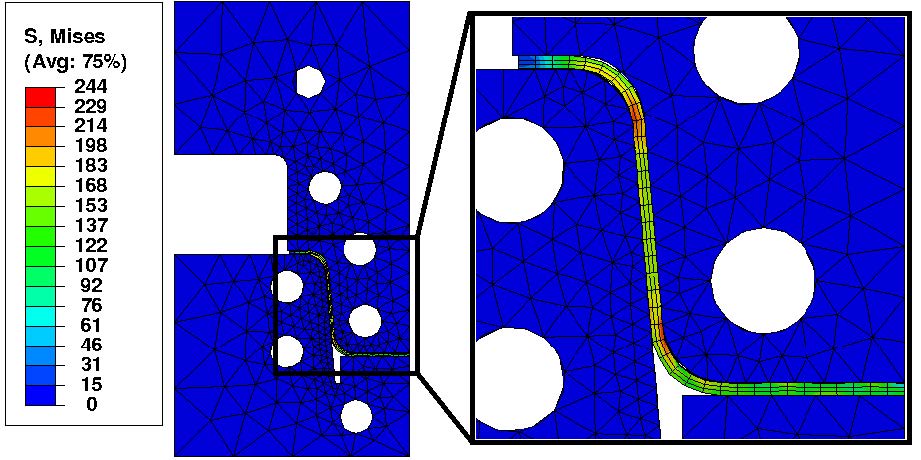
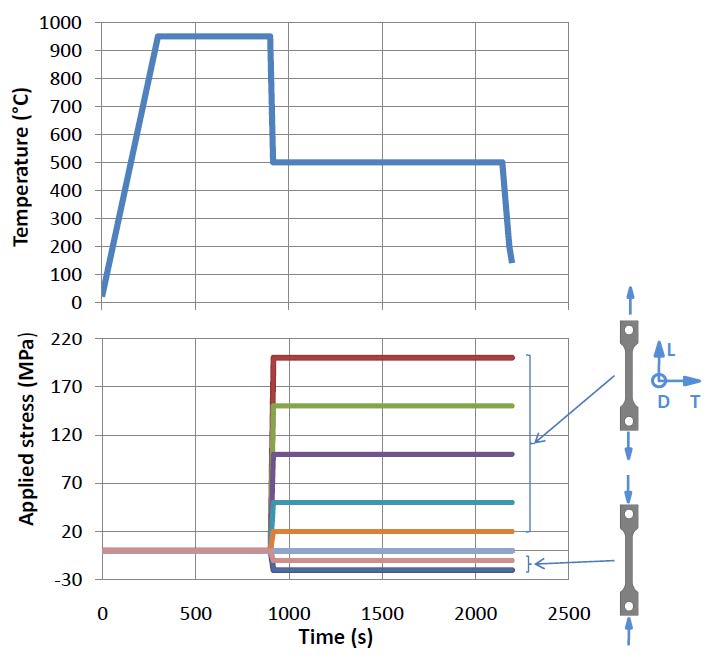
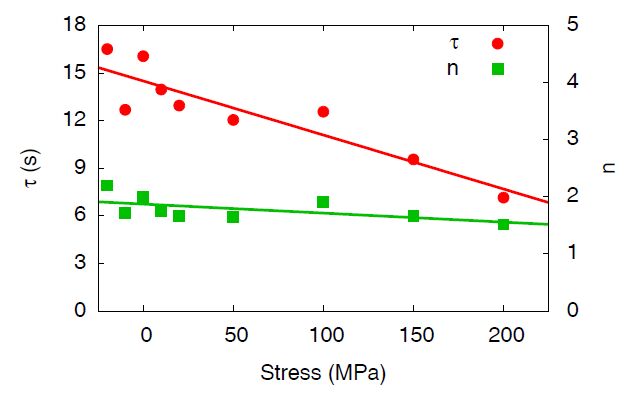
We give an excerpt of recent developments in the experimentally benchmarked modeling of bainite formation in the press hardening process. As the press hardening process poses a heavily multi-parameter dependent modeling challenge, we focus on three main branches which complement each other. We emphasise the combination of basic sharp interface and phase field models with pragmatically adapted multi phase field models and experimentally parametrized implementations of the Johnson-Mehl-Avrami model. In the basic thermodynamic modeling part, we review fundamental aspects of displacive and diffusional-displacive transformations to predict dominant transformation morphologies. These results provide a link to multi-phase-field implementations which allow to simulate isothermal bainitic transformations, supported by available material data from thermodynamic databases. Excellent agreement with experiments, e.g. scanning electron microscopy for the transformed bainite in the high-carbon steel 100Cr6 shows the value of these model implementations. The further connection to Johnson-Mehl-Avrami models offers to extend the understanding to transformation plasticity for the press hardening steel 22MnB5.
1.
Introduction
The effect of radiation on a living organism is assumed to be proportional to the energy imparted and absorbed in the unit mass of the exposed bodies. Geometrical modeling of the human body plays an important role in the calculation of the energy deposited in the tissues and organs of the body [1]. In medical physics terminology, these geometrical models are called phantoms and are classified in three categories of stylized, voxelized and hybrid models [2].
Stylized phantoms, sometimes called mathematical phantoms, are the first generation of the anthropomorphic phantoms that are used for dose calculations in the human body [3]. In stylized phantoms, 3D shapes of different sizes/materials are defined in the computer memory to represent different organs of the body [4]. Stylized phantoms can only be used to characterize the gross shape of the human anatomy.
In the 1980s, voxel-based phantoms were introduced to represent the detailed geometry of the human body. These phantoms are normally generated from the computed tomography scans or magnetic resonance images [5]. The difficulty in the generation of digital phantoms involve the segmentation of tissues and assignment of the material composition to the voxels of phantoms. In recent years, many digital phantoms have been introduced to provide much better anatomical realism compared to stylized phantoms. Depending on the resolution of the tomographic image, it is sometimes difficult or even impossible to segment small or tortuous tissues in the generation of digital phantoms [6]. These phantoms have limited flexibility to change the shape/posture of the organs.
To overcome the limitations of digital phantoms, researchers have focused on combining the realism of voxel phantoms with the flexibility of mathematical phantoms to generate hybrid phantoms [7]. Non-uniform rational B-spline or polygon-mesh surfaces provide great flexibility to define the organs and the organ motion in hybrid phantoms [8]. Despite all of the theoretical advantages, it is not yet possible to integrate a hybrid phantom into the geometry used in a Monte Carlo (MC) simulation. In practice, a hybrid phantom generator produces one or more digital phantoms at the desired spatial/time resolution that can be integrated into the geometry of simulations. The conversion procedure always has some degree of digitization error that becomes prominent in the voxels at the boundary of moving tissues. Such voxels may become a mixture of bordering tissues representing uncharacteristic properties/compositions. The main advantage of hybrid phantoms is that they provide the opportunity to consider organ motion in imaging studies [9].
In practice, digital phantoms are the most widely used geometrical model for medical dosimetry. However, they are mainly used to represent large-scale geometries (e.g., body, torso, head) at the pixel size of millimeters, which is not suitable for dosimetry at a microscopic level [10]. Due to the limitations of current imaging systems, the production of high-resolution digital phantoms is not possible, although radiation interacts with atoms and molecules and radiation damage starts at cellular levels. Moreover, many radionuclides emit very short-range particles (such as alpha and Auger electrons), delivering very high doses in a small spot. Therefore, nuclear medicine therapy with short-range particles requires microscale dosimetry. Dosimetry in nuclear medicine is based on the Medical Internal Radiation Dosimetry method, which is a semi-analytical method based on slowing-down approximation, to calculate the fraction of energy released from the source component that is absorbed in the target component [11].
One of the critical microstructures of tissues in the human body are the nephrons inside the kidneys. Kidneys act as the main excretory pathway for the radiopharmaceuticals administrated to the body, and are therefore a critical organ in radionuclide therapy [12]–[14]. Nephrons are functional subunits of kidneys, and each are individually responsible for excess substances from the blood. A healthy adult has 0.8 to 1.5 million nephrons in each kidney with slightly different sizes and postures. Nephrons are classified as cortical or juxtamedullary nephrons. Cortical nephrons have small, short loops of Henle and are largely located at the outer renal medulla. They make up around 85% of the nephron population in a human kidney and perform the excretory functions over radiopharmaceuticals. Juxtamedullary nephrons are much smaller in population, and their main function is controlling the concentration of urea.
A nephron is itself composed of thousands of cells in a complex arrangement in the shape of a narrow, long, curved tube. Nephrons perform different actions (i.e., excretion, reabsorption) on different types of radiopharmaceuticals within their substructures (i.e., glomeruli, tubules). Dose distribution along a nephron varies with the type of radiopharmaceutical administered. The probability of radiation nephropathy is consequently dependent on the distribution of dose along the nephron or, more correctly, the dose distribution within the nephron cells. Deterring the dose distribution in nephrons requires a high-resolution phantom because, in macroscale dosimetry, only the average dose to the nephron population can be estimated. Experiential studies have shown signs of radiation toxicity when the average dose to the mouse kidney is well below the threshold level [15],[16]. These observations also evoke the need for investigation of the dose distribution at the microscopic level.
A digital phantom representing a typical nephron can be helpful to estimate the dose distribution between the cells of nephrons and investigate the subunit that receives the highest dose and is therefore the most likely to be damaged by a given radiopharmaceutical.
In this paper, an anatomical model of a kidney based on a 3D high-resolution digital phantom is introduced. The constructed phantom represents a typical cortical nephron with a detailed anatomy. In order to validate the phantom, MC simulations are performed using a similar method to Hobbs et al. [17], who used a stylized phantom of a nephron for the microdosimetry of alpha-emitting radionuclides; our results are compared to the results published by them. S-values for the electron source are also calculated, and the differences between the two phantoms are discussed.
2.
Materials and methods
2.1. Geometry input file
Voxelized phantoms can represent the complex geometry at the desired size and resolution. The procedure for generating a phantom is represented in Figure 1. In this study, a 3D Wavefront OBJ format containing the polygonal mesh structure of the nephron surface was created. Using commercial software, different components of the nephron (i.e., the glomeruli, proximal and distal tubules, and loops of Henle) were separated. Binvox freeware was used to convert each component into the 3D voxelized format. Binvox is a command-line program that rasterizes a 3D model into a binary 3D voxel grid. The generated phantoms were processed independently to segment each compartment into the urinary duct and epithelial cells. In the case of the glomeruli, they were segmented into the Bowman's capsule, Bowman's space and glomerulus. The outer shell in each subunit is the cell region, and the remaining voxels represent the pathway of urine through which the source is distributed. Different tissue indexes have been devoted to different segments of each compartment as identification indexes. The resultant files were finally converted into the interfile format. Interfile is a file format developed for nuclear medicine image data. An interfile data set consists of two files, i.e., a binary file containing image data and an ASCII format containing information about the dimensions, identification and processing history. The interfile format can be recognized by the GATE toolkit. To adjust the size of each compartment to suit the morphological data, the voxel sizes were set individually in each header file.
Figure 2 illustrates the morphological analysis of the generated nephron phantom. The voxelized phantom and its compartments are shown in this Figure. Each subunit of a nephron has an endothelial cell layer and a lumen. The matrix sizes of the glomeruli, tubules and loop of Henle were set to be 160×300×80, 357×257×286 and 357×57×459, respectively. The corresponding voxel sizes of the glomeruli, tubules and loop of Henle were set to be 1.5×1.5×1.5, 1×1×1 and 0.85×0.85×0.85 µm3, respectively. The arrangement of the voxels representing glomerular endothelial cells is also shown in Figure 3. All three components of the nephron were imported into the gate geometry simultaneously. The placement was correctly adjusted to make the three components represent a single nephron. All of the geometrical structures were made up of water because more than 70% of the mammalian body is made up of water (unit density).
The problem with particle tracking inside of the voxelized phantom is changing the material properties of voxels and the need to renew cross sections at the boundaries between voxels with different materials. Gates have three extra navigating algorithms to save time and memory when tracking particles inside voxelized phantoms. The native regular matrix algorithm was selected since all of the voxel material was set to be water and the voxel boundary problem does not exist.
A specific index number was allocated to each compartment of the nephron. The material composition and activity distribution was independently set for the voxels with the same index number. The index number was also used for dose calculation and output data extraction.
The volumes of the phantom compartments were calculated according to the number of voxels encountered in each part and the voxel size. This ensured that, not only would the shape of the nephron be realistic, but the volumes would be equivalent. For the current work, the phantom was filled with water in consideration of the fact that biological material consists of about 70% water. This is still a simple approximation, and it would be interesting to produce the current work while taking into consideration the concentration of the various elements found inside a nephron; however, this requires further information about the chemical composition of nephrons.
2.2. Monte Carlo simulation
All simulations in this study were performed using GATE version 7.2. GATE is a general-purpose MC code that simulates the transport of particles over a wide range of energies. It is becoming increasingly popular in the field of medical physics and a good method to investigate cellular-level dosimetry. Although numerical approaches have many advantages, MC simulations can track particles with more precision than numerical approaches [18]–[20]. GATE has three different physics lists for the simulation: Livermore, Penelope and Geant4-DNA physics [21]. In the case of the first two physics lists, a condensed history algorithm is used to track charged particles. In the case of the Geant4-DNA physics list, a track structure algorithm is used to track charged particles. Geant4-DNA was used to score the deposited energy of the electrons in each voxel of the phantom. In this physics list, electrons are tracked down to 11 eV while considering all the necessary interactions by using ENDL97 cross-section tables. Geant4-DNA was developed to provide predictions of the biological effects at the cellular level [22]. Although the track structure is the most advanced algorithm for electron tracking for microscale geometries, its application is limited to a water medium, and its computational time is considerably long. In GATE terminology, the required medium for Geant4-DNA physics is G4_WATER.
To evaluate the digital phantom using the data published by Hobbs et al., similar simulations were performed using alpha-emitting radionuclides. However, alpha emitters are rarely used in radionuclide therapy, and the most widely used radionuclides are beta emitters. All particles were assumed to be independently uniformly distributed inside the glomeruli and proximal tubules of the digital phantom. The number of historical records in the simulations was set to be 106 for alpha particles to keep the uncertainty in dose calculation under 5%. In the case of a stylized phantom GATE provides the uncertainty of dose per compartment, but, for a digital phantom, some additional calculation is required. GATE provides the uncertainty of dose per pixel. The uncertainty of the dose in the nephron compartment was calculated by using the root mean squares method. The uncertainty of voxels was squared and summed up. The result was divided by the number of pixels in the compartment and the square root was accepted as the uncertainty of dose in the compartment.
The first stage in this study involved making a comparison with the results derived by using the voxelized and stylized phantom used by Hobbs et al [14]. In their study, the energy deposited by the alpha particles emitting to the glomeruli and the proximal tubules of the phantom were calculated. The same energy values as those reported by Hobbs et al [14] were used for the alpha particles. Simulations were performed for each radionuclide independently. The dose delivered to each compartment was finally summed up after normalization of the yields and branching ratios.
The simulations were conducted by using a high-power computer with a Linux Ubuntu 16.04 operating system. The simulations were performed in parallel by using 60 CPUs simultaneously. The duration of simulation was between 30 hours and 60 days. No variance reduction technique was used in the simulations.
The dose derived in the simulations were scaled based on their history number and corresponding radiation yield and used to calculate the S-values for the single-unit nephron geometrical model (u S-values), as explained in the Hobbs et al. study [23],[24].
For further investigation of the digital phantom, the electron source (energy range: 1, 10, 20, 30, ...70 keV) was independently distributed uniformly inside the glomeruli and the tubules of the digital phantom. The history number in each simulation varied from 106 to 109 to keep the uncertainty under 5%. The DNA physics library was used to score the deposited energy of the electrons in each voxel of the phantom. Simulations were performed to calculate the electron specific absorbed fraction (SAF) for the glomeruli and the tubules of the digital phantom.
The absorbed energy in each compartment was calculated by averaging the voxel values in the entire region of the components. The absorbed energy in the voxels of the target region was divided by the total energy emitted from the source region. The result was divided by the total mass of the voxels in the target region to calculate SAF values.
Similar simulations were performed using the stylized phantom, and the corresponding SAF values were calculated.
3.
Results
3.1. Alpha S-values
Table 1 presents the S-values for the human nephron model generated in this study, as well as the Hobbs et al. S-values given for their single-unit model. The relative differences (RDs) between the results of the models were calculated as follows:
where SD and SH represent the S-values calculated using our digital phantom and the Hobbs et al. model, respectively.
The RDs were up to 12.46% for self-absorption, but a little higher (17%) for cross-absorption. Self-absorption may be defined as the absorption of radiation when the source and target are the same. The self-absorbed dose that commonly provides the largest fractional contribution to the total absorbed dose in a target region refers to the case when the source and target regions are identical. The cross-absorbed dose refers to the case when the source and target regions are different. Pearson's correlation analysis confirmed a good linear correlation (R2 = 0.99) for the self-absorption and cross-absorption between two data series (R2 = 0.96). Figure 3(a) illustrates the linear curve that has been fitted to the scatter plot of the S-values. A high linear correlation (R2 = 0.991) can be seen between the two series of data. The slope of the fitted linear curve was + 0.95 higher than unity. Figure 3(b) includes the scatter plot of the RD between two series of data. This Figure demonstrates the Bland-Altman plot to reveal the RD versus reference values (Hobbs et al. S-values). The average value of the RDs, i.e., the bias, demonstrates a systematic difference in the MC simulation. As the plot shows, 95% of the data points were inside the limits of agreement (average of RD ± 1.96 × standard deviation of RD) and the statistical difference is acceptable (≈ 5%). There was a high bias (5.27%) between the two sets of data.
3.2. Electron sources
The variations of the self-absorption and cross-absorption SAF values according to electron energy are presented in Figure 4. As the graph shows, for the glomeruli as the source, the calculated SAF values derived using the stylized and digital phantoms were in good agreement. The maximum difference of the self-absorption in the glomeruli was -4.78% for the 1-keV electrons. Similar curves for the glomeruli as the source and the proximal tubules as the target (cross-absorption) are also shown in Figure 4. The RDs between the results obtained by using the digital and stylized phantoms for electrons were up to 9.54%. Although a greater difference was observed in the case of cross-absorption as compared to self-absorption, the trends of variation were similar for the two phantoms. The RD for the electrons in the range of 1 to 10 keV was a little higher than that for other energies for both the self-absorption and cross-absorption.
Figures 5 illustrates the Bland-Altman plots for the self-absorption and cross-absorption SAF values for the electron source within the energy range of 1 keV to 70 keV. The graph shows the RD between the results derived using the digital and stylized phantoms as a function of the energy of the electrons. The plots illustrate the agreement between two data series. The bias between the two data series (the average of RD%) was -0.65%, showing an almost perfect agreement. The plot reveals that the SAF values derived using the digital phantom were 1% smaller than the corresponding values derived using the stylized phantom. The limit of agreement (average ±1.98 times the standard deviation) is normally used for evaluation of the statistical variation between the two data series. As can be seen, 95% of the data points were inside the limits of agreement. For electrons with energy < 30 keV, the RDs were high (between 4% to 10%).
4.
Discussion
An obstacle in MC simulations at the microscopic level is the lack of high-resolution phantoms. The phantoms that are currently in use are stylized phantoms that simplify the geometries. This model only includes the glomeruli and proximal tubules in simple shapes. This is an important problem because a small variation in target and source volumes may lead to a considerable difference in the results of microscale simulations [20],[23]. Moreover, it is not possible to make a stylized phantom at the desired resolution. Therefore, the phantom must be close to the anatomy of the object to be represented. In the present study, a simple method was developed to generate digital phantoms from tessellated 3D graphical images. The method is expected to be useful for investigating the absorbed dose in organs on the microscale. A digital phantom representing the detailed anatomical properties of cortical nephrons in human kidneys was modeled in this study.
One of the main advantages of using the digital phantom is the possibility to investigate the dose distribution in voxels that can be approximate values for the dose distribution among cells. It is not necessary to have voxels at the size of cells in the tissue. It is always possible to consider a combination of voxels to represent the average size of the cells. This can be different for different locations of phantoms. The dose distribution in the cells is an important index to predict the response of tissues to radiation.
Another advantage of using the digital phantom is the possibility to consider the non-uniform distribution of radiopharmaceuticals in source components. The nephron digital phantom can also take into account the possible differentiation of uptake between superficial and juxtamedullary nephrons [24].
At present, there is no experimental data available for the validation of the results derived using the digital phantom of a nephron. However, the consistency with the results derived using the stylized phantom may be regarded as a type of validation. The maximum difference was up to 20%, which is not acceptable when the uncertainty of simulation is around 5% (95% confidence interval).
The S-values calculated using the digital phantom were all smaller than the values reported in the study by Hobbs et al. This can be due to the different energy spectra used in the two studies. In the present study, alpha energy spectra were derived using the MIRD radionuclide data and decay scheme [25]. Hobbs et al. derived the decay schemes from another data center [26],[27]. The difference can also be due to small differences in the shapes of the nephron components [27]. The volumes of nephron components are equal, but it is not possible to equalize the shapes simultaneously. A considerable part of these differences is due to the simplification of nephron anatomy. Therefore, it is obvious that the deviation from the real anatomy of a nephron leads to considerable differences in the S-values and dose calculations.
To some extent, the difference between the results of two phantoms could just be due to statistical variation (uncertainty) in the MC simulation. When the energy of particles is low, most of the energy of particles is absorbed in the source components, and only a small fraction of particle energy is released in the target components. From the statistical point of view, smaller values indicate higher statistical uncertainty. However, this does not explain the smaller S-values derived by using the digital phantom compared to the stylized phantom.
Despite the advantage of digital phantoms, tracking particles in discrete environments is much slower than in continuous mediums. The main reason is the need for calculation of the material properties each time a particle enters a voxel. This becomes a significant problem when the number of voxels is large and the voxel size is small. This may be the reason why the digital phantoms are not so popular in microdosimetry. However, high-power computers can overcome this difficulty.
The digital phantom developed in this study permits the calculation of the dose in fine spatial resolution. As the results showed, the average dose to cells is considerably different from the maximum and minimum doses to the cells. Depending on the threshold dose for cell damage, the relative number of cells that receive a dose higher than the threshold can be an index for the protection of normal cells or damage of malignant cells.
5.
Conclusions
A digital phantom of a nephron was modeled in this study. This phantom provides the possibility to measure dose at the cellular level, and it can be helpful in the estimation of the kidney response to radionuclide therapy. The phantom represents the real anatomy of a nephron in detail, and it can be used to assess the effect of inhomogeneous activity distribution in the absorbed dose of a nephron. So, a generated phantom can be useful for obtaining accurate absorbed dose estimations for different radiation protection situations, as well as for the more precise evaluation of biological effects. This study showed that, depending on the radionuclide spectra, the dose to the nephron may be overestimated or underestimated, and that this is something expected in general. It would be useful to quantify this difference in more detail. This may be regarded as a sample for the development of a more accurate high-resolution digital phantom. The phantom is freely available from the corresponding author of this paper.










 DownLoad:
DownLoad: