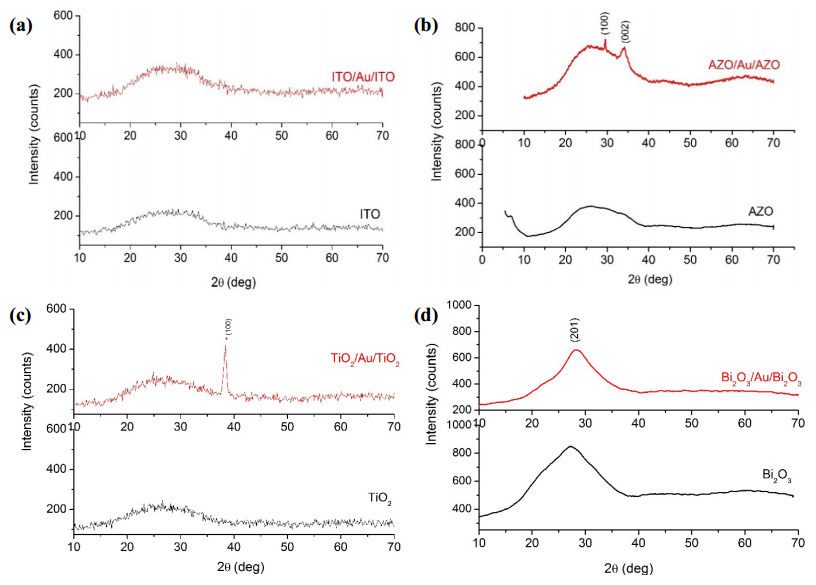
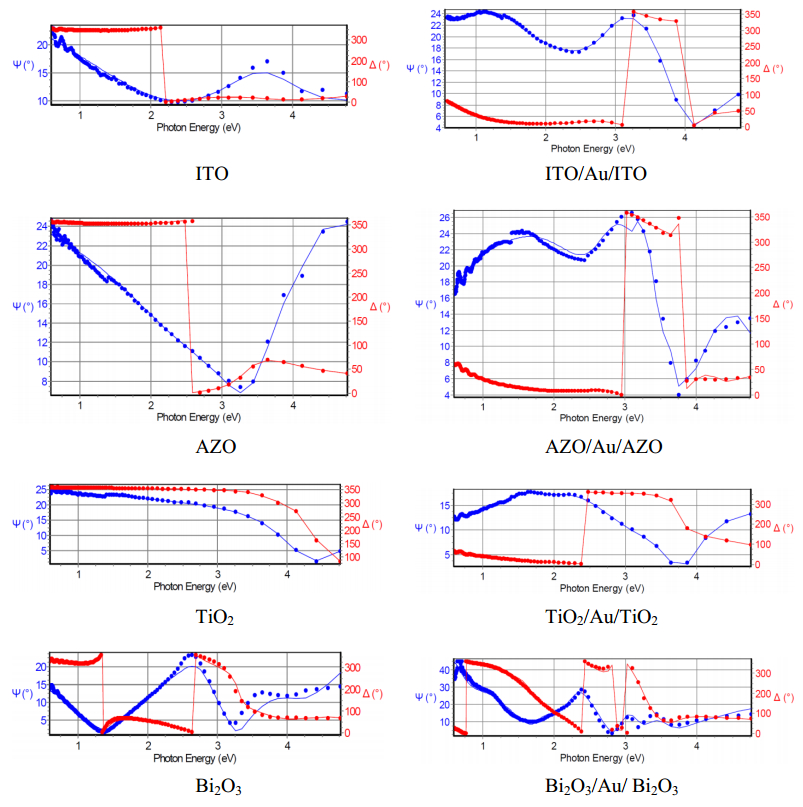
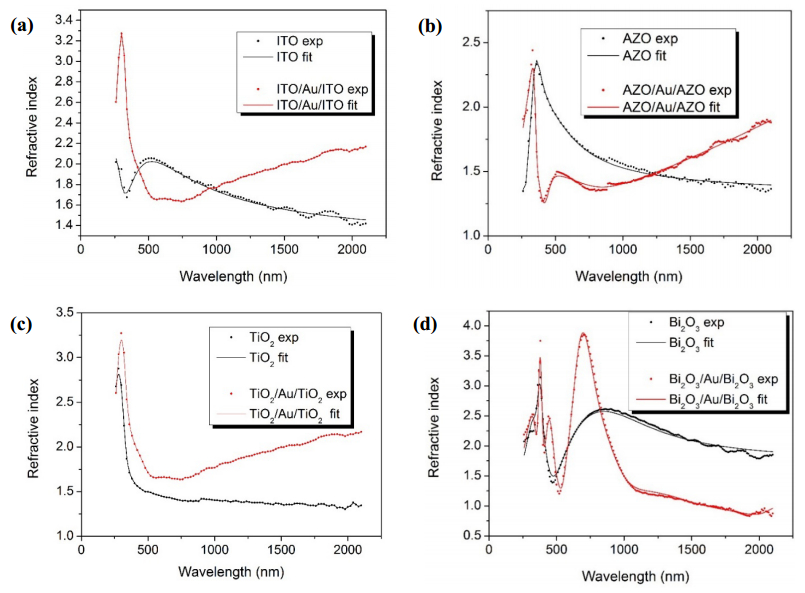
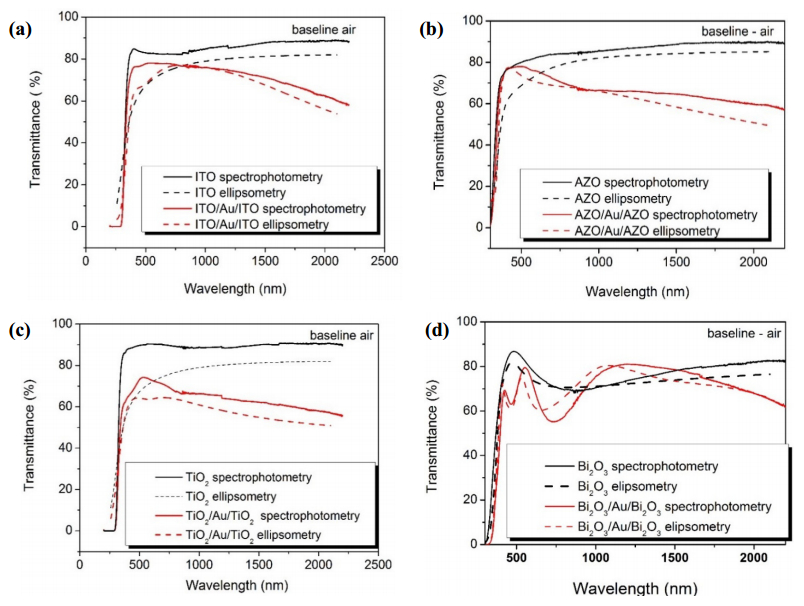
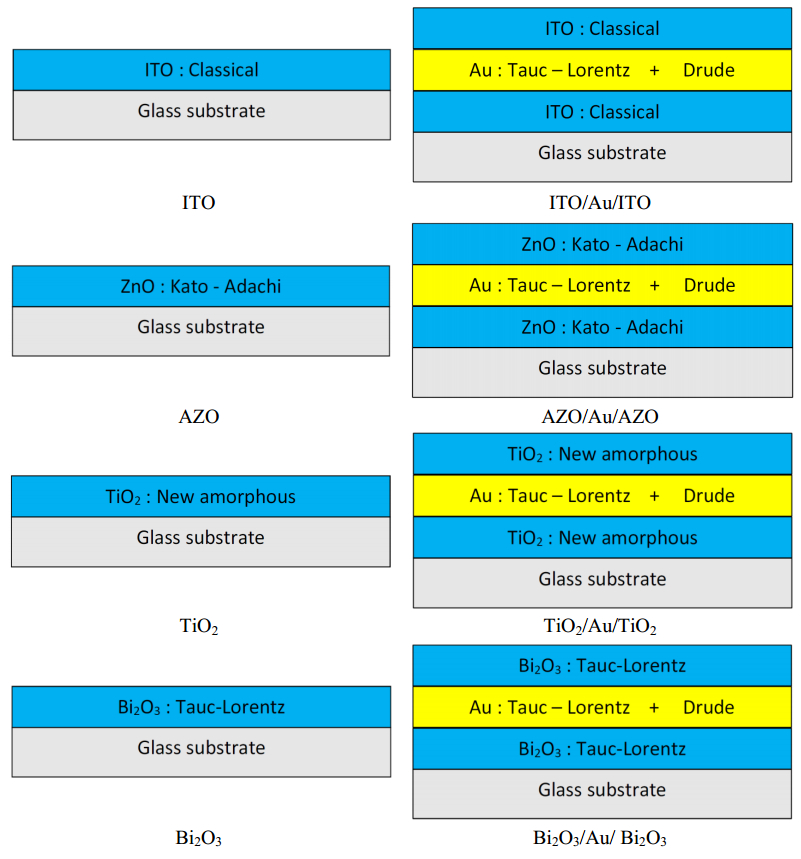
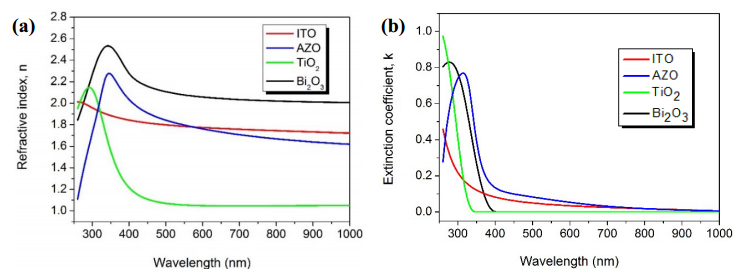
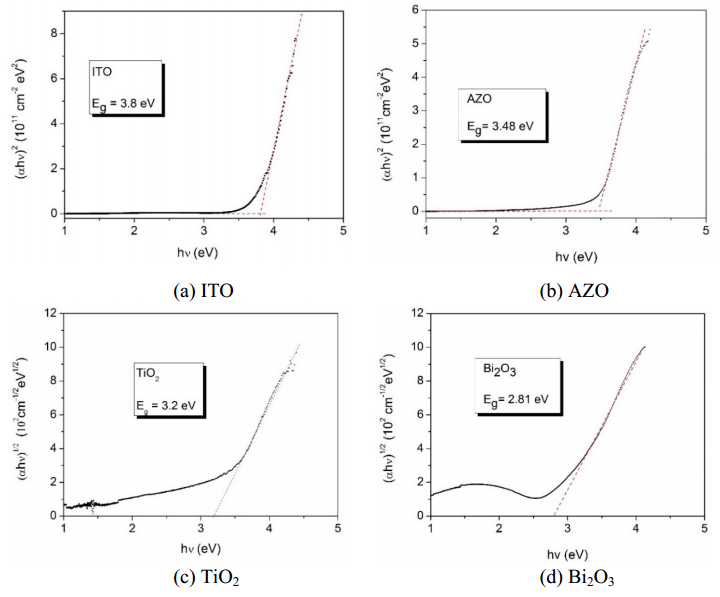
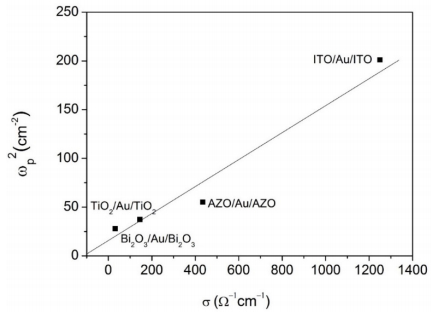
A comprehensive study of a class of Oxide/Metal/Oxide (Oxide = ITO, AZO, TiO2 and Bi2O3, Metal = Au) thin films was done by correlating the spectrophotometric studies with the ellispometric models. Films were deposited by successive sputtering from metallic targets In:Sn, Zn:Al, Ti and Bi in reactive atmosphere (for the oxide films) and respective inert atmosphere (for the metallic Au interlayer films) on glass substrates. The measurements of optical constants n—the refractive index and k—the extinction coefficient, at different incident photon energies for single oxide films and also for the three layers films oxide/metal/oxide samples were made using the spectroscopic ellipsometry (SE) technique. The ellipsometry modelling process was coupled with the recorded transmission spectra data of a double beam spectrophotometer and the best fitting parameters were obtained not only by fitting the n and k experimental data with the dispersion fitting curves as usual is practiced in the most reported data in literature, but also by comparing the calculated the transmission coefficient from ellipsometry with the experimental values obtained from direct spectrophotometry measurements. In this way the best dispersion model was deduced for each sample. Very good correlations were obtained for the other different thin films characteristics such as the films thickness, optical band gap and electrical resistivity obtained by other measurements and calculation techniques. The ellipsometric modelling, can hence give the possibility in the future to predict, by ellipsometric simulations, the proper device architecture in function of the preferred optical and electrical properties.
1.
Introduction
In this article we consider the following quasilinear boundary value problem
where Ω⊂Rn, with n≥3, f,u:Ω→RN, with N≥2, and a:Ω×RN→RN2n2 is a matrix valued function whose entries are aα,βi,j(x,u) with i,j∈{1,…,n} and α,β∈{1,…,N}. Therefore the first line in (1.1) is a system of N equations of the form
For the treated problem there is an extensive literature in the scalar case N=1.
In particular, for the existence of a suitably defined solution, the Reader can refer to the papers [9,10,14,58,69] while, relatively to uniqueness and a priori estimates, we can quote respectively the papers [67] and [3]. For what concerns the regularity of a solution we cite the works [35,38]. Moreover, similar conclusions for the nonlinear case can be found in [2,8,12] and for the anisotropic case in [4,36]. Subsequently the aforementioned results have been extended to the operator with lower order terms too (see also [15,16,17,20,51]). In this context one can also see [7,11,12,24,25,30]. Furthermore, in [37] the right hand side appears in divergence form, that is f=−divF and in [1] the biharmonic operator is studied.
For further regularity results concerning elliptic operators the Reader is invited to refer to the foundamental works [5,6,26,27,28,41,42,43,44,45,46,47,48,64] and the survey [65].
As it is shown by the De Giorgi's counterexample [29], see also [39,40,49,60,61], the good regularity properties obtained in the scalar case can not be in general extended to the vectorial one, unless new structural assumptions are introduced.
An existence result of bounded weak solution for nonlinear degenerate elliptic systems is obtained in [55], using a componentwise coercivity condition. In several other papers, conditions on the support of the off-diagonal coefficients aα,βi,j(x) have been used to address different problems. Let us mention that a maximum principle result is obtained in [66] where the assumption is aα,βi,j(x,y)=0 for α≠β when yα is large and in [52] where different shapes of support are considered. Hölder continuity of the solutions is proved in [70] for a tridiagonal system, aα,βi,j=0 for β>α. L∞ regularity results are obtained in [53] for an oblique type of support for the coefficients and in [54] for a butterfly support. Measure data problems are faced in [56] and [57] where the support of aα,βi,j(x,y) is contained in squares along the yα=±yβ diagonals.
These kind of assumptions on the coefficients have been recently employed also to deal with degenerate elliptic systems. In this context there are results on problem (1.1) when the datum f∈Lm, which extend the ones contained in [14] for the scalar case. Namely, in [31] the existence of a bounded solution is proved when m>n2, assuming a butterfly support for the off-diagonal coefficients; moreover in [32] the case of a datum f with an intermediate grade of integrability (m<n2) is treated, thanks to an appropriate choice of the support for the off-diagonal coefficient.
In this paper we extend to the degenerate vectorial problem (1.1) an existence result concerning degenerate scalar operators, with the datum f in a suitable Marcinkiewicz space, contained in [14,62,63] (see also [21,22]). Since we are dealing with the vectorial case the support of the coefficients is required to have a particular structure. In Section 2 we give the precise notions of degenerate ellipticity and Marcinkiewicz spaces, see respectively (A2) and definition 1, while the assumption on the shape of the support of the coefficients is stated in (A3).
Also in this context the extension to the vectorial case of the known result in the scalar one is not obvious. Indeed, starting from De Giorgi's counterexample, it is possible to construct an example of an elliptic system with datum f∈Lp for every p<n, whose unique solution is unbounded and has low integrability, see [31] for details on the counterexample.
When dealing with systems of N equations, like (1.2), whose coefficients are only measurable with respect to x, little is known. Most articles are devoted to study existence or regularity of solutions of systems with right hand side fα∈Lm, either when m is large, or when m is small. When m is large, namely m>n2, existence of bounded solutions is obtained in [31].
When m is small, namely m=1, or even when fα is a measure, existence of solutions have been studied for general systems
under structure conditions on Aαi. Namely, in [33] and [34], authors assume that
for every b∈RN with |b|≤1. On the other hand, in [71], the author assumes the componentwise sign condition
for every α=1,…,N. When N=2, (1.4) implies (1.5): it is enough to take first b=(1,0), then b=(0,1). Note that, in the present paper, we address the quasilinear case
in this case, as far as one off-diagonal coefficient a˜α,˜β˜i,˜j(x,y) is non zero, then (1.5) is no longer true: it is enough to take α=˜α, ξβj=0 if β∉{˜α,˜β}, ξ˜αi=0 if i≠˜i, ξ˜α˜i=1, ξ˜βj=0 if j≠˜j, ξ˜β˜j=ta˜α,˜β˜i,˜j(x,y)|a˜α,˜β˜i,˜j(x,y)|2 with t→−∞. When N=2, failure of (1.5) implies failure of (1.4). We recall that the study of quasilinear systems (1.2) with fα∈L1 is contained in [57] under the assumption that the support of off-diagonal coefficients is contained in a sequence of squares with side lenght r along the diagonals of the yα−yβ plane.
Concerning existence and regularity of suitable defined solutions of linear ellitptic systems
with VMO coefficients and datum f=(fα) in a Lebesgue space Lγ with γ∈(1,2nn+2] (i.e., below the duality exponent) or in a suitable Lorentz-Morrey space one can refer also to [50]. While if f belongs to the natural dual Lebesgue space but the linear operator in not coercive due to the presence of a lower order term, called "drift term",
then existence and regularity results can be found in [19]. The above result has been extended to non linear operator under the so-called Landes condition (similar to (1.4)) with datum being in L1 or in L2nn+2 respectively in [18,23].
In the present work we address the existence of a regular solution to (1.2) when fα has an intermediate degree of integrability, namely, fα∈Mm with 1<2nn+2−θ(n−2)<m<n2 and Mm is the Marcinkiewicz space. In this case, the higher degree of integrability of the right hand side fα allows us to weaken the condition on the support of off-diagonal coefficients.
In the next section we present assumptions on the coefficients and on the datum f and our result. In Section 3 we consider a sequence of approximating non degenerate problems and we prove estimates on their weak solutions; then, with a limit procedure, we get the result for our problem.
2.
Assumptions and result
For all i,j∈{1,…,n} and all α,β∈{1,…,N} we assume that aα,βi,j:Ω×RN→R satisfies the following conditions:
(A0) x↦aα,βi,j(x,y) is measurable and y↦aα,βi,j(x,y) is continuous;
(A1) (boundedness of all the coefficients) there exists c>0 such that
for almost every x∈Ω and for all y∈RN;
(A2) (degenerate ellipticity of all the coefficients) there exist constants ν>0 and θ∈(0,1) such that
for almost every x∈Ω, for all y∈RN and ξ∈RN×n;
(A3) (support of off-diagonal coefficients) there exists L0≥1 such that (A′3) and (A″3) hold, where
(A′3) (support of off-diagonal coefficients contained in a central square) if aα,βi,j(x,y)≠0 and 0≤|yα|<L0, then it holds also 0≤|yβ|<L0;
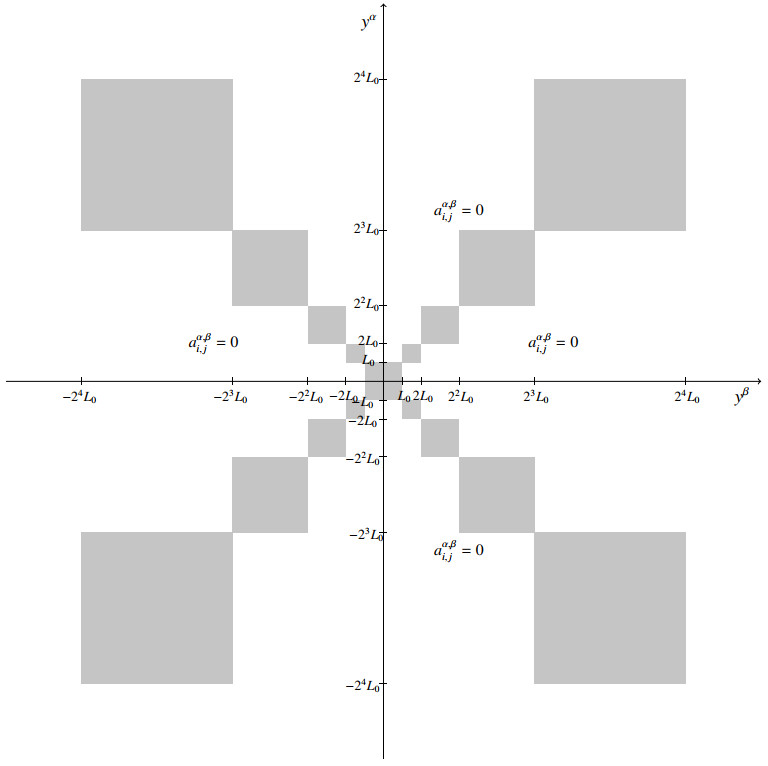
(A″3) (support of off-diagonal coefficients contained in the union of a geometric progression of squares) if aα,βi,j(x,y)≠0 and there exists t∈N∪{0} such that 2tL0≤|yα|<2t+1L0, then it holds also 2tL0≤|yβ|<2t+1L0.
Let us remark that from assumption (A2) it follows that we have degeneracy in the α equation when uα is large. In [13] is treated for N=2 the case in which degeneracy in the α equation arises when uβ is large, with β≠α.
Note that (A′3) and (A″3) are always fulfilled when α=β. On the contrary, when α≠β, (A3) forces the support of aα,βi,j(x,y) to be contained in the union of infinite squares along the diagonals, see grey region in Figure 1.
On f we assume that it belongs to the Marcinkiewicz space Mm(Ω,RN), with
For the convenience of the Reader, we recall the definition of Marcinkiewicz spaces, also known as weak Lebesgue spaces.
Definition 2.1. Let m be a positive number. We say that a measurable function f:Ω→R belongs to the Marcinkiewicz space Mm(Ω,R) if there exists a positive constant c sucht that
in such a case we set
Mm(Ω,RN) is the space of functions f=(f1,…,fN) such that fi∈Mm(Ω,R) for each i. Moreover Mm(f)=∑Nα=1Mm(fα).
We recall some properties on Marcinkiewicz spaces:
and
For more details on Marcinkiewicz space see [10,68].
Let us explicitly remark that, being 0<θ<1, from (2.2) it follows that
Under our set of assumptions we prove the following theorem:
Theorem 2.1. Assume (A0), (A1), (A2), (A3), with n≥3. If f∈Mm(Ω,RN), with 2nn+2−θ(n−2)<m<n2, then there exists u∈W1,20(Ω,RN)∩Mr(Ω,RN), with
weak solution of the problem (1.1), that is such that
for all φ∈W1,20(Ω,RN).
3.
Approximation and estimates
We set for all k∈N
with
We consider the following family of approximating problems
We want to show the existence of a weak solution for each problem (˜Pk), that is a function uk∈W1,20(Ω,RN) such that
for all φ∈W1,20(Ω,RN).
Let us first show some properties of the coefficients ˜aα,βi,j,k. From assumption (A1) it follows that
Using assumption (A2) we have the following non degenerate ellipticity condition
Now let us show that for all f∈Mm(Ω,RN), with m>2nn+2−θ(n−2), the linear operator
is continuous. Indeed, using Hölder inequality, (2.4) and Sobolev embedding, we have for a suitable constant C>0
and the continuity of F is proved. Therefore we can apply the surjectivity result of Leray-Lions, see [59], and we have the existence of a weak solution uk for the problem (˜Pk), that is, there exists uk∈W1,20(Ω,RN) such that (3.1) holds true for every φ∈W1,20(Ω,RN).
In the next Lemma 3.1, arguing as in [14], we prove that the sequence {uk}k∈N is bounded in W1,20(Ω,RN)∩Mr(Ω,RN). We first recall the following elementary inequalities that will be used in the proof of Lemma 3.1. We have
provided aα,bα≥0 for all α∈{1,…,M} and p>0.
Lemma 3.1. Assume that f∈Mm(Ω,RN) with 2nn+2−θ(n−2)<m<n2 and let uk be a weak solution of (˜Pk). Then the sequences ‖uk‖W1,20(Ω,RN) and Mr(uk,Ω), with r given in (2.5), are bounded by a positive constant which depends only on L0, θ, m, n, N, ν, |Ω| and Mm(f,Ω).
Proof. For any t∈N∪{0} and for L0≥1 given by assumption (A3), we define the following functions
and
We consider as test function in (3.1) the function φt∈W1,20(Ω,RN) defined as
We introduce the sets
For all α∈{1,…,N} we have
where IB(x)=1 if x∈B and IB(x)=0 otherwise. Moreover, using (A″3), we have
Indeed, if aα,βi,j(x,uk(x))=0 or x∉Bαk,2tL0, then the (3.7) is obvious. If aα,βi,j(x,uk(x))≠0 and x∈Bαk,2tL0, that is 2tL0≤|uαk|<2t+1L0, then for (A″3) we have 2tL0≤|uβk|<2t+1L0 so that x∈Bβk,2tL0.
From (3.6), (3.7) and (A2) we have
Then, replacing in the left side of (3.1) the test function (3.5) and using (3.8), we get
Combining (3.9) with (3.1), we get
Using Sobolev's embedding and (3.10) we have
where CS is the Sobolev embedding constant. Summing on α in (3.11) and using (3.10), we have
From (2.4) we have f∈L2nn+2(Ω) and, by Sobolev immersion, we have also φt∈L2∗=L2nn−2. Then, using the Hölder inequality with exponents 2nn+2 and 2nn−2=2∗ and applying (2.3) to the function |fα|2nn+2∈M(n+2)m2n(Ω), we deduce for all α=1,…,n
From (3.12) and (3.13) it follows that
where C1 is a constant depending only on Cs, ν, Mm(f,Ω).
Now, using last inequality and (3.3), (3.4), (3.2), we have
Therefore
Since φαt=T2tL0(G2tL0(uαk)), for all t∈N∪{0}, we have
Then, summing on α and using (3.2) we have
From (3.14) and (3.15) it follows that
and then
From the last inequality and using (3.3) and (3.2) we have
Therefore
where C2 is a positive constant depending only on N, n, CS, ν and Mm(f,Ω).
Let us set
and let us remark that for r given in (2.5) the following equality holds
Now, for all h>0 and for r given in (2.5), let us define
For all t∈N∪{0}, it follows from (3.16) that
Therefore we obtain that there exists a constant C3=max(1,2rC2)≥1, depending only on N, n, CS, ν, Mm(f,Ω), θ and m such that, for all t∈N∪{0}, we have
and, arguing by induction, it follows that
Being γ<1 and ρ(L0)≥0, the elementary inequality
holds. Using the notation C4=C∑+∞h=0γh3=C11−γ3 and putting together (3.19) and (3.20), we have
where C4≥1 is a constant depending only on N, n, CS, ν, Mm(f,Ω), θ and m.
Using (3.21), we want to prove that there exists a constant C5 depending only on N, n, CS, ν, Mm(f,Ω), θ, m, L0 and |Ω| such that
Indeed, for h∈[L0,2L0], we have
For all h≥2L0 there exists s∈N and w∈[L0,2L0) such that h=2sw. Then, using (3.21) and (3.23), we have for all h≥2L0
From (3.23) and (3.24) follows (3.22).
For all h≥L0, using (3.22), we have
for h∈(0,L0) we have
Then, setting C6=max(C5,N|Ω|Lr0), from (3.25) and (3.26), we get
proving the boundness of the sequence {uk}k∈N in Mr(Ω).
It remains to prove that the sequence {uk}k∈N is bounded in W1,20(Ω,RN).
From (3.10), for all t∈N∪{0}, we have
Now we estimate the right hand side of (3.27).
Observing that |φαt(x)|≤2tL0, for all x and for all t∈N∪{0}, and using (2.3), we have
Summing on α=1,..,N the previous inequality, by (3.2), the definition of ρ in (3.18) and (3.22), we get
From this inequality it follows that
Since 2nn+2−θ(n−2)<m<n2, it results that θ+1−r(1−1m)<0 and the series in the right side of the last inequality converges; we have
where C7 is a positive constant depending only on n,N,m,θ,ν,Mm(f,Ω),|Ω|,CS,L0.
Now, let us prove that ∑Nα=1∫{|uαk|<L0}|Duαk(x)|2dx is bounded.
To this aim we use ψ=(ψ1,...,ψN)=(TL0(u1k),...,TL0(uNk)) as a test function in the weakly formulation (3.1) of problem (˜Pk). Observing that
where Bαk,0={x∈Ω:0≤|uαk(x)|<L0}, we have
From (A′3), we get
Combining (3.30), (3.31) and (A2), we deduce that
From (3.32) and (2.3), it follows that
Therefore, combining (3.27), (3.29) and (3.33), we have
where C8 is a positive constant depending only on n,N,m,θ,ν,Mm(f,Ω),|Ω|,CS,L0, and the boundedness of uk in W1,20(Ω,RN) is proved.
Proof of Theorem 2.1
Proof. Let uk be a solution of (˜Pk). Lemma 3.1 states that the sequence of {uk} is uniformly bounded in Mr(Ω,RN) and in W1,20(Ω,RN). Then there exists a positive constant C such that Mr(uk,Ω)≤C and ‖uk‖W1,20(Ω,RN)≤C for all k∈N. Being {uk} bounded in W1,20(Ω,RN) there exists a subsequence {ukλ} weakly converging in W1,20(Ω,RN) to a function u∈W1,20(Ω,RN). Moreover, by Rellich-Kondrachov embedding Theorem, Sobolev space W1,20(Ω,RN) is compactly embedded in L2(Ω,RN); then, there exists a subsequence, not relabeled, also in the sequel, strongly converging to u in L2. From L2 convergence we get pointwise convergence almost everywhere, up to a further subsequence. Briefly we write
Now, we pass to the limit as λ→+∞, in the weak formulation of problem (˜Pk), written when k=kλ, to prove that u solves problem (2.6). More precisely, we verify that for all φ∈W1,20(Ω,RN)
To this aim, we estimate
We obtain the result by proving that Ikλ,IIkλ,IIIkλ tend to zero as λ→+∞. We start to estimate Ikλ. Using Hölder inequality and boundedness of the sequence {ukλ} in W1,20(Ω) we have
For any i,j=1,…,n and for any α,β=1,…,N, using pointwise convergence in (3.34) and continuity of functions y→aα,βi,j(x,y) we have that
moreover from (A1) we get
therefore, by dominated convergence theorem, we obtain that
The above limit and (3.35) imply that Ikλ tends to zero as λ→+∞.
Observing that uβkλ⇀uβ in W1,20(Ω), for any i,j=1,…,n and for any α,β=1,…,N, we have
hence IIkλ tends to zero as λ→+∞.
Using Hölder inequality and (3.34), it results that
Passing to the limit as λ→+∞, we obtain that IIIkλ tends to zero and the proof is completed.
Acknowledgments
We acknowledge the support of GNAMPA, INdAM, MIUR, UNⅣAQ. S. Leonardi has been supported by Piano della Ricerca di Ateneo 2020-2022–PIACERI: Project MO.S.A.I.C. "Monitoraggio satellitare, modellazioni matematiche e soluzioni architettoniche e urbane per lo studio, la previsione e la mitigazione delle isole di calore urbano", Project EEEP & DLaD. S. Leonardi is member of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM), codice CUP_E55F22000270001.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: