1. Introduction
Renewable energy sources produce clean energy with no emission and provide less dependency on limited fossil fuel resources. Microgrid (MG) provides an efficient power system structure to manage, control and integrate renewables as Distributed Generators (DG) within utility grid [1,2]. MG has two modes of operation, grid-connected and islanded [3]. However, the presence of renewables at MGs may cause problems of stability due to their high degree of uncertainty resulting in voltage fluctuations and low power quality [4]. The phenomena of voltage fluctuations is more evident for islanded MGs where power flow is limited. Uncontrolled power flow could negatively affect all MG components [5].
Flexible AC Transmission Systems (FACTS) [6] are devices that enhance the efficiency and performance of power systems. FACTS devices have been implemented successfully to improve the overall performance of MGs [7]. Among FACTS devices, Static VAR Compensators (SVCs) are widely used as reactive power compensators [8]. They have the ability to respond quickly to load disturbance in order to minimize the effect of transients and maintain acceptable steady state voltage levels [9,10,11]. In literature, the placement of the SVCs and its effect on power system stability have been discussed [12]. References [13,14,15,16,17] discussed SVCs performance dependency on implemented control algorithms that control the flow of reactive power. In [10], PI SVC controller is used to stabilize the load bus voltage. Authors assumed a linear system dynamics and they neglected the nonlinearity and parameter variation of the system. References [13] proposed a control strategy based on energy function. Authors developed two control laws, one for the SVC and the second for thyristor-controlled series capacitor (TCSC). Their control law of SVC was based on the first derivative of the square voltage (power). Hence, the control algorithm can be considered as a simple proportional controller which cannot compensate for parameter variation and nonlinearity. For further improvement, a model reference adaptation mechanism was added to the PI controller [17]. Their proposed algorithm extend the dynamic performance of fixed-gain PI controller over a wide range of operating conditions by implementing a model reference adaptive control (MRAC). Yet, nonlinearity of power system cannot be justified by linear PI controller with adaptation mechanism which can perform well only for smooth nonlinear dynamics. A nonlinear control surface with an adaptation mechanism would present the power system better with fast transient and more stability performance.
Fuzzy Logic controllers (FLC) [18] have a great advantage over conventional control techniques for the following reasons: 1) They can present nonlinear mapping surface by membership functions and inference mechanism inherited in their structure; 2) They are independent on mathematical modeling and require only behavioral performance to set out linguistic variables and rule basis; and 3)They are better to present system uncertainties. In [19,20,21], a fuzzy controller is implemented to control, activate and deactivate the number of Thyristor Switched Capacitor (TSC), to maintain operational voltage as required. In addition, genetic algorithm is used to find the optimal firing angle of SVC [19]. The system has no ability to adapt for load variation as fuzzy controller has no adaptation mechanism and genetic optimization cannot be implemented online. Moreover, the simulation conducted was based on a connected mode MG. Hence, control algorithm with SVC has less evident effect on system performance due to presence of utility grid that has greater ability to compensate for load variation. Authors in [22] designed two parallel controllers, instantaneous reactive power compensator and fuzzy controller. The fuzzy controller is equipped with rule adaptation mechanism; however, it has the same inputs of the fuzzy controller. Hence, both FLC and its adaptation mechanism can be combined in one controller. Their control algorithm can be considered as a linear controller, presented by instantaneous reactive power compensator, supported by parallel FLC to compensate for system nonlinearity. Yet, the control algorithm has no adaptation mechanism that can
compensate for load variation.
FLC with adaptive capabilities was developed by Procyk and Mamdani [23]. The parameters of the fuzzy controller are subjected to adaptation during system operation to meet a predefined performance under plant parameter variation. Fuzzy model reference learning control (FMRLC)[24,25] uses reference models to describe the required performance to the adaptation mechanism. The term learning reflects the memorizing capability of the fuzzy controller where enhancement in the system performance can be experienced by frequent exposure of the system to the same dynamic range of state variables. The algorithm was successfully implemented to control the speed of induction motor drives [26,27]. Adaptive fuzzy controller for SVC based on Oscillation Energy Function (OEF) was introduced [28]. The mean objective was to design effective SVC fuzzy-logic damping controller for the power system. The authors show enhanced transient performance with less oscillation.
The contribution of this paper is the implementation of a PID-FMRLC in control loop of SVC for islanded mode MG. The proposed control algorithm compresses fuzzy controller subjected to adaptation that is able to compensate for power systems nonlinearity. Hence, the system’s performance can be kept as required during wide ranges of operating conditions. The MG together with the controller represents a linear system that matches the reference model. Moreover, learning mechanism insures updating controller parameters to compensate for load variation within MG. With its high sensitivity to load disturbance, islanded MG is used as challenging power system to verify the proposed control algorithm dynamic and stability performance.
This paper is organized as follows. Section 2 discusses the FMRLC algorithm, section 3 introduces the structure of the case study and simulations are presented in section 4. Conclusions are presented in the last section.
2. Control algorithm
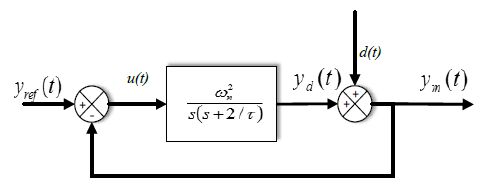
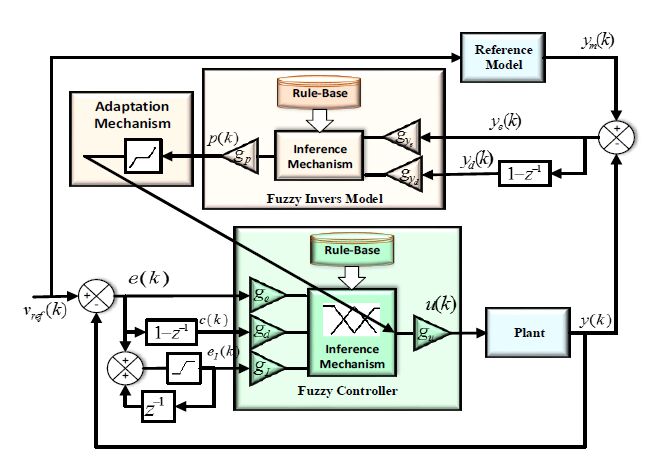
Figure 1 shows the proposed control structure. The algorithm consists of reference model, inverse model, adaptation mechanism, and fuzzy controller. Reference model presents desired achievable performance required to follow by the system. Reference model parameters should be chosen reasonably to avoid instability of learning mechanism[29,30].
A reasonable time constant of reference model can be achieved by observing the behavior of MG for different loads. The reference model is a disturbance rejection 2nd order system as shown in Figure 2. Its forward transfer function is of type one to insure disturbance rejection with zero steady state error and is given by:
|
Yd(s)Ym(s)=ω2ns(s+2/τ)
|
(1) |
where ωn is calculated by the desired overshoot and τ as follow:
|
ωn=1τ√π2+ln2(%OS/100)−ln(%OS/100)
|
(2) |
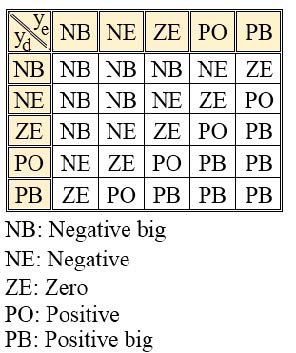
The inverse model is a first order (PD) fuzzy system with rule-base set to describe inverse dynamics of MG. It generates adequate amount of control action that forces the system to follow the reference model. Based on knowledge of system dynamics, fuzzy inverse dynamics was encoded in rule base of the inverse model as shown in Table 1. The inputs to the inverse model are given by:
|
yd(k)=(ye(k)−ye(k−1)T)
|
(4) |
where
y,ym,ye and
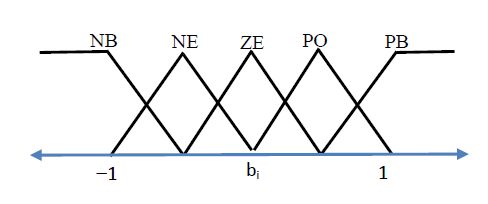
yd are the output of the process, the output of reference model, the error between reference model output and process output, and the derivative of that error respectively. The third part of control algorithm is learning and adaptation mechanism that is responsible for encoding the output of inverse model into the rules at the rule-base of fuzzy controller. The fuzzy controller rules describe the nonlinear control surface that compensates and linearizes the overall system to match the reference model. The adaptation mechanism is also responsible for adapting the control surface to compensate for time varying parameters of connected loads to MG. Triangular membership functions are used for fuzzy controller as shown in
Figure 3 where its centers
bi subjected to adaptation as follow:
|
bi(k)={bminbi(k−1)+Δbi(k)≤bminbi(k−1)+Δbi(k)bmin<bi(k−1)+Δbi(k)<bmaxbmaxbi(k−1)+Δbi(k)≥bmaxΔbi(k)=ηgpp(k)
|
(5) |
where,
η is the learning factor,
gp is the adaptation gain,
p(k) is the output of the inverse model
bmin and
bmax and are the minimum and maximum control action values respectively. Both and can be combined as a one gain (
gp).
Table 1. Rule-base for the fuzzy Inverse model.
The addition of limit values to bi(k) (bmin and bmax) is used to avoid generating control actions exceeding process input limits.
Equation (5) shows that FMRLC algorithm provides both adaptation and learning capabilities. This is due to the fact that adaptation process is independent of inputs of the main fuzzy controller. In addition, adaptation process is seeking a certain performance defined by reference model regardless of MG parameters change. To avoid learning instability, dead band was added to adaptation mechanism according to following equation:
|
bi(k)={bi(k−1)+gpp(k)−pDB≥gpp(k)≥pDBbi(k−1)otherwise
|
(6) |
where
pDB is the dead band limit of the learning process. Note that
ηgp is replaced by
gp in equation (6). The main fuzzy controller is a PID fuzzy controller with inputs described by following equations:
|
eI(k)=T(e(k)+k−1∑i=1e(i))
|
(9) |
Where e,c, and eI are the error between reference input r and the measured output y, its derivative and its integral respectively in the current sample k. (While PD fuzzy controllers are commonly used in control loop of nonlinear systems, it was found that the system with the PD fuzzy controller would possess a large steady state error. A PI fuzzy controller would experience undesired transient performance. Although the PID fuzzy controller increases the dimension of the rule-base matrix (and hence complicate the learning process), it has better performance. The dynamic range that is covered by the membership functions is set to the interval [−1, 1]. The adjustment of the signals dynamic range to dynamic range covered by the membership functions is carried out by the input-output scaling factors gx where x represents the label of the signal at which the gain is placed on.
In order to avoid accumulated large values during transient period from integral part, a limiter is added after digital integrator described by equation (9). Such large values (over the dynamic range of the proper signal) could cause slowdown of the controller performance. The limiter maximum and minimum values are set in order of magnitude of output signal dynamic range.
The activation level of rule primes is given by:
where
i is the index of the rule,
Aj is linguistic value for the input (center of the
ith input membership function i.e.
A0 = negative big,
A1 = negative … etc), and finally,
μ1Aj is membership value of 1st input
Aj linguistic value. Center Of Area (COA) is used for the defuzzification process and is given by:
|
ycrisp=∑Ri=1bisupy{μˆBi(y)}∑Ri=1supy{μˆBi(y)}
|
(11) |
where
ycrisp is the crisp outputs,
R is the numbers of rules at rule base, (
sup (x) denotes supremum value of
μ(x) which can be assumed as the upper bound of the chopped output membership function) and
ˆBi is the implied fuzzy sets for the
ith rules of fuzzy controller. The implied fuzzy set
ˆBi is given by:
where
μBi(y) represents the membership function of the output (a triangle membership function was used). Assuming the use of minimum and maximum function for inference mechanism then:
and hence equation (11) can be rewritten as:
|
ycrisp=∑Ri=1biμiA∑Ri=1μiA
|
(14) |
The stability of conventional and Fuzzy model reference control has been discussed analytically in literature [31,32]. In this paper, the stability of the proposed controller will be examined practically using phase plane and will be presented in section IV.
3. Case study
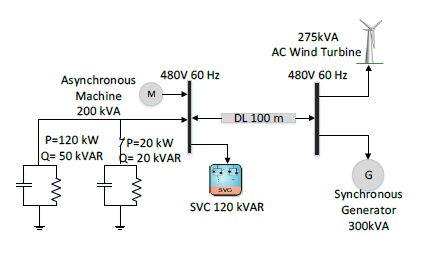
A MG in islanded mode is used to verify the performance of proposed FMRLC algorithm. The structure of MG power system used for the simulation is shown in Figure 4.
The system is composed of PV bus supplied by two sources, wind turbine and asynchronous generator and PQ bus with two loads, linear load and induction motor. The PV and PQ buses are connected via 100 m distribution line. The wind turbine represents a renewable source. The synchronous generator is used as a synchronous condenser that controls the grid voltage by its excitation system during load or/and wind variation [33] and in addition, it generates the required active power to balance between supply and demand. SVC is used to balance reactive power and keep voltage level within MG as required. The induction motor is 200 kW while the linear load consists of 220 kW active load and 100 kVAR capacitive load connected continuously to the bus and 20 kW active load and 20 kVAR capacitive load connected after 2.5 seconds of the simulation.
A 120 kVAR Static VAR Compensator (SVC) is connected at load side. The mathematical model of the SVC is presented in [34]. The simplified SVC phasor model block of the FACTS library of MATLAB/SIMULINK is used for the simulation. The original model of SVC applies PI controller. The controller was modified to switch between PID conventional control algorithm and FMRLC algorithm.
4. Simulation results
The objective of simulations is to verify the enhancement of MG performance in islanded mode using proposed FMRLC against performance of applying a well-known PID controller that is used as a benchmark for comparing different control algorithms. Moreover, to show effectiveness of SVC, performance of the two control algorithms were compared with MG performance without SVC. In this case, asynchronous generator is used as a synchronous condenser and its excitation system controls the grid voltage at its nominal value.
The simulation is conducted using the system described in section 3 for 15 sec. A load change is applied to the induction motor by a repeating pattern. In addition, a variable wind speed from 6 m/s to 16 m/s with 0.5 Hz frequency is applied to the wind turbine. The load and wind speed profiles are shown in Figure 5. The objective of the repeating pattern of load change and wind speed variation is to expose learning algorithm repeatedly to possible variations that could take place within the power system. Hence, the system would form and memorize proper control surface for different operating points. In addition, a linear load has been connected to MG after 2.5 sec to allow MG to operate on its edge of power follow (the load was not connected at start of simulation to avoid MG instability during its transient).
The reference model parameters were calculated from equation (1) and (2). After set of different load experiments, the time constant was set to 0.04 sec. The required OS% is set to 1%, hence, A PID FMRLC was used in control loop of SVC. It was found that PI or PD FMRLC wouldn’t perform adequately as it will be shown in results discussion. Eleven membership functions are used for fuzzy controller and three for inverse model.
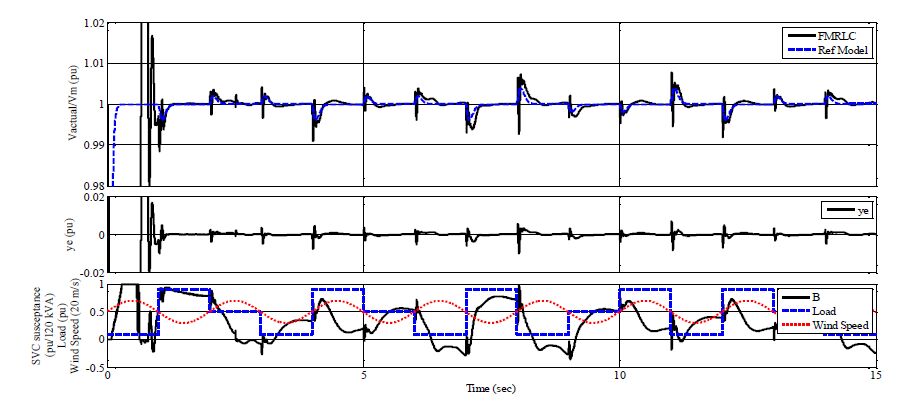
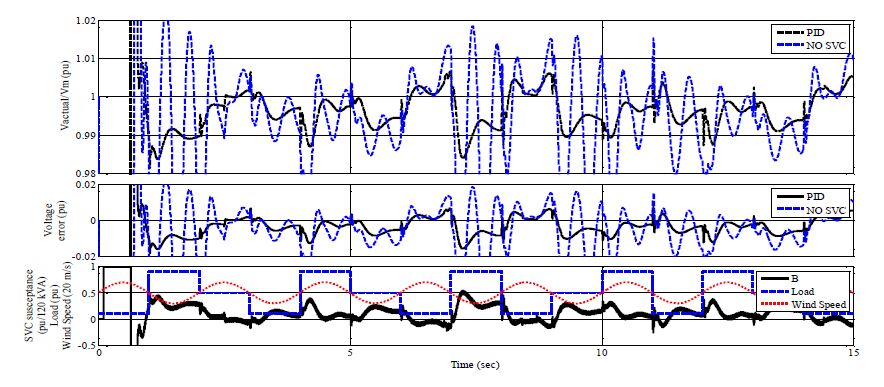
Figure 5 shows simulation result for the proposed PID-FMRLC. Figure 6 shows the same simulation using PID SVC and without SVC. The scales in Figure 5 and Figure 6 are the same for convenience. Top curves, in Figure 5, show bus voltage (pu) for FMRLC (in solid black line) and reference model in (in dashed blue line) and, in Figure 6, for PID controller (in solid black line) and without SVC (in dashed blue line). It can be noted that FMRLC algorithm was able to maintain line voltage to the required level with minimal disturbance compared to both conventional PID controller and simulation without SVC. The transient behavior of the system follows closely the reference model transient. The second curve in Figure 5 shows the error between reference model output and measured bus voltage for FMRLC algorithm. The learning algorithm was able to store information about proper control action during grid transient and recall it to minimize error during the full simulation run. On the other hand, PID controller shows steady performance that does not improve with time as expected as shown in second curve in Figure 6. The grid without SVC has degraded performance.
The bottom curves, in both Figure 5 and 6, show the measured susceptance of the SVC voltage regulator for both FMRLC and PID controller respectively. In addition the load variation of the induction motor and the wind speed are presented (note wind speed is normalized to 20 m/s for convenience). The proposed PID-FMRLC algorithm was able to generate strong control action and deploy the full capacity of SVC to compensate for load disturbance. The PID controller was not able to generate strong control action despite of it operation close to the critical stability region.
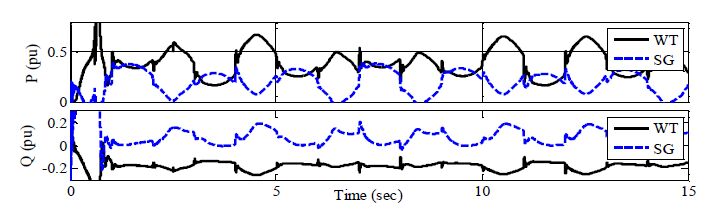
Figure 7 shows the active and reactive power generated from both wind turbine and synchronous generator. It can be noted that synchronous generator compensates for the variation of generated power of the wind turbine (as a result of wind speed variation) and load variation. Due to its slow dynamics, synchronous generator is not able to compensate for fast variation while SVC do (due to its fast response) as can be noted from Figure 5 and 6 (compare between bus voltages in presence of SVC and without SVC).
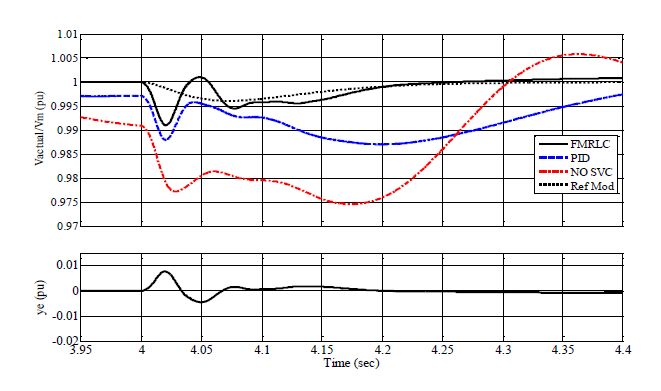
Figure 8 shows the bus voltage and the voltage error in the period from 3.95 sec to 4.4 sec. At time 4 sec, the machine load increased from 0.1 pu to 0.9 pu. The measured overshoot was 0.9% for the FMRLC algorithm while it was 1.2% using the PID controller. Without SVC, the overshoot was 1.8%. The voltage settle within 5% of its maximum deviation from desired bus level after 0.25 sec (four to five times the time constant) for the FMRLC while it takes 2.3 sec with the PID controller.
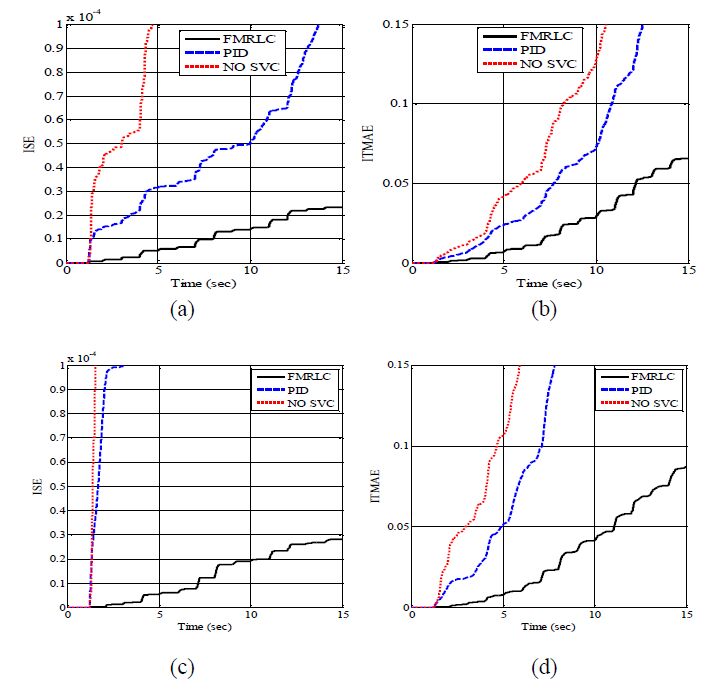
Figure 9 shows the Integral-of-Time Multiplied Absolute Error (ITMAE) and integral square error (ISE) for the three cases for 15 sec simulation. The measurement of both error parameters (ITMAE and ISE) was performed after the 1st 1.2 sec of simulation to avoid building high values during MG transient operation that would hide the details of system performance during the rest of simulation period. The performance indices are applied to MG for two cases, (1) no wind speed variation (shown in Figure 9(a) and (b)) and (2) with wind speed variation (shown in Figure 9(c) and(d)).
While the ISE measures the system oscillation and steady state error, ITMAE measures the system performance improvement with time by giving error at later control stage more significance than error at early control stage. The curves show that the FMRLC is outperforming PID controller. FMRLC keeps MG performance even with wind speed variation that affect operating conditions of MG. PID controller has larger slope for the ISE and exponential rising curve for the ITMAE (no improvement of performance with time indicating no learning capabilities). Without SVC, both indicators show detuned performance. MG performance with wind speed variation processes a total detuned performance when applying PID and without SVC. Table 2 shows a summary of performance indices for the two control algorithms and the MG without SVC that were indicated before.
Table 2. Performance indices of the simulation.
| Overshoot (OS%) | Settling time (Ts sec) | ITMAE | ISE |
| FMRLC | 0.9 | 0.25 | 0.066 | 2.35 × 10-5 |
| PID | 1.2 | 2.3 | 0.275 | 1.2 × 10-4 |
| No SVC | 1.8 | - | 0.9 | 8 × 10-4 |
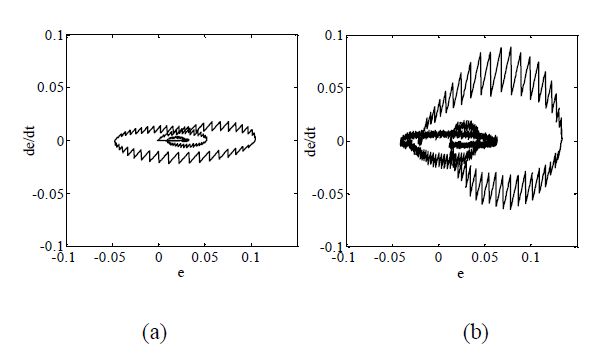
For stability investigation purposes, Figure 10 (a) and (b) introduce the phase plane for PID-FMRLC and PID controller respectively. It can be noted that both control algorithm provides asymptotically stability that approaches the equilibrium point however PID-FMRLC is more stable than the PI controller.
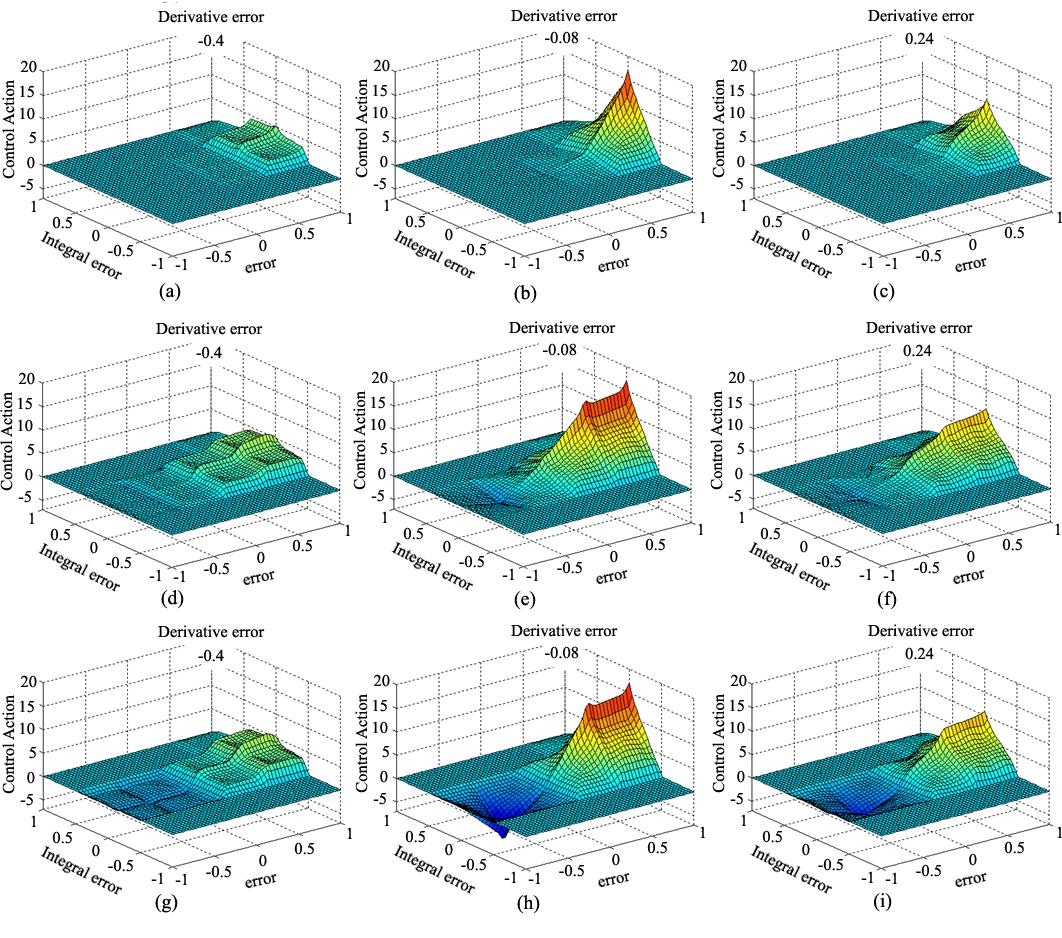
Figure 11 shows the FMRLC control surface. The control surface of the system is four-dimensional where e,c, and eI represent the controller inputs and y represents the controller output. To visually demonstrate this surface, the control surface between e, eI (as inputs) and y as an output with different values c of is presented. The objective of presenting control surfaces is to verify nonlinear relationship between the controller inputs and output and to study the effect of controller adaptation and training mechanism on control relations. Figure 11(a), (b), and (c) present the control surface after 0.2 seconds of training for derivative error −0.4, −0.08 and 0.23 respectively. Figure 11(d), (e) and (f) present the same control surface after 5 sec of training, while (g), (h) and (I) present the same control surface after 10 sec of training.
It can be noted that at the first 0.2 seconds, the adaptation and training mechanism is able to form the control surface using transient information. However, Figures from (g) to (i) clearly show that the more the system is subjected to load variation the more the adaptation and learning mechanism is able to modify the control surface. The adaptation and learning mechanism adequately match the desired performance given by the reference model and encode all the transient behavior of the system into control surface. After 15 sec of simulation, the control surface (not presented in Figure 10 to avoid repetition) is very close to the one achieved after 10 sec of training. This confirms that whenever the system is subjected to repeated load pattern, adequate control action will be generated and no more learning or adaptation is required. Comparing the control surface to the simulation results shown in Figure 5, it can be noted that most of control effort were positive (injecting reactive power form SVC to MG) which match the formulation of the control surface that built large positive control surface with moderate negative one.
Figure 11 confirms the nonlinearity of the control surface and validates the results presented in Figure 9 and Table 2 that shows superior performance of proposed control algorithm over conventional linear PI controller. Moreover, Figure 11shows that the dynamic range of integral error is limited between the interval [−0.5 0.5]. This is due to the selection of the scaling gain of the integral action in addition to the limiter that is used to avoid accumulation of large values during transient period.
Indeed the addition of the derivative error to the control action enhances the system performance. This can easily be concluded by revisiting Figure 11 and comparing the difference in nonlinearity of the control surface for different values of . Hence, the proposed controller achieves more accurate results compared to conventional PID controller that is commonly used to control the SVC voltage regulator, even in islanded mode MG that has been rarely tested in recorded research.
5. Conclusion
A fuzzy model reference learning control algorithm has been implemented to control SVC voltage regulator for MG operating in islanded mode. The design of reference model was conducted based on aggregated active and reactive power flow of MG. The MG was subject to load change by load variation of 200 kVA induction machines (nonlinear dynamics). A MG in islanded mode is used as a case study to represent a challenging control case where power flow is limited and large disturbance can cause severe detuned performance and voltage instability. Moreover, a linear load was connected after MG transient to force MG to operate on the edge of its power flow. The performance of FMRLC was compared to conventional PID controller and to MG without SVC. Both IMTAE and ISE are used as a performance indices. The simulation results show an outstanding performance of FMRLC. It is not only able to compensate for load variation but also improves its performance during the learning process.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: