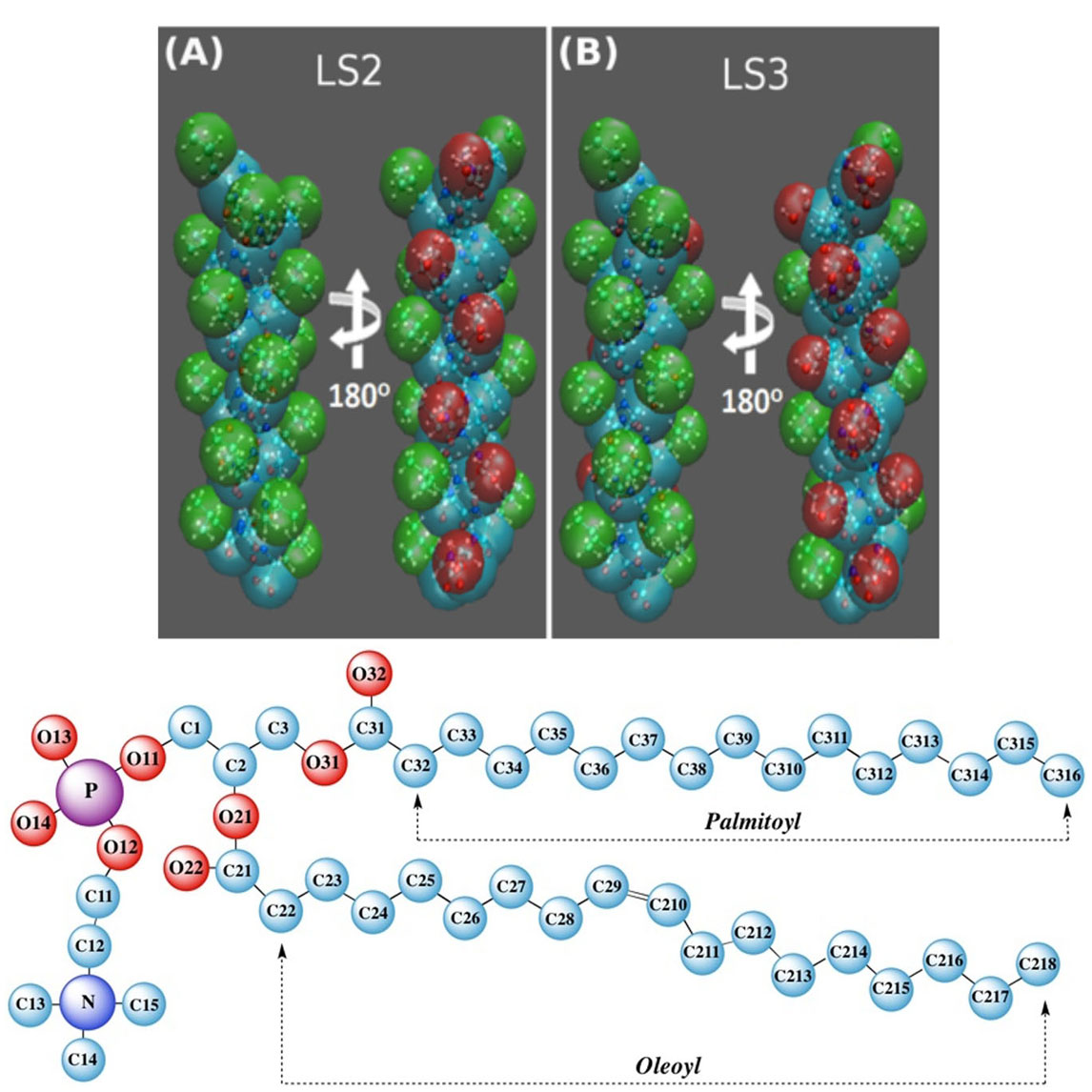
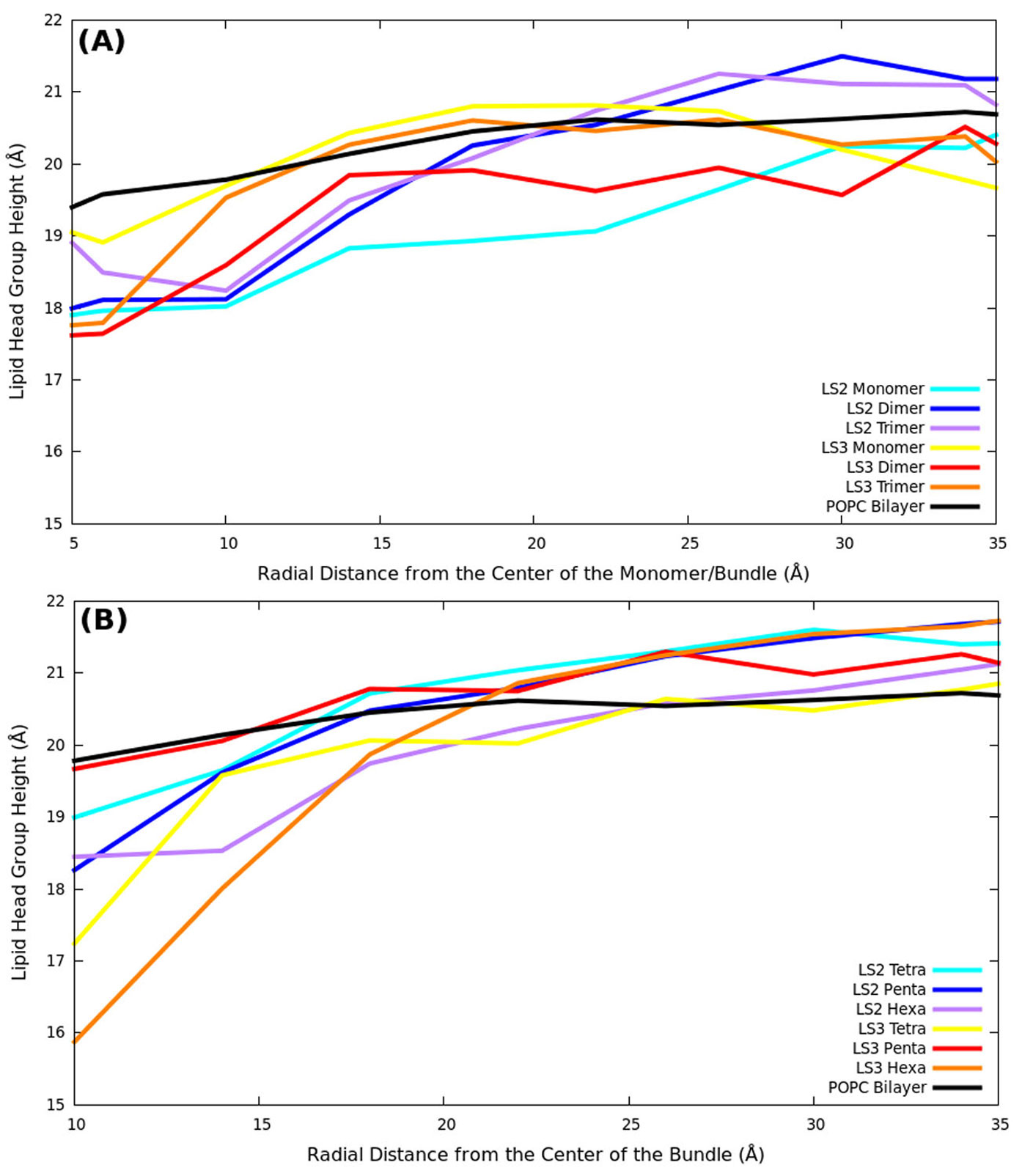
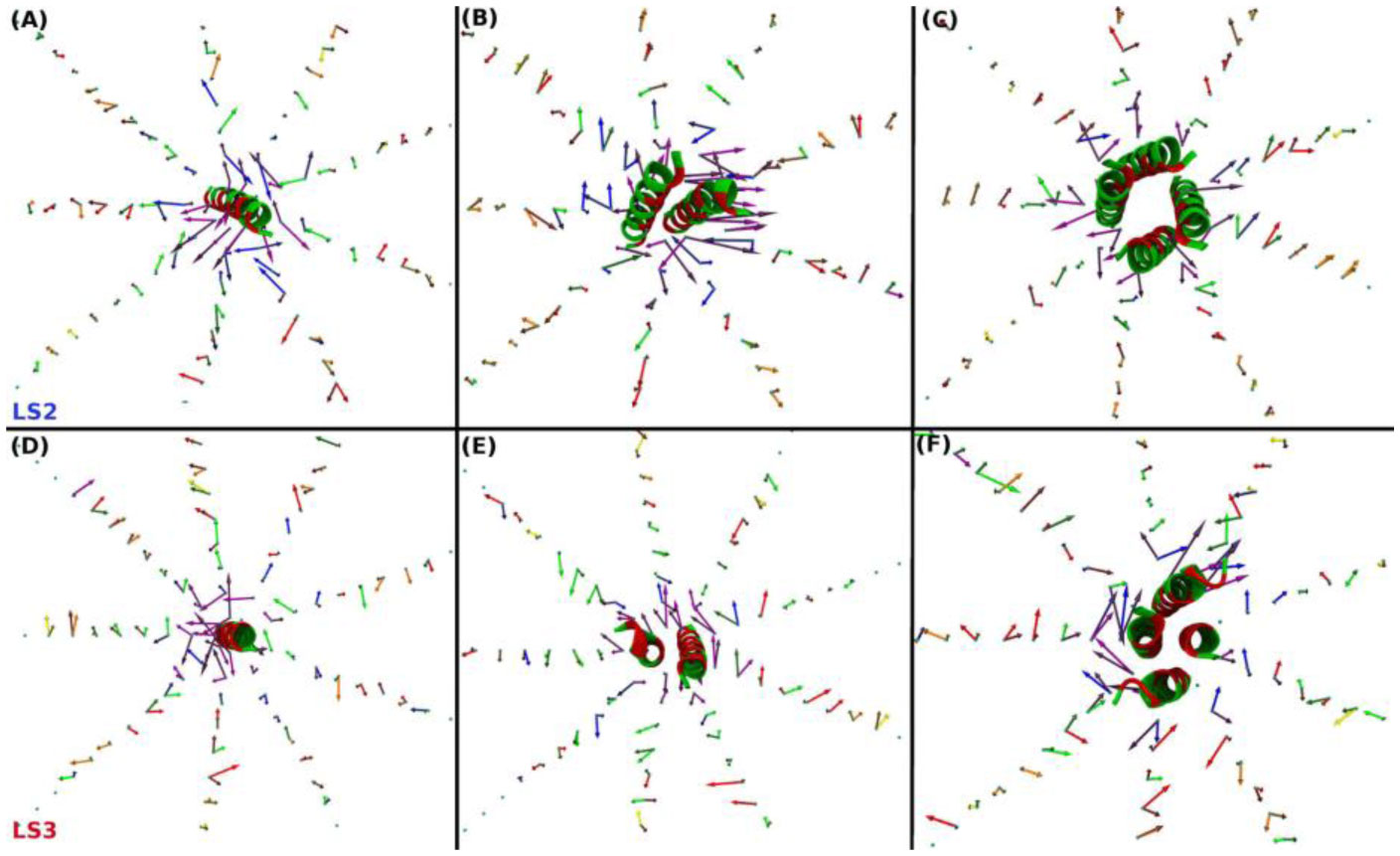
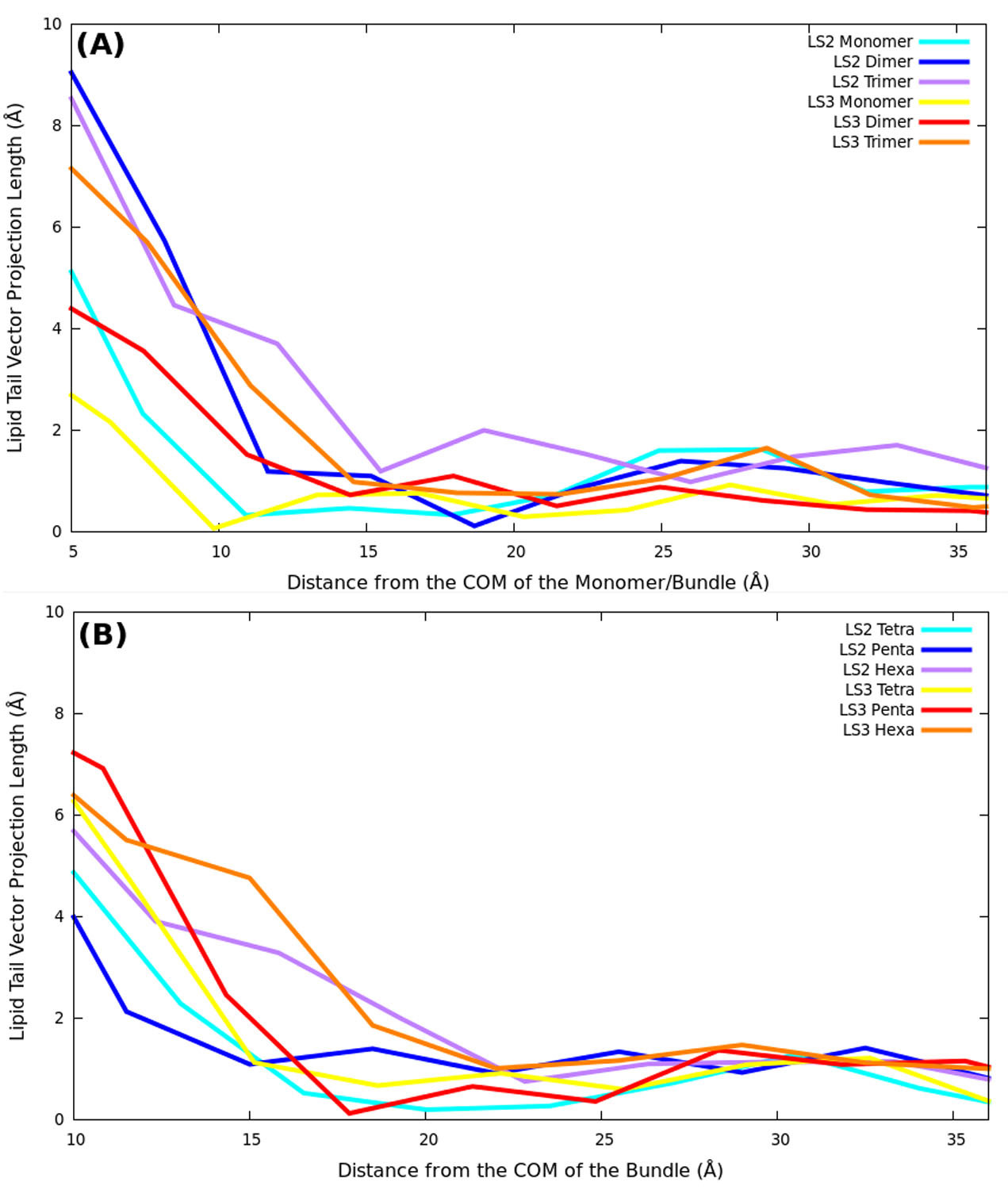
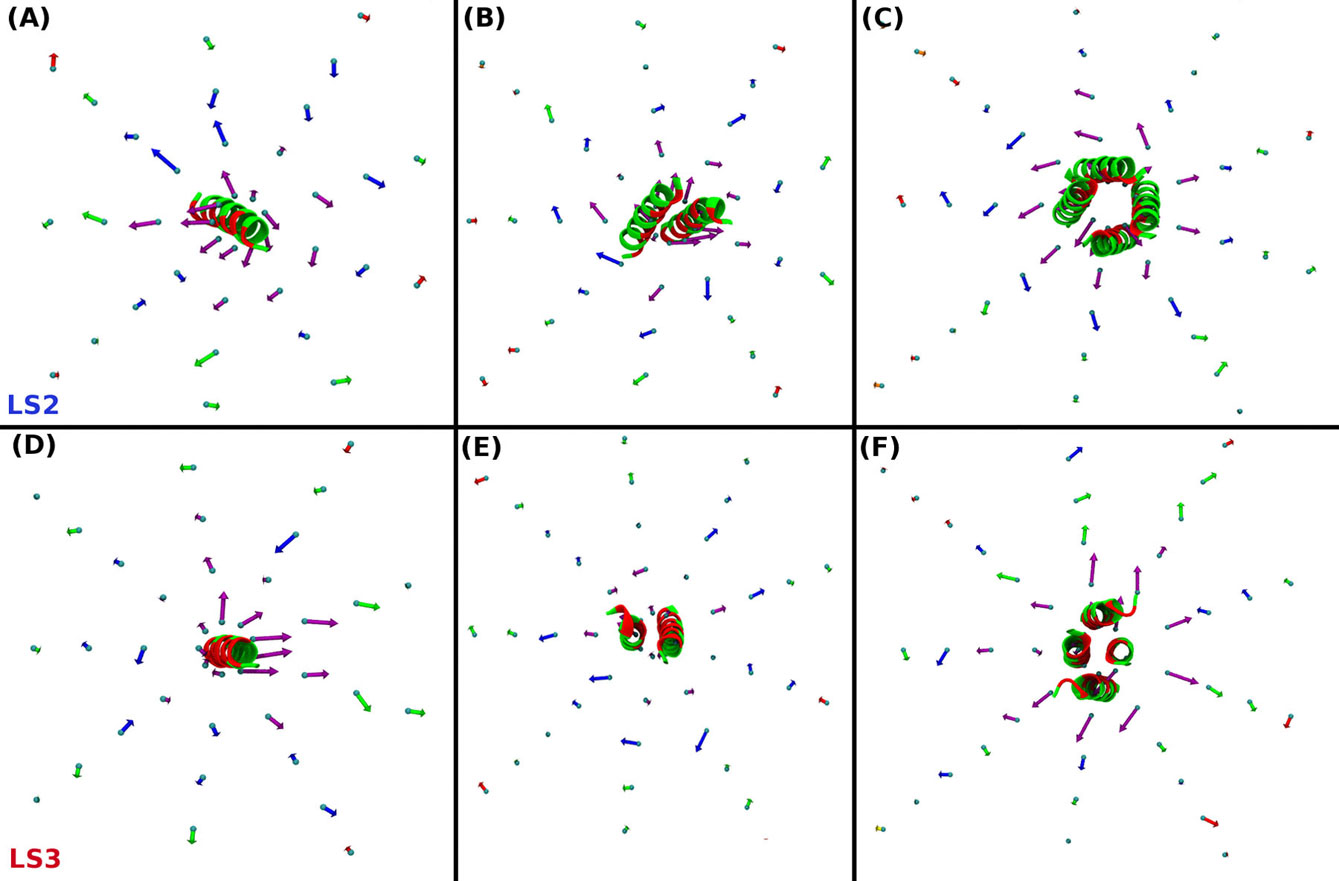
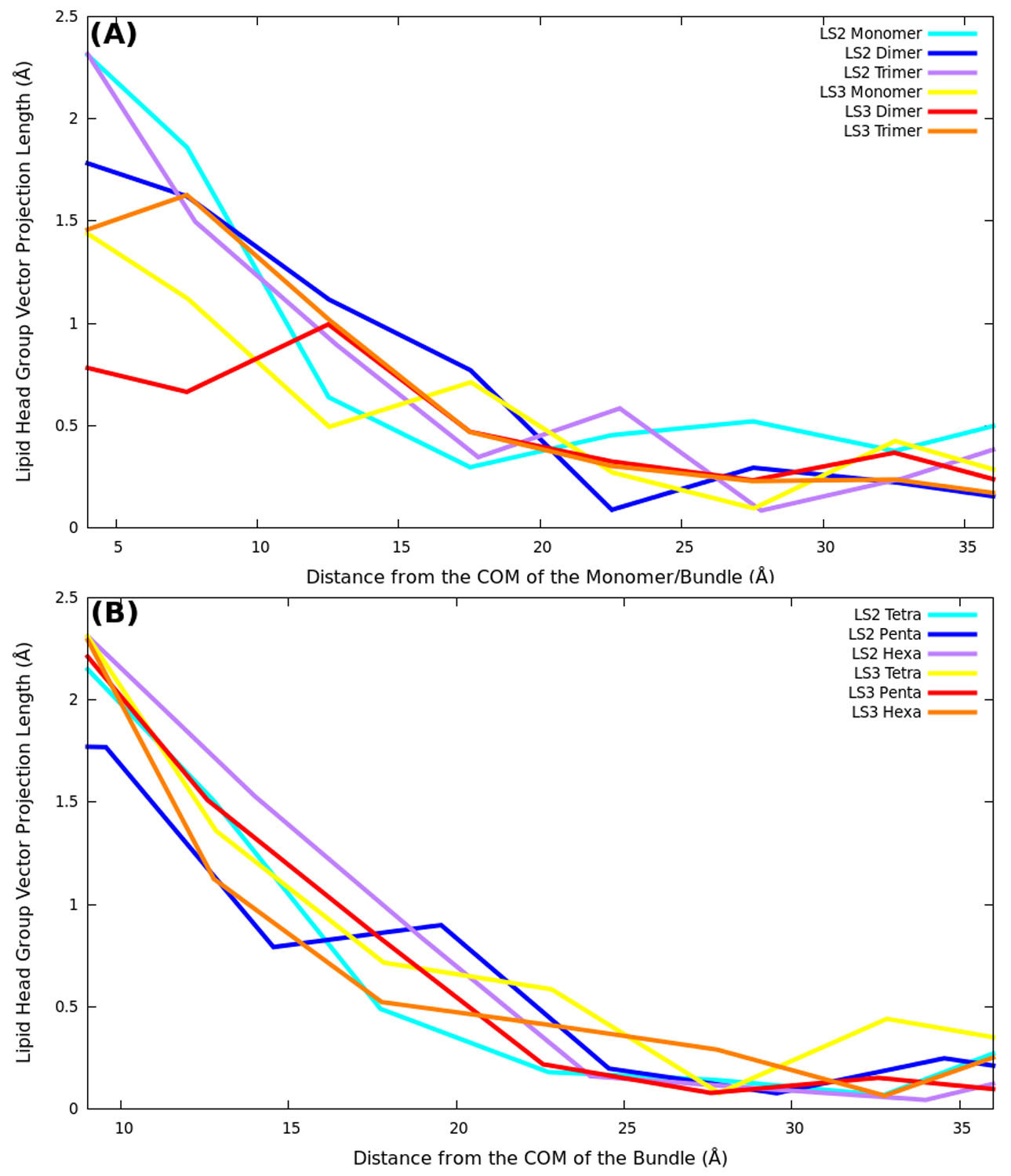
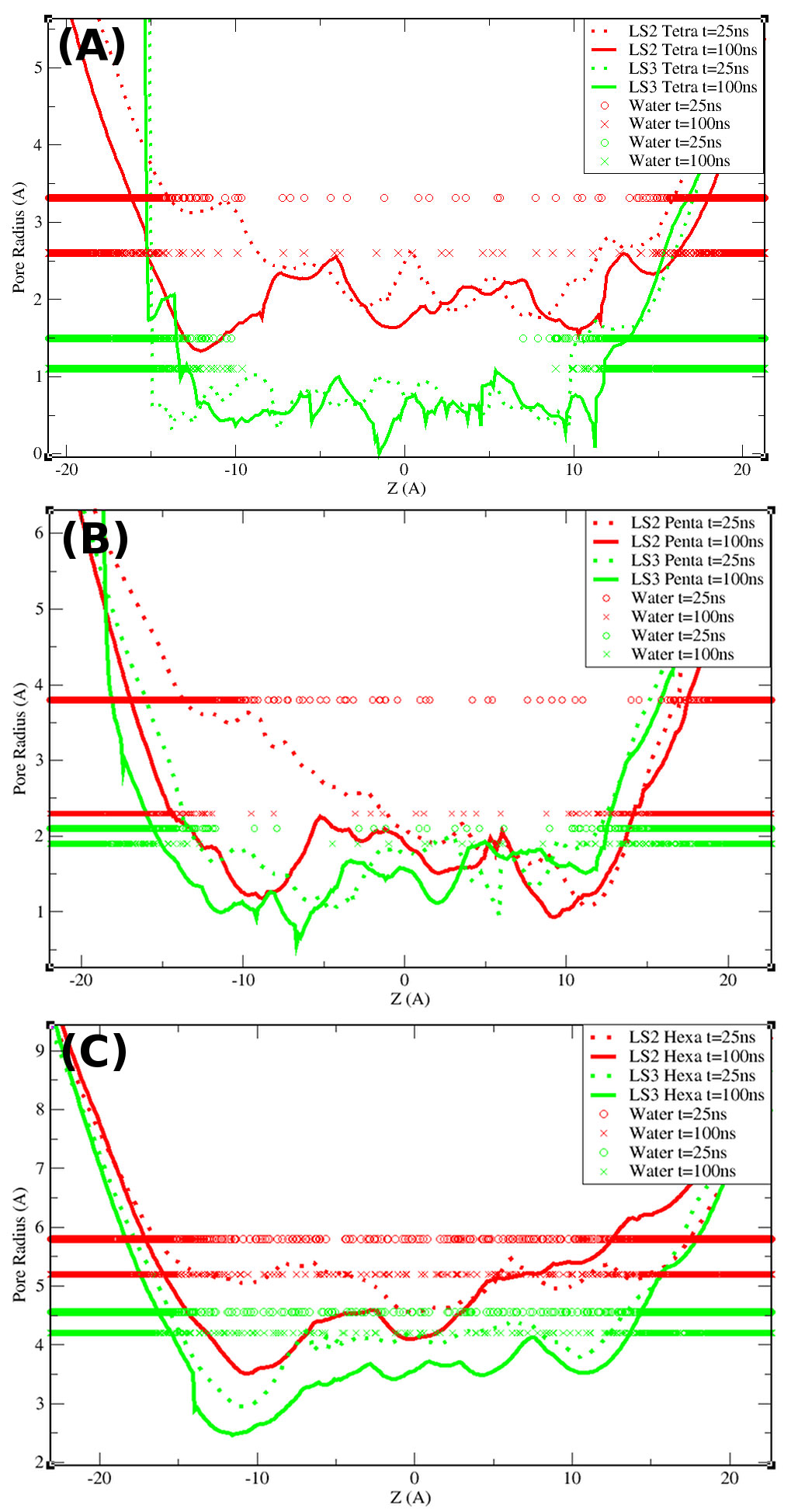
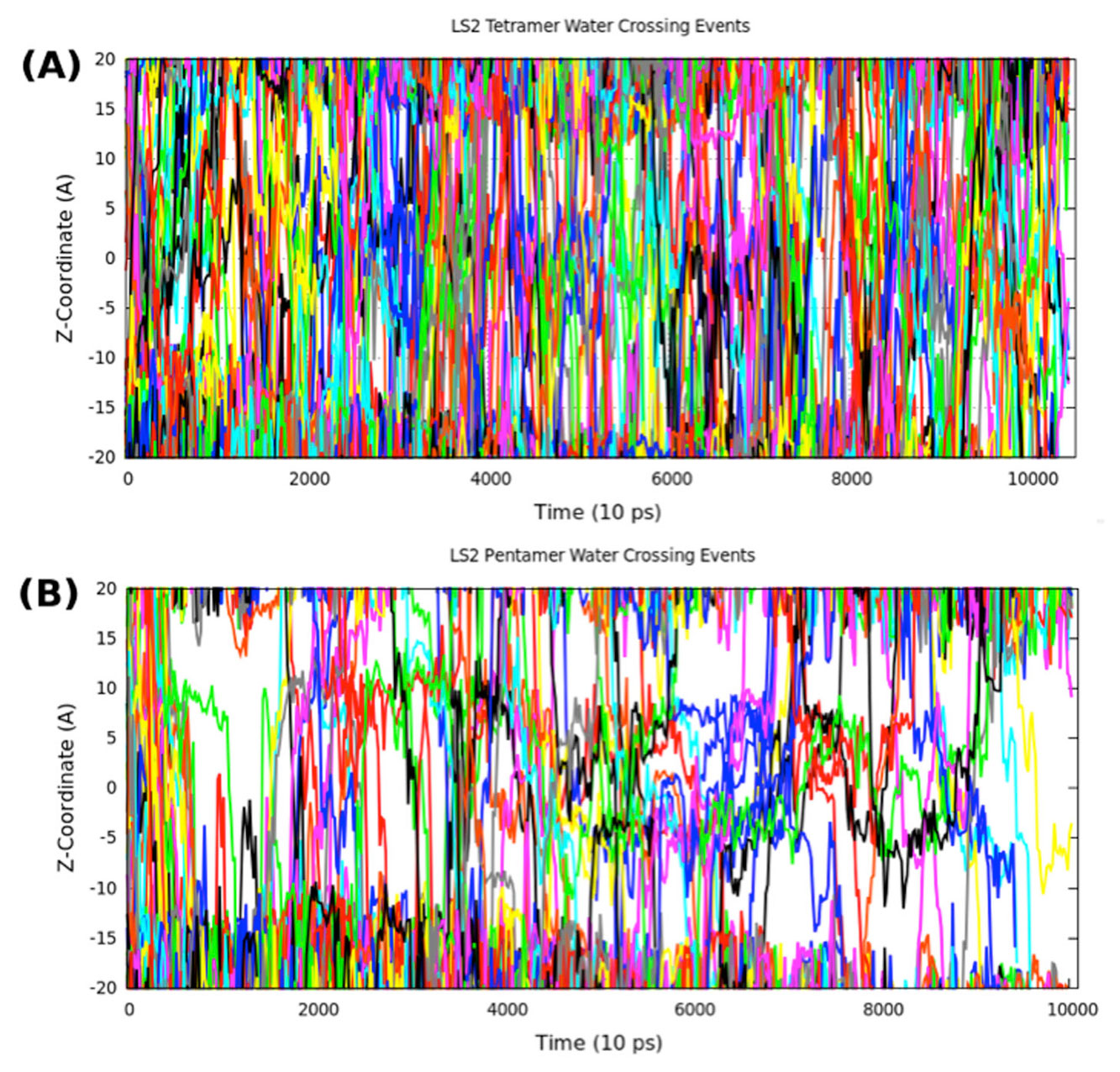
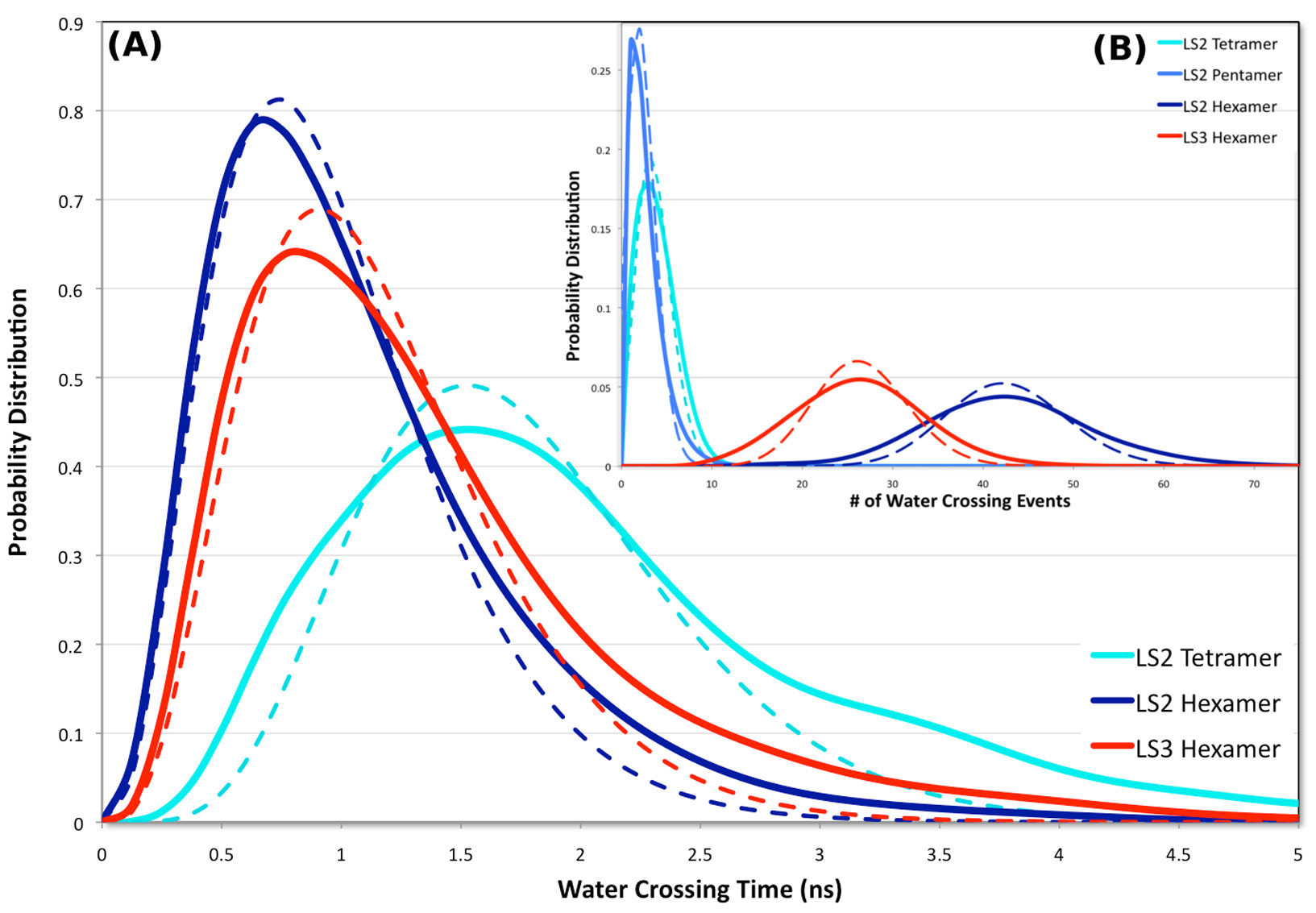
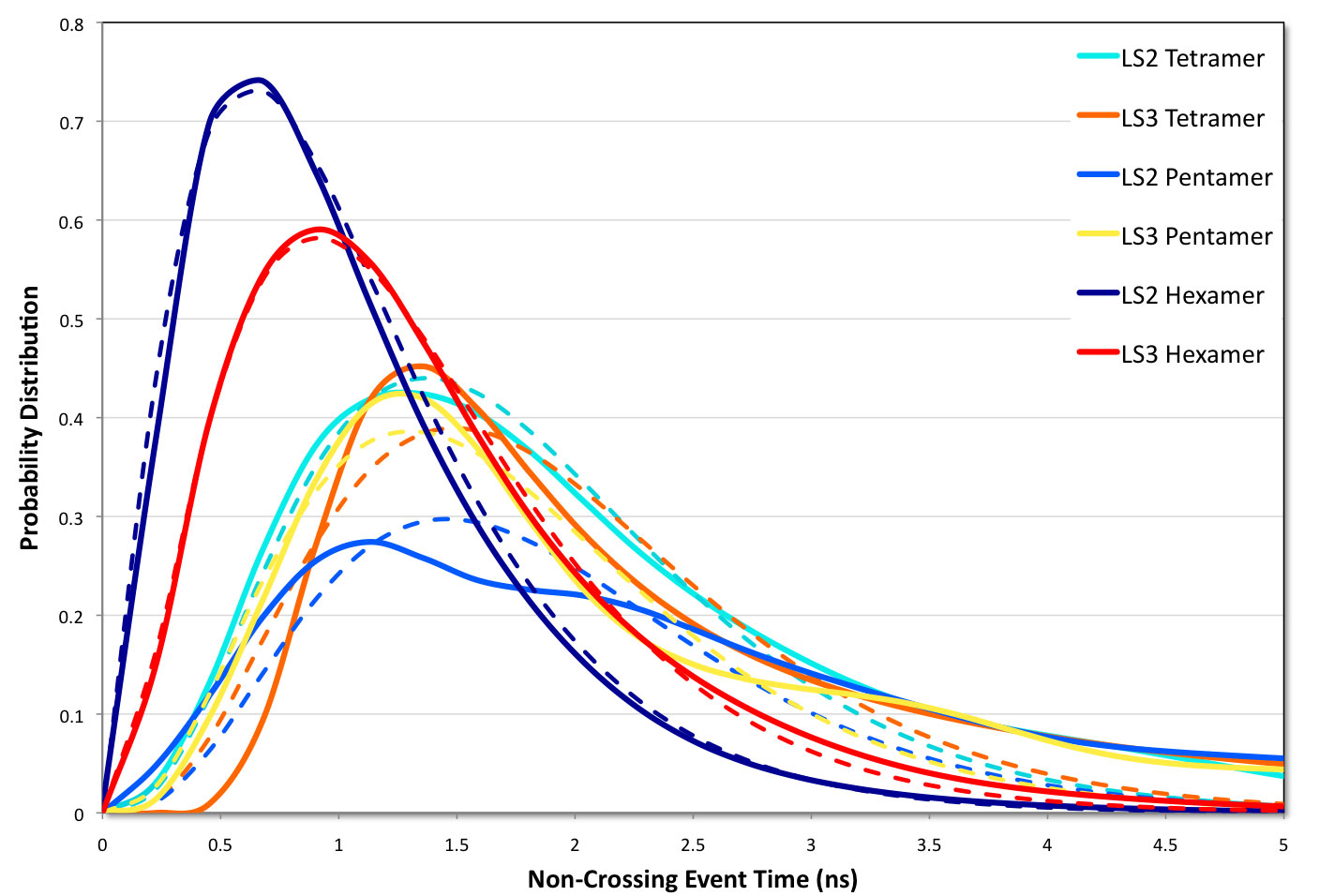
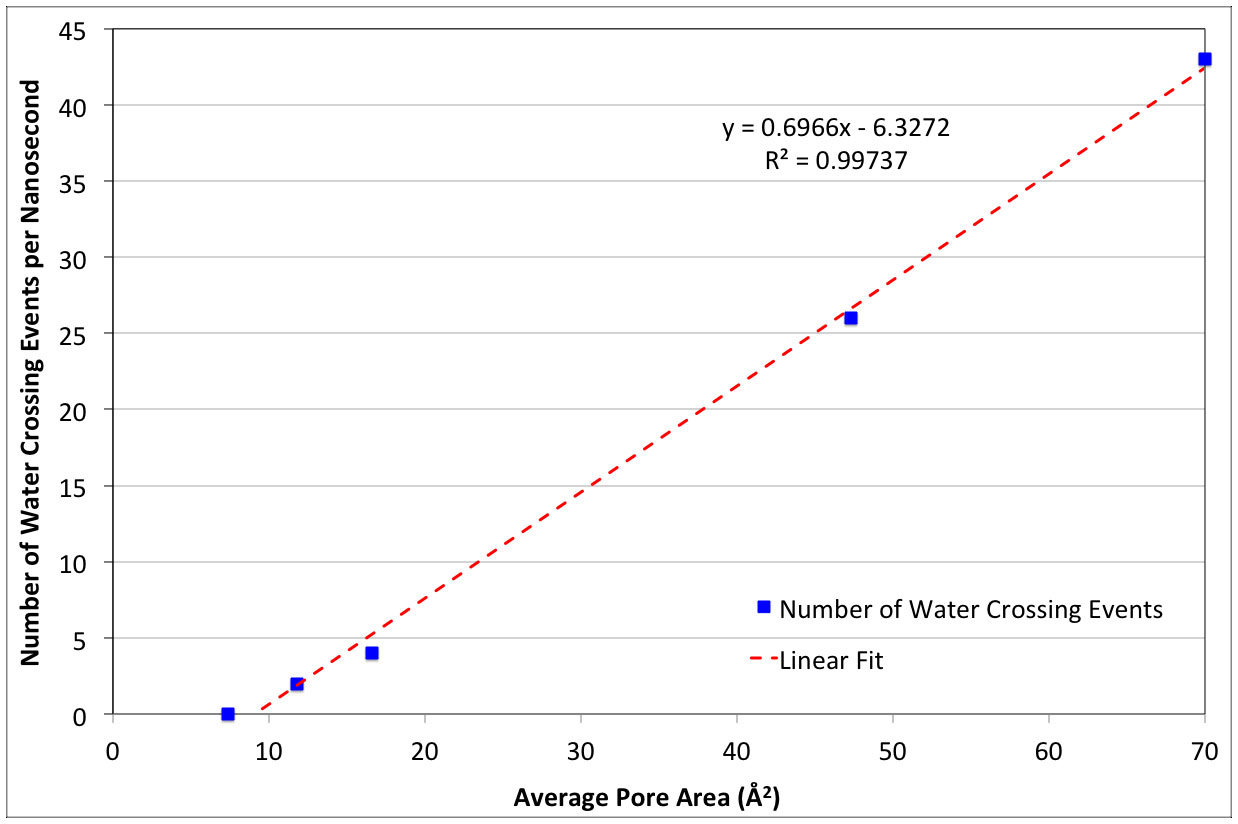
Molecular dynamics study of homo-oligomeric ion channels: Structures of the surrounding lipids and dynamics of water movement

1.   Introduction

Shells are three-dimensional bodies with one dimension that is largely smaller than the others. This geometric class of bodies includes plates, the relaxed shape of which is flat, and thin films, characterized by vanishing thickness. Such geometric features suggest to represent shells by looking at their middle surface only, with the proviso of assigning to each point of such a surface information on the through-the-thickness behavior. Every point of the middle surface is thus endowed with degrees of freedom that are additional to those natural for a point in $ 3D $ space; they summarize the through-the-thickness behavior in a way rendered precise in each specific model. The variability of possible choices generated a number of models, each implying peculiar analytical problems. However, pertinent analyses appear in a sense more manageable than those based on looking at shells as genuine three-dimensional bodies. A related question concerns the rigorous justification of such approximate models. In the elastic case, non trivial relevant results are available. For them, the energy scaling with the thickness plays a crucial role (pertinent analyses are in reference ^[10]; see also ^[9,16,21] on this matter).

In 1958 ^[8], Jerald LaVerne Ericksen and Clifford Ambrose Truesdell III resumed the 1909 theory by Eugène and François Cosserat, noticing that Cosserat's surfaces were an appropriate ground for models of beams and shells. Such surfaces are endowed with out-of-surface vector field. Every element of this field is in principle free to rotate independently of its neighbors, along any deformation, but constrained to avoid falling within the tangent plane to the surface at each point. In this way, looking at shells, one considers at each point on the middle surface any out-of-middle-surface material fiber as a rigid body. Of course the scheme can be further enriched but also reduced, as, for example, when we consider such an additional vector field to coincide with the fields of normal to the middle surface that we consider to be smooth.

This last choice is the one that we adopt in the analyses presented here. With it we avoid considering through-the-thickness shear. We have however the advantage to look at the deformed shell as the Gauss graph of a smooth surface. Such a graph is the set of pairs $ (y, \nu(y)) $, where $ y\in\mathbb{R}^{3} $ is a point over the deformed surface and $ \nu(y) $ the pertinent normal to the surface itself. Of course, with $ u $ a deformation from $ \Omega $, a bounded domain in $ \mathbb{R}^{2} $, into $ \mathbb{R}^{3} $, we have a map $ \Phi_u $ assigning to each $ x\in\Omega $ the pair $ (u(x), \nu_{u}(x)) = (y, \nu(y)) $. In such a setting, we consider an elastic shell with an energy given by

where $ {\mathop{{\rm{adj}}}\nolimits}_2\nabla u $ indicates the second-rank minors of $ \nabla u $, $ {{\mathscr{E}}}(u) $ is a potential of external body actions, $ f $ a convex function, and $ |D\Phi_u(x)|^2 = |\nabla u(x)|^2+|\nabla {{\nu}_u}(x)|^2 $ (in (1.1) unitary dimensional constants are left understood, for the sake of simplicity). With this energy we account for bending and in-tangent-plane stretching and shear. We leave a part out-of-tangent-plane shear and thickness stretching, the latter due to Poisson's effect.

We prove here existence of minimizers for such an energy in terms of currents carried by Gauss graphs. For this reason we speak of our result as describing weak deformations for shells. In the proof we adopt minimizing sequences of deformed shells with non-vanishing thickness. Physics suggests the existence of at least subsequences of this type. Roughly speaking, under elongation in the middle surface tangent plane, Poisson's effect does not allow a reduction of shell thickness below the one of a single atomic layer.

With this type of sequences, we are able to assure that each their element avoids self-penetration of matter. And such a property is stable in the limit process.

2.   Background analytical material

First, we collect some basic aspects concerning currents associated with graphs of approximately differentiable maps. Then, we connect them with Gauss graphs of surfaces in the Euclidean space. Eventually, we recall some structure properties about weak limits of currents carried by Gauss graphs.

2.1.   Currents carried by approximately differentiable maps

The theory of currents is systematically discussed in the two-volume treatise ^[13,14] (see also ^[15]). Here, we limit ourselves to maps $ u: \Omega\to{{\mathbb{R}}}^3 $, where $ \Omega $ is a bounded domain in $ {{\mathbb{R}}}^2 $. We indicate by $ y $ points in $ \mathbb{R}^{3} $ while with $ x $ those in $ \mathbb{R}^{2} $.

For $ u\in L^1(\Omega, {{\mathbb{R}}}^3) $ an almost everywhere (a.e.) approximately differentiable map, we denote by $ \nabla u $ its approximate gradient. Measurable functions into topological spaces with a countable basis can be approximated by continuous functions on arbitrarily large portions of their domain (this is Lusin's theorem). Such continuous functions are what we call the Lusin representatives of the original functions. So, the map $ u $ has a Lusin representative on the subset $ \widetilde \Omega $ of Lebesgue points pertaining to both $ u $ and $ \nabla u $. Also, we have $ {{\mathscr{L}}}^2(\Omega \setminus \widetilde \Omega) = 0 $. We shall thus denote by $ {\mathop{{\rm{adj}}}\nolimits}_2F\in {{\mathbb{R}}}^3 $ the 3-vector given by the $ 2\times 2 $ minors of a matrix $ F\in {{\mathbb{M}}}^{3\times 2} $.

Definition 2.1. We say that $ u $ belongs to $ {{\mathscr{A}}}^1(\Omega, {{\mathbb{R}}}^3) $ if $ \nabla u\in L^1(\Omega, {{\mathbb{M}}}^{3\times 2}) $ and $ {\mathop{{\rm{adj}}}\nolimits}_2\nabla u \in L^1(\Omega, {{\mathbb{R}}}^3) $.

The graph of a map $ u\in{{\mathscr{A}}}^1(\Omega, {{\mathbb{R}}}^3) $ is defined by

where $ \widetilde {u}(x) $ is the Lebesgue value of $ u $. It turns out that $ {{\mathscr{G}}}_u $ is a countably 2-rectifiable set of $ \Omega \times{{\mathbb{R}}}^3 $, with $ {{\mathscr{H}}}^2({{\mathscr{G}}}_u) < \infty $, where $ {{\mathscr{H}}}^k $ denotes the $ k $-dimensional Hausdorff measure. The approximate tangent plane at $ (x, u(x)) $ is generated by the vectors $ {{\mathbf{t}}}_1(x) = (1, 0, \partial_1 u(x)) $ and $ {{\mathbf{t}}}_2 = (0, 1, \partial_2 u(x)) $, where the partial derivatives are the column vectors of the gradient $ \nabla u $, and we take $ \nabla u(x) $ as the Lebesgue value of $ \nabla u $ at $ x\in \widetilde \Omega $. Therefore, the 2-vector

provides an orientation to the graph $ {{\mathscr{G}}}_u $.

Integration of compactly supported smooth 2-forms $ \omega $ in $ {{\mathscr{D}}}^2(\Omega \times{{\mathbb{R}}}^3) $ on $ {{\mathscr{G}}}_u $ defines the current $ G_u $ carried by the graph of $ u $, namely

$ G_u $ is called an integer multiplicity (in short i.m.) rectifiable current in $ {{\mathscr{R}}}_2(\Omega \times{{\mathbb{R}}}^3) $, with mass $ {{\mathbf{M}}}(G_u) $ equal to the area $ {{\mathscr{H}}}^2({{\mathscr{G}}}_u) $ pertaining to the graph of $ u $, so a finite mass. (We write $ \mathscr{R}_{2} $ instead of the common (natural) notation $ \mathscr{D}_{2} $ to recall the rectifiable nature of the current.) Since the Jacobian of the graph map $ x\mapsto(x, u(x)) $ is equal to $ |{{\mathbf{t}}}_1(x)\wedge {{\mathbf{t}}}_2(x)| $, by the area formula we get

By duality, the boundary of $ G_u $ is the $ 1 $-current $ \partial G_{u} $ acting on $ {{\mathscr{D}}}^{1}(\Omega\times {{\mathbb{R}}}^3) $, the space of compactly supported smooth $ 1 $-forms $ \eta $ in $ \Omega\times{{\mathbb{R}}}^3 $, as

where $ d \eta $ is the differential of $ \eta $. By Stokes theorem we get

if $ u $ is of class $ C^1 $. However, in general, the boundary $ \partial G_u $ does not vanish and may not have finite mass in $ \Omega \times{{\mathbb{R}}}^3 $. On the other hand, if $ \partial G_u $ has finite mass, the boundary rectifiability theorem states that $ \partial G_u $ is an i.m. rectifiable current in $ {{\mathscr{R}}}_1(\Omega \times{{\mathbb{R}}}^3) $.

Example 2.1. If $ u $ is a Sobolev map in $ W^{1, q}(\Omega, {{\mathbb{R}}}^3) $, with $ q\geq 1 $, the approximate gradient agrees with the density of the weak derivative of $ u $. Moreover, since $ |{\mathop{{\rm{adj}}}\nolimits}_2\nabla u|\leq c\, |\nabla u|^2 $, we get $ W^{1, 2}(\Omega, {{\mathbb{R}}}^3)\subset{{\mathscr{A}}}^1(\Omega, {{\mathbb{R}}}^3) $.

The null-boundary condition (2.1) holds true for Sobolev maps $ u\in W^{1, 2}(\Omega, {{\mathbb{R}}}^3) $, by approximation. In fact, if $ \{u_h\} \subset C^1(\Omega, {{\mathbb{R}}}^3) $ is such that $ u_h\to u $ strongly in $ W^{1, 2} $, by dominated convergence we infer that $ G_{u_h} $ converges to $ G_u $ weakly as currents, i.e., $ \langle G_{u_h}, \omega \rangle\to \langle G_{u}, \omega \rangle $ for each $ \omega\in {{\mathscr{D}}}^2(\Omega \times{{\mathbb{R}}}^3) $. So, condition (2.1) is preserved in the weak limit process.

Take $ \Omega = B^2 $, with $ B^2 $ the unit disk centered at the origin $ O $, and $ u:B^2\to{{\mathbb{R}}}^3 $ as the zero-homogeneous map

for some Lipschitz-continuous map $ \varphi: \partial B^2\to{{\mathbb{R}}}^3 $. Then, $ u\in W^{1, q}(B^2, {{\mathbb{R}}}^3) $ for each $ q < 2 $, and $ {\mathop{{\rm{adj}}}\nolimits}_2\nabla u = 0 $, by the area formula, whence $ u\in{{\mathscr{A}}}^1(B^2, {{\mathbb{R}}}^3) $. However (compare Example 2 in reference [13, Sec. 3.2.2]), we compute

where $ \delta_O $ is the Dirac mass at the origin and $ \varphi_\#{[\![\, { \partial B^2}\, ]\!]} $ is the image through the map $ \varphi $ of the 1-current $ {[\![\, { \partial B^2}\, ]\!]} $ associated with the naturally oriented unit circle $ \partial B^2 $. Therefore, condition (2.1) fails to hold whenever $ \varphi_\#{[\![\, { \partial B^2}\, ]\!]} $ is non-trivial (see Examples 7.1 and 7.2 below).

2.2.   Gauss graphs of smooth surfaces

We summarize in this section some issues concerning Gauss graphs of surfaces with codimension one. Our main reference is ^[5] (see also ^[4]). Such notions are essential for the rest of this work because we refer to functionals depending on curvatures.

Given a smooth (say $ C^2 $), bounded, and oriented surface $ {{\mathscr{M}}} \subset{{\mathbb{R}}}^3 $, with smooth boundary $ \partial{{\mathscr{M}}} $, the Gauss map $ \nu:{{\mathscr{M}}}\to {\mathbb S}^2 $ associates to each point $ y $ in $ {{\mathscr{M}}} $ the unit normal $ \nu(y)\in {\mathbb S}^2 $, where

The graph of such a map, or Gauss graph, is the 2-dimensional surface in $ {{\mathbb{R}}}^6 $ given by

where $ {{\mathbb{R}}}^3_{z} $ is the isomorphic copy of $ {{\mathbb{R}}}^3 $ in which we consider embedded the sphere $ {\mathbb S}^2 $.

Therefore, we shall denote by $ (\varepsilon_1, \varepsilon_2) $ and $ (e_1, e_2, e_3) $ the canonical bases of $ {{\mathbb{R}}}^2 $ and $ {{\mathbb{R}}}^3_y $, respectively, and by $ (\varepsilon^1, \varepsilon^2) $ and $ (e^1, e^2, e^3) $ the natural dual bases defined by $ \varepsilon_i\cdot\varepsilon^j = \delta^{\; j}_{i} $ and $ e_h\cdot e^k = \delta^{\; k}_{h} $, where the interposed dot means dual pairing. In particular, we will identify the dual bases with $ (dx^1, dx^2) $ and $ (dy^1, dy^2, dy^3) $, which are naturally dual to $ (\frac{\partial}{\partial x^{1}}, \frac{\partial}{\partial x^{2}}) $ and $ (\frac{\partial}{\partial y^{1}}, \frac{\partial}{\partial y^{2}}, \frac{\partial}{\partial y^{3}}) $. We also correspondingly denote by $ (\epsilon_1, \epsilon_2, \epsilon_3) $ the canonical basis of $ {{\mathbb{R}}}^3_z $, and by $ (dz^1, dz^2, dz^3) $ the dual basis, after adopting the previous identification.

The Hodge star, applied to the normal vector $ \nu(y) $, defines a 2-form over the tangent space at $ y $. We then have a field, that we call a tangent 2-vector field $ \tau:{{\mathscr{M}}}\to\bigwedge^2 T{{\mathscr{M}}} \subset\bigwedge^2{{\mathbb{R}}}^3_y $ with values $ \tau(y) = \ast \nu(y) $. Denoting by $ \Phi:{{\mathscr{M}}}\to{{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $ the graph map $ \Phi(y): = (y, \nu(y)) $, a continuous tangent 2-vector field $ \xi: {{{\mathscr{G}}}\!{{\mathscr{M}}}}\to\bigwedge^2({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ is given by $ \xi(y, \nu(y)): = \bigwedge^2 d\Phi(\tau(y)) $. Since $ | \xi|\geq 1 $ on $ {{{\mathscr{G}}}\!{{\mathscr{M}}}} $, the normalized $ 2 $-vector field $ \overrightarrow \zeta: = \xi/| \xi| $ determines an orientation to $ {{{\mathscr{G}}}\!{{\mathscr{M}}}} $. Therefore, the corresponding i.m. rectifiable $ 2 $-current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]} $ in $ {{\mathscr{R}}}_2({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ carried by the Gauss graph has multiplicity one and support contained in $ \overline{{\mathscr{M}}} \times {\mathbb S}^2 $. Its action on compactly supported smooth 2-forms $ \omega $ in $ {{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $ is (by integration) given by

By Stokes' theorem, the boundary current $ \partial {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]} $ acts by integration of 1-forms on the naturally oriented boundary of $ {{{\mathscr{G}}}\!{{\mathscr{M}}}} $, so that $ \partial {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]} = 0 $ if $ {{\mathscr{M}}} $ is a closed smooth surface.

The tangential Jacobian $ J^{{\mathscr{M}}}_\Phi $ of the graph map is given by

where $ {\bf{k}}_1 = {\bf{k}}_1(y) $ and $ {\bf{k}}_2 = {\bf{k}}_2(y) $ are the principal curvatures at $ y\in{{\mathscr{M}}} $. In fact, we have $ J^{{\mathscr{M}}}_\Phi(y) = | \xi(y, \nu(y))| $. Moreover, denoting by $ \tau_1 $ and $ \tau_2 $ the principal directions, and considering the natural homomorphism $ v\mapsto \widetilde v $ from $ {{\mathbb{R}}}^3_y $ onto $ {{\mathbb{R}}}^3_z $, we get

Also, with the mean curvature and the Gauss curvature given by

so that $ {\bf{k}}_{1, 2} = {{\mathbf{H}}}\pm\sqrt{{{\mathbf{H}}}^2-{{\mathbf{K}}}} $, we may equivalently write

Therefore, by the area formula, area of the Gauss graph is

It agrees with the mass $ {{\mathbf{M}}}({[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]}) $ of the current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]} $.

The curvature functional $ \Vert {{\mathscr{M}}}\Vert $ of a smooth surface $ {{\mathscr{M}}} \subset{{\mathbb{R}}}^3_y $ is defined in reference ^[5] to be

It can be equivalently written as

so that, by formula (2.4), we obtain bounds such as

Also, two real measures on $ {{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $ are naturally associated with mean and Gauss curvatures ^[5]:

Consequently, for any $ \psi\in C_0({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ we have

and

In terms of the current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}}\, ]\!]} $, such curvature measures read

$ \Theta_\ell = \Theta_\ell(y, z) $ are 2-forms in $ {{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $, defined in ^[5]. For two-dimensional surfaces they are explicitly given by

Remark 2.1. The dependence of mean curvature from the sign of principal curvatures motivates the introduction of a factor $ -1 $ in order to recover, for parametric surfaces, standard notations (see expression (3.13) below).

2.3.   Weak limits of Gauss graphs

Weak limits $ \Sigma $ of sequences of currents carried by Gauss graphs of smooth surfaces $ \{{{\mathscr{M}}}_h\} $ are analyzed in reference ^[5]. Assuming for simplicity that each $ {{\mathscr{M}}}_h $ is closed, supported in a given compact set $ K \subset{{\mathbb{R}}}^3 $, and $ \sup_h\Vert{{\mathscr{M}}}_h\Vert < \infty $, it turns out that possibly passing to a subsequence the currents $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_h}\, ]\!]} $ weakly converge in $ {{\mathscr{D}}}_2({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ to an i.m. rectifiable current $ \Sigma $ in $ {{\mathscr{R}}}_2({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $, with null boundary, $ \partial \Sigma = 0 $, and with support contained in $ K \times {\mathbb S}^2 $.

We thus have

for some 2-rectifiable subset $ R $ of $ K \times {\mathbb S}^2 $, some positive and integer-valued $ {{\mathscr{H}}}^2∟ R $-measurable multiplicity function $ \theta:R\to{{\mathbb{N}}}^+ $, and some $ {{\mathscr{H}}}^2∟ R $-measurable function $ \overrightarrow\eta:R\to\bigwedge^2({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ such that $ \overrightarrow\eta(y, z) $ is a unit 2-vector orienting the approximate tangent 2-space $ T_{(y, z)}R $ to $ R $ at $ (y, z) $, for $ {{\mathscr{H}}}^2 $-a.e. $ (y, z)\in R $. In that case, one usually writes $ \Sigma = {[\![\, {R, \theta, \overrightarrow\eta}\, ]\!]} $. We also denote by

the orthogonal projection onto the first factor. Therefore, $ P: = p(R) $ is a 2-rectifiable set. Finally, $ \varphi $ and $ \varphi^\ast $ denote the canonical $ 1 $-form and $ 2 $-form, respectively given by

Theorem 2.1. (^[5]) With the previous notation, the following statements hold:

1) $ \langle \Sigma, \eta \wedge \varphi \rangle = 0 $ for each $ \eta\in{{\mathscr{D}}}^1({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $\,;

2) $ \langle \Sigma, \psi\, \varphi^\ast \rangle\geq 0 $ for each $ \psi\in C({{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z) $ such that $ \psi\geq 0 $\,;

3) for $ {{\mathscr{H}}}^2 $-a.e. $ y\in P $

where $ \nu:P\to {\mathbb S}^2 $ is an $ {{\mathscr{H}}}^2∟ P $-measurable map with $ \nu(y) $ orthogonal to the approximate tangent 2-space $ T_yP $, for $ {{\mathscr{H}}}^2 $-a.e. $ y\in P $.

Remark 2.2. We finally recall from reference ^[5] that property (1) is equivalent to the orthogonality condition

for $ {{\mathscr{H}}}^2 $-a.e. $ (y, z)\in R $, where $ \bullet $ denotes the scalar product in $ {{\mathbb{R}}}^6 $. As in reference ^[5], the stratification

holds, where according to the number of $ \epsilon_j $-entries we have set

Then, it turns out that properties (1) and (2) are equivalent to

3.   Two-dimensional representation of plates and shells, and the related Gauss graphs

As already recalled in the Introduction, shells (we include plates and thin films in the nomenclature, as special cases) are bodies for which one dimension is largely smaller with respect to the others. This geometric peculiarity suggests approximate representations of shells as two-dimensional bodies, each point of which is endowed with additional information on what happens in the (real) thickness (essential references on the matter are ^[2,8,22,23]; see also ^[3,17,19,20]).

In this view, we consider a planar reference configuration for the shell middle surface, i.e., we refer in essence to something that can be a plate in some configuration. So, we select a two-dimensional smooth domain $ \Omega $ in $ \mathbb{R}^{2} $, where Cartesian coordinates $ x = (x_1, x_2) $ are fixed. A differentiable map $ u: \Omega\to{{\mathbb{R}}}^3 $, say $ u = (u^1, u^2, u^3) $, represents a deformation. It is taken to determine an immersion of $ \Omega $ into $ \mathbb{R}^{3} $. The tangent plane to the deformed shape is assumed not to degenerate. Formally, it is tantamount to impose $ |\text{adj}_2\nabla u(x)| > 0 $ for any $ x\in \Omega $. In other words, if $ \partial_iu $ denotes a column vector of the gradient matrix $ \nabla u $, the previous condition is equivalent to say that the vector product $ \partial_1u\times \partial_2u $ does not vanish at every point. Normal to the deformed configuration

is the unit vector

It can be considered as a descriptor of out-of-middle-surface shell behavior. However, such an information can be carried out by an $ {{\mathbb{S}}}^2 $-valued vector field $ x\mapsto \zeta(x) $ defined over $ \Omega $ and constrained to be at every $ x\in\Omega $ such that

where $ \bullet $ is the scalar product in $ {{\mathbb{R}}}^3 $. In both cases we are representing a shell as a Cosserat surface (see ^[8,22,23]). By choosing $ \zeta $ we allow the description of through-the-thickness shear, while with $ \nu_{u} $ we exclude it. We adopt here this last choice so that smooth deformed shells are represented by parametric surfaces.

3.1.   Gauss graphs of parametric surfaces

In the present setting, the Gauss graph of the surface $ {{\mathscr{M}}}_u = u(\Omega) $ is described by

where $ \Phi_u: \Omega\to {{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $ is the smooth map

The first fundamental form of $ {{\mathscr{M}}}_u $ is given by the symmetric matrix

with determinant

Second derivatives $ \partial^2_{i, j}u $ of the deformation map $ u $, where $ \partial^2_{2, 1}u = \partial^2_{1, 2}u $, determine the second fundamental form given by the symmetric matrix

where, for short-hand notation, we have denoted $ {{\mathbf{n}}}: = \partial_1u \times \partial_2u $, so that $ g_u = |{{\mathbf{n}}}|^2 $. Therefore, the mean curvature at $ u(x) $ becomes

and the Gauss curvature is then

The tangent space at a point $ (y, z) $ in the Gauss graph $ {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u $ is oriented by the wedge product

We have

and hence, according to the number of $ \epsilon_j $-entries, we can write as before the stratification

where

As a consequence of the expression (2.4), by the area formula we can write the Gauss graph area $ {{\mathscr{H}}}^2({{{\mathscr{G}}}\!{{\mathscr{M}}}}_u) $ as

which yields a formula for the Jacobian $ J_{\Phi_u} $ of $ \Phi_u $:

Finally, by the expression (2.3) we infer

3.2.   Currents carried by Gauss graphs of parametric surfaces

Let $ u: \Omega\to{{\mathbb{R}}}^3 $ a smooth function with $ \partial_1 u \times \partial_2u\neq 0 $ everywhere. Assume $ \Vert u\Vert_\infty\leq K < \infty $. The current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $ in $ {{\mathscr{R}}}_2({{\mathbb{R}}}^6) $ is defined as above, with $ {{\mathscr{M}}}_u = u(\Omega) $. The Gauss graph surface $ {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u $ is equipped with the natural orientation induced by the function $ u $, so that

We shall restrict to the action of compactly supported forms in $ {{\mathbb{R}}}^3 \times {\mathbb S}^2 $. By the definition (3.3) we thus equivalently have $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} = \Phi_{u\, \#}{[\![\, { \Omega}\, ]\!]} $, that is

Moreover, recalling the notation (2.8), we have (see also formula (5.1) below)

3.3.   Absence of cancellations

A property that we call the absence of cancellations plays a role here. So far we left a part direct references to the shell thickness, considering it implicitly very thin. Take it to be vanishing, i.e., infinitesimal. Take also circumstances in which two pieces of the deformed shell $ {{\mathscr{M}}}_u = u(\Omega) $ are in contact, with the same or opposite orientation. More precisely, we have two pairwise disjoint and connected open sets $ A, B \subset \Omega $ such that both the restrictions $ u_{\vert A} $ and $ u_{\vert B} $ are injective, but $ u(A) = u(B) $. Then, for each $ x\in A $ there exists a unique point $ \widetilde x = \widetilde x(x)\in B $ such that $ u(x) = u(\widetilde x) $, and the map $ x\mapsto \widetilde x(x) $ is a diffeomorphism from $ A $ to $ B $. Moreover, notice that a unit 2-vector field orienting the tangent plane to $ {{\mathscr{M}}}_u $ at $ y = u(x) $ is

Therefore, one of the two following alternatives holds: either $ \tau_u(x) = \tau_u(\widetilde x(x)) $ for all $ x\in A $, or $ \tau_u(x) = -\tau_u(\widetilde x(x)) $ for all $ x\in A $, according to the fact that the diffeomorphism from $ A $ to $ B $ preserves or reverses the natural orientation. In both cases, the tangent plane to $ u(\Omega) $ at $ u(x) $ agrees with the one at $ u(\widetilde x(x)) $. In the first case, $ u_\#{[\![\, A\, ]\!]} = u_\# {[\![\, B\, ]\!]} $ and the image current $ u_\#{[\![\, {A\cup B}\, ]\!]} $ has multiplicity two, whereas in the second one $ u_\#{[\![\, A\, ]\!]} = -u_\# {[\![\, B\, ]\!]} $, whence $ u_\#{[\![\, {A\cup B}\, ]\!]} = 0 $, a cancellation occurs and actually

However, since in the second case $ \nu_u(x) = - \nu_u(\widetilde x(x)) $ for each $ x\in A $, by the expressions (3.8) we infer

for some $ \alpha, \, \beta > 0 $, whence $ \xi_u(x)\neq \pm \xi_u(\widetilde x(x)) $, and definitely no cancellation occurs in the Gauss graph current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $. In conclusion, even in the presence of cancellations for the projected current $ u_\#{[\![\, { \Omega}\, ]\!]} = p_\#{[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $, we always have

Compare Example 7.2 below for a deformation with folding.

3.4.   Action of the Gauss graph current and curvature measures formulas

For the sake of completeness, we compute the action of a current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $ over the Gauss graph and explicit formulas for the curvature measures $ \chi_\ell^{{{\mathscr{M}}}_u} $.

Since for $ i, j = 1, 2, 3 $

the pull-back of the basis of $ 2 $-forms in $ {{\mathbb{R}}}^3_y \times{{\mathbb{R}}}^3_z $ gives the fifteen formulas

Therefore, for each compactly supported smooth function $ \psi\in C^\infty_c({{\mathbb{R}}}^3 \times {\mathbb S}^2) $ we obtain

By referring to the expressions (2.6), if $ {{\mathscr{M}}} = {{\mathscr{M}}}_u $ for some smooth and injective function $ u: \Omega\to{{\mathbb{R}}}^3 $ as above, we may write

where $ {{\mathbf{H}}}_u $ and $ {{\mathbf{K}}}_u $ are given by (3.6) and (3.7). In terms of the Gauss graph current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $, on account of definitions (2.7) we thus get

In fact, recalling that $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} = \Phi_{u\, \#}{[\![\, { \Omega}\, ]\!]} $ we obtain the following formulas:

where $ g_u $ is given by (3.5). Therefore, for any $ \psi\in C^\infty_c({{\mathbb{R}}}^3 \times {\mathbb S}^2) $ we have

We omit any further detail and address to reference ^[18] for a similar computation involving Gauss graphs of smooth Cartesian surfaces.

4.   The energy

If we consider only pure bending, the energy refers to the curvature functional $ \Vert {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u\Vert $ defined by the expression (2.5). By the area formula, it agrees with the energy functional $ {{\mathscr{E}}}(u) $ defined by

On account of the expressions (3.9), (3.10), and (3.11), we get

where $ | \xi_u|^2 = | \xi_u^{(0)}|^2+| \xi_u^{(1)}|^2+| \xi_u^{(2)}|^2 $ and, by (3.8),

On account of the expression (3.12), we have

We aim at a bound for the total variation of the function $ u $ and of the Gauss map $ {{\nu}_u} $. Also, we wish to preserve condition $ \partial_1 u \times \partial_2 u\neq 0 $, where $ | \partial_1 u \times \partial_2 u| = |{\mathop{{\rm{adj}}}\nolimits}_2\nabla u| $. These two issues suggest us to work with an expression of the energy given by

for some real exponent $ q > 1 $. The map $ \Phi_u $ is given by formula (3.4), so that

and $ f:]0, +\infty[\to {{\mathbb{R}}}^+ $ is a positive and convex function with linear growth at $ +\infty $ and such that $ f(\rho)\to +\infty $ as $ \rho\to 0^+ $, as e.g., $ f(\rho) = \rho^{-1}\vee\rho $.

Here, the presence of $ \nabla u $ implies considering middle surface stretch and shear. We leave a part the consequent thickness stretching (due to the Poisson's effect), considering it not prominent from an energetic point of view as the thickness is thin and possibly vanishing in the minimizing sequences.

5.   Closure properties

Theorem 5.1. For $ q > 1 $ and $ K > 0 $, let $ \{u_h\} \subset C^2(\Omega) $ a sequence satisfying $ \sup_h{{\mathscr{F}}}_q(u_h) < \infty $ and $ \sup_h\Vert u_h\Vert_\infty\leq K $. There exists a map $ u\in W^{1, q}(\Omega, {{\mathbb{R}}}^3) $, with $ \Vert u\Vert_ \infty\leq K $, and a (not relabeled) subsequence such that

1) $ u_h \rightharpoonup u $ weakly in $ W^{1, q}(\Omega, {{\mathbb{R}}}^3_y) $,

2) for $ {{\mathscr{L}}}^2 $-a.e. $ x\in \Omega $, one has $ \partial_1 u \times \partial_2 u\neq 0 $, and $ |{\mathop{{\rm{adj}}}\nolimits}_2\nabla u|\in L^1(\Omega) $, and

3) $ \nu_{u_h} \rightharpoonup \nu_u $ weakly in $ W^{1, q}(\Omega, {{\mathbb{R}}}^3_z) $, where the approximate normal $ \nu_u(x) $ is defined for $ {{\mathscr{L}}}^2 $-a.e. $ x\in \Omega $ by (3.1), but in terms of the approximate gradient $ \nabla u $.

Proof. We repeatedly pass to not relabeled subsequences. The first assertion is trivial. Since

by formulas (4.1) and (4.2) we get $ \sup_h{{\mathbf{M}}}(G_{u_h}) < \infty $. Therefore, by the closure theorem for Cartesian currents (see ^[13,14]) there exists a current $ T $ such that

with $ G_{u_h} \rightharpoonup T $ weakly in $ {{\mathscr{D}}}_2(\Omega \times{{\mathbb{R}}}^3) $ and $ S_T\in {{\mathscr{D}}}_1(\Omega \times{{\mathbb{R}}}^3) $, which we write in short $ T\in \mathop{{\rm{cart}}}\nolimits(\Omega \times{{\mathbb{R}}}^3) $. This implies $ |{\mathop{{\rm{adj}}}\nolimits}_2\nabla u|\in L^1(\Omega) $. Moreover, since the integrand $ f $ is a convex function, by $ {{\mathscr{L}}}^2 $-a.e. convergence of the gradients $ \nabla u_h $ to the approximate gradient $ \nabla u $, which follows from $ L^q $-convergence, we get

Hence, condition $ \partial_1 u \times \partial_2 u\neq 0 $ holds a.e. in $ \Omega $. We finally obtain weak $ W^{1, q} $ and $ {{\mathscr{L}}}^2 $-a.e. convergence of $ \nu_{u_h} $ to $ \nu_u $. □

If $ u $ is the limit function in Theorem 5.1, we can express the energy $ {{\mathscr{E}}}(u) $ by equation (4.1), where the three terms $ | \xi_u^{(\ell)}| $, $ \ell = 0, 1, 2 $, are defined $ {{\mathscr{L}}}^2 $-a.e. on $ \Omega $ by the right-hand side of the system (4.2), now in terms of the approximate gradient of $ u $ and $ \nu_u $.

We impose Dirichlet-type boundary conditions as follows:

(H) there exists an open set $ \widetilde \Omega \subset{{\mathbb{R}}}^2 $, with $ \overline \Omega \subset \widetilde \Omega $, and an injective function $ \widetilde u\in C^2(\widetilde \Omega) $ such that each $ u_h $ can be smoothly extended to $ \widetilde \Omega $ so that $ u_h = \widetilde u $ on $ \widetilde \Omega \setminus \Omega $.

Recalling the notation (2.8), we also denote by $ \widetilde \pi:{{\mathbb{R}}}^2 \times{{\mathbb{R}}}^3_y\to{{\mathbb{R}}}^3_y $ the orthogonal projection onto the second factor.

Theorem 5.2. Let $ \{u_h\} $ as in Theorem 5.1. Assume that condition $ (H) $ holds. Then, passing to a (not relabeled) subsequence, the Gauss graphs $ {[\![\, {{{\mathscr{M}}}_{u_h}}\, ]\!]} $ weakly converge to a current $ \Sigma\in{{\mathscr{R}}}_2({{\mathbb{R}}}^3 \times {\mathbb S}^2) $ satisfying the properties listed in Theorem 2.1. Moreover,

where $ T = G_u+S_T $ is the current in $ \mathop{{\rm{cart}}}\nolimits(\Omega \times{{\mathbb{R}}}^3) $ obtained in Theorem 5.1. In addition, the estimates $ \Vert \Sigma\Vert\geq {{\mathscr{E}}}(u) $ and $ {{\mathscr{E}}}(u)\leq\liminf\limits_{h\to\infty}{{\mathscr{E}}}(u_h) $ hold. Eventually, $ {{\mathscr{F}}}_q(u)\leq\liminf\limits_{h\to \infty}{{\mathscr{F}}}_q(u_h) $.

Proof. The boundary condition (H) yields a uniform bound on mass and curvatures of the boundary currents $ \partial u_{h\#}{[\![\, { \Omega}\, ]\!]} = u_{h\#}{[\![\, { \partial \Omega}\, ]\!]} $. Therefore, we can apply the closure theorem on Gauss graphs proven in reference ^[5], obtaining the current $ \Sigma $ that satisfies the properties listed in Theorem 2.1. Since

by the weak convergence $ G_{u_h} \rightharpoonup T $ in the proof of Theorem 5.1, we get the projection formula (5.1).

Even if a cancellation may occur in the projected current $ p_\# \Sigma $, the argument exploited in Section 3.3 (see relations (3.12)) allows us to conclude that

As a consequence, by lower semicontinuity we get

where $ \Vert {\Phi_u}_\#{[\![\, { \Omega}\, ]\!]}\Vert = {{\mathscr{E}}}(u) $ and $ \Vert{[\![\, {{{\mathscr{M}}}_{u_h}}\, ]\!]}\Vert = {{\mathscr{E}}}(u_h) $ for each $ h $. The lower semicontinuity inequalities readily follow. □

6.   Avoiding self-penetration

Under large bending, distant portions of shells may touch. Physics, however, suggests that an appropriate model should avoid solutions describing self-penetration of the matter. A constraint excluding such a possibility is then required in the setting represented here. Evidently, for it the shell thickness – otherwise not exploited directly so far – should play a role. We propose a way to obtain such a necessary constraint on the basis of what is done for fully three-dimensional bodies.

Let $ u:\overline \Omega\to{{\mathbb{R}}}^3 $ be a map of class $ C^2(\overline \Omega) $, with $ \partial_1 u \times \partial_2 u\neq 0 $ on $ \overline \Omega $. For $ s > 0 $ let $ v_{u, s}:U\to{{\mathbb{R}}}^3 $, where $ U: = \Omega \times(-\frac{h}{2}, \frac{h}{2}) $, $ h $ the constant shell thickness, be given by

We compute

on $ U $, where

and

By the equiboundedness of $ \lambda_u(x) $ and $ \mu_u(x) $, we infer that $ s^{-1}\det\nabla v_{u, s}\to | \partial_1 u \times \partial_2 u| $ as $ s\to 0^+ $ uniformly on $ U $. Hence, we get

if $ s > 0 $ is sufficiently small. On account of the relations (4.2) and (4.4), we also estimate

for some absolute constant $ c > 0 $ not depending on $ u $.

Moreover, since the principal curvatures of the deformed surface $ u(\Omega) $ are bounded, there exists $ s = s(u) > 0 $ such that for each $ (x_1, x_2)\in \Omega $ we can find a neighborhood $ V $ of $ (x_1, x_2) $ in $ \Omega $ such that the restriction of $ v_{u, s} $ to $ V \times(-\frac{h}{2}, \frac{h}{2}) $ is injective.

In order to obtain global injectivity, one may e.g., impose the well-known Ciarlet-Nečas condition ^[6]. In reference ^[7], under suitable additional hypotheses, the inequality

is proposed. However, it is violated by a folding deformation. Then, what is suggested in reference ^[7] is to adopt a notion of approximately injective deformations. It requires (in a sense not specified here) that the parametric surface $ u: \Omega\to{{\mathbb{R}}}^3 $ can be approximated by sequences of functions $ u_h $ such that each $ u_h $ can be seen as a parameterization of the middle surface of a thick shell satisfying the Ciarlet-Nečas condition, and we can take the thickness so that it gradually disappears. This property yields to a more reasonable scenario from a physical point of view.

6.1.   Possible admissible deformations

We go along the path summarized above to avoid self-penetration of matter. We start by a condition introduced in 1989 by M. Giaquinta, G. Modica, and J. Souček ^[11,12] (see also [14, Sec. 2.3.2]). It is equivalent to Ciarlet-Nečas' one.

For a sufficiently smooth map $ v:U\to{{\mathbb{R}}}^3 $ with $ \det\nabla v > 0 $ a.e. in $ U $, a fit region in $ {{\mathbb{R}}}^3 $, by setting $ w = (x_1, x_2, x_3) $, the global invertibility condition above mentioned reads

for every compactly supported smooth function $ f:U \times{{\mathbb{R}}}^3\to[0, + \infty) $. Weak convergence in terms of currents preserves such condition. It implies $ {{\mathscr{L}}}^3 $-a.e. injectivity.

Theorem 6.1. Let $ \{u_h\} $ satisfy assumptions in Theorems 5.1 and 5.2. Assume that, for every $ h $, the function $ v_h = v_{u_h, s_h} $ given by expression (6.1) satisfies the global invertibility condition (6.3), for some $ s_h\in(0, 1) $. The weak limit deformation map $ u $ is the trace on $ x_3 = 0 $ of a function $ v:U\to{{\mathbb{R}}}^3 $ satisfying $ |\nabla v|, \, |{\mathop{{\rm{adj}}}\nolimits}_2\nabla v|, \det\nabla v\in L^1(U) $, $ \det\nabla v\geq 0 $ a.e. in $ U $, and condition (6.3).

Proof. For every $ h $, we have already seen that by taking $ s_h\in(0, 1) $ sufficiently small, the function $ v_h = v_{u_h, s_h} $ also satisfies $ \det\nabla v_h > 0 $ on $ U $. Furthermore, on account of the estimate (6.2), we infer that the current $ G_{v_h} $ carried by the graph of $ v_h $ has finite mass, which satisfies the bound

Therefore, we get $ \sup_h{{\mathbf{M}}}(G_{v_h}) < \infty $, whereas, by the smoothness hypothesis, $ \partial G_{v_h} = 0 $ on $ U \times{{\mathbb{R}}}^3 $. As a consequence, by the closure theorem for Cartesian currents, it turns out that a (not relabeled) subsequence satisfies $ G_{v_h} \rightharpoonup \widetilde T $ weakly in $ {{\mathscr{D}}}_3(U \times{{\mathbb{R}}}^3) $ for some Cartesian current $ \widetilde T\in \mathop{{\rm{cart}}}\nolimits(U \times{{\mathbb{R}}}^3) $. Let $ v $ denote the underlying function to $ \widetilde T $, so that $ \widetilde T = G_v+S_{ \widetilde T} $. We find that $ v:U\to{{\mathbb{R}}}^3 $ is approximately differentiable a.e. in $ U $. Also, all the minors of its approximate gradient $ \nabla v $ are in $ L^1(U) $.

By the weak convergence $ G_{v_h} \rightharpoonup \widetilde T $, it turns out that the function $ v $ satisfies the global invertibility condition (6.3), too, whereas $ \det\nabla v\geq 0 $ a.e. in $ U $.

In addition, if we look at $ G_{v_h} $ as an i.m. rectifiable current in $ {{\mathbb{R}}}^3_w \times{{\mathbb{R}}}^3_y $, slicing theory implies that the restriction of $ G_{v_h} $ to $ (\Omega \times\{0\}) \times{{\mathbb{R}}}^3 $ agrees with the graph current $ G_{u_h} $. Therefore, by the weak convergence of $ G_{v_h} $ to $ \widetilde T $ and of $ G_{u_h} $ to $ T $, where, we recall, $ \widetilde T = G_v+S_{ \widetilde T} $ and $ T = G_u+S_{T} $, it turns out that the restriction of $ \widetilde T $ to $ (\Omega \times\{0\}) \times{{\mathbb{R}}}^3 $ agrees with the current $ T $. This property indicates us that $ u $ is the trace of $ v $ on $ \Omega \times\{0\} $. So, the proof is complete. □

Remark 6.1. A sort of thickness condition holds if we choose a size $ s_0 > 0 $ and assume that $ v_h = v_{u_h, s_h} $ satisfies the constraint (6.3) and $ \det \nabla v_h > 0 $ on $ U $ for some $ s_h\geq s_0 $. In this case the function $ v $ is given $ {{\mathscr{L}}}^3 $-a.e. by (6.1), where $ s\geq s_0 $ and the unit normal $ {{\nu}_u} $ is defined $ {{\mathscr{L}}}^2 $-a.e. in $ \Omega $ by the formula (3.1), now in terms of the approximate gradient $ \nabla u $ of the limit deformation $ u $.

Moreover, in order to preserve the local orientation, namely $ \det\nabla v > 0 $ a.e. on $ U $, we may add to the energy functional (4.3) a term of the type

6.2.   Weak deformations for shells

Fix $ q > 1 $, $ K > 0 $, and $ \widetilde u: \widetilde \Omega\to{{\mathbb{R}}}^3 $, together with the boundary condition (H). On account of the above results, we may say that a function $ u: \Omega\to{{\mathbb{R}}}^3 $ represents a weak deformation for a shell, and we write for short $ u\in{{\mathscr{A}}} = {{\mathscr{A}}}(q, K, \widetilde u) $, provided that the following properties hold:

$ 1) \; u\in W^{1, q}(\Omega, {{\mathbb{R}}}^3) $ with $ \Vert u\Vert_ \infty\leq K $, $ \partial_1 u \times \partial_2 u\neq 0 $ for $ {{\mathscr{L}}}^2 $-a.e. $ x\in \Omega $, and $ |{\mathop{{\rm{adj}}}\nolimits}_2\nabla u|\in L^1(\Omega) $ (see Theorem 5.1); moreover, the approximate normal $ \nu_u $ belongs to $ W^{1, q}(\Omega, {\mathbb S}^2) $ (see definition (3.1));

$ 2) \; u = \widetilde u $ on $ \widetilde \Omega\setminus \overline \Omega $ (see Theorem 5.2); moreover, there exists a current $ \Sigma\in{{\mathscr{R}}}_2({{\mathbb{R}}}^3 \times {\mathbb S}^2) $ satisfying Theorem 2.1, such that the projection formula (5.1) holds, where $ T = G_u+S_T\in \mathop{{\rm{cart}}}\nolimits(\Omega \times{{\mathbb{R}}}^3) $, and $ \Vert \Sigma\Vert\geq {{\mathscr{E}}}(u) $;

$ 3) \; u $ is the trace on $ x_3 = 0 $ of a function $ v:U\to{{\mathbb{R}}}^3 $ satisfying $ |\nabla v|, \; |{\mathop{{\rm{adj}}}\nolimits}_2\nabla v| $, $ \det\nabla v\in L^1(U) $, $ \det\nabla v\geq 0 $ a.e. in $ U $, and the global invertibility condition (6.3) (see Theorem 6.1).

For future use, we also denote by $ \widetilde {{\mathscr{A}}} = \widetilde {{\mathscr{A}}}(q, K, \widetilde u) $ the class of maps $ u $ that are generated by a weak limit process as in Theorems 5.1, 5.2, and 6.1. It may be called the class representing smoothly accessible weak deformations for shells.

Therefore, $ \widetilde {{\mathscr{A}}}\subset{{\mathscr{A}}} $, and we expect that equality holds: if $ u $ represents a weak deformed shell. Then, we can find a sequence $ \{u_h\} $ as in the above mentioned theorems such that $ u_h \rightharpoonup u $ weakly in $ W^{1, q}(\Omega, {{\mathbb{R}}}^3) $.

The smooth density property for a generic weak deformation $ u $ of a shell is an open question. However, due to the Dirichlet-type boundary condition (H), and to the equiboundedness hypothesis, all the involved weak convergences as currents, say $ G_{u_h} \rightharpoonup T $, $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_{u_h}}\, ]\!]} \rightharpoonup \Sigma $, and $ G_{v_h} \rightharpoonup \widetilde T $ are metrizable. Therefore, we can apply a diagonal argument and prove the following existence result:

Theorem 6.2. For $ q > 1 $, $ K > 0 $, and $ \widetilde u $ as in $ (H) $, let $ \widetilde {{\mathscr{A}}} $ denote the class of smoothly accessible weak deformation of shells. Then, the problem

for the energy defined by formula (4.3) has a solution in the class $ \widetilde {{\mathscr{A}}} $.

Proof. Let $ \{u_k\} \subset \widetilde {{\mathscr{A}}} $ a minimizing sequence. Then, possibly passing to a (not relabeled) subsequence $ u_k \rightharpoonup u_ \infty $ weakly in $ W^{1, q} $ to some $ u_ \infty\in W^{1, q}(\Omega, {{\mathbb{R}}}^3) $, and $ \nu_{u_k} \rightharpoonup \nu_{u_ \infty} $ weakly in $ W^{1, q} $ where, we recall, $ \nu_{u_k} $ is defined $ {{\mathscr{L}}}^2 $-a.e. in $ \Omega $ as in formula (3.1), for each $ k\in\overline{{\mathbb{N}}}: = {{\mathbb{N}}}\cup\{ \infty\} $. Moreover, for each $ k\in{{\mathbb{N}}} $ we can find a sequence $ \{u^{(k)}_h\} $ that satisfies Theorems 5.1, 5.2, and 6.1, such that $ u^{(k)}_h \rightharpoonup u_k $ weakly in $ W^{1, q} $, as $ h\to \infty $. Due to the metrizable character of the (weak) convergences involved, by a diagonal argument we infer that actually $ u\in \widetilde {{\mathscr{A}}} $. Moreover, arguing as in the proof of Theorem 5.2, by the weak convergences $ u_k \rightharpoonup u_ \infty $ and $ \nu_{u_k} \rightharpoonup \nu_{u_ \infty} $ in $ W^{1, q} $, where $ q > 1 $, we obtain

where $ \Vert {\Phi_{u_k}}_\#{[\![\, { \Omega}\, ]\!]}\Vert = {{\mathscr{E}}}(u_k) $ for each $ k\in\overline{{\mathbb{N}}} $. We thus get

and the proof is complete. □

7.   Shells with holes and fractures

If $ u $ represents a weak deformation for a shell, as in the previous section, where $ q = 2 $, the membership of $ u $ to the Sobolev class $ W^{1, 2}(\Omega, {{\mathbb{R}}}^3) $ yields that the graph current $ G_u $ satisfies the null-boundary condition (2.1). On account of the Dirichlet-type condition (H), this implies that $ \partial u_{\#}{[\![\, { \Omega}\, ]\!]} = u_{\#}{[\![\, { \partial \Omega}\, ]\!]} $. Therefore, when $ q\geq 2 $, we are actually avoiding the formation of fractures.

Things change when the growth exponent $ q $ is lower than two.

Let $ \Omega = B^2 $ be the unit disk at the origin $ O $. Let $ u:B^2\to{{\mathbb{R}}}^3 $ be given by

for some Lipschitz-continuous map $ \varphi: \partial B^2\to{{\mathbb{R}}}^3 $. We have $ u\in W^{1, q}(B^2, {{\mathbb{R}}}^3) $ and $ {\mathop{{\rm{adj}}}\nolimits}_2\nabla u\in L^q(B^2, {{\mathbb{R}}}^3) $ for each $ q < 2 $, whence $ u\in{{\mathscr{A}}}^1(B^2, {{\mathbb{R}}}^3) $.

Consequently, we are presuming the existence of a hole at the origin in $ B^2 $, and the deformed hole has a boundary that is described by the map $ \varphi $. Moreover, formula (2.2) continues to hold. More precisely, viewing the graph $ G_u $ as a current in $ {{\mathscr{R}}}_2({{\mathbb{R}}}^2 \times{{\mathbb{R}}}^3) $, one gets

where $ \Psi[\varphi]: \partial B^2\to{{\mathbb{R}}}^2 \times{{\mathbb{R}}}^3 $ is the Lipschitz map $ \Psi[\varphi](x): = (x, \, 2 \varphi(x)) $ parameterizing the exterior boundary of the graph associated with $ u $.

Example 7.1. We can stretch the hole (without bending) by taking, in polar coordinates, $ \varphi(\cos \theta, \, \sin \theta): = (\cos \theta, \, \sin \theta, \, 0) $, so that

Denoting by $ {[\![\, {D^2}\, ]\!]} $ the 2-current given by integration of 2-forms on the positively oriented disk

we get

Example 7.2. We can stretch, bend, and fold the hole by letting

In this case, we get

and a cancellation occurs. We have the same phenomenon in the image current $ u_\#{[\![\, {B^2}\, ]\!]} $. In fact, let us denote by $ \Omega_k $, for $ k = 1, \ldots, 4 $, the four quarters of the holed unit disk $ B^2\setminus\{O\} $. We have

so that it turns out that $ u(\Omega_2) = u(\Omega_4) $. In other words, folding without self-penetration of matter occurs but $ u_\#{[\![\, { \Omega_2}\, ]\!]} = -u_\#{[\![\, { \Omega_4}\, ]\!]} $ and, actually,

More precisely, coming back to Remark 3.3, the map

is an orientation reversing diffeomorphism from $ \Omega_2 $ to $ \Omega_4 $ such that

Thus, by formulas (3.8) we have $ \xi^{(0)}_u(x) = - \xi^{(0)}_u(\widetilde x(x)) $ and $ \xi^{(2)}_u(x) = \xi^{(2)}_u(\widetilde x(x)) $ for each $ x\in \Omega_2 $, whence no cancellation occurs in the Gauss graph current $ {[\![\, { {{{\mathscr{G}}}\!{{\mathscr{M}}}}_u}\, ]\!]} $.

In our results above collected, when $ q < 2 $ we do not consider an energy term accounting for the occurrence of holes. For it, a physically reasonable choice could be given by the hole boundary size in the deformed surface $ u(\Omega) $. In Example 7.1, the latter contribution might be represented by the graph current boundary mass

In fact, sequences of currents $ G_{u_h} $ carried by the graph of functions $ u_h\in W^{1, q}(\Omega, {{\mathbb{R}}}^3) $, which satisfy

for some $ q > 1 $, sub-converge (in the sense of currents) to an element $ G_u $ in the same class. Two drawbacks appear.

In general, the term $ {{\mathscr{H}}}(u) $ does not have a satisfactory physical significance. The map in Example 7.2, e.g., satisfies $ {{\mathscr{H}}}(u) = {{\mathbf{M}}}(\varphi_\#{[\![\, { {\mathbb S}^1}\, ]\!]}) = 4\pi $, but the curve $ \varphi: \partial B^2\to{{\mathbb{R}}}^3_y $ describing a hole in the deformed configuration has length equal to $ 4(\pi+1) $.

Also, an essential difficulty in this framework is that we are not allowed to apply the closure theorem on Gauss graphs (see results in ^[5]). In fact, since equality $ \partial u_{\#}{[\![\, { \Omega}\, ]\!]} = u_{\#}{[\![\, { \partial \Omega}\, ]\!]} $ fails to hold, the boundary condition (H) does not guarantee a uniform bound on curvatures of the boundary terms produced by the holes.

Similar problems appear if one tries to analyze fractured shells. In that case, a natural ambient is given by suitable deformations $ u: \Omega\to{{\mathbb{R}}}^3 $ that belong to the class of special functions of bounded variation. Referring to the treatise ^[1] for an accurate analysis of $ SBV $ functions, we only observe here that the jump set $ S(u) $ describes a crack path in the reference configuration, whereas fractures in the deformed shape may be described again by the term $ {{\mathscr{H}}}(u) $. In fact, a map $ u\in{{\mathscr{A}}}^1(\Omega, {{\mathbb{R}}}^3) $ satisfying $ {{\mathscr{H}}}(u) < \infty $, actually belongs to the class $ SBV(\Omega, {{\mathbb{R}}}^3) $ (compare [15, Prop. 3.3.1]).

For those reasons, in order to apply the closure theorem on Gauss graphs by reference ^[5] (that in Theorem 5.2 – where we worked with Cartesian currents – led to the validity of Theorem 2.1), one has to introduce a further energy term that bounds the curvature of the Gauss graph boundary of the deformed surface $ u(\Omega) $. For these issues, future work is necessary.

8.   Additional remarks

The analyses presented here can be extended variously:

● We could consider through-the-thickness shear by opting for an out-of-tangent-plane vector field $ \zeta $ in the deformed shape.

● We could look at multi-layer shells, with consequent need of refining the scheme adopted here.

● Different modeling needs would emerge if we would consider a through-the-thickness microstructure. An example is a thin film of a smectic liquid crystal.

All the previous issues involve both modeling and analytical questions. Looking back to what we have discussed here, a purely analytical open problem emerges: the regularity of minimizers assured by Theorem 6.2. This is probably a nontrivial matter of future specialist work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work has been developed within the activities of the research group in "Theoretical Mechanics" of the "Centro di Ricerca Matematica Ennio De Giorgi" of the Scuola Normale Superiore in Pisa. We acknowledge also the support of GNFM-INDAM (to PMM) and GNAMPA-INDAM (to DM).

Conflict of interest

The authors declare no conflict of interest.