1. Introduction
Recently, draft human proteome map project has catalogued more than 92% of the protein coding genes in human by profiling 60 human tissues, 13 body fluids and 147 cancer cell lines using combined computational and mass spectrometry techniques [1]. Another study has mapped more than 96% of the human proteome with ample experimental evidence for protein expression by profiling > 800 tissue/cell types/body fluids using integrated bioinformatics approach [2]. Among many other families of proteins, secreted proteins always remains in the limelight due to their exploitation as candidate biomarkers. Cells secrete wide variety of cytokines, chemokines, hormones, digestive enzymes, toxins, antimicrobial peptides as well as components of extracellular matrix into the extracellular space under different conditions [3,4]. Some of these secreted proteins are also exploited as potential therapeutic targets to treat various disease conditions. In humans, secretory proteins is known to account for about one-tenth of the human proteome [5]. However, a catalogue of up-to-date human secreted proteins is missing and the exact number of secreted proteins remains elusive.
Proteins mainly gets secreted into the extracellular space through classical secretory (also known as ER/Golgi-dependent) [6] and non-classical secretory [7] (also known as ER/Golgi-independent) pathways. The proteins secreted through classical secretory pathway were known to contain specific signal sequence known as signal peptide and it is known to be hallmarks of classically secreted proteins. In contrast to the well-defined ER/Golgi-dependent pathway, the mechanism by which the proteins are secreted non-classically is poorly characterized.Currently, at least five non-classical secretory mechanisms are characterized i, exosomes ii, shedding microvesicles iii, ectodomain shedding and iv, membrane transport channels [8]. Majority of the proteins secreted through non-classical pathway were known to be of biomedical importance [9]. Identification and study of such proteins secreted through these mechanisms under normal and pathological conditions would further benefit in understanding detail pathophysiology of the cells and/or microenvironment.
Currently many tools and methods are available for the prediction of secreted proteins from different organisms. Majority of them predict either classical or non-classical secretory proteins using various algorithms. To our knowledge, there is only one freely available web-based database namely Secreted Protein Database (SPD) known to host secreted proteins from human, mouse and rat [4]. But, the actual number of predicted secreted proteins from human cannot be confirmed due to error in the download link. Also, another limitation of this database is it contains only classically secreted protein list and was last updated in 2006.
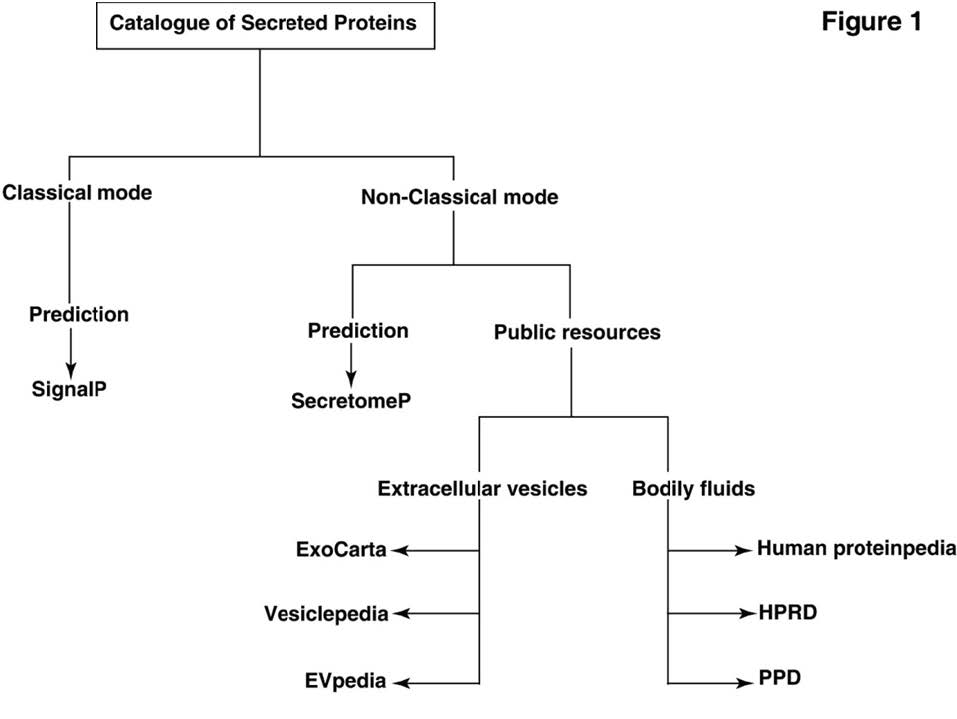
Here, using simple and integrative bioinformatics approach, human secreted proteins likely to get secreted both through classical and non-classical secretory pathways were catalogued. The list of secreted proteins was collated by using both prediction tools and from different database resources (Figure 1). Among the list of prediction tools, a widely used signal peptide prediction tool namely ‘SignalP v.4.1’ [10] and ‘SecretomeP v.1.0’ [11] for the prediction of secreted proteins through classical and non-classical secretory pathway was used respectively. Further list of secreted proteins known to be found in extracellular vesicles (EVs) and in human body fluids (blood, serum, plasma, saliva, semen, tear and urine) were merged from public databases namely ExoCarta [12,13], Vesiclepedia [14], EVpedia [15], Plasma Proteome Database (PPD) [16], Human Proteinpedia [17,18] and HPRD [19]. By integrating these tools resources, a high confidence list of human secreted proteins was generated. Based on their mode of secretion, these secreted proteins were known to be involved in many heterogeneous biological process, function and expression.
2. Materials and Methods
2.1. Standard human dataset
Human RefSeq protein sequence database was downloaded (08/09/14 version) from NCBI [20] and used as standard input dataset for the prediction of secreted proteins.
2.2. Prediction tools used
SignalP: The SignalP v.4.1 a stand-alone tool compatible with Linux platform was downloaded and installed. SignalP predicts the presence and location of signal peptide cleavage sites in amino acid sequences based on the combination of several artificial neural networks.
SecretomeP: The SecretomeP v.2.0 a stand-alone tool compatible with Linux platform was downloaded and installed. SecretomeP predicts non-classical secreted proteins using ab-initio approach.
The downloaded human protein RefSeq sequence dataset was split into batch of 10K sequences and each of these batches were searched against SignalP and SecretomeP using default parameters for the prediction of proteins secreted through classical and non-classical secretory pathways respectively. Further, the predicted list of secreted proteins at isoform level was converted to its gene level using in-house python scripts.
FunRich: A customizable venn diagrams were generated using FunRich [21], a windows based free software tool mainly used for the functional gene set enrichment and protein-protein interaction network analysis.
2.3. Resource of extracellular vesicles (EVs)
Vesiclepedia: This contains manually curated compendium of molecular data (proteins, lipids, RNA) identified in different class of EVs from more than 300 independent published studies from different organisms.
ExoCarta: This database contains manually curated molecular data identified only in Exosomes from both published and unpublished studies from different organisms.
EVpedia: EVpedia is an integrated and comprehensive proteome, transcriptome, and lipidome database of EVs derived from archaea, bacteria, and eukarya, including human.
Extracellular vesicular proteins pertaining to human were collated from these resources.
2.4. Resource of bodily fluids
Plasma Proteome Database (PPD): This database currently contains details of more than 10000 human proteins detected in serum/plasma curated from > 500 published studies.
Human Proteinpedia: This is a unified human proteomics resource that contains thousands of subcellular localizations, protein-protein interactions, protein expression annotations and millions of MS/MS spectra collated from both published and unpublished proteomic data contributed by biomedical community participation.
Human Protein Reference Database (HPRD): This is a database of manually curated proteomic data pertaining to protein-protein interactions, protein expression, sub-cellular localization, domain architecture and post-translational modifications collated from > 400000 published studies.
The list of human proteins annotated in bodily fluids was compiled and merged from these above freely available current database versions.
3. Results and Discussion
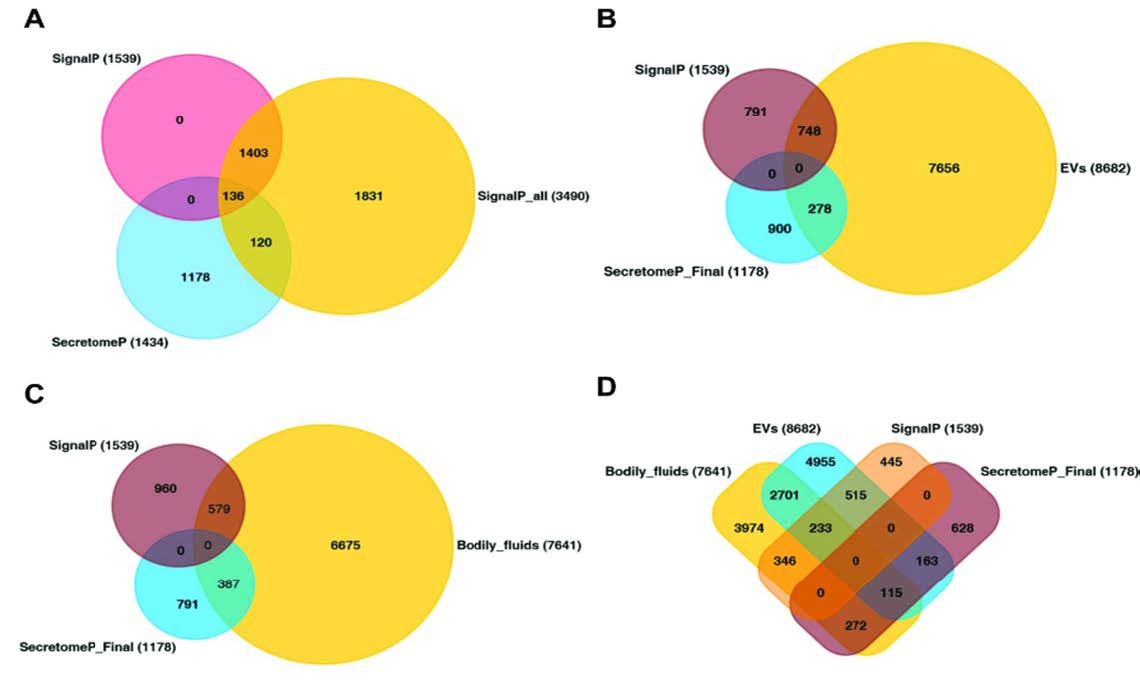
Then entire human protein sequences from the NCBI’s RefSeq database was searched using the most commonly used signal peptide prediction tool namely SignalP. The SignalP method predicted 3490 protein coding genes as secreted proteins having signal peptide sequence. Out of which, after applying stringent criteria based on D-score (discrimination score) > 0.8, a total of 1539 protein coding genes were selected (Supplementary Table 1).
Similarly, the entire human protein sequences were searched for the prediction of non-classical secretory protein using SecretomeP tool. Based on the stringent criteria of NN-score ≥ 0.9 (neural network score) and odds score > 0.6, SecretomeP method predicted 1434 protein coding genes likely to get secreted through non-classical secretory pathway. Due to its capable of predicting signal-peptide containing proteins, 136 overlapping protein coding genes predicted also by SignalP tool were further removed. To be more stringent in cataloguing these proteins, the remaining 1298 protein coding genes were further compared with 3490 protein coding genes predicted by SignalP method, irrespective of the any stringent criteria. As a result, further 120 overlapping protein coding genes between these two datasets were removed to generate high confidence 1178 (Supplementary Table 2) secreted protein coding genes (Figure 2A).
Using these combined prediction methods, ~8% (1539) of the total human proteome is likely to be secreted through classical secretory pathway where as another ~6% (1178) of the total human proteome is likely to be secreted through non-classical secretory pathway. In this study, using prediction approach alone, 14% of the human proteome is likely to be secreted.
Recent studies have elucidated the role of extracellular vesicles (EVs) in intercellular communication, pathogenesis, drug and vaccine delivery as well as possible reservoirs of biomarkers. These EVs are known to contain proteins, RNA and lipids [22]. A manually curated list of proteins isolated from these EVs secreted by variety of human cell types having experimental evidence was collated from ExoCarta, Vesiclepedia and EVpedia.
Using these EVs resources, nearly 40% (8682) of human protein coding genes were likely to be present in these EVs under different biological context. Out of which, ~9% (748) and 3% (278) of these protein coding genes were found in common with the SignalP (Supplementary Table 3) and SecretomeP method (Supplementary Table 4), respectively. On the other hand, ~49% of the secreted proteins predicted using SignalP method and ~24% of the secreted proteins predicted by SecretomeP method were also detected in these EVs (Figure 2B). Proteins containing signal peptides that are secreted by the ER-Golgi pathway are also detected in EVs suggesting an unknown mechanism of sorting secreted proteins into EVs.
In order to check the accessibility of theses secreted proteins in bodily fluids, the proteins were compared against bodily fluid dataset. To this end, freely available and manually curated public databases namely Plasma proteome database (PPD), Human Proteinpedia and HPRD were downloaded and collated. The body fluid datasets comprised of 38% (7641) of the human protein coding genes that was detected in plasma, serum, saliva, tear, semen and urine.
Out of 8682 protein coding genes collated from ExoCarta, Vesiclepedia and EVpedia, 35% (3049) of EV protein coding genes were likely to be present in human bodily fluids. Besides, ~38% (579/1539) of predicted classically secreted protein coding genes (Supplementary Table 5 and Figure 2C) and ~33% (387/1178) of predicted non-classically secreted protein coding genes (Supplementary Table 6 and Figure 2D) were also detected in human bodily fluids respectively.
4. Conclusions
Overall, using our integrated bioinformatics approach, we could show for the first time that ~14% of the human proteome is secreted, by prediction method alone. Out of which, ~38% of these predicted proteins were known to be found in EVs whereas 94% of these predicted proteins were known to be found in human bodily fluids. By assigning experimental evidence to those predicted secreted proteins, we anticipate that catalogue of these proteins secreted by various human tissues and/or cell types in different biological context could serve as reservoir of candidate biomarkers. Besides, the compendium may also aid in understanding disease mechanism.
Acknowledgments
I thank Suresh Mathivanan for editing the manuscript.
Conflict of Interest
Authors declare no conflict of interest.
Supporting Information
Supplementary Table 1: A list of secreted protein coding gene details predicted fromSignalP method.
Supplementary Table 2: A list of secreted protein coding gene details predicted from SecretomeP method.
Supplementary Table 3: A list of predicted secreted protein coding gene details from SignalP method present in Extracellular Vesicles (EVs).
Supplementary Table 4: A list of predicted secreted protein coding gene details from SecretomeP method present in Extracellular Vesicles (EVs).
Supplementary Table 5: A list of predicted secreted protein coding gene details from SignalP method detected in human bodily fluids.
Supplementary Table 6: A list of predicted secreted protein coding gene details from SecretomeP method detected in human bodily fluids.









 DownLoad:
DownLoad: