The Laplace transform as an alternative general method for solving linear ordinary differential equations

1.   Introduction

Switched systems (SSs) are a significant subclass of hybrid systems consisting of a series of subsystems and a signal for controlling the switch among them ^[1]. Over the last few decades, SSs have been applied in various domains, such as DC-DC power converters ^[2], inverter circuits ^[3], unmanned vehicles ^[4], secure communication ^[5], fault estimation ^[6] and image encryption ^[7]. At the same time, stability analysis and controller design for SSs, as fundamental issues in the control area, have been intensively studied and a significant amount of results have been proposed in the international literature; see, e.g., ^{[8,9,10,11,12,13,14,15,16]}.

The stability of an SS is dependent on each subsystem and highly affected by the switching frequency. Although all subsystems are asymptotically stable (AS), the entire SS may have a non-convergent solution trajectory caused by fast switching ^[17]. However, the stability can be maintained when the switching is sufficiently slow in the sense that the running time of each active subsystem is not less than a specified threshold called the dwell time (DT) ^[18]. Actually, this is also true even when fast switching occurs occasionally, as long as the average dwell time (ADT) is long enough ^[19].

In 2004, a type of switching signal, called the persistent DT (PDT) switching signal, was introduced in ^[20] to represent the switching signal that has infinitely many intervals of length no less than a given positive constant $\varepsilon$ (i.e., the PDT) during which no switch occurs, and distance between two consecutive intervals with this property does not surpass a period of persistence $\delta$. As explained in ^[20], the PDT switching is more common and suitable than DT and ADT switching for describing switching phenomena associated with hybrid systems.

There have been various control strategies, including uniform tube-based control ^[21], fault-tolerant control ^[22], quasi-synchronization control ^[23], quantized fuzzy control ^[24], $\mathcal{L}_1$ finite-time control ^[25], dynamic output-feedback control ^[26], sliding mode control ^[27] and model predictive control ^[28], that have been introduced for discrete-time SSs with PDT switching over the past few years. To the best of our knowledge, however, there are no available reports on the energy-to-peak control of continuous-time SSs (CTSSs) with PDT switching. Energy-to-peak control can guarantee that the infinity norm of the controlled output is less than a certain disturbance attenuation level ^[29]. In many practical situations, such a control approach serves as an appropriate selection for system design because it is insensitive to specific statistical characteristics of the noise signals and exhibits good robustness ^[30].

In this paper, we are interested in the energy-to-peak control for CTSSs with PDT switching. Our objective is to ensure that the CTSS is AS with a certain energy-to-peak disturbance-attenuation performance (EPDAP) level ^[31]. We first introduce a lemma regarding the asymptotic stability and EPDAP analysis of the PDT-based CTSS. Then, we propose a time-independent state-feedback controller design approach using a Lyapunov function (LF) and decoupling techniques. To reduce conservatism, we further present a quasi-time-dependent (QTD) controller design method. The required gains of these two types of controllers can be obtained by means of feasible solutions of linear matrix inequalities (LMIs), which are known to be easily solved with available tools in MATLAB ^[32]. Finally, we give an example to illustrate the effectiveness of our controller design strategies.

Notation: We denote by $\mathbb{R}^{n}$ the $n$-dimensional Euclidean space, by $\mathbb{Z}_{+}$ the set of non-negative integers, by $\mathbb{R}$ the set of real numbers, by $\Vert \cdot\Vert$ the $2$-norm, and by $\lfloor \cdot\rfloor$ the round-down operator. We apply an asterisk "$\ast$" to represent a symmetric term in a matrix and the superscript "$T$" to stand for the transpose operator. For any square matrix $X$, we utilize $X > 0\, (<0)$ to imply that the matrix is symmetric positive-definite (negative-definite) and define $\mathscr{S}(X)$ as $X+X^{T}$. Moreover, we let $\mathcal{K}_{\infty }$ be a class of continuous and strictly increasing functions $\beta(\cdot)$ that satisfy $\beta(0) = 0$.

2.   Preliminaries

In the field of control for SSs with PDT switching, the majority of published work primarily focuses on the discrete-time setting; see, e.g., ^{[21,22,23,24,25,28]}. In this paper, we will consider CTSSs with PDT switching as in ^[33,34]. The system model is described by

within which $\psi(t) \in \mathbb{R}^n$, $\phi(t) \in \mathbb{R}^p$ and ${u(t)} \in \mathbb{R}^q$ stand for the state, controlled output and control input, respectively; ${\varpi(t)} \in \mathbb{R}^r$ denotes the exterior disturbance that belongs to $\mathcal{L}_2[0, \, \infty]$ ^[35]; $A_{\varsigma (t)}$, $B_{\varsigma (t)}$, $E_{\varsigma (t)}$ and $G_{\varsigma (t)}$ are the given system matrices; $\varsigma (t)$ denotes the switching rule, which is a right-continuous function defined on $[0, \infty)$ and takes values in $\mathcal{M} = \{1, \ldots, M\}$. The sequence formed by all switching moments is given as $t_{0} = 0, \ldots, t_{l}, \ldots$. The minimum time interval between any two switching moments is defined by $h_{t} = \min \{t_{l+1} - t_l\}$ ($l \in \mathbb{Z}_{+}$). To avoid Zeno behavior, we set $h_{t} \geq C_0$, where $C_0$ is a positive constant.

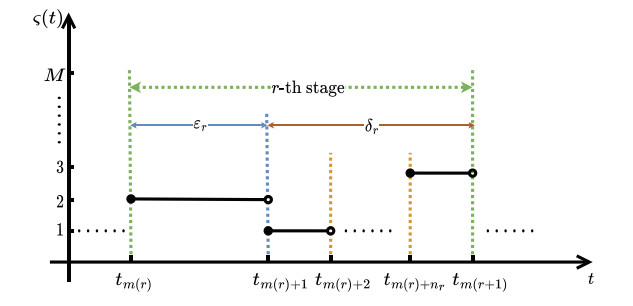
As described in Figure 1, the whole time axis is divided into infinitely many stages, where each stage consists of two parts, namely the slow switching part (i.e., $\varepsilon$-part) and the frequent switching part (i.e., $\delta$-part). We denote by ${\varepsilon_{r}}$ and ${\delta_{r}}$ the duration of each of these two parts in the $r$-th stage, respectively. Additionally, we use $t_{m(r)}$ to represent the initial moment of the $r$-th stage and $n_{r}$ to stand for the number of switches within the period of $(t_{m(r)}, \, t_{m(r+1)})$. Evidently, $\varepsilon_{r}$ and $\delta_{r}$ satisfy $\varepsilon_{r}\geq\varepsilon$ and $\delta_{r}\leq\delta$, respectively, and the switching moments within the interval $(t_{m(r)}, \, t_{m(r+1)})$ can be shown as $t_{m(r)+1}, \ldots, t_{m(r)+\kappa}, \ldots, t_{m(r)+n_{r}}$. For all $\kappa \in \mathbb{Z}_{+}$, we denote further that ${\delta_{r, \, \kappa}} = t_{m(r)+\kappa+1}-t_{m(r)+\kappa}$. Then, according to the meaning of the symbols introduced, it can be seen that ${\delta_{r, \, \kappa} \leq \delta}$ and $t_{m(r+1)} = t_{m(r)+n_{r}+1}$.

Remark 1. According to the PDT switching scheme, in the $r$-th stage, the duration of the slow switching part is at least ${\varepsilon}$, and the duration of the frequent switching part does not surpass ${\delta}$. As compared to the DT and ADT switching schemes, the PDT switching scheme is more general. To be more specific, when ${\delta}$ takes values of zero and infinity, the PDT switching scheme degenerates into the DT and weak DT switching schemes, respectively ^[20]. Furthermore, unlike the ADT switching scheme, the PDT switching scheme does not impose any restrictions on the switching frequency of the frequent switching part ^[36].

Let us now introduce the concepts concerning the asymptotic stability and EPDAP:

Definition 1. We say that CTSS (2.1) is AS if there is a function $\beta(\cdot) \in \mathcal{K}_{\infty }$ such that

holds in the case of ${\varpi(t)} = 0$.

Definition 2. Given a scalar $\gamma > 0$, we say that CTSS (2.1) has the EPDAP level ${\gamma}$ if

holds under $\psi(0) = 0$, where $\Vert \phi(t)\Vert_\infty = \sup_{t\geq 0}\Vert \phi(t)\Vert$.

Before ending the section, we state three preliminary propositions that we are going to use to prove our main results.

Proposition 1. ^[37] Given a scalar $\rho > 0$ and two locally integrable functions $\mathscr{V}(t)$ and $\Gamma(t)$ defined on $[0, \infty)$, if $\dot{\mathscr{V}}(t)\leq -\rho \mathscr{V}(t)+\Gamma(t)$ holds, then we obtain

Proposition 2. ^[38] Given a real number $\eta$ and real matrices $\mathcal{X}$, $\mathcal{Y}$, $\mathcal{U}$ and $\mathcal{W}$,

holds if and only if both $\mathcal{X} < 0$ and $\mathcal{X}+\mathscr{S}\{\mathcal{Y}^{T}\mathcal{U}\} < 0$ hold true.

Proposition 3. ^[39] For any real matrices $\mathcal{N}_{1}$, $\mathcal{N}_{2}$ and $\mathcal{N}_{3}$,

holds if and only if

3.   Main results

We will give the following lemma, which provides a criterion for the analysis of the asymptotic stability and EPDAP.

Lemma 1. Given scalars ${\delta}\geq0, \, \mu > 1, \, \rho > 0, \, \gamma > 0$ and ${h_{t} > 0}$, suppose that there is an LF $\mathscr{V}_{\varsigma (t)}(\psi(t), \, t)$$:(\mathbb{R}^{n}, \mathbb{Z}_{+})\rightarrow \mathbb{R}$ and two classes of functions $\beta_1(\cdot), \ \beta_2(\cdot)\in \mathcal{K}_{\infty}$ such that

hold. Then, for any PDT switching signal satisfying

CTSS (2.1) is AS with the EPDAP level $\bar{\gamma} = \gamma \sqrt{\mu ^{{\delta}\left/ h_{t}\right. +1}}$.

Proof. Denote by $N(a, \, b)$ the count of switched times within any left-open time interval $(a, \, b]$. Then, for any $t \in [t_{\kappa}, \, t_{\kappa+1}), \, \kappa \in \mathbb{Z}_{+}$, one has

Inequality (3.6) can be shown by mathematical induction. In fact, for $t\in (t_{0}, \, t_{1})$ (i.e., $\kappa = 0$), using Proposition 1, one can get from (3.3) that

Because of $N(\sigma, \, t) = 0$ for $\sigma \in [t_{0}, \, t)$, the inequality (3.6) obviously holds. For $t\in [t_{1}, \, t_{2})$ (i.e., $\kappa = 1$), from (3.2) and (3.3), one can obtain

which means that the inequality (3.6) is satisfied. Next, assume that (3.6) holds for $t\in [t_{k}, t_{k+1})$ ($k > 1, k\in \mathbb{Z}_+$). Then, one can write the following inequality:

For $t\in [t_{k+1}, t_{k+2})$, using (3.2) and (3.3) and noticing that $N(0, t) = k+1$, one has

It follows from (3.7) that

which means that (3.6) holds true for $t\in [t_{k+1}, t_{k+2})$.

When ${\varpi(t)} = 0$, for $t > 0$, one obtains from (3.6) that

which, together with

results in

From (3.5), one can find that

It follows from (3.1), (3.10) and (3.11) that

which means that

Thus, CTSS (2.1) is AS in light of Definition 1.

When ${\varpi(t)}\neq 0$, given that $\psi(0) = 0$, from (3.6), one has

for any $t > 0$, which, together with (3.4), yields that

From (3.9)–(3.12), one has

Thus, CTSS (2.1) has the EPDAP level $\bar{\gamma}$ according to Definition 2. □

Now, as in ^[40,41,42], we consider a state-feedback-based controller as

Based on Lemma 1, a design approach of the controller in (3.13) is given as follows:

Theorem 1. Given scalars ${\delta}\geq0, \, \mu > 1, \, {\rho > 0}, \, \gamma > 0$, ${\theta > 0}$ and ${h_{t} > 0}$, suppose that, for $i_{1} \in \mathcal{M}$, there exist matrices $P_{i_{1}} > 0$, $X_{i_{1}}$ and $Y_{i_{1}}$ such that (3.5) and

hold, where

Then, CTSS (2.1) is AS with the EPDAP level $\bar{\gamma} = \gamma \sqrt{\mu ^{{\delta}\left/ h_{t}\right. +1}}$ if the controller gains are chosen as

Proof. Consider the LF

Under the conditions of $P_{i_{1}} > 0$, $P_{i_{2}} > 0$ and (3.15), the conditions (3.1) and (3.2) hold true. For any $\varsigma(t) = i_{1}$, taking the derivative along CTSS (2.1), we have

where

Because $K_{i_{1}} = X_{i_{1}}^{-1}Y_{i_{1}}$, we can obtain that $\mathscr{S}\{P_{i_{1}}B_{i_{1}}K_{i_{1}}\} = \mathscr{S}\{B_{i_{1}}Y_{i_{1}}+(P_{i_{1}}B_{i_{1}}-B_{i_{1}}X_{i_{1}})X_{i_{1}}^{-1}Y_{i_{1}}\}$. Then, utilizing Proposition 2, from (3.14) we have that $\Lambda _{i_{1}} < 0$, which means that (3.3) is satisfied. Furthermore, by applying Proposition 3 to (3.16), (3.4) in Lemma 1 can be guaranteed. Thus, from Lemma 1, CTSS (2.1) is AS with the EPDAP level $\bar{\gamma}$. □

The controller designed in (3.13) is time-independent. Next, we focus on the time-dependent design. The controller to be determined takes the form of

where $q_{t}$ is a time scheduler that takes values in $\mathcal{N} = \{0, \ldots, \left\lfloor {\varepsilon} / {h_{t}} \right\rfloor \}$, described by

with $t_{\eta}\triangleq \max_{t_l \in [0, \, t]} \{t_{l} \}$.

The following result can be deduced from Lemma 1.

Lemma 2. Given scalars ${\delta}\geq0, \, \mu > 1, \, \rho > 0, \, \gamma > 0$ and ${h_{t} > 0}$, suppose that, for $t > 0$ and $r \in \mathbb{Z}_{+}$, there exists a QTD LF $\mathscr{V}_{\varsigma (t)}(\psi(t), \, q_{t})$$:(\mathbb{R}^{n}, \mathbb{Z}_{+})\rightarrow \mathbb{R}$ and two classes of functions $\beta_1(\cdot), \ \beta_2(\cdot)\in \mathcal{K}_{\infty}$ such that

hold, where

Then, for any PDT switching signal satisfying (3.5), CTSS (2.1) is AS with the EPDAP level $\bar{\gamma} = \gamma \sqrt{\mu ^{{\delta}\left/ h_{t}\right. +1}}$.

Proof. Let $\breve{\mathscr{V}}_{\varsigma (t)}(\psi(t), \, t) = \mathscr{V}_{\varsigma (t)}(\psi(t), \, q_{t})$. Then, we deduce from (3.20)–(3.22) that

which correspond to (3.1), (3.3) and (3.4) in Lemma 1, respectively.

Next, we need to prove that

holds, which corresponds to (3.2) in Lemma 1. Obviously (3.24) holds true when $t$ is not a switching instant. When $t = t_{m(r)+1}$ ($r\in \mathbb{Z}_{+}$), from (3.23), we obtain

and for $t = t_{m(r)+\kappa}$ ($\kappa = 2, \ldots, n_{r}+1, \, r\in \mathbb{Z}_{+}$), we have

Thus, (3.24) also holds when $t$ is a switching instant. The proof is finished. □

Then, based on Lemma 2, the desired QTD controller can be constructed according to the following theorem.

Theorem 2. Given scalars ${\delta}\geq0, \, \mu > 1, \, {\rho > 0}, \, \gamma > 0$, ${\theta > 0}$ and ${h_{t} > 0}$, suppose that, for $i_{1}\in \mathcal{M}$, ${i_{2}\in \{0, \ldots, M_{\varepsilon}-1 \} }$ and $i_{3}\in \mathcal{M}$, there exist matrices $\tilde{P}_{i_{1}, \, i_{2}} > 0$, $\tilde{P}_{i_{1}, \, M_{\varepsilon}} > 0$, $X_{i_{1}, \, i_{2}}$, $X_{i_{1}, \, M_{\varepsilon}}$, $Y_{i_{1}, \, i_{2}}$ and $Y_{i_{1}, \, M_{\varepsilon}}$ satisfying

and

for $i_{1}\neq i_{3}$, where

Then, for any PDT switching signal satisfying (3.5), the time-dependent controller in (3.18) can ensure that CTSS (2.1) is AS with the EPDAP level $\bar{\gamma} = \gamma \sqrt{\mu ^{{\delta}\left/ h_{t}\right. +1}}$ if the control gains are chosen as

Proof. Define $\eta_{i_{2}} = i_{2}h_{t}.$ Then, the switching interval $[t_{m(r)}, \, t_{m(r)+1})$ can be reformulated as

Consider the following LF

where

Note that $\mathscr{V}_{\varsigma (t)}(\psi(t), q_{t})$ is continuous on $[t_{m(r)}, t_{m(r+1)})$ and differentiable at $t\neq t_{m(r)+\kappa}$. Obviously, (3.20) is satisfied. In addition, (3.23) is guaranteed by (3.31).

Next, we only need to show that (3.21) and (3.22) hold true for any $t \geq 0$. In order to simplify the notations, we take $\varsigma (t) = i_{1}$ and $q_{t} = i_{2}$. For any $r\in\mathbb{Z}_+$, when $t\in \lbrack t_{m(r)}, \, t_{m(r)}+\eta _{M_{{\varepsilon} }})$, we can get from (3.33) that

Then, we obtain

According to CTSS (2.1) and (3.35), we have

where

In addition, utilizing CTSS (2.1) and (3.34), we can get

Similarly, when $t\in \lbrack t_{m(r)}+\eta _{M_{{\varepsilon} }}, \, t_{m(r)+1})$, we have from (3.33) that

This, together with CTSS (2.1), enables us to get that

where

Utilizing Proposition 2, we can deduce from (3.25)–(3.27) that

where

From (3.32) and (3.40)–(3.42), we can obtain that $\Theta_{1i_{1}i_{2}} < 0$, $\Theta_{2i_{1}i_{2}} < 0$ and $\Theta_{3i_{1}{M_{\varepsilon}}} < 0$, which, together with (3.36) and (3.38), ensure (3.21) for $t\in \lbrack t_{m(r)}, \, t_{m(r)+1})$. In addition, by means of Proposition 3, (3.28)–(3.30), (3.37) and (3.39) ensure (3.22) for $t\in \lbrack t_{m(r)}, \, t_{m(r)+1})$. Furthermore, due to the fact that $M_{r, \, \kappa}\leq M_{{\varepsilon} }$, (3.25)–(3.30) guarantee (3.21) and (3.22) for $t\in \lbrack t_{m(r)+1}, \, t_{m(r+1)})$. Thus, (3.21) and (3.22) hold true for any $t\in \lbrack t_{m(r)}, \, t_{m(r+1)})$. Considering the arbitrariness of $r$, by Lemma 2, CTSS (2.1) is shown to be AS with the EPDAP level $\bar{\gamma} = \gamma \sqrt{\mu ^{{\delta}\left/ h_{t}\right. +1}}$. The proof is finished. □

Remark 2. As commonly reported in the literature on SSs with PDT switching (see, e.g., ^[43,44,45], the design strategy proposed in Theorem 1 is time-independent. In order to reduce conservativeness, Theorem 2 presents a QTD design strategy by incorporating the time scheduler $q_{t}$ effectively. The benefits of this approach will be demonstrated in Section 4. However, it may be worth noting that this improvement comes at the cost of increased computational complexity.

4.   Example

Consider CTSS (2.1) subject to the following parameters:

We set ${\delta} = 2$, $h_{t} = 0.2$ and $\theta = 0.1$. Then, by solving the LMIs of Theorems 1 and 2, respectively, we can get the comparison outcomes of the optimal EPDAP level $\bar{\gamma}_{min}$ for different values of $\rho$ and $\mu$, as described in Tables 1 and 2, respectively. From these two tables, we have two observations. First, when one of the values of $\rho$ and $\mu$ is fixed, the optimal EPDAP level $\bar{\gamma}_{min}$ increases as the value of the other parameter increases. Second, when comparing the controller design method given in Theorem 1 with the one in Theorem 2, it is evident that the latter always yields better performance levels $\bar{\gamma}_{min}$. This improvement can be attributed to the fact that the design method in Theorem 2 is QTD.

Next, we set $\rho = 0.4$ and $\mu = 1.1$. By solving the LMIs of Theorem 2, we get the EPDAP level $\bar{\gamma}_{min} = 0.0866$ and the controller gains as follows:

In the simulation, we take the exterior disturbance as ${\varpi(t)} = e^{-0.2t}\sin(2t)$ and set the initial value as $\psi(0) = [5 \, -2]^{T}$. Figures 2–4 show the trajectories of PDT switching mode $\varsigma(t)$, time scheduler $q_{t}$ and states of the closed-loop CTSS, respectively. It is evident from Figure 4 that the open-loop CTSS is unstable. The trajectories of the states and control input of the closed-loop CTSS are depicted in Figure 5. It is apparent that the curves tend to zero as time $t\rightarrow \infty$, indicating that QTD controller (3.18) can ensure that the closed-loop CTSS is AS.

At last, we introduce

Figure 6 further describes the curve of $\gamma(t)$ given that $\psi(0) = [0 \quad 0]^{T}$. Apparently, $\gamma(t)$ progressively converges to $0.0077$, which is smaller than the optimal EPDAP level $\bar{\gamma}_{min} = 0.0866$. This shows the effectiveness of controller (3.18) in ensuring the EPDAP of the closed-loop CTSS.

5.   Conclusions

This work investigated the issue of energy-to-peak control for CTSSs with PDT switching. With the aid of an LF and a few decoupling techniques, a time-independent controller design approach was proposed in Theorem 1. To reduce conservatism, a QTD controller design method was further presented in Theorem 2. The required gains of these two types of controllers can be acquired by solving LMIs. Finally, an example was utilized to illustrate the validity of our controller design approaches.

The controllers under consideration are based on full-state feedback, which utilizes state variables as feedback signals to generate control inputs. However, there are certain scenarios in which implementing such controllers becomes challenging because directly measuring all of the state variables is often difficult ^[46]. The issue of energy-to-peak control for CTSSs with PDT switching based on output feedback will be explored as an extension of the current work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.