A review on bioremediation by microbial immobilization-an effective alternative for wastewater treatment

1.   Introduction

The viscous Stokes problem seeks unknown functions ${\bf u}$ and $p$ that fulfill the following equations,

where $\Omega$ is a polygonal domain in $\mathbb{R}^2$. For the nonhomogeneous boundary condition ${\bf u} = {{\bf g}}\; \mbox{on}\; \partial\Omega$, one can use the standard procedure by letting ${\bf u} = {\bf u}_0+ {\bf u}_g$. ${\bf u}_g$ is a known function satisfying ${\bf u}_g = {{\bf g}}$ on $\partial\Omega$ and ${\bf u}_0$ is zero at $\partial\Omega$ and satisfies (1.1) and (1.2) with different righthand sides. For the sake of simplicity, we only consider the homogeneous boundary condition, i.e., ${{\bf g}} = \mathbf{0}$. The scheme can be extended to the nonhomogeneous boundary condition. Using the standard notation for the Sobolev spaces, the weak formulation for the Stokes problems (1.1)–(1.3), in the primary velocity-pressure form, we seek ${\bf u}\in [H_0^1(\Omega)]^2$ and $p\in L_0^2(\Omega)$ such that,

In the standard finite element discretization schemes, pressure and velocity unknowns are approximated simultaneously via a saddle-point system. To avoid solving such an indefinite system, the divergence-free finite element methods have been proposed to compute the numerical velocity by solving a symmetric positive-definite system in a divergence-free subspace. Due to the discrete or exact divergence-free property, such a method eliminates the pressure from the coupled systems, resulting in a symmetric positive definite system with a smaller size. Previously, a divergence-free basis was constructed for different finite element methods, e.g., ^[1,2,3,4]. The original divergence-free weak Galerkin (WG) method was proposed in ^[3].

Unlike most existing divergence-free finite element methods, the discrete divergence-free WG method considered in this paper allows the meshes to consist of a mix of general polygons and hanging nodes. However, although the basis functions are discrete divergence-free, they may not guarantee good velocity approximation since the velocity error may depend on viscosity and pressure. This is because the div-free scheme is non-pressure-robust; thus, the velocity error bound depends on viscosity and pressure. Small viscosity values or inaccurate pressure approximations may produce an incorrect velocity solution to ruin the simulation.

This paper shows that the numerical pollution mentioned above, caused by small viscosities or large pressure errors, also appears for the previous discrete divergence-free WG method. In this paper, we contribute to modify the original scheme and investigate the technique to remove viscosity and pressure effects in the velocity approximations with minimal effort. The technique follows the previous work of the authors and employs the velocity-reconstruction operator to modify the load term. This reconstruction technique was first proposed by Linke ^[5,6] and was then widely used to modify the existing finite element scheme for Stokes problems ^{[7,8,9,10,11,12,13,14,15,16]} and other incompressible fluid problems due to the minimal efforts required to achieve the desired good quality in numerical solutions ^{[17,18,19,20,21,22]}. Unlike using the H(div) basis functions in H(div) finite element methods, the velocity reconstruction operator is designed to map the original velocity basis functions to a suitable subspace of the H(div) space. Then, this modification only changes the load term assembly, but the stiffness matrix remains the same. In addition to the velocity reconstruction operator, we also mention that there are other advanced approaches to achieve the desired pressure-robustness ^[17,23,24]. Due to the page limitation, we only cite an incomplete list of the previous schemes featuring pressure-robustness. For example, Zhang ^[25,26] constructed divergence-free pairs of finite element spaces and used it to solve incompressible fluid problems ^[27,28]. Another successful strategy is to employ the Stokes complex of the lowest regularity ^[29] and the approximate velocity in the H(div) space ^[30]. A similar approach has been used in hybrid discontinuous Galerkin methods (HDG) to achieve the desired pressure-robustness ^[31,32,33]. More details on divergence-free and pressure-robust schemes can be found in the review paper ^[34]. Recently, there is another approach to achieve the desired robustness by enriching the Raviart-Thomas (RT) basis functions into the $H^1$ -finite element spaces ^[35,36]. In this paper, we focus on designing the proper velocity-reconstruction operator and modifying the source term assembly to achieve robustness. The advantages of this modification lie in the potential to recycle the researchers' previous codes and enhance the former work with minimal changes to the reliable numerical approximation. We also demonstrate the pressure recovery procedure for the case that requires a pressure approximation.

The rest of this paper is organized as follows. In Section 2, we first introduce the notation and two existing numerical algorithms and then propose the robust pressure algorithm and the pressure recovery scheme. In Section 3, we demonstrate the main error estimates for the Stokes problem. Several numerical experiments are presented in Section 4. We conclude this paper in Section 5.

2.   Numerical scheme

This section recalls the standard WG method and proposes our new divergence-free and pressure-robust WG methods. Let ${\cal T}_h$ be a partition of the domain $\Omega$ consisting of a mix of polygons satisfying the set of conditions specified in ^[37]. Let ${\cal E}_h$ denote the set of all edges in ${\cal T}_h$ and ${\cal E}_h^0 = {\cal E}_h\backslash\partial\Omega$ be the set of all interior edges. Based on the partition $\mathcal{T}_h$, we introduce the following finite element spaces $W_h$ and $V_h$ for the pressure and velocity variables, respectively,

where $P_k(\omega)$ denotes the space of polynomials of degree at most $k$ restricted to $\omega = e$ or $T$.

The discrete weak gradient and divergence operators are defined locally on each $T\in {{\mathcal T}}_h$ as follows.

Definition 2.1. The discrete weak gradient $\nabla_{w}: V_h \mapsto [P_0(T)]^{2\times 2}$ and weak divergence operator $\nabla_w\cdot: V_h \mapsto P_{0}(T)$ are defined as follows,

For each edge $e\in {\cal E}_h$, let $Q_{b}$ be the $L^2$ projection from $[L^2(e)]^2$ onto $[P_{0}(e)]^2$. Then, we define

Here, $h_T$ denotes the mesh size for the element $T$. Then, a standard WG algorithm (see ^[38]) is as follows.

Algorithm 2.1. Standard weak Galerkin algorithm (SWG) A numerical approximation for (1.1)–(1.3) is to seek ${\bf u}_h = \{ {\bf u}_0, {\bf u}_b\}\in V_h$ and $p_h\in W_h$ such that

Algorithm 2.1 produces a saddle system, which can be challenging due to its indefiniteness, strong coupling between velocity and pressure, and large size. In some cases, linear solvers for this large system involving both velocity and pressure may not be effective. Instead, we use the divergence-free basis to decouple the velocity and pressure and solve a smaller system, which is symmetric positive definite.

2.1.   Divergence-free finite element basis

In this section, we introduce the divergence-free basis. First, we define the discrete divergence-free subspace $D_h$ of $V_h$ in the usual way (see ^[1,2,3]) as follows,

Following the techniques introduced in ^[3] and using the definition (2.1), we explicitly construct the basis functions as the following three types.

$1)$ Type 1 ($\Psi_0$): For each $T_i \in{{\mathcal T}}_h$, $i = 1, \cdots, N_K$ with $N_K$ being the number of elements, all the six linearly independent linear functions $\Phi_{6(i-1)+1}, \Phi_{6(i-1)+2}, \cdots, \Phi_{6(i-1)+6}$ in $V_h$ are discrete divergence-free since they are nonzero only in the interior of element $T_i$.

$2)$ Type 2 ($\Psi_t$): For each $e_i\in{{\mathcal E}}_h^0$, $i = 1, \cdots, N_E$ with $N_E$ being the number of interior edges, let ${\bf t}_{e_i}$ be its tangential vector and $\Psi_{e_i, 1}$ and $\Psi_{e_i, 2}$ be the two basis functions of $V_h$ that are nonzero only on $e_i$. Define $\Upsilon_i: = C_1\Psi_{e_i, 1}+C_2\Psi_{e_i, 2}$ such that $\Upsilon_i|_{e_i} = {\bf t}_{e_i}$. It is easy to verify that $\Upsilon_i$ is discrete divergence-free using the divergence theorem. Note that $\Upsilon_i$ is nonzero only on $e_i$.

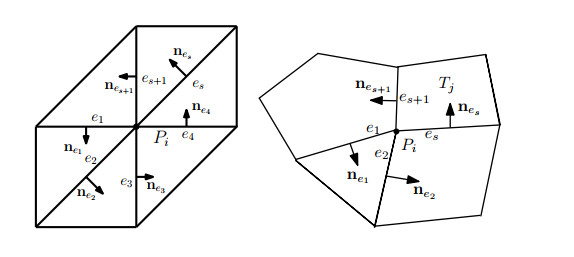
$3)$ Type 3 ($\Psi_V$): For each interior vertex $P_i\in {\cal V}_h$, $i = 1, \cdots, N_V$ with $N_V$ being the number of interior vertices, there are $r$ elements sharing $P_i$ which form a hull ${\cal H}_{P_i}$ as shown in Figure 1. Consequently, there are $r$ interior edges $e_j$ ($j = 1, \cdots, r$) incident with $P_i$. Let ${{\bf n}}_{{e_j}}$ be a normal vector on $e_j$, and we assume that the normal vectors ${{\bf n}}_{e_j}$ $j = 1, \cdots, r$ are counterclockwise around the vertex $P_i$ as shown in Figure 1. For each $e_j$, let $\Psi_{e_j, 1}$ and $\Psi_{e_j, 2}$ be the two basis functions of $V_h$, which are nonzero only on $e_j$. Define $\Theta_j = C_1\Psi_{e_j, 1}+C_2\Psi_{e_j, 2}\in V_h$ such that $\Theta_j|_{e_j} = {{\bf n}}_{e_j}$ and then define $\Lambda_i = \sum_{j = 1}^r \frac{1}{|e_j|}\Theta_j$, which is discrete divergence-free by the divergence theorem. The construction can be applied to triangular and polygonal grids, as shown in Figure 1.

Figure 1.  Hull ${\cal H}_{P_i}$ for triangular grids and polygonal grids.

DownLoad: Full-Size Img PowerPoint

The dimension of $V_h$ is $6N_K + 2N_E$. Since we use a piecewise constant space $W_h$ for the pressure, there are $N_K-1$ divergence-free constraints. Subtracting the number of divergence-free constraints from the total degrees of freedom (DoFs), $(6N_K + 2N_E)-(N_K - 1) = 6N_K + N_E + N_V$ (where we use the Euler's formula in 2D), we get the dimension of the discrete divergence-free subspace $D_h$. Note that the total number of the three types of divergence-free basis functions is exactly $6N_K + N_E + N_V$, indicating that we found all the basis functions that are supported locally. Specifically, the above basis functions correspond to the components of ${\bf u}_0$ and ${\bf u}_b = \{ {\bf u}_t, {\bf u}_V\}$. The basis functions for ${\bf u}_0$, i.e., $\{\Psi_0\}$, are defined only on the interior of each element $T$, which is the same as the previous SWG element. The basis functions for ${\bf u}_t$, that is, $\{\Psi_t\}$, are defined only on each edge $e\in\mathcal{E}_h^0$ along the tangential direction, and the basis functions for ${\bf u}_V$, i.e., $\{\Psi_V\}$, are defined only on the edges incident with the vertex $V$.

Using the divergence-free basis (2.2), the decoupled algorithm can be proposed to solely solve the velocity ${\bf u}_h$ as follows; see ^[3] for more details.

Algorithm 2.2. Divergence-free WG algorithm A discrete divergence free approximation for (1.1)–(1.3) is to find ${\bf u}_h = \{ {\bf u}_0, {\bf u}_b\}\in D_h$ such that

Although this algorithm decouples the unknown variables in ${\bf u}$ and $p$, it is essentially equivalent to the SWG Algorithm 2.1. Thus, the velocity error still depends on the pressure error (see Theorem 1 and Table 2). This may cause inaccuracy and instability when problems occur with a low viscosity and a pressure singularity. This computational challenge can be resolved using the pressure-robust enhancement, which will be discussed in the next section.

2.2.   Pressure robust enhancement

We shall employ the velocity reconstruction operator to enhance Algorithm 2.2. The reconstruction operator $\Pi_h {\bf v}: D_h\to \tilde{D}_h\subset H(\text{div}; \Omega)$ is defined as

Let $\tilde{D}_h|_T = \text{RT}_0(T)\cap H(\text{div}; \Omega)$. As the fact that $\Psi_t$ is aligning the tangential direction on each edge, we only need to compute the reconstruction operator corresponding to $\Psi_V = \{\Lambda_1\cdots\Lambda_{N_V}\}$. It gives

Here, it is easy to verify that in (2.3): $\Pi_h\Lambda_i = \sum_{j = 1}^r\text{sign}_{e_j}\phi_{e_j}^{\text{RT}_0},$ where $\phi_{e_j}^{\text{RT}_0}$ is the corresponding $\text{RT}_0$ basis on the edge $e$. We associate a unit normal vector ${{\bf n}}_e$ with $e\in\mathcal{E}_h^0$, which is assumed to be oriented from $T^+$ to $T^-$. If $e$ is a boundary edge/face, then ${{\bf n}}_e$ is the unit outward normal vector to $\partial\Omega$. For the outer normal ${{\bf n}}$, if $[{{\bf n}}\vert_T]_{e_j} = {{\bf n}}_{e_j}$, we assign $\text{sign}_{e_j} = 1$; if $[{{\bf n}}\vert_T]_{e_j} = -{{\bf n}}_{e_j}$, we assign $\text{sign}_{e_j} = -1$. Thus, by employing $\Pi_h$, we propose the following pressure-robust scheme.

Algorithm 2.3. Pressure-robust divergence-free WG algorithm A pressure-robust divergence-free approximation for (1.1)–(1.3) is to find ${\bf u}_h = \{ {\bf u}_0, {\bf u}_b\}\in D_h$ satisfying

As we can see from the discretization, the stiffness matrix is the same as Algorithm 2.2, but only the load vector changes. By this minor modification, the desired pressure-robustness can be achieved. The results will be demonstrated in Theorem 2 and validated in numerical experiments.

Remark 2.1. For triangular, rectangular, tetrahedral, and cubic meshes, we can directly employ the associated RT$_0$ or RT$_{[0]}$ basis functions to perform the velocity reconstruction. For polygonal / polyhedral meshes, the techniques in ^[7,8] can be used to build the operator $\Pi_h {\bf v}$.

2.3.   Pressure recovering

In Algorithms 2.2 and 2.3, we decouple the unknowns and only compute the velocity solution ${\bf u}_h$. In some cases, the pressure variable is also needed. In this section, we propose the following procedure that computes the pressure after obtaining the velocity ${\bf u}_h$.

Algorithm 2.4. Pressure recovering algorithm The pressure can be obtained by solving the following equation: find $p_h\in W_h$ such that

Here, $\ell({\bf v}) = ({{\bf f}}, {\bf v}_0)$ for Algorithm 2.2 and $\ell({\bf v}) = ({{\bf f}}, \Pi_h {\bf v})$ for Algorithm 2.3. As ${\bf v}\in{{\bf V}}_h\backslash D_h$, let us assume $p_h^- = p_h|_{T}$ is already known, and we can choose ${\bf v} = \{ {\bf v}_0 = 0, {\bf v}_b = {{\bf n}}_e\}$ with $e\in\partial T$ and the value of $p_h^+ = p_h$ on the adjacent element sharing the edge $e$ is not computed. Then, the definition of $b(\cdot, \cdot)$ implies $b({\bf v}, p_h) = (\nabla_w\cdot {\bf v}, p_h) = \sum_T \langle {\bf v}_b\cdot{{\bf n}}_e, p_h\rangle_{\partial T} = \langle {\bf v}_b\cdot{{\bf n}}_e, {{[\![}} p_h{{]\!]}}\rangle_e = |e|\left(p_h^+-p_h^-\right).$ Here, ${{\bf n}}_e$ denotes the normal direction from the current element $T$ to its adjacent element that shares the edge $e$. In the implementation, we can assume $p_h|_{T_1} = 0$ to start and compute all the values in $p_h|_T$ as above sequentially and locally. There is no need to form the global matrix explicitly.

2.4.   Further DoFs reduction by eliminating ${\bf u}_0$ unknowns

In the above proposed algorithms, we can do further DoFs enhancement by eliminating the unknowns corresponding to ${\bf u}_0$ to obtain a smaller system. This elimination can be done locally when the global matrix is assembled via static condensation. To state the local elimination procedure, denote by $D_h(T)$ the restriction of $D_h$ on $T$, i.e.,

Algorithm 2.5. An approximation to the problem (1.1)–(1.3) is given by seeking ${\bf u}_h = \{ {\bf u}_0, {\bf u}_t, {\bf u}_b\}\in D_h$ satisfying a global equation

and a local system on each element $T\in\mathcal{T}_h$,

Remark 2.2. The above algorithm consists of a local system solved on each element $T\in\mathcal{T}_h$ to eliminate ${\bf u}_0$ and a global system for ${\bf u}_b$, and a global system has ${\bf u}_b$ as its only unknowns that will reduce the number of unknowns of the WG system. The comparison of DoFs is shown in Figure 2.

Figure 2.  Sparsity pattern for Algorithm 2.2/2.3 (left) and Algorithm 2.5 (right) for uniform mesh with $h = 1/16$.

DownLoad: Full-Size Img PowerPoint

3.   Convergence results

In this section, we present the error analysis of Algorithm 2.3 to demonstrate its advantages. Denote by $Q_{0}$ the $L^2$ projection operator from $[L^2(T)]^2$ onto $[P_1(T)]^2$. Define $Q_h {\bf u} = \{Q_0 {\bf u}, Q_b {\bf u}\}\in V_h$ and let ${\mathbb{Q}}_h p$ be the local $L^2$ projections onto $P_{0}(T)$. Furthermore, we define the following norm corresponding to {the} WG finite element methods:

The following optimal error estimates have been derived in ^[3,38].

Theorem 3.1. (Non-pressure robust scheme) Let $({\bf u}; p)\in [H_0^1(\Omega)\cap H^{2}(\Omega)]^2\times (L_0^2(\Omega)\cap H^{1}(\Omega))$ be the solution of (1.1)–(1.3) and $({\bf u}_h; p_h)\in V_h\times W_h$ be the solutions of (1.1)–(1.3) and Algorithm 2.1 or Algorithms 2.2–2.4, respectively. Then, the following error estimate holds true,

Proof. The proofs can be found in ^[3]. □

Theorem 3.2. (Pressure-robust scheme) Let $({\bf u}; p)\in [H_0^1(\Omega)\cap H^{2}(\Omega)]^2\times (L_0^2(\Omega)\cap H^{1}(\Omega))$ be the solution of (1.1)–(1.3) and $({\bf u}_h; p_h)\in V_h\times W_h$ be the solution of (1.1)–(1.3) and Algorithms 2.3 and 2.4, respectively. Then, the following error estimate holds true,

Proof. By estimating the inconsistent errors caused by changing the righthand load vector and following the techniques in ^[3], the theorem can be proved. □

Remark 3.1. Although the divergence-free scheme only needs to solve the velocity component, the velocity error may still depend on the pressure, which is a non-pressure-robust scheme as shown in Theorem 1. By modifying the load vector, we completely remove the pressure dependence in the error estimate to achieve the desired pressure robustness. Besides, the pressure-robust error analysis can be obtained similarly to the rigorous analysis in ^[7].

4.   Numerical experiments

In this section, we test several benchmark problems to report numerical performance and validate the convergence results shown in Theorems 1 and 2. In all numerical tests, triangular meshes have been used.

4.1.   Example 1. Homogeneous Dirichlet boundary condition.

Let $\Omega = (0, 1)\times(0, 1)$ and the exact solution ${\bf u}$ and $p$ be,

Denote the errors ${\bf e} = \{(Q_0 {\bf u}- {\bf u}_0, Q_b {\bf u}- {\bf u}_b)\}$ and $\epsilon = \mathbb{Q}_h p-p_h$. We first compare the computational cost corresponding to Algorithm 2.1, Algorithm 2.2/2.3, and Algorithm 2.5. Since the stiffness matrix corresponding to Algorithms 2.2 and 2.3 is identical, we only compute the DoFs for Algorithm 2.2. The profiles for DoFs are reported in Table 1. Here, we exclude the unknowns for ${\bf u}_b$ for the Dirichlet boundary as computing the required DoFs.

Table 1.  Example 4.1: Comparison of DoFs for different algorithms. Here, "DoFs" denotes the degrees of freedom and "nnz" denotes the number of nonzeros of the stiffness matrix.

	Algorithm 2.1			Algorithm 2.2/2.3		Algorithm 2.5
N	DoFs$_u$	DoFs$_p$	DoFs	DoFs	nnz	DoFs	nnz
4	272	32	304	241	1861	49	360
8	1120	128	1248	993	8805	225	1984
16	4544	512	5056	4033	38, 245	961	9168
32	18, 304	2048	20, 352	16, 257	159, 333	3969	39, 280
64	73, 472	8192	81, 664	65, 281	650, 341	16, 129	162, 480
128	294, 400	32, 768	327, 168	261, 633	2, 627, 685	65, 025	660, 784
256	1, 178, 624	131, 072	1, 309, 696	1, 047, 553	10, 563, 685	261, 121	2, 665, 008

---

 | Show Table

DownLoad: CSV

In this table, we first observe that the required DoFs can be significantly reduced by employing the divergence-free basis. Since we only modify the assembly of the source term in Algorithm 2.3, the required DoFs in Algorithms 2.2 and 2.3 remain the same. As static condensation is employed (Algorithm 2.5), the DoFs of the global system can be further reduced. For example, when $N = 256$, the size of the global system is reduced from 1 M to 0.2 M, while the density of the matrix increased from 1E-5 to 4E-5.

Next, we will test the performance corresponding to non-pressure-robust scheme, Algorithm 2.2/Algorithm 2.4, and pressure-robust scheme, Algorithm 2.3/Algorithm 2.4, for a sequence of meshes and varying values in $\nu$. In Table 2, we report the error profiles and the convergence results. We observed that:

Table 2.  Example 4.1: Error profiles and convergence results.

$1/h$	$\|{\bf e}_0\|$	order	$\|\nabla{\bf e}_0\|$	order	$\|\epsilon\|$	order	$\|{\bf e}_0\|$	order	$\|\nabla{\bf e}_0\|$	order	$\|\epsilon\|$	order
	Algorithm 2.2/Algorithm 2.4						Algorithm 2.3/Algorithm 2.4
	$\nu = 1$
8	6.30E-2		5.23E-1		1.29E+0		8.27E-3		1.70E-1		2.71E-2
16	1.72E-2	1.9	2.84E-1	0.9	6.31E-1	1.0	2.17E-3	1.9	8.74E-2	1.0	1.17E-2	1.2
32	4.47E-3	1.9	1.47E-1	0.9	3.00E-1	1.1	5.50E-4	2.0	4.41E-2	1.0	5.32E-3	1.1
64	1.13E-3	2.0	7.44E-2	1.0	1.44E-1	1.1	1.38E-4	2.0	2.21E-2	1.0	2.57E-3	1.0
128	2.84E-4	2.0	3.74E-2	1.0	6.98E-2	1.0	3.46E-5	2.0	1.10E-2	1.0	1.27E-3	1.0
	$\nu = 1$E-2
8	6.21E+0		5.10E+1		1.29E+0		8.27E-3		1.70E-1		2.71E-4
16	1.70E+0	1.9	2.79E+1	0.9	6.31E-1	1.0	2.17E-3	1.9	8.74E-2	1.0	1.17E-4	1.2
32	4.41E-1	1.9	1.45E+1	0.9	3.00E-1	1.1	5.50E-4	2.0	4.41E-2	1.0	5.32E-5	1.1
64	1.12E-1	2.0	7.32E+0	1.0	1.44E-1	1.1	1.38E-4	2.0	2.21E-2	1.0	2.57E-5	1.0
128	2.80E-2	2.0	3.68E+0	1.0	6.98E-2	1.0	3.46E-5	2.0	1.10E-2	1.0	1.27E-5	1.0
	$\nu = 1$E-4
8	6.21E+2		5.10E+3		1.29E+0		8.27E-3		1.70E-1		2.71E-6
16	1.70E+2	1.9	2.79E+3	0.9	6.31E-1	1.0	2.17E-3	1.9	8.74E-2	1.0	1.17E-6	1.2
32	4.41E+1	1.9	1.45E+3	0.9	3.00E-1	1.1	5.50E-4	2.0	4.41E-2	1.0	5.32E-7	1.1
64	1.12E+1	2.0	7.32E+2	1.0	1.44E-1	1.1	1.38E-4	2.0	2.21E-2	1.0	2.57E-7	1.0
128	2.80E+0	2.0	3.68E+2	1.0	6.98E-2	1.0	3.46E-5	2.0	1.10E-2	1.0	1.27E-7	1.0
	$\nu = 1$E-6
8	6.21E+4		5.10E+5		1.29E+0		8.27E-3		1.70E-1		2.71E-8
16	1.70E+4	1.9	2.79E+5	0.9	6.31E-1	1.0	2.17E-3	1.9	8.74E-2	1.0	1.17E-8	1.2
32	4.41E+3	1.9	1.45E+5	0.9	3.00E-1	1.1	5.50E-4	2.0	4.41E-2	1.0	5.32E-9	1.1
64	1.12E+3	2.0	7.32E+4	1.0	1.44E-1	1.1	1.38E-4	2.0	2.21E-2	1.0	2.57E-9	1.0
128	2.80E+2	2.0	3.68E+4	1.0	6.98E-2	1.0	3.46E-5	2.0	1.10E-2	1.0	1.27E-9	1.0
	$\nu = 1$E-8
8	6.21E+6		5.10E+7		1.29E+0		8.27E-3		1.70E-1		2.71E-10
16	1.70E+6	1.9	2.79E+7	0.9	6.31E-1	1.0	2.17E-3	1.9	8.74E-2	1.0	1.17E-10	1.2
32	4.41E+5	1.9	1.45E+7	0.9	3.00E-1	1.1	5.50E-4	2.0	4.41E-2	1.0	5.32E-11	1.1
64	1.12E+5	2.0	7.32E+6	1.0	1.44E-1	1.1	1.38E-4	2.0	2.21E-2	1.0	2.57E-11	1.0
128	2.80E+4	2.0	3.68E+6	1.0	6.98E-2	1.0	3.46E-5	2.0	1.10E-2	1.0	1.27E-11	1.0

---

 | Show Table

DownLoad: CSV

● All the error profiles produced by Algorithm 2.2/Algorithm 2.4 and Algorithm 2.3/Algorithm 2.4 result in the optimal convergence rate: the velocity error measured in $H^1$-norm and pressure error measured in $L^2$-norm are of order $\mathcal{O}(h)$; the velocity error measured in $L^2$-norm is of order $\mathcal{O}(h^2)$. The convergence rates stay the same for different viscosity values $\nu$.

● The velocity errors produced by the non-pressure-robust scheme Algorithms 2.2–2.4 depend on the viscosity $\nu$. When $\nu$ decreases, the velocity error measured in the norms $H^1$- and $L^2$- increases on the order of $\frac{1}{\nu}$. In contrast, the pressure errors measured in $L^2$-norm stay the same as $\nu$ varies. These observations agree with (3.1).

● The velocity errors produced by pressure-robust scheme Algorithms 2.3 and 2.4 do not depend on the viscosity $\nu$. When $\nu$ decreases, the velocity error measured in the norms $H^1$- and $L^2$- remains the same. In contrast, the pressure error measured in $L^2$-norm decreases at the order $\nu$. These observations agree with (3.2).

● The above observations validate that, although the scheme can decouple the unknowns in velocity and pressure and solve them independently, the div-free finite element space is sometimes insufficient to ensure the accuracy of numerical solutions with satisfaction.

4.2.   Example 2 - Nonhomogeneous Dirichlet boundary condition

In this test, we shall consider the nonhomogeneous Dirichlet boundary conditions. Let $\Omega = (0, 1)\times(0, 1)$ and the exact solution is taken as

It is easy to see that ${\bf u}\vert_{\partial\Omega}\neq 0$. Thus, one needs to modify the method in order to deal with nonhomogeneous Dirichlet boundary conditions.

Table 3 reports the error profiles and convergence results. We compare the performance of Algorithm 2.2/2.4 and Algorithm 2.3/2.4 on a sequence of meshes with different values of $\nu$. To start, non-pressure-robust scheme Algorithm 2.2 and pressure-robust scheme Algorithm 2.3 have been employed to simulate the numerical velocity component. Then, when the velocity approximation is available, Algorithm 2.4 is used to recover the unknown pressure. As in the above test, though Algorithm 2.2 can decouple velocity/pressure and solely solve the unknown velocity, Algorithm 2.2 fails to produce reliable numerical solutions when the viscosity values are small. In contrast, the pressure-robust scheme Algorithm 2.3 is able to produce a viscosity-independent simulation for the velocity. As viscosity values vary, velocity errors (measured in the $L^2$-norm and the $H^1$-norm) remain the same. Furthermore, reducing viscosity values $\nu$ produces a more accurate numerical pressure, which gives a convergence rate for the pressure measured in the $L^2$-norm as $\mathcal{O}(h).$ These numerical results confirm the theoretical conclusions in the above section.

Table 3.  Example 4.2: Error profiles and convergence results.

$1/h$	$\|{\bf e}_0\|$	order	$\|\nabla{\bf e}_0\|$	order	$\|\epsilon\|$	order	$\|{\bf e}_0\|$	order	$\|\nabla{\bf e}_0\|$	order	$\|\epsilon\|$	order
	Algorithm 2.2/Algorithm 2.4						Algorithm 2.3/Algorithm 2.4
	$\nu = 1$
8	5.12E-2		5.83E-1		4.57E-1		2.81E-2		8.76E-1		7.62E-1
16	1.28E-2	2.0	2.91E-1	1.0	2.36E-1	1.0	7.69E-3	1.9	4.54E-1	0.9	4.41E-1	0.8
32	3.18E-3	2.0	1.46E-1	1.0	1.19E-1	1.0	2.00E-3	1.9	2.30E-1	1.0	2.37E-1	0.9
64	7.95E-4	2.0	7.29E-2	1.0	5.95E-2	1.0	5.06E-4	2.0	1.15E-1	1.0	1.23E-1	0.9
128	1.99E-4	2.0	3.65E-2	1.0	2.98E-2	1.0	1.27E-4	2.0	5.78E-2	1.0	6.29E-2	1.0
	$\nu = 1$E-2
8	3.80E-1		2.87		1.99E-2		2.81E-2		8.76E-1		7.43E-3
16	9.79E-2	2.0	1.47	1.0	1.01E-2	1.0	7.69E-3	1.9	4.54E-1	0.9	4.36E-3	0.8
32	2.47E-2	2.0	7.44E-1	1.0	5.16E-3	1.0	2.00E-3	1.9	2.30E-1	1.0	2.36E-3	0.9
64	6.20E-3	2.0	3.73E-1	1.0	2.63E-3	1.0	5.06E-4	2.0	1.15E-1	1.0	1.23E-3	0.9
128	1.55E-3	2.0	1.87E-1	1.0	1.33E-3	1.0	1.27E-4	2.0	5.78E-2	1.0	6.28E-4	1.0
	$\nu = 1$E-4
8	3.51E+1		2.91E+2		2.41E-2		2.81E-2		8.76E-1		1.43E-4
16	9.06	2.0	1.51E+2	0.9	1.24E-2	1.0	7.69E-3	1.9	4.54E-1	0.9	2.40E-5	2.6
32	2.29	2.0	7.65E+1	1.0	6.36E-3	1.0	2.00E-3	1.9	2.30E-1	1.0	1.29E-5	0.9
64	5.74E-1	2.0	3.84E+1	1.0	3.24E-3	1.0	5.06E-4	2.0	1.15E-1	1.0	9.36E-6	0.5
128	1.44E-1	2.0	1.92E+1	1.0	1.64E-3	1.0	1.27E-4	2.0	5.78E-2	1.0	5.53E-6	0.8
	$\nu = 1$E-6
8	3.50E+3		2.92E+4		2.41E-2		2.81E-2		8.76E-1		2.08E-4
16	9.05E+2	2.0	1.51E+4	0.9	1.24E-2	1.0	7.69E-3	1.9	4.54E-1	0.9	5.40E-5	1.9
32	2.29E+2	2.0	7.65E+3	1.0	6.37E-3	1.0	2.00E-3	1.9	2.30E-1	1.0	1.37E-5	2.0
64	5.74E+1	2.0	3.84E+3	1.0	3.25E-3	1.0	5.06E-4	2.0	1.15E-1	1.0	3.40E-6	2.0
128	1.44E+1	2.0	1.92E+3	1.0	1.64E-3	1.0	1.27E-4	2.0	5.78E-2	1.0	8.26E-7	2.0
	$\nu = 1$E-8
8	3.50E+5		2.92E+6		2.41E-2		2.81E-2		8.76E-1		2.09E-4
16	9.05E+4	2.0	1.51E+6	0.9	1.24E-2	1.0	7.69E-3	1.9	4.54E-1	0.9	5.44E-5	1.9
32	2.29E+4	2.0	7.65E+5	1.0	6.37E-3	1.0	2.00E-3	1.9	2.30E-1	1.0	1.39E-5	2.0
64	5.74E+3	2.0	3.84E+5	1.0	3.25E-3	1.0	5.06E-4	2.0	1.15E-1	1.0	3.50E-6	2.0
128	1.44E+3	2.0	1.92E+5	1.0	1.64E-3	1.0	1.27E-4	2.0	5.78E-2	1.0	8.80E-7	2.0

---

 | Show Table

DownLoad: CSV

4.3.   Example 3 - Mixed boundary condition

In this test, let $\Omega = (0, 1)\times(0, 1)$ and the exact solution ${\bf u}$ and $p$ be,

In this test, the top ($y = 1$), left ($x = 0$), and bottom ($y = 0$) boundaries are assumed to be the Dirichlet boundary conditions. The right boundary ($x = 1$) employs the Neumann boundary condition.

We perform convergence tests on a sequence of meshes with varying viscosity values $\nu$. The error profiles for the velocity and pressure solutions are plotted in Figures 3–5, in which we vary the mesh size $h$. The numerical results are similar to the two examples above. Figure 3 demonstrates the velocity errors measured in the $L^2$-norm. When we use the non-pressure-robust scheme Algorithm 2.2/2.4, the errors converge at the second order for different values of $\nu$. However, the velocity error depends on $\nu$ and the pressure. As the pressure error does not dominate the velocity errors, the error increases as a factor $1\nu$. This means that Algorithm 2.2/2.4 fails to produce reliable numerical solutions for the velocity. In contrast, Algorithm 2.3/2.4 outperforms Algorithm 2.2/2.4 and produces a robust numerical simulation. The velocity errors show an invariant behavior for varying viscosity values $\nu$.

Figure 3.  Example 4.3: Convergence results for Algorithm 2.2/2.4 (Left) and Algorithm 2.3/2.4 (Right) for velocity errors measured in $L^2$-norm.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Example 4.3: Convergence results for Algorithm 2.2/2.4 (Left) and Algorithm 2.3/2.4 (Right) for velocity errors measured in $H^1$-norm.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Example 4.3: Convergence results for Algorithm 2.2/2.4 (Left) and Algorithm 2.3/2.4 (Right) for pressure errors measured in $L^2$-norm.

DownLoad: Full-Size Img PowerPoint

The $H^1$-error of the velocity is plotted in Figure 4. We observe the same behavior and can draw the same conclusion as above.

Lastly, the $L^2$-error of the pressure is plotted in Figure 5. Algorithm 2.2/2.4 first produces a better pressure approximation before the dominance of pressure error $h\|p\|_1$. However, as the viscosity variable $\nu$ decreases, the pressure term will dominate the error, i.e., $h\|p\|_1 \gg h\nu \| \mathbf{u} \|_2$. Thus, pressure errors show a constant behavior on the same mesh with decreasing values of $\nu$. On the other hand, Algorithm 2.3/2.4 outperforms Algorithm 2.2/2.4. For small $\nu$, Algorithm 2.3/2.4 produces much better pressure solutions. All of the above tests validate our theoretical conclusions.

5.   Conclusions

In this paper, we enhanced the divergence-free WG finite element method proposed in ^[3] by modifying the load function via the velocity reconstruction operator. Our proposed algorithm results in a symmetric positive definite matrix, and the velocity error is pressure-robust. Moreover, we illustrated the procedure for recovering the pressure variables. Numerical experiments are presented to validate the theoretical results. As a future work plan, we will consider the development of an effective preconditioner, which may improve the efficiency further. In addition, the construction of a high-order ($k > 2$) divergence-free basis will be given and analyzed in our future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Jay Chu is partially supported by the Ministry of Science and Technology of Taiwan under the research grant MOST 111-2115-M-007-012. Xiaozhe Hu is partially supported by the National Science Foundation under the grant DMS-2208267. Lin Mu is partially supported by the National Science Foundation under the grant DMS-2309557.

Conflict of interest

The authors declare there are no conflicts of interest.