1.
Introduction
Bipolar disorder is a challenging neurological condition that is described by repetitive episodes of depression and mania, involving extreme mood swings that can have a considerable amount of influence on an individual's daily experiences [1]. People suffering from bipolar disorder will encounter periods of intense sadness or depression, as well as periods of heightened mood, known as mania or hypomania [2]. The underlying molecular process contributing to the development and advancement of bipolar disorder remain puzzling. Still, unfolding evidence hints that dysregulation of microRNAs (miRNAs) in bipolar disorder play a key role in the physiopathology of the given disorder. MicroRNAs are non-coding small (approximately 21 nucleotides) [3],[4] RNA molecules that govern gene expression post transcriptionally by binding to mRNA transcripts, and thus either inhibit their translation or promote their degradation. It is well established that miRNAs play crucial roles in the regulation of various biological processes, including metabolism, growth, development, and cell differentiation. These miRNAs are highly conserved across eukaryotic cells and are considered evolutionary ancient genes with a significant importance in gene regulation. RNA polymerase II polymerizes the genes for miRNA, resulting in the production of primary miRNAs (Pri-miRNAs). These Pri-miRNAs are subsequently cleaved by a microprocessor complex within the nucleus, generating stem-loop structures known as precursor miRNAs. Then, the precursor miRNAs are taken to the cytoplasm and are cleaved by DICER to form mature miRNAs; these miRNAs can further modulate gene expression by guiding the RNA-induced silencing complex (RISC) to target mRNAs, thus leading to either their degradation or translational repression. Considering that the human genome contains approximately 1900 miRNA genes, [3] many of which are implicated in human diseases, it is increasingly important to employ appropriate methods to study the expression and regulation of miRNAs in both physiological and pathological contexts.
Differentially expressed genes (DEGs) are kind of genes whose expression level or read count are significantly different from others between two experimental conditions, such as in a patient and in a healthy person [5]. DEGs play the most important part of clinical and pharmaceutical research, as they can easily help to identify therapeutic targets, biomarkers, and molecular signatures for a particular diagnosis [6]. The identification of DEGs have increased our understanding of bipolar disorder; unfortunately, the treatment has not advanced. Several research studies have used in silico methods to find genes that are differently expressed in bipolar disorder. In a study, a group of genes that were differentially expressed in the prefrontal cortex of people with bipolar disorder were identified using gene expression data from postmortem brain samples [7]. One study showed that lithium is the one of the most commonly used treatments for bipolar disorder [8]. Due to many limitations and a lack of research, the main therapeutic phytochemical that should be used as a drug in bipolar disorder is still not understood [9].
This research about bipolar disorder, a disease characterized by recurring instances of mania and depression, examines whether the medicinal plant Centella asiatica might prove to be of great help. We performed an in-silico analysis to explore the interaction between microRNAs (miRNAs) and genes that play key roles in bipolar disorder's neural circuitry. MiRNAs, small non-coding RNA molecules who regulate gene expression, are scrutinized for their connections to the disorder's major receptors. This investigation aims to discern whether Centella asiatica could be efficacious to mitigate bipolar disorder's impact by influencing miRNA expression. Our study ties traditional herbal knowledge with modern computational wisdoms, thus presenting a potential channel to evolve our understanding and treatment of bipolar disorder.
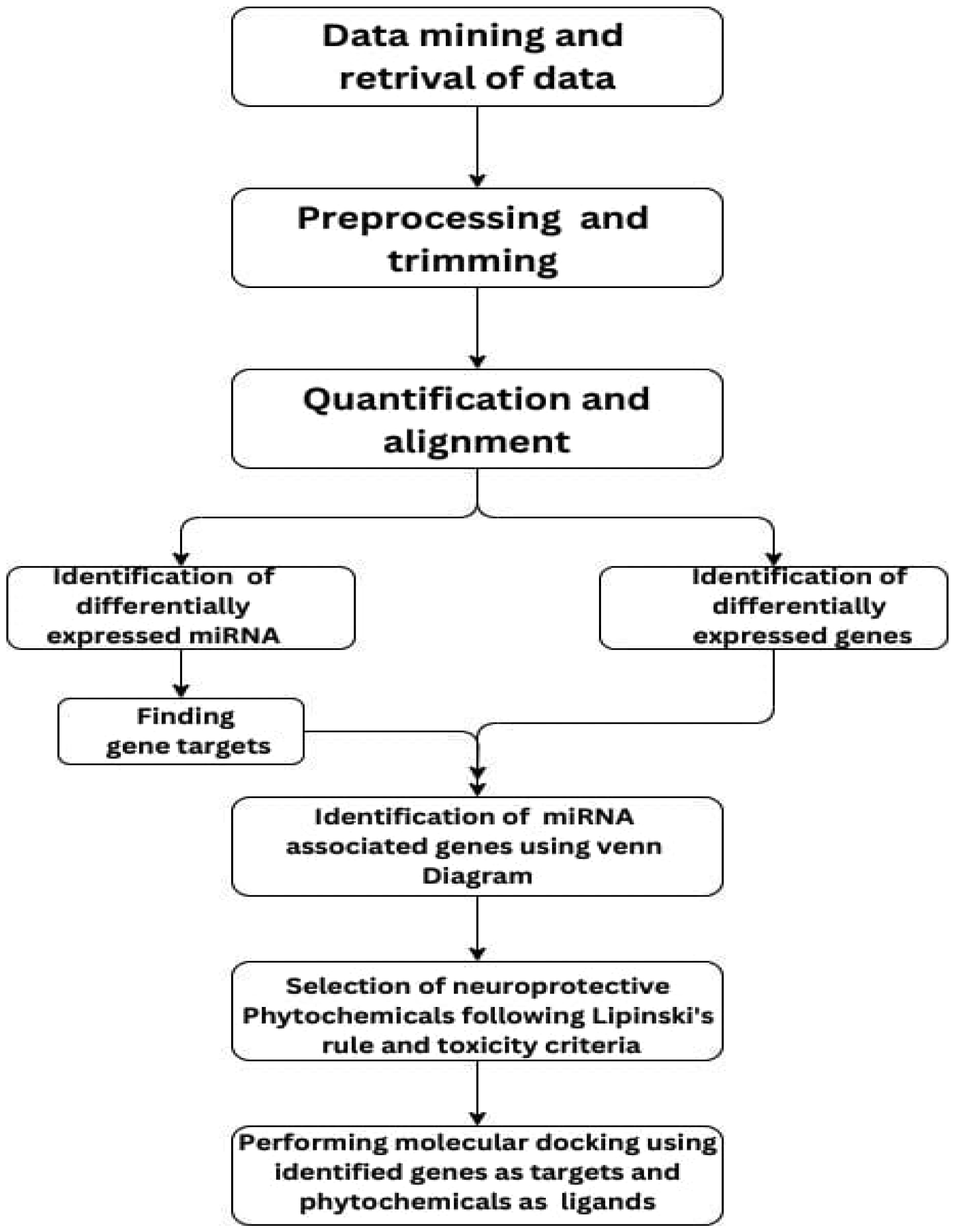
2.
Materials and methods
2.1. Retrieval of data
This study uses transcriptomic RNA-sequencing data of patient and control samples. As shown in Figure 1, the Gene Expression Omnibus (GEO) [10], the Sequence Read Archive (SRA) [11], and the PubMed databases from National Center for Biotechnology Information (NCBI) were used for data retrieval as the major platform for the collection of samples and related information.
2.2. Quality control and trimming
FASTQC was used to check the quality of each sample [12]. FASTQC is a widely used tool for quality control of high-throughput sequencing data; it assesses the quality and composition of sequencing reads in FASTQ files. The input involved utilizing FASTQ files, which were processed and read; the results are presented in the form of plots, except for basic statistics and overrepresented sequences. Low-quality bases, adapters, and unwanted sequences from the sample sequence were removed using Trim Galore and Trimmomatic tools. Trimming improves the data quality, normalizes the read length, mitigates biases, and enhances the accuracy of downstream analyses. FASTQC, Trim Galore, and Trimmomatics were accessed from the GALAXY server [13].
2.3. Alignment and quantification
The reference genome of Homo sapiens (h38) was aligned to all the samples utilized in this study using MiRDeep2 mapper and the Hisat2 tool [14],[15]. MiRdeep2 Mapper utilizes the mapping program Bowtie to perform the alignment and is specifically designed to map miRNA reads to a reference genome and to identify potential miRNA candidates. The hierarchical index of the human genome in HISAT is comprised of 48,000 local Ferragina-Manzini (FM) indexes that represent 64,000bp genomic regions. Once the Alignment was completed, MiRDeep2 quantifier and feature counts were used to count the number of expressed miRNAs and genes in the control and patient samples [16],[17].
2.4. Identification of differentially expressed miRNAs and genes
The differentially expressed miRNAs and genes were identified using the DESeq2 package [18]. DESeq2 is a very commonly used package to visualize and differentially analyze the count data by utilizing a negative binomial distribution; moreover, it assesses the relationship between the mean and the variance in the count data, which were obtained through high throughput sequencing assays.
2.5. Identification of targeted miRNA
The downregulated miRNA that was identified earlier was further used for the gene target identification. The gene targets of the miRNAs were identified using TargetScan and DIANA [19]. A popular belief is that miRNA binds to the 3′-UTRs of the targets transcript with the help of complementary base pairing in either one of the two classes of binding patterns. This understanding has led to the development of TargetScan and DIANA.
2.6. Identification of differentially expressed miRNA associated genes
The gene target list of differentially expressed miRNA and differentially expressed genes was added to make a vein diagram to identify the differentially miRNA associated genes using Venny [20]. A Venn diagram is a graphical representation that used to identify the list of common genes found in both of the two different spaces; it can also be thought of as a union feature of sets.
2.7. Identification of variations in differentially expressed miRNA associated genes
The differentially expressed genes were identified and the mutational variants were discovered using variation viewer, which is a tool that enables the user to search, view, and navigate variations accumulated in ClinVar (Database that stores information about relationship between human health and variations), dbSNPs (Database for Single Nucleotide Polymorphisms), and dbVar (Database of large scale genomic variants) with reference to genomics. The basis of the searches can be the gene name, chromosomal locations, phenotypes, or variant ID of dbVar and dbSNPs; the results can be explored with the help of annotated tables of variations and a dynamic sequence viewer.
2.8. Identification of phytochemicals with antipsychotic potential
After going through some already published papers on PubMed Central, we identified certain antipsychotic drugs that could act as therapeutics that targeted our associated genes. The compound for Lipinski's Rule of 5 was discovered using Molinspiration [21], which is an online tool to validate for drug likeness, which requires the Smile structure of the phytochemical. For the final selection of our compound, we performed a toxicity check using ProTox II [22].
2.9. Molecular docking studies to identify potential drug against bipolar disorder
To identify the drug binding to all associated miRNA genes, we performed docking using AutoDock 4.2 [23]. AutoDock 4.2 comprehends the binding interactions between a ligand (phytochemical molecule) and a receptor/target (the protein coded by our gene) and uses a Lamarckian genetic algorithm as a search algorithm to reduce the ligand scoring function. Finally, we performed Cygwin for molecular docking and analyzed our potential drug for bipolar disorder.
3.
Results
3.1. Retrieval of data
The transcriptomic RNA-sequencing sample of patients with bipolar disorder were retrieved from the GEO dataset of the NCBI. The selection of samples was performed under certain criteria, which included the age of the sample (studies should range between 40–55 years old), the species (which should be Homo sapiens in bipolar patients), and the experiment type (which included profiling by high throughput screening); illumine instruments should be preferably used for sequencing, the library source should be a transcriptomic data type, the library selection should include complimentary DNA (cDNA), and the considered disease should be neurological, hence the sample data should also be taken from somewhere within the brain. For the present study, a 2-year time frame between 2016–2018 was considered for data retrieval. Table 1 enlists the GEO datasets taken for the present study.
3.2. Identification of differentially expressed genes
The DESeq2 package in R was used to identify the DEGs. The criteria established to identify the upregulated DEGs was a p adjusted value less than 0.05 and a log2foldchange greater than 0. The number of upregulated genes obtained after performing the metanalysis (i.e., the data analysis technique) involved combining all the individual studies to produce a combined result; from this, we obtained 327 upregulated DEGs.
3.3. Identification of differentially expressed miRNAs
The DESeq2 package in R was used to identify DEGs and miRNAs. MiRNAs with a p adjusted value less than 0.10 and a log2foldchange less than 2 were considered as downregulated miRNAs. The study identified only 1 downregulated miRNA among patients with bipolar disorder, hsa-miR-3960, which had a p-adjusted value of 0.08 and a log2foldchange of −2.98.
3.4. Identification of gene targets of differentially expressed miRNA
After identifying a differentially expressed miRNA, we obtained 485 gene targets from targetscan and 58 gene targets from the DIANA tool. The total non-duplicate gene targets, which were selected from both DIANA and targetscan, were found to be 489.
3.5. Identification of differentially expressed miRNA associated genes
Three common genes between differentially expressed miRNAs and genes identified with the help of a Venn diagram were found to be CITED, NUDT4, and Arl8B, as mentioned in Figure 2. These three genes have been found to play a major role in regulating bipolar disorder.
3.6. Variations in differentially expressed miRNA associated genes
Variants in the DEGs were identified using Variation Viewer. Those variations that either had a pathogenic or likely pathogenic clinical significance were retrieved from the Variation Viewer database. Most of the mutations that were identified as pathogenic in CITED2, ARL8b, and NUDT4 were copy number variations. The details of the variants and their clinical significance in the gene of interest are listed in Table 2.
3.7. Identification of phytochemicals with antipsychotic potential
Following an intensive data mining procedure, a few neuroprotective phytochemicals were selected, which went through certain levels of selection, that is, they were finalized if they were found to follow Lipinski's rule of 5 and did not exceed the toxic class IV, thus signifying that they were not harmful if swallowed at concentrations below 300mg/kg. The toxicity class and allowed dosage of the phytochemicals is listed in Table 3 below.
3.8. Molecular docking studies to identify potential drug against bipolar disorder
Molecular docking was performed with the three identified genes as targets and the selected phytochemicals as ligands; the finalized compound that had the highest binding energy will all three of our gene/targets was found to be Asiatic acid. This signifies that this ligand can serve as the best possible phytochemical among this given list for managing bipolar disorder. The interactions of the molecular docking complex were visualized using the Discovery Studio Visualizer [51]. The binding energy of the phytochemicals with the protein receptor is given in Table 4 below. The results are shown in Figures 3–5 below.
4.
Discussion
Bipolar disorder is a substantial mood disorder that has a notable impact on both psychosocial and economic aspects. Despite being more prevalent than previously believed, it has received comparatively less research attention compared to disorders such as schizophrenia and major depression. There has been a growing need to focus on this disorder, as the global lifetime prevalence rate of bipolar disorder lies well within the range of 1.4–6.4% [52]; moreover, it is an incapacitating condition with substantial risk of mortality, presenting a 20 times greater suicide risk than the normal unaffected population [53].
Previous studies have fascinatingly revealed the key role of hsa-mir-3960 in amyotrophic lateral sclerosis (ALS) patients, which is a neurodegenerative disorder in which a patient gradually loses control over voluntary muscles [54]; the primary etiology of this disease has still not been discovered, but can be associated with neuronal degeneration. In this study, hsa-mir-3960 has emerged as the sole downregulated miRNA when the metanalysis was performed. Therefore, hsa-mir-3960 appears to play a key role in neuronal degradation.
This study revealed three miRNA-associated genes: CITED2, NUDT4, and Arl8B. A subsequently analysis disclosed CITED2's substantial role in governing neocortical layer II/III formation, the development of somatosensory callosal sensory projection neurons [55], and its involvement in neuroinflammation [56]. Additionally, this study highlights the pivotal role of neuroinflammation in mood-related disorders such as bipolar disorder. Moreover, CITED2 was found to minimize the pathogenic responses of innate immune cells by moderating a broad spectrum of inflammatory genes in macrophages, thus offering protection against harmful inflammation [57]. Arl8B emerged as a key regulator in neuronal connectivity, thereby directing axon branch positioning through the spatial control of autophagy [58] and impacting the mobility of lysosomes [59]. Most interesting, Arl8B has been identified as a novel biomarker for Alzheimer's disease [60]. NUDT4, or nudix hydrolase 4, regulates the degradation of diphosphoinositol polyphosphates, which are high-energy molecules [61]; on this note, a captivating study has suggested that targeting the enzyme responsible for dephosphorylating diphosphoinositol polyphosphates could serve as a novel therapeutic strategy for bipolar disorder, which potentially involves lithium therapy [62].
Through molecular docking of the three identified genes, the neuroprotective antipsychotic drug was finally found to be Asiatic acid, which is one of the main components of Centella Asiatic. Its chemical formula is pentacyclic triterpenoid, C30H48O5, and its molecular weight is 488.70kD [63]. It is a medicinal plant which was culturally used to improve memory and learning [64]; additionally, it promotes nerve growth and dendric branching [65] and is involved in protecting neurons from oxidative stress [66]. A study supported our results by pointing out the role of Asiatic acid in preventing cognitive defects with the help of the preservation of synaptic and mitochondrial function [67]; Several studies in the past have also mentioned the effect of mitochondrial dysfunction as a cause of bipolar disorder [68]. Asiatic acid is helpful to prevent oxidative stress and apoptosis by restraining the movement of α-synuclein into the mitochondria [69]. This actively plays a key role as a neuroprotectant in cerebral ischemia [70].
5.
Conclusions
In conclusion, this computational analysis provides a promising avenue for a therapeutic breakthrough in the vast field of bipolar disorder by exploring miRNA-correlated DEGs. This study underlines 3 notable genes, namely CITED2, NUDT4, and Arl8B, as significant regulators, thus implying the multifaceted therapeutic role of Asiatic acid in managing bipolar disorder. These findings extend promising prospects for targeted therapies to manage bipolar disorder.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.









 DownLoad:
DownLoad:







