A proof of Kirchhoff's first law for hyperbolic conservation laws on networks

1.   Introduction

In the dynamical systems community, networks are largely studied as families of Euclidean edges $\mathcal{E} := ([0, w_e])_{e \in E}$, with $w_e \in \mathbb{R}_{ > 0}$ and $E$ being an index set. The network's structure is often only incorporated by defining a family of dynamical systems $\Phi_e: [0, T] \times \mathcal{E} \to \mathcal{S}, e \in E$, where $\mathcal{S}$ models some state-space, $T \in \mathbb{R}_{ > 0}$, and the systems are coupled by their boundary conditions. Networks typically do not appear explicitly as mathematical objects and are not subject to further study.

In this work, however, we construct networks as metric spaces $(\mathcal{N}, d)$, where $d$ is a notion of path distance. We show that sufficiently regular networks $(\mathcal{N}, d)$ are Polish metric spaces—a convenient setting for deriving basic measure-theoretic notions underpinning abstract analysis. Although Euclidean calculus does not immediately apply to such networks, we develop, with minimal assumptions, a metric calculus for networks that preserves the properties of the known Euclidean setting.

Using such network calculus we introduce a weak notion of hyperbolic conservation laws, for which our main theorem, Theorem 4.2, states equivalence with an edge-wise system $(\Phi_e)_{e \in E}$ if all $\Phi_e$ are a solution to a hyperbolic conservation law on a Euclidean edge and Kirchhoff's algebraic boundary conditions hold for each $t \in [0, T]$. The theorem applies, in particular, if a solution to a hyperbolic conservation law admits a quasi-linear form (see Remark 8). Theorem 4.2 therefore implies that an arguably universal calculus for networks exists for which hyperbolic conservation laws can be stated without explicit Kirchhoff-type boundary conditions. Concerning the uniqueness of quasi-linear hyperbolic conservation laws, an Entropy condition is required edge-wise and additional conditions need to be satisfied at the boundaries. A global analysis perspective could help here as well and one could expect to formulate an Entropy condition on the entire network without a specific emphasis on the nodes and boundary conditions.

The results of our work thereby contribute to unifying the study of global objects relevant to dynamical systems, such as time-limiting phenomena or approximations, with the study of physically-plausible transport models in a mostly Euclidean setting. Furthermore, our work derives from the most basic axioms of mathematical analysis, a widely observed and practically essential phenomenon of mathematical physics.

Motivation and related work Networks are essential models in many applications such as information technology, chemistry, power systems, transportation, neuroscience, and social sciences. In light of such broad applicability, a general theory of (dynamical systems on) networks may

● derive system properties from basic axioms, in particular, when they cannot be validated precisely by the experimental method of physics, such as in traffic system modeling,

● provide a setting for describing abstract concepts, such as Kirchhoff's law, and

● make existing mathematical results applicable, e.g., limit theorems from probability or the theory of $L^p$-spaces.

Rather recently, the study of networks was, therefore, extended by a global—as opposed to edgewise-Euclidean—perspective based on modeling networks as abstract metrizable spaces ^[12,23,25]. While such network spaces, often also called quantum graphs, have been studied greatly before ^{[1,22,27,31,32,33]}, novel global phenomena may now be studied from the abstract perspective.

Transport on networks, modeled by coupled Euclidean hyperbolic conservation laws, has been of particular interest to the mathematical, science, and engineering communities ^{[2,3,4,5,9,10,11,13,14,15,16,17,18,19,24,28,29]}. Thus, we seek to derive a coupling of hyperbolic conservation laws as a consequence of the network's geometry and an associated abstract calculus characterized by universal properties. With such derivation, Kirchhoff's first law for hyperbolic conservation laws is provable and replaces a set of phenomenological model axioms.

Outline In Section 2, we introduce a particularly accessible setting for constructing networks based on graph data and equivalence relations, discuss the (un)suitability of graphs for the purpose of network modeling, rule out pathological examples of networks to develop a notion of regularity, and motivate the notion of path distance.

We continue constructing a Lebesgue-like measure for networks, developing differentiability, derivatives, and integration by parts in Section 3.

We close with motivating a notion of a weak hyperbolic conservation law for networks in Section 4, which lets us derive our main theorem, Theorem 4.2, an analog of Kirchhoff's law for these abstract dynamical systems.

2.   Networks

Our initial goal of this work is to introduce a rigorous notion of a network. Networks ought to be the central objects on which the rest of the theory will build. A guiding perspective is taken in classical mechanics, built into many of the mathematical terms used in this section. The decisive impact of this perspective will be demonstrated first.

Due to the widespread use of graphs in discrete mathematical modeling of related real-world phenomena, it is of interest to discuss their relevance to the purpose of network modeling. Classically, only when modeling pairwise relations of elements of a set $V$ called vertices, one resorts to graphs $(V, E)$, with $E: K \to V \times V$, where $E(k)$ is called an $edge$, $K$ is an index set and $k \in K$. This representation includes multiple edges with the same vertices. Possibly, one assigns a weight $W: K \to \mathbb{R}_{ > 0}$ to each edge to describe additional structure.

Definition 2.1 (Positively weighted graph). A positively weighted graph is a tuple $(V, E, W)$, where $V$ is a set, $E: K \to V \times V$ is a function from an index set $K$ to the product of $V$ with itself, and $W: K \to \mathbb{R}_{ > 0}$ is a function from $K$ to the positive reals. It is required that $E(K)_1 \cup E(K)_2 = V$, ^* that is, all vertices are connected to an edge.

^*The subscript denotes the projection on the respective element of the tuple.

As a network model and for the purpose of modeling in this work, however, graphs will not be sufficient. In mathematical terms, one can find an indication of the unsuitability of graphs in Lemma 2.1.

Lemma 2.1. Every metric, path-connected, finite vertex space has only one vertex.

Proof. A finite metric space $(V, d)$ has the discrete topology as for all $x \in V$ the ball with a radius smaller than

contains only $x$. If $V$ carries the discrete topology all subsets of $V$ are clopen. If $V$ is additionally path-connected, it is also connected, and thus the only clopen sets are $\varnothing$ and $V$. This implies $V = \{x\}$. □

Lemma 2.1 characterizes the incompatibility of graphs and the continuity of real numbers embedded into much of the mathematical language. This is relevant to practical problems, as continuity is the defining structure in continuum mechanics and is thus an inherent property in modeling network phenomena. In applications, the following, slightly informally stated properties are expected to be fulfilled.

Nonetheless, it turns out that one can construct networks that fulfill Property 2.1 from graphs but not as graphs—as will be shown by Definition 2.2 and Theorem 2.1. That is, positively weighted graphs non-uniquely encode the information of a specific network among all networks. Yet additional information is supplied by intervals of real numbers to obtain a general network setting with Property 2.1.

2.1.   Construction of networks

A quite elementary way to construct a network with such properties is as a set of equivalence classes of elements of intervals in $\mathbb{R}$ with a notion of path distance. While there are multiple ways to construct such spaces mathematically, even such that do not rely on graphs, the Definition 2.2 networks will be constructed as a set and equipped with a distance function. Some pathological examples of networks will then be ruled out in Definition 2.3, and Property 2.1 proven in Theorem 2.1. This presentation may be relatively accessible for interdisciplinary study, as it requires only a small amount of abstract language. Two examples of street networks are visualized in Figure 1.

A topological construction of networks, on the other hand, is given in ^[26]. Although the topological setting is arguably elegant, the presented quotient topology in general agrees with the path distance topology only for (in the work termed "combinatorically") locally finite networks (see "middle" of Figure 3). As a benefit of such a setting, it becomes clear that networks are topologically characterized by the universal property of the quotient topology. In this work, it will be shown that the assumption of a countable number of edges can be recovered from the regularity assumptions of Definition 2.3.

To define networks in a concise way, the following tools are introduced. Given a family $(I(w_j))_{j \in J}$ of intervals $I(w_j) : = [0, w_j] \subseteq \mathbb{R}$ with $w_j > 0$ for all $j \in J$ and $J$ being a non-empty index set. The disjoint union of these intervals is defined as

and an extended metric on $\mathrm{Un}\big((I(w_j))_{j \in J}\big)$ is defined as

Definition 2.2 (Network). Given a positively weighted graph $(V, E, W)$, one can define an equivalence relation$\sim$on the disjoint union $\mathrm{Un}\big((I(W(k)))_{k \in K}\big)$ by

A network associated with $(V, E, W)$ is defined as the set $\mathcal{N}$ of equivalence classes

where

A network is endowed with a function

Remark 1 (Network). In $\mathcal{N}$, the equivalence classes of the boundaries of intervals are called vertices of the network and denoted with $\mathcal{V}$. The set $\mathcal{E}$ is called edges of the network $\mathcal{N}$, where an element is a set that contains the equivalence classes of elements with the same index. The vertices of an edge $e \in \mathcal{E}$ are denoted by $0_e$ and $w_e$. Note that the distance function $d$ does not regard the orientation of the edges. The edges that contain the vertex $v$ will be denoted with $\mathcal{E}_v$.

Essentially, intervals are "glued" together, and a universal extension from distances along intervals to distances along simple paths is constructed. At this point, paths have not been defined rigorously. In fact, paths will be recovered from the distance function $d$—which will be shown to be a metric—in the case of regular networks.

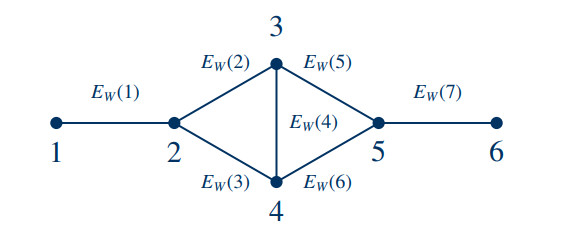
A classic example of a network is the Wheatstone network, which originated from electrodynamics ^[34] and is seminal in the study of transportation systems ^[7].

Example 2.1 (Wheatstone network). As per Definition 2.2, one can characterize a network by a positively weighted graph $(V_{wh}, E_{wh}, W_{wh})$, where $V_{wh}: = \{1, \dots, 6\}$, $K_{wh} : = \{1, \dots, 7\}$, and $E_{wh}: K_{wh} \to V_{wh} \times V_{wh}$, and

The weight function can be picked rather arbitrarily, but an embedding into $\mathbb{R}^2$ preserves vertex distances, e.g., for $W_{wh} \equiv 1$. The network $\mathcal{N}_{wh}$ characterized by the graph $(V_{wh}, E_{wh}, W_{wh})$ is called Wheatstone network. See Figure 2 for a visualization of the Wheatstone network.

2.2.   Properties of networks

There are certain networks, depicted in Figure 3, that do not carry the structure required in Property 2.1. These networks turn out to be somewhat pathological and do not lend themselves well to the purpose of modeling real-world networks. However, the following definition describes networks that fulfill all of the requirements of Property 2.1.

Definition 2.3 (Regularity). A network $\mathcal{N}$ is called regular if

● it is locally finite, i.e., each vertex is included in at most a finite number of edges,

● there exists a positive lower bound of the edge lengths, and

● it is connected with respect to the topology induced by $d$.

Regular networks allow the description of Lebesgue integration, continuous functions, and paths. These constructs are essential to the theory and practice of modeling transport phenomena on networks. The following theorem, therefore, describes several mathematical qualities of networks that enable their study.

Theorem 2.1 (Regularity). Regular networks $(\mathcal{N}, d)$ are path-connected, complete, locally compact, separable metric spaces with a countable number of edges.

Remark 2 (Regularity). Regularity, therefore, implies that networks are Polish spaces. All networks considered will be regular for the remainder of this work.

Proof.

1. It is shown that $d$ is an extended metric (may take the value $\infty$) on a regular network.

$Identitity ~~of ~~indiscernibles:$ Let $x, y \in \mathcal{N}$. If $x \neq y$ their distance $d(x, y)$ is not smaller than the length of a subinterval of some edge. To see why that is, consider the following cases.

$x$ is a vertex: Either $y$ must be an inner point of one of the finite number of edges connected to $x$. In this case (in slight abuse of notation) $d(x, y) \geq \min \{|{x-y}|, \varepsilon\}$, where $\varepsilon$ is a positive lower bound to the edge lengths. Otherwise, $y$ is contained in an edge not connected to $x$. In this case $d(x, y) \geq \varepsilon$.

$x$ is not a vertex: $d(x, y)$ is larger or equal to the shortest distance of $x$ to the closest vertex (see previous case) or (in slight abuse of notation) $d(x, y) = |{x-y}|$ if $x$ and $y$ are on the same edge.

If $x = y$, one has $d(x, y) = 0$ as for $p_1\sim x$, $q_1\sim y$ there is the extended metric distance $d'(p_1, q_1) = 0$.

$Symmetry:$ By the reversal of finite sequences and commutativity of addition, $d$ is symmetric.

$Triangle~~ inequality:$ Pick sequences $(p_i, q_i)_{i \in \mathbb{N}}, (p_i', q_i')_{i \in \mathbb{N}}$ and let $x, y, z \in \mathcal{N}$ and for $\gamma > 0$ (see Definition 2.2) with

Such sequences exist by definition of $d$. By concatenation of the sequences, one has

As this holds for all $\gamma > 0$, the triangle inequality follows.

2. It is shown that regular networks $(\mathcal{N}, d)$ are path-connected. By assumption, regular networks are connected. Regular networks are also locally path-connected by the argument following below. Generally, topological spaces that are connected and locally path-connected are path-connected. All of the above arguments are with respect to the topology induced by the extended metric $d$.

Let $x \in \mathcal{N}$, then one can pick $\varepsilon > 0$ such that $U_\varepsilon(x)$ contains only elements of $\mathcal{N}$ that share an edge with $x$. This is done such that $U_\varepsilon(x)$ is only a subset of one edge if $x$ is not a vertex. Otherwise, $\varepsilon$ should be picked as a lower bound of the edge lengths. $U_\varepsilon(x)$ is path-connected as edges are path-connected, and its restriction onto each edge is a subinterval.

3. By the following argument, one can show using the path-connectedness of $\mathcal{N}$ that the extended metric $d$ takes only finite values, i.e., that $d$ is a metric.

For $x, y \in \mathcal{N}$ pick a path $\gamma: [0, 1] \to \mathcal{N}$ with $\gamma(0) = x$ and $\gamma(1) = y$. As $[0, 1]$ is compact, $\gamma([0, 1])$ is also compact and in particular bounded. Therefore, $d(x, y)$ is bounded by the same bound.

4. A regular network $(\mathcal{N}, d)$ has a countable number of edges.

Let $\varepsilon > 0$ be the positive lower bound of the edge lengths and $x \in \mathcal{V}$. The initial goal is to show that for all $n \in \mathbb{N}_0$

is finite. This can be proved by an inductive argument. Clearly, $|{A_\varepsilon}| = 0$ and thus assume that $A_{\varepsilon n}$ is finite for some $n \in \mathbb{N}_0$. The vertices in $A_{\varepsilon(n+1)} \setminus A_{\varepsilon n}$ are connected to $A_{\varepsilon n}$ by single edges, as per the lower bound of edge lengths $\varepsilon$. However, as $A_{\varepsilon n}$ is finite and all $v \in A_{\varepsilon n}$ are only connected to a finite number of edges, one has

This implies that by the countable union of finite sets, the set of vertices $\bigcup_{n \in \mathbb{N}_0} A_{\varepsilon n}$ is finite, and the set of edges is countable.

5. A regular network $(\mathcal{N}, d)$ is a complete space, as for all Cauchy sequences $(x_n)_{n \in \mathbb{N}} \in \mathcal{N}$ one can pick $N \in \mathbb{N}$ such that $(x_{n+N})_{n \in \mathbb{N}}$ is contained in a finite number of edges, which by restriction, is therefore included in a compact and thus complete subset.

6. A regular network $(\mathcal{N}, d)$ is locally compact, as it is complete and neighborhoods contain bounded closed neighborhoods.

7. Generally countable unions of separable spaces are separable. Thus, regular networks are separable as they are countable unions of edges, which are separable.

□

Lastly, for the following work, a precise notion of a path and its length is useful as it relates $d$ and shortest paths.

Definition 2.4 (Path). A path in a regular network $\mathcal{N}$ is a continuous function $p: [0, l] \to \mathcal{N}$, where $l > 0$. The length of a path is defined as

A path $p: [0, l] \to \mathcal{N}$ is called parameterized by its length if $\ell(p_{|[0, l']}) = l'$ for all $l'\leq l$.

Remark 3 (Path). Given an edge $e_k \in \mathcal{E}$, in slight abuse of notation $\ell(e_k): = W(k)$ will also be written for any $k \in K$, where $K$ is the index set of the graph associated with the network. For a path $p:[0, l] \to \mathcal{N}$, if $p(0) = x$ and $p(l) = y$, it is said that $x \rightsquigarrow y$ for $p$.

Theorem 2.2. In a regular network $\mathcal{N}$, for any $x, y \in \mathcal{N}$, there exists at least one shortest path $x \rightsquigarrow y$ parametrized by its length $d(x, y)$.

Proof. For $x, y \in \mathcal{N}$, set $\varepsilon : = d(x, y)$. The lower bound on edge lengths implies that there is a finite number of paths $x \rightsquigarrow y$ in $\mathcal{N} \cap U_\varepsilon(x)$ that are parametrized by the length of each edge they can be restricted to. One of such that is shortest exists in this finite set of paths and must have length $d(x, y)$ by definition of $d$. □

3.   Calculus on networks

One may desire a medium to localize a notion of mass in networks and describe concentrations thereof. This mass may be a homogeneous object, unlike, e.g., a set of distinguished agents. This perspective is particularly meaningful in what one may call "egalitarian systems", as those of infrastructure or platform providers. Mathematical measure theory provides a framework to study such objects and includes a notion of signed, discrete, and continuous media.

3.1.   Measures and integration

There is a unique measure on a network that assigns each edge and subinterval thereof its length. Measures of this type are essential for classical integration and the modeling of densities. As regular networks are metric spaces, one can consider their Borel $\sigma$-algebra $\mathcal{B}(\mathcal{N})$ as a set of measurable sets. An example of a discrete measure often encountered in practice in the form of data is pictured in Figure 4.

Definition 3.1 (Lebesgue measure). A measure $\lambda$ is called the Lebesgue measure on a regular network $(\mathcal{N}, \mathcal{B}(\mathcal{N}))$ if for all $U \subseteq \mathcal{N}$ that are isometrically isomorphic to a possibly degenerate interval, i.e. $U \cong [0, l]$, $\lambda_{|U}$ is the classical Lebesgue measure.

Remark 4 (Isometric isomorphism). Two metric spaces $(U, d_U), (V, d_V)$ are isometrically isomorphic if there exists a bijective function $f: U \to V$ that preserves the metric distance, i.e., for all $u_1, u_2 \in U$

One writes $U \cong V$.

Lemma 3.1. On regular networks, a unique Lebesgue measure exists and is $\sigma$-finite.

Proof. For all elements $x \in \mathcal{N}$, one finds a neighborhood $U_x$ of $x$ that is isometrically isomorphic to a possibly degenerate interval. Due to the compactness of single edges and the countability of the edges (see Theorem 2.1), one can find a countable set of elements $B \subset \mathcal{N}$ such that

Without loss of generality, assume that $(U_x)_{x \in B}$ are disjoint, as otherwise a disjoint cover can be constructed from $(U_x)_{x \in B}$ by subtraction and intersection of sets. Therefore, by $\sigma$-additivity every such measure $\lambda$ must for all $A \in \mathcal{B}(\mathcal{N})$ satisfy the equation

where $\lambda_{|U_x}$ is the classical Lebesgue measure on the interval $U_x$. The right-hand serves as the unique definition of a networks' Lebesgue measure, as for other covers of $\mathcal{N}$ one can show equality by refinement of the cover $(U_x)_{x \in B}$. The Lebesgue measure is clearly $\sigma$-finite on regular networks as $U_x$ includes only a vertex and has measure zero, or is included in an edge with a finite length. □

The Lebesgue measure can be used to define an integral, called the Lebesgue integral (for the Lebesgue measure). The construction of this integral, a standard procedure, will not be covered. One also obtains Lebesgue densities, which will capture the notion of media defined by locally integrable functions and represent the state space of the dynamical systems studied in Section 4.

3.2.   Spatial derivatives and integration by parts

Some of the key uses of derivatives of mathematical objects are linear approximation and the representation of (physical) structures through differential equations. It is essential for this work to have a notion of differentiability for networks.

The common Euclidean theory of differentiation does not apply to networks as they are abstract metric spaces with non-oriented edges and vertices as non-trivial boundary. Therefore, it is tough to find a general notion of differentiability. The notions of differentiability differ depending on how much one likes to think of vertices as a boundary. The following definition may be the best choice since it enforces continuity constraints on values a function takes on vertices. Its offer of the existence of continuous differentiability may be essential to many use cases.

Definition 3.2 (Differentiability). A function $f: \mathcal{N} \to \mathbb{R}$ on a regular network is called k-(continuously) differentiable if $f\circ p$ is k-times (continuously) differentiable for all isometric paths $p: [0, l] \to \mathcal{N}$.

This notion of differentiability requires differentiability along all "structured" paths, yet does not require a notion of orientation, as only for derivatives one needs to pick a (local) orientation. Next to differentiability along edges, the definition turns out to impose an additional constraint of zero-derivatives on all vertices with more than two edges and differentiability across vertices with two edges (see Figure 5).

Differentiable functions are still missing a derivative. For a derivative, one has to pick an orientation for the edges. The orientation of network edges can be adapted to the orientation of a graph's edges that encodes the network, but it does not have to be. A problem that may appear is that there are vertices with two edges for which one picks different orientations. The following global object can solve this problem.

Definition 3.3 (Spatial derivative). An operator $D: C^1(\mathcal{N}) \to C(\mathcal{N})$ is called spatial derivative if it resembles a classical derivative, i.e., if for all open $U \subseteq \mathcal{N}$ for which there is an isometric isomorphism $p: (0, l) \to U$ it holds that for all $f \in C^1(\mathcal{N})$

Remark 5 (Orientation of 1-d components).

1. In the setting of dynamical systems, the notation $(\cdot)_x : = \tfrac{{\rm{d}}}{{\rm{d}} x} : = D$ will also be used.

2. Each spatial derivative provides a specific assignment of $0_e$ and $w_e$ for each edge $e \in \mathcal{E}$, as each edge inherits an orientation that is embedded into the definition. This fact can be characterized by monotonicity of functions: A function $f \in C^1(\mathcal{N})$ is said to be strictly monotonous on $e$ if $(Df)_{|e} > 0$. Then the definition

does not depend on the choice of $f$.

3. Given $D$, one can define the incoming and the outgoing edges of vertex $v$ as

4. A spatial derivative can be computed by a simple reduction to the real-valued case. Indeed, for all $e \in \mathcal{E}$ there exists a unique path $p$ parametrized by length $0_e \rightsquigarrow w_e$. As $p$ is locally an isometric isomorphism, one has for all $x \in e$

One obtains such a derivative by splitting the network on all vertices with more than two edges and picking an orientation for all parts. The partition's remaining elements are either isometric to intervals, or the original network is (topologically) a sphere. Piecewise derivatives are then compatible as they are zero at vertices with more than two edges, as this is required as per the differentiability of functions.

An analog of the classical product rule and the related integration by parts formula also holds for all spatial derivatives of a regular network. These properties are essential when dealing with certain dynamical systems that describe the transport of media in Section 4.

Lemma 3.2 (Product rule). A spatial derivative $D: C^1(\mathcal{N}) \to C(\mathcal{N})$ fulfills the product rule, i.e., for all $x \in e \in \mathcal{E}$ and $f, g \in C^1(\mathcal{N})$

Proof. Straightforward. □

Theorem 3.1 (Integration by parts). Let $D: C^1(\mathcal{N}) \to C(\mathcal{N})$ be a spatial derivative on a regular network $\mathcal{N}$ that is compact. Then, for all $f, g \in C^1(\mathcal{N})$

where $0_e, w_e$ are the endpoints of edge $e$ the order of which depends on $D$.

Proof. Let $f, g \in C^1(\mathcal{N})$ and $D: C^1(\mathcal{N}) \to C(\mathcal{N})$. One has

where $0_e, w_e$ are the endpoints of $e$, the order of which depends on $D$. One obtains the second identity in the theorem's statement because each edge is incoming into exactly one vertex and outgoing from exactly one vertex. □

4.   Weak solutions on networks and Kirchhoff's first law

Weak solutions to differential equations can be a generalization of the notion of a solution from continuously differentiable functions to Lebesgue densities. In the case of networks, this generalization manifests as both a generalization to a non-Euclidean setting and a generalization to less regular initial data.

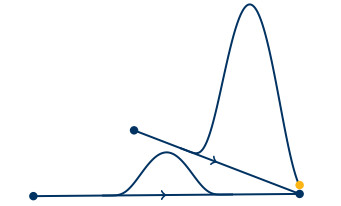
In Figure 6, it can be seen that even in "simple" networks, there may not exist a differentiable or even continuous solution to a conservation law. This fact and the possible generalization to less regular initial measures, such as $L^1_{loc}(\mathcal{N})$, suggest a weak solution theory for networks. This setting will turn out to yield a coupled system of weak solutions for each edge and thereby recover Kirchhoff's first law from the network's topology.

The following conservation law captures the dynamical systems of Lebesgue densities that will be treated in this work.

Remark 6 (Notation). For functions $\rho: [0, T] \times \mathcal{N} \to \mathbb{R}$ and $A \subseteq \mathcal{N}$, the notation $\rho_{|A} : = \rho_{|(0, T) \times A}$ will be used. Note that in the following for functions, unless otherwise specified, $(\cdot)_{|\cdot}$ will denote the restriction, $(\cdot)_{\cdot}$ a partial derivative, and $(\cdot)_{\underline{\cdot}}$ the projection onto a factor of the codomain.

For example, for a continuously differentiable function

it will be written

The time integrals $\int \, \cdot \, \, {\rm{d}} t$ considered will be Lebesgue integrals. Further, $A^\circ$ will denote the interior of $A \subseteq \mathcal{N}$.

Definition 4.1 (Conservation laws on networks). The functions

fulfill a conservation law with a spatial derivative $\tfrac{{\rm{d}}}{{\rm{d}} x}$ on the regular network $\mathcal{N}$, if for all $\phi \in C_c^\infty([0, T] \times \mathcal{N})$

It is important to mention that the above solution concept enforces the flow to be zero on vertices included in only one edge. That is, there is no in- or outflow of the network. These edges may be seen as dead-ins or dead-ends. Excluding them is a purely technical feature that offers a slightly more condensed description. Even in this setting, one can always introduce "dummy edges" and not lose generalization.

To validate the introduced solution concept, it should be made sure it is compatible with the classical setting in the sense of Theorem 4.1.

Theorem 4.1 (Classical solutions). In the setting of Definition 4.1, if $\mathcal{N}$ has only one edge $e$ and $\rho, \nu \in C^1([0, T] \times \mathcal{N})$, then $\rho$ fulfills a conservation law with $\nu$ and $\tfrac{{\rm{d}}}{{\rm{d}} x}$ if and only if

Proof. Assume $\rho$ fulfills a conservation law with $\nu$ and $\tfrac{{\rm{d}}}{{\rm{d}} x}$. Let $\mathcal{N}$ be a network with only one edge $e$ and $\rho, \nu \in C^1([0, T] \times \mathcal{N})$ and $\phi \in C_c^\infty([0, T] \times \mathcal{N})$, then

The previous equation must hold for all $\phi \in C_c^\infty([0, T] \times \mathcal{N})$; in particular if $\phi$ is zero at the domain's boundary. Therefore, $\rho_t + (\nu \rho)_x$ must be zero everywhere by the fundamental lemma of the calculus of variations [20,p. 6,Lemma 1.1.1]. If $0_e \neq w_e$, then through arbitrary localization on the boundaries $[0, T] \times \{0_e\}$ and $[0, T] \times \{w_e\}$ one obtains by

and the fundamental lemma of the calculus of variations that

The opposite direction of the statement is trivial. □

One of the central ideas towards simulating and optimizing network flows is their characterization as flows on edges coupled by the conservation of their boundary flow at mutual vertices. This reduces the presented abstract setting to a more classical one that turns out to lend itself well to computation. To this end, Theorem 4.2 can be understood to recover Kirchhoff's first law ^[21] for conservation laws of Definition 4.1. To get a sense of the meaning of boundary evaluations of $L^1$-functions, the following lemma is derived in preparation of Theorem 4.2.

Lemma 4.1 (Boundary evaluations). Let

● $f \in L^1\big([0, T] \times (0, w)\big)\cap C_u\big((0, w), L^1([0, T])\big)$ for some $w > 0$,

● $\tau \in C^\infty_c([0, T])$,

● $\tau_\gamma \in C^\infty_c\big([0, T] \times (0, \tfrac{1}{\gamma})\big)$ for all $\gamma \in (\frac{1}{w}, \infty)$ with

and such that there exists $M \in \mathbb{R}$ with

By completeness define $f_0 : = \lim_{x \to 0} f(\cdot, x) \in L^1([0, T])$. Then,

Remark 7 (Right-limits for boundary evaluations). $C_u$ denotes uniformly continuous functions. In the following, the limit

will be heavily used in boundary evaluations of functions $f$ that fulfill the regularity assumptions of Lemma 4.1. Note that such limits may differ in network vertices based on the edge in which the limit is considered.

Proof. Let $\varepsilon > 0$ and pick $\alpha > \tfrac{1}{w}$ such that for all $x < \tfrac{1}{\alpha}$

One has for all $\gamma \in (\alpha, \infty)$

□

Theorem 4.2 (Kirchhoff's first law). In the setting of Definition 4.1, if for all edges $e \in \mathcal{E}$

then $\rho$ fulfills a conservation law with $\nu$ and $\tfrac{{\rm{d}}}{{\rm{d}} x}$ if and only if

Proof. The proof is broken down into several steps.

● Let $\rho$ fulfill a conservation law with $\nu$ and $\tfrac{{\rm{d}}}{{\rm{d}} x}$. Then, by extension of test functions from edges to the network with $0$, it is clear that $\rho$ is a weak solution on edges.

● To show that the flow is conserved at vertices let $v \in \mathcal{V}$ and $\phi \in C_c^\infty([0, T] \times \mathcal{N})$ such that the support of $\phi$ is contained in an $\varepsilon$-ball $U_\varepsilon(v)$ around $v$ at all times, where $2\varepsilon$ is smaller than the smallest edge length, i.e.,

Note that $U_\varepsilon(v)$ can be contracted with a continuous bijection $c_\gamma: U_\varepsilon(v) \to U_{\varepsilon/\gamma}(v)$ uniquely, such that,

For all $\gamma \geq 1$ define $\phi^\gamma: [0, T] \times \mathcal{N} \to \mathbb{R}$ by

Generally, as $\rho$ fulfills a conservation law with $\nu$ and $\tfrac{{\rm{d}}}{{\rm{d}} x}$

● Therefore, by the fact that

with $n : =|{\mathcal{E}_v}|$ being the number of edges connected to $v$, and the latter factor $2$ due to possible self-edges, it follows that

By

one has

● One therefore has

(by Equations (4.4) to (4.6))

(linearity)

(Lemma 4.1, see below argument)

($\phi(\cdot, v)$ was arbitrary, fundamental lemma c.v. [20,p. 6,Lemma 1.1.1])

To see why Lemma 4.1 is applicable for all $e \in \mathcal{E}_v$, without loss of generalization, assume $e \in \mathcal{E}_v^{out}$; if $0_e = w_e$, the two halves of the edge need to be treated separately. In the notation of Lemma 4.1 let

Then, by Eq (4.3) and the fact that

it remains to show that Eqs (4.1) and (4.2) hold. By Theorem 3.1 and the definition of $\phi^\gamma$, Eq (4.1) holds, i.e., for all $t \in [0, T]$

Again by definition of $\phi^\gamma$, Eq (4.2) holds, i.e.,

(by ${\phi_x^\gamma}_{|e} \leq \gamma ||{\phi_x}||_{L^\infty([0, T]\times e)}$)

● The converse statement of this theorem holds by the following argument. Assume that $\rho$ is a weak solution on edges with flow conservation at all vertices. The goal is to show that for all $\psi \in C_c^\infty([0, T] \times \mathcal{N})$

It is equivalent to verify Eq (4.7) for test functions of type $\psi \phi^\gamma$, where $\phi^\gamma$ is a localized function, such that,

and for a vertex $v \in \mathcal{V}$ and $\varepsilon > 0$ (as above)

This is because $\phi^\gamma$ can be part of a partition of unity such that all other terms are zero by the assumption of $\rho$ being a weak solution on open edges. Therefore, the value of

is constant in $\gamma > 1$ and converges as $\gamma \to \infty$—by the exact analog derivation as above —to the difference of incoming and outgoing flow, which is zero by assumption.

□

Remark 8 (Generality of the solution concept). It is essential to note that Theorem 4.2 does not make a statement on the existence or uniqueness of solutions. The solution concept at hand relaxes the widely known setting of the existence of a solution $\rho$ for a given $\rho \mapsto \tilde{\nu}(\rho)$ to the assumption of the existence of a solution tuple $(\nu, \rho)$. In particular, there may be a representation $\nu \equiv \tilde{\nu}(\rho)$. Therefore, the statement of Theorem 4.2 applies in greater generality, in particular, to hyperbolic conservation laws that admit a quasi-linear form. Generalizations to vector-valued conservation laws modeling multi-commodity flows as well as to balance laws are possible. An introduction to hyperbolic conservation laws can be found in ^[8].

5.   Future work

We see the most promising focus of future work building on the described theory in

● Robust solutions to hyperbolic conservation laws: The fact that regular networks are Polish spaces suggests the application of existing tools from probability to meaningfully model scenarios, e.g., hyperbolic conservation laws with random initial data;

● Convergence of solutions in time: Long-time behavior/stability of physically-plausible hyperbolic conservation laws on networks could be studied for its dependence on the network geometry; and

● Localization in networks: Uncertain measurements of characteristics of hyperbolic conservation laws on networks, which are embedded into a higher-level space, could model real-world localization problems. Such models would include information about the network geometry in the localization problem.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there is no conflicts of interest.