1. Introduction
The atmospheric corrosion of metal systems is among the common types of degradation of structural materials. The corrosion mass loss or depth of corrosion damage depends on the atmosphere corrosivity and varies in a broad range under real conditions of each atmosphere type. According to the experimental data of one-year corrosion tests under the ISO CORRAG [1] and UNECE international programs [2,3], MICAT project [4,5] and the Russian program [6], in continental regions of the world the ranges of first-year corrosion losses are 5.4–685 g/m2 for carbon steel, 0.65–38.4 g/m2 for zinc, 0.76–18.31 g/m2 for copper, and 0.027–2.57 g/m2 for aluminum. Taking into account the considerable difference in the corrosion resistance of metals in the atmosphere, the design of metal structures and their protection from atmospheric corrosion require data on the atmosphere corrosivity category and corrosion mass losses in various climate zones and atmosphere types over various periods of time. The K1 value is an important parameter: a) based on K1, the atmosphere corrosivity categories are estimated [7]; b) K1 values are used for long-term predictions of corrosion mass losses of metals, e.g., see [8,9,10,11,12,13,14,15,16]. The power-linear [17] and power [18,19] functions for the prediction of corrosion mass losses in any world regions are based on K1 values predicted using DRFs (K1pr) [18,19,20]. The K1pr values at any location should match the long-time annual average meteorological and aerological atmosphere parameters. An advantage of DRFs is that they make it unnecessary to perform numerous one-year exposures at every location in order to obtain valid mean K1 values corresponding to the current natural conditions.
All the DRFs were developed using regression analysis, with consideration for the identified or assumed regularities of the effect of separate atmosphere corrosivity parameters on the corrosion. Therefore, they can have various mathematical forms. Currently, no model is perfect due to, at least, the following factors: a) imprecise mathematical form of the DRFs; b) imprecise values of the coefficients that are used in the DRFs and are calculated from regression analysis; c) incomplete set of atmosphere corrosivity parameters that affect corrosion [20]. Therefore, DRFs can be improved based on the gained knowledge about the effect of each atmosphere corrosivity parameter on the corrosion.
The DRFs for carbon steel and zinc [7] developed for various world regions have nearly the same mathematical form for K1 prediction. The results of K1 predictions for continental regions using these models differ considerably, as shown in [18,21]. This is due to the difference in the coefficients used in these DRFs. Ref [21] presents new DRFs for these metals based on the K = f([SO2]) relationship obtained, and gives a comparative estimate of the values of the coefficients in the DRFs.
The purpose of this paper is to obtain the K = f([SO2]) relationships for copper and aluminum and to develop new DRFs for K1 predictions on these metals based on the K = f([SO2]) relationship coefficients and meteorological parameters of atmosphere corrosivity obtained. Yet another purpose is to give a comparison of K1 predictions for these metals based on the new and earlier DRFs [7,18] for continental territories of the world, and to analyze the coefficients in these DRFs.
2. Procedure
2.1. Development of DRFs for continental territories
The corrosion of metals is affected by numerous factors that currently cannot all be taken into account. Therefore, in order to develop a DRF, one primarily needs to choose its mathematical form and the atmosphere parameters that affect corrosion most strongly. As a rule, two main parameters were taken into account for the prediction of metal corrosion in continental regions: SO2 concentration in air and time of wetting (TOW) of the metal surface. The relationship was studied between the TOW, on the one hand, and the mean annual temperature (T) and air relative humidity (RH), on the other hand. It was shown that the temperature dependence of the time of surface wetting (at RH > 80% and T > 0 ℃) has a maximum around T = +10…+13 ℃ [22,23]. In view of this, it was suggested to describe the temperature dependence of metal corrosion rate in two ranges, T ≤ Tlim and T > Tlim, by simple relationships of ln(K – T) type. Tlim is the temperature corresponding to the maximum K values. The boundary between the ranges, Tlim, is not necessarily the same as the maximum in the TOW—temperature plot due to complex changes in the state of the adsorbed water layers that also depend on T [22,24]. The temperature dependence of corrosion for the majority of metals has a maximum in the range of T = +9…+11 ℃ [22]. The plot of K versus RH is close to an exponent if the RH range is sufficiently wide. In development of the new DRFs, the main attention was given to the determination of the relationship between the corrosion losses of copper and aluminum, on the one hand, and the concentration of sulfur dioxide in air, on the other hand.
To develop the DRFs, we used experimental data from all exposures over the first test year in continental regions with in the МICAT [4,5] (8 countries, 26 locations, copper and aluminum tests) and UN/ECE [2,3] international programs (11 countries, 27 locations, copper tests) and the Russian program [6] (12 locations, copper and aluminum tests). The background chloride precipitation at the locations did not exceed 1.5 g/(m2·day). The test locations (country, location name, code), atmosphere corrosivity parameters, and experimental K1 values obtained from 1–3 one-year exposures are resented in Tables 1–3. The test results obtained under the ISO CORRAG program [1] are not provided in this paper because they lack the atmosphere corrosivity parameters required for K1 prediction. We used them only to find the K = f([SO2]) dependences for copper and aluminum.
Table 1. UN/ECE program. Test locations, atmosphere corrosivity parameters, K1 (g/m2) of copper from one-year exposures, and location numbers in the order of increasing K1.
| Country |
Test location |
Designation |
T, ℃ |
RH, % |
O3, μg/m3 |
Prec, mm/y |
SO2, μg/m3 |
H+, mg/L |
Cu |
| K1, g/m2 |
No. |
| Czech Republic |
Prague |
CS1 |
9.5 |
79 |
- |
639.3 |
77.5 |
0.1 |
10.87 |
13 |
| Kasperske Hory |
CS2 |
7.0 |
77 |
- |
850.2 |
19.7 |
0.1 |
15.04 |
22 |
| Kopisty |
CS3 |
9.6 |
73 |
- |
426.4 |
83.3 |
0 |
27.59 |
27 |
| Finland |
Espoo |
FIN4 |
5.9 |
76 |
- |
625.9 |
18.6 |
0.1 |
7.44 |
10 |
| Ähtäri |
FIN5 |
3.1 |
78 |
52 |
801.3 |
6.3 |
0 |
11.87 |
18 |
| Helsinki Vallila |
FIN6 |
6.3 |
78 |
- |
673.1 |
20.7 |
0 |
5.89 |
6 |
| Germany |
Waldhof Langenbrügge |
GER7* |
9.3 |
80 |
59 |
630.6 |
13.7 |
0.1 |
15.78 |
24 |
| Aschaffenburg |
GER8 |
12.3 |
77 |
27 |
626.9 |
23.7 |
0 |
6.05 |
7 |
| Langenfeld Reusrath |
GER9 |
10.8 |
77 |
30 |
782.9 |
24.5 |
0 |
6.95 |
9 |
| Bottrop |
GER10 |
11.2 |
75 |
- |
873.8 |
50.6 |
0 |
11.71 |
17 |
| Essen Leithe |
GER11 |
10.5 |
79 |
- |
713.1 |
30.3 |
0 |
9.06 |
11 |
| Garmisch Partenkirchen |
GER12 |
8.0 |
82 |
50 |
1491.5 |
9.4 |
0 |
11.42 |
15 |
| Netherlands |
Eibergen |
NL18 |
9.9 |
83 |
40 |
904.2 |
10.1 |
0.0036 |
13.37 |
19 |
| Vredepeel |
NL19 |
10.3 |
81 |
36 |
845 |
13 |
0.0048 |
16.79 |
25 |
| Wijnandsrade |
NL20 |
10.3 |
81 |
39 |
801.3 |
13.7 |
0.0188 |
13.92 |
20 |
| Norway |
Oslo |
NOR21 |
7.6 |
70 |
- |
1023.8 |
14.4 |
0.0334 |
6.95 |
8 |
| Birkenes |
NOR23 |
6.5 |
80 |
60 |
2144.3 |
1.3 |
0.0567 |
10.97 |
14 |
| Sweden |
Stockholm South |
SWE24 |
7.6 |
78 |
44 |
531 |
16.8 |
0.045 |
5.33 |
5 |
| Stockholm Centre |
SWE25 |
7.6 |
78 |
- |
531 |
19.6 |
0.045 |
4.40 |
4 |
| Aspvreten |
SWE26 |
6.0 |
83 |
55 |
542.7 |
3.3 |
0.0541 |
10.71 |
12 |
| Spain |
Madrid |
SPA31 |
14.1 |
66 |
26 |
398 |
18.4 |
0.0055 |
3.12 |
1 |
| Toledo |
SPA33 |
14.0 |
64 |
77 |
785 |
3.3 |
0.0054 |
3.54 |
2 |
| Russian Federation |
Moscow |
RUS34 |
5.5 |
73 |
- |
575.4 |
19.2 |
0.0007 |
4.14 |
3 |
| Estonia |
Lahemaa |
EST35 |
5.5 |
83 |
- |
447.8 |
0.9 |
0.0221 |
11.47 |
16 |
| Canada |
Dorset |
CAN37 |
5.5 |
75 |
59 |
961.1 |
3.3 |
0.0541 |
14.68 |
21 |
| USA |
Research Triangle Park |
US38 |
14.6 |
69 |
54 |
846.7 |
9.6 |
0.0517 |
15.48 |
23 |
| Steubenville |
US39 |
12.3 |
67 |
42 |
733.1 |
58.1 |
0.1008 |
18.96 |
26 |
| * The concentration of chloride the in precipitations was [Cl–] = 3.92 mg/L. |
Table 2. МICAT program. Test locations, atmosphere corrosivity parameters,
K1 (g/m2) of copper and aluminum from one-year exposures, and location numbers in the order of increasing K1.
| Country |
Test location |
Designation |
T, ℃ |
RH, % |
Rain, mm/y |
SO2, μg/m3 |
Cl–, mg/(m2·d) |
Cu |
|
Al |
| K1, g/m2 |
No. |
K1, g/m2 |
No. |
| Argentina |
Villa Martelli |
A2 |
16.7 |
75 |
1729 |
10 |
Ins |
7.23 |
29 |
|
0.378 |
30 |
| A2 |
17.1 |
72 |
983 |
10 |
Ins |
5.63 |
20 |
0.216 |
18 |
| A2 |
17.0 |
74 |
1420 |
9 |
Ins |
8.30 |
37 |
0.405 |
32 |
| Iguazu |
A3 |
20.6 |
76 |
2158 |
Ins |
Ins |
0.82 |
* |
0.27 |
* |
| A3 |
20.9 |
74 |
2624 |
Ins |
Ins |
0.81 |
* |
0.567 |
* |
| A3 |
22.1 |
75 |
1720 |
Ins |
Ins |
0.7 |
* |
0.756 |
* |
| San Juan |
A4 |
18.0 |
51 |
35 |
Ins |
Ins |
1.70 |
5 |
0.162 |
15 |
| A4 |
20.0 |
49 |
111 |
Ins |
Ins |
1.43 |
2 |
0.405 |
31 |
| A4 |
18.3 |
51 |
93 |
Ins |
Ins |
1.52 |
3 |
0.108 |
12 |
| La Plata |
A6 |
17.0 |
78 |
1178 |
6.22 |
Ins |
11.79 |
41 |
0.351 |
25 |
| A6 |
16.7 |
77 |
1263 |
8.21 |
Ins |
15.63 |
46 |
0.54 |
35 |
| A6 |
16.6 |
78 |
1361 |
6.2 |
Ins |
14.56 |
45 |
0.324 |
23 |
| Brasil |
Caratinga |
B1 |
21.2 |
75 |
996 |
1.67 |
1.57 |
1.09 |
* |
0.297 |
* |
| Sao Paulo |
B6 |
19.7 |
75 |
1409 |
67.2 |
Ins |
18.31 |
47 |
1.836 |
40 |
| B6 |
19.5 |
76 |
1810 |
66.8 |
Ins |
14.29 |
44 |
1.458 |
39 |
| B6 |
19.6 |
75 |
1034 |
48.8 |
Ins |
12.59 |
43 |
1.242 |
38 |
| Brasil |
Belem |
B8 |
26.1 |
88 |
2395 |
Ins |
Ins |
5.72 |
21 |
0.594 |
|
| Brasilia |
B10 |
20.4 |
69 |
1440 |
Ins |
Ins |
1.12 |
* |
0.729 |
* |
| Paulo Afonso |
B11 |
25.9 |
77 |
1392 |
Ins |
Ins |
1.86 |
* |
1.485 |
* |
| Porto |
B12 |
26.6 |
90 |
2096 |
Ins |
Ins |
1.94 |
* |
- |
- |
| Colombia |
Cotove |
CO2 |
9.6 |
98 |
1800 |
0.56 |
Ins |
9.56 |
38 |
0.432 |
33 |
| CO2 |
11.4 |
90 |
1800 |
0.56 |
Ins |
8.13 |
36 |
0.648 |
36 |
| CO2 |
13.5 |
81 |
1800 |
0.56 |
Ins |
10.36 |
40 |
- |
- |
| Guayaquil |
CO3 |
27.0 |
76 |
900 |
0.33 |
Ins |
0.73 |
* |
- |
- |
| CO3 |
27.0 |
76 |
900 |
0.33 |
Ins |
0.63 |
* |
0.378 |
* |
| CO3 |
27.0 |
76 |
900 |
0.33 |
Ins |
0.94 |
* |
- |
- |
| Ecuador |
Riobamba |
EC1 |
26.1 |
71 |
635 |
4.2 |
1.5 |
5.89 |
22 |
0.081 |
9 |
| EC1 |
26.9 |
82 |
635 |
2.72 |
1.31 |
6.43 |
25 |
0.081 |
10 |
| EC1 |
24.8 |
75 |
564 |
2.1 |
1.66 |
6.79 |
26 |
- |
- |
| Leon |
EC2 |
12.9 |
66 |
554 |
1.0 |
0.4 |
3.21 |
9 |
- |
- |
| EC2 |
13.2 |
71 |
598 |
1.35 |
1.14 |
4.38 |
15 |
- |
- |
| Spain |
Tortosa |
E1 |
12.0 |
69 |
652 |
1.18 |
1.5 |
9.73 |
39 |
0.378 |
26 |
| E1 |
10.6 |
65 |
495 |
1.18 |
1.5 |
7.95 |
35 |
0.297 |
20 |
| E1 |
11.1 |
63 |
334 |
1.18 |
1.5 |
4.11 |
12 |
0.378 |
27 |
| Granada |
E4 |
18.1 |
65 |
554 |
8.3 |
1.5 |
6.79 |
27 |
0.297 |
21 |
| E4 |
17.0 |
63 |
521 |
5.7 |
1.5 |
7.41 |
30 |
0.135 |
14 |
| E4 |
17.2 |
62 |
374 |
1.9 |
1.5 |
7.59 |
32 |
0.216 |
16 |
| Arties |
E5 |
16.3 |
59 |
416 |
10.3 |
1.5 |
2.51 |
* |
0.135 |
* |
| E5 |
15.0 |
59 |
258 |
5.4 |
1.5 |
1.97 |
* |
0.081 |
* |
| E5 |
15.6 |
58 |
266 |
2.8 |
1.5 |
1.34 |
* |
0.081 |
* |
| E8 |
8.8 |
52 |
738 |
9.1 |
1.8 |
5.54 |
19 |
0.378 |
29 |
| E8 |
6.9 |
52 |
624 |
8.9 |
1.6 |
4.73 |
16 |
0.216 |
17 |
| Spain |
Arties |
E8 |
7.8 |
52 |
681 |
9.0 |
1.7 |
6.25 |
24 |
0.324 |
24 |
| Mexico |
Mexico (a) |
M1 |
15.1 |
63 |
743 |
14.9 |
1.5 |
5.36 |
18 |
0.432 |
34 |
| M1 |
14.6 |
63 |
743 |
17.6 |
1.5 |
7.50 |
31 |
0.216 |
19 |
| M1 |
15.6 |
63 |
743 |
3.5 |
1.5 |
4.29 |
14 |
- |
- |
| Mexico (b) |
M2 |
21.0 |
56 |
1352 |
6.7 |
1.5 |
2.05 |
7 |
0.378 |
28 |
| M2 |
21.0 |
56 |
1724 |
9.9 |
Ins |
2.50 |
8 |
0.297 |
22 |
| M2 |
21.0 |
56 |
1372 |
7.1 |
Ins |
3.57 |
10 |
1.242 |
37 |
| Cuernavaca |
M3 |
18.0 |
51 |
374 |
31.1 |
Ins |
5.98 |
23 |
- |
- |
| M3 |
18.0 |
62 |
374 |
10.9 |
Ins |
4.29 |
13 |
1.674 |
* |
| M3 |
18.0 |
60 |
374 |
14.6 |
Ins |
3.84 |
11 |
1.242 |
* |
| Peru |
San Luis Potosi |
PE4 |
16.4 |
37 |
17 |
Ins |
Ins |
1.70 |
4 |
0.027 |
1 |
| PE4 |
17.2 |
33 |
34 |
Ins |
Ins |
1.79 |
6 |
0.027 |
2 |
| Arequipa |
PE5 |
12.2 |
67 |
632 |
Ins |
Ins |
0.81 |
1 |
0.027 |
3 |
| PE5 |
12.2 |
67 |
672 |
Ins |
Ins |
- |
- |
0.081 |
8 |
| Arequipa |
PE6 |
25.4 |
84 |
1523 |
Ins |
Ins |
5.00 |
17 |
0.108 |
11 |
| PE6 |
25.8 |
83 |
1158 |
Ins |
Ins |
- |
- |
0.027 |
4 |
| Uruguay |
Pucallpa |
U1 |
16.8 |
74 |
1182 |
0.6 |
1.8 |
7.05 |
28 |
0.027 |
5 |
| U1 |
16.6 |
73 |
1324 |
0.8 |
1.2 |
7.59 |
34 |
0.027 |
6 |
| U1 |
16.7 |
76 |
1306 |
Ins |
Ins |
7.59 |
33 |
0.054 |
7 |
| Trinidad |
U3 |
17.7 |
79 |
1490 |
Ins |
Ins |
11.97 |
42 |
0.108 |
13 |
| * discarded data. |
Table 3. Test locations, atmosphere corrosivity parameters, K1 (g/m2) of copper and aluminum from one-year exposures, and location numbers in the order of increasing K1.
| Location |
Т, ℃ |
RH, % |
Prec, mm/y |
SO2, μg/m3 |
Cu |
|
Al |
| K1, g/m2 |
No. |
K1, g/m2 |
No. |
| Bilibino |
–12.2 |
80 |
218 |
3 |
0.84 |
2 |
|
0.177 |
2 |
| Oimyakon |
–16.6 |
71 |
175 |
3 |
0.76 |
1 |
0.189 |
3 |
| Ust-Omchug |
–11 |
70 |
317 |
5 |
0.92 |
3 |
0.242 |
5 |
| Atka |
–12 |
72 |
376 |
3 |
0.98 |
4 |
0.164 |
1 |
| Susuman |
–13.2 |
71 |
283 |
10 |
1.37 |
5 |
0.474 |
12 |
| Tynda |
–6.5 |
72 |
525 |
5 |
1.62 |
6 |
0.280 |
8 |
| Klyuchi |
1.4 |
69 |
253 |
3 |
2.82 |
10 |
0.310 |
11 |
| Aldan |
–6.2 |
72 |
546 |
5 |
1.78 |
7 |
0.205 |
4 |
| Pobedino |
–0.9 |
77 |
604 |
3 |
6.69 |
12 |
0.285 |
10 |
| Yakovlevka |
2.5 |
70 |
626 |
3 |
4.06 |
11 |
0.259 |
7 |
| Pogranichnyi |
3.6 |
67 |
595 |
3 |
2.79 |
9 |
0.258 |
6 |
| Komsomolsk-on-Amur |
–0.7 |
76 |
499 |
10 |
2.45 |
8 |
0.285 |
9 |
2.2. Predictions of first-year corrosion losses
The corrosion losses for the first year of exposure (K1) were predicted for continental test locations at background Cl– precipitation ≤1.5 mg/(m2·day). The DRFs presented in this article (hereinafter referred to as New DRF), in the Standard [7] (hereinafter—Standard DRF), and in Ref [18] (hereinafter—Unified DRF) were used.
The standard DRFs are intended for the prediction of K1 (rcorr in the original, μm) for two temperature ranges.
For copper, Eq 1:
|
K1=0.0053⋅Pd0.26⋅exp(0.059⋅RH+fCu)+0.01025⋅Sd0.27⋅exp(0.036⋅RH+0.049⋅T),fCu=0.126⋅(T−10)atT≤10℃;fCu=−0.080(T−10)atT>10℃
|
(1)
|
For aluminum, Eq 2:
|
K1=0.0042⋅Pd0.73⋅exp(0.025⋅RH+fAl)+0.0018⋅Sd0.60⋅exp(0.020⋅RH+0.094⋅T),fAl=0.009⋅(T−10)atT≤10℃;fAl=−0.043⋅(T−10)atT>10℃
|
(2)
|
where Т is the temperature (℃) and RH (%) is the relative humidity of air; Pd and Sd are the SO2 and Cl– deposition rates expressed in mg/(m2·day), respectively.
In Eqs 1 and 2, the contributions to corrosion due to SO2 and Cl– are presented as separate components, therefore only their first components were used for continental territories.
The Unified DRFs are intended for long-term predictions of mass losses K (designated as ML in the original). It is stated that the calculated values are given in g/m2.
For copper, Eq 3:
|
K=0.0027⋅[SO2]0.32⋅[O3]0.79⋅RH⋅exp{+0.083⋅(T−10)}⋅τ0.78+0.050⋅Rain⋅[H+]⋅τ0.89,T≤10℃;K=0.0027⋅[SO2]0.32⋅[O3]0.79⋅RH⋅exp{−0.032⋅(T−10)}⋅τ0.78+0.050⋅Rain⋅[H+]⋅τ0.89,T>10℃
|
(3)
|
For aluminum, Eq 4:
|
K=0.0021⋅[SO2]0.23⋅RH⋅exp{+0.031⋅(T−10)}⋅τ1.2+0.000023⋅Rain⋅[Cl−]⋅τ,T≤10℃;K=0.0021⋅[SO2]0.23⋅RH⋅exp{−0.061⋅(T−10)}⋅τ1.2+0.000023⋅Rain⋅[Cl−]⋅τ,T>10℃
|
(4)
|
where [SO2] is the concentration of SO2, μg/m3; Rain is the rainfall amount, mm/y;
[H+] is the acidity of the precipitations; [O3] is the ozone concentration in the air, μg/m3; [Cl–] is the concentration of chlorides in rain water, mg/L; and τ is the exposure time, years.
To predict the first-year corrosion losses, τ = 1 was taken.
The K1 values in μm were converted to g/m2 using the specific densities of copper and aluminum equal to 8.96 and 2.7 g/cm3, respectively. Furthermore, the relationship Pd, p = 0.67 Pd, c was used, where Pd, p (mg/(m2·day)) is the SO2 deposition rate and Pd, c (μg/m3) is the SO2 concentration [7].
The K = f([SO2]) relationship is nonlinear, therefore the background SO2 concentrations at the test locations cannot be smaller than 1 μg/m3, since at [SO2] < 1 μg/m3 the calculated K1 values would be smaller than the experimental K1. In our calculations, we used the value of 1 μg/m3 for SO2 concentrations indicated in Tables 1 and 2 as "Ins." or ≤1 μg/m3, whereas the remaining SO2 concentrations were taken from the Tables.
The K1 predictions obtained by different DRFs are compared to the experimental K1 values for each test location, which provides a clear idea about the specific features of predictions by each DRF.
3. Results and discussion
3.1. Development of New DRFs
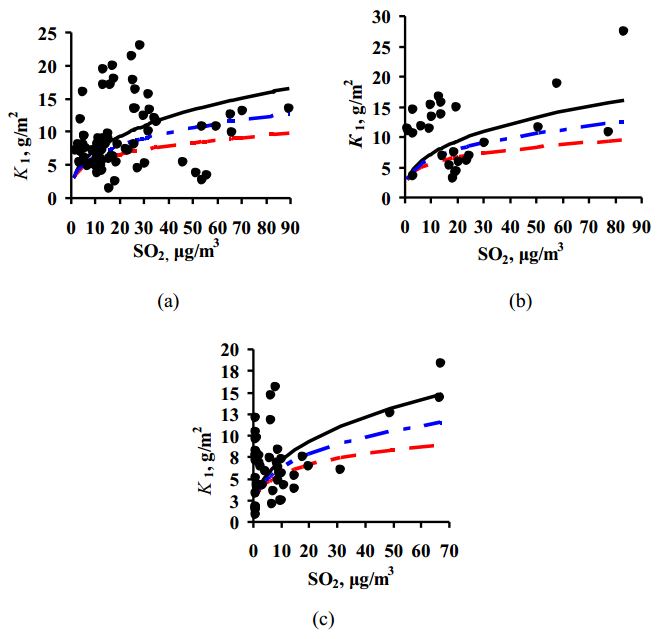
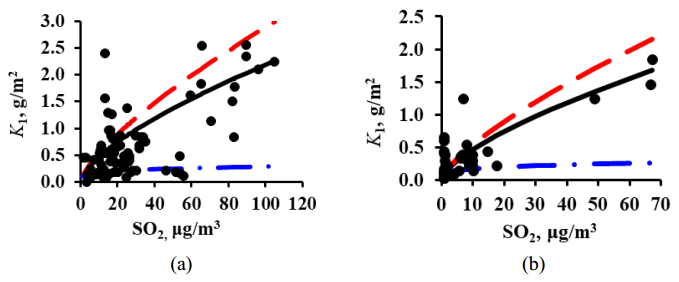
To develop a DRF, it is first of all necessary to estimate the effect of sulfur dioxide on corrosion, i.e., find the mathematical relationship K = f([SO2]). The estimate was based on actual data on K1 and SO2 concentrations from all one-year exposures under each of the programs.
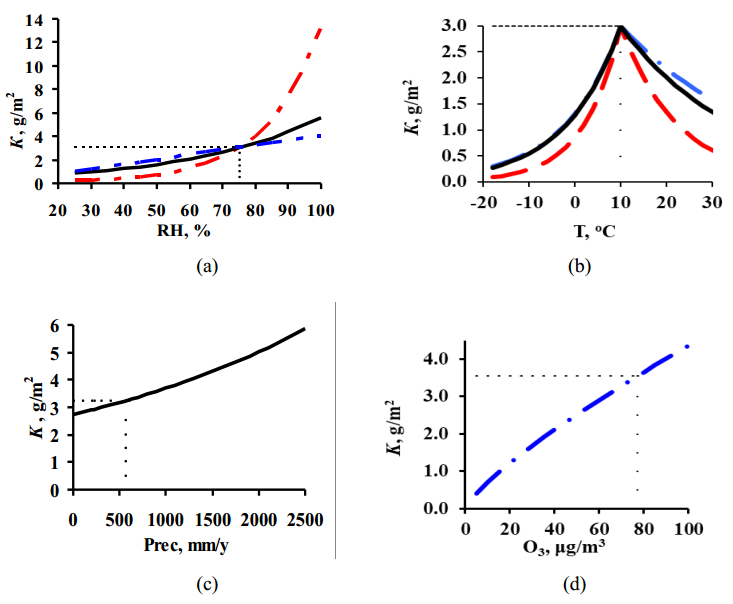
Despite the considerable scatter of experimental K1 values (Figures 1 and 2) obtained in broad ranges of meteorological atmosphere parameters, it is evident that, in a first approximation, this relationship can be described by a function that has the form:
where Ǩ10 is the mean value of the first-year corrosion losses (g/m2) in a pure atmosphere and α is the exponent that depends on the metal nature.
Selection of Ǩ10 values proved to be complicated due to a scatter in the experimental K10 values in a pure atmosphere. An inaccurate Ǩ10 value would result in an inaccurate estimate of the α value that is used in the DRF. We chose the Ǩ10 values of 3 and 0.1 g/m2 and the α values of 0.38 and 0.67 for copper and aluminum, respectively, as the most suitable values for the averaged description of the experimental data. The K = f([SO2]) relationships obtained for each program based on the selected Ǩ10
и α values are shown in Figure 1 for copper and in Figure 2 for aluminum. In a first approximation, the lines of the relationships obtained pass through the mean experimental points.
In the development of the New DRF, the K1 values for copper and aluminum were determined using the mathematical form of the New DRFs developed for carbon steel and zinc. The Prec parameter, including Rain and solid precipitation, was introduced in the DRFs [21]. DRFs were also developed for two temperature ranges.
In addition to the parameters mentioned above, the Unified DRFs include [H+]—acidity of precipitation and [O3]—ozone concentration for copper, as well as [Cl–]—concentration of chlorides in rain water for aluminum. Ozone is certainly among the important parameters that affect the corrosion of metals. For example, it is noted that ozone can stimulate the formation of oxides and their effect on the protective properties of corrosion products [25,26]. Despite the importance of this factor in the estimation of corrosion effects, in reality the ozone concentration is only measured in a small number of locations. Data on [H+] and [Cl–] are also available for a small number of test locations. In view of this, these parameters are currently not used in the New DRFs.
The New DRFs developed for the prediction of K1 (g/m2) have the form:
For copper, Eq 6,
|
K1=0.5⋅[SO2]0.38⋅exp{0.025⋅RH+0.085⋅(T−10)+0.0003⋅Prec},T≤10℃;K1=0.5⋅[SO2]0.38⋅exp{0.025⋅RH−0.040⋅(T−10)+0.0003⋅Prec},T>10℃
|
(6)
|
For aluminum, Eq 7,
|
K1=0.01⋅[SO2]0.67⋅exp{0.039⋅RH+0.032⋅(T−10)−0.0001⋅Prec},T≤10℃;K1=0.01⋅[SO2]0.67⋅exp{0.039⋅RH−0.065⋅(T−10)−0.0001⋅Prec},T>10℃
|
(7)
|
The coefficient at Prec was found to be negative for aluminum. Attempts to use a positive coefficient for Рrec with various combinations of other coefficients gave poorer results of K1 prediction. It has been shown [26] that dust can accelerate the adsorption of moisture and SOx from the atmosphere, which results in long-term surface acidification. Protective aluminum coatings are unstable under these conditions. Furthermore, carbon-containing dust can initiate pitting due to galvanic effects. Apparently, precipitations wash the dust off, thus favoring a decrease in aluminum corrosion, as the negative coefficient at Prec in Eq 7 shows. It should however be noted that the coefficient values and signs found by regression analysis may be unexplainable in a rational manner.
3.2. Screening the test locations for copper and aluminum K1 prediction
The K1 predictions for carbon steel and zinc [21] were also performed within the UN/ECE and RF programs and the МICAT project. The number of test locations (taking the number of exposures at each location into account) was 77 and 94 under the UN/ECE program, 63 and 61 under the МICAT program for steel and zinc, respectively, and 12 locations for each metal under the RF program. It was shown that for steel and zinc, some test locations under the МICAT project had considerably higher experimental K1 values (K1exp) in comparison with the K1 values predicted using various DRFs (K1pr). This regularity indicates a possible inaccuracy of K1exp or corrosivity parameters at these locations. Screening of these locations was not performed. These locations were attributed to locations with doubtful data.
Сopper and aluminum have been tested in a smaller number of locations and with smaller number of exposures in these locations. The number of test locations for copper is 27 under the UN/ECE program and 61 under the MICAT program. Aluminum was not tested within the UN/ECE program. It was tested in 53 locations (the largest number of locations) under the MICAT project. For copper and aluminum, preliminary data screening was performed in the MICAT project for those locations where K1pr provided by various DRFs considerably differed from K1exp for steel and zinc [21]. These are the following locations: А3 (3 exposures), В1, В10,
В11, В12, СО3 (3 exposures), and E5 (3 exposures) for copper, and additionally М3 (3 exposures) for aluminum. These locations are shown in italics in Table 3. After screening of the locations used in the MICAT project, 47 test locations remained for copper and 40 for aluminum. No screening of test locations was performed for copper data in the UN/ECE program.
3.3. K1 predictions for copper using various DRFs
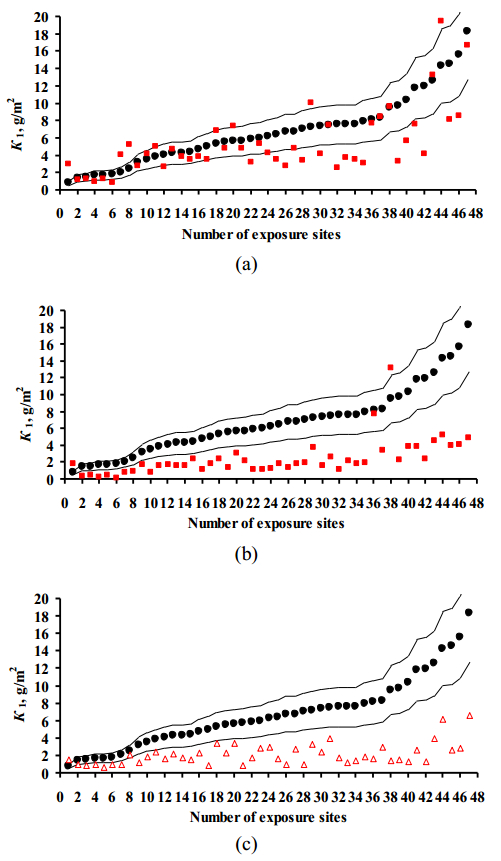
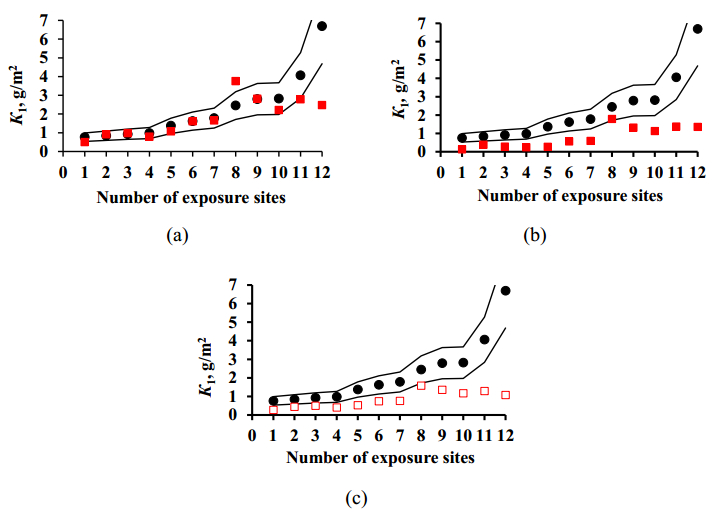
The K1pr results for copper obtained using the Standard DRF (Eq 1), Unified DRF (Eq 3), and the New DRF (Eq 6) are presented separately for each test program. To build the plots, the test locations were arranged in the order of increasing experimental K1exp values. Their sequence numbers are given in Tables 1–3. All the plots are drawn on the same scale. The plots show the prediction error lines δ = ±30% (range: 1.3K1exp–0.7K1exp). This provides a visual picture of how K1pr compares with K1exp for each DRF. No estimate on the difference between the K1pr values obtained using various DRFs and the K1exp values for each test locations within each program was made. The scatter of points is inevitable. It results from the imperfection of each DRF and the inaccuracy of experimental data on meteorological parameters, SO2 content, and K1exp values. Let us just note the general regularities of the results on K1pr for each DRF.
The results on K1pr for copper under the MICAT project and the UN/ECE and RF programs are presented in Figures 3–5, respectively. It should be noted that the K1pr values for copper obtained using the Unified DRF (Eq 3) were quite insignificant. Apparently, like for carbon steel [21], the K1pr values were calculated in μm rather than in g/m2 as the authors assumed. To convert K1pr in μm to K1pr in g/m2, the prediction results were multiplied by 8.96, which corresponds to an 8.96-fold increase in the coefficients (0.0027 and 0.05) in Eq 3.
The K1pr values calculated by the New DRFs in the test locations of the MICAT project either lie in the range of δ = ±30% or are considerably underestimated in comparison with K1exp, Figure 3а, indicating that the prediction errors are distributed nonuniformly. As one can see in Figure 1c, many test locations with insignificant [SO2] have high K1exp values. Perhaps, despite the preliminary screening, certain locations have unreasonably overestimated K1exp values. For locations within the UN/ECE program, the K1pr error has a symmetric distribution at first approximation, while there are few locations with K1pr within δ = ±30%, Figure 4а. It is evident from Figure 1b that the K1exp values at [SO2] < 20 μg/m3 are higher or much higher than those at [SO2] > 20 μg/m3. Taking into account that no screening of test locations used in the UN/ECE program was done, we present only a comparison of K1exp values, e.g., for SWE24 (No. 5), SWE25 (No. 4) and SWE26 (No. 12) (the test location numbers are given according to Table 1). Under practically equal climatic conditions, in SWE26 at [SO2] = 3.3 μg/m3,
K1exp = 10.71 g/m2, which is approximately two times higher than in SWE25 and SWE24: K1exp = 4.40 and 5.33 g/m2 at higher [SO2] concentrations of 19.6 and 16.8 μg/m3, respectively. If K1exp were 4.40 or 5.33 g/m2 at [SO2] = 3.3 μg/m3, and K1exp were 10.71 g/m2 at [SO2] = 19.6 or 16.8 μg/m3, then K1pr would have matched K1exp. In these locations, the [O3] values differ insignificantly according to data of other exposures [2,3] (these data are not reported there since copper was not exposed in those periods). Therefore, it is hard to explain the observed difference in K1exp in these locations. It is possible that, apart from ozone, other parameters affecting copper corrosion were not taken into consideration, or not all locations in this program had reliable data. For locations under the RF program, except for 2 locations, nearly all K1pr values are within the δ = ±30% range, Figure 5a. In total, the K1pr error is nearly symmetrical with respect to K1exp.
The K1pr values calculated by the Standard DRF for almost all the test locations are considerably lower than K1exp, Figure 3b. Under the UN/ECE program, the K1pr values for some locations are within the range of δ = ±30%, but for the other locations these values are considerably lower than K1exp, Figure 4b. In locations under the RF program, the K1pr values are also lower than K1exp, Figure 5b.
It is difficult to estimate K1pr using Unified DRF since no [O3] and [H+] data required for Eq 3 are available in many locations. Under the UN/ECE program, for the locations with a full set of parameters used in the DRFs, the K1pr errors are within the δ = ±30% range or slightly exceed it, while if ozone is not taken into account, the K1pr values are considerably underestimated, Figure 4c. It should be noted that at [O3] = 27–77 μg/m3 (Table 1), K1pr can be increased 14–31 fold. Taking this effect of ozone into account, K1pr can be highly overestimated at some locations. In locations under the MICAT project and RF program, the K1pr values are also lower than K1exp, Figure 5c, due to the lack of [O3] data (MICAT project) or both [O3] and [H+] data (RF program). The corrosion losses due to the acidity of precipitation (∆K1Н+) in Eq 3 are taken into account by a separate component. For example, the ∆K1Н+ value can reach 11.8 g/m2 at US39 (No. 26, UN/ECE program). Comparison of K1pr and K1exp allows one to assume that in an atmosphere contaminated with SO2, ozone and acidic precipitations affect corrosion more significantly than SO2, but we believe this to be unlikely. Let us remind the reader that we increased the K1pr results obtained by Eq 3 by a factor of 8.96.
Comparison of the K1pr results for all DRFs with K1exp indicates that none of the models is perfect. New tests are required for copper, with simultaneous recording of meteorological and aerochemical parameters that affect copper corrosion. Let us just note that currently the New DRFs give the most reliable K1pr values in comparison with the K1pr values calculated by the Standard DRF and Unified DRF.
3.4. Analysis of DRFs for copper
The DRFs were analyzed by comparison of the coefficients used in these DRFs. The nonlinear New DRFs (Eq 6) and Standard DRFs (Eq 1) can be represented in the form:
|
K1=A⋅[SO2]α⋅exp{k1⋅RH+k2⋅(T−10)+k3⋅Prec}=K10⋅[SO2]α
|
(8)
|
where K10 = А·exp{k1·RН + k2·(Т – 10) +
k3·Рrec}.
Unified DRFs (Eq 3) can be presented in the form:
|
K1=A⋅[SO2]α⋅[O3]β⋅RH⋅exp{k2⋅(T−10)}+B⋅Rain⋅[H+];orK1=A⋅[SO2]α⋅[O3]β⋅RH⋅exp{k2⋅(T−10)}+B⋅Rain⋅[H+]≈K10⋅[SO2]α
|
(9)
|
where K10 = А·[O3]β·RH·exp{k2·(Т – 10)}, provided that ozone is considered to be a parameter of pure atmosphere and that the В·Rain·[H+] member can be neglected.
The values of the coefficients used in Eqs 1, 3 and 6 are presented in Table 4.
Table 4. The values of coefficients used in DRF for copper.
| DRF |
А |
α |
β |
k1 |
k2 |
k3 |
В |
| μm |
g/m2 |
Т ≤ 10 ℃ |
Т > 10 ℃ |
μg |
g/m2 |
| New |
0.0558 |
0.50 |
0.38 |
- |
0.025 |
0.085 |
–0.040 |
0.0003 |
- |
- |
| Standard |
0.0053 |
0.047 |
0.26 |
- |
0.059 |
0.126 |
–0.080 |
- |
- |
- |
| Unified |
0.0027 |
0.024 |
0.32 |
0.79 |
- |
0.083 |
–0.032 |
- |
0.050 |
0.448 |
To compare the [SO2]α plots, with the α values taken into account for all DRFs, Eq 5 used Ǩ10 = 3 g/m2 at [SO2] = 1 μg/m3, which at first approximation corresponds to an average K1 value in a pure atmosphere for the entire set of experimental data. The plots for all the programs are presented in Figure 1. For the New DRF, the line K = f([SO2]) at α = 0.38 passes approximately through the mean experimental points from all the test programs. Therefore, one should expect a relatively uniform distribution of prediction errors (Figures 3a, 4a and 5a). For the Standard DRF, α = 0.26 is somewhat lowered, which may result in a small K1 range as a function of [SO2], i.e., in underestimated K1pr values, especially at high [SO2] (Figures 3b, 4b and 5b). For Unified DRF, α = 0.32 is slightly underestimated. However, with a full set of corrosivity parameters in Eq 3, the K1pr values match K1exp at first approximation (Figure 4с), which may be due to a combined effect of other parameters, e.g., due to ∆K1H+ = В·Rain·[H+].
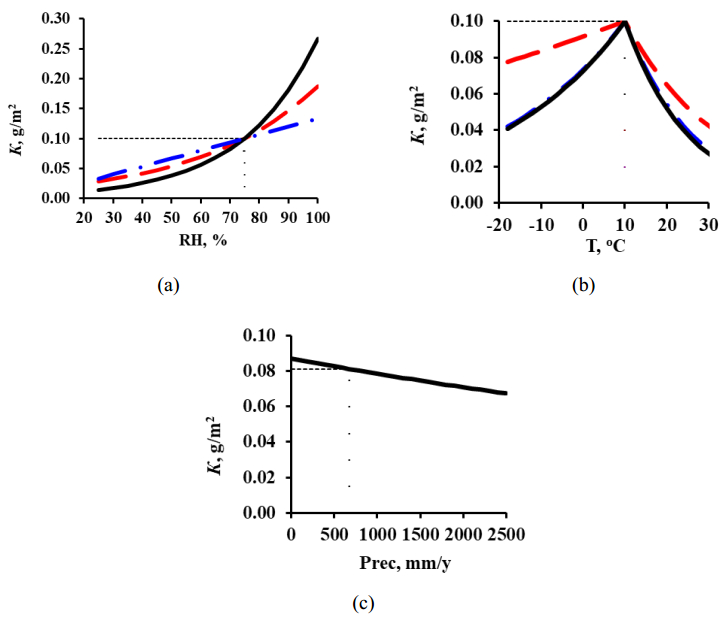
To perform a comparative estimate of k1 and k2, let us use the value where a change in the temperature dependence is observed, i.e., Тlim = 10 ℃ accepted in the DRF. Let us assume that at Тlim = 10 ℃ and the most common RH = 75%, K1 = 3 g/m2. The dependences of K on Т and RH under these conditions and with consideration for the corresponding k1 and k2 values for each DRF are presented in Figure 6.
According to the New DRF (k1 = 0.025), K may decrease from 3 to 0.97 g/m2 upon RH change from 75 to 30%, while an increase in RH to 100% increases K to 5.61 g/m2, i.e., K changes 5.8-fold upon RH variation from 30 to 100% (Figure 6a). For the Standard DRF (k1 = 0.059), K changed abruptly, i.e., it increases 62-fold upon RH variation from 30 to 100%. In Unified DRF (Eq 3), K linearly depends on RH, hence K can increase 3.3-fold in the same range of RH variation.
For all the DRFs, the absolute value of k2 is larger at Т ≤ 10 ℃ than at Т > 10 ℃, i.e., K decreases more abruptly upon a temperature decrease than upon its increase from 10 ℃ (Figure 6b). According to the Standard DRF, the most abrupt decrease should be observed for two temperature ranges. At k2 = 0.126 and –0.080, the K value decreases from 3 to 0.09 g/m2 (upon temperature decrease to –18 ℃) and to 0.61 g/m2 (upon temperature increase to 30 ℃). This corresponds to 33- and 6.8-fold K decrease, respectively.
The nonlinear effect of Рrec on corrosion is only taken into account in the New DRF. This effect is represented using ЕС2 data (MICAT project): at Т = 12.9 ℃, RH = 66%, [SO2] = 1 μg/m3 and Рrec = 554 mm/y, K1 equals 3.2 g/m2. A change in Рrec from 500 to 2500 mm/y at k3 = 0.0003 can increase K to 6 g/m2, i.e., almost twofold, Figure 6c. The effect of О3 was only used in Unified DRF, Figure 6d. Owing to О3, in locations with climate conditions similar to SPA33 (UN/ECE program, Т = 14 ℃, RH = 64%, Рrec = 785 mm/y, [SO2] = 3.3 μg/m3, [O3] = 77 μg/m3), variation of О3 concentration from 10 to 100 μg/m3 can increase K 6-fold (at β = 0.79). In Unified DRF, the separate contribution of ∆K1H+ = В·Rain·[H+] to corrosion linearly depends on Rain and [H+]. It is known that in case of a linear dependence, a combination of high constituent values can result in a high ∆K1H+ value.
The А values are 0.50 in the New DRFs and 0.047 and 0.024 g/m2 in the Standard DRF and Unified DRF, respectively, i.e., the А values differ 10.6- and 20.8-fold.
It has been shown that the K1pr values obtained for copper using DRFs with different parameters affecting corrosion and/or their combinations are taken into account, as well as having different coefficients at similar parameters, differ considerably, Figures 3–5.
3.5. K1 predictions for aluminum using various DRFs
The difficulty of K1 prediction for aluminum lies in the possibility that large errors in K1exp determination may have to be tolerated. For example, the K1exp values in a pure atmosphere may lie within the experimental error due to the complexity of removal of corrosion products from pits, etc. Under the same test conditions, the variation of K1exp is many times greater than for other metals. For example, in the MICAT project, the K1exp values vary 68-fold for aluminum (0.027–1.836 g/m2) but only 23-fold for copper. It is more difficult to predict such differences using the same parameters in the DRFs.
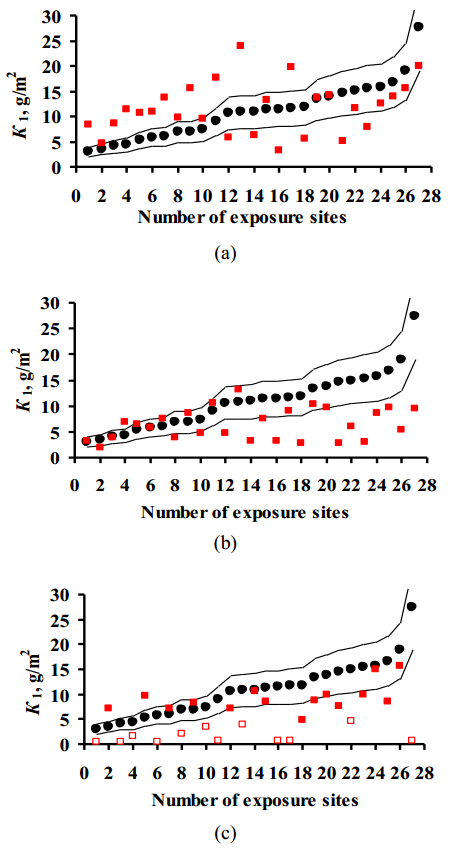
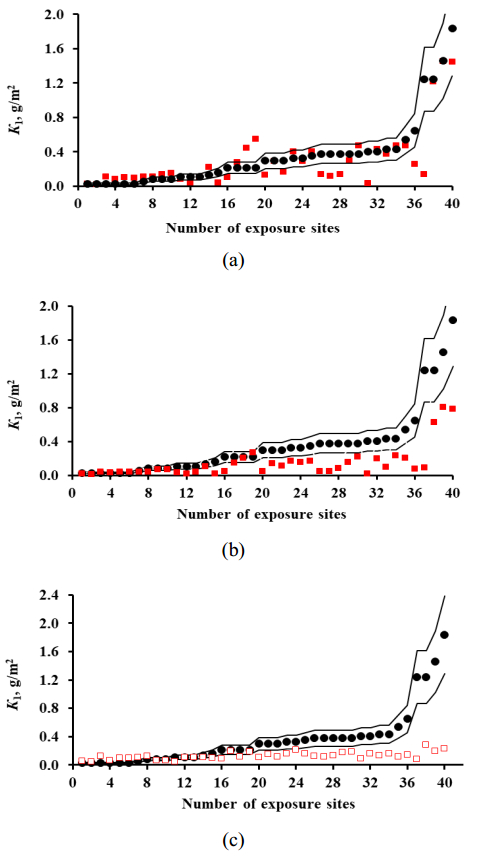
The K1pr results for aluminum obtained using the Standard DRF (Eq 2), Unified DRF (Eq 4), and the New DRF (Eq 7) are presented separately for each test program. To build the plots, the test locations were arranged in the order of increasing K1exp values. Their sequence numbers are given in Tables 2 and 3. The plots are built on the same scale. They show the prediction error lines δ = ±30% (range: 1.3K1exp–0.7K1exp). The results on K1pr for locations used in the MICAT project and the RF program are presented in Figures 7 and 8, respectively. Notwithstanding the preliminary screening in the MICAT project, let us additionally compare the K1exp values obtained in a number of locations. For example, in the pure atmosphere in РЕ4 (No. 1 and 2, Table 2) at low RH (37 and 33%) and Prec values (17 and 34 mm/y), the K1exp value amounts to 0.027g/m2. The same K1exp value was obtained in РЕ5, РЕ6, and U1 locations (No. 3, 4, 5, 6, respectively, Table 2) at higher RH (67–83%) and Prec values (632–1324 mm/y), which is hardly possible. Thus, it follows that the experimental data in some other locations are also doubtful.
Let us note the general regularities of the results on K1pr for each DRF.
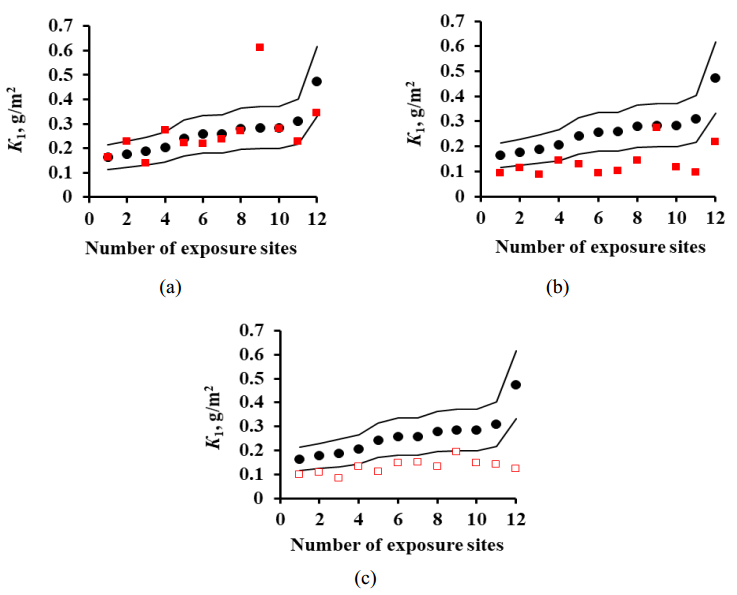
For locations under the MICAT project, the K1pr values calculated using the New DRFs fit in the range δ = ±30% and are either under- or overestimated in comparison with K1exp, Figure 7а. At first approximation, the K1pr error has a symmetric distribution. Overestimated K1pr values are mainly observed in locations with K1exp within 0–0.2 g/m2, whereas underestimated K1pr—at locations with higher K1exp. For locations under the RF program, except for one location, nearly all K1pr values are within the δ = ±30% range, Figure 8a. In total, the K1pr error is nearly symmetrical with respect to K1exp for both programs.
The K1pr values calculated by the Standard DRF lie in the range δ = ±30% for the test locations under the MICAT project only at K1exp up to 0.2 g/m2, Figure 7b. For the other locations, the K1pr values are lower or much lower than K1exp. For locations under the RF program, the K1pr values are also underestimated in comparison with K1exp, Figure 8b.
In the K1pr values obtained using Unified DRF, the component of corrosion losses due to the content of chlorides in deposits, ∆K1Cl–, is not taken into account. Without this component, the mainly underestimated K1pr values manifest themselves as a nearly horizontal band for both programs, Figures 7с and 8с. Hence higher K1pr values in an atmosphere contaminated with SO2 can be obtained only from the presence of chloride ions in deposits, which is unlikely for continental territories.
In the MICAT project, data on the concentration of chlorides in deposits are unavailable. Therefore, to estimate the possible ∆K1Cl– value, let us use the data on chloride concentration in precipitates for locations under the UN/ECE program. Of all test locations under this program, with insignificant salt content in the atmosphere (1.5 mg/(m2·day)) in Waldhof Langenbrügge GER7, the highest chloride concentration in the precipitates is [Cl–] = 3.92 mg/L, Table 1. This value is applicable for K1pr calculations in two locations: Brazil, Belem, B8 (Т = 26.1 ℃, RH = 88% Rain = 2395 mm/y, [SO2] = Ins, [Cl–] = Ins., Table 2) and Brazil, Sao Paulo, B6 (Т = 19.5 ℃, RH = 76%, Rain = 1810 mm/y, [SO2] = 66.75 μg/m3 and [Cl–] = Ins., Table 2). In these locations, K1exp amounted to 0.378 g/m2 and 1.458 g/m2, respectively. The K1exp were 0.378 g/m2 and 1.458 g/m2, respectively, in these locations. The K1pr values determined using Eq 4 with consideration for corrosion due to chlorides in rain water (∆K1Cl–) at [Cl–] = 3.92 mg/L were found to be 0.126 + 0.582 = 0.708 g/m2 in Belem and 0.195 + 0.440 = 0.635 g/m2 in Sao Paulo. In the pure atmosphere of Belem, K1pr can match K1exp due to the ∆K1Cl– component at a lower chloride concentration in the precipitation, while ∆K1Cl– predominates in the overall corrosion effect. In Sao Paulo, even taking the ∆K1Cl– component into account, the K1pr value is 2.3 times higher than K1exp, though the [Cl–] amount in the precipitation is the largest among the continental territories.
Comparison of the K1pr values with K1exp for all the DRFs indicates that the New DRFs currently give the most reliable K1pr values in comparison with the K1pr values calculated by the Standard DRF and Unified DRF.
3.6. Analysis of DRFs for aluminum
The DRFs were analyzed by comparison of the coefficients used in these DRFs. The nonlinear New DRFs (Eq 7) and Standard DRFs (Eq 2) can be represented in the form: New DRFs (Eq 6) and Standard DRFs (Eq 1) can be represented in the form:
|
K1=A⋅[SO2]α⋅exp{k1⋅RH+k2⋅(T−10)+k3⋅Prec}=K10⋅[SO2]α
|
(10)
|
where K10 = А·exp{k1·RН + k2·(Т – 10)
+ k3·Рrec}.
Unified DRF (Eq 4) can be represented as:
|
K1=A⋅[SO2]α⋅RH⋅exp{k2⋅(T−10)}+B⋅Rain⋅[Cl−]≈K10⋅[SO2]α
|
(11)
|
where K10 = А·RH·exp{k2·(Т – 10)}, provided that В·Rain·[Cl–] = 0 in SO2-containing atmospheres, which is only possible at [Cl–] = 0.
The values of the coefficients used in Eqs 2, 4, and 7 are presented in Table 5.
Table 5. The values of coefficients used in DRF for aluminum.
| DRF |
А |
α |
k1 |
k2 |
k3 |
В |
| μm |
g/m2 |
Т ≤10 ℃ |
Т > 10 ℃ |
μg |
g/m2 |
| New |
0.0037 |
0.010 |
0.67 |
0.039 |
0.032 |
–0.065 |
–0.0001 |
- |
- |
| Standard |
0.0042 |
0.0113 |
0.73 |
0.025 |
0.009 |
–0.043 |
- |
- |
- |
| Unified |
0.00078 |
0.0021 |
0.23 |
- |
0.031 |
–0.061 |
- |
0.000023 |
0.000062 |
To compare the K–[SO2]α plots with the α values for all the DRFs taken into account, in Eq 5 we used K10 = 0.1 g/m2 at [SO2] = 1 μg/m3, which at first approximation corresponds to the average K1 value in a pure atmosphere for the entire set of experimental data. These plots for the test locations under all the programs are presented in Figure 2. For the new DRF, the K = f([SO2]) line at α = 0.67 passes approximately through the mean experimental points of all the test programs. Therefore, one should expect a relatively uniform distribution of prediction errors (Figures 7a and 8a). The value for the Standard DRF, α = 0.73, is somewhat overestimated. The value for Unified DRF, α = 0.23, is considerably underestimated. This α value makes it impossible to obtain a large K1pr variation range. As a result, K1pr is considerably smaller than K1exp (Figures 7c and 8c), thus the mass losses had to be increased by adjusting other atmosphere corrosivity parameters.
Let us make a comparative estimate of k1 and k2, assuming that K1 = 0.1 g/m2 at Т = 10 ℃ and RH = 75%. The plots of K vs. Т and RH under these conditions and with consideration for the corresponding k1 and k2 for each DRF are presented in Figure 9.
In the New DRF, the effect of RH (k1 = 0.039) on corrosion is higher than in the other DRFs. On RH variation from 30 to 100%, K сan increase from 0.014 to 0.266 g/m2, in the Standard DRF (k1 = 0.025) from 0.033 to 0.188 g/m2, whereas in Unified DRF (linear K–RH relationship) K should increase 3.3-fold, i.e., from 0.04 to 0.133 g/m2.
The effect of temperature on corrosion at Т ≤ 10 is weaker in the Standard DRF, k2 = 0.009. This corresponds to a K decrease from 0.1 to 0.08 g/m2 upon a Т decrease from 10 ℃ to –18 ℃. A strong temperature effect is expected by the New DRF (k2 = 0.032) and Unified DRF (k2 = 0.031): under the same conditions, K decreases from 0.1 to 0.04 g/m2, respectively. A temperature increase from 10 to 30 ℃ results in an abrupt K decrease to 0.021, 0.023 and 0.036g/m2 according to the New DRF (k2 = –0.065), Unified DRF (k2 = 0.061) and Standard DRF (k2 = –0.043).The adverse effect of Рrec on corrosion is only taken into account in the New DRF. This relationship was presented using data from РЕ5 (MICAT project, at Т = 12.2 ℃, RH = 67%, [SO2] = 1 μg/m3 and Рrec = 672 mm/y, K1 = 0.081 g/m2). A change in Рrec from 500 to 2500 mm/y at k3 = –0.0001 can decrease K from 0.083 to 0.067 g/m2, i.e., 1.2-fold, Figure 9c. For Unified DRF, the separate contribution of ∆K1Cl– = В·Rain·[Cl–] to mass losses linearly depends on Rain and the [Cl–] concentration therein.
The A values are 0.010, 0.0113 and 0.0021 g/m2 in the New, Standard and Unified DRF, respectively. The А value differs 0.88- and 4.8-fold in comparison with the New DRFs.
The K1pr values obtained for each DRF using the presented combinations of considerably different coefficients for parameters affecting corrosion are shown in Figures 7 and 8.
4. Conclusions
1. The K = f([SO2]) relationships for corrosion losses of copper and aluminum vs. sulfur dioxide concentration have been obtained.
2. Based on the K = f([SO2]) relationships obtained, new DRFs for copper and aluminum have been developed for continental territories.
3. The predicted corrosion losses of copper and aluminum in the first year of exposure using the New DRF, Standard DRF, and Unified DRF are compared with experimental data for continental test locations under the UN/ECE, RF programs and MICAT project.
4. An analysis of the values of the coefficients used in the DRFs for the prediction of corrosion losses of copper and aluminum is presented. It is shown that the most accurate DRFs can only be developed based on the knowledge about the effects of each atmosphere corrosivity parameter on corrosion. Using this knowledge, it is possible to correctly choose the analytical form of the DRF, the coefficients in it, and to develop the most perfect DRFs.
Conflicts of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: