1.
Introduction
Penne [1] presented the classical model for governing heat transfer in tissues. The formulation is simplistic and is composed of an energy conservation balance with a source term. Penne's equation is the most used among the various models proposed to study heat transfer in biological tissues [2],[3]. This is because of its mathematical simplicity and its ability to predict the temperature field reasonably well in various applications [4].
The simplicity of bioheat transfer modeling is associated with the absence of convective terms in the mathematical formulation. This feature is usually positive, making computational approaches more stable. However, bioheat transference problems can present high numerical complexity due to the presence of source terms, non-trivial boundary conditions [5], and complex geometries [6].
Analytical solutions to specific bioheat transfer problems are available in the literature [7]–[9]. However, [10] noted that there is not yet a general analytical form for the solution of Penne's equation. In this way, accurate numerical solutions remain essential for the resolution of the model in question.
The Radial Basis Function (RBF) method was applied by [11] to solve partial differential equations and thus garnered the attention of engineers and scientists because of its simplicity, even with complex geometries and non-linear problems of different dimensions [12]. However, the application of the RBF method for heat bioheat transfer problems is still in development [13]. It is currently restricted to applications and evaluations of the RBF method to classical problems (burns and thermotherapy in different dimensions and multi-domains) [14],[15].
One of the main characteristics of the RBF method is that it does not make use of a mesh, which facilitates the construction of complex geometries in complex dimensions and enables the development of spatial adaptive algorithms. The literature on the RBF method presents a series of spatial adaptive algorithms for classical convection-diffusion equations [16],[17]. The mentioned authors present different algorithms for choosing the best node location. They presented enthusiastic results involving convective problems and functions with high gradient regions. However, they have limitations concerning the domain's dimension. On the other hand, [18] presented the multi-domain Residual Subsampling Method (RSM), an adaptive node refinement strategy that enables the user to set parameters allowing the addition and removal of nodes based on residuals evaluated at a finer point set. This fact might be of interest to bioheat numerical problems since RSM can be useful to refine the boundary domain's (regions with high gradients in bioheat problems) and coarse-smooth gradient regions (usually on the internal nodes in bioheat problems), reducing computational time, and lowering the integration errors. However, the mentioned algorithms were not evaluated for the classical bioheat applications, and their stability and convergence in transient problems are still being researched. To our knowledge, for conventional bioheat modeling, no work involving the RBF technique has presented a spatial adaptive numerical solution. The presence of non-linear source terms and Neuman and Mixed boundary conditions suggests the implementation of such algorithms aiming at solutions of high accuracy and high computational performance as performed in applications concerning mesh-based methods [19], neural network modeling [20] and boundary value methods [21],[22].
Recently [23] proposed a bioheat transfer study implementing the Radial Basis Function method. In this study, constant and sinusoidal boundary conditions were evaluated in three types of heat transfer models, i.e., Penne's bioheat model, single-phase lag model. The authors contributed with a physical analysis restricted to sinusoidal and constant heating boundary conditions and the physical parameters. However, the quality of numerical RBF solutions was no discussed or compared with benchmark solutions. The bioheat model and its respective boundary conditions and physical parameters directly impact the propagation of the tissue's thermal signals. Additionally, the precision of the numerical methodology may be a source of solution errors and numerical instability. This investigation topic becomes essential when the modeler proposes adopting numerical methods with empirical parameters and mesh refinement strategies. Moreover, the numerical method should overcome the complexity inherent to transient models, source terms, and step/sinusoidal boundary conditions. The importance of a performance analysis concerning RMS as a methodology for solving transient problems is emphasized by [18].
The present work aims to evaluate a spatial adaptive methodology coupled with the RBF-meshless method to obtain numerical solutions of the classic bioheat model.
The analytical solutions developed by [8] by Green's function method will be applied to evaluate the numerical solution in three scenarios: constant skin surface heating, heating the skin surface using a step function, and heating the skin surface using a periodic function.
2.
Materials and method
2.1. The bioheat transfer model
Most theoretical analyses on heat transfer in living tissues are based on Penne's equation, which describes the influence of blood flow on the temperature distribution in tissue.
In this work, in line with [8], only one-dimensional models with constant thermal parameters will be used, which results in a good approximation when heat propagates in the direction perpendicular to the skin surface.
Penne's bioheat transfer general equation for one-dimension analysis can be described as;
where ρ, c and k are the density, specific heat, and thermal conductivity of the tissue, respectively; ρb and cb denote the blood's specific density and heat; ωb blood perfusion; Ta the arterial temperature that is treated as a constant; T the temperature of the tissue; Qm the heat generated by metabolism; and Qr(x, t) is the source of heat due to external applied heat.
According to [8], the initial temperature profile for the rest state of biological bodies can be obtained by solving the following equation and its boundary conditions.
where, T(x, 0) = T0(x) is the steady-state temperature profile before heating, Tc is the blood temperature and often considered as constant, h0 is the apparent heat convection coefficient between the surface of the skin and the surrounding air physiologically in the basal state, and is a general contribution of natural convection and radiation, and Tf is the air temperature. The surface's skin is set on x = 0 while the center of the body in x = L.
During a practical thermal process, the boundary condition presented by Eq 4 is always dependent on time, which can be generalized to:
Or
where, f1(t) represents the surface heat flux dependent on time, and f2(t) is the medium cooling temperature on the time and the coefficient of heat convection between the medium and the surface of the skin. In this work, the body temperature was considered constant (Tc) considering that the biological body tends to maintain a stable central temperature, i.e.,
2.2. The Radial Basis Function Method
A radial base function φ(r) is a radially symmetrical n-dimensional function: Rn→R which depends only on the Euclidean distance (r=∥x−xj∥) between a center x and a point evaluated in xj. In this work, multiquadric radial base function was applied to interpolate an f(x) function into Rn assuming that
where φj(r)=2√ϵ2+(x−xj)2 and ϵ is a non-zero empirical parameter.
The coefficients λ are calculated by solving the linear system presented in the form λ=Ø−1f(x).
2.3. Discretization of bioheat transfer equation by Radial Basis Function Method
Beginning from Eq 8, the partial derivatives can be easily obtained from the following Eqs 9 and 10:
And
Consider Eq 1 as a function temperature T(x, t). The Crank-Nicolson [24] discretization scheme consists of a finite difference approach to approximate partial derivatives on T(x, t) by the following equation.
Considering the terms Qm and Qr as constant in the Eq 1 and expanding the Eq 11 will result in:
where α=kρc and Π represents the sum of the constant terms contained in the model Π=wcbTa+qm+qr. From Eq 12, two new operators will be defined, H+ and H−, considering T(x,t)≈Ø(x,t) and ∂2T∂x2≈∂2Ø∂x2 as follows:
Finally, the operators H+ and H− will be used to approximate the function T(x, t) using the radial base function, shown below:
Equation 15 generates a system of linear equations, which can be solved by LU decomposition to obtain the unknowns, λt+Δt from the known values of λt, at a previous time step. Then they give rise to T(x, t) by means of Eq 8.
2.4. Meshfree node adaptive algorithms – Residual Subsampling Method
The residual subsampling method developed by [18] is a simple and easy method to add, reallocate, and remove the nodes based on an interpolation process.
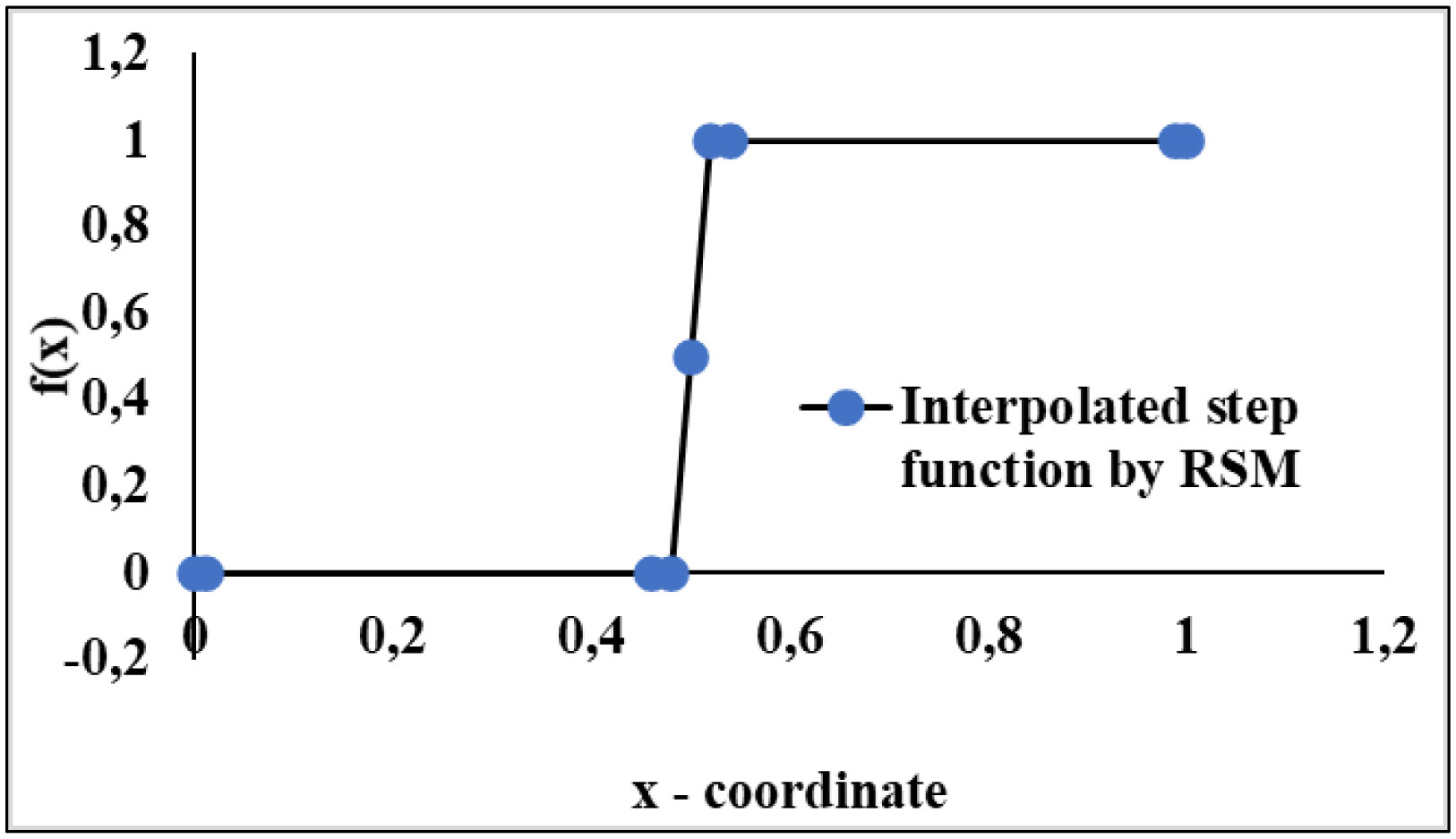
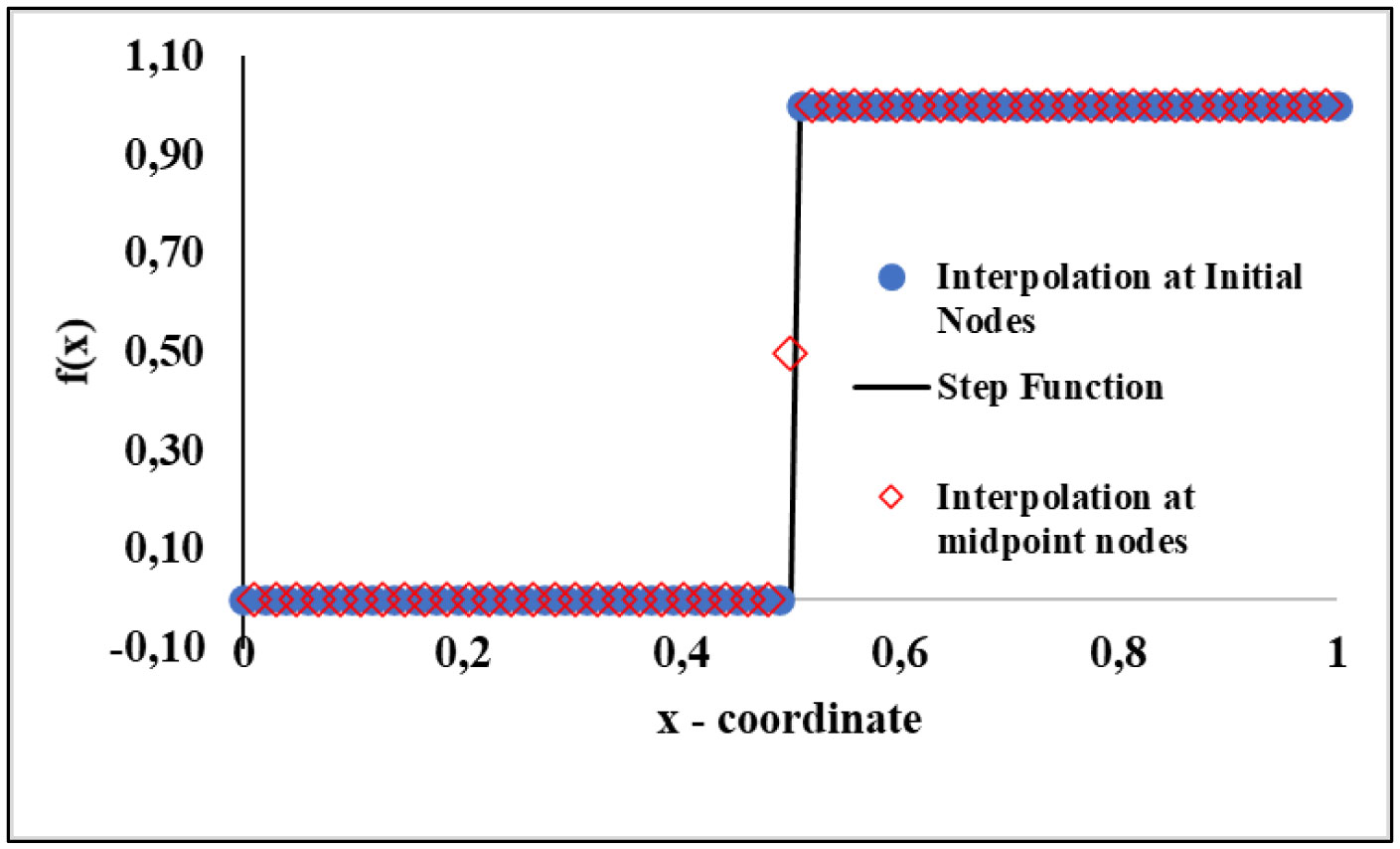
This method consists of generating an initial discretization using equally spaced N points and finding the Radial Basis Function approximation. The Figure 1, illustrate this first RSM step for interpolate a step function.
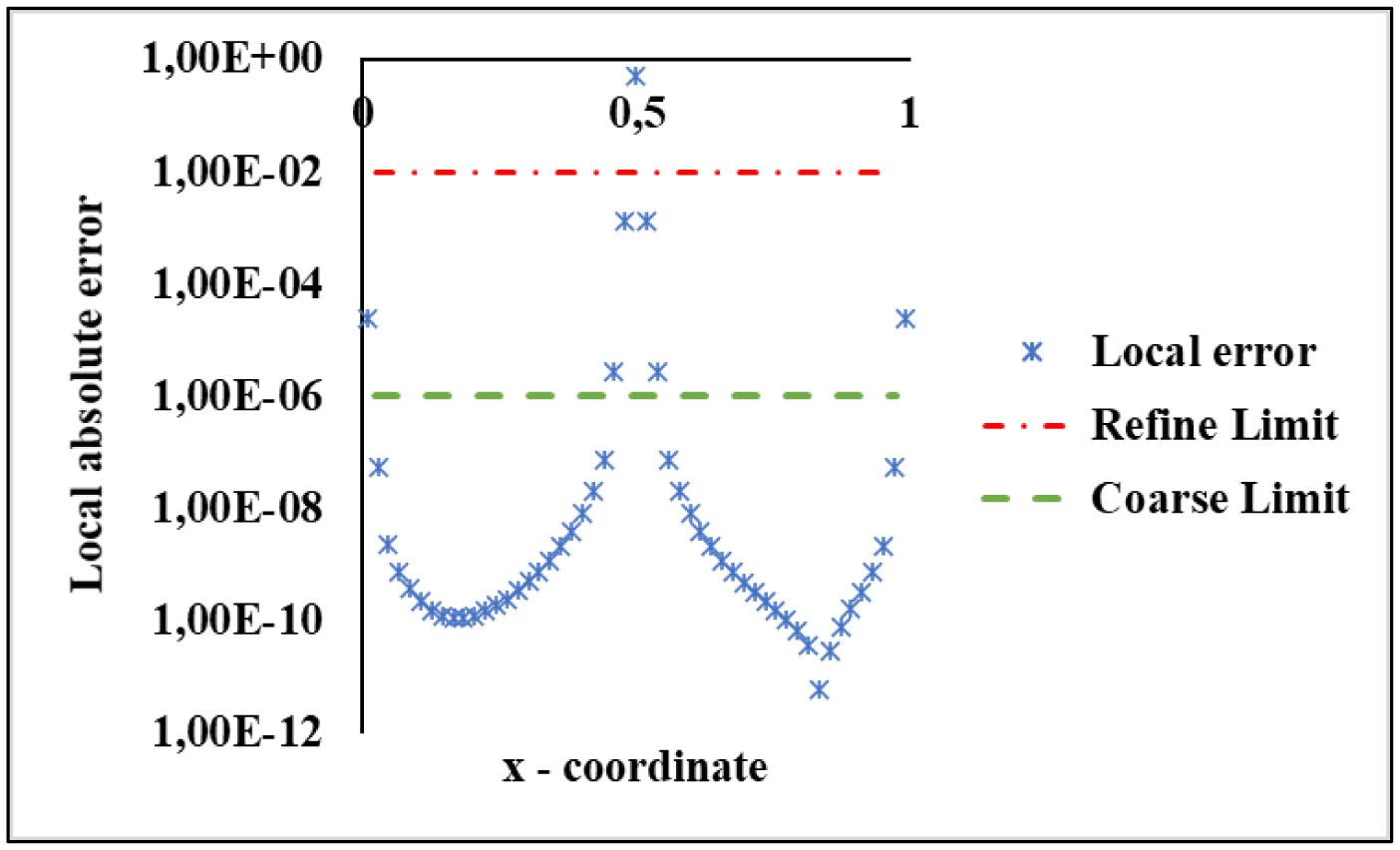
Next, the interpolation error of the midpoints between the nodes is calculated as illustrated in Figure 2.
Points at which the error exceeds a threshold become (refine limit) θr centers, and the centers that are between two points whose error is below a lower threshold (coarse limit) θc are removed. Contour nodes are always left intact. Figure 3 shows the final set node after an iteration of RSM for interpolating a step function.
The shape parameter of each center is chosen based on spacing with the nearest neighbors, and the Radial Basis Function approximation is recalculated using the new center set. The original approach by the Residual Subsampling Method is made by Multiquadrics RBF. However, it should be easily adapted to other global support RBFs. The coarse and refinement process should be repeated until an error criterion be reached.
In short, the adaptation process follows the family paradigm of resolving estimating/approaching until a stopping criterion is met [18].
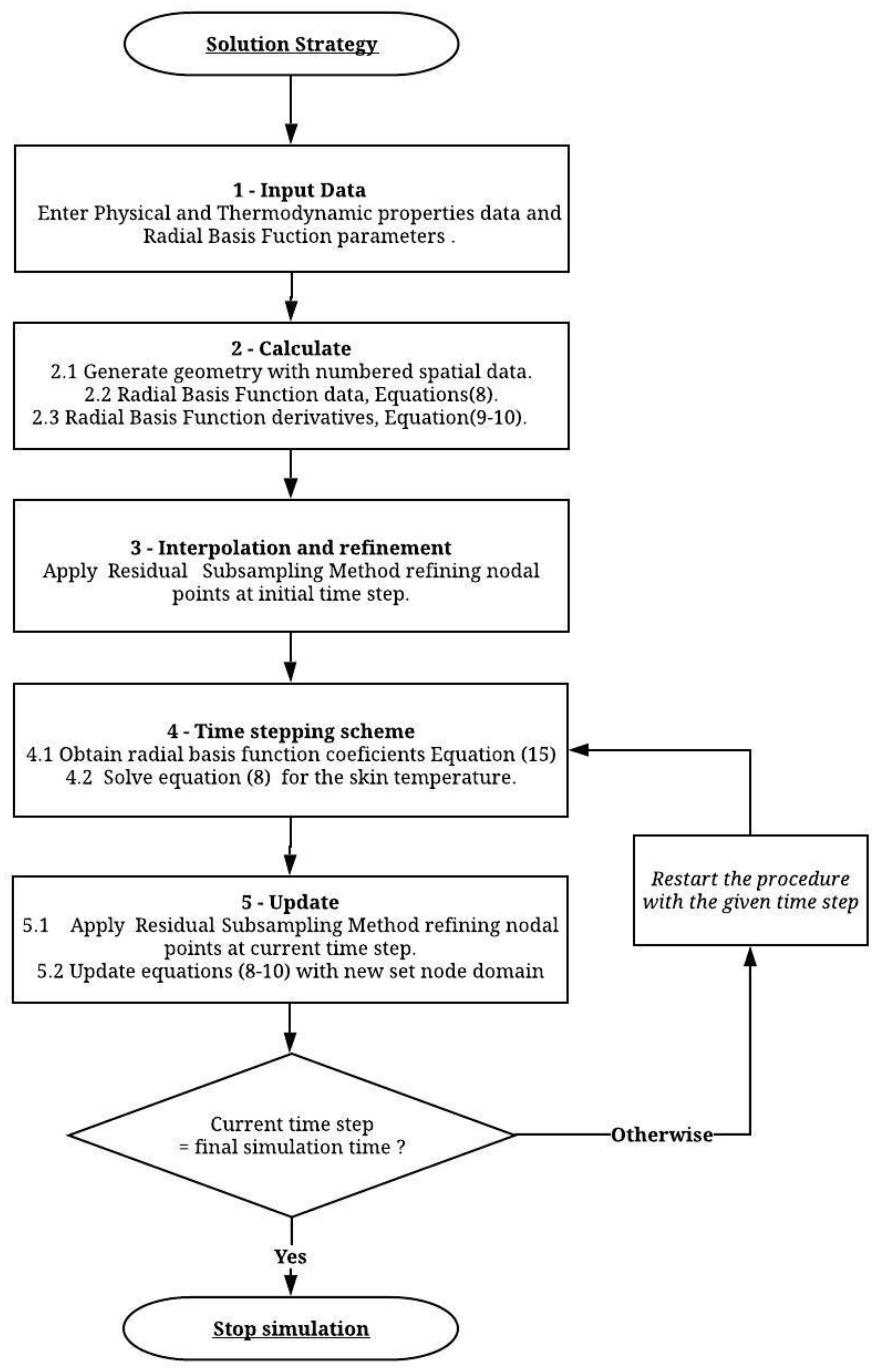
The Residual Subsampling Method can be easily modified to solve linear or non-linear problems of contour value. Figure 4 shows the flowchart of this method applied to the present study.
3.
Results and discussion
In the following calculations, the typical skin physical properties will be applied as proposed by [8]: ρ = ρb = 1000 kg/m3, c = cb = 4200 J/(kg·K), Ta = Tc = 37 °C, k = 0.5 W/(m·K), ωb = 0.0005 m3/s/m3, Qm = 33800 W/m3. The convection coefficient of apparent heat due to natural convection and radiation is taken as h0 = 10 W/(m2·K). The forced convection coefficient is applied as hf = 100 W/(m2·K), while the temperature of the surrounding fluid was chosen as Tf = 25 °C. Also, as demonstrated in many works [6],[25],[26], the indoor temperature of the tissue usually tends to be constant at a short distance, such as 2 to 3 cm, so it will be used in L = 3 cm in this study.
The local (E∞) and global (E2) errors will be calculated using the following equations:
where f(x) is the analytical solution, and s(x) is the numerical solution.
3.1. Skin surface under constant heating
This method of heating is often used in hot plate tests. This test was introduced in pharmacology by [27] to test the efficiency of new analgesics in use at the time and has since been widely used by researchers and scientists in the field [28],[29]. The hot plate test evaluates the reaction time to thermal stimuli of mice placed on hot plates at 55 °C [27],[29].
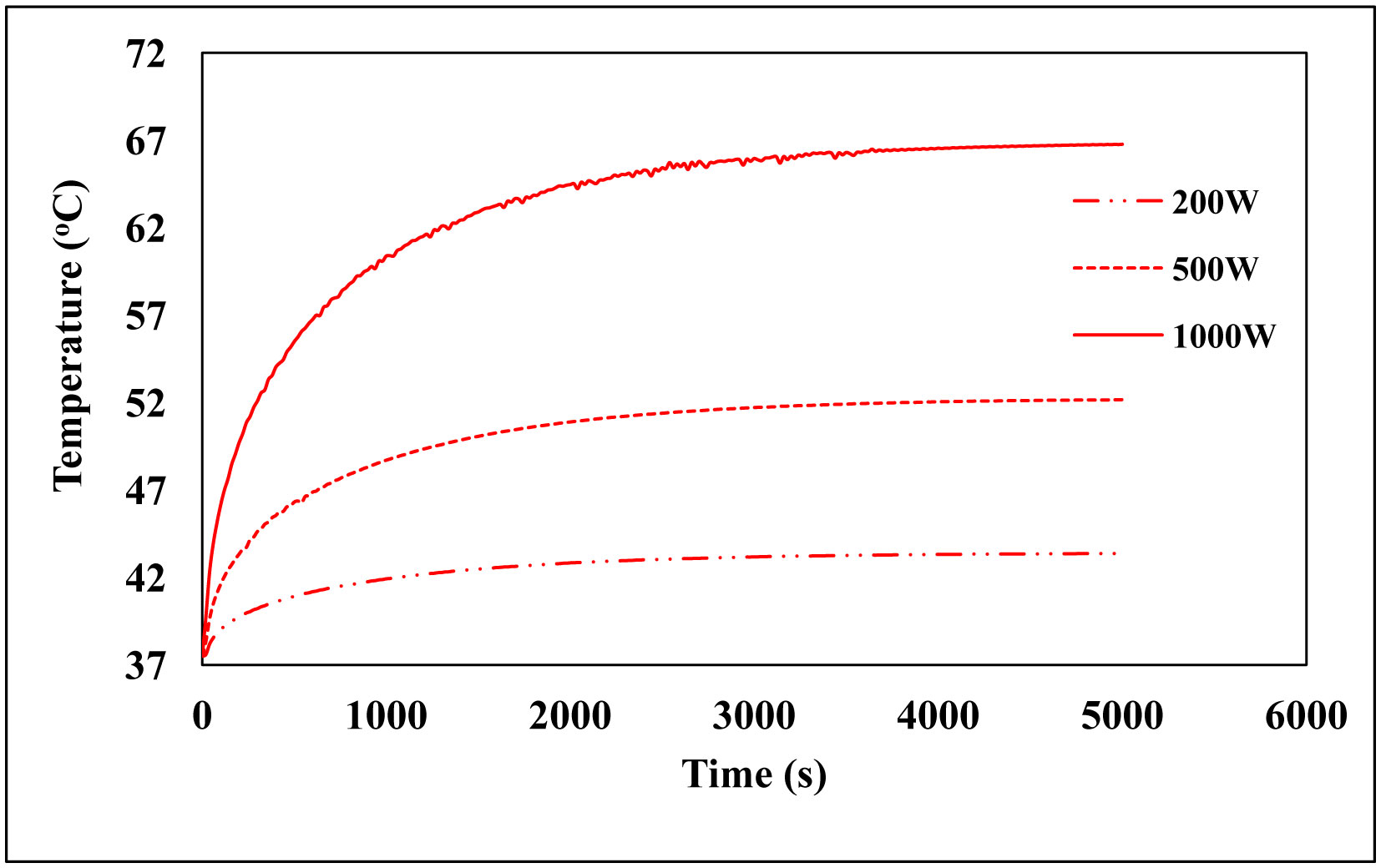
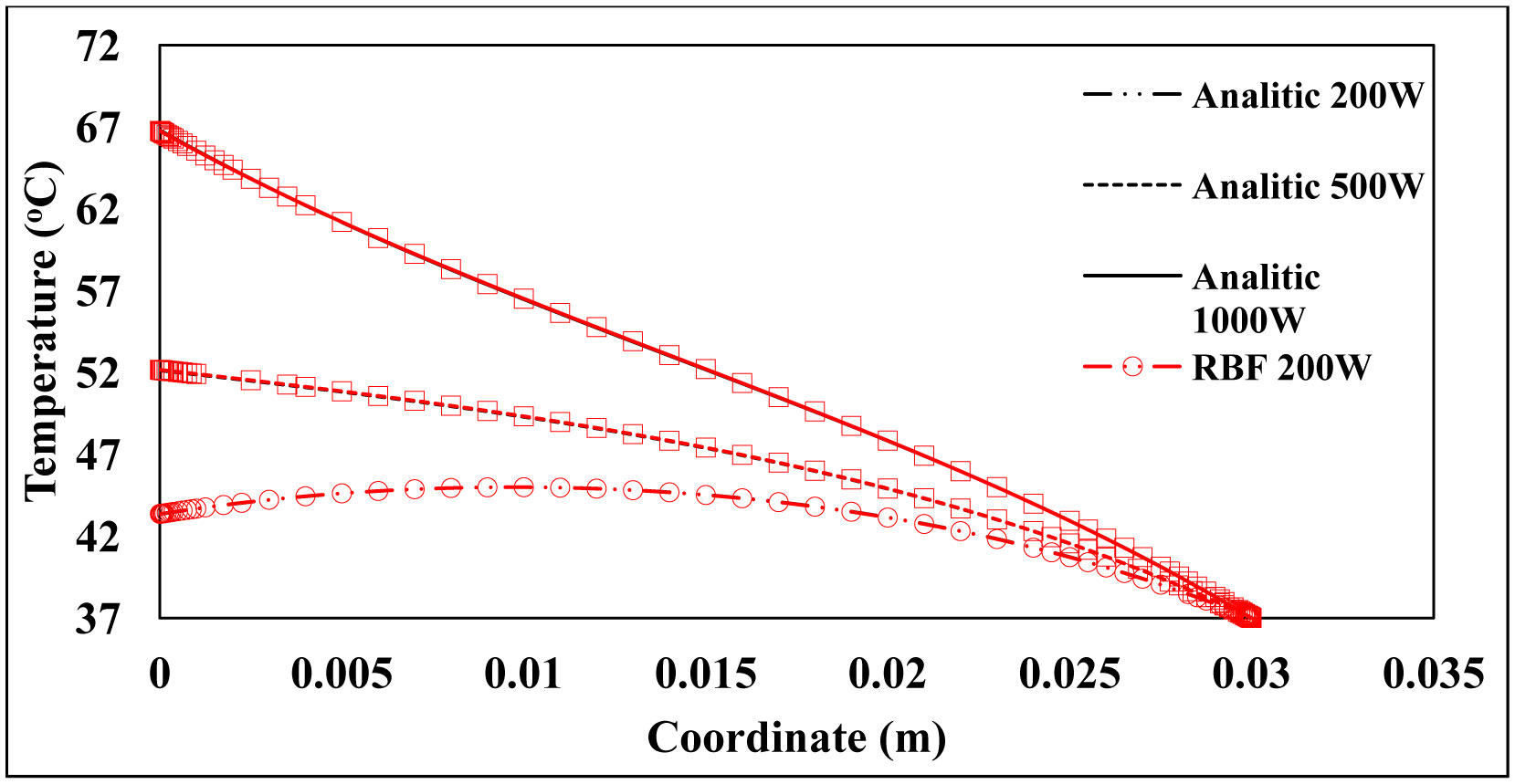
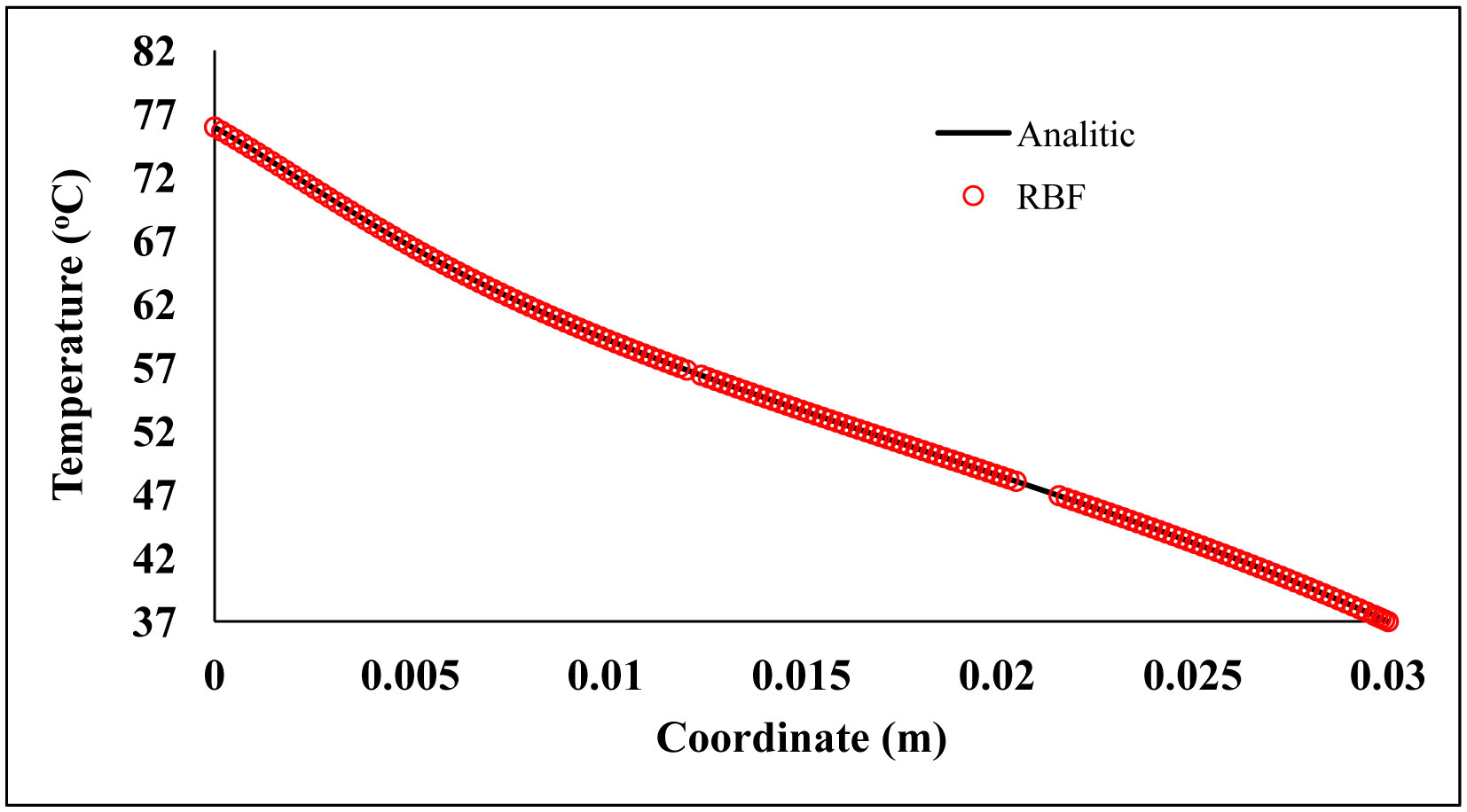
The numerical solution for surface temperature response is shown in Figure 5, while the numerical solution of the temperature response along the tissue compared to its analytical solution is shown in Figure 6. The curves presented are the transient temperatures of the tissues subject to three surface heating constants: P0(t) = 1000 W/m2, P0(t) = 500 W/m2, and P0(t) = 200 W/m2.
Table 1 shows the values of the shape parameters used for model calibration and the values of errors E2 and E∞ resulting from the comparison of numerical results with the analytical solution for the constant heating condition of the surface.
Analyzing Figures 5 and 6, and the results presented in Table 1, it was concluded that all error rates were below 0.1%. Also, the final values of nodes were extremely low for the three powers used, indicating an excellent performance of the proposed numerical methodology. It is important to focus on the uniformity of the errors presented by the technique, which can be observed more specifically in Table 1, which presents the maximum errors close to the global errors. Another phenomenon to be highlighted is the greater concentration of nodes on the boundaries, indicating that the contour regions present greater instability, caused by the formulation of the boundary condition or the non-linear terms of the equation. Table 2 corroborates the mentioned results when comparing the RBF adaptive node strategy in Table 1 against the RBF uniform node strategy in Table 2.
3.2. Surface heating by a step function
Practical examples of this case can be found in ophthalmologic surgeries through a single laser pulse [30] or skin burns due to an instant fire, hot plate, liquid, and gas for a short period. In the atomic explosion, the burn caused by the high-temperature shock wave also belongs to this problem [8].
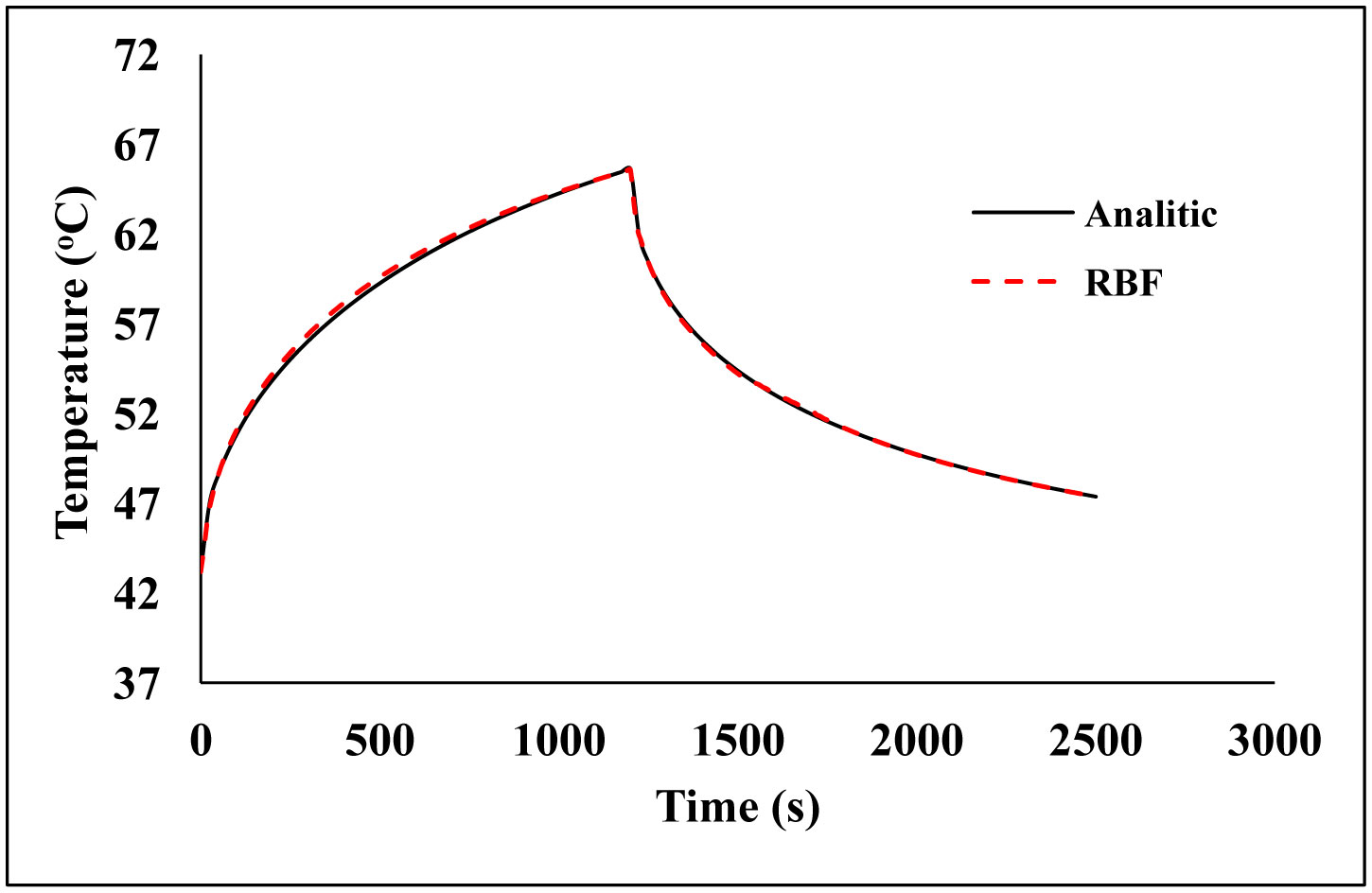
Figure 7 shows the transient temperature response to a heating on the surface of the step function P0(t) = 1000 W/m2 for t < 1200 s and P0(t) = 0 for t ≥ 1200 s, while spatial heating Qr = 0 and ωb = 0.0005 m3/s/m3.
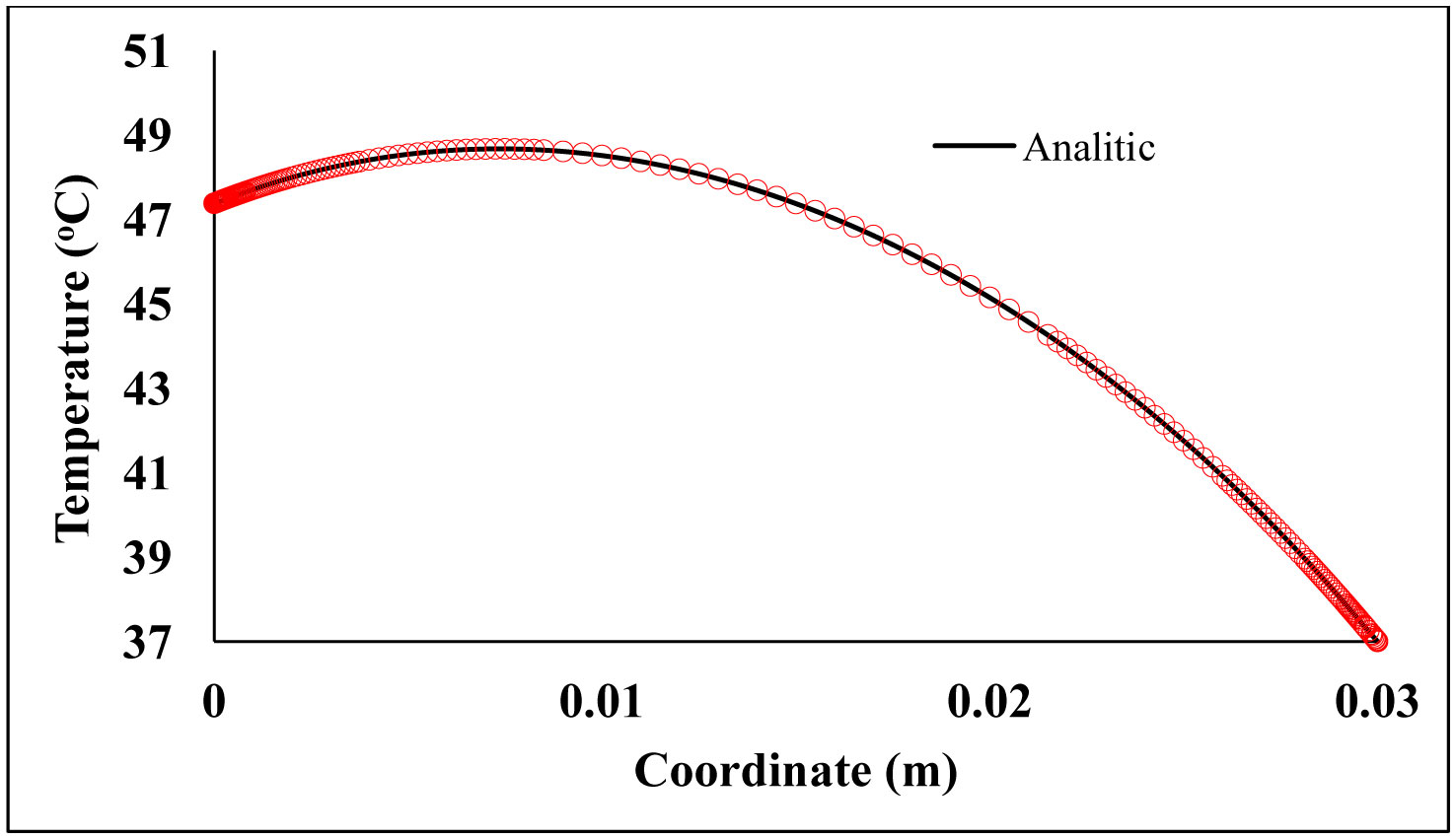
The numerical solution of the temperature response to heating by a step function compared to its analytical solution is presented in Figure 8, as well as the distribution of the resulting nodes in solving the problem.
Table 3 shows the respective values of the shape parameters used for RBF mesh refinement strategy and regular node distribution. The values of errors E2 and E∞ result from the comparison with the analytical solution for the condition of the heating of the surface by a step function.
To preserve good performance, the form factor of the multiquadric function had to be changed during the simulation, justified by the behavior of the step function in the contour. Therefore, for heating times below 1200 s, the applied value was ϵ1 = 0.673, and for longer times ϵ2 = 0.448.
Analyzing Figures 7 and 8, and the results presented in Table 3, it was concluded that the error rates presented values below 0.1%. The final number of nodes was very low, thus supporting the application of the proposed numerical methodology. It was also observed that the regions with the highest concentration of nodes were on the boundaries. The skin surface is a region of greater instability in the execution of the model, due to the sudden change of heat flux on the surface. This fact raises the difficulty of maintaining the desired stability and convergency criteria and makes it necessary to triple the number of nodes compared to the previous scenario.
3.3. Surface heating under a periodic function
Many researchers have investigated the effects of warming by a periodic function of biological tissues [32],[25],[33]. This type of heating is used in medicine and reflects a situation in which heating is caused by repeated laser irradiation in thermotherapy procedures [8], and is also used to measure blood perfusion in biological tissues [25].
Using the current solution in the finite domain, the temperature for periodic heating – both of the skin surface and inside biological bodies – can be easily obtained. Periodic surface heating can be expressed as [8].
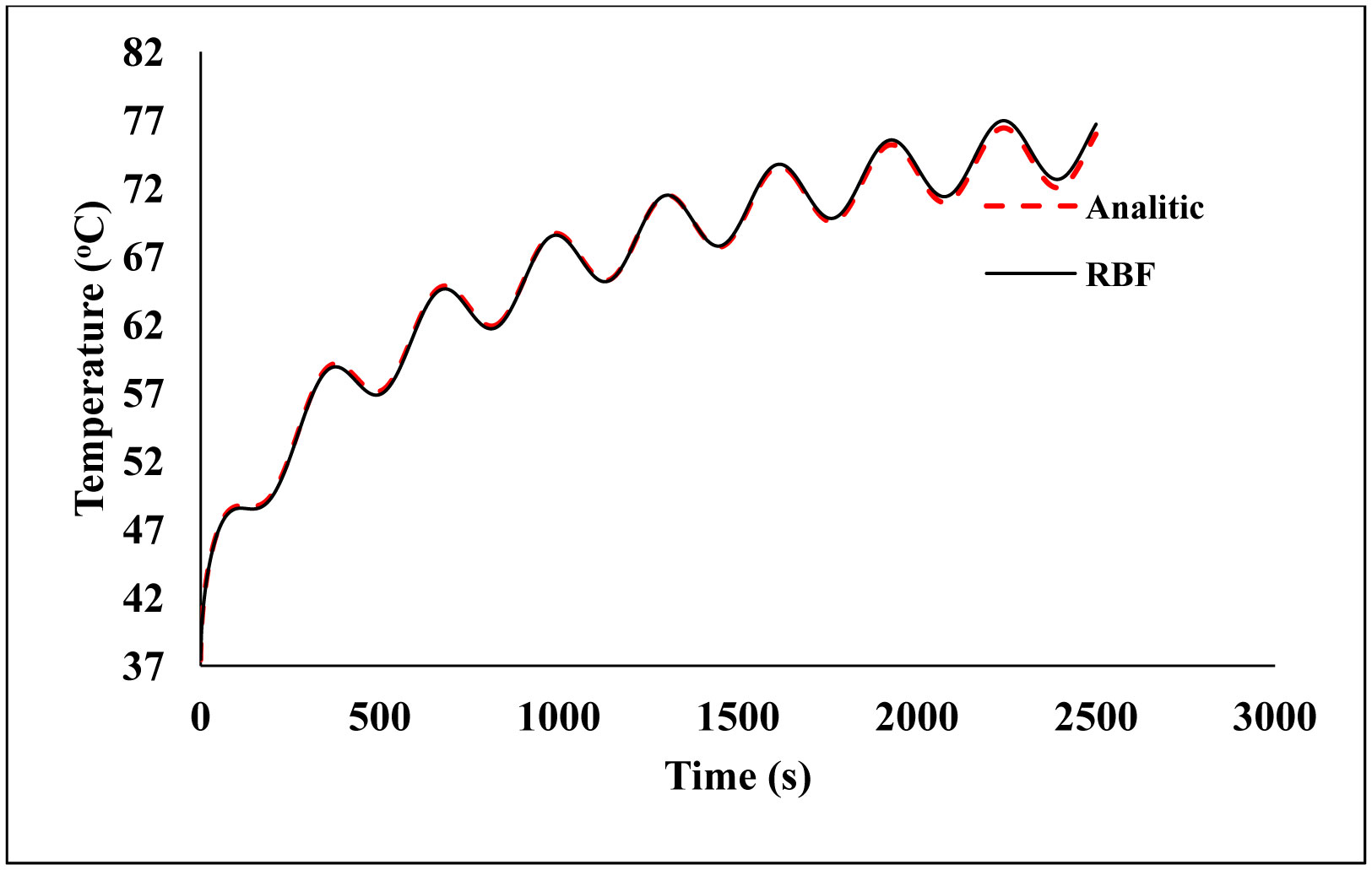
Figure 9 shows the response of transient temperature in biological bodies subject to surface heating by a periodic function.
The numerical solution of the temperature response to heating by a periodic function compared to its analytical solution is presented in Figure 10, as well as the distribution of the resulting nodes in solving the problem.
Table 4 shows the values of the shape parameters used for model calibration and the values of errors E2 and E∞ resulting from the comparison with the analytical solution for the condition of the heating surface by a periodic function.
Analyzing Figures 9 and 10, and Table 4, it was concluded that the error rates were around 0.1%, which are acceptable considering that only 162 nodes were needed to solve the problem. The points were distributed almost evenly along the tissue, but in the central region, it can be noted that there was a slight absence of points because the tendency is for the points to focus on the contours. It is essential to highlight the error uniformity of adaptive strategy when compared against the regular node distribution. This is a desirable phenomenon for numerical approaches representing the numerical stability and absence of local oscillations.
4.
Conclusion
Here we have presented a performance evaluation of the RBF node refinement strategy to solve bioheat transfer problems.
The numerical results had an excellent approximation relative to the analytical solutions, thus confirming that RBFs (coupled with a spatial node refinement strategy) are acceptable methods for solving bioheat transfer problems with low set of nodes. The novel RBF approximation for boundary condition involving step function presented excellent results. Additionally, the numerical solution showed uniformity on local and global error norms for all simulated scenarios.
However, it is essential to highlight that for surface heating by step function and periodic function, the transient terms in these respective boundary conditions directly affected the proposed methodology's performance. Additionally, the adaptive strategy may work excessively to maintain the error precision imposed by θr and θc parameters inducing instability in integration on time—however, the numerical approach still presenting good results. This fact should be considered in problems with irregular geometries. It should not be trivial to guarantee the presence of nodes only inside the domain coordinates. Additionally, remove a boundary node in 2D or 3D models within complex geometries may generate serious stability problems.
As a proposal for future work, we suggest expanding the adaptive technique proposed in this work for applications in 2- and 3-dimension bioheat transfer models involving multilayer problems, complex geometries, and the presence of convective terms. Practical adaptive radial basis function approach by bio-heat transfer modeling computed together with biomechanics may present complex modeling phenomena as soft tissue movement and thermal expansion/shrinkage effect [34],[35] and should be investigated.









 DownLoad:
DownLoad: