1.
Introduction
In the early outbreaks of COVID-19, many countries have banned public gatherings, closed down schools, restaurants, land, and sea borders, and forced people to stay at home in an attempt to curb the spread of this disease [1,2,3]. Few countries such as the Republic of Korea and Singapore focused their control measures on intensive contact tracing and testing [2,4]. Without vaccines and medicine, controlling the spread of COVID-19 relied mainly on non-pharmaceutical interventions (NPIs). These control measures were essential to public health but have caused an immense burden on the social and economic aspects of life [5,6].
During the early stages of COVID-19, most countries have monitored incidence cases and deaths and relied on this information in crafting policies [2,3]. The development of vaccines and oral antiviral drugs greatly impacted public health by reducing the severity of infections [7]. The fast rollout of vaccines, use of highly effective vaccines and medicine, and implementation of strict social distancing policies are expected to greatly minimize infections [8,9,10]. However, the protection given by pharmaceutical interventions alone did not guarantee the suppression of COVID-19 as variants of the virus continued to emerge. During the highly-transmissible omicron wave, the focus of control shifted to managing severe cases and minimizing deaths. The timing of lifting and intensity of easing NPIs have been important policy questions during the course of the COVID-19 pandemic. To this end, mathematical models that incorporate various aspects of COVID-19 and NPIs are proving to be important decision support tools [11,12,13,14].
Motivated by the events of the COVID-19 pandemic, we aim to provide a framework for planning social distancing policies based on the number of infections requiring hospitalization. The approach utilizes a Susceptible-Exposed-Infected-Isolated-Recovered (SEIQR) model that distinguishes mild from severe cases and includes a parameter that quantifies NPIs. The policy period is divided into two phases: a prevaccination phase, where only NPIs are implemented, followed by a vaccination phase, where vaccines are assumed to be available as additional control measures. We formulate optimization problems that minimize the stringency of NPIs during the prevaccination and vaccination phases and guarantee that cases requiring hospitalization will not exceed the number of available hospital beds. A measure of cost-effectiveness is presented as a basis for the choice of the frequency of policy change. To solve the optimization problems, we transform the constrained problems into unconstrained ones and implement a metaheuristic algorithm called the improved multi-operator differential evolution (IMODE) [15]. We compare IMODE with 20 other global optimization algorithms to demonstrate its effectiveness.
The presented framework can address key policy issues on the timing and level of adjusting NPIs. It is most relevant during an early epidemic phase, wherein pharmaceutical interventions are not yet available but managing the number of infections is a top priority. The timing of easing of NPIs is crucial at the start of vaccination in order not to compromise the benefits of vaccines [16,17,18]. Since a time-dependent epidemiological model is embedded in the method, data can be readily updated to fit the country or region where the framework is applied. As an application, we forecast the optimal intensity and timing of social distancing policies in Korea. An extended, more elaborate epidemiological model is adopted that includes variants, vaccination with primary and booster shots, waning of immunity, and administration of oral antiviral drugs [19]. Optimal solutions during the vaccination phase are determined under different scenarios.
2.
Materials and methods
In this section, we present the epidemiological models utilized in the optimization problems. We formulate the optimization framework and transform the constrained into unconstrained problems via the penalty method. We also present a measure of the cost-effectiveness of the strategies and discuss IMODE in more detail.
2.1. Epidemiological model
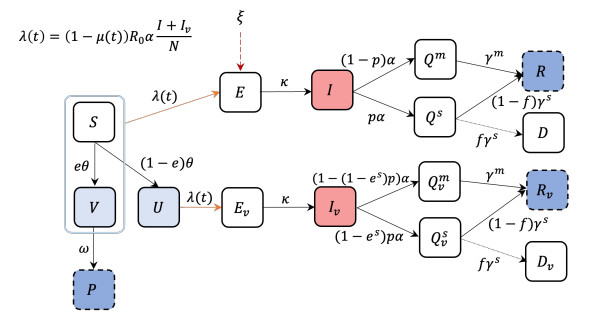
The mathematical model, illustrated in Figure 1, follows an SEIQRD structure. Susceptible class (S) can be effectively (V) or ineffectively (U) vaccinated with vaccine effectiveness e. The subscript v denotes vaccination and θ is the number of people vaccinated per day. After an average of 1/ω days, individuals in V develop full immunity to the disease (P). Without full immunity, susceptible individuals (S,U,V) can become exposed (E) with a force of infection λ(t), infectious (I) after 1/κ days, confirmed and isolated in 1/α days on average. Infection can be classified as mild (Qm) or severe (Qs). The parameter p represents the severe rate or the proportion of infected individuals that becomes severe. Isolated individuals can recover (R) at a rate γm or γs. A proportion f of severe cases is assumed to die (D). We assume that the severity of symptoms is reduced by a factor of 1−es for the vaccinated classes. The number of daily imported cases (ξ) is depicted by the red dashed arrow going into E.
The non-infected compartments are described by the following differential equations
The infected, recovered, and death compartments are given by
The force of infection λ(t) is defined as
where N=S+V+U+P+E+Ev+I+Iv+R+Rv, μ(t)∈(0,1) is a time-dependent parameter representing the intensity of NPIs, and R0 is the basic reproductive number. A μ value close to 1 translates to a high reduction in transmission, which is assumed to be a result of strict implementation of NPIs. On the other hand, a μ value close to 0 implies more relaxed NPIs. The model parameters are summarized in Table 1.
The number of administered vaccines per day (θ), imported cases (ξ), periods from confirmation to isolation (1/α), and hospitalization (γm,γs) are specific to a country's policies and resources. In the prevaccination phase, we simply set θ to zero. If ξ is zero, then screening measures are assumed to detect all non-locally transmitted cases. Other parameters in Table 1 can be obtained from the literature. Because vaccines have different effectiveness, we considered low and high values for e and es. The initial susceptible, exposed E0, and infectious I0 population are set to 999945, 50, and 5, respectively. The rest of the state variables are initially set to zero. The initial total population N0 is 1000000.
2.2. Formulation of the optimization problem
The stringency of NPIs is incorporated into the model as a factor in (2.3) that reduces transmission by 1−μ(t). In the optimization problem, we aim to determine the least value of μ(t) such that the number of severe patients Qs(t)+Qsv(t) throughout the policy period does not exceed the maximum severe bed capacity Hmax. Payoff constraints to ensure that daily cases are decreasing at the end of the prevaccination period and there are minimal cases at the end of the vaccination period are incorporated. A gradual easing of policies during the vaccination phase is also added as a constraint.
Suppose that the prevaccination phase is divided into n1 equal periods P1(t),P2(t),…,Pn1(t) and the vaccination phase into n2 equal periods Pn1+1(t),Pn1+2(t), …,Pn1+n2(t). We assume that μ(t) is a piecewise constant function over disjoint periods given by
where χi(t) is the characteristic function of Pi(t),i=1,2,…,n1+n2. Note that each μi assumes a constant value between 0.05 and 0.95. The goal in the prevaccination phase is to
such that
The objective in (2.4) means that we want to find the set of μi (i=1,…,n1) that gives the minimum average value. Here, Qs(t;μ) is solved from (2.1) to (2.3). Constraint (2.5) ensures that the number of severe cases at any time during the prevaccination period does not exceed the threshold value Hmax. Furthermore, we include a payoff constraint which guarantees that the number of cases at the end of the prevaccination phase is decreasing. That is,
where Pendn1 is the last time point on period Pn1, ρ is a constant less than 1, and Rt(t) is the effective reproduction number given by
Hence, the optimization problem for the prevaccination phase consists of (2.1) to (2.6).
For the vaccination phase, we consider the following objective function,
such that
and
where Pendn2 denotes the last time point on period Pn2. The payoff constraint (2.9) ensures that the number of severe patients by the end of the vaccination phase is less than a constant ˜H, with ˜H<Hmax. To have a gradual easing of policies during the vaccination phase, we further impose that
This means that successive values of μi in the vaccination phase are decreasing. The full optimization problem for the vaccination phase is given by (2.7)–(2.10) and the model (2.1)–(2.3).
To solve the constrained optimization problems, we use a penalty method and convert them into unconstrained problems. For the prevaccination phase, we minimize over [0,1]n1 the objective function
where the penalty terms η1,η2>>1. For the vaccination phase, the unconstrained problem is to minimize
over [0,1]n2, where η3,η4>>1. Note that the penalty terms chosen are exact [34], which means that the solution of the unconstrained problem is the same as the constrained one.
The lengths of the prevaccination and vaccination periods and frequency of policy change are decided by the user. In the simulations, we assume that the entire policy period is 18 months (540 days), consisting of 9-month prevaccination and 9-month vaccination phases. In the prevaccination phase, we vary the frequency of policy change, that is, we set n1=1 (uniform), n1=3 (quarterly), n1=9 (monthly), n1=18 (biweekly), or n1=36 (weekly). We assume that the severe bed capacity Hmax is 100, which is 0.01% of the initial total population N0, and the number of severe cases by the end of the vaccination phase ˜H is 1% of Hmax. Moreover, vaccination is assumed to proceed at a constant rate of θ=0.8N0/30σ, where σ is the number of months it takes to vaccinate 80% of N0. Different speeds of vaccination is considered: σ=6, 9, 12, or 24 months. To investigate the effect of importation, we also perform simulations on varying ξ. Because the constraints have different magnitudes relative to the objective functions, we chose appropriate weight constants ηi. The parameter settings used in the simulations are summarized in Table 2. To solve (2.11) and (2.12), we implement the metaheuristic algorithm IMODE.
2.3. Mathematical model of COVID-19 in Korea
As variants, booster vaccines, antiviral drugs, and waning of immunity have emerged as critical drivers of infection, a model that captures these factors is considered. We adopt the model in [19], which is an extension of the previously presented model to describe COVID-19 transmission in Korea.
The model illustrated in Figure 2 is divided into two parts: infection flow (top) and vaccination flow (bottom). In the vaccination flow, S denotes the susceptible group with no vaccine- or infection-induced immunity. The number of people administered with primary and booster vaccines per day are denoted by θv and θb, respectively. The protected class for the pre-delta and delta variants is P2, and against all variants is P3. Note that e1 is the primary vaccine effectiveness and e∗3=e3/e1 is a conditional probability depending on the vaccine effectiveness against the different variants. We assume that vaccine-induced immunity of the protected groups wanes after 1/τv days on average. Those in the waned group W will go to Vb after getting a booster shot three or four months after completing the primary vaccines. After an average of 1/ωb days, those in Vb move back to the protected groups depending on the probabilities e∗b,j, which are computed similarly as before.
In Figure 2, the variable X denotes the class where the infection was from and it can be sus (from S or V), U (from U), or P (from P1, W, or Vb). The subscript j denotes the variant and it can be 1 (infected by pre-delta), 2 (infected by delta), or 3 (infected by omicron). The reason for dividing the infectious group is to distinguish the different characteristics of infection, e.g. effect of vaccines for those infected, and the transmissibility and latent period of the variants. The E, I, Qm, Qs, R, and D classes are the same as in the simple model, each having nine variations depending on the subscripts. The probability of getting severe symptoms is assumed to be reduced by a factor (1−esX,j)(1−epill) due to the antiviral drugs. To include the waning of natural immunity depicted by the green arrow in Figure 2, individuals in R are assumed to have immunity only for 1/τX,n days on average. Note that the natural waning rate and vaccine effectiveness against severe disease are different for sus,V, and P. The system of differential equations describing the model is in Appendix A.
Before applying the optimization framework using model (A.1), we first establish the baseline value for μ in Korea by fitting the model to the cumulative confirmed cases data from February 26, 2021, when vaccination began, until February 3, 2022, when the testing method was changed. We then forecast the number of infections given a fixed μ value and different amounts of antiviral drugs and compare the results to the forecasts using the optimal μ values.
The estimation period covered four distinct social distancing phases in Korea: Social Distancing level 2 (SD2) from February 26 until July 11, 2021, Social Distancing level 4 (SD4) from July 12 until October 31, 2021, Gradual Recovery (GR) from November 1 until December 17, 2021, and Suspended Gradual Recovery (SGR) from December 18, 2021 to February 3, 2022. These phases do not directly reflect the stringency of NPIs. For example, the number of people in a private gathering, which is an important policy in controlling transmission, changed multiple times during SGR. We divide the estimation period every two weeks and determine μ on each interval by fitting the model to the cumulative confirmed data (Y(t)) using IMODE. That is, we look for the best-fitted μ value by minimizing the objective functional
As of April 29, 2022, Korea had used 2504630 drugs (Paxlovid: 2328610, Lagevrio: 176020) and has a remaining supply of 5775670 drugs (Paxlovid: 4942710, Lagevrio: 832960) [35]. This means that the proportion of Paxlovid among the used antiviral drugs is 93%, among the reserve antiviral drugs is 86%, and the total supply is 88%. We investigate future scenarios by first considering a fixed μ=0.1, 0.3, 0.5, 0.7 and setting the number of antiviral drugs to five or seven million. Then we apply the optimization framework to determine the optimal μ with varying amounts of antiviral drugs (five million, six million, and seven million) and proportions of Paxlovid ϕ (80%, 84%, 88%, 92%, 96%, and 100%) among the antiviral drugs used. We assume that the reduction in severity by Paxlovid and Lagevrio are 89% [36] and 30% [37], respectively. Simulation for the forecast starts on February 3, 2022, which is the final time of estimation, and ends on December 31, 2022. The threshold value on the number of severe cases at the end of the simulation period ˜H is set to 500.
2.4. Measure of cost-effectiveness
To determine the frequency of policy change, we adopt a measure of cost-effectiveness based on the cost of implementation of NPIs and the number of cases averted by the intervention strategy [38]. The cost-effectiveness ratio (CER) is the basis for choosing n1,n2=9 (monthly policy change) and is used to compare the optimal strategies under different amounts of antiviral drugs in Korea.
The total cost of implementation of NPIs is given by C⋅1n1n1∑i=1ui=C⋅μave, where C is the average cost of implementation of NPIs for the whole population for n1 periods and μave is the average of all the μi in the prevaccination phase. The CER is computed as
where k=1 or 2,
and
The number of averted severe cases Ak is computed as the relative difference between the number of severe cases when there are no NPIs and when there are NPIs with intensity μ⋆. In A2, φ denotes the number of antiviral drugs and φ⋆ can be five, six, or seven million. We use A2 in comparing the optimal strategies in Korea depending on the supply of antiviral drugs (Figure 2 model). Meanwhile, A1 is used in comparing the strategies resulting from different frequencies of policy change (Figure 1 model). For simplicity of calculations, we set C=1 since it only appears as a factor in the CER in (2.14) and will not affect the ranking of the different policies.
2.5. Improved multi-operator differential evolution
In Figure 3, we observe a non-convex and multi-modal surface plot of the objective function (2.11) with n1=2. Since the surface has many local minima near the global minimum, a local optimizer is not suitable for this problem. Evolutionary algorithms have become popular because of their capability of obtaining global minimum and ease of use. They only use function evaluations and do not require the derivative of the function. Applications of these algorithms have been explored in many areas of science and engineering [39,40,41,42,43,44,45].
Several algorithms are continuously being developed that can obtain the global minimum with high accuracy and low computational time [46,47,48,49,50,51]. In 2020, the Competition on Single Objective Bound Constrained Numerical Optimization was held and the Improved multi-operator differential evolution (IMODE) [15] ranked first in this competition. Hence, we use IMODE in solving the minimization problems (2.11) and (2.12). Since evolutionary algorithms have been shown to be effective in estimating parameters of biological systems [52,53,54,55,56], we also use IMODE in estimating the parameters for Korea using (A.1) by minimizing (2.13).
The inputs of IMODE are the objective function, dimension, and bound constraints. At the beginning of the IMODE process, an initial population from the search space is generated. The objective function using each population member is calculated and then sorted in ascending order. IMODE divides the population into several sub-populations, which are all evolved using three mutation operators. To preserve population diversity, archiving is done. The three operators are given as follows:
where r1,r2,r3≠i are randomly generated integers, →xr1,→xr3 are randomly chosen from the population, →xϕ is selected from the top 10% members of the population, and →xr2 is randomly selected from the union of the archive and the population. The scaling factor Fi is assigned based on success-historical memory [57]. Operators 1 and 2 move the member in the current population to the best points with and without archiving, respectively [58]. Operator 3 is a weighted random-member-to-best operator [15]. The size of each sub-population (NPop,op=1,2,3) is iteratively adjusted based on the diversity of the sub-populations and the quality of the solutions. The size of the population per generation (NPG) is also reduced linearly [57]. After the mutation operators are carried out, crossover is implemented randomly to create a new set of solutions. To speed up the convergence of IMODE, a local search is implemented when the number of function evaluations exceeds 85% of the maximum function evaluations (MAXFES). Figure 4 shows the flowchart of the IMODE algorithm. For a detailed discussion of the IMODE, we refer the readers to [15].
We compare IMODE to 20 other global optimization techniques in Appendix B by solving (2.11) for n1=3. The best, worst, mean, median, and standard deviation of the cost function values obtained from the 20 independent runs of each algorithm are computed. The hyperparameters of the algorithms are set to their default values except for the maximum function evaluations (MAXFES), which is set to 10000. If the stopping criterion of the algorithm is based on the number of iterations, we fix the population (or swarm) size (NP) to the default value and set the maximum number of iterations to ⌈MAXFES/NP⌉. For (2.11), (2.12), and (2.13), we use IMODE and set MAXFES to 20000 times the dimension of the problem. The other hyperparameters are fixed to their default values.
3.
Results
3.1. Comparative analysis of performance of IMODE with other metaheuristic algorithms
Appendix B summarizes the results using various metaheuristic algorithms. The top five with the least cost function values for each metric are written in boldface. Notably, IMODE ranked first in the mean and median. Eight other algorithms, RACS [59], LSHADE-cnEpSin [60], EBOwithCMAR [61], LSHADE-SPACMA [62], WFS [63], ABC [64], GBO [65], and AMO [66], have obtained 100% feasibility rate and have metric scores of less than 1. These algorithms may also perform well in solving the optimization problems given enough function evaluations or tuning of some hyperparameters.
3.2. Optimal solutions and cost-effectiveness analysis during the prevaccination phase
Figure 5 shows the results of the optimization problem (2.11) during the prevaccination phase for different frequencies of policy change. Here we considered uniform (n1=1), quarterly (n1=3), monthly (n1=9), biweekly (n1=18), or weekly (n1=36) policy changes in a span of nine months. The black curves are the plots of the severe patients Qs(t) and the colored lines are the optimal values of μ per period.
In the uniform policy, the optimal value of μ that should be maintained throughout the prevaccination phase is 0.630. The number of severe patients grew exponentially, almost reaching Hmax=100 by the end of this phase. Having two constraints on a one-dimensional optimization problem may result in an infeasible solution. For this reason, although the severe patients did not exceed Hmax, the payoff constraint, which ensures that incidence cases are decreasing by the end of the period, is not satisfied.
If the policy is changed every three months, the resulting optimal values of μ on the three consecutive periods are 0.873, 0.214, and 0.708. If the policy is changed monthly, the optimal values of μ on the consecutive months are 0.363, 0.812, 0.355, 0.944, 0.778, 0.917, 0.207, 0.085, and 0.787. The optimal solutions for the biweekly and weekly policies are illustrated in Figure 5. The average values of μ and the corresponding CER for the different policies are calculated using (2.14). The resulting CER are 0.016, 0.017, 0.012, 0.014, and 0.031 and are shown at the bottom right panel in Figure 5. In the succeeding simulations, we set n1,n2=9, which translates to a monthly policy change.
3.3. Optimal policy strategies during the vaccination phase
Figure 6 shows the optimal solutions and number of severe patients (Qs(t)+Qsv(t)) considering high (solid) or low (dashed) vaccine effectiveness (e and es) and speeds of vaccination depending on the value of σ.
If vaccination proceeds at a speed equivalent to vaccinating 80% of the initial total population in six months (red solid) using a highly effective vaccine, the optimal strategy is to keep the value of μ at around 0.785 from the start of the vaccination phase until day 359, when the first small noticeable reduction in μ to 0.733 is observed. This value of μ is reduced further to 0.05 on day 390. If the speed of vaccination is slowed down and vaccinating 80% of the initial total population is achieved in 9 (black solid), 12 (blue solid), or 24 months (green solid), the first observable easing of NPIs is delayed to day 419,449, and 479, respectively. Despite the delay, the corresponding reduction in the value of μ is greater. The value of μ decreased to 0.530 (black solid), 0.303 (blue solid), or 0.146 (green solid). In all scenarios, the number of severe patients by day 540 is around ˜H=1. Notably, a small peak in severe patients is observed on day 480 when the speed of vaccination is the fastest (red solid).
When a low effective vaccine is used, the first significant reductions in NPIs are further delayed. From around μ=0.785 at the start of the vaccination phase, the value of μ noticeably reduced to 0.145 (red dashed) or 0.687 (black dashed) on day 450. Meanwhile, if the speed of vaccination is slower, the first noticeable reduction in μ is on day 480 to 0.075 (blue dashed) or 0.403 (green dashed). In all cases, the number of severe patients declined.
3.4. Effects of importation and initial number of infection on NPIs
On the left panel in Figure 7, we set the severe bed capacity Hmax to 50,100,150, and 200, and vary the initial number of infected individuals I0. We assume that the daily imported cases ξ is zero and E0=10⋅I0. For simplicity, we assume that there is a uniform policy (n1=1) throughout the prevaccination phase. Results show that for Hmax=150 or 200, the optimal values of μ range from 0.61 to 0.69 as the initial number of infections varies from 0 to 500. If Hmax=100, the optimal values of μ can climb to 0.7 or higher if I0 is at least 350. If Hmax=50 and the initial number of infections is at least 420, the maximum value for μ is reached.
On the right panel in Figure 7, we fix ξ to 0, 5, 10, or 20, and vary Hmax. If Hmax is only 0.001% of the total population, then the optimal values of μ are 0.818, 0.750, 0.714, and 0.657 if ξ=20,10,5, or 0, respectively. Meanwhile, if Hmax is increased to 0.025% of the total population, then the optimal values of μ range from 0.689 to 0.704 as ξ varies from 0 to 20. As Hmax goes to 0.1% of the total population, all four cases converge to an optimal μ value of about 0.6.
3.5. Application of the framework using COVID-19 data of Korea
The estimation results for μ from February 26, 2021, when vaccination was begun, until February 3, 2022, when the testing method changed are shown in Figure 8 and summarized in Table 3. The lowest μ value was 0.590 during GR, and the highest value was 0.795 during SD4. Considering the average values in each phase, GR (0.623) was the most relaxed, followed by SD2 (0.665), SGR (0.682), and SD4 (0.744). If we compare the length of time for the variants to reach 90% of the infections, delta took 16 weeks while omicron took 10 weeks. In the final two weeks of the estimation period (January 19 to February 3, 2022), daily cases exceeded 30000 and μ was estimated at 0.653.
Figure 9 shows the forecasts for the daily confirmed cases and severe patients for different values of μ and amounts of antiviral drugs from February 3 to December 31, 2022. In this simulation, the amount of antiviral drugs is set to seven million (solid) or five million (dashed), and μ is kept constant until the end of the year. The horizontal line on the right panel depicts the severe bed capacity on February 3, 2022 equal to 2825. Note that the drugs only affect the severe patients and not the daily confirmed cases since the drugs are assumed to reduce the severity of infections. If μ is fixed at 0.10 or 0.30, the number of severe patients surpasses the threshold. If the amount of antiviral drugs is limited to five million, a surge in severe infections starting from around July 2022 may occur if μ=0.10,0.30, or 0.50. Moreover, if μ=0.10 and with five million antiviral drugs, the number of severe patients may once more exceed the threshold. In the next simulations, we apply the framework and investigate when and by how much should NPIs be eased given different amounts of antiviral drugs.
Because Korea is in the vaccination phase, the optimal μ is solved by minimizing (2.12), where the number of severe patients is obtained by solving system (A.1). We set the upper bound for μ to 0.653, which was the last estimated value of μ, and set different amounts of antiviral drugs (five, six, or seven million). Figure 10 shows that if the amount of drugs is five million (red), the optimal values of μ are around 0.6 until July 2022, then around 0.48 until the end of the year. A rise in severe patients may occur towards the last quarter of the year when the supplies are all used up. Meanwhile, if the amount of drugs is six million (blue), the optimal values of μ range from 0.487 to 0.438 until around October 2022 before it is reduced to 0.365. If the supply of antiviral drugs is seven million (green), the optimal values of μ are 0.534 at the beginning, eased to 0.318 from March 2022, then reduced significantly to 0.05 from April 2022. At the end of the forecast period, the cumulative severe cases are 18494, 11152, and 13233 for the five, six, and seven million supply of antiviral drugs, respectively. The corresponding CER values are 0.652, 0.493, and 0.124.
Figure 11 shows the optimal policy plans and the resulting number of severe and cumulative severe patients from February 3 until December 31, 2022, assuming different proportions ϕ of administered antiviral drug Paxlovid. Since the effectiveness of Paxlovid (89%) is assumed to be much higher than Lagevrio (30%), the net effectiveness of using both antiviral drugs would vary depending on how much of each drug is administered. For example, ϕ=0.8 means out of all the administered antiviral drugs, 80% is Paxlovid and 20% is Lagevrio. This results in a net effectiveness of 77%. In the forecast, the optimal values of μ on the first period, if ϕ=1 (green) or ϕ=0.96 (teal), are 0.534 or 0.617, respectively. On the other hand, if ϕ=0.92,0.88,0.84 and 0.8, the optimal values of μ are 0.674, 0.706, 0.728, and 0.743, respectively, which are higher than the estimated value of μ=0.653 before February 3, 2022. At the end of the forecast period, the optimal value of μ reached the minimum (0.05) in all scenarios and the cumulative severe cases are 23861, 21815, 20100, 17922, 15656, and 13231 for ϕ=0.8,0.84,0.88,0.92,0.96, and 1, respectively. The corresponding CER values are 0.290, 0.272,213, 0.181, 0.166, and 0.124.
4.
Discussion
In Figure 5, the oscillating values of μ, which results in the shifts in the number of severe patients, are observed on the quarterly, monthly, biweekly, and weekly policy changes. In the quarterly policy change (n1=3), relaxation of NPIs is suggested to be implemented from months 3 to 6. Correspondingly, we observe a very small number of severe cases until towards the end of the sixth month. Under this strategy, NPIs should be intensified in the last period as the number of severe cases increased and peaked at almost the capacity Hmax before it declined. As the frequency of policy change is increased, there are more frequent adjustments in the intensity of NPIs, depicted by the jumps in the values of μ. Consequently, more peaks in the number of severe patients occur. Naturally, a rise or drop in cases follows when the policy is eased or relaxed. In all cases, Hmax is always almost reached to allow the most relaxed level of NPIs possible, as long as the number of severe cases is kept below the capacity. Results of the cost-effectiveness analysis show that the monthly policy change has the least CER (0.012) and hence, the most cost-effective strategy. On the other hand, the weekly policy change is the least cost-effective (0.031).
In Figure 6, we see that a gradual easing of NPIs (or decreasing values of μ) is possible in all scenarios. We observe that NPIs can be noticeably eased much earlier if the vaccines used are highly effective. Moreover, if vaccination is slow (green curves), then strict NPIs (μ≈0.78) are maintained longer, even if the vaccine has high or low effectiveness (easing on day 479 for high and day 480 for low vaccine effectiveness). These emphasize the importance of not only using highly effective vaccines but also fast administration of the vaccines to the population.
In Figure 7, results show that with higher Hmax, a lower value for the optimal μ is possible. For low values of initial infections (I0 less than 150), the level of NPIs is relatively stable (μ from 0.61 to 0.69). As I0 increases and Hmax reduces, the importance of maintaining strict NPIs is more evident. For example, if I0=500 (or 0.05% of N0) and Hmax=50 (or 0.005% of N0), the healthcare capacity can be overwhelmed with severe cases even with the most strict level of NPIs (μ≈0.95). This approach can serve as a guide in assessing the adequacy of severe beds given that the initial number of infections is known. Furthermore, the impact of daily imported cases on the optimal values of μ is more apparent for smaller values of Hmax. Here, the severe bed capacity Hmax is presented as a percentage of the total population. For example, in Germany and the USA in 2020, the number of ICU beds is more than 0.025% of the population, while in most African and Southeast Asian countries, this percentage is less than 0.001% [67]. In Figure 7, if the severe bed capacity is 0.001% of the initial population, the intensity of NPIs is less if there are fewer imported cases (μ=0.657 if ξ=0, while μ=0.818 if ξ=20). Therefore, for countries with a low number of severe beds, NPIs such as screening measures at the border are crucial in keeping a minimal number of imported cases and preventing strict NPIs.
From February 26, 2021 to February 3, 2022, the estimated μ values in Korea and the number of daily confirmed cases during SD2 and SD4 were relatively stable except around July 12, 2021, when the proportion of the delta variant among the infections increased rapidly. On November 1, 2021, GR was implemented and the maximum number of people allowed in a private gathering increased to eight. As a result, daily confirmed cases soared, even though the proportion of omicron among the cases was still below 10%. As daily confirmed cases reached 7000, the government suspended the GR policy. Since SGR initially had a stricter private gathering policy, the daily confirmed cases decreased. However, the daily confirmed cases increased again as the proportion of the omicron variant rose to over 50%. Despite the increasing number of cases towards the end of the estimation period, policies in Korea kept easing.
Furthermore, we investigate the effects of antiviral drugs and the easing of NPIs in the number of severe patients. We see in Figure 9 that for non-optimal μ values of 0.1 or 0.3, even with seven million antiviral drugs, the number of severe patients may surpass the severe bed capacity. Moreover, with μ=0.5 or lower and five million antiviral drugs, a surge in severe patients is likely to happen. Results in Figure 10 with the optimal μ values show that in all three cases, a gradual easing of NPIs is possible without exceeding the severe bed capacity, even during the second surge of cases when all the five million supply of antiviral drugs are used up. We note that all the obtained optimal μ values are less than the estimated μ values during SD2, SD4, GR, and GR (see Table 3). Although the cumulative cases by the end of the year when the antiviral drugs are six million (11152) are less compared to when the supply is seven million (13233), the CER for the seven million supply (0.124) is considerably less than the six million supply (0.493). Finally, we see on the bottom left panel in Figure 11 that if the proportion of administered Paxlovid is 92% or less (blue, black, purple, and red), then more strict NPIs, greater than the previously estimated μ=0.653, should be implemented at the beginning of the forecast period so that the number of severe patients will not exceed the set threshold of 2825 beds. In all cases, a relaxed level of NPIs (μ=0.05) is possible starting June 2022. A lower proportion ϕ may delay the peak of severe infections but the wave is wider resulting in higher cumulative cases. For instance, if ϕ=0.80, the predicted cumulative severe cases are almost double compared to when ϕ=1. This is interesting because social distancing policies are more relaxed if ϕ=1 compared to when ϕ=0.8. Thus, the use of highly effective antiviral drugs not only reduces the number of severe cases but may also lead to earlier easing and less strict intensity of NPIs. In Korea, COVID-19 restrictions were eased in April 2022, while the relaxation of mask mandates began in May 2022. Since 93% of antiviral drugs used in Korea were Paxlovid, the results of the simulations support the Korean policies on the easing of restrictions.
5.
Conclusions
In this work, we have formulated nonlinear optimization problems that minimize the intensity of NPIs (such as social distancing and mask-wearing) and ensure that the number of severe cases will not surpass the severe bed capacity during the prevaccination and vaccination phases. An epidemiological model that considers vaccination, reduction in transmission due to NPIs, and severe cases is embedded in the optimization problem. The constrained optimization problem is transformed into an unconstrained one using the penalty method. Because we use exact penalty functions, the resulting objective function is non-differentiable, non-convex, and highly multi-modal. The metaheuristic optimization algorithm IMODE, which is capable of obtaining the global minimum, is used to solve the problems.
In the simulations, we observed in the prevaccination phase that more frequent policy changes result in more oscillations in the number of severe cases and a lower average μ. However, results of the cost-effectiveness analysis show that a monthly policy change is the most cost-effective. In the vaccination phase, faster administration of highly effective vaccines results in the earlier easing of NPIs. If vaccine rollout is slow (80% of the population is vaccinated in 24 months), vaccine effectiveness does not impact the timing of easing of NPIs. Moreover, we have demonstrated that the initial number of infected individuals and daily imported cases should be kept at a minimum value especially when the severe bed capacity is low.
As an application, we determine optimal social distancing policy plans in Korea considering different amounts and types of antiviral drugs. A mathematical model that includes variants, booster vaccines, antiviral drugs, and waning of immunity was used. To establish the relationship between social distancing policies and the values of μ, the model is first fitted to the data on confirmed cases by minimizing a least-squares formulation using IMODE. Forecast results for the optimal μ values show that gradual easing of policies is possible and the number of severe patients can be maintained below capacity even with at most five million antiviral drugs, compared to when μ is kept fixed to 0.3 or below. The easing of NPIs may occur earlier and with less intensity, if the supply of antiviral drugs is enough and the antiviral drugs are highly effective in reducing the severity of the disease.
Results in Appendix B show that recent algorithms performed better compared to classical algorithms when solving the proposed optimization problem. Hence, this study contributes to the growing importance of optimization algorithms that converge faster with more accurate solutions. Since the study of evolutionary algorithms is an active research area, we expect that new algorithms will be developed which can be used to solve the constrained problems. In our simulations, a constant value for the severe bed capacity Hmax was assumed. However, the optimization problem can be reformulated to allow Hmax to be time-dependent, as in the case when there is a surge of infections and hospital bed capacity needs to be increased to accommodate more patients. A study that considers a time-dependent Hmax can be done in future work. One can also consider a more general optimization problem that allows for a non-constant duration of policies (e.g. P1 is 30 days, P2 is 15 days, and so on). Furthermore, we assumed that both the prevaccination and vaccination phases span 9 months. Depending on the capability to implement and availability of resources of a region or country, the length of these phases can be modified, and consequently, the optimal strategies will change. In the application using COVID-19 data of Korea, second booster shots and possible underreporting of cases were not considered. Nevertheless, the epidemiological model can be modified to incorporate these and other factors, and the framework is still applicable. The proposed scheme is general enough that it can be applied to any model, regardless of complexity, as long as NPIs are quantified as a reduction in the force of infection, and the severe case has a separate compartment. Finally, the presented framework may be applied to other variants of COVID-19 or other infectious diseases.
Acknowledgments
This paper is supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021M3E5E308120711). This paper is also supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021R1A2C100448711).
Conflict of interest
All authors declare no conflicts of interest in this paper.
Supplementary
A. Equations of the COVID-19 model in the application using data of Korea
The system of differential equations describing the model are given by
where
The model parameters and their values considering the pre-delta, delta, and omicron variants are shown in Table S1. The parameters ω, f, p, and vaccine effectiveness (e,eb,es) are from the literature and adjusted to fit Korea (e.g. vaccines administered, age structure, etc.).
B. Application of different metaheuristic algorithms in solving the prevaccination phase optimization problem
Table S2 summarizes the results of the 21 metaheuristic algorithms in solving (2.11) for n1=3. The following abbreviations are used: Improved Multi-operator Differential Evolution (IMODE), Ranking-based Adaptive Cuckoo Search (RACS), Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood (LSHADE-cnEpSin), Effective Butterfly Optimizer with Covariance Matrix Adapted Retreat Phase (EBOwithCMAR), LSHADE with Semi-Parameter Adaptation Hybrid with CMA-ES (LSHADE-SPACMA), Wingsuit Flying Search (WFS), Artificial Bee Colony(ABC), Gradient-based Optimizer (GBO), Animal Migration Optimization (AMO), Ant Lion Optimizer (ALO), Simulated Annealing (SA), Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), Elephant Herding Optimization (EHO), Genetic Algorith, (GA), Mexican Axolotl Optimization (MAO), Harris Hawks Optimizer (HHO), Generalized Pattern Search (GPS), Whale Optimization Algorithm (WOA), Chimp Optimization Algorithm (ChOA), Bat Algorithm (BA).









 DownLoad:
DownLoad:














