Positivity analysis for the discrete delta fractional differences of the Riemann-Liouville and Liouville-Caputo types

1.   Introduction

In recent years, the inverse problem has aroused the research interest of scholars. Keller first proposed the concept of positive and inverse problems in ^[1]. Solving problems based on known data and definite solution conditions is called a positive problem (also known as a direct problem). On the contrary, problems like those of interest in this paper are called inverse problems if we solve or estimate unknown data based on measurement data. Hadamard ^[2] first proposed the concept of well-posedness. That is, a problem is well-posed if its solution exists and is unique and stable to the given data. If one of these is not satisfied, then the problem is ill-posed. With the study of the inverse problem, people find that the inverse problem is usually ill-posed. So, studying the solution of the inverse problem is a challenging task. The heat conduction equation is a classical mathematical physics equation, which describes the process of temperature change with time in a certain region. If we already know the initial temperature and boundary conditions of the equation, and we obtain the temperature at any time by solving the equation, this is called the forward heat conduction problem, and the forward problem is well-posed in general. In real life, since the initial temperature in the heat equation is unknown, then we have to use some conditions to obtain the initial temperature and the temperature distribution at any time. This kind of problem is called the backward heat conduction problem. For example, in the field of biomedicine, through changes in the body's perceived temperature, we can determine that a disease is occurring in one of the body's organs ^[3,4,5]. The BHCP is also called the final value problem ^[6], which is a seriously ill-posed problem ^[7]. Usually, there is no solution, or if there is a solution, it will be discontinuously dependent on the given data. So, it is very difficult to get its numerical solution. A specific method (called the regularization method) is required to obtain stable numerical solutions. For this reason, many scholars have done a lot of research.

The Tikhonov regularization method to solve the BHCE by W. B. Muniz et al. was proposed in ^[8,9]. The author transforms this inverse problem into an optimization problem. The regular term is introduced into the objective function, and a good approximation is obtained. In ^[10], in order to solve the inverse heat equation, the author proposes a new Tikhonov method. In ^[11], the Lie-group shooting method is used to numerically integrate the ordinary differential equations. S. M. Kirkup and M. Wadsworth proposed operator splitting in ^[12] and obtained the solution of the inverse heat equation. The Adomian decomposition method was proposed by G. Adomian, R. Grzymkowski, and M. Pleszczynski in ^[13,14]. In ^[15], a new spatiotemporal radial Trefftz collocation method was proposed to solve the inverse heat conduction problem with time-dependent source terms.

In recent years, the Fourier regularization method has been found to be highly efficient in solving inverse problems. In ^[16,17], Fourier regularization was applied to study the heat equation. In ^[18], the author studied numerical differentiation. In ^[19], a posterior truncation method was proposed to solve ill-posed problems. In ^[20,21], the author solved the Cauchy problem of Helmholtz equation by a truncation method. In ^[22], the authors studied the Cauchy problem of the inhomogeneous Helmholtz equation. In ^[23], the initial data of the BHCP with non-uniform time fraction was determined by the Fourier truncation method. In ^[24], a new technique for determining the truncation singular value when regularization is applied in ill-posed inverse problems is discussed. Besides, the Fourier-type inversion has been characterized in a general setting of the filter regularization operators in ^[25]. Other methods for solving the inverse problem of heat conduction can be found in references ^{[26,27,28,29,30]}.

Although the authors in the above literature have obtained the solution of the BHCE through some regularization methods, the error estimation is basically the traditional $H\ddot{o}lder$ type estimation, and the estimation at $t = 0$ is neglected. In addition, the traditional heat conduction equation does not take into account the uncertainty of the parameters and regards the parameters as definite values, which is a big defect when we solve real-world problems. For example, in the process of the spacecraft returning to the land surface, due to the effect of aerodynamic heating of the atmosphere, the temperature of the spacecraft surface rises instantaneously with the passage of time. Therefore, we must get the surface temperature in time to ensure the safety of the astronauts. But, this temperature is often difficult to measure, and when it is measured, it is uncertain. For instance, in the high-temperature smelting furnace in the high-temperature smelting operation, we need to regularly measure the temperature of the furnace surface to ensure safety. However, due to the extremely high temperature of the furnace surface, the data measured by physical means are often uncertain. In order to deal with the uncertainty in parameters, we use fuzzy numbers to model the uncertainty in parameters and define the BHCE with uncertainty. Since the BHCE with uncertainty is a fuzzy differential equation in essence, some literature on fuzzy differential equations is introduced here for the convenience of analysis.

The theories related to fuzzy differential equations have been extensively studied, but because of the operation property of fuzzy subtraction, it is very difficult to define the derivative of fuzzy numbers, which is a great challenge. The development of derivatives of fuzzy numbers is described below.

In 1965, Zadeh proposed the concept of fuzzy sets for the first time in ^[31]. The fuzzy mapping function was introduced by Chang and Zadeh in ^[32]. In 1972, under the influence of the extension principle, Dubois et al. ^[33] proposed elementary fuzzy operation. The cauchy problem for fuzzy differential equations (FDEs) were studied by Kaleva in ^[34]. The fuzzy initial value problem was studied by Seikkala in ^[35]. Based on the Hukuhara derivative operation, Bade applied it to the solution of FDEs in ^[36]. A differential transform method to solve fuzzy partial differential equations (FPDEs) was studied by Mikaeilvand and Khakrangin in ^[37]. Zadeh's extension principle was applied to the solution of FDEs by M. S. Cecconello, M. Oberguggenberger et al. in ^[38,39]. S. Abbasbandy and M. Chen proposed solving fuzzy differential equations based on differential inclusion theory in ^[40,41], which forms a differential inclusion family by taking the level set of fuzzy vector fields. In ^[42], based on the Hukuhara derivative and the generalized Bede derivative, a fuzzy differential equation was solved by R. Agarwal and M. Chen et al. In 1997, Zadeh put forward the idea of fuzzy information granulation in ^[43]. In 2018, M. Mazandarani proposed a new method for solving fuzzy differential equations, namely granular differentiability, in ^[44]. This method overcomes the disadvantages of previous methods and makes the solution of fuzzy differential equations simple and convenient. According to our literature review, the conventional fuzzy differential equation is generally based on the $\mu$-level set of fuzzy numbers into two crisp differential equations to obtain the solution interval. However, in this paper, we use the concept of the granular differentiability to transform the fuzzy differential equation into a granular differential equation, thus improving the efficiency of the calculation.

In this paper, we will regard the parameters in the BHCE as uncertain parameters, and define the BHCE with uncertainty. It is found that most of the papers are on the forward problem of fuzzy differential equations, while there are very few papers on the inverse problem (such as ill-posedness, regularization methods, etc). The representative studies are mainly the following articles by Gong and Yang. In ^[45], Gong and Yang studied fuzzy initial boundary value problems in 2015. A regularization method was proposed to restore numerical stability. In 2019, Yang and Gong first proposed the concept of ill-posedness of the first kind of the fuzzy Fredholm integral equation in ^[46]. In ^[47], Yang and Gong proposed an iterative method for solving the fuzzy integral equation. The error estimation under this method is also given.

The remaining portion of the current paper is arranged as follows. In Section 2, the basic knowledge used in this paper is given. In Section 3, the BHCE with uncertain parameters is defined and the granular representation is derived. Then, it is proved to be a seriously ill-posed equation. In Section 4, the Fourier regularization method is introduced, and the granular representation of the approximate solution is given. Under the condition of proper selection of regularization parameters, the error estimation between approximate solution and exact solution is proved. In Section 5, a numerical example is given to illustrate the feasibility and practicability of the method. Section 6 gives the conclusion of this paper and future prospects.

2.   Preliminaries

We stipulate that the fuzzy number space is represented by $E^{1}$. For $0 < \mu \leq1,$ the $\mu$-level set of $\tilde{u}\in E^{1}$ is defined by $[ \tilde{u} ]_{\mu} = \{x\in \mathbb{R}^{n}| \tilde{u} (x)\geq \mu\}.$

Theorem 2.1. (^[48]) If $\tilde u\in E^{1}$, then $\tilde u = \bigcup\limits_{\mu\in[0, 1]}(\mu\cdot[\tilde u]_{\mu})$.

Definition 2.2. (^[44]) Let $\tilde{u} : [a, b] \subseteq \mathbb{R}^{n} \rightarrow [0, 1]$ be a fuzzy number. The horizontal membership function $u^{gr} : [0, 1]\times[0, 1] \rightarrow [a, b]$ is a representation of $\tilde{u} (x)$ as ${u}^{gr}(\mu, \alpha_{u}) = x$ in which "gr" stands for the granule of information included in $x \in [a, b], \mu \in [0, 1]$ is the membership degree of $x$ in $\tilde{u} (x), \alpha_{u} \in [0, 1]$ is called relative-distance-measure (RDM) variable, and $u^{gr}(\mu, \alpha_{u}) = \underline{u}^{\mu} + (\overline{u}^{\mu}-\underline{u}^{\mu})\alpha_{u}$.

By definition, for fuzzy numbers $\tilde{u} = (a, b, c)$, we have $\mathcal{H}(\tilde{u}) = [a + (b-a)\mu] + [(1 - \mu)(c - a)]\alpha_{u}$.

Remark 2.3. (^[44]) The horizontal membership function of $\tilde{u}(x)\in E^{1}$ is also denoted by $\mathcal{H}(\tilde u (x)) = u^{gr}(\mu, \alpha_{u})$. Moreover, using

the $\mu$-level sets of the vertical membership function of $\tilde{u}(x)$, which is in fact the span of the information granule, can be obtained.

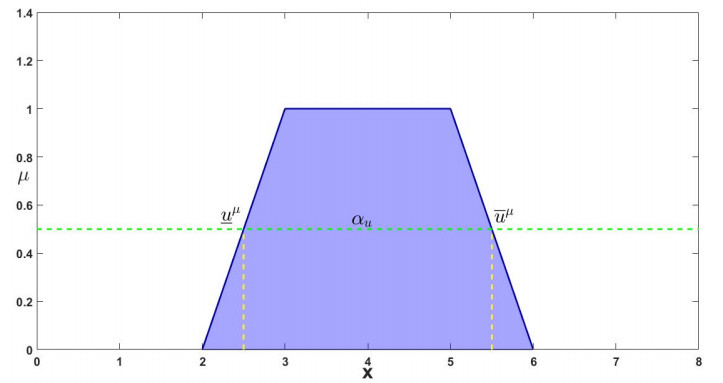
Example 2.4. For $\tilde{\mu} = (2, 3, 5, 6)\in E^{1}$,

Figure 1 shows its horizontal membership function.

Definition 2.5. (^[44]) Two fuzzy numbers $\tilde{u}$ and $\tilde{v}$ are said to be equal if and only if $\mathcal{H}(\tilde{u}) = \mathcal{H}(\tilde{v})$ for all $\alpha_{u} = \alpha_{v} \in [0, 1],$ and $\mu \in [0, 1]$.

Definition 2.6. (^[44,49]) Let $\tilde{f} : [a, b] \subseteq \mathbb{R}^{n} \rightarrow E^{1}$. The horizontal membership function of $\tilde{f}(t)$ at the point $t\in[a, b]$ is denoted by $\mathcal{H}(\tilde{f}(t))\triangleq f^{gr}(t, \mu, \alpha_{f})$, and defined as $f^{gr}:[a, b]\times[0, 1]\times\underbrace{[0, 1]\times\cdots\times[0, 1]}_{n}\rightarrow [c, d]\subseteq \mathbb{R}$ in which $\alpha_{f}\triangleq(\alpha_{u_{1}}, \alpha_{u_{2}}, \cdots, \alpha_{u_{n}})$ are the RDM variables corresponding to the fuzzy numbers.

Theorem 2.7. (^[44]) The fuzzy-number-valued function $\tilde{f} : [a, b] \subseteq \mathbb{R}^{n} \rightarrow E^{1}$ is said to be gr-differentiable at the point $t \in [a, b]$ if and only if its horizontal membership function is differentiable with respect to $t$ at that point. Moreover, $\mathcal{H}\left(\dfrac{d\tilde{f}(t)}{dt}\right) = \dfrac{\partial f^{gr}(t, \mu, \alpha_{f})}{\partial t}.$

Definition 2.8. ^[44] Let $\int_{a}^{b}\tilde f(t)dt$ denote the integral of $\tilde f$ on $[a, b]$. Then, the fuzzy function $\tilde f$ is said to be granular integrable on $[a, b]$ if there exists a fuzzy number $\tilde m = \int_{a}^{b}\tilde f(t)dt$ such that $\mathcal{H}(\tilde m) = \int_{a}^{b}\mathcal{H}(\tilde f(t))dt$.

Definition 2.9. ^[44] Let $\tilde u$ and $\tilde v$ be two fuzzy numbers whose horizontal membership functions are $u^{gr}(\mu, \alpha_{u})$ and $v^{gr}(\mu, \alpha_{v})$, respectively, and "$\odot_{gr}$" denotes one of the four basic operations, i.e., addition, subtraction, multiplication, and division. Then, $\tilde u\odot_{gr}\tilde v$ is a fuzzy number $\tilde m$ such that $\mathcal{H}(\tilde m)\triangleq u^{gr}(\mu, \alpha_{u})\odot_{gr}v^{gr}(\mu, \alpha_{v})$.

Remark 2.10. ^[44] Let $\tilde m = \tilde u\odot_{gr}\tilde v$. Then, $[\tilde m]_{\mu} = \mathcal{H}^{-1}(u^{gr}(\mu, \alpha_{u})\odot_{gr}v^{gr}(\mu, \alpha_{v}))$ always presents $\mu$-level sets of the fuzzy number $\tilde m$.

Remark 2.11. ^[44] Consider the differential equation

where $\tilde x:[t_{0}, t_{f}]\subseteq\mathbb{R}\rightarrow E^{1}$ includes $n\in \mathbb{N}$ distinct fuzzy numbers $\tilde u_{1}, \tilde u_{2}, ..., \tilde u_{n}$, $\dot{\tilde x}(t)$ represents the gr-derivative of $\tilde x$ with respect to $t$, and $\tilde x_{0}\in E^{1}$ is a fuzzy initial condition. Based on Definition $2.5$, the fuzzy differential Equation $(2.3)$ can be rewritten as

and then, using Theorem $2.7$, we have

Definition 2.12. Let $\tilde f(t)$ be a bounded and continuous fuzzy-number-valued function. Then, the fuzzy Fourier transform of $\tilde f(t)$ is given by the following formula:

Definition 2.13. If $\tilde F(w)$ is the fuzzy Fourier transform of $\tilde f(t)$, then the inverse fuzzy Fourier transform of $\tilde F(w)$ is

Remark 2.14. Let $\tilde f(x)$ be a fuzzy-number-valued function. According to Definition $2.8$, for any $\mu, \alpha_{f}, \alpha_{F}\in [0, 1]$, the following formula holds:

and Eq $(2.7)$ can also be rewritten as

Example 2.15. ^[50] Consider the following fuzzy heat conduction equation:

where $k \in \mathcal{R}$ represents the coefficient, and $\tilde \varphi(x)$ is the fuzzy initial condition. If we assume that the exact solution $\tilde u(x, t)$ of the above equation has a fuzzy Fourier transform of $\mathcal{F}\{\tilde u(x, t)\}$ with respect to the variable $x$, then by Definition $2.12$, we have

and according to Definition $2.13$, we have

We apply the fuzzy Fourier transform to the variable $x$ in Eq $(2.10)$, and obtain its exact solution by the variable separation method as follows:

where $\tilde F(\lambda, 0)$ is the fuzzy Fourier transform of fuzzy initial data $\tilde \varphi(x)$, i.e.,

Then, we substitute $\tilde F(\lambda, t)$ into the Eq $(2.12)$, and obtain

where the exponent part can be written as

Let

If we set $\lambda-i\dfrac{x-\zeta}{2kt} = \dfrac{l}{\sqrt{kt}}$, then $d\lambda = \dfrac{1}{\sqrt{kt}}dl$. According to $Euler^{'}s$ equation (denoted as $\int_{-\infty}^{+\infty}e^{-l^{2}}dl = \sqrt{\pi}$), we obtain

We get the solution of the fuzzy heat conduction equation as follows:

and according to Definition $2.8$, we have

Definition 2.16. (^[51]) Let the fuzzy-number-valued function $\tilde f(x)$ be granular improper integrable on the infinite interval $[a, \infty)$, where $a\geq0$. For any fixed $\mu, \alpha\in[0, 1]$, then $L^{2}$-norm of $f^{gr}(x, \mu, \alpha)$ on $\mathbb{R}$ is defined as

3.   Ill-posedness of the BHCE with uncertainty

In this section, we consider the following BHCE with uncertainty:

where $\tilde\varphi_{T}(x)$ is the data known at time $T$. We want to find the temperature distribution $\tilde u(\cdot, t)$ at time $0\leq t < T$ from the data we know, $\tilde\varphi_{T}(x)$.

According to Remark $2.11$, the above Eq $(3.1)$ can be rewritten as

Based on the Definition $3.1$ below, we will show that the BHCE with uncertainty is seriously ill-posed.

Definition 3.1. An equation is well-posed if its solution satisfies the following three properties:

$(1)$ Existence;

$(2)$ Uniqueness;

$(3)$ Continuous dependence on given data.

On the contrary, if only one of these three conditions is not satisfied, then it is ill-posed.

Theorem 3.2. If Eq $(3.2)$ has no solution, then Eq $(3.1)$ has no solution.

Proof. If Eq $(3.2)$ has no solution, for any $\mu, \alpha\in[0, 1]$, then $u^{gr}(x, t, \mu, \alpha)$ does not exist. From Remark $2.3$, we can get that $\mathcal{H}^{-1}(u^{gr}(x, t, \mu, \alpha)) = [\tilde u(x, t)]_{\mu}$ does not exist. According to Theorem $2.1$, $\tilde u(x, t)$ does not exist. Therefore, Equation $(3.1)$ has no solution. □

Theorem 3.3. If the solution of Eq $(3.2)$ exists and it is not unique, then a solution of Eq $(3.1)$ exists and it is not unique.

Proof. For $x\in\mathbb{R}$, $t\in(0, T]$, $\mu, \alpha\in[0, 1]$, assume $u_{1}^{gr}(x, t, \mu, \alpha_{u})$ and $u_{2}^{gr}(x, t, \mu, \alpha_{u})$ are the solution of Eq $(3.2)$ which correspond to the data $\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})$, respectively, and $u_{1}^{gr}(x, t, \mu, \alpha_{u})\neq u_{2}^{gr}(x, t, \mu, \alpha_{u})$. According to the Eq $(3.2)$, we have the following equation:

For Eq $(3.3)$, we have

For any $\mu, \alpha_{u}\in[0, 1]$, according to Remark $2.11$, we have

For Eq $(3.6)$, we have

and, according to Definition $2.5$ and Eq $(3.7)$, we have

For Eq $(3.8)$, we have

In the same way, for Eq $(3.4)$, we can also get the following equations:

For any $\mu, \alpha\in[0, 1]$, because $u_{1}^{gr}(x, t, \mu, \alpha_{u})$ and $u_{2}^{gr}(x, t, \mu, \alpha_{u})$ are the solutions of Eqs $(3.2)$ which correspond to the data $\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})$, respectively, and $u_{1}^{gr}(x, t, \mu, \alpha_{u})\neq u_{2}^{gr}(x, t, \mu, \alpha_{u})$, according to Remark $2.3$, $\mathcal{H}\left(u_{1}(x, t, \mu, \alpha)\right)\neq\mathcal{H}\left(u_{2}(x, t, \mu, \alpha)\right)$. According to Definition $2.5$, $\tilde u_{1}(x, t)\neq\tilde u_{2}(x, t)$. From Eqs $(3.9)$ and $(3.10)$, we can obtain that $\tilde u_{1}(x, t)$ and $\tilde u_{2}(x, t)$ are two different solutions of the Eq $(3.1)$. □

Theorem 3.4. For any $\alpha_{\varphi}$, $\mu \in[0, 1]$, a solution of Eq $(3.2)$ does not depend continuously on the data $\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})$.

Theorem 3.5. A solution of Eq $(3.1)$ does not depend continuously on the data $\tilde \varphi_{T}(x)$.

Proof. Using the fuzzy Fourier transform to Eq $(3.1)$ with respect to the variable $x$, we can get the fuzzy Fourier transform $\hat{\tilde u}(\xi, t)$ of the exact solution $\tilde u(x, t)$ of Eq $(3.1)$

or equivalently

Moreover, there holds

or equivalently

Now we consider Eq $(3.12)$. Assume $\tilde F:R\rightarrow E^{1}$ is a fuzzy-number-valued function. Let $\tilde u_{1}(x, t)$ and $\tilde u_{2}(x, t)$ be the solutions of Eq $(3.1)$ which correspond to the data $\tilde\varphi_{1}(x) = \tilde\varphi_{T}(x)$ and $\tilde\varphi_{2}(x) = \tilde\varphi_{1}(x)\oplus_{gr}\epsilon\sin(\omega x)\odot_{gr}\tilde F(x)$ (where $\epsilon$ is a nonzero constant). Then, we have the following two equations:

From Eqs $(3.15)$ and $(3.16)$, we have

From Eq $(3.17)$, we obtain

For any $\mu, \alpha\in[0, 1]$ and Eq $(3.18)$, according to Remark $2.11$ and Definition $2.8$, we have

From equation $\tilde\varphi_{2}(x) = \tilde\varphi_{1}(x)\oplus_{gr}\epsilon\sin(\omega x)\odot_{gr}\tilde F(x)$, we obtain

For any $\mu, \alpha\in[0, 1]$ and Eq $(3.20)$, according to Remark $2.11$ and Definition $2.8$, we have

and according to the Riemann-Lebesgue Lemma, as $\omega\rightarrow0$, we have the equation

However, as $\omega\rightarrow0$,

where $\lVert\cdot\rVert$ denotes the $L^{2}$-norm. (See Definition $2.16.$)

The theorem has been proved. □

We will give the following example to help understand Theorem $3.5$.

Example 3.6. Consider the following BHCE:

According to Remark $2.11$, we have the following granular differential equation:

Let $\tilde \varphi_{T_{1}}(x) = 0$. Then, the corresponding granular equation is $\varphi_{T_{1}}^{gr}(x, \mu, \alpha_{\varphi}) = 0$. It is easy to verify that, at this time, the solution of the above equation is $u_{1}^{gr}(x, t, \mu, \alpha_{u}) = 0$.

Let $\tilde \varphi_{T_{2}} = \tilde m \cdot \dfrac {1}{n}sin\dfrac{n\pi}{l}x$, where $\tilde m$ is a fuzzy-number-valued function, i.e., $\tilde m = (-1, 0, 1)$, which has the following expression:

Then, according to Definition $2.6$, we obtain $m^{gr}(\mu, \alpha_{m}) = -1+\mu+2(1-\mu)\alpha_{m}$. Therefore, the corresponding granular equation is $\varphi_{T_{2}}^{gr}(x, \mu, \alpha_{\varphi}) = [-1+\mu+2(1-\mu)\alpha_{m}]\cdot \dfrac{1}{n}sin\dfrac{n\pi}{l}x$, for all $\mu, \alpha_{m} \in[0.1]$. In this case, Equation $(3.25)$ corresponding to the data $\varphi_{T_{2}}^{gr}(x, \mu, \alpha_{\varphi})$ can be solved by the following granular equation:

The solution of the above granular differential equation can be easily obtained by the method of separating variables as follows

Based on the above discussion, the continuous dependence of the solution on the given data is analyzed, and we have

However, for any $\mu, \alpha_{m} \in [0, 1]$,

Therefore, from Eqs $(3.29)$ and $(3.30)$, we can conclude that Eq $(3.22)$ is seriously ill-posed.

4.   Fourier regularization and error estimates for the BHCE with uncertainty

We consider the BHCE with uncertainty

where $\tilde\varphi_{T}(x)$ is the data known at time $T$.

Based on Theorems $3.4$ and $3.5$, we mainly consider the Fourier regularization of the granular differential equation of the BHCE with uncertainty:

We need to determine the temperature distribution $u^{gr}(x, t, \mu, \alpha_{u})$ for $0\leq t < T$ from the given data $\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})$. Applying the fuzzy Fourier transform method to Eq $(4.2)$, we can obtain the fuzzy Fourier transform $\hat{u}^{gr}(x, t, \mu, \alpha_{u})$ of the solution $u^{gr}(x, t, \mu, \alpha_{u})$ of Eq $(4.2)$ as follows:

and, according to the Definition $2.9$ and Remark $2.10$, we can obtained the inverse fuzzy Fourier transform of $\hat{u}^{gr}(\lambda, t, \mu, \alpha_{u})$:

where $\hat{\varphi}_{T}^{gr}(\lambda, \mu, \alpha_{\varphi})$ is the fuzzy Fourier transform of the given data $\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})$.

For Eq $(4.3)$, let $t = 0$. Then, we have

Denoting $u^{gr}(x, 0, \mu, \alpha_{u}) = \varphi_{0}^{gr}(x, \mu, \alpha_{\varphi})$, in order to give an error, we make the following assumption:

where $A$ represents a positive constant, and $\parallel\cdot\parallel_{H^{k}}$ represents the Sobolev norm.

Based on Eq $(4.5)$, Eq $(4.6)$, and the Parseval identity, we have

We find that $e^{\lambda^{2}T}\rightarrow \infty$ when $|\lambda|\rightarrow \infty$, so Eq $(4.6)$ implies a rapid decay of $\hat{\varphi}_{T}^{gr}(\lambda, \mu, \alpha_{\varphi})$ at high frequencies. Since the data $\varphi_{\delta, T}^{gr}(x, t, \mu, \alpha_{\varphi})$ at time $t = T$ is measured by a physical instrument, there is a certain error. We know that the ill-posedness of the BHCE with uncertainty is caused by the high-frequency disturbance in the solution. Therefore, in this paper, we apply the Fourier regularization method to stabilize the numerical solution, and instead consider Eq $(4.4)$ only for $|\lambda| < \lambda_{max}$, where $\lambda_{max}$ is an appropriate positive constant which will be selected as a regularization parameter so that the solution tends to be stable for given noisy data.

Let $\varphi_{T}^{gr}(x, t, \mu, \alpha_{u\varphi})$ and $\varphi_{\delta, T}^{gr}(x, t, \mu, \alpha_{\varphi})$ denote the exact data and measured data at $t = T$, respectively, and they satisfy

where $\delta$ denotes the error level, and we assume Eq $(4.6)$ holds.

Next, we define a regularization solution of Eq $(4.2)$ for the measured noisy data, which we call the Fourier regular solution of Eq $(4.2)$ as follows:

where $\hat{\varphi}_{\delta, T}^{gr}(\lambda, \mu, \alpha_{\varphi})$ is the fuzzy Fourier transform of measured the data $\tilde \varphi_{\delta, T}(x, t)$ at $t = T$, and $\zeta_{\max}$ is the characteristic function of the interval $[-\lambda_{\max}, \lambda_{\max}]$, i.e.,

and $\lambda_{\max}$ will be selected appropriately as a regularization parameter.

The following theorem illustrates that the Fourier regular solution defined by Eq $(4.9)$ continuously depends on the given data $\varphi_{\delta, T}^{gr}(x, t, \mu, \alpha_{\varphi})$.

Theorem 4.1. Let $u_{\lambda_{\max}}^{gr}(x, t, \mu, \alpha_{u})$ and $u_{\delta, \lambda_{\max}}^{gr}(x, t, \mu, \alpha_{u})$ be solutions to Eq $(4.9)$ corresponding to the data $\varphi_{T}^{gr}(x, t, \mu, \alpha_{\varphi})$ and $\varphi_{\delta, T}^{gr}(x, t, \mu, \alpha_{\varphi})$, respectively. Then, for $0\leq t < T$, there is

Proof. Due to the Parseval formula

we have

Therefore, the proof of convergence estimate is completed. □

This theorem shows the stability of the Fourier regularization method. When the input data is noisy, the results indicate that the regularized solution can stay within a reasonable and relatively stable range and will not deviate significantly from the original solution. Thus, it can ensure the reliability and effectiveness of the solution in practical applications.

Note that $\parallel u_{\lambda_{\max}}^{gr}(\cdot, t, \mu, \alpha_{u})\ominus_{gr} u_{\delta, \lambda_{\max}}^{gr}(\cdot, t, \mu, \alpha_{u})\parallel \rightarrow 0$ as $\delta \rightarrow 0$. That is, the Fourier regular solution defined by Eq $(4.9)$ continuously depends on the given data $\varphi_{\delta, T}^{gr}(x, t, \mu, \alpha_{\varphi})$.

Theorem 4.2. Let $u^{gr}(x, t, \mu, \alpha_{u})$ and $u_{\delta, \lambda_{\max}}^{gr}(x, t, \mu, \alpha_{u})$ be the exact solution and the Fourier regular solution we defined for the Eq $(4.2)$, respectively. Then, for $0\leq t\leq T$, assuming that conditions $(4.6)$ and Eq $(4.8)$ hold, if we select the regularization parameter

we have the following conclusion:

Proof. Due to the Parseval formula and Eqs (4.3)–(4.5), (4.7), and $(4.8)$, we find

Therefore, the proof of convergence estimate is completed. □

This theorem shows the error estimation of the Fourier regularization method. When the input data is noisy, the results show that the error between the regularized solution and the exact solution can be effectively controlled within a certain range. When certain conditions are met, with the reduction of the noise level, the regularized solution will converge to the exact solution at a certain rate, which provides a solid theoretical basis for evaluating and optimizing the Fourier regularization method in practical applications.

Remark 4.3. When $k = 0$, Eq $(4.14)$ becomes

We know this is a $H\ddot{o}lder$ error estimate. At $t = 0$, it just means that, with $2A$ as the error bound, you cannot actually tell whether the regular solution is stable at $t = 0$. However, this defect can be corrected by Eq $(4.14)$. In fact, for $t = 0$, Equation $(4.14)$ becomes

as $\delta\longrightarrow0$ and $k > 0$.

Remark 4.4. We know that in actual calculation, the prior bound $A$ given by us is unknown. For the convenience of calculation, if we take the prior bound as $A = 1$, then

and we also have the estimate

5.   Numerical example

Example 5.1. The initial value problem of the following form of the BHCE with uncertainty in an unbounded region is considered:

where $\tilde v(x)$ is a fuzzy-number-valued function, i.e., $\tilde v(x) = (-5, 0, 5)$, and we have the following expression:

and, according to Definition $2.2$, $v^{gr}(x, \mu, \alpha_{v}) = (-5+5\mu)+10(1-\mu)\alpha_{v}$. Based on Remark $2.11$, we obtain the granular differential equation as follows:

Then, from Eq $(2.20)$, the exact solution of Eq $(5.3)$ is

and, according to Remark $2.3$, the $\mu$-level sets of the exact solution can be obtained as

Therefore, $\tilde u^{\ast}(x, t)$ is also a solution to the following fuzzy backward heat conduction equation

Numerical experiments will be performed below. Then, according to the Fourier regularization method, the Fourier regular solution of the above Eq $(5.6)$ is constructed as follows:

where $\zeta_{\max}$ is the characteristic function of the interval $[-\lambda_{\max}, \lambda_{\max}]$, and $\hat{\varphi}_{\delta, T}^{gr}(\lambda, \mu, \alpha_{\varphi})$ is the fuzzy Fourier transform of the measurement data $\varphi_{\delta, T}^{gr}(x, \mu, \alpha_{\varphi})$ obtained by physical instruments at time $t = T$, which is usually with errors. Noise data is generated by the $rand(\cdot)$ function of MATLAB.

where $(\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi}))_{i}$ is the exact data and $rand(size(\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi})))_{i}$ is a random number of the same dimension as $(\varphi_{T}^{gr}(x, \mu, \alpha_{\varphi}))$ on $[0, 1]$. The magnitude $\epsilon$ indicates the noise level of measurement data by physical instruments, and this noise level has an expression as follows:

In this experiment, we mainly used $MATLAB\; R\; 2016a$ for numerical simulation and calculation. Before regularization, we first present the results obtained unregularization. Figures 2 and 3 show the results for noise levels $\epsilon = 6\times10^{-2}$ and $\epsilon = 6\times10^{-4}$, respectively, with $T = 1$ and $t = 0$.

It is evident that the higher the noise level, the less accurate the unregularized solution becomes. Therefore, when the input data is not processed through regularization, even minor perturbations in the input data can lead to significant changes in the solution, rendering the numerical solution highly unstable.

Figure 4 show the exact solution of the Eq $(5.1)$, taking $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1, respectively. In these figures, the upper and lower halves of the graph represent the left and right endpoints of the $\mu$-level sets of the exact solution, respectively, and the red curve represents $\mu = 1$.

Figure 5 show the Fourier regular solution of Eq $(5.1)$ obtained by Fourier regularization, taking $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1, respectively. The regularization parameter $\lambda_{\max} = 0.9124$.

From Figures 4 and 5, we can clearly see that appropriate selection of regularization parameter values can make regular solutions stably approximate the exact solution. To further investigate this example under the granular differentiability concept, here we take special values $x = 1$ and $t = 1$ to observe the numerical results, i.e., we fix $x = 1$ and $t = 1$, respectively, to observe the relationship between the exact and regular solutions.

Figure 6 shows the exact solution of Eq $(5.1)$ when $x = 1$ is fixed, with $\mu$ taking values of 0, $0.25$, $0.5$, $0.75$, and 1, respectively. The blue and red curves show left and right endpoints of the $\mu$-level sets of the exact solution of the Eq $(5.1)$, respectively, and the black curve corresponds to the level $\mu = 1$.

Figure 7 shows that when $x = 1$ is fixed, the Fourier regular solution of Eq $(5.1)$ obtained by Fourier regularization takes $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1, respectively. The regularization parameter $\lambda_{\max} = 0.9124$.

Figure 8 shows that when $t = 1$ is fixed, the exact solution of Eq $(5.1)$ takes values corresponding $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1, respectively.

Figure 9 shows that when $t = 1$ is fixed, the Fourier regular solution of Eq $(5.1)$ obtained by Fourier regularization takes $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1, respectively.

The above numerical experiments are done with noise level $\epsilon = 6\times10^{-2}$ on the given data. As can be seen from Figures 8 and 9, Fourier regularization method can stabilize regular solutions to exact solutions well if appropriate regularization parameter values are selected. From the fixed $x = 1$ and $t = 1$, it is not difficult to find that when $\mu = 1$, the solution of the uncertain reverse heat conduction equation obtained by Fourier regularization is completely consistent with the solution in the classical sense.

In the following, we illustrate the numerical results of the Fourier regularization method when taking different regularization parameters. The purpose is to prove that the exact solution can be approached well by selecting suitable regularization parameters, and the optimal regularization parameters can also be found by this method. It can also be further explained that the regularization parameter selection scheme we give, that is, Equation $(4.13)$, is very effective.

Figures 10–12 are the results of Fourier regularization with regularization parameter $\lambda_{\max} = 1.1736$ and noise level $\epsilon = 6\times10^{-2}$. In Figures 11 and 12, $x = 1$ and $t = 1$ are fixed, respectively. It is obvious that the Fourier regularization results are not optimistic when the regularization parameter values are large.

Figures 13–15 are the results of Fourier regularization when the regularization parameter $\lambda_{\max} = 0.5697$ and the noise level $\epsilon = 6\times10^{-2}$. In Figures 14 and 15, $x = 1$ and $t=1$ are fixed, respectively. It is obvious that Fourier regularization results are not optimistic when the regularization parameter values are small.

We can see from the graph above that if the regularization parameter value is large or small, there will be a large error between the regular solution and the exact solution. Therefore, choosing the appropriate regularization parameter value is the key to solving this kind of problem. According to the selection scheme of regularization parameters given in this paper, the regular solution can well approach the exact solution. In this example, we can also observe that when $\mu = 1$, the solution of the BHCE with uncertainty is the solution of the BHCE in the classical sense.

This not only shows the validity of our method, but also provides a new solution for solving the inverse problem of the uncertainty equation. Compared with the deterministic equation, the solution of the uncertain equation is an interval, which increases the control range and can improve the precision accordingly.

Through the above analysis, it can be seen that the regularization parameter rule given by Eq $(4.13)$ is valid. For this example, when the value of the regularization parameter is 0.9124, the regular solution and the exact solution have the best stability. The figure below shows that the numerical solution of the proposed method is stable at $t = 0$. This is consistent with our theoretical results.

We already know that, the higher the value of $T$, the flatter the exact solution. Therefore, as the $T$-value increases, we also adjust the regularization parameters accordingly, so that the regular solution is stabilizes well to the exact solution. The following two figures show the regularization results for $T = 10$ and $T = 100$, respectively. It can be seen that Fourier regularization yields satisfactory results in these cases.

Through the analysis of the above example, even if there is noise in the given data, we can make it tend to a stable solution through the Fourier regularization method. This numerical example also further verifies the effectiveness and practicability of the Fourier regularization method proposed in this paper.

The following example shows that Fourier regularization is still valid under different fuzzy initial conditions.

Example 5.2. We consider the following BHCE with uncertainty:

where $\tilde{v}(x) = (-1, 0, 1)$ is a fuzzy-number-valued function, and, according to Definition $2.2$, we have $v^{gr}(x, \mu, \alpha_{v}) = (\mu-1)+2(1-\mu)\alpha_{u}$. Based on Remark $2.11$, we obtain the granular differential equation as follows:

The exact solution of Eq $(5.11)$ is

and according to Remark $2.3$, the $\mu$-level sets of the exact solution can be obtained:

Therefore, $\tilde u^{\ast}(x, t)$ is also a solution to the following fuzzy backward heat conduction equation:

In the following experiment, we also tested under the software $MATLAB\; R\; 2016a$. Here, the noise data is generated in the same way as in the previous example. Our main purpose here is to study the accuracy of regularization methods under different fuzzy initial conditions.

Figures 19 and 20 are the result of the unregularization of this example when $T = 1$, and the noise levels $\epsilon = 6\times10^{-2}$ and $\epsilon = 6\times10^{-4}$ are taken, respectively.

As can be seen from Figures 19 and 20, in the case of unregularization, small perturbations in the input data will cause huge changes in the solution, and this problem is seriously ill-posed. Next, we apply the regularization method to stabilize the numerical solution.

For this example, we calculated the regularization parameters applicable to this example according to the regularization parameter selection scheme, namely Eq $(4.13)$, and compared the difference between the obtained regularization solution and the exact solution of the equation so as to test the stability of the proposed regularization method.

Figure 21 is the result of Fourier regularization. With regularization parameter $\lambda_{\max} = 0.9124$, it can be seen that the regular solution is effectively stable to the exact solution.

Next, we will discuss the stability of the regularization method when fixing $x = 1$ and $t = 1$, respectively.

Figures 22 and 23 show the interval solution plots for fixed $t = 1$ and $x = 1$, respectively, in this example.

It can be seen from the figure that the interval solution obtained by Fourier regularization method is stable even if $t = 1$ and $x = 1$ are fixed.

Next, we take $T = 10$ and $T = 100$ respectively to observe the stability of Fourier regularization method.

From the above example, we can observe that small perturbations in the data can cause large changes in the solution. Fourier regularization method is used to stabilize the numerical solution. By fixing the graph of $t = 1$ and $x = 1$, respectively, it is not difficult to find that when $\mu = 1$, the result obtained is consistent with the result in the classical sense.

The calculation of the above numerical examples were performed using the MATLAB software. Given the small scale of the problem, the limited amount of data, and the high efficiency of the algorithm employed, the computational time for these examples is very brief, typically taking only a few seconds to complete. Specifically, using MATLAB's built-in timer function, we measured the computational time to be approximately 1.2 seconds. This further demonstrates the efficiency and applicability of our algorithm.

6.   Conclusions and prospects

In this study, we propose the backward heat conduction equation (BHCE) with uncertainty, in which the uncertainty of parameters is expressed by fuzzy numbers. This equation is essentially an inverse fuzzy differential equation, and we study its numerical solution. Second, it is proved that the backward heat conduction equation (BHCE) with uncertainty is a seriously ill-posed problem, so a specific regularization method is needed to solve its numerical solution. Last, the Fourier regularization method under the granular differentiability concept is used to solve the numerical solution. The granular representation of the regular solution is given, and the convergence and stability estimations of the method are proved under the prior assumptions of the exact solution.

In numerical examples, we use the $rand(\cdot)$ function in MATLAB to randomly generate numbers in the interval $[0, 1]$ to simulate noise in the given data. In this example, we take the noise level of the data $\epsilon = 6\times10^{-2}$. We find that when the regularization parameter $\lambda_{\max}$ is calculated according to Eq $(4.13)$, the approximate effect is significant. We also compare different regularization parameters and find that when the regularization parameter is greater than or less than this value, the error between the exact solution and the regular solution is relatively large. At the same time, we also analyze the relationship between the regular solution and the exact solution when $\mu = 0$, $0.25$, $0.5$, $0.75$, and 1 with fixed variables $x = 1$ and $t = 1$, respectively. We find that when $\mu = 1$, the solution of the uncertain BHCE is exactly that of the classical BHCE. This numerical example also shows the practicability and effectiveness of the proposed method.

At present, we define the inverse heat transfer equation based on the granular differentiability concept of fuzzy numerical functions. When uncertainty is represented by fuzzy numbers, the complexity of fuzzy number operation may affect the efficiency of the model. In the future, we can further expand and deepen the definition of fuzzy number differentiability, explore its application in a wider range of mathematical-physical scenarios, and study the properties and solutions of reverse heat conduction equations under different differentiability conditions. Even though we have used the Fourier regularization method, regularization theory is an evolving field. We can explore other types of regularization methods and compare the advantages and disadvantages of different methods in dealing with uncertain reverse heat conduction equations. In practical engineering, the heat conduction process is often coupled with other physical processes. In the future, our method could be extended to the inverse problems of such multi-physical coupling to study its effectiveness in complex practical scenarios. We can apply this method to the field of real-time monitoring and control, such as real-time monitoring of the heat conduction state and feedback control in the industrial production process. Moreover, we can study how to optimize the method to meet the real-time requirements and enhance its practicality in real-world applications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China (NO. 12161082) and Gansu Province Outstanding Youth Fund project (Grant No. 24JRRA121). The authors are very grateful to the anonymous referees for their valuable suggestions.

Conflict of interest

The authors declare that they have no conflict of interest.