Thermal vibration in rotating nanobeams with temperature-dependent due to exposure to laser irradiation

1.   Introduction

Nanotechnology is an expanding topic of research with numerous fields, for example, nanomedicine, nanofabrication, nanoelectronics, and nanomachines. These areas require novel devices, such as nano water harvesters, oscillators, load sensors, nano-scale mass sensors, field-emitting devices, biological tissues, and nano-electrical devices. Although the movement of nuclear energy and the forces working between them is usually successful, engineers rely on continuous theories that describe the influence of those phenomena in a far wider and intermediate sense in the case of the deformation of solids ^[1]. Even current digital computers need too much processing capacity to be used by the designer in comprehensive atomic simulations of engineering structures and components; the fundamental reason for these approximation theories is efficiency ^[2]. Continuous theories such as linear elasticity, plasticity, etc. give approximately a fraction of the cost of a simple nuclear simulation to approximate response engineers.

Several bulk material theories, such as the local beam, shell, and plate, were used in classical continuum mechanics to study the mechanical nanostructure of large-scale systems. While many studies have been done using classical continuum mechanics, its use at the nanoscale is unclear. Because in conventional continuum mechanics, small-scale factors such as Van der Waals, surface influences, lattice distance, energy, and chemical bonds are ignored ^[3].

Experimental as well as atomic simulation results show that these small-scale effects cannot be ignored at the nanoscale ^[4]. As the lattice distance between the atoms becomes increasingly relevant on a small scale, the discrete structure (interior) of the material cannot be homogenized into a continuum anymore. Nonlocal continuum theories have been defined to treat small-scale effects. In continuum modeling, this incorporates a size-dependent parameter to reflect the modest effect ^[5]. The theory of strain gradient, stress theory, the theory of micropolar, and the nonlocal theory of elasticity are among the most popular non-local theories ^[6,7].

Eringen's nonlocal elasticity theory is effective in dealing with phenomena that have fewer origins in systems than in traditional models of communication ^[8,9,10]. The internal size or scale in this theory may be described simply as material parameters in the constitutive equations. These nonlocal mechanics are widely recognized and used for many issues, including wavy diffusion, dislocation, problems with cracks, etc. It has recently been shown that the application of non-local continuum mechanics to the modeling and analysis of nanostructures is very interesting ^[11]. Furthermore, few studies have reached the same conclusions as the classical theory of nonlocal elasticity ^[12].

Lim et al. ^[13] introduced the higher-order nonlocal strain gradient theory (NSGT) with two separate small-scale parameters in order to solve these problems with the nonlocal theory of elasticity. According to the NSGT, stress is the function of strain and a larger order strain gradient at every point in the domain. This theory takes into account both the interatomic forces and the deformation process of the higher-order microstructure. Subsequently, many studies using the NSGT theory have been carried out to examine the mechanical interaction of nanostructures ^[14]. The wave dispersion achieved by the NSGT theory is found to be extremely close to what was predicted by the dynamic molecular modeling of the nanopillars ^[15]. Liu et al. ^[16] evaluated the significant nanowire deformation behavior in terms of its surface influences (surface elasticity and residual surface stress). They constructed the governing equation in combination with the residual surface stress and surface elasticity of nanowires with large displacements and different boundary conditions. Many researchers in many different applications ^{[16,17,18,19,20,21,22,23,24,25]} have used these modified models. The study of the dynamic behavior of rotating nanobeams is a growing research topic, due to its potential for application in various rotating NEMS such as nanomotors, nanoturbines, rotating nanomotors, etc. ^{[26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]}.

Generalized thermoelasticity theories have been developed to solve the infinite speed heat propagation problems predicted by the classical thermoelastic theory. By substituting a unique law of thermal conductivity for the standard Fourier law, Lord and Shulman ^[42] proposed one of the modified generalized thermoelasticity theories with one relaxation time. Recently, the Tzou model is one of the most recent models that has gained fame in the field of thermoelasticity ^[43,44,45]. In order to address the problems of the infinite speed of thermal waves, which are anticipated by conventional thermoelastic theory, several proposals have been offered in addition to the above-mentioned models ^{[46,47,48,49]}.

Many studies focusing on the dynamics, bending, statics, and vibrational properties of nanobeams have been presented, with few studies focusing on the thermal elastic behavior of small-sized rotating beams with variable physical properties. In this paper, motivated by the need for improvement, the dynamic transverse vibration properties and thermal vibration analyzes of rotating nanobeams are studied based on the proposal of a new methodology based on nonlocal strain gradient theory (NSGT) that captures the small-scale effects. Also, the equations for the governing system were derived based on the Euler-Bernoulli theory and generalized thermoelasticity with two-phase lag (DPL). Contrary to many other concerns, the thermal conductivity and specific heat of the material have been considered variable and linearly dependent on changes in temperature.

The proposed model is able to study rotating nanobeams under thermal loads and includes Coriolis effects caused by rotation. To the authors' knowledge, for the first time, a rotational model of a thermal nanobeam has been reported whose properties depend on the temperature change. This study will also contribute to a full understanding of the behavior of rotating nanobeams, which have variable physical properties. The Laplace transform method was used to solve constitutive equations and partial differential governing equations, and is an important addition to this article. The Laplace transforms are inverted using a numerical approach based on Fourier series expansions. According to the numerical results, the mechanical and thermal wave responses of the rotating nanobeam are greatly influenced by many parameters such as temperature change, angular velocity, nonlocality parameters, and thermal conductivity change. The results of this study may be useful for future research and accurate design of nanomachines, such as nanoparticle bearings and nanogears, etc.

2.   Theoretical preliminaries and basic equations

2.1.   The nonlocal elasticity theory

According to the nonlocal elasticity theory of Eringen ^[8,9,10], the nonlocal stress-tensor ${\tau }_{ij}$ can be expressed as

where ${\sigma }_{ij}\left(\boldsymbol{x}'\right)$ is the classical local stress tensor given by

The strain tensor ${\varepsilon }_{ij}$ at any two adjacent points ${\boldsymbol{x}}^{'}$ and $\boldsymbol{x}$, is defined by

In these equations, $\gamma = \frac{{\alpha }_{t}E}{\left(1-2\nu \right)} = {\alpha }_{T}E$, $\nu$ Poisson's ratio, $E$ Young's modulus, ${\alpha }_{t}$ linear thermal expansion, ${u}_{i}$ displacement components, ${\delta }_{ij}$ is the Kronecker delta, $\theta = T-{T}_{0}$ temperature change, and ${T}_{0}$ environmental temperature. The Lamé constants $\lambda$ and $\mu$ can be written as $\lambda = E\nu /(1+\nu)(1-2\nu)$ and $\mu = E/2(1+\nu)$. Also, ${K}_{1}\left(\left|{\boldsymbol{x}, \boldsymbol{x}}^{'}\right|, {\xi }_{1}\right)$ scalar kernel function, $‖{\boldsymbol{x}-\boldsymbol{x}}^{'}‖$ Euclidean distance, ${\xi }_{1} = {e}_{0}a/l$ nonlocal scale parameter, $a$ internal characteristic length, $l$ external characteristic length, and ${e}_{0}$ determined experimentally. When the kernel ${K}_{1}$ is chosen as ^[50,51]:

where ${K}_{0}$ is the modified Bessel function, Eq (1) is given by ^[8,9,10]:

Using Eq (4) in (1), the nonlocal constitutive is obtained as

According to the NSGT, the total stress tensor ${T}_{ij}\left(\boldsymbol{x}\right)$ can be expressed as ^[17,52]

where ${\sigma }_{ij}^{\left(1\right)}$ is the higher-order stress tensor given by ^[52,53]

The material length scale parameter ${l}_{m}$ was introduced to describe the importance of the higher-order strain gradient stress field, the additional attenuation kernel ${K}_{2}\left(\left|{\boldsymbol{x}, \boldsymbol{x}}^{'}\right|, {\xi }_{2}\right)$ was introduced to describe the nonlocal effect of the higher-order strain gradient field, ${\xi }_{2} = {e}_{1}a/l$, and ${e}_{1}$ the related material constant ^[13]. By assuming that the attenuation kernels satisfy the conditions of Eringen's nonlocal elasticity, the differential counterpart of Eq (4) is written as ^{[13,52,53,54,55]}:

For simplicity, assuming that ${\xi }_{2} = {\xi }_{1} = \xi$, the first-order nonlocal strain gradient model (NSGT) is given by

By inserting Eq (2) into (10), then we have

When ${l}_{m} = 0$, the constitutive equation for the nonlocal elasticity theory can be obtained. On the other hand, if we set ${\xi }^{2} = {\left({e}_{0}a\right)}^{2} = 0$, we may get the constitutive equation for strain gradient theory.

A micro/nanoscale size influence, for example, is represented by a stiffer elastic response to external stresses. This has been found in the plastic deformation of metals and polymers. In terms of the size effect on elasticity, Lam et al. ^[54] discovered a rise in the bending rigidities of epoxy micro-beams. When the beam thicknesses were reduced from 120 to 20 μm, the bending rigidities were roughly 2.4 times higher than expected by conventional theory. Similarly, additional studies have revealed an apparent rise in Young's modulus without reference to higher-order models. In the absence of strain gradients (for instance, in uniaxial tensile testing), Lam et al. ^[54] demonstrated that the elastic response of epoxy is independent of sample thickness, which is supported by strain gradient theories.

2.2.   The dual-phase-lag thermoelastic mode (DPL)

The classical Fourier's law and energy equation for a homogeneous, isotropic, thermoelastic are as follows:

Combining (1) and (2) yields the classical heat conduction equation as

Tzou ^[43,44,45] devised the dual-phase-lag (DPL) model that ignores instantaneous temperature-energy interactions. The DPL model, in particular, makes heat transmission in thermoelastic materials accurate and easy. The modified Fourier law, which has been superseded by Tzou ^[43,44,45], can be expressed as

The proposed new generalized dual-phase-lag thermoelastic model can be obtained by combining (13) and (15) as

In Eqs (12)-(16), $\overrightarrow{q}$ is the heat flux vector, $Q$ is the heat source, $K$ is the thermal conductivity, ${C}_{E}$ is the specific heat, $\rho$ is the material density, $e = \mathrm{d}\mathrm{i}\mathrm{v}\overrightarrow{u}$, ${\tau }_{q}$ is the phase lag of heat flux, and ${\tau }_{\theta }$ is the temperature gradient's phase lag. Equation (16) is simplified to the constitutive relation of the LS model by setting ${\tau }_{\theta } = 0$ and omitting the influence of the term ${\tau }_{q}^{2}$. Equation (7) can be reduced to the classical Fourier law when ${\tau }_{q} = {\tau }_{\theta } = 0$.

3.   Problem formulation

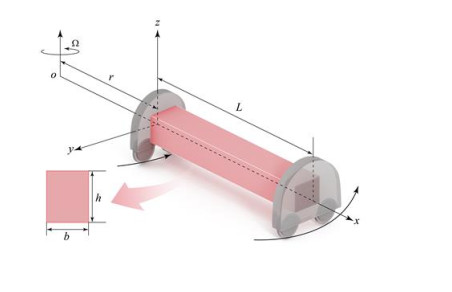
As shown in Figure 1, a nanobeam with length $L$, width $b$ and thickness $h$, internal cross-sectional area $A$, and bending stiffness $EI$ are the components of the system under discussion. Under the Euler-Bernoulli principle, every plane cross-section is perpendicular to the nanobeam pivot in the beginning and perpendicular to the unbiased surface. The displacements are given by ^[53]

where $w$ is the deflection.

Equation (17) can be used to simplify Eq (9) as

where ${\sigma }_{x}$ is the nonlocal axial stress, ${\alpha }_{T} = {\alpha }_{t}/\left(1-2\nu \right)$ and $\xi = {\left({e}_{0}a\right)}^{2}$.

The bending moment $M\left(x, t\right)$ is given by:

Substituting Eq (18) into Eq (19), we get

where $I = b{h}^{3}/12$ and

The transverse motion equation can be written as ^[51]

We suppose that the nanobeam rotates about an axis parallel to the $z$-axis with an angular velocity ${\Omega }$ centered at a small distance $r$ from the first edge of the nanobeam. The centrifugal tensional force $R\left(x\right)$ is introduced because of rotation. In this case, the equation of transverse motion (22) can be written as ^[27,28]

The axial force $R\left(x\right)$ due to centrifugal stiffening at a distance $x$ from the origin (Figure 1) is given by ^[27,28,39]

After integration, Eq (24) can be simplified as

By inserting (25) into Eqs (20) and (23), we can obtain

The modified heat conduction Eq (16) can be written as $\left(Q = 0\right)$

4.   Thermal properties of materials

The conductivity $K$ is considered a linear function of the temperature variation as ^[23,39,40]

where ${K}_{0}$ denotes the thermal conductivity at temperature ${T}_{0}$ and ${K}_{1}$ is the temperature-dependent thermal conductivity fluctuation.

By substituting Eq (29) into (28), we obtain

To linearize the governing equation (30), we define a variable $\psi$ as follows ^[39,40]

After inserting Eq (29) into Eq (31) and integrating, we have

By differentiating the relationship (31) times in terms of distances and once in terms of time, we get

Then, the heat conduction equation can be expressed as

5.   Sinusoidal solution

To solve the problem, we take the temperature change solution as a sinusoidal function as

Presenting Eq (35) in Eqs (26), (27) and (34) leads to

The following non-dimensional variables are provided for convenience

We can get the following after introducing dimensionless quantities (39) into the Eqs (36)-(38) (primes are omitted)

The maximum axial force $R\left(x\right)$ due to centrifugal stiffening at the root ($x = 0$) is given by ^[38,39]

The motion Eq (40) can therefore be described as

The bending moment $M\left(x, t\right)$ in Eq (42) can also be expressed as

6.   Laplace transform strategy

Using the Laplace technique under the initial conditions

Then, Eqs (41), (44) and (45) are converted as

where

We obtain from Eqs (47) and (48) the following

where

Equation (50) has a general solution that can be written as

where the parameters ${C}_{j}, \mathrm{ }(j = \mathrm{1, 2}.., 8)$ are the integrated parameters. Also, the parameters ${m}_{1}^{2}$, ${m}_{2}^{2}$, ${m}_{3}^{2}$ and ${m}_{4}^{2}$ satisfy the equation

With the help of Eqs (48) and (52), we have

where ${H}_{j} = -\frac{{A}_{5}{m}_{j}^{2}}{{m}_{j}^{2}-{A}_{6}}$.

The axial displacement $\stackrel{-}{u}$ is given by

After using the Laplace transform to Eq (35), the temperature $\stackrel{-}{\theta }$ may be calculated as

The bending moment $\stackrel{-}{M}$ can be obtained from (48) after using the solutions (52) and (54).

7.   Application

We assume that the nanobeam fulfills the following boundary conditions:

i) Mechanical boundary conditions ^[55]

ii) Thermal boundary conditions:

In Eq (58), ${t}_{p}$ is the time length of a laser pulse and ${L}_{0}$ the laser intensity. Introducing Eqs (32) and (33) into Eqs (58) and (59), we get

In the Laplace transform domain, the boundary conditions (57)-(61) can be written as

When the previously mentioned conditions are applied, then we have

By solving the aforementioned system equations, the unknown parameters ${C}_{j}, \mathrm{ }(j = \mathrm{1, 2}.., 8)$ may be computed.

8.   Laplace transform inversion

The Fourier series expansion, as well as the Honig and Hirdes technique ^[56], will be briefly introduced in this paper. In this method, all functions $\stackrel{-}{g}\left(x, s\right)$ in the Laplace field can be converted to the time field $\stackrel{-}{g}\left(x, s\right)$ by using the following relation:

where the parameter ${t}_{1}$ denotes the time interval and $\mathrm{R}\mathrm{e}$ stands for the real part of the complex function. By summing a specific number of $N$, Equation (80) can now be calculated numerically. As a result, $c$ and $N$ must be adjusted to improve accuracy ^[57,58].

9.   Results and discussion

In this work, numerical results are provided by focusing on physical parameters and constants in SI units, which are used in formulating the physical variables under study, and by using silicon as a material. The following physical values are used ^[39]:

We divided graphical representations of several properties, such as size-dependent effects ($\xi$ and ${l}_{m}$), parameter change of thermal conductivity ${K}_{1}$, and rotation ${\Omega }$ on the investigated thermal-physical fields, into three groups in order to analyze their effects.

The current work was prompted by a strong fit between the conclusions of nonlocal strain gradient theory and evidence from experimental research and molecular dynamics simulations. The investigation of wave propagation in the classical theory was established using the NSG theory and the DPL heat transfer theory, and the calculation results were compared with the theoretical and experimental results ^[59,60]. The nonlocal strain gradient elasticity model, unlike the conventional model, can demonstrate good agreement with experimental results.

9.1.   Effect of nonlocal and material length scale coefficients

Nonlocal gradient theory (NSGT) has been used to capture the size-dependent effect of the nanobeam, as well as other specific cases such as classical theory (CET), nonlocal theory (NET), and strain regression theory (SGT). A stress-gradient parameter $\xi$ is also included to account for the stress gradient effect, as well as a strain-gradient parameter ${l}_{m}$ to account for the strain gradient effect. If ${l}_{m} = 0$, the introduced nonlocal gradient theory (NSGT) model may be reduced to a nonlocal elastic model (NET), and if $\xi = 0$, to a strain gradient model (SGT).

Figures 2-5 show the dimensionless studied fields for various nonlocal parameter ($\xi$) and material length scale parameter (${l}_{m}$) values. For the purposes of computing, the values ${K}_{1} = -0.3$, ${\Omega } = 0.3$, ${\tau }_{q} = 0.02$ and ${\tau }_{\theta } = 0.01$ are taken. The NSGT incorporates the impacts of both nonlocal and material length scale factors, allowing for a better understanding of the implications of these two parameters on the dynamic responses of the nanobeam. From the numerical results and figures, the following can be noted:

• It is clear that the non-local parameter and the stress gradient modulus have a great influence on the interactions within the nanobeam.

• The dimensionless values of deflection $w$ and displacement $u$ grow in proportion to the nonlocal parameter values. From Figures 2 and 4, it is apparent that the magnitudes of NSGT, SGT and NET models for deflections $w$ and displacement $u$ have greater values than those achieved using conventional continuum theory (CET).

• When the parameter ${l}_{m} > \xi$, the NSGT model yields lower results than the nonlocal elastic model (NET). These facts suggest the nanobeam has a stiffness-reduction impact when the length scale parameter is lower than the non-local parameter, and when the parameter of the material length scale is higher than the non-local parameter, the nanobeam exerts a stiffness-reduction effect. Thus, it can be said that the non-local parameter has the effect of stiffness-softening while the gradient modulus has the effect of stiffness-hardening. Similar results were also found in several papers, such as in ^[60,61,62] on the dynamic response of beam-type structures based on NSGT.

• From the figures, it is clear that the difference between the NSGT and SGT models is less pronounced at lower non-local parameter values but becomes more pronounced at larger non-local parameter values. This pattern applies to both the CET and the NET. Indeed, regarding the reduction of the results due to the raising of the non-local parameter values, one can mention that the strain increases while stress is reduced in Eringen's differential formulation. This phenomenon causes a softening of the effect. Thus, an increase in the non-local parameter decreases the aberrations within the nanobeam. Compared with the published results, the collected results show good agreement, for example, with those of Jena et al. ^[22] and Zeng et al. ^[23].

• Also, when the parameter ${l}_{m}$ is smaller than the parameter $\xi$; the nonlocal effect predominates, which leads to a stiffness-softening effect of the nanobeam. When the parameter $\xi$ is greater than the parameter ${l}_{m}$, the effect of the stress gradient takes precedence, causing the nanobeam to stiffen.

Figure 2 shows that the deflection $w$ starts and terminates at zero values and fulfills the boundary conditions at $x = 0$ and $x = L$. It is further shown that the aberrations recorded by the Euler-Bernoulli beam theory are usually slower than those predicted by non-local beam theories, indicating that the nanobeam is attenuated and softened when the size-dependent is taken into account.

• From Figure 3, we notice that the parameters $\xi$ and ${l}_{m}$ have a very weak influence on the distribution of temperature change $\theta$. Thermal waves are continuous and smooth phenomena that reach a steady state depending on the phase lag factors, which means that heat transfers easily from one particle to another, causing the temperature to drop even more. This phenomenon is in contrast to the traditional theory of thermal elasticity, which predicts that the rate of propagation of thermal perturbation is infinite.

• Increases in temperature and thermal load cause a drop in beam stiffness, which reduces thermal and mechanical waves.

• As seen in Figure 4 it is evident that the magnitude of the displacement $u$ in the NSGT, SGT and NET models is less than that obtained using standard contact theory (CET).

• In contrast to the behavior shown in Figures 2 and 3, the bending moment $M$ behavior as shown in Figures 5. It is clear that the sizes of the NSGT, SGT, and NET models of the bending moment $M$ have lower values than those achieved using the conventional contact theory (CET). In other words, the bending moment decreases with the height of the nonlocal modulus.

• Finally, the classical theory, which does not take into account the size dependence and can yield results suitable for studying narrow beams, is well known. However, in non-local models, the effect of size-dependent mechanical behavior becomes significant and cannot be ignored. From theoretical calculations, we may conclude that the nanobeam can display either a hardening softening or a hardening-stiffness effect, depending on the relative amplitude of the non-local factor and the length-scale factor of the material.

• This may explain why the stiffness-hardening effect of nanobeams is frequently found in experimental studies as in ^[61], but the stiffness-softening effect of nanostructures is more common as discussed in ^[62].

9.2.   The effect of the variability of thermal conductivity

Thermal conductivity is an important property of a material that is often taken for granted. On the other hand, many experimental and theoretical investigations have shown that thermal conductivity is closely related to temperature change ^[63,64]. Depending on the general one-dimensional thermoplastics problem, Xiong and Guo ^[65] emphasized the effect of changing temperature-dependent properties on field variables. As described earlier, the thermal conductivity $K$ is assumed to be a linear function of the temperature change (see Eq (25)). A material with a high $K$ is considered an excellent conductor of heat, while a material with a low $K$ is considered a good thermal insulator. As a result, this parameter has a significant impact on both the working conditions in deep mines and the ability of subterranean vents to store thermal energy. It is also related to geothermal energy generation and radioactive waste disposal.

In this subsection, the effect of the variability parameter of thermal conductivity ${K}_{1}$ on the non-dimensional deflection, temperature spread, displacement, and bending moment is investigated. When the coefficient of thermal conductivity is dependent on heat, there will be two separate examples to study the change of thermal conductivity. The values ${K}_{1} = -1$ and ${K}_{1} = -0.5$ are used when the thermal conductivity is dependent on the temperature change. The value ${K}_{1} = 0.0$ is utilized if the thermal conductivity is constant. The non-dimensional values $\xi = 0.01$, ${l}_{m} = 0.01$, ${\Omega } = 0.3$, ${\tau }_{q} = 0.02$ and ${\tau }_{\theta } = 0.01$ are taken. The numerical results of the studied field variables are depicted in Figures 6-9.

As can be seen from Figure 6, the magnitudes of $w$ decrease as the parameter ${K}_{1}$ increases. As illustrated in Figure 7, as the distance $x$ increases, the temperature drops, driving wave propagation. The temperature distribution is increased when the parameter ${K}_{1}$ is reduced. Physically, increasing the parameter ${K}_{1}$ improves the heat transfer process and raises the local temperature of the beam. It is also noted that with an increase in the parameter ${K}_{1}$, the temperature rises. The results were compared with those presented in ^[66] and it was found that there was agreement in the results.

Figure 8 shows that the displacement $u$ increases when $0.0\le x\le 0.1$ for the greatest amplification and drops when $0.1\le x\le 0.6$. In the last range $0.6\le x\le 1$ of wave propagation, the displacement $u$ is traveling straight. The variability parameter ${K}_{1}$ has a significant impact on the displacement. In Figure 9, the increase in the parameter ${K}_{1}$ is designed to enhance the distribution of the bending moment $M$.

The results demonstrate that the change in thermal conductivity has an effect that should not be ignored ^[67]. The mechanical and thermal distributions of the nanobeam reveal that the wave propagates as a velocity-limited wave in the medium and depends on the coefficient of change of thermal conductivity ${K}_{1}$ ^[34]. We may deduce from the analysis that the thermoelastic behavior is affected by variations in thermal material characteristics, and these impacts are mostly focused on the distribution's peak values.

9.3.   Effects of the rotation speed

As mentioned earlier, spinning nanobeams play an important role in many nano-devices, and properly modeling and studying them is a very challenging task. In this section, a study was conducted to investigate the effect of rotational speed ${\Omega }$ on the functions of the physical fields. Numerical calculations were performed when the values of the other effective parameters were constant. This work will use non-local gradient theory (NSGT) to elucidate the vibrational behavior of nanobeams for size-dependent beams, as there has been no precise inquiry into the nanobeams' rotation. It is found that the speed of rotation, elastic media, and non-local scaling factors greatly influence the bending vibration of the system.

Figures 10, 11, 12, and 13 show the variance of the investigated fields for three distinct angular velocity values (${\Omega } = 0, \mathrm{ }0.1, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }0.3$). The rotation coefficient is zero (${\Omega } = 0$) in the absence of rotation, which is a special case of the current work. Figure 10 depicts the rotation ${\Omega }$ that affects the deflection $w$. In the presence and absence of rotation (centrifugal force), this parameter was shown to have a significant impact on the deflection $w$ and variance in results. It is noticeable that increasing the angular velocity ${\Omega }$ reduces the deflection $w$ of the non-local transverse nanobeam. These findings and behavior are similar to those seen in ^[68,69]. In Figure 11, the effect of angular velocity on temperature change $\theta$ is examined and displayed. We note from the figure that the effect of rotation on the temperature change is very slight. The results of the preceding literature are compatible with those of the author, such as the equivalent results achieved in ^[37,38,39].

The effect of the angular velocity of rotation ${\Omega }$ on the variance of the displacement $u$ is shown in Figure 12. It is found that the speed of rotation ${\Omega }$ most prominently affects the curves reflecting the displacement field. The figure also displays that the displacement distribution $u$ decreases in certain periods with increasing rotation and rises in other periods along the axis of the beam. Figure 13 shows the changes in bending moment $M$ for different values of rotational velocity ${\Omega }$. The graph indicates that rotation greatly affects the moment curves and that as the angular velocity ${\Omega }$ values decrease, the bending moment amplitude $M$ increases. Ultimately, the amplitude of the studied fields changes as the non-dimensional angular velocity increases. In other words, the speed of rotation ${\Omega }$ is most prominently responsible for the stiffening effect of the centrifugal force. The functional features of rotating structures with diverging effects of external stimulation can be improved based on understanding the influence of rotational speed in hybrid nano-generators to achieve better shaft motion.

10.   Conclusions

In the current work, a nonlocal strain gradient beam model is constructed to examine the vibration response of the thermoelastic nanobeam, including its rotational effect. The Euler-Bernoulli beam theory coupled with the generalized thermoelastic model with phase delays and nonlocal strain-gradient theory, is used to construct the governing equations for the rotating nanobeam. It was taken into consideration that the thermal conductivity coefficient and the specific heat of the nanobeam are temperature dependent. The effect of nonlocal, material length scale parameters, rotation, and thermal conductivity variability on thermal and mechanical wave scattering is investigated. The following important outcomes are achieved:

• The non-local gradient elasticity model showed results that were different from the results of the traditional model, and this is in agreement with the previous literature.

• Deflections and displacement are reduced as the non-local parameters increase. The strain gradient effect is a priority when the non-local parameter is greater than the length scale parameter of the material, which results in the annealing of the nanobeam.

• The difference between NSGT and SGT is less pronounced at lower non-local parameter values, but becomes more pronounced at larger non-local parameter values. This pattern applies to both the CET and the NET.

• The behavior of different fields is affected by changes in the thermal properties of materials, and these effects appear mostly in the peak values of the distributions.

• Depending on the relative amplitude of the nonlocal factor and the material length-scale parameter, the nanobeam may show the effect of stiffness-softening or stiffness-hardening.

• The fluctuation of thermal conductivity and its dependence on temperature change have a significant impact on different physical fields.

• The angular velocity of rotation is most prominently responsible for the strengthening effect of the centrifugal force.

• The effect of rotation on the temperature change is very slight. The fundamental effect of rotation on the behavior of different physical distributions can also be inferred from the obtained results and should be taken into account in production and design procedures.

• Temperature-dependent and size-dependent structures may both be found in nanoscale materials. This indicates that external temperature has a significant impact on nonlocality behavior. The rotating nanobeam can also respond as a temperature-dependent structure.

• Our findings reveal that the dependent size impact on the thermoelastic vibration of nanobeams could be significant, emphasizing the relevance of dependent size effects in nanoscale device and system design.

Conflict of interest

The authors declared no potential conflicts of interest with respect to the research.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Jouf University for funding this work through research grant No. (DSR2020-05-426). We would also like to extend our sincere thanks to the College of Science and Arts in Al-Qurayyat for its technical support.